Abstract
The flip regression procedure that we used earlier for handling the dibenzofuran system has been applied to xanthones. The MAO-A inhibitory activity expressed as IC50 of the xanthones is known to correlate with E-state, molecular connectivity, shape indices and in this contribution it is shown that the orientation of nodes in their occupied π orbitals explain a further large portion of the variance in their inhibitory activity.
Introduction
Monoamine oxidase (MAO) plays a critical role in the regulation of monoamine neurotransmitters such as serotonin, nor adrenaline and dopamine. MAO isoenzymes are classified on the basis of their substrate preference, sensitivity towards specific inhibitors, and tissue distribution into MAO-A and MAO-B. Selective MAO-A inhibitors have been used clinically in the treatment of depression and anxiety, while MAO-B inhibitors have been used in the treatment of Parkinson's and Alzheimer's diseases. Many plant-derived and synthetic compounds such as isoquinoline, xanthones have been identified as MAO inhibitors.
The xanthones (9H-xanthen-9-ones) of natural and synthetic origin are of biological and pharmacological interest. Recently in the literature, a special issue of “Current Medicinal Chemistry” was dedicated to xanthones Citation1-5.
It has been demonstrated that in most cases the orientations of nodes in π -like orbitals of aromatic molecules are a critically important feature in understanding their activity. This was first found in phenylalkylamine hallucinogens [Citation6], carbonic anhydrase, trypsin, thrombin and bacterial collagenase inhibitors [Citation7], tryptamine hallucinogens [Citation8] as well as polychlorodibenzofurans [Citation9]. The present contribution extends this to some xanthone derivatives.
A QSAR study among the MAO-A inhibitory activity of xanthones series was recently studied [Citation10] and shown to correlate with descriptors like the E-state index, molecular connectivity and shape. In this contribution it is hoped to improve the correlation by including the nodal orientations. The calculation of nodal orientation is done with the program NODANGLE [Citation11], which has been described previously. NODANGLE calculates the angle between the nodes in π-like orbitals and a reference point on the aromatic ring. NODANGLE works by for each ring analytically least-squares fitting the coefficients of the pz orbitals on the ring atoms to those of the degenerate HOMO and LUMO of benzene. The 10 highest occupied and 10 lowest unoccupied orbitals of the compound in question are searched, and an error term is calculated for each - a scaled sum of squares of the difference between the coefficients of the pz orbitals of the compound and those of benzene with the same nodal orientation as the ring in question. For an exact match to benzene this error term is zero. For an exact match for an orbital of the wrong symmetry it is unity. NODANGLE prints out angles and orbital energies for those orbitals for which the error term is less than 0.5. These are π-like orbitals, and provided the error term is small have nodal orientations that closely match benzene of the appropriate nodal orientation. This calculation is done for each of the three rings of the xanthones.
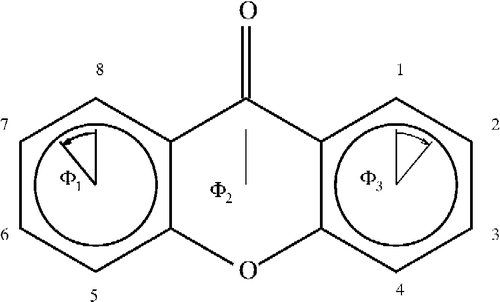
For the xanthones, calculating the angles in the three rings can be accomplished in two MOPAC calculations by entering the atom as numbered in . In labeling 1, rings 1 and 3 are 6-membered rings numbered 1–6 and 9–14 for ring 1 and 3, respectively. In labeling 2, ring 2 is also a 6-membered ring numbered 5–10. The angles calculated by NODANGLE are then Θ1, Θ2 and Θ3 in that figure, measured at atoms 1, 9 (in labeling 1) and 5 (in labeling 2), respectively. For final interpretation, the final angles are related to the calculated angles, assuming the rings are regular polygons, Φ2 = Θ2 – 120, Φ1 = Θ1 − 60 and Φ3 = 120 – Θ3 as shown in .
Figure 1 Numbering of xanthones skeleton used in the HyperChem and NODANGLE calculations. (compound 1 in Table I).
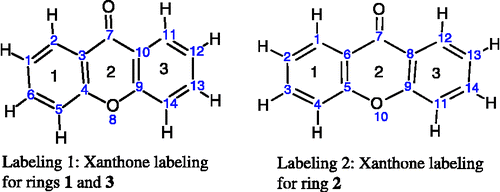
Figure 2 Numbering of the xanthones skeleton and angles used in the interpretations. Angles shown are for compound 1.
summarizes the MAO-A inhibitory activity of 42 xanthones derivatives [Citation10] expressed as IC50 values, where C is the effective concentration of the compound to achieve 50% MAO-A inhibition in a micro molar range.
Table I. MAO Inhibitory activities of xanthone derivatives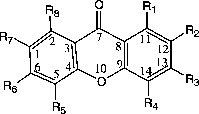 .
.
A problem arises from the symmetry of the parent molecule and to deal with this problem, we use the program FLIPSTEP, a component of the MARTHA [Citation12] statistical package, which has been described previously [Citation12,Citation13]. FLIPSTEP calculates regressions for all possible combinations of compounds with Φ1 exchanged with Φ3 and Φ2 with – Φ2 and selects that combination with the regression with the best Fisher F-ratio, after eliminating descriptors that are either collinear with other descriptors or are of poor statistical significance.
Calculations
The molecules were setup with HyperChem [Citation14] and optimized at the AM1 level with MOPAC 6 [Citation15]. An AM1 optimization was considered adequate for these compounds, as AM1 was developed and parameterized for common organic structures, and also because the calculated angles (but not the orbital energies) are extremely insensitive to the level of theory. A NODANGLE calculation was run on the MOPAC output file to identify the relevant orbital and obtain the angles and corresponding orbital energies. The angles and orbital energies were correlated with the activities taken from the literature [Citation10] with the program FLIPSTEP.
Results
In this study the HOP (highest occupied π orbital) is not identical to HOMO and also LUP (lowest unoccupied π orbital) is not identical to LUMO. In general we restrict our attention to π – like orbitals and, in particular, to those four orbitals that most resemble the degenerate HOMO and LUMO of benzene. SHOP and SLUP refer to the energies of the second highest occupied and second lowest unoccupied π-orbital respectively, and they are not necessarily the same for all rings, hence HOP1, HOP2 and HOP3 refer to orbital energies for the relevant orbitals for the three rings of the xanthones. summarizes the orbital energies and angles of the compounds in .
Table II. Orbital energies (eV) and angles (°) of the compounds in Table 1.
NODANGLE does not print out values of angles or energies for non π – like orbitals for which the error term for the angle exceeds 0.5. summarizes the calculated angles and their error terms. The different descriptors used in this study are summarized in .
Table III. Calculated angles and their error terms.
Table IV. Descriptors used in this study.
The best model as given in [Citation10] after excluding compounds 12,16,18,33,37,38,40 and 41 was:
where n is the number of compounds used in the fit, r2 is the squared correlation coefficient, S is the standard deviation, and F is the overall F-statistics for the addition of each successive term. The ai values are at 90% confidence limit of each coefficient. The data Xi are the E-state for atoms level (Si), molecular connectivity (χ), shape (κ) indices and finally the constant term.
In flip regression in the present case, flipping consist of changing the sign of Φ2 and swapping Φ1 and Φ3, and also swapping HOP1 with HOP3, SHOP1 with SHOP3, LUP1 with LUP3 and SLUP1 with SLUP3.
Compounds 28 and 41 has no nodal angle with error term (α) less than 0.5 which indicates that the symmetry of the π-like orbitals in ring 2 in these compounds is not close to that of the π orbitals for benzene ring. Hence, two regression analyses was performed, one using all of the compounds and only the ring1 and ring 3 variables, and the second using all variables for the three rings with all compounds except compounds 28 and 41, for which some values were not available. Two runs of FLIPSTEP, that performs a backward-stepwise variable selection, were carried out using the default setting of VIFMAX value of 35 and a reduced VIFMAX value of 15. VIFMAX is the criterion for excluding variables that are collinear with other variables in the regression. The variance inflation factor (VIF) is defined for each independent vatriable i as 1/(1 − Ri2), where Ri2 is the R2 for independent variable i regressed on all of the other independent variables. VIFMAX is the value of VIF above which a variable will be removed from the regression early in the procedure. In general a value of VIF above 10 is cause for concern. By default VIFMAX is set to 35. With this value, the maximum VIF in the final equation is usually much less than 35.
Using VIFMAX value of 15 resulted in removing C4Φ1L, C4Φ3L, SLUP1, SLUP2, and LUP1 due to colinearity. LUP1 and HOP2 are removed because they are statistically insignificant.
FLIPSTEP stepwise regression with VIFMAX = 15 gives:
Here, R2 is the square of the multiple correlation coefficients. F is the Fisher variance ratio. S is the standard error of estimate. Q2 is the square of the multiple correlation coefficients based on the leave-one-out residuals. The numbers in parentheses are Student's t values; a value greater than approximately 2 is indicative of significance at the 0.05 level.
Using VIFMAX = 35, SLUP1 and LUP2 were removed because of colinearity. SHOP3 and SHOP1 were removed because they are statistically insignificant. FLIPSTEP stepwise regression with VIFMAX = 35 gives:
Here α is the statistical significance of the regression based on 5000 randomizations of the dependent variable [Citation9]. Equation (3) has a higher R2 than that for Equation (2), which implies that using VIFMAX = 35 gives a better model than that obtained by using VIFMAX = 15, at the cost of introducing a small colinearity.
Reduced Model:
Flip regression was applied on the reduced model, in which variables for rings 1 and 3 for all compounds were entered in regression analysis. Removing ring 2 variables from the descriptors set would result in a set of 12 variables that are: HOP1, SHOP1, LUP1, SLUP1, HOP3, SHOP3, LUP3, SLUP3, Φ1H, Φ1L, Φ3H, Φ3L. These variables are then flipped. Flipping consists of interchanging ΦH and ΦL for ring 1 with the parallel angles for ring 3. However, the nodal angles are then converted to sin 2ΦH, cos 2ΦH, sin 4ΦL and cos 4ΦL and ΦH and ΦL are removed from the variables set. As a result of the flipping process, we will have a set of variables which consists of: HOP1, SHOP1, LUP1, SLUP1, HOP3, SHOP3, LUP3, SLUP3, C2Φ1H, S2Φ1H, C2Φ 3H, S2Φ 3H, C4Φ 1L, S4Φ 1L, C4Φ 3L, S4Φ 3L. These variables are defined in . Applying FLIPSTEP on the reduced model resulted in removing LUP1 due to colinearity and removing S4Φ3L and S4Φ1L because they are statistically insignificant. shows the progress of FLIPSTEP for the reduced model. The variables SLUP1 and SLUP3 are a flipped pair. One is of poor significance and the other very poor, so they can advantageously be deleted, reducing the number of variables.
Table V. Progress of FLIPSTEP for the reduced model.
The results for the reduced model with ring 1 and ring 3 variables for all compounds as well as the results for the model with all variables for all compounds but 28 and 41, were checked by running the regression 5000 times with the dependent variable randomized (randomization test). Statistical significance was tested for using MARTHA routine FLIPRAND [Citation7]. For the set using the rings 1 and 3 variables significance was satisfactory (2.47 × 10− 6), and for the run using all of the variables the regression was totally nonsignificant (1.13 × 10− 1).
Finally, a multi-linear regression analysis was carried out on the variables selected by FLIPSTEP regression using the program multlr from the Martha package [Citation12]. Multilinear regression of Log(CI50) with the π-like HOP and LUP energies as well as the converted angles trigonometric functions gives:
Again, n is the number of compounds used, R2 is the square of the multiple correlation coefficients, F is the Fisher variance ratio, S is the standard error of estimate and α is the statistical significance of the regression based on 5000 randomizations of the dependent variable. The numbers in parentheses are standard errors of estimates, or approximate 90% confidence intervals. It should be noted that in contrast to Equation (1) no compound has here been deleted.
shows the flip status and flip significance from FLIPSTEP carried out on the reduced model (with ring 1 and ring 3 variables for all compounds) and the first model with all variables for all compounds but compounds 28 and 41. A value of the significance greater than 0.05 is indicative that flipping the corresponding compound makes little difference to the quality of the regression. A flip status of 1 indicates that the compound has not flipped in the final regression, and − 1 that it has. This has only relative significance, and flipping all of the compounds in a flip regression has no effect.
Table VI. Flip status and flip significance for Equations (3) and (4).
Equation (4) is reasonably good but could be improved by incorporating more descriptors from the classical work done [Citation10], but in this case the number of descriptors will be too large. Equation (4) and show that R2 obtained from FLIPSTEP is better than that obtained from multilinear regression analysis while F is better for the latter. However, the differences between the two regressions are not large.
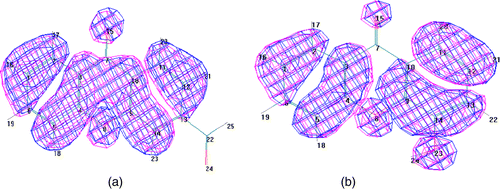
shows HOMO orbitals for two sample compounds of the 42 compounds. HOMO orbitals for the 42 compounds are similar to the molecular orbitals shown in either (a) or (b). As shows, pz orbital on furan's oxygen prevents the formation of a nodal plane on ring 2. Hence, the withdrawal of ring 2 variables is supported.
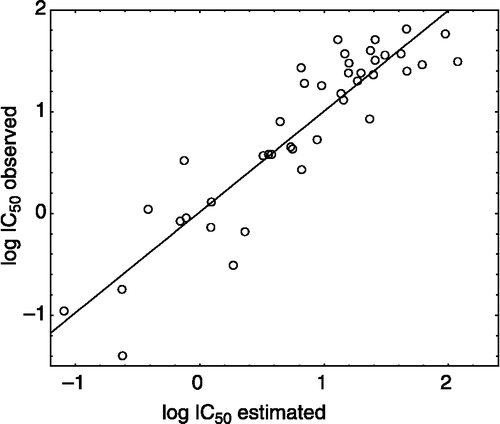
summarizes the observed activity as well as the estimated activity according to the reduced model for the 42 compounds of xanthones in , while shows the plot of the logarithm of the observed activity against the logarithm of the estimated activity.
Table VII. Observed Log IC50 versus estimated.
Comparison with the QSAR of Castro et al.
The quality of a QSAR is assessed on a number of criteria. The commonest is goodness of fit, usually assessed as R2. As well as having a high R2, all of the terms in a QSAR should be statistically significant, conventionally at the 0.05 level. Further, it is necessary to exclude colinearities between independent variables for a QSAR to be reliable. It is also highly desirable, but not essential, that there be an intuitively apparent relationship between the variables considered and the dependent variable. Finally, from a statistical viewpoint, it is desirable to have fewer rather than more independent variables. It is unreasonable however to expect that an outcome such as inhibition of an enzyme would be well described by very few variables. This could only be the case if the structural variation in the inhibitors is strictly limited, so that the variation in activity is confined to a narrow aspect of the variation between the drugs.
Because we are considering the same group of drugs the structural diversity in the two studies is identical. Our R2 for Equations (2) and (4) are 0.833 and 0.825, with 12 and 10 variables respectively. Castro et al. get 0.586 [Citation10] with 10 variables and 42 compounds in Equation (1), but increased this to 0.847 only at the cost of discarding 8 compounds, which we consider not to be a legitimate procedure. Thus we obtain a much better fit with a similar number of variables than does Castro et al.
Castro et al. controlled colinearity by excluding descriptors with a pairwise R2 greater than 0.80. This procedure however does not pick up colinearities that involve 3 or more descriptors. In contrast, we control colinearity using the variance inflation factor (VIF). This procedure picks up all colinearities. It is conventional to regard with suspicion any variable with a VIF greater than 10. In our Flipstep program we use a criterion VIFMAX, which by default is set to 35. Variables with a VIF greater than VIFMAX are excluded early in the stepwise regression. This often results in a regression in which the maximum VIF is much less than VIFMAX, and valuable descriptors can be lost. This is why we do not routinely set VIFMAX to 10.
Castro et al. do not cite values that allow us to assess the individual statistical significance of their terms in their equations, but do state that they are better than 10% confidence. We use a value of 5% confidence, but with a proviso that is uniquely relevant to flip regression. This is that if one of a pair of flipped variables is significant and the variable is included, then so is its partner, even if not significant. If this is not done it is impossible to use flip regression predictively. The significance of the terms in our regressions may be gauged from the t values in Equations 2-4. A value greater than approximately 2 is significant at the 5% level.
Finally, the variables used by Castro et al. include e-state, shape, size, connectivity and topological descriptors. These are legitimate descriptors, but are obscure in meaning, especially when many of them are used together in the same equation. The e-state variables are probably a measure of polarization of charge in a molecule. In other studies we have used quantum chemically calculated descriptors such as mean absolute charge or local dipole index, which are probably measures of the same thing, but we usually cannot use both of these in the same equation. They show too much colinearity. We have not used them here because they would expand by too much the number of descriptors used. We do use as descriptors the orientation of nodes in the π orbitals of the drugs, and also the energies of some of the π orbitals. We believe, and hope to show in a future publication, that these are intimately related to intermolecular forces between two aromatic molecules. It is not however as simple as alignment of nodes in an orbital in the drug with one in the receptor. At least two orbitals on each are involved in most cases. Since we have been using these descriptors we have not encountered a single example of a series of aromatic drugs in which at least one of them is not a major term in the QSAR equation.
Conclusions
The nodal orientation terms have a powerful explanatory value in that they account for much more of the variance in activity than is possible using the classical descriptors alone. Were it not for the large number of descriptors already in the equation in comparison to the number of molecules, a combination of the classical descriptors and the nodal orientation terms would probably give an even better explanation of the MAO-A inhibitory activity of the xanthones.
This study has used two relatively new techniques. The first is flip regression, for handling the symmetry of the xanthone system, which is C2v, like the dibenzofurans studied earlier and the phenylalkylamines for which the method was devised. A similar approach was pioneered 25 years ago by Kishida and Manabe [Citation16] in their study of the QSAR of benzenedisulfonamide carbonic anhydrase inhibitors. The second is the use of the orbital nodal angle descriptors. This is based on the concept that the stability of stacked aromatic systems is highly orientation dependent, and is also dependent on the energies of the orbitals in the two aromatic systems that resemble the degenerate HOMO and LUMO of benzene. It is envisaged that the benzene rings of the xanthones are interacting with aromatic systems on the receptor (here MAO), and that alignment occurs between the π-orbital nodes on the pair. Precisely which rings are involved becomes apparent from the identity of the descriptors that remain in the equations. We hope to publish in the near future a computational and theoretical study of these interactions.
References
- Vieira LMM, Kijjoa A. Curr Med Chem 2005; 12: 2413
- Sila AMS, Pinto DCGA. Curr Med Chem 2005; 12: 2481
- Gales L, Damas AM. Curr Med Chem 2005; 12: 2499
- Pinto MMM, Sousa ME, Nascimento MSJ. Curr Med Chem 2005; 12: 2517
- Riscoe M, Kelly JX, Winter R. Curr Med Chem 2005; 12: 2539
- Clare BW. J Med Chem 1998; 41: 3845–3856
- Supuran CT, Clare BW. J Enz Inhib Med Chem 2004; 19: 237–248
- Clare BW. THEOCHEM 2004; 712: 143–148
- Clare BW. THEOCHEM 2006; 763: 207–215
- Nunez MB, Maguna FP, Okulik NB, Castro EA. Bioogan Med Chem Lett 2004; 14: 5611
- Clare BW. nodangle.zip http://www.chem.biomedchem.uwa.edu.au/staff/homepages/BrianClare 2005.
- Clare BW. martha.zip http://www.chem.biomedchem.uwa.edu.au/staff/homepages/BrianClare 2005.
- Clare BW, Supuran CT. Bioorg Med Chem 2005; 13: 2197–2211
- Hypercube Hyperchem 1115 NW 4th Street, Gainesville, Florida 32601-4256 U.S.A.
- Stewart JJP. Q.C.P.E. Bull 1990; 10: 86
- Kishida K, Manabe R. Med J Osaka Univ 1980; 30: 95–100