QSAR of aromatic substances: EGFR inhibitory activity of quinazoline analogues

Abstract

The flip regression procedure that we used earlier for handling the xanthones system has been applied to phenylaminoquinazoline analogues. It is known that the substituents at the 6- and 7- positions of the polycyclic system have been identified as the most important structural features. The steric as well as the electrostatic interactions proved to be the most important for the inhibitory effect. In this contribution it is shown that the orientation of nodes in their occupied π orbitals, and also the energies of these orbitals explains a further large portion of the variance in their inhibitory activity.

Keywords::

• Aromatic
• QSAR
• Flip-regression
• Orbital nodes
• quinazolines
• inhibitors
• EGFR

Introduction:

It is accepted that there is a critical need for new targets, in addition to DNA, for anticancer drug development [1]. Epidermal growth factor receptor (EGFR) that has been identified as a kind of protein tyrosine kinase (PTK) and has been demonstrated to be related to many human cancers such as breast and liver cancers [2–4], leading many to believe that EGFR is an attractive target for anti-tumor drug discovery [5].

In the past few years, quantitative structure-activity relationships (QSAR) for different groups of compounds, which have been evaluated as EGFR inhibitors, have been reported [6–9].

It has been demonstrated that in most cases the orientations of nodes in π -like orbitals of aromatic molecules are a critically important feature in understanding their activity. This was first found in phenylalkylamine hallucinogens [10], carbonic anhydrase, trypsin, thrombin and bacterial collagenase inhibitors [11], tryptamine hallucinogens [12] as well as polychlorodibenzofurans [13]. The present contribution extends this to some quinazoline analogues.

A QSAR and 3D QSAR of 134 structurally diverse inhibitors of the EGFR was recently reported, using comparative molecular field analysis (CoMFA) and comparative molecular similarity indices analysis (CoMSIA), in which the steric and electrostatic interactions proved to be the most important for the inhibitory effect [14].

In this contribution it is hoped to improve the correlation by including the nodal orientations. The calculation of nodal orientation is done with the program NODANGLE [15], which has been described previously. NODANGLE calculates the angle between the nodes in π-like orbitals and a reference point on the aromatic ring. NODANGLE works by for each ring analytically least-squares fitting the coefficients of the p_z orbitals on the ring atoms to those of the degenerate HOMO and LUMO of benzene. The 10 highest occupied and 10 lowest unoccupied orbitals of the compound in question are searched, and an error term is calculated for each - a scaled sum of squares of the difference between the coefficients of the p_z orbitals of the compound and those of benzene with the same nodal orientation as the ring in question. For an exact match to benzene this error term is zero. For an exact match for an orbital of the wrong symmetry it is unity. NODANGLE prints out angles and orbital energies for those orbitals for which the error term is less than 0.5. These are π-like orbitals, and provided the error term is small have nodal orientations that closely match benzene of the appropriate nodal orientation. This calculation is done for each of the three rings of the quinazoline analogues.

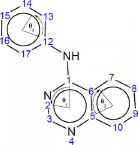
For the quinazoline, calculating the angles in the three rings can be accomplished in one MOPAC calculations by entering the atom as numbered in Figure 1. The three rings are 6-membered rings numbered 1–6, 5–10 for ring 1 and 2, respectively. Ring 3 is also a 6-membered ring numbered 12–17. The angles calculated by NODANGLE are then Θ1, Θ2 and Θ3 in that figure, measured at atoms 1, 5 and 12 respectively.

Figure 1.  Numbering of quinazolines skeleton used in the HyperChem and NODANGLE calculations and angles used in the interpretations. Angles shown are for compound 1. The angle subscript indicates the ring number.

Table I summarizes the quinazoline-inhibitory activity of 63 analogues [14] expressed as log IC₅₀, where IC₅₀ is the effective concentration of the compound required to inhibit by 50% the phosphorylation of a 14-residue fragment of phosphorylase C_{γ − 1} (prepared from A431 human epidermoid carcinoma cells through immunoaffinity chromatography) by EGFR.

Table I.  Structures and activities (log 1/IC₅₀) of 4-(3-bromo-aniline)- 6,7-dimethoxyquinazoline analogues.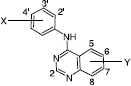

Compound	X	Y	log 1/IC50
1	H	H	6.46
2	3-F	H	7.25
3	3-Cl	H	7.64
4	3-Br	H	7.57
5	3-I	H	7.10
6	3-CF3	H	6.24
7	H	6-OMe	7.26
8	3-Br	6-OMe	7.52
9	H	6-NH2	6.11
10	3-CF3	6-NH2	6.24
11	3-Br	6-NH2	9.11
12	H	6-NO2	5.30
13	3-Br	6-NO2	6.04
14	H	7-OMe	6.92
15	3-Br	7-OMe	8.00
16	H	7-NH2	7.00
17	3-F	7-NH2	8.70
18	3-Cl	7-NH2	9.60
19	3-Br	7-NH2	10.00
20	3-I	7-NH2	9.46
21	3-CF3	7-NH2	8.48
22	H	7-NO2	4.92
23	3-F	7-NO2	5.21
24	3-Cl	7-NO2	6.09
25	3-Br	7-NO2	6.00
26	3-I	7-NO2	6.27
27	H	6,7-diOMe	7.54
28	3-F	6,7-diOMe	8.42
29	3-Cl	6,7-diOMe	9.51
30	3-Br	6,7-diOMe	10.6
31	3-I	6,7-diOMe	9.05
32	3-CF3	6,7-diOMe	9.62
33	3-Br	6-NHMe	8.40
34	3-Br	6-NMe2	7.08
35	3-Br	6-NHCO2Me	7.92
36	3-Br	7-OH	8.33
37	3-Br	7-NHAc	7.40
38	3-Br	7-NHMe	8.15
39	3-Br	7-NHEt	7.92
40	3-Br	7-NMe2	7.96
41	3-Br	6,7-diNH2	9.92
42	3-Br	6-NH2, 7-NHMe	9.16
43	3-Br	6-NH2, 7-NHMe2	6.80
44	3-Br	6-NH2, 7-OMe	8.42
45	3-Br	6-NH2, 7-Cl	8.19
46	3-Br	6-NO2, 7- NH2	7.28
47	3-Br	6-NO2, 7-NHMe	7.17
48	3-Br	6-NO2, 7-NMe2	5.70
49	3-Br	6-NO2, 7-NHAc	7.55
50	3-Br	6-NO2, 7-OMe	7.82
51	3-Br	6-NO2, 7-Cl	7.60
52	3-Br	5,6-diOMe	5.86
53	3-Br	5,6,7-triOMe	9.17
54	2-Br	6,7-diOMe	6.89
55	4-Br	6,7-diOMe	9.02
56	3,4-diBr	6,7-diOMe	10.14
57	3-Br	6,7-diOH	9.77
58	3-Br	6,7-diOEt	11.22
59	3-Br	6,7-diOPr	9.77
60	3-Br	6,7-diOBu	6.98
61	3,5-diBr	6,7-diOMe	6.95
62	3-Br	6,7-OCH2O	7.82
63	5-Br	2-NH2,6,7-diOMe	6.33

A problem arises from the symmetry of the parent molecule; to deal with this problem we use the program FLIPSTEP, a component of the MARTHA [16] statistical package, which has been described previously [16,17]. The phenyl ring in our system has symmetry, and the two o- positions, and also the two m- positions are related. We refer to these as flippable, and FLIPSTEP calculates regressions for all possible combinations of each flippable descriptor (a property of one of the two o- or m- substituents) exchanged with its flippable partner (the corresponding property of the other of the two), and selects that combination with the regression with the best Fisher F-ratio, after eliminating descriptors that are either collinear with other descriptors or are of poor statistical significance. In the present case only two flippable variables are present, and these are the angles the nodes in the HOPO and LUPO in the phenyl ring make with the 1-position of the phenyl ring. Flipping in this case consists of changing the signs of these angles.

Calculations

The molecules were setup with HyperChem [18] and optimized at the AM1 level with MOPAC 6 [19]. An AM1 optimization was considered adequate for these compounds, as AM1 was developed and parameterized for common organic structures, and also because the calculated angles (but not the orbital energies) are extremely insensitive to the level of theory. A NODANGLE calculation was run on the MOPAC output file to identify the relevant orbital and obtain the angles and corresponding orbital energies. The angles and orbital energies were correlated with the activities taken from the literature [14] with the program FLIPSTEP.

The classical descriptors LDI, MEANQ and solvation energy were calculated with Mopac 93, while the diagonal components of the polarizability tensor were obtained from Mopac 6. MEANQ is the mean absolute Mulliken charge calculated over all atoms in the compound, while LDI (local dipole index) is the mean of the absolute difference in Mulliken charge between bonded pairs of atoms, calculated over all bonded pairs of atoms in the molecule. Both are measures of charge polarization in the molecule.

Results

In this study the HOP (highest occupied π orbital) is not identical to HOMO and also LUP (lowest unoccupied π orbital) is not identical to LUMO. In general we restrict our attention to π – like orbitals, and in particular, to those four orbitals that most resemble the degenerate HOMO and LUMO of benzene. SHOP and SLUP refer to the energies of the second highest occupied and second lowest unoccupied π-orbital respectively, and they are not necessarily the same for all rings, hence HOP1, HOP2 and HOP3 refer to orbital energies for the relevant orbitals for the three rings of the quinazoline analogues. Table IIA and IIB summarizes the orbital energies and angles and other variables of the compounds in Table 1.

Table IIA.  Orbital energies (eV) and angles (°) of the compounds in Table I.

Compound	HOP1	SHOP1	LUP1	SLUP1	ΘH1	ΘL1	HOP2	SHOP2	LUP2	SLUP2	log 1/IC50
1	− 8.708	− 10.133	− 0.669	− 0.281	73	47	− 8.708	− 9.495	− 0.669	− 0.281	6.46
2	− 8.866	− 10.227	− 0.792	− 0.384	72	46	− 8.866	− 9.554	− 0.792	− 0.384	7.25
3	− 8.849	− 10.214	− 0.774	− 0.369	72	46	− 8.849	− 9.557	− 0.774	− 0.369	7.64
4	− 8.868	− 10.221	− 0.782	− 0.377	71	46	− 8.868	− 9.585	− 0.782	− 0.377	7.57
5	− 8.864	− 10.218	− 0.778	− 0.374	71	46	− 8.864	− 9.603	− 0.778	− 0.374	7.1
6	− 9.027	− 10.31	− 0.895	− 0.472	70	46	− 9.027	− 9.837	− 0.895	− 0.472	6.24
7	− 8.505	− 10.105	− 0.675	− 0.275	62	42	− 8.505	− 9.257	− 0.675	− 0.275	7.26
8	− 8.638	− 10.194	− 0.782	− 0.366	60	42	− 8.638	− 9.384	− 0.782	− 0.366	7.52
9	− 8.335	− 9.935	− 0.592	− 0.196	53	43	− 8.335	− 9.935	− 0.592	− 0.196	6.11
10	− 8.527	− 10.119	− 0.798	− 0.363	49	42	− 8.527	− 10.119	− 0.798	− 0.363	6.24
11	− 8.444	− 10.031	− 0.698	− 0.285	51	43	− 8.444	− 10.031	− 0.698	− 0.285	9.11
12	− 9.161	− 10.034	− 1.585	− 1.042	82	69	− 10.034	− 10.863	− 1.585	− 1.042	5.3
13	− 9.324	− 10.943	− 1.67	− 1.139	81	68	− 10.238	− 10.943	− 1.67	− 1.139	6.04
14	− 8.724	− 9.686	− 0.682	− 0.254	80	50	− 8.724	− 9.3	− 0.682	− 0.254	6.92
15	− 8.883	− 9.476	− 0.767	− 0.327	74	49	− 8.883	− 9.476	− 0.767	− 0.327	8
16	− 8.634	− 9.511	− 0.548	− 0.124	84	49	− 8.634	− 8.876	− 0.548	− 0.124	7
17	− 8.782	− 9.545	− 0.668	− 0.22	89	48	− 8.782	− 8.961	− 0.668	− 0.22	8.7
18	− 8.772	− 9.552	− 0.653	− 0.211	88	48	− 8.772	− 8.957	− 0.653	− 0.211	9.6
19	− 8.788	− 9.579	− 0.661	− 0.218	90	48	− 8.788	− 8.966	− 0.661	− 0.218	10
20	− 8.785	− 9.601	− 0.658	− 0.215	89	48	− 8.785	− 8.965	− 0.658	− 0.215	9.46
21	− 8.917	− 9.833	− 0.77	− 0.307	102	48	− 8.917	− 9.072	− 0.77	− 0.307	8.48
22	− 9.146	− 10.011	− 1.584	− 1.112	78	22	− 10.011	− 10.955	− 1.584	− 1.112	4.92
23	− 9.307	− 11.044	− 1.677	− 1.216	76	23	− 10.264	− 11.044	− 1.677	− 1.216	5.21
24	− 9.287	− 11.029	− 1.662	− 1.199	76	22	− 10.217	− 11.029	− 1.662	− 1.199	6.09
25	− 9.31	− 11.035	− 1.668	− 1.206	76	22	− 10.226	− 11.035	− 1.668	− 1.206	6
26	− 9.307	− 11.037	− 1.665	− 1.202	76	22	− 10.215	− 11.029	− 1.665	− 1.202	6.27
27	− 8.715	− 9.854	− 0.785	− 0.476	70	47	− 8.715	− 9.486	− 0.785	− 0.476	7.54
28	− 8.866	− 9.937	− 0.899	− 0.571	68	46	− 8.866	− 9.546	− 0.899	− 0.571	8.42
29	− 8.849	− 9.924	− 0.882	− 0.557	69	46	− 8.849	− 9.549	− 0.882	− 0.557	9.51
30	− 8.866	− 9.931	− 0.889	− 0.564	68	46	− 8.866	− 9.577	− 0.889	− 0.564	10.6
31	− 8.863	− 9.928	− 0.886	− 0.561	68	46	− 8.863	− 9.595	− 0.886	− 0.561	9.05
32	− 9.015	− 10.006	− 0.994	− 0.652	66	46	− 9.015	− 9.826	− 0.994	− 0.652	9.62
33	− 8.372	− 9.982	− 0.682	− 0.254	49	43	− 8.372	− 9.982	− 0.682	− 0.254	8.4
34	− 8.471	− 9.944	− 0.712	− 0.319	53	46	− 8.471	− 9.944	− 0.712	− 0.319	7.08
35	− 8.768	− 10.204	− 0.94	− 0.542	58	48	− 8.768	− 10.204	− 0.94	− 0.542	7.92
36	− 8.93	− 9.732	− 0.839	− 0.388	75	49	− 8.93	− 9.566	− 0.839	− 0.388	8.33
37	− 8.902	− 10.941	− 0.821	− 0.443	78	45	− 8.902	− 9.284	− 0.821	− 0.443	7.4
38	− 8.72	− 10.81	− 0.641	− 0.187	109	48	− 8.72	− 8.861	− 0.641	− 0.187	8.15
39	− 8.694	− 10.793	− 0.627	− 0.171	114	48	− 8.694	− 8.839	− 0.627	− 0.171	7.92
40	− 8.788	− 10.759	− 0.605	− 0.161	55	48	− 8.625	− 8.788	− 0.605	− 0.161	7.96
41	− 8.497	− 8.987	− 0.671	− 0.242	46	46	− 8.497	− 8.987	− 0.671	− 0.242	9.92
42	− 8.32	− 8.947	0.121	0.187	42	43	− 8.32	− 9.253	− 0.615	− 0.19	9.16
43	− 8.349	− 10.292	− 0.664	− 0.238	47	41	− 8.349	− 9.329	− 0.664	− 0.238	6.8
44	− 8.417	− 10.69	− 0.688	− 0.255	46	46	− 8.417	− 9.506	− 0.688	− 0.255	8.42
45	− 8.545	− 10.82	− 0.885	− 0.485	51	39	− 8.545	− 9.918	− 0.885	− 0.485	8.19
46	− 9.124	− 10.2	− 1.514	− 0.82	105	65	− 9.124	− 9.385	− 1.514	− 0.82	7.28
47	− 9.06	− 10.154	− 1.475	− 0.8	114	66	− 9.06	− 9.275	− 1.475	− 0.8	7.17
48	− 11.127	—	− 1.392	− 0.907	159	64	− 9.057	− 9.243	− 1.392	− 0.907	5.7
49	− 9.216	− 10.253	− 1.583	− 0.959	101	66	− 9.216	− 9.454	− 1.583	− 0.959	7.55
50	− 9.278	− 10.333	− 1.596	− 0.994	85	66	− 9.894	− 10.049	− 1.596	− 0.994	7.82
51	− 9.395	− 10.691	− 1.684	− 1.35	83	65	− 10.282	− 10.691	− 1.684	− 1.35	7.6
52	− 8.731	− 10.23	− 0.882	− 0.489	71	48	− 8.731	− 9.467	− 0.882	− 0.489	5.86
53	− 8.659	− 9.561	− 0.8	− 0.391	73	51	− 8.659	− 9.424	− 0.8	− 0.391	9.17
54	− 8.766	− 9.467	− 0.849	− 0.426	67	50	− 8.766	− 9.467	− 0.849	− 0.426	6.89
55	− 8.766	− 9.467	− 0.849	− 0.426	67	50	− 8.766	− 9.467	− 0.849	0.672	9.02
56	− 8.805	− 9.626	− 0.91	− 0.463	60	47	− 8.805	− 9.446	− 0.91	− 0.463	10.14
57	− 8.824	− 9.489	− 0.908	− 0.439	57	45	− 8.824	− 9.489	− 0.908	− 0.439	9.77
58	− 8.662	− 9.284	− 0.715	− 0.27	52	45	− 8.662	− 9.284	− 0.715	− 0.27	11.22
59	− 8.658	− 9.28	− 0.711	− 0.267	52	45	− 8.658	− 9.28	− 0.711	− 0.267	9.77
60	− 8.658	− 9.279	− 0.71	− 0.266	52	45	− 8.658	− 9.279	− 0.71	− 0.266	6.98
61	− 8.845	− 9.545	− 0.877	− 0.443	58	47	− 8.845	− 9.545	− 0.877	− 0.443	6.95
62	− 8.87	− 9.734	− 0.89	− 0.57	60	46	− 8.87	− 9.548	− 0.89	− 0.57	7.82
63	− 8.468	− 10.815	− 0.614	− 0.168	49	46	− 8.468	− 9.414	− 0.614	− 0.168	6.33

Energy of: HOP, Highest Occupied π Orbital; SHOP, Second Highest Occupied π Orbital; LUP, Lowest Unoccupied π Orbital; SLUP, Second Lowest Unoccupied π Orbital; H, HOP; L, LUP, log 1/IC₅₀(obs), θ angles (as in Figure 1).

Table IIB.  Table IIA continued.

Compound	ΘH2	ΘL2	HOP3	SHOP3	LUP3	SLUP3	ΘH3	ΘL3	log 1/IC50
1	72	75	− 8.708	− 9.495	0.293	0.458	86	36	6.46
2	71	75	− 9.554	− 9.883	0.043	0.114	47	36	7.25
3	71	75	− 9.557	− 9.847	0.069	0.105	52	45	7.64
4	71	75	− 9.585	− 9.861	0.003	0.063	56	71	7.57
5	71	75	− 9.603	− 9.868	0.004	0.07	63	71	7.1
6	69	75	− 9.837	− 10.425	− 0.342	− 0.157	90	77	6.24
7	75	80	− 9.257	− 9.759	0.327	0.505	84	37	7.26
8	74	80	− 9.384	− 9.786	0.046	0.104	70	68	7.52
9	78	78	− 9.105	− 9.739	0.364	0.527	85	36	6.11
10	77	79	− 9.48	− 10.356	− 0.276	− 0.086	89	77	6.24
11	77	78	− 9.251	− 9.754	0.071	0.134	75	71	9.11
12	50	56	− 9.161	− 10.034	− 0.207	0.076	86	41	5.3
13	46	56	− 9.324	− 9.972	− 0.369	− 0.234	80	49	6.04
14	63	71	− 8.724	− 9.686	0.294	0.461	86	36	6.92
15	73	72	− 9.876	—	0.016	0.075	150	71	8
16	56	72	− 9.746	—	0.368	0.521	175	35	7
17	43	72	− 9.545	− 9.841	0.12	0.178	39	34	8.7
18	45	72	− 8.772	− 9.552	0.146	0.169	81	46	9.6
19	42	72	− 8.788	− 9.579	0.07	0.135	83	74	10
20	43	72	− 8.785	− 9.601	0.071	0.143	84	74	9.46
21	25	72	− 9.833	− 10.352	− 0.272	− 0.078	91	79	8.48
22	59	6	− 10.011	− 10.081	− 0.174	0.124	69	40	4.92
23	56	5	− 9.96	− 10.264	− 0.37	− 0.159	21	40	5.21
24	56	5	− 9.955	− 10.217	− 0.342	− 0.161	21	43	6.09
25	56	5	− 9.976	− 10.226	− 0.363	− 0.238	23	49	6
26	56	5	− 10.005	− 10.215	− 0.357	− 0.232	26	50	6.27
27	75	75	− 8.715	− 9.486	0.247	0.438	86	38	7.54
28	74	75	− 8.866	− 9.546	0.003	0.097	77	38	8.42
29	74	75	− 8.849	− 9.549	0.028	0.089	81	44	9.51
30	74	75	− 8.866	− 9.577	− 0.023	0.034	83	65	10.6
31	74	75	− 8.863	− 9.595	− 0.021	0.041	84	66	9.05
32	72	75	− 9.826	− 10.44	− 0.359	− 0.19	91	76	9.62
33	77	78	− 9.203	− 9.739	0.081	0.145	76	72	8.4
34	75	75	− 9.214	− 9.741	0.063	0.126	76	71	7.08
35	76	71	− 9.465	− 9.868	− 0.047	0.009	70	64	7.92
36	73	72	− 8.93	− 9.566	− 0.015	0.041	82	69	8.33
37	63	77	− 9.674	− 9.897	− 0.006	0.05	41	69	7.4
38	20	73	− 8.861	− 9.558	0.08	0.146	82	74	8.15
39	15	73	− 8.839	− 9.547	0.088	0.154	82	75	7.92
40	2	73	− 8.788	− 9.527	0.094	0.163	82	75	7.96
41	91	75	− 9.322	− 9.755	0.084	0.146	72	72	9.92
42	90	78	− 9.253	− 9.714	0.121	0.187	73	73	9.16
43	83	81	− 9.133	− 9.329	0.093	0.154	78	72	6.8
44	86	75	− 9.185	− 9.753	0.085	0.146	77	71	8.42
45	79	83	− 9.332	− 9.808	− 0.006	0.048	74	65	8.19
46	27	59	− 9.124	− 9.385	− 0.207	− 0.114	81	52	7.28
47	16	58	− 9.275	− 9.872	− 0.187	− 0.098	79	52	7.17
48	14	59	− 9.243	− 9.873	− 0.197	− 0.108	80	53	5.7
49	35	58	− 9.216	− 9.94	− 0.273	− 0.042	81	50	7.55
50	18	58	− 9.278	− 9.894	− 0.298	− 0.186	80	50	7.82
51	30	59	− 9.395	− 10.021	− 0.434	− 0.279	80	48	7.6
52	70	73	− 9.467	− 9.797	0.023	0.087	65	62	5.86
53	74	71	− 9.424	− 9.777	0.048	0.105	68	62	9.17
54	81	71	− 8.766	− 9.467	− 0.06	0.221	87	41	6.89
55	81	71	− 8.766	− 9.467	− 0.06	0.221	87	41	9.02
56	82	74	− 8.805	− 9.446	− 0.271	− 0.108	85	55	10.14
57	86	76	− 8.824	− 9.489	− 0.038	0.018	83	64	9.77
58	88	75	− 9.284	− 9.489	0.047	0.106	74	71	11.22
59	88	75	− 9.28	− 9.485	0.049	0.108	74	71	9.77
60	88	75	− 9.279	− 9.484	0.05	0.109	74	71	6.98
61	81	74	− 9.66	− 9.771	− 0.293	− 0.172	76	8	6.95
62	84	75	− 8.87	− 9.548	− 0.039	0.018	83	63	7.82
63	86	74	− 9.265	− 9.721	− 0.019	0.192	94	20	6.33

NODANGLE does not print out values of angles or energies for non π – like orbitals for which the error term for the angle exceeds 0.5, or for which coefficients of s, p_x or p_y atomic orbitals are large compared with those of p_z. Table III summarizes the calculated angles and their error terms and Table IV the classical descriptors. The different descriptors used in this study are summarized in Table V.

Table III.  Calculated angles and their error terms.

Compound	ΘH1	αH1	ΘL1	αL1	ΘH2	αH2	ΘL2	αL2	ΘH3	αH3	ΘL3	αL3
1	73	0.3450	47	0.1955	72	0.1920	75	0.1803	86	0.0536	36	0.0030
2	72	0.3312	46	0.1822	71	0.1783	75	0.1949	47	0.0051	36	0.0017
3	72	0.3319	46	0.1843	71	0.1794	75	0.1925	52	0.0025	45	0.0004
4	71	0.3294	46	0.1837	71	0.1773	75	0.1933	56	0.0014	71	0.0054
5	71	0.3295	46	0.1842	71	0.1776	75	0.1927	63	0.0011	71	0.0065
6	70	0.3152	46	0.1732	69	0.1628	75	0.2065	90	0.0096	77	0.0150
7	62	0.3470	42	0.2165	75	0.0904	80	0.1554	84	0.0065	37	0.0038
8	60	0.3348	42	0.2023	74	0.0824	80	0.1673	70	0.0044	68	0.0042
9	53	0.3172	43	0.1876	78	0.0820	78	0.1905	85	0.0096	36	0.0033
10	49	0.3025	42	0.1634	77	0.0801	79	0.2180	89	0.0211	77	0.0160
11	51	0.3078	43	0.1744	77	0.0802	78	0.2048	75	0.0079	71	0.0055
12	82	0.3838	69	0.2925	50	0.1447	56	0.0596	86	0.0332	41	0.0127
13	81	0.3634	68	0.2863	46	0.1113	56	0.0609	80	0.0320	49	0.0031
14	80	0.3644	50	0.2170	63	0.2151	71	0.1568	86	0.0502	36	0.0030
15	74	0.3241	49	0.1809	73	0.2083	72	0.2020	150	0.0050	71	0.0056
16	84	0.3730	49	0.1962	56	0.2155	72	0.1861	175	0.0008	35	0.0029
17	89	0.3913	48	0.1828	43	0.1892	72	0.2021	39	0.0057	34	0.0016
18	88	0.3885	48	0.1842	45	0.1911	72	0.2002	81	0.0601	46	0.0006
19	90	0.3934	48	0.1837	42	0.1861	72	0.2011	83	0.0600	74	0.0067
20	89	0.3928	48	0.1842	43	0.1866	72	0.2005	84	0.0609	74	0.0072
21	102	0.4489	48	0.1731	25	0.1537	72	0.2159	91	0.0136	79	0.0172
22	78	0.3771	22	0.2355	59	0.1019	6	0.0655	69	0.0001	40	0.0115
23	76	0.3596	23	0.2270	56	0.0734	5	0.0687	21	0.0096	40	0.0054
24	76	0.3607	22	0.2283	56	0.0789	5	0.0681	21	0.0069	43	0.0049
25	76	0.3567	22	0.2276	56	0.0784	5	0.0682	23	0.0061	49	0.0026
26	76	0.3563	22	0.2280	56	0.0801	5	0.0680	26	0.0042	50	0.0025
27	70	0.3439	47	0.2213	75	0.1616	75	0.1571	86	0.0532	38	0.0037
28	68	0.3292	46	0.2061	74	0.1481	75	0.1702	77	0.0612	38	0.0023
29	69	0.3302	46	0.2085	74	0.1492	75	0.1681	81	0.0582	44	0.0010
30	68	0.3276	46	0.2078	74	0.1473	75	0.1688	83	0.0595	65	0.0033
31	68	0.3278	46	0.2084	74	0.1476	75	0.1683	84	0.0620	66	0.0041
32	66	0.3131	46	0.1959	72	0.1341	75	0.1807	91	0.0184	76	0.0151
33	49	0.3159	43	0.1777	77	0.0797	78	0.2016	76	0.0195	72	0.0060
34	53	0.3232	46	0.1825	75	0.0717	75	0.1954	76	0.0100	71	0.0056
35	58	0.3079	48	0.2067	76	0.0941	71	0.1689	70	0.0076	64	0.0031
36	75	0.3290	49	0.1945	73	0.2124	72	0.1877	82	0.0548	69	0.0046
37	78	0.3454	45	0.1997	63	0.2052	77	0.1807	41	0.0025	69	0.0046
38	109	0.4776	48	0.1868	20	0.1572	73	0.1987	82	0.0538	74	0.0071
39	114	0.4953	48	0.1858	15	0.1550	73	0.2000	82	0.0557	75	0.0072
40	55	0.2609	48	0.1779	2	0.1662	73	0.2094	82	0.0622	75	0.0074
41	46	0.2321	46	0.1748	91	0.1078	75	0.2161	72	0.0098	72	0.0061
42	42	0.2327	43	0.1657	90	0.1116	78	0.2227	73	0.0134	73	0.0064
43	47	0.2826	41	0.1751	83	0.0921	81	0.1988	78	0.0248	72	0.0065
44	46	0.2552	46	0.1687	86	0.1029	75	0.2230	77	0.0215	71	0.0056
45	51	0.3093	39	0.2073	79	0.0840	83	0.1560	74	0.0158	65	0.0037
46	105	0.4526	65	0.3786	27	0.2259	59	0.0624	81	0.0473	52	0.0015
47	114	0.4964	66	0.3665	16	0.2112	58	0.0639	79	0.0292	52	0.0014
48	159	0.0201	64	0.3139	14	0.2098	59	0.0621	80	0.0330	53	0.0014
49	101	0.4235	66	0.3539	35	0.2647	58	0.0608	81	0.0364	50	0.0020
50	85	0.3749	66	0.3187	18	0.1058	58	0.0609	80	0.0348	50	0.0021
51	83	0.3727	65	0.2945	30	0.0937	59	0.0612	80	0.0318	48	0.0042
52	71	0.3519	48	0.2401	70	0.1423	73	0.1459	65	0.0024	62	0.0020
53	73	0.3516	51	0.2537	74	0.1661	71	0.1402	68	0.0052	62	0.0029
54	67	0.3257	50	0.1898	81	0.1551	71	0.1902	87	0.0479	41	0.0023
55	67	0.3257	50	0.1899	81	0.1550	71	0.1902	87	0.0480	41	0.0023
56	60	0.2981	47	0.1763	82	0.1154	74	0.2111	85	0.0590	55	0.0100
57	57	0.2708	45	0.1907	86	0.1241	76	0.2010	83	0.0637	64	0.0030
58	52	0.2458	45	0.1567	88	0.1231	75	0.2426	74	0.0149	71	0.0056
59	52	0.2461	45	0.1568	88	0.1232	75	0.2422	74	0.0160	71	0.0056
60	52	0.2459	45	0.1567	88	0.1230	75	0.2424	74	0.0162	71	0.0056
61	58	0.2791	47	0.1809	81	0.1100	74	0.2051	76	0.0059	8	0.0016
62	60	0.2777	46	0.1667	84	0.1588	75	0.2208	83	0.0609	63	0.0028
63	49	0.1769	46	0.2200	86	0.1662	74	0.1925	94	0.0213	20	0.0011

H, HOP; α, error; θ, angle (as in Figure 1).

Table IV.  Calculated classical descriptors.

Compound	MEANQ	LDI	Pxx	Pyy	Pzz	SE	Log 1/IC50
1	0.167	0.248	255.210	160.880	51.266	− 16.465	6.46
2	0.168	0.273	256.430	166.420	50.849	− 16.537	7.25
3	0.160	0.244	264.510	173.180	54.439	− 16.506	7.64
4	0.163	0.243	266.490	177.050	57.907	− 17.151	7.57
5	0.168	0.255	271.140	180.180	60.879	− 16.856	7.1
6	0.175	0.291	259.650	179.450	64.255	− 17.589	6.24
7	0.158	0.241	285.440	180.380	61.332	− 18.857	7.26
8	0.155	0.237	291.210	204.060	66.243	− 19.527	7.52
9	0.172	0.271	271.940	177.840	55.529	− 21.527	6.11
10	0.181	0.312	273.830	202.770	66.458	− 22.708	6.24
11	0.169	0.267	278.560	200.070	61.446	− 22.166	9.11
12	0.204	0.333	291.210	185.980	54.888	− 24.676	5.3
13	0.200	0.330	298.800	204.490	61.851	− 25.626	6.04
14	0.169	0.278	293.750	170.750	60.986	− 19.851	6.92
15	0.166	0.274	307.820	183.560	66.422	− 19.777	8
16	0.188	0.321	288.020	165.800	52.620	− 22.210	7
17	0.190	0.346	288.850	172.320	52.147	− 22.227	8.7
18	0.181	0.317	294.950	180.570	56.006	− 22.156	9.6
19	0.184	0.316	295.170	186.280	59.494	− 22.805	10
20	0.190	0.327	298.430	190.820	62.485	− 22.526	9.46
21	0.194	0.356	289.870	187.660	65.706	− 23.192	8.48
22	0.194	0.298	294.470	178.700	54.493	− 24.546	4.92
23	0.195	0.321	295.910	182.910	54.738	− 24.868	5.21
24	0.195	0.305	309.630	195.790	67.117	− 25.178	6.09
25	0.190	0.294	305.560	192.540	63.543	− 25.455	6
26	0.195	0.305	309.640	195.770	67.131	− 25.174	6.27
27	0.154	0.243	308.860	183.230	78.823	− 19.864	7.54
28	0.155	0.263	309.350	190.720	77.305	− 19.988	8.42
29	0.148	0.240	314.610	201.000	80.288	− 19.915	9.51
30	0.150	0.239	314.430	208.670	82.154	− 20.575	10.6
31	0.155	0.248	316.920	214.640	84.504	− 20.253	9.05
32	0.161	0.279	311.260	207.630	88.123	− 21.080	9.62
33	0.157	0.248	295.580	211.110	70.424	− 20.798	8.4
34	0.147	0.230	300.050	218.430	82.694	− 19.567	7.08
35	0.182	0.293	330.800	224.070	79.702	− 27.196	7.92
36	0.181	0.299	284.860	178.610	58.469	− 21.316	8.33
37	0.193	0.319	324.320	199.080	94.632	− 30.836	7.4
38	0.171	0.292	314.910	196.680	66.802	− 21.358	8.15
39	0.166	0.292	335.220	195.250	76.172	− 21.038	7.92
40	0.160	0.271	333.780	202.300	74.423	− 20.228	7.96
41	0.180	0.301	304.910	202.990	63.476	− 26.230	9.92
42	0.168	0.279	324.790	209.710	72.462	− 26.326	9.16
43	0.155	0.256	334.170	213.830	83.598	− 22.304	6.8
44	0.166	0.269	318.450	205.880	70.176	− 23.634	8.42
45	0.162	0.260	306.950	200.620	62.189	− 21.552	8.19
46	0.229	0.406	331.170	211.330	64.006	− 28.429	7.28
47	0.211	0.373	354.910	216.780	72.519	− 26.736	7.17
48	0.191	0.336	362.850	223.270	84.651	− 26.536	5.7
49	0.232	0.408	382.300	230.730	76.459	− 36.868	7.55
50	0.203	0.352	340.050	211.960	69.876	− 28.614	7.82
51	0.193	0.324	314.810	204.500	74.083	− 25.728	7.6
52	0.150	0.239	295.210	218.360	81.700	− 18.104	5.86
53	0.156	0.263	346.830	228.350	80.983	− 20.195	9.17
54	0.156	0.261	310.540	209.550	83.336	− 19.983	6.89
55	0.156	0.263	358.530	185.430	75.066	− 21.609	9.02
56	0.154	0.251	370.680	207.800	76.236	− 21.553	10.14
57	0.181	0.287	291.360	189.970	60.779	− 26.242	9.77
58	0.150	0.255	343.760	228.520	95.850	− 22.768	11.22
59	0.144	0.242	363.170	242.890	114.280	− 22.331	9.77
60	0.140	0.234	382.270	257.320	132.200	− 22.405	6.98
61	0.152	0.251	341.480	211.760	93.624	− 21.480	6.95
62	0.161	0.246	301.450	198.210	67.089	− 21.150	7.82
63	0.173	0.302	340.940	215.990	87.650	− 25.333	6.33

MEANQ is mean of absolute charge (charge polarization) LDI is Local Dipole Index, SE is solvation energy, P_xx, P_yy and P_zz are the diagonal components of polarizability.

Table V.  Descriptors used in this study

Name	Descriptor
HOP1	Energy of highest occupied π orbital for ring 1
SHOP1	Energy of second highest occupied π orbital for ring 1
LUP1	Energy of lowest unoccupied π orbital for ring 1
SLUP1	Energy of second lowest unoccupied π orbital for ring 1
HOP2	Energy of highest occupied π orbital for ring 2
SHOP2	Energy of second highest occupied π orbital for ring 2
LUP2	Energy of lowest unoccupied π orbital for ring 2
SLUP2	Energy of second lowest unoccupied π orbital for ring 2
HOP3	Energy of highest occupied π orbital for ring 3
SHOP3	Energy of second highest occupied π orbital for ring 3
LUP3	Energy of lowest unoccupied π orbital for ring 3
SLUP3	Energy of second lowest unoccupied π orbital for ring 3
S2θ1H	sin(2* the nodal angle in the highest occupied π orbital in ring 1)
C2θ1H	cos(2* the nodal angle in the highest occupied π orbital in ring 1)
S4θ1L	sin(4* the nodal angle in the lowest unoccupied π orbital in ring 1)
C4θ1L	cos(4* the nodal angle in the lowest unoccupied π orbital in ring 1)
S2θ2H	sin(2* the nodal angle in the highest occupied π orbital in ring 2)
C2θ2H	cos(2* the nodal angle in the highest occupied π orbital in ring 2)
S4θ2L	sin(4* the nodal angle in the lowest unoccupied π orbital in ring 2)
C4θ2L	cos(4* the nodal angle in the lowest unoccupied π orbital in ring 2)
S2θ3H	sin(2* the nodal angle in the highest occupied π orbital in ring 3)
S4θ3L	sin(4* the nodal angle in the lowest unoccupied π orbital in ring 3)
C2θ3H	cos(2* the nodal angle in the highest occupied π orbital in ring 3)
C4θ3L	cos(4* the nodal angle in the lowest unoccupied π orbital in ring 3)
MEANQ	mean of absolute charge (charge polarization)
LDI	Local Dipole Index
SE	Solvation energy
Pxx	diagonal components of polarizability in x-direction
Pyy	diagonal components of polarizability in y-direction
Pzz	diagonal components of polarizability in z-direction

The best model as given in [7] for quinazoline analogues was: where n is the number of compounds used in the fit, R² is the squared correlation coefficient, S is the standard deviation, and Q² is the square of the multiple correlation coefficients based on the leave-one-out residuals. The indicator variable I = 1 is for 6,7-OMe derivatives. B1_Y,7 is the steric effect (y- substituent at 7-position). B1_X,3 is the same but for x- substituent at the 3-position of the 4-phenylamino moiety. σ⁻ _Y are electron donating groups as y-substituent. ClogP is the hydrophobicity.

The nodal angles are converted to sin 2θ_H, cos 2θ_H, sin 4θ_L and cos 4θ_L and then θ_H and θ_L are removed from the variables set. As a result, we will have a set of variables consists of: HOP1, SHOP1, LUP1, SLUP1, HOP2, SHOP2, LUP2, SLUP2, HOP3, SHOP3, LUP3, SLUP3, C2θ₁H, S2θ₁H, C2θ₂H, S2θ₂H, C2θ₃H, S2θ ₃H, C4θ₁L, S4θ ₁L, C4θ₂L, S4θ₂L, C4θ₃L, S4θ₃L. These variables are defined in Table V.

NODANGLE did not print out a value for either the energy of SHOP1 for compound 48 or the energy of SHOP3 for compounds 15 and 16 because the error term was larger than 0.5. Hence, these variables were excluded from the regression analysis.

A FLIPSTEP calculation, that performs a backward-stepwise variable selection, was carried out using the default setting of VIFMAX value of 35. VIFMAX is the criterion for excluding variables that are collinear with other variables in the regression. The variance inflation factor (VIF) is defined for each independent variable i as 1/(1-R_i²), where R_i² is the R² for independent variable i regressed on all of the other independent variables. VIFMAX is the value of VIF above which a variable will be removed from the regression early in the procedure. In general a value of VIF above 10 is cause for concern. By default VIFMAX is set to 35. With this value, the maximum VIF in the final equation is usually much less than 35.

This set of quinazolines separates into two parts (symmetry wise): the singly-substituted quinazoline ring system, and the singly substituted phenyl ring. The quinazoline ring system has no vertical mirror planes or axes. Hence, ring 1 cannot be flipped into ring 2. Thus for this part of the molecule flip regression is not applied. The singly substituted phenyl ring has C_2v symmetry, so flip regression is applicable to this. Thus only ring 3 should be flipped. Applying FLIPSTEP on this model resulted in removing S4θ₂L, C4θ₂L, LUP2 and SLUP1 due to colinearity. C4θ₁L, HOP1, LUP1, C2θ₁H and S2θ₁H were deleted because they are statistically insignificant. FLIPSTEP stepwise regression gives:

Here, F is the Fisher variance ratio. The numbers in parentheses are Student's t values; a value greater than approximately 2 is indicative of significance at the 0.05 level. Table VI shows the progress of FLIPSTEP for this model.

Table VI.  progress Of Flipstep For Quantum Descriptors.

Variable	Coefficient	T	Significance	VIF
HOP2	− 1.7828	4.32	0.00008	11.05
SHOP2	1.7771	6.54	0.00000	5.95
SLUP2	1.2678	2.89	0.00578	5.58
HOP3	2.1062	6.25	0.00000	3.81
LUP3	5.4061	4.09	0.00016	15.42
SLUP3	− 8.6831	6.93	0.00000	12.30
S4θ1L	0.60493	2.87	0.00612	2.24
C2θ2H	− 0.92009	5.21	0.00000	2.64
S2θ2H	1.3927	3.99	0.00022	2.31
C2θ3H	− 0.25315	1.01	0.31766	3.93
S2θ3H	− 0.12697	0.77	0.44367	1.52
C4θ3L	0.58047	3.07	0.00344	2.96
S4θ3L	1.2140	11.13	0.00000	1.51

F = 31.47, R² = 0.8930, S = 0.5244, Q² = 0.8346

Multi-linear regression analysis was carried out on the flipped variables selected by FLIPSTEP regression using the program MULTLR from the Martha package [16]. Multilinear regression analysis applied to all variables in Table VI without removing the variables with high significance leads to precisely the values given by FLIPSTEP. Removal of the two variables of poor significance (C2θ₃H and S2θ₃H) leads to Equation (3). For example, C2θ₃H and its flippable partner S2θ₃H are of very poor significance, and their removal is justified. These variables are not independent, but are orthogonal to their partner terms. If only one of them were removed because of insignificance it would become impossible to carry out the prediction, because there is nothing to be flip into. If FLIPSTEP is to be used predicatively, then each variable and its flippable partner should be retained if one of them is significant. Removing one or other of the sine or cosine terms would force the angle to be either 0 or 90 degrees, which is not justifiable. The angle may well be 0 or 90 degrees as far as it can be determined, within the confidence limits set, but saying that the optimum angle is 0 is not the same thing as saying the angle does not matter. Deleting S2θ₃H and retaining C2θ₃H would have the effect of forcing the angle θ₃H to be 0 degrees, rather than its maximum likelihood value of approximately 4°. In the present case both variables are deleted, because of their very poor significance, and the functions of θ₃L, which are both very highly significant are retained. In regression analysis it is usual to delete variables that are not significant, usually taking the 0.05 significance level as the criterion. In the special case of flip regression we consider the flippable pairs as a whole, deleting them only if both are nonsignificant, as in the case of 2θ₃H they are.

Multilinear regression analysis shows that SLUP3 and S4θ₃L are the most critical variables, by the magnitude of the standardized regression coefficient and Student's t criteria respectively. Both the HOP and LUP orbital energies on ring 3 are very significant. The orientation of the node in the HOP orbital present on ring 3 is not very significant while the orientation of the node in the LUP orbital present on ring 3 is very highly significant, and is in fact the most significant term in the regression. The orientation of the nodes in the occupied and virtual orbitals present on rings 1 and 2, except for θ₂H, are not very significant. Regression of Log 1/IC₅₀ with the previous variables but deleting the nonsignificant θ₃H terms gives:

P is the significance level based on a randomization test, using the Martha routine FLIPRAND. This procedure involves repeatedly running randomization of dependent variable followed by flip regression 1000 times, preserving the independent variables. The correlation coefficient for each randomization is saved, and the significance, calculated after Fisher normalization. In contrast to Equation (2) the coefficients given here are the standardized regression coefficients. Their magnitudes are a measure of the relative importance of the contributions of the terms in the model to Log 1/IC₅₀. In applying Equation 3 it must be remembered that not the raw descriptor values should be used, but rather the values standardized to zero mean and unit variance. It should be noted that in contrast to Equation (1) no compound has here been deleted. Deleting the two insignificant terms, leads to very little deterioration of the model; it gives a correlation coefficient of 0.9431 that is very close to that obtained when retaining these variables in Equation (2), 0.9450, which justifies our choice for removing these variables.

Equation (2) and Table III show that R² obtained from FLIPSTEP is the same as that obtained from multilinear regression analysis. The quality of the correlations is quite good and in Equation (3) we have about 6 points per variable, which is well within acceptable limits [20–22]. This entire regression was done with only the orbital energies and nodal angles, and could probably be substantially improved by including classical variables.

Including classical variables

Some classical descriptors were added to the previous set of variables. These variables are LDI, MEANQ, polarizabilities and solvation energies. These variables are shown in Table IV. Flip regression was applied on the new set of quantum and classical variables. Adding the classical variables would result in a set of 28 variables defined in Table V. The variables that entered the FLIPSTEP calculations are: HOP1, LUP1, SLUP1, HOP2, SHOP2, LUP2, SLUP2, HOP3, LUP3, SLUP3, C2θ₁H, S2θ₁H, C4θ₁L, S4θ₁L, C2θ₂H, S2θ₂H, C4θ₂L, S4θ₂L, C2θ₃H, S2θ₃H, C4θ₃L, S4θ₃L, MEANQ, LDI, P_xx, P_yy, P_zz and SE. These variables are then flipped as described above. Applying FLIPSTEP stepwise regression resulted in deleting S4θ₂L, C4θ₂L, LUP2, SLUP1, MEANQ and HOP2 due to colinearity. S2θ₁H, P_yy, SE, HOP1, S4θ₁L, SLUP2, LDI, LUP1, C2θ₂H and HOP3 were deleted because they are statistically insignificant. Flip regression with quantum and classical descriptors gives:

Table VII shows the progress of FLIPSTEP for this model.

Adding the classical variables to the set of variables improves R² value, but only marginally. The best descriptor is still SLUP3. LUP3 is highly significant but HOP3 is not significant now. The orientation of the node in the LUP orbital present on ring 1 is very significant while the orientation of the node in the HOP orbital present on rings 2 and 3 is not very significant..P_xx and P_zz which are the polarizability tensor component in the directions of highest and lowest polarizability (and highest and lowest inertia) are very highly significant. We have one fewer variables than in Equation (2).

Finally, following the same argument when performing multilinear regression for the quantum descriptors, a multi-linear regression analysis was carried out on Log 1/IC₅₀ with the variables in Table VII, without removing the variables with poor significance (S2θ₃H and C4θ₃L), because their flippable partners are very significant.

Table VII.  progress of FLIPSTEP for quantum and classical descriptors.

Variable	Coefficient	T	Significance	VIF
SHOP2	− 0.71655	3.36	0.00149	4.06
LUP3	8.2831	7.10	0.00000	13.31
SLUP3	− 9.6185	8.92	0.00000	10.14
C2θ1H	− 1.8925	6.30	0.00000	2.83
C4θ1L	− 3.1242	7.73	0.00000	6.01
S2θ2H	− 1.3632	3.07	0.00348	4.16
Pxx	0.03688	7.80	0.00000	5.07
Pzz	− 0.05298	6.55	0.00000	3.71
C2θ3H	− 0.46731	3.34	0.00159	1.36
S2θ3H	0.08549	0.57	0.56988	1.40
C4θ3L	− 0.07838	0.51	0.61539	2.22
S4θ3L	1.1329	11.27	0.00000	1.38

F = 38.21, R² = 0.9017, S = 0.4977, Q² = 0.8550

Multiple regression analysis shows that SLUP3 is the most critical variable. LUP3 has very high significance while SHOP2 has a low significance, as measured by the standardized coefficients in Equation (5). The orientations of the nodes in the LUP orbital in rings 1 and 3 have a very high significance. Also, P_zz and P_xx have high significance. Regression of Log 1/IC₅₀ with the previous variables gives:

As with Equation (3) the coefficients are the standardized values.

Equations (4) and (5) show that R² obtained from FLIPSTEP the same as that obtained from multilinear regression analysis. In this equation, unlike Equation (3), no terms have been deleted due to non-significance. Equation (5) gives an R² of 0.9017, compared with 0.8895 for Equation (3), at the expense of increasing the number of descriptors by 1.

Table VIII shows the flip status and flip significance from FLIPSTEP calculations carried out on quantum variables alone and that carried on quantum and classical variables together. A value of the significance greater than 0.05 is indicative that flipping the corresponding compound makes little difference to the quality of the regression. A flip status of 1 indicates that the compound has not flipped in the final regression, and − 1 that it has. This has only relative significance, and flipping all of the compounds in a flip regression has no effect.

Table VIII.  Flip status and flip significance for Equations (2) and (4).

	Equation (2) (quantum descriptors only)		Equation (4) (quantum and classical descriptors)
Comp.	Flip status	Flip significance	Flip status	Flip significance
1	− 1	0.039724	− 1	0.037336
2	− 1	0.051305	− 1	0.033844
3	− 1	0.759420	− 1	0.951920
4	1	0.000069	1	0.000628
5	1	0.000122	1	0.000694
6	1	0.007975	1	0.011471
7	1	0.088653	1	0.043051
8	1	0.000068	1	0.000222
9	1	0.083033	− 1	0.045017
10	1	0.014573	1	0.011355
11	− 1	0.000476	− 1	0.000627
12	− 1	0.413540	1	0.319210
13	1	0.355810	1	0.406050
14	− 1	0.043405	− 1	0.030024
15	− 1	0.005024	1	0.000948
16	1	0.124220	1	0.091302
17	1	0.062726	1	0.007508
18	1	0.801980	− 1	0.920900
19	1	0.003916	− 1	0.002337
20	1	0.005221	− 1	0.002042
21	− 1	0.031814	− 1	0.019038
22	1	0.588510	1	0.237880
23	− 1	0.418130	− 1	0.217000
24	1	0.838300	1	0.551420
25	1	0.233760	1	0.371060
26	1	0.149000	− 1	0.279950
27	1	0.073178	1	0.058749
28	− 1	0.086832	− 1	0.049363
29	1	0.929320	1	0.761500
30	− 1	0.000114	− 1	0.000228
31	1	0.000164	− 1	0.000143
32	− 1	0.003838	− 1	0.004150
33	− 1	0.000526	− 1	0.000689
34	1	0.000226	1	0.000739
35	− 1	0.000334	1	0.003100
36	1	0.000249	1	0.000311
37	1	0.000200	1	0.001998
38	1	0.002864	1	0.001365
39	1	0.003638	1	0.001633
40	1	0.014457	1	0.004109
41	− 1	0.000525	− 1	0.002716
42	− 1	0.000292	− 1	0.001112
43	1	0.000203	1	0.000825
44	− 1	0.000096	1	0.000452
45	− 1	0.000178	1	0.000688
46	1	0.072142	1	0.127250
47	− 1	0.073628	1	0.125180
48	1	0.065791	1	0.555230
49	− 1	0.212830	− 1	0.296540
50	− 1	0.169710	1	0.231520
51	− 1	0.423840	− 1	0.514300
52	1	0.000243	1	0.002493
53	− 1	0.000233	1	0.001317
54	− 1	0.389380	1	0.367510
55	1	0.812650	1	0.393690
56	− 1	0.036152	1	0.096367
57	− 1	0.000196	− 1	0.000652
58	− 1	0.000391	− 1	0.000647
59	− 1	0.000202	− 1	0.001318
60	1	0.000170	1	0.010127
61	− 1	0.135880	− 1	0.079706
62	1	0.000320	1	0.000917
63	− 1	0.000235	− 1	0.000523

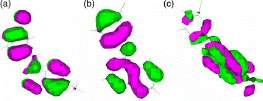
Figure 2 shows HOMO orbitals for three sample compounds of the 63 compounds. HOMO orbitals for the 63 compounds are similar to the molecular orbitals shown in either (a), (b) or (c). As Figure 2 shows, the p_z orbitals of ring 3 looks more similar to benzene π-orbitals than those for rings 1 and 2. This enhances the high coefficient for ring 3 LUP orbitals.

Figure 2.  HOMO orbitals for quinazolines.

Table IX summarizes the observed activity as well as the estimated activity according to the multilinear regression carried out on quantum variables alone and that carried on quantum and classical variables together, while Figure 3 shows the plot of the logarithm of the observed activity against the logarithm of the estimated activities in both cases.

Table IX.  Observed Log 1/IC₅₀ versus estimated.

Compound	Log 1/IC50 (Obs)	Log 1/IC50 (Calc) [Q]	Log 1/IC50 (Calc)[Q,C]
1	6.46	6.9396	6.3127
2	7.25	6.6668	7.1034
3	7.64	7.4556	8.2490
4	7.57	6.9810	7.1982
5	7.10	6.8524	7.2556
6	6.24	6.7698	6.3829
7	7.26	6.9909	7.4116
8	7.52	7.2190	7.1066
9	6.11	6.0045	6.1376
10	6.24	6.1728	5.9253
11	9.11	8.5908	9.0829
12	5.30	5.3718	5.2401
13	6.04	6.7331	6.3958
14	6.92	7.2540	6.8085
15	8.00	8.8157	7.7006
16	7.00	6.9864	7.2232
17	8.70	8.8975	9.1057
18	9.60	9.8487	9.1202
19	10.00	9.5176	9.7261
20	9.46	9.4997	9.6197
21	8.48	8.4893	8.4692
22	4.92	4.7750	4.6423
23	5.21	5.5360	5.2501
24	6.09	6.2378	5.7781
25	6.00	6.2162	5.9476
26	6.27	6.0550	6.5052
27	7.54	7.8866	7.8523
28	8.42	8.0823	7.9904
29	9.51	8.8927	9.0478
30	10.60	10.7130	10.0870
31	9.05	8.2043	10.0390
32	9.62	8.7237	8.9480
33	8.40	8.6838	9.0407
34	7.08	6.3716	6.6572
35	7.92	8.0230	8.5615
36	8.33	8.4814	8.1863
37	7.40	7.3080	6.9286
38	8.15	8.3457	8.0505
39	7.92	8.1873	8.2882
40	7.96	7.5683	8.2218
41	9.92	9.6712	9.4811
42	9.16	9.1641	9.4966
43	6.80	7.4089	7.2909
44	8.42	9.1804	7.7161
45	8.19	8.6888	7.8784
46	7.28	7.2086	7.0859
47	7.17	7.4932	7.2296
48	5.70	6.2020	5.7885
49	7.55	7.3267	7.7056
50	7.82	7.3967	7.9648
51	7.60	6.8222	7.4098
52	5.86	6.6127	6.8614
53	9.17	8.9068	8.8656
54	6.89	7.0002	6.9464
55	9.02	8.9432	9.1544
56	10.14	10.0060	9.7535
57	9.77	10.6880	10.2620
58	11.22	9.7935	9.7861
59	9.77	9.7998	9.5199
60	6.98	7.3697	7.1649
61	6.95	7.9379	8.2493
62	7.82	7.9915	8.2686
63	6.33	5.9599	6.4426

Log 1/IC₅₀ (Calc) [Q] is Log 1/IC₅₀ (Calc) obtained from regression analysis carried on quantum descriptors only (Equation 3), and Log 1/IC₅₀ (Calc) [Q,C] is Log 1/IC₅₀ (Calc) obtained from regression analysis carried on quantum and classical descriptors (Equation 5).

Figure 3.  Observed Log 1/IC₅₀ versus estimated for regression analysis carried out for quantum descriptors and that carried out for quantum and classical descriptors.

Comparison with other QSAR studies of quinazoline analoges

The results that we obtained in this study are better than the results obtained in [7], in which number of compounds are 51 as reported in Equation (1) while we include all the compounds, also the R² value (0.9011) that we obtained is much higher than they obtained (0.852). In [14], the steric as well as the electrostatic interactions proved to be the most important for the inhibitory effect and this is represented qualitatively while we represent these results quantitatively.

Conclusions

The nodal orientation terms have a powerful explanatory value in that they account for much more of the variance in activity than is possible using the classical descriptors alone. Were it not for the large number of descriptors already in the equation in comparison to number of molecules, a combination of the classical descriptors and the nodal orientation terms gives even better explanatory of activity of the quinazolines analogues.

This study has used two relatively new techniques. The first is flip regression, for handling the symmetry of the phenylaminoquinazoline system. The second is the use of the orbital nodal angle descriptors. Their descriptors are interesting ones but their application is limited: they can be used for the same structural family only. (within one core) This is based on the concept that the stability of stacked aromatic systems is highly orientation dependent, as we have found in previous studies [10–13], and is also dependent on the energies of those orbitals in the two aromatic systems that resemble the degenerate HOMO and LUMO of benzene. It is envisaged that the benzene rings of the quinazolines are interacting with aromatic systems on the receptor and that alignment occurs between the π-orbital nodes on the pair. Precisely which rings are involved becomes apparent from the identity of the descriptors that remain in the equations. SLUP3 was identified to be an important descriptor. Adding classical variables improves the correlation but only marginally. The only classical variables found to be significant were the polarizability components. High polarizability in the highest inertia direction was found to be favorable to high activity, while high polarizability in the lowest inertia direction was detrimental.