Bernal’s road to random packing and the structure of liquids

Abstract

Until the 1960s, liquids were generally regarded as either dense gases or disordered solids, and theoretical attempts at understanding their structures and properties were largely based on those concepts. Bernal, himself a crystallographer, was unhappy with either approach, preferring to regard simple liquids as ‘homogeneous, coherent and essentially irregular assemblages of molecules containing no crystalline regions’. He set about realizing this conceptual model through a detailed examination of the structures and properties of random packings of spheres. In order to test the relevance of the model to real liquids, ways had to be found to realize and characterize random packings. This was at a time when computing was slow and in its infancy, so he and his collaborators set about building models in the laboratory, and examining aspects of their structures in order to characterize them in ways which would enable comparison with the properties of real liquids. Some of the imaginative – often time consuming and frustrating – routes followed are described, as well the comparisons made with the properties of simple liquids. With the increase of the power of computers in the 1960s, computational approaches became increasingly exploited in random packing studies. This enabled the use of packing concepts, and the tools developed to characterize them, in understanding systems as diverse as metallic glasses, crystal–liquid interfaces, protein structures, enzyme–substrate interactions and the distribution of galaxies, as well as their exploitation in, for example, oil extraction, understanding chromatographic separation columns, and packed beds in industrial processes.

Keywords:

• liquid structure
• random packing
• Voronoi polyhedra

1. Introduction

John Desmond Bernal (1901–1971) was a major polymath of the twentieth century. He played a key role in the early development of crystallography, advancing instrumentation and methods that became standard procedures in X-ray crystallography well into the 1960s. Seeing the potential of crystallography in determining the structures of biological molecules as a way to understanding biological processes, with Dorothy Hodgkin he took the first X-ray photograph of a wet protein [1], and while in Cambridge in the 1930s he was instrumental in starting off Max Perutz in his pioneering work to solve the structure of haemoglobin.

His interest in the structural basis of biological functioning was also instrumental in raising his interest in liquids. As he himself said in his 1962 Royal Society Bakerian Lecture [2]:

My interest in the subject is of long standing. It came about in the first place through my biochemical interests, in that all living structures are mostly composed of water. This was to lead, thirty years ago now, to the paper on water and ionic solutions which Professor R. H. Fowler and I brought out in the first number of the Journal of Chemical Physics. [3]

Considering the state of knowledge of water and aqueous solutions in the early 1930s, this paper was an amazing tour de force. On the basis of a model of the water molecule derived from the limited spectroscopic and X-ray data available at the time (a model which interestingly bears a strong resemblance to some of the most successful potential functions used in modern computer simulations of aqueous systems), Bernal and Fowler were able to deduce ‘quantitatively in good agreement with experiment’ the X-ray diffraction curve for water (see Figure 1, taken from a manuscript draft of the paper), as well as the structure of ice, the total energy of water and ice, and various hydration and mobility properties of ions. They were also able to infer ‘in a qualitative way’ the density of water and how it changes with temperature (one of the so-called anomalies of water), the dielectric properties of water and ice and explain the ‘unique position of water among molecular liquids’. Quite a list.

Figure 1 The X-ray diffraction pattern of water compared with those predicted by Bernal’s quartz-like model, taken from a draft of the original 1933 paper [3].

Despite this success, he was dissatisfied:

My … approach to this problem was, frankly, one of crystal structure, trying to picture water structure as a mixture of the analogous four co-ordinated structures of silicon dioxide, quartz and tridymite. [2]

In essence, he was seeing the structure of the liquid as explainable on the basis of crystal structures that he saw the water molecule – by analogy with the geometrically similar SiO₄ building block of silica structures – capable of forming. He may have tried to introduce a degree of disorder into this picture, but it was still essentially a crystalline mixture model of a liquid structure.

Realizing that water was rather a difficult problem, and commenting that ‘It is not worth tackling complicated liquids until we understand simple ones’ [4], he moved his liquid focus to so-called ‘normal’ liquids – those of monatomic systems of which the inert gases looked the simplest to address. He made two main attempts in the 1930s. The first of these [2] was based on the analogy pointed out by Zernike and Prins [5] between the (smooth but bumpy) scattering pattern of a liquid and that (sharp peaky) one of a crystalline solid. This analogy he interpreted as ‘the peaks of the first, second and third co-ordination spheres corresponding to the reflections from planes of the same spacings in a crystal’ [2]. He found this ultimately to be a delusive approach, ‘postulating a greater degree of order, particularly long-range order, in the liquid than actually exists there. A liquid … is not simply a blurred solid’ [2] (author’s emphasis). The second approach, published in 1937 [6], attempted to describe a liquid in terms of coordination – it should be describable in terms of the number of atoms in each of the first, second, third etc. coordination spheres of given radius and width. In retrospect [2], he saw this as a ‘highly artificial’ description which could not be made quantitative as there was no means of calculating the values the theory required.

There is evidence in the development of his thinking of an increasing scepticism of the value of modelling the structure of a liquid in terms of related crystal structures – an interesting move for a crystallographer, with the underlying basis of experimental and theoretical crystallography being that of a regularly repeating lattice.

2 Previous approaches to the structures of liquids

In the period up till the 1960s or so, there were in essence two conceptual approaches to liquid structures. The first of these envisages a liquid as a disordered crystal. This has the advantage of being mathematically tractable (we can easily deal with crystalline order and limited departures from it), and yielding good results for properties such as density. They are, however, too ordered, giving entropies that are too low. At the opposite end of the structural spectrum, liquids became increasingly considered as dense gases. This fixed the entropy problem, but the mathematical approximations needed meant that the approach failed at realistic liquid densities.

There were, however, other theoretical approaches that were developed in this period. Although ‘in a sense their approach approximates to the theory of dense gases’ [7] and hence relates to the gas-like approach just mentioned, the massive literature and extensive intellectual effort that have gone into first principles theories of liquids mean that we cannot really avoid mentioning them briefly. In essence, these theories attempt to relate the pair distribution function that describes the structure of a simple liquid to the mutual potential between the molecules. For full discussions of these methods, see for example Hansen and McDonald [8]. The treatments are complicated and difficult to apply to real liquids, but if this connection between structure and potential function can be made, we would have a good theory of the thermodynamic properties of liquids [9]. In fact, an equation can be written down to connect these two quantities; the problem is that the equation also involves the distribution function for triplets of molecules. This in itself is unknown, but can in turn be written in terms of the (also unknown) quadruplet distribution function, and that also can be written in terms of the quintuplet distribution, etc.

To break this chain, we need to ‘step off the staircase’ [10] and look for another connection between the distribution functions. Several people (Bogoliubov, Born and Green, Kirkwood and Yvon) have implemented an approximation of Kirkwood [11] that expresses the triplet distribution in terms of the product of the three related pair distributions. Implementing this leads to an integral equation (‘BBGKY’) that indeed relates the pair distribution function to the interatomic potential, the temperature and the density of the liquid. However, problems observed when comparing predictions with experiment have led many to conclude that the approach is unsatisfactory. Refinements are possible – for example going to a higher level in the hierarchy and making a similar approximation relating the quadruplet to the triplet distributions. However, the computational resources required to solve the resulting equation numerically mean it cannot then be reasonably described as an analytical theory [10]. If we want such a theory, then perhaps there are other ways forward.

‘Having abandoned the mathematical solidity of the staircase of canonical distribution functions’ Ziman argued [10] ‘we really have no better guide than inspired phenomenology’. One such well-explored line of thought, and one of the most successful, measures the effects of geometrical constraints and physical forces on the statistical independence of the atomic positions, in essence trying to quantify the departure from the perfect randomness of the ideal gas. However, the equations obtained do not really say very much [10], and simplifying assumptions are still needed. One of these assumptions in fact brings us back to a version of the BBGKY equation. Others take us to, for example, the well-explored Percus–Yevick and hypernetted chain equations.

Ziman concludes: ‘Unfortunately the experimental evidence doesn’t decisively favour any single one of these alternative theories for all simple liquids at all densities’ [12]. Furthermore: ‘Formulae derived by [these methods] are not rigorous and should not be treated with exaggerated respect’ [10].

Though he did it some 30 years before it was given, Bernal seems to have followed Ziman’s advice and found all these approaches unsatisfactory. In his own words [2]:

Throughout this period I found all these theories fundamentally unsatisfying to a crystallographer, however much they might appeal to a physical chemist or a mathematician. I wanted a more concrete picture of the structure and one making use of Ockham’s razor ‘Not to multiply entities beyond necessity’. I wished to get some kind of theory of liquids that would be homologous to that of the crystalline solid as well as radically different in kind, and have a general quality of homogeneity without the assumption of any special groups, although … such groups may arise spontaneously and out of necessity.

So was born – with some stimulation from Frank’s work on packings in complex metal alloys [13] – his ‘most general hypothesis’ [4] of liquids as ‘homogeneous, coherent and essentially irregular assemblages of molecules containing no crystalline regions nor, in their low temperature form, holes large enough to admit another molecule’[2].

How this concept was realized in practice as random packings of spheres, and some of its potential applications in other areas of science and technology, forms the rest of this paper.

2 Earlier work on random packings

2.1 Primary structural properties

To be acceptable, a model of any phenomenon needs to have properties consistent with those of the phenomenon being modelled. Bernal seemed to have considered three primary experimental properties that a liquid model should quantitatively reproduce:

• Density.

• Average coordination number and its variability.

• The radial distribution function.

Clearly the density is likely to be the easiest of these to measure. The most critical and most easily accessible with respect to the detailed structure is the radial distribution function which can be obtained for real liquids by X-ray or neutron diffraction.

2.2 Early random packings of spheres

In 1930, Westman and Hugill published work [14] on particle packing that was initiated in the Department of Electrochemistry at the University of Toronto much earlier in 1923. Although not relating their work to the liquid problem (their primary interest seemed to be related to ceramics), they saw the potential relevance of particle packings to a range of science and industry, and their study looked at mixtures of up to five different sizes of spheres. The packings were produced by periodically vibrating a cylindrical vessel containing the spheres until a minimum volume was thought to have been obtained. For the particles they used which were most uniform (lead shot and steel ball bearings), packing densities of between 0.608 and 0.631 were obtained. Although liquid structure was not relevant to the intentions of this work, when compared to the density of a face-centered-cubic crystal of hard spheres (0.7405), this first set of density measurements suggested a density difference between crystalline close packing and random close packing of between about 15 and 20%. Over a decade later, Rice [15] also measured the density of a random close packing of glass spheres by measuring the volume of water needed to fill the interstices of a packing. After addressing corrections from edge effects, he concluded the volume of his random packing was 15(±3)% greater than that of regular cubic close packing.

As Bernal was to point out later [16], this is the order of magnitude of the change in volume on melting of an inert gas crystal.

Six years after Westman and Hugill, Morrell and Hildebrand (another giant of twentieth century science) constructed random packings specifically to try to model a liquid [17]. Quoting earlier work in two dimensions by Menke (steel spheres) [18] and Prins (seeds) [19], they used gelatin spheres as their model molecules, and neutralized effects of gravity by placing their gelatin spheres in a gelatin solution. To make possible measurement of sphere coordinates, a few spheres were coloured black and photographic images obtained from two directions. Many such exposures were made, between which the system was ‘shaken somewhat’, the photographs being recorded before the consequent sphere motion had ceased. A range of packing densities were explored. Though none of these approached the generally accepted density of random close packing of close to 0.637 (see below), their comparison with the experimental radial distribution function of liquid mercury is encouragingly good (Figure 2).

Figure 2 The radial distribution function of Morrell and Hildebrand’s densest model (lower panel) compared with the experimental function for liquid mercury (top panel). Reprinted with permission from Morrell and Hildebrand [17]. Copyright 1936, American Institute of Physics.

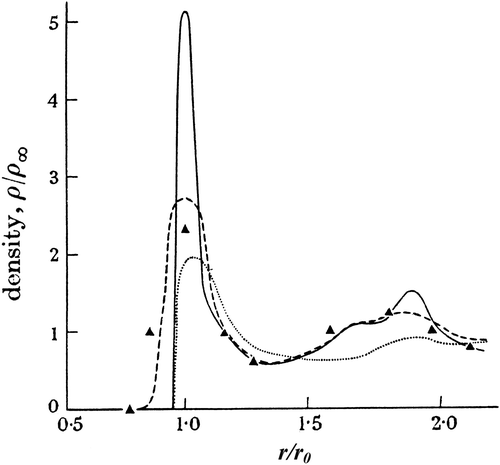
Two decades later, the development of computers had begun to make computer simulations possible – though severely limited by the computational power then available. Nevertheless in 1955, Alder et al. [20] reported a series of Monte Carlo calculations on boxes of around 80–100 hard spheres. The primary intention was to compare the simulations with theoretical methods of obtaining the radial distribution function. As mentioned above, these methods are limited to relatively low densities, so the work focused on low densities, concluding that up to around 20% of (crystal) close packing, the results were in good agreement with those calculated theoretically. For one calculation at 72% of closest packing (a packing density of 0.54 or 85% of random dense packing density) the radial distribution function was published (Figure 3). Inspection of this suggests the system may not have melted, still retaining significant crystalline character (compare for example with the liquid Mercury radial distribution function in Figure 2).

Figure 3 The radial distribution function of Alder et al.’s densest Monte Carlo-computed hard sphere assembly. Reprinted with permission from Alder et al. [20]. Copyright 1955, American Institute of Physics.

Perhaps, it is worth noting here that Bernal – who had essentially no experience in computing – was in the vanguard of seeing the possibilities of computer simulations. When he set up his Biomolecular Research Laboratory at Birkbeck College, London, opened by Sir Lawrence Bragg in 1948, (his dream Institute that he sometimes called ‘The Institute for the Study of Things’) [21], it included a computing laboratory headed by Donald Booth. Dorothy Hodgkin comments [21] that setting up a computing laboratory at that time was ‘one of Bernal’s most far sighted projects – advances in computing were to be essential for the solution of the problems he cared about … Booth developed many good ideas on computer building including computer-graphics’. Ultimately the computer unit joined forces with the main University of London computer centre. It was on that central computer system that Bernal was able in 1959 to report his first attempts to bring computing to the liquid problem [4]:

We have now started these computations by the use of the Mercury machine at London University and with the help of Dr A.D. Booth and my son Dr M.J.M. Bernal. These calculations not only confirm the earlier results obtained by the ball and spoke models [q.v. below], but also provide a good approximation to the radial distribution function.

What appear to have been the results of this early computer-based calculation are revisited in Section 3.2 below.

3 Bernal’s road to random packings

3.1 The difficulty of describing irregularity

Describing regularity is essentially trivial: for a crystallographic structure you merely repeat the contents of a unit cell in three dimensions. When there is no unit cell, then the whole framework of classical crystallography cannot help.

As mentioned earlier at the end of the Introduction, Bernal returned to the problem in the late 1950s after a 20-year break. In the 1930s, he could not see how to extend the ideas he had put forward in the 1933 paper on water [3]; as he said in the late 1950s [4]:

Twenty years ago I tried to extend these ideas to get a theory of liquids but gave it up because I did not know then how to get further than the very rough idea that a liquid was an irregular structure. I was baffled by the difficulty of describing irregularity. (my emphasis)

He made four main attempts to ‘unbaffle’ himself on the road to random close packing.

3.1.1 The first ball and spoke model

Before computer graphics, models were mainstream in understanding crystal structures. It was perhaps natural therefore that Bernal should see how far model building could take him. From the known radial distribution function of a simple liquid, we can get information on the distances between neighbouring atoms and the frequencies of occurrence of each distance. Bernal took this information, had it converted to a set of spokes cut to sizes consistent with the experimental radial distribution function, and proceeded to build a ball and spoke model from these [4]. The rationale was that the resulting model would be consistent with the diffraction pattern of the real liquid and, as the diffraction pattern is the Fourier transform of the structure, it would be a good bet that the resulting model would be a reasonable model of the structure of the liquid.

Building a model by hand, however, can be problematical in a number of ways. One particularly important one is to try to avoid bias in the building of it. One could perhaps throw dice to decide where next to add a spoke, or use a random number generator. But perhaps as effective is what Bernal did – he built it in his office where he was frequently interrupted, to the extent that when he went back to the model he did not remember what he had just done.

Figure 4 shows the model in process of construction.

Figure 4 Bernal building his first simple liquid model in his office.

Perhaps, three main points came from this model-building exercise [4]. First, the estimated density was about 10% less than that of a completely regular packing and, secondly, the calculated energy comes out about right – as would be expected from a distribution of neighbour distances that is consistent with the conclusions from diffraction data. Thirdly, an examination of the model showed that it could be considered as a packing of polyhedra. Remembering the work of Frank on local coordination polyhedra in metal structures [13], perhaps this was a way to proceed?

3.1.2 Elucidating and assembling coordination polyhedra

There are many ways of looking at atomic arrangements in crystals. One is the ball and spoke picture above. Another is to look at the arrangements of atoms around a central atom – what we might call the coordination polyhedron. In a crystal there will be a limited number of these local atomic arrangements and these will fit against one another in a regular way. Without this constraint of regularity, however, there will be many more local coordination polyhedral arrangements that do not fit together in a regular fashion. Bernal’s thesis in this context was that with the variety of local (irregular) coordination you could build up a reasonable model of a liquid. So he set about enumerating the different ways that spheres could be arranged around a central sphere [4], using the magnetic sphere arrangement shown in Figure 5(a). He found 54 of these for four up to twelve neighbours, and postulated he might find another hundred if he extended the exercise to 14 surface spheres.

Figure 5 (colour online) (a) Magnetic sphere arrangement used to build irregular coordination models. (b) An example of an irregular coordination arrangement together with the equivalent Voronoi polyhedron. Reprinted by courtesy of the Royal Institution of Great Britain from Proc. Roy. Instn. 37 (1959) p.373.

The problem then is how to take the next step and try to pack these together. As each neighbouring sphere will be a central sphere for another local arrangement, we cannot just pack together these local arrangements. Instead, the equivalent Voronoi polyhedra can be elucidated (Figure 5(b)). The problem then reduces to that of assembling a three-dimensional jigsaw puzzle of the set of equivalent Voronoi polyhedra. This ‘reduced’ problem is, however, still a challenging one:

If I knew the actual sizes of the polyhedra I could work out the ways in which they combine. I would then have the clue to all such arrangements of points, and, according to my view, to the arrangements of molecules in liquids. But to do this by the kind of process I have been discussing … would be an incredibly tedious process, and, indeed, would only be the beginning because I still would not know how many of each kind to use. [4]

So not surprisingly, the process was not followed. Instead, it led to the next idea.

3.1.3 Determining the Voronoi polyhedra and how they pack together: ‘rougher methods’

His next approach to trying to find the arrangement of molecules in liquids takes us closer to realizing random packings. In his 1958 Royal Institution Friday evening lecture (lectures which are renowned for imaginative demonstrations), Bernal described this next step – shaking together a heap of marbles – as follows [4]:

I will pass therefore to the use of rougher methods to give you some idea of this arrangement. The roughest of these is to assume that such an arrangement as I obtained by throwing the balls together early on in the lecture, represents a really random arrangement of spheres. The problem then simply remains to find out what the precise arrangement of these marbles is.

But as he admitted at the time, this is difficult to do with marbles. So instead he took a number of plasticine balls, covered them with chalk to prevent them sticking together, jumbled them inside a football bladder and then removed the air by pumping it out. The atmospheric pressure then would push the balls together to fill the interstices, resulting in an array of polyhedra that fit together to fill space. This was, in fact, the very kind of arrangement he had envisaged trying to construct ‘the other way round’ from the different kind of coordination polyhedra he had tried to elucidate as described in Section 3.1.2 above.

Figure 6 shows the kind of mass that resulted, broken apart to show exposed polyhedral faces. When the individual polyhedra were separated out, Bernal observed that they were ‘nearly all of them … quite different’. He then set about examining the shapes of these polyhedra, discovering that the commonest number of faces was 13 (average around 13.5) while the commonest face had five edges.

Figure 6 An exposed surface of the compressed plasticene sphere assembly.

Five. Not a number that is comfortable for a crystallographer, as an extended crystal can only be built on a lattice with underlying symmetries of 2, 3, 4 or 6. Never five. A regular repeating structure is just not possible with that symmetry. Again, Bernal’s words here are interesting [4]:

Now you can see how very shocking such an arrangement would be to a crystallographer because it is impossible to fit these five-sided figures together in any regular (my emphasis) way; … in other words such an arrangement of points is radically different from that of a crystal – I could not get a regular from an irregular structure except by a very marked transition of the same nature as that between one crystalline structure and another. … The co-ordinations are different. … This explains why melting is a marked phase transition. … My analysis would show that it is impossible to pass in a continuous way from a crystalline solid to its corresponding liquid.

So here is a simple, convincing structural rationalization of the discontinuity of the melting transition. In essence it involves a change of symmetry, and such changes are of their nature discontinuous.

After performing this kind of experiment, Bernal acknowledged that it had been performed over 200 years earlier by the Reverend Stephen Hales in trying to see the swelling properties of peas [22]. In the 1940s, the botanist Edwin Matzke, in exploring the role of surface forces in the determination of the three-dimensional shapes of plant cells examined the shapes of the bubbles in a foam and came to similar conclusions to Bernal concerning the prevalence of fivefold faces and obtained a similar value of 13.70 for the average number of faces per polyhedron [23]. Half a decade earlier, James Marvin [24] had done similar analyses on compressed lead shot and also come to similar conclusions (as also had Matzke in similar experiments published [25] in the same issue of the American Journal of Botany).

3.1.4 ‘Crazy fishing’

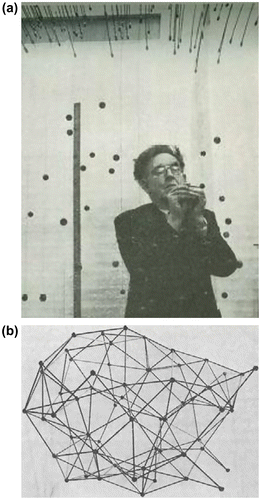
Bernal was still unsure he had achieved ‘absolute irregularity’ so he tackled the problem in yet another way: start with a number of molecules arranged at random and imagine what would happen if this assembly were compressed uniformly. First, in two dimensions he started off with an arrangement of points on a board placed according to a table of random numbers. Taking the closest pair, these are moved apart to a certain distance. Then taking another close pair, do the same and repeat until all pairs are separated by this minimum distance. Then continue the process with slightly longer minimum distance etc. Eventually a situation should be reached in which no further moves can be made.

Two dimensions, however, is a problem as there is a strong tendency to crystallize (the average number of edges per polygon in two dimensions is six, whether or not the arrangement is crystalline, whereas in three dimensions there is a discontinuity in the average number of faces per polyhedron in going from a disordered to a regular structure). He therefore had a three-dimensional jig set up in which small spheres were hung in positions determined by random number tables and proceeded to move apart the nearest pair to a given distance, repeating the process similar to that explored in two dimensions. Figure 7(a) shows Bernal at work – ‘crazy fishing’ as he called it – while Figure 7(b) shows the ball and spoke model constructed from the final arrangement of ‘hanging balls’. This looks similar to the first ball and spoke model he built in his office (Figure 4) but, as he pointed out [4], the earlier model had been made ‘arbitrarily by hand’ while the second one ‘was made more or less at random’.

Figure 7 (colour online) (a) Bernal ‘crazy fishing’, with (b) the ball-and-spoke model constructed from the resulting high density arrangement of the hanging balls in (a). Reprinted by courtesy of the Royal Institution of Great Britain from Proc. Roy. Instn. 37 (1959) p.385.

3.2 But is it the structure of a liquid?

This can really only be confirmed by demonstrating that the structure is the same as that reported by a diffraction experiment. Or alternatively that the model structure gives the same diffraction pattern as is observed from a liquid. In this situation, the latter is the easier approach as light can be used to obtain the diffraction pattern of an appropriately scaled projection of the laboratory-constructed model. This experiment was indeed carried out on a Lipson optical diffractometer at the Medical Research Laboratory at Mill Hill – and the picture obtained was ‘of the same kind as those given by liquids’ [4]. Though this may have been only a qualitative demonstration, it did indeed suggest to him that he was on the right track.

This conclusion was backed up by a further attempt to build a random model for which the radial distribution function could be calculated, but this time on the computer in a calculation carried out by his son Mike Bernal. This time the method of construction differed from that used in ‘crazy fishing’ – though later work using that approach does successfully result in the random close packed structure (see for example [26]). The coordinates of points were chosen at random, keeping all of them that were not less than a certain distance from the points already chosen [4]. As Bernal noted [2], this method was inefficient in that towards the end of the process, many hundreds of points had to be chosen before one could be accepted. Although this was clearly a random model, it was not a close packed one. Nevertheless, its radial distribution function (Figure 8) has the features of that of a real liquid.

Figure 8 The radial distribution function of Bernal’s computer-constructed random hard sphere model, together with that of the subsequently ‘squeezed’ densified model, compared to that of liquid lead. Reprinted by permission from Macmillan Publishers Ltd.: Nature 185 (1960) 68, copyright 1960.

The solid line in the figure is the radial distribution function from what is called a ‘squeezed random model’. This refers to a densification of the computer model, but not one densified by using the computer (for which the computer power at the time was inadequate). Instead he returned to model-building, taking the machine coordinates of the above computer-generated model and ‘by a process of manipulation [I was able to] reduce most, but by no means all, of the distances between neighbouring points to approximately identical minimum values’ [27]. The agreement of the density of this denser model (estimated as 0.61, only about 0.02 less than what is now considered the maximum random packing density) with experiment is very encouraging (the very high first peak is an expected consequence of the hard spheres so should not be seen as a serious discrepancy). Particularly interesting is the splitting of the second peak – a feature later found to be characteristic of random close packing (see below).

3.3 The concept of the ideal structure of a liquid

The ‘bond-equalised model’ of the previous paragraph led Bernal to the concept of an ideal structure of a liquid – ideal in that all the distances between nearest neighbours are equal, an ideal that corresponds to ideal structures in crystallography. Just as in the crystalline case where actual structures differ in detail from ideal ones, no actual liquid structure would be an ideal one but would be close to it.

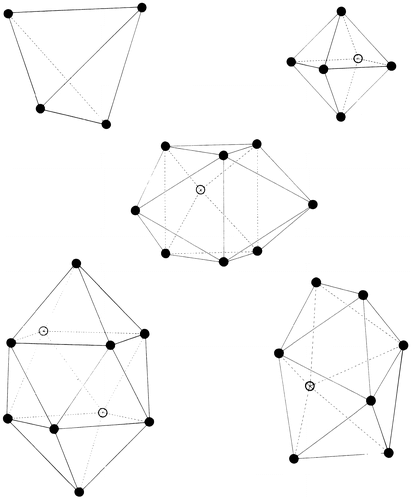
This ideal structure could be characterized as an assembly of the five basic polyhedra that Bernal identified by inspection of this bond-equalized model. Shown in Figure 9, these are the familiar tetrahedron and (half)octahedron found frequently in crystals, together with the trigonal prism, Archimedean antiprism and tetragonal dodecahedron. These polyhedra can be envisaged as packed together through the sharing of triangular or square faces in an unlimited number of ways. In fact, using a number of polyhedra of these types made from extensible plastic foam (which allowed for small differences of the order of 5% in edge lengths), one of his assistants (Wilkinson) explored how they could fit together, establishing that it was possible to fit these together in at least 197 different ways around a given point [2]. However, without the relaxation of the constraint of equality of near-neighbour distances (a relaxation that was accomplished in Wilkinson’s experiments by the flexibility of the foam), this packing cannot fill space. Moreover, the introduction of the three less-frequently occurring polyhedra (trigonal prism, Archimedean antiprism and tetragonal dodecahedron) prevents any long-range order and therefore permits fluidity, with the proportion of these larger polyhedra determining the volume at a given temperature and perhaps opening up a way of estimating entropy. Additionally, the possible clustering of locally low-density tetrahedral units in ‘Boerdijk spiral’ [28] arrangements that are incompatible with a crystalline structure was pointed out as a possible explanation of supercooling.

Figure 9 The five ‘canonical holes’ identified by Bernal in random sphere packings.

4 The geometry of random close packing

The path described above may seem rather tortuous. Trying to get to grips with ‘the difficulty of describing irregularity’ [4] Bernal had approached the problem from a number of different directions, eventually coming to a point at which there was encouraging semi-quantitative agreement between realizations of the conceptual model and measured properties of real simple liquids. Examination of various geometrical characteristics of these models had produced some possible ways of describing irregularity. To progress further, however, the model had to become more quantitative. ‘In the end I fell back on the study of a model of a large number of ball-bearings’ [2]. This is perhaps where the random close packing story really takes off.

4.1 Bernal’s first steel ball random packing

Bernal’s first real random packing hard sphere models were obtained by in essence replacing the plasticene spheres of the earlier ‘Hales-type’ experiment by about 1000–5000 ¼″ ball bearings, shaking down and compressing the assembly by winding it round with thick rubber bands [16]. The mass was fixed by soaking with black paint, which was, after draining of the excess liquid, allowed to dry. The object here was again focused on trying to get a handle on the local coordinations of the spheres. However, having noted that his idea of an idealized liquid structure built up of the five ‘canonical polyhedra’ revealed in his earlier work (Section 3.3 above) required a relaxation of the condition of equality of near-neighbours, he required information not only on actual contacts, but also near contacts. As illustrated in Figure 10, an actual contact would be indicated by a ring of dried paint, while near contacts would be marked by dots. Preliminary work had established that this method would record near contacts up to a radius of 5% greater than the sphere diameter.

Figure 10 The ‘paint’ method of marking (left) close and (right) near contacts between spheres. Reprinted by permission from Macmillan Publishers Ltd.: Nature 188 (1960) 910, copyright 1960.

Unwrapping the mass after the paint had dried revealed structures ‘with an appearance like caviare’ (Figure 11). Taking samples from the centre of the mass to try to avoid surface effects (the outer smooth surface would induce a certain degree of regularity that would penetrate some way into the mass), many of the structural features observed in earlier work were observed – for example the ‘pseudonuclei’ Boerdijk spiral arrangements of face-sharing tetrahedra. What this experiment primarily established, however, was

… one further clue of great importance, namely, that the numbers of contacts were arranged in some definite statistical order, that is, the number of balls having five, six, seven, etc. up to eleven contacts formed a determinate curve and was absolutely distinct from the regular arrangement, where every ball must have twelve contacts. It was evident that this variation of contact numbers or co-ordination was one of the most significant features, possibly the most significant feature of the irregular liquid arrangement.

Figure 11 Part of a random packing of steel balls taken from a paint-fixed model.

For his densest packing (estimated at 0.62 – a little less than the recognized close packed density of 0.637), he obtained an average near-neighbour coordination of 8.5, 6.4 of these being close contacts [16]. The corresponding figures for a looser packing of density around 0.6 (which he observed contained a number of ‘large holes’) were, respectively, 7.1 and 5.5, with the coordinations of some balls – many of them facing one of these holes – being highly unsymmetrical.

In discussing these results [16], he argued that he would expect each sphere to be in contact with at least four others, this being a necessary condition of stability, and at the most twelve. This absolute upper limit (that found in crystalline close packing) he saw as extremely improbable. He also was perhaps the first to argue here that the most probable average would be six, with each sphere in general resting on three others and in turn support another three.

Also on the basis of these results, he made some early comparisons with the actual properties of liquid argon, assuming the random close packing structure was a good model of the structure of the liquid at the melting point. The agreement of the increase in volume on melting has already been commented on above (Section 2.2). He was also able to argue from these results that the latent heat of melting of argon should be between a quarter and a sixth of the energy of evaporation as against the observed value of 1/5.5. Considering also random loose packing in terms of a higher temperature liquid, he also suggested a change in configurational energy between the melting and critical points within about 12% of the observed value. Semi-quantitatively, the model continued to look promising.

4.2 Seeing through caviare: the first expanded hard-sphere model

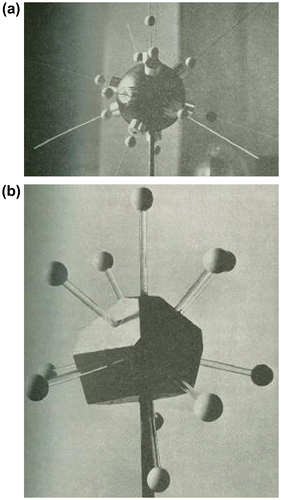
Models of crystallographic structures can be made in several ways. These can be represented as regular packings of (generally more than on sized) spheres, or as ball-and-spoke models that allow viewing of the structure internally. Bernal argued in a parallel way that in order to study the random packing arrangements adequately, it was necessary to be able to see through the model. Accordingly, a milling machine was rigged up as a triaxial measuring machine and was used to measure the coordinates of about 1000 of the balls at the centre of one of the paint-fixed ‘caviare’ models [16]. This first expanded ball-and-spoke model is shown in Figure 12.

Figure 12 (colour online) The first expanded ball-and-spoke model built using the sphere coordinates measured from a paint-fixed random packing of steel spheres.

Examination of this model confirmed the earlier conclusions that in terms of the links between near neighbours (the spokes connecting neighbouring balls), a random sphere packing could be seen as a packing of five different kinds of polyhedra (see Section 3.3 and Figure 9). It also enabled an enumeration of the percentages of occurrence of the five polyhedra, with the tetrahedron and half octahedron dominating (together making up some 75% of the volume, with the tetrahedral holes themselves making up nearly three-quarters of the polyhedra by number). Again, he argued that as temperature increases, the proportion of the larger polyhedra would increase suggesting a volume expansion of some 17% could be accommodated before other ‘icosahedral and larger’ holes would be needed. Such a model of volume expansion would be consistent with evidence from X-ray diffraction of real simple liquids which showed about the same mean distance between neighbouring molecules as temperature increased, but a reduction in the coordination number.

This expanded model also underlined the existence of long strings of molecules in more or less straight lines – ‘collineations’ (see Figure 13). While at first sight this might seem counter-intuitive for a model that is referred to as random, it is in fact a natural consequence of the symmetry of the fairly high coordinations about each point; Bernal’s analysis [16] suggested the length of such straight lines could range up to about eight spheres, though averaging at four.

Figure 13 Looking down part of a collineation in an expanded ball and spoke model.

4.3 The Canadian connection: David Scott and the upper density limit

In the early 1960s, David Scott in Toronto (perhaps interestingly the same university where Westman and Hugill constructed their random packings in the 1930s [14]) had also begun to build random packings of hard spheres. At the beginning of his 1960 paper [29], he commented:

J. D. Bernal has directed attention to the importance of geometrical models to represent the structure of liquids. A random packing of equal spheres may provide a useful model for an ideally simple liquid. One of the basic parameters related to an array of spheres is the packing density.

Noting that earlier work of both Westman and Hugill [14] and Rice [15] was not meant to be precise and was probably perturbed by surface effects, he set about building large models that were not perturbed by small amounts of ordering from the presence of the containing vessel wall, and using such models to correct the measured packing density for such peripheral effects as were present. The former was achieved by using dimpled glass flasks and copper cylinders while the correction for remaining surface effects was achieved by extrapolating density measurements made on different sized containers to infinite volume. Consequently, he concluded an upper density limit of 0.637 for random close packing and a lower stability limit (‘random loose packing’) of 0.601.

4.4 Coordinate measurements and the radial distribution function: the model works!

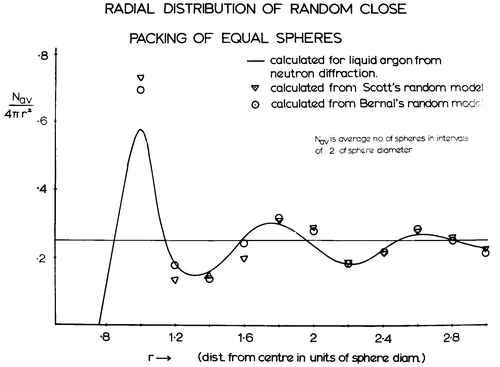
Two years later, Scott took his work further by also measuring the coordinates of the spheres in a random packed structure of spheres, using paraffin wax rather than paint to fix the sphere assembly and a modified optical comparator to measure the coordinates [30]. Bernal and Scott were in contact over this work and exchanged data between them (in fact, the expanded model of a random packed structure in the Science Museum was one constructed from Scott’s coordinates [31]). Both sets of data were used to calculate the radial distribution function, the comparisons with experimental results from neutron scattering for liquid argon being shown in Figure 14. The agreement between the two models and with the experimental data was more than encouraging. In Bernal’s words [2]:

His [Scott’s] measurements and ours … [show] that within the limits of the method the results are identical. Both radial distribution functions correspond within the limits of experiment, with that found for ideal liquids by X-ray scattering methods.

Figure 14 The experimental radial distribution function of liquid argon compared with those predicted from both the random packing models of Scott and Bernal.

And he continued with a strong statement that perhaps summed up his view that the idea was now experimentally verified:

We may therefore say that the first question of what is a structure of a liquid, at least of a simple liquid, has effectively been solved. The hypothesis of homogeneous, coherent and essentially irregular assemblages has been justified. We cannot consider this an absolute proof, but at any rate it cannot be disproved on the basis of the scattering results alone. As will be seen, it fits in very well with other results of the properties of liquids.

Perhaps we should also add that his conviction that the structure was determined essentially by repulsive forces that determined packing constraints on the constituent molecules (the property of ‘impenetrability’ as he was fond of quoting from Alice through the looking glass) was also backed up by these results. It was also a model that fitted his requirement to satisfy Ockham’s razor – not to multiply entities beyond necessity.

With respect to Bernal’s reference to other properties of liquids, we have already commented above on a number of these, such as the volume change on melting, the latent heat of melting and the change in configurational energy in going from melting to the critical point. Now that actual coordinate data were available, it became possible to make more quantitative comparisons with experiment, including attempting to take account of the softness of the intermolecular potential functions between ‘real’ atoms. This was later done with respect to heats of fusion of inert gases by superimposing Lennard-Jones potentials for neon, argon, krypton and xenon onto the innermost spheres of the Scott random close packed model, resulting in encouragingly good results for both the heats of fusion and volume changes on melting at pressures up to 6000 atmospheres pressure 3233. These and other calculations were, however, limited by (a) the sizes of the available models, (b) the accuracy of the coordinate measurements (∼ ±1% for the Scott measurements) and (c) the limitations of the structural characterization methods used. Both these issues were then tackled by the construction of a much larger model and the development of a much more sensitive structural characterization.

5 The large random packing model and its Voronoi analysis

5.1 Model construction and measurement

A large random sphere packing was constructed from around 17,000 ¼″ diameter steel balls using a refinement of the approach taken with the models fixed with black paint. The balloon in which the packing was confined was surrounded by two hemispherical surfaces which had been covered in steel spheres of a range of sizes (Figure 15(a)). After extensive kneading of the mass, which was tightly confined by about 50 m of rubber strip (Figure 15(b)), the assembly was heated to around 70 °C by hot compressed air and a liquid microcrystalline wax poured into the sample to fix the sphere positions. After cooling and unwrapping, spheres were removed from the top and bottom of the approximately spherical mass so that its height (about 11.5 cm) could be accommodated on the measuring machine, which was essentially a toolmaker’s microscope fitted with two perpendicular movements in the horizontal plane and a further vertical movement of the microscope itself 3134. The mass was then pressed into a 15 cm² 2.5 cm deep tray containing wet stone plaster which was allowed to set firm. Figure 15(c) shows the sample in position near the end of the measurements while Figure 15(d) shows a section of the packing in close-up.

Figure 15 Building and measuring the large hard sphere model. (a) One of the two hemispherical surfaces used to suppress any crystallization at the surface; (b) the sample after binding with rubber strip; (c) the converted toolmaker’s microscope used to measure the sphere coordinates with the sample towards the end of the measurements; (d) a close-up of an exposed plane of the model.

After cleaning with an appropriate (heated) solvent (2,2,4-trimethyl pentane), the coordinates of each sphere were located by coincidence of a pair of images of a triangular graticule reflected from each sphere surface through a double-image ocular. The coordinates were read via digitizers attached to the three leads screws that facilitated movement of both the tray (x and y) and the microscope (z). Preliminary tests of the mechanics and optical system established the precision of the overall system. The standard error for each sphere position was 0.2% of a sphere diameter 3134.

The final model contained 7934 spheres.

5.2 Model analysis

This ‘final’ random close packed model was important for both its size and the accuracy with which the constituent sphere coordinates were measured. The most important conclusions drawn from the model were [35] (a) its density, (b) its radial distribution function and (c) its statistical structure as described by its constituent Voronoi polyhedra: this is the polyhedron defined about a point by the bisecting planes of lines connecting that point with its neighbours, and, by its very definition, contains all points closer to the central point than any other. An assembly of Voronoi polyhedra fills space. They are essentially the polyhedra obtained from the plasticene ball compression described in Section 3.1.3.

Taking each of these quantities in turn, the density (calculated as the average occupied volume of the equivalent assembly of Voronoi polyhedra) came out to be 0.6366 ± 0.0004. This is essentially the same as obtained by Scott’s 1960 value of 0.637 (see Section 4.3 above), and is also supported by a later measurement of 0.6366 ± 0.0008 by Scott and Kilgour [36]. Although at the time it was difficult to assert with real confidence that this value is the real upper limit, later work using advanced computer construction techniques have come up with the same value [37]. Its closeness to Buffon’s constant 2/π (0.636620) – a figure of relevance to one of the oldest problems in geometrical probability (the probability that a dropped needle intersects one of a set of parallel lines separated by the needle’s length) – is particularly tantalizing.

Secondly, the radial distribution function (Figure 16) shows a new feature not visible in the earlier models (though perhaps presaged by Bernal’s squeezed computer-built model – see Figure 8 and the end of Section 3.2 above) – a clearly split second peak. Remembering the description of random packing in terms of an assembly of five polyhedral types, of which the tetrahedron and half octahedron are the dominant ones, this comes as no surprise. The peak at 1.99 diameters can be taken as reflecting the existence of collineations (with the steep drop-off above this value consistent with this interpretation), while the peak close to 1.73 could be explained in terms of two coplanar tetrahedral bases. That this split second peak is not observed in real liquids could be put down to its being washed out by the soft potential in real liquids – a point verified by later studies mentioned below. Though – also as mentioned later – it is retained in other disordered real systems where the soft potential is less relevant.

Figure 16 The radial distribution function of the large model at two different resolutions. First published in [35].

Thirdly, the random packing could be characterized in terms of the topology of the constituent Voronoi polyhedra. Several characteristics can be envisaged, including average and distribution of number of faces per polyhedron (giving a natural definition of ‘geometrical’ neighbours), average and distribution of edges per face, and distribution of actual polyhedron types in terms of the numbers of faces of n sides – [F₃, F₄, F₅, F₆, F₇, …]. Taking note of the topological condition on a three-dimensional polyhedral network

and noting that the number of seven-edged faces and above found in the array is small [35], this suggest to a good approximation that considering polyhedral types in terms of just [F₃, F₄, F₅] is a realistic simplification.

The values and distributions of these various polyhedral statistics (478 different types were found among the 5500 polyhedra elucidated in the model) demonstrate a difficulty in using this detailed characterization as a description of random close packing, though it was found of considerable use in comparing different assemblies [38]. Within the limited statistics of the smaller model, the various quantities – topological as well quantitative – for the Scott model were similar to those of the large model [35], arguing that the two models were indeed essentially (statistically) the same structure.

5.3 How good is random packing as a model of liquid structure?

We have mentioned above a number of comparisons of properties of liquids derived from the realizations of random close packing of spheres. The Voronoi analysis opens up further possibilities.

For example, attempts were made to estimate the configurational entropy of a random close packed structure, using a definition of a polyhedron type to define a state i. If the fraction of polyhedra of type i is f_i, then the configurational entropy is simply –RΣ_if_ilnf_i. Using the number of nearest neighbours as the state criterion, Everett estimated [39] a value which came out to be about 80% of the experimental value for liquid argon. Using geometrical neighbours as defined by the Voronoi construction gave a value only 3% lower than the experimental value. Coincidental, perhaps, but interesting.

By the time the large model had been built and structurally characterized, computer simulation of simple liquids had become possible. It therefore became feasible to examine the detailed structure of a simulated liquid using the tools discussed above and compare it with that of random close packing to see how well the latter stands up as an ideal model of a simple liquid. This was attempted using simulations of liquid and crystalline argon, with the liquid just above its melting temperature. In order to explore how the hardness of the hard sphere potential might affect the detailed structure, in addition to simulating argon with a standard 12:6 Lennard-Jones potential, Monte Carlo calculations were also made with potentials with harder repulsive cores, namely 25:6, 40:6 and 75:6 [40].

Taking as an example the distribution of Voronoi edges per face, there are clear differences between the distribution for the crystal and that of the liquid (Figure 17). Moreover, the simulated liquid distribution is similar to that for the random packing, though the latter is slightly sharper. That the structure is essentially similar is further strengthened by the sharpening up of this distribution as the potential function is hardened. Also of note is the average number of edges per face which jumps discontinuously from 5.148(5) to 5.170(6) from the crystal to the liquid at the melting temperature, underlining the discontinuity in structure on melting. A discontinuity is also found in the average number of faces per polyhedron which jumps from 14.10(2) to 14.46(2) as the crystal melts.

Figure 17 The distribution of edges per face of the Voronoi polyhedra elucidated from Monte Carlo simulations of crystalline argon at three temperatures up to the melting point, of liquid argon just above the melting point, together with that of the random hard sphere packing and two Monte Carlo simulations of the liquid using ‘hardened’ potentials. First published in [40].

The difference in structure between crystal and liquid is also clear from the radial distribution plots in Figure 18. As the temperature of the crystal rises, the peaks relating to the main intermolecular distances broaden as expected but remain identifiable right up to the melting temperature. They collapse as the crystal melts, with the second and third peaks of the crystal function being replaced by the second broad peak of the liquid. As the potential is hardened, we begin to see the second peak beginning to split, as is found in the hard sphere packing. Thus this split second peak does indeed appear to be a consequence of the hardness of the potential.

Figure 18 The radial distribution functions of Monte Carlo simulations of crystalline and liquid argon, of the liquid using ‘hardened’ potentials, together with that of the random hard sphere packing. First published in [40].

5.4 Random packing and other systems

Bernal died in 1971, the date at which the above discussion essentially closes. However, work on random packings was taken up by others in the years that followed. A particular engine driving this subsequent work was the increasing computer power which enabled exploration of different construction techniques and the examination of possible influences – e.g. gravity – on the structures of random packings. To mention just a few of the early attempts, one of the earliest to explore the sequential deposition of spheres was Bennett [41] who although unable to construct a packing of the maximum density obtained radial distributions similar to those of the large steel ball model. Mason [42] and Finney [26] independently implemented the hard-sphere-gas compression procedure that Bernal had used earlier (see Section 3.2), obtaining again radial distribution functions that were consistent with those obtained from the large laboratory model. These methods were, however, restricted at that time to building finite clusters with free boundaries, structures which could not be considered as fully space-filling assemblies. Perhaps the first computer simulation that successfully produced a pseudo-infinite packing of maximum density (i.e. with periodic boundaries) was the molecular dynamics calculation of Woodcock [37].

Furthermore, the core concept underlying his use of random packing as a liquid model has proved fruitful in many other areas, as have the various analysis techniques used in characterizing non-regular structures. Some of these later developments are discussed in several of the papers in this special issue. Others that might be noted include:

• A model structure for metallic glasses. Here, the split second peak of the radial distribution function (Figure 16) was to prove a key point – the metallic glasses appeared to be real systems in which this splitting was not washed out by thermal fluctuations. Following a presentation of the detailed structural data from the large model by one of Bernal’s team (me!) at the International Union of Crystallography Congress in 1969, Cargill, who was working with David Turnbull on metallic glasses and who had observed this split peak experimentally, published a direct comparison of the experimental data with the model radial distribution function [43].

• It was increasingly realized that many other structures could be considered as primarily determined by packing constraints, perhaps one of the most complex being the atoms in protein molecules. Though complicated further by specific attractive interactions (charged and hydrogen bonded), these molecules were seen to be locally densely packed structures 4445.

• Packed beds are used widely in a number of industrial and laboratory processes and knowledge of their structures is a way of understanding their action and potentially improving their efficacy. Examples here include exchange columns [46], the (now discontinued) pebble bed nuclear reactor [47] and chromatographic separation columns [48]. The coordinates of the large random packing also appear to have been used in aiding commercial oil extraction. They are also still requested from time-to-time by researchers concerned with both fundamental understanding of the structure as well as a range of other possible applications.

The Voronoi subdivision has also been exploited in a wide range of problems where the distribution of space allocation is of interest. Examples include the distribution of galaxies [49], nucleation and growth of crystal nuclei from the liquid [50] and the structure of the liquid–crystal interface [51]. The generalization of the Voronoi tessellation that handles multisized spheres more realistically – the radical plane construction [52] – has been used in exploring the local structures of, for example, multicomponent glasses [53] and proteins [54].

Other ways of describing non-regular packed structures have also been developed for particular purposes. For example, the interstices and their connectivity have been used in studies of flow through packed beds [48], work which interestingly also showed that softening the potential resulted in a significant reduction in the population of the three larger polyhedral holes identified by Bernal (see Section 3.3 above). This work suggested that a random packing of soft spheres could indeed be considered as a packing largely of tetrahedra and octahedra, and tetrahedron–tetrahedron, octahedron–octahedron and tetrahedron–octahedron correlation functions used 5556 to throw a different light on the structures of the packings and the local environments of the spheres (interestingly showing the relative paucity of pseudo-regular local structures such as the icosahedron, backing up the conclusion drawn earlier from looking at Voronoi polyhedra statistics [38]). Other work 5758 has explored the structure of random packings in terms of Dirichlet polyhedra – essentially the dual of the Voronoi polyhedra. Theoretical work has elucidated the statistics of self-avoiding walks and closed loops in random close packings [59]. This interestingly concluded that the irregularity did not significantly affect the results obtained from equivalently coordinated defective crystalline systems, confirming that the critical exponents that arise in the self-avoiding walk problem depends on dimensionality rather than structural regularity.

6 Summary

The comparisons and calculations discussed above form an assembly of data that demonstrates not only the essential validity of Bernal’s ideal model of a simple liquid, but also the fruitfulness of the concept itself and the ways of characterizing random packings in a range of other scientific areas and technological applications. His general hypothesis of the liquid as a homogeneous, coherent and essentially irregular assemblage of molecules does seem to be essentially correct. Interestingly, the path he took to getting to this demonstration was long and apparently tortuous, focusing initially on the variability of coordination rather than the detailed nature of the extended disordered structure that is the physical realization of his general hypothesis. We may still be a long way from having an ability to deal with random packing analytically – we still have not managed to develop the statistical geometry that Bernal argued was needed. But with the advent of computer simulations, the old ideas of liquids as disordered crystals have been completely invalidated. Interesting that it was a crystallographer who was concerned to develop an inherently non-crystalline model of a liquid.

Speaking in 1958 at The Royal Institution, Bernal accepted that although these ideas – in essence relating a crystal to a regular pile of atoms and a liquid to an irregular heap – may [4]

… be crude as well as very old-fashioned, they give a reasonable picture of why liquids exist and why they have the properties they have. I apologise to the modern theoretical physicists for introducing such a simple way of looking at things but I believe on the whole that it is better to start with a model which has some semblance to reality …

… Thermodynamic experts demand, with justification, that I calculate from first principles the properties such as partition functions, pressures, melting and critical points before any theory of mine will have any chance of acceptance. The fact that on existing theory these constants come out all wrong is to their minds preferable to not being able to calculate them at all.

Perhaps, it was his frustration with the inability of early versions of the complex theoretical ‘first principles’ approaches summarized in Section 1 to deliver the goods (‘intractability’ of the theories, according to Norman Cusack [60], another major figure of twentieth century liquid physics) that incited Bernal to cut through what he might have seen as a Gordian knot by developing his conceptually very simple random packing picture.

Things have changed since 1958. As John Ziman, one of the great theoretical physicists of the second half of the twentieth century, who did major work on liquid metals, puts it [61]:

This simple idea … is now seen to be the key to any qualitative or quantitative understanding of the physics of liquids.

Similar comments were made in 1970 by John Rowlinson [62], one of the foremost theoretical chemists who has spent a lifetime working on liquids:

It has therefore been hard to admit that the form or even the existence of the attractive forces has little direct effect on the structure of a liquid, as described, for example, by the pair distribution function g(r). The recent realization of this truth has followed the extensive studies … of the properties of assemblies of hard spheres without attractive forces.

A random packing of hard spheres may indeed be a simple way of looking at a complex system like a liquid. But it seems to work.

Acknowledgements

Bernal’s laboratory work was made possible by the imagination and expertise of the members of the liquids team that Bernal assembled over a period of perhaps three decades. In alphabetical order these unsung heroes include G. Atkinson, I.A. Cherry, S. King, K.R. Knight, K.P.N. Kutty, J. Mason and J. Wilkinson. I am also much indebted to the late John Ziman for discussions and inspiration – not all of which had to do with liquid state physics.