Continuous description of a grain boundary in forsterite from atomic scale simulations: the role of disclinations

Abstract

We present continuous modelling at inter-atomic scale of a high-angle symmetric tilt boundary in forsterite. The model is grounded in periodic arrays of dislocation and disclination dipoles built on information gathered from discrete atomistic configurations generated by molecular dynamics simulations. The displacement, distortion (strain and rotation), curvature, dislocation and disclination density fields are determined in the boundary area using finite difference and interpolation techniques between atomic sites. The distortion fields of the O, Si and Mg sub-lattices are detailed to compare their roles in the accommodation of lattice incompatibility along the boundary. It is shown that the strain and curvature fields associated with the dislocation and disclination fields in the ‘skeleton’ O and Si sub-lattices accommodate the tilt incompatibility, whereas the elastic strain and rotation fields of the Mg sub-lattice are essentially compatible and induce stresses balancing the incompatibility stresses in the overall equilibrium.

Keywords:

• Grain boundary
• continuum mechanics
• atomistic simulation
• dislocation
• disclination
• forsterite

1. Introduction

Olivine, (Mg,Fe)₂SiO₄, the most abundant and weakest mineral in the earth’s upper mantle, has attracted intensive research work during the past decade owing to its considerable importance in mantle rheology [1–3]. In this literature, the mechanisms for olivine plasticity include shear by dislocation glide and transport of matter by diffusion, but since dislocation-mediated plasticity of olivine is challenged by a lack of independent slip systems, grain boundaries (GBs) are seen as potential providers of complementary mechanisms for creep [4–7].

Low-angle boundaries are rather well described by the classical Read-Shockley dislocation-based model [8]. In a recent experimental study of GBs in Mg₂SiO₄ (forsterite: the Mg-rich end member of olivine), Heinemann et al. [9] showed that the Read-Shockley model applies for misorientation angles up to ca. 20° in this silicate. For higher angles, dislocation cores overlap, invalidating this description. The atomic structure of high-angle GBs has been investigated in olivine using atomistic simulations, including first principles calculations based on density functional theory (DFT) and simulations with empirical potentials. For instance, Adjaoud et al. [10] used molecular dynamics (MD) simulations to explore the structure of forsterite tilt GBs with misorientation angles ranging from 9.6° to 60.8°. Their study suggests that the molecular modelling approach can be used as an efficient tool to predict the configuration and energy of forsterite GBs. Ghosh and Karki [11] simulated different types of tilt GBs with stepped and non-stepped surfaces in forsterite using DFT, and presented their detailed atomic and electronic structures. Using classical interaction potentials, Leeuw et al. [12] performed MD simulations to study the effect of proton-containing defects on the atomic structure and stability of a series of stepped high-angle tilt boundaries in forsterite. However, although atomistic models are useful in studying the material properties of GBs, they do not provide a direct insight into their mechanical properties, because the latter is derived from the stress and strain fields, and their relationships in the body, particularly in the GB area.

So far, GB descriptions in olivine were restricted to their structure, giving no link with their possible mechanical behaviour. Considering the need in olivine to identify active deformation mechanisms involving GBs, another approach was needed. Continuous modelling of the structure of GBs using smooth distortion (strain and rotation) fields at inter-atomic scale is attractive because it provides the basis for a mechanical description of the lattice defects. In such descriptions, matter is assumed to be able to transmit stresses and couple stresses, and work density is defined at this scale [13]. Further, attractiveness of continuous modelling of GB structure also derives from its ability to serve as a basis for coarse-grained representations of polycrystalline media [14]. Based on a continuous description of crystal defects, high-angle tilt boundaries have been modelled as periodic arrays of disclination dipoles [14–18]. For instance, disclination dipole arrays were found to decorate GBs in olivine samples, and it was shown that their shear-coupled migration could provide the missing mechanism for deforming olivine-rich rocks in the mantle [19]. However, properly defining the distortion field of the lattice at inter-atomic resolution length scale from the input provided by the discrete atomic structure of the GB is still a challenging task [20,21].

In order to do so, we proposed a continuous dislocation/disclination-based model for GBs built from the atomic structure of the relaxed and unrelaxed configurations [22]. To initiate the procedure, the discrete values of the transformation gradient tensor are calculated at each atomic position from finite difference approximations of , where the vectors and are the positions in the reference state and the deformed state, respectively. The reference configuration is chosen to be the low-energy relaxed structure and the current configuration is the initial un-relaxed configuration in the atomistic simulation. Then, the distortion tensor components in the GB area are calculated from the transformation gradient using the standard relationships of continuum mechanics (also shown in the Appendix 1). Since there is more than one atom in each atomic neighbourhood, averaging procedures are needed. Finally, linear interpolation is used to generate spatial field distributions between atoms. The method was applied to the 18.9° copper symmetrical tilt boundary to set a benchmark, and its accuracy was validated by comparison with recent similar techniques [20,21].

In the present work, we use the above method to build a continuous description of a high-angle 60.8° symmetric tilt GB in forsterite, as generated by atomic scale simulations. The continuous strain, rotation, curvature, dislocation and disclination fields are calculated in the GB area for the three O, Si and Mg sub-lattices of forsterite. The aim of the paper is to give a detailed description of the elastic structure of the tilt GB, by elucidating the respective mechanical roles of these sub-lattices in the accommodation of lattice incompatibility across the GB. The outline of the paper is as follows. In Section 2, details of the calculation techniques are described. In Section 3, the results on the strain, rotation, dislocation and disclination fields are presented. Discussions about the dislocation and disclination fields are detailed in Section 4, and a summary of the results and conclusions follow in Section 5.

2. Calculation techniques

2.1. Atomic scale modelling of GBs

The continuous description of the boundary is built by bottom-up processing. By this, we mean that the various tensors describing the deformation of the body from its low energy configuration, such as the transformation gradient and elastic strain tensors, are computed from incremental atomic displacements generated by atomistic simulations. The GB is a (0 1 1)/[1 0 0] tilt boundary of misorientation θ = 60.8°, which was recently modelled using atomistic simulations [10] and dipoles of wedge disclination densities [19].

The method for constructing the forsterite GB is described in detail in [10]. In a first step, a supercell of forsterite is rotated to align the (0 1 1) plane parallel to the GB plane. Then, the crystal is cut in the (0 1 1) plane and one grain is rotated by 180° around [0 1 1]. The cut is made such that SiO₄ tetrahedra remain as intact units, since cutting through the tetrahedra would lead to structures with higher GB energy [10]. To avoid close contact between atoms, the two grains are initially separated by 2 Å normal to the GB plane. Using periodic boundary conditions results in two distinct GBs in the simulation cell. In a next step, the two grains are translated with respect to each other parallel to the GB plane to identify low energy structures. Atomic interactions are described by an advanced polarizable and deformable ion potential [23]. For each translation, atomic positions are relaxed using the conjugate gradient method. Some of the low energy structures are then used as input structures for MD simulations at ambient pressure and a temperature of 100 K. Temperature and pressure are controlled by an anisotropic barostat coupled to a Nosé-Hoover thermostat [24]. After a few ps of MD simulation, the GB structures reach a relaxed stable state. The lowest energy structure is used as input for disclination modelling. The time step of MD simulations is chosen as 1 fs, and periodic boundary conditions are applied in all three directions. Visualisation is carried out using the Visual Molecular Dynamics (VMD) tool [25].

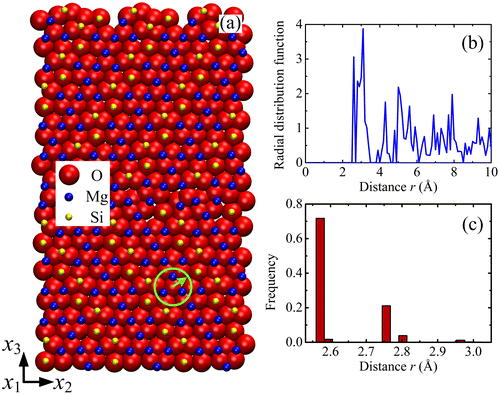
The relaxed configuration of forsterite GB with misorientation θ = 60.8° is shown in Figure 1(a). The structure of forsterite can be regarded as an hcp array of oxygen anions stacked along the [1 0 0] direction of an orthorhombic array of Mg cations, in which one-half of the available octahedral interstitial sites are occupied by Mg cations and one-eighth of the tetrahedral sites by Si cations [26]. It is characterised by strong distortions of the O hcp sub-lattice, which can be explained by the partial filling of the interstitial sites and electrostatic forces due to cation–cation repulsion.

Figure 1. (colour online) Cut-off distance in forsterite GB. (a) Configuration of forsterite GB with misorientation θ = 60.8°. Atom colours are: red for oxygen, blue for magnesium and yellow for silicon. Forsterite can be regarded as a close-packing of oxygen ions (close to hcp). Some empty tetrahedral sites are filled with Si⁴⁺, some octahedral sites are filled with Mg²⁺. (b) Radial distribution functions (RDF) of O sub-lattice. (c) Distribution of nearest distances for O-O pairs.

2.2. Linking atomic scale and continuum

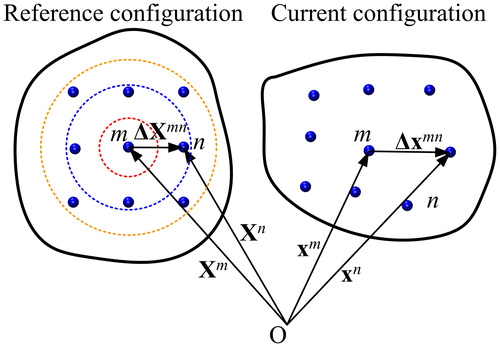
In continuum mechanics, calculation of the transformation gradient tensor requires information on the reference and current configurations. In the present work, the reference configuration is chosen to be the low-energy relaxed GB structure, and the current configuration is the initial un-relaxed configuration. If we use the vector X to denote the position of a point in a solid material with respect to a reference coordinate system and the vector x to represent the new position in the current configuration, the transformation gradient writes(1)

The transformation gradient field associated with the current and reference atomic configurations is calculated by the following method. As shown in Figure 2, an atom m is located at a position in the reference configuration. In the current configuration, this atom reaches its new position . The relative position of a neighbouring atom n with respect to atom m is(2)

Figure 2. (colour online) Transformation gradient associated with the motion of material particles from the reference state to the current state.

in the reference configuration and(3)

in the current configuration. Then, the components of the transformation gradient at atom m induced by the variation of the relative position of atom n are approximated by(4)

Because there may be more than one neighbouring atom near the atom m, the component of transformation gradient at the atom location is averaged over all neighbouring atoms n:(5)

where r_mn is the distance between atoms m and n in the reference configuration, is a cut-off distance used to verify whether an atom n is in the neighbourhood of atom m, and N is the total number of neighbouring atoms identified within the cut-off distance.

The cut-off distance should not be too large (sketched by the orange circle in Figure 2) otherwise the local value of the transformation gradient would be overly smoothed. Conversely, it should not be too small or there would be no surrounding atom (sketched by the red circle in Figure 2). Thus, an appropriate cut-off distance should cover and only cover the nearest neighbouring atoms (sketched by the blue circle in Figure 2). In the case of face-centred cubic (fcc), body-centred cubic (bcc) and hexagonal-close packed (hcp) lattices, the nearest neighbour distances are , and a, respectively, where a is the lattice parameter.

The lattice structure of the forsterite is more complicated than the simple fcc, bcc or hcp lattices. To determine the appropriate cut-off distance, the Radial distribution functions (RDF) and the distribution of nearest distances are calculated for the different sub-lattices. The RDF is a measure of the probability of finding a particle at a distance of r from a given reference particle. Figure 1(b) shows the RDF of the O sub-lattice. The first peak at r = 2.56 Å indicates the smallest distance with other O atoms, and the major peak shows that the highest probability to find a neighbouring O atom occurs at the distance r_p = 3.1 Å. Hence, the cut-off distance should not be smaller than r_p. In addition, Figure 1(c) shows the distribution of the smallest distance between O atoms, which ranges from 2.55 Å to r_m = 3.02 Å. The cut-off distance should not be smaller than r_m, otherwise some O atom surroundings would not contain other O atoms. Therefore, it is chosen as r_cut-off = max{r_p, r_m}. By using this method, the cut-off distances for the O, Mg and Si sub-lattices are found to be 3.1, 3.9 and 5.0 Å, respectively.

To avoid the singular behaviour in Equation (4(4) ) where becomes too small, an interior cut-off distance is used to filter out neighbouring atoms which are too close. In the following, we use such three-dimensional finite difference methods to calculate the components of the transformation gradient and all other derivatives. Using the equations set out in Ref [22] (see also the Appendix 1) and the similar finite difference/interpolation method, the elastic strain, rotation and curvature fields and the disclination and dislocation density fields can be calculated in turn in the boundary area. Once local values at atomic positions are gotten, all the atoms are projected onto plane , then two-dimensional linear interpolation is used to obtain spatial field distributions in between atoms.

3. Results

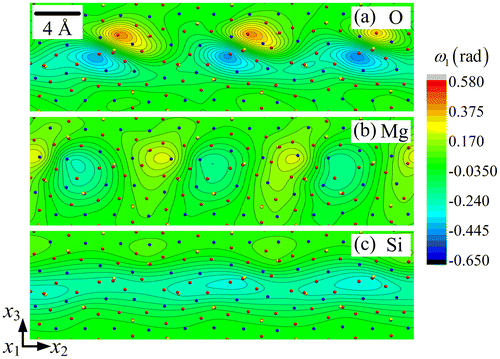
The strain fields E₂₂, E₃₃ and E₂₃ are shown in Figures 3–5, respectively, for each sub-lattice of the forsterite GB. A first striking feature is their periodicity in a narrow layer along the boundary, with alternating zones of tension-compression and shear, and their organisation into dipoles, particularly in the O and Si sub-lattices. Each of the Si sub-lattice strain fields is seen to follow closely its counterpart from the O sub-lattice, both in the distribution and extreme values, whereas the Mg sub-lattice field shows anti-phased distribution with respect to the other two sub-lattices. For example, the maximum values in the Mg sub-lattice field are found at locations where the corresponding field shows minimum values in the O/Si sub-lattices. This property is clearly in evidence in Figures 4 and 5 for the strain fields E₃₃ and E₂₃, while E₂₂ shows similar but less striking features. The slave/master relationship of the Si–O sub-lattice strain fields is indication of the mild deformations of Si–O tetrahedra, whereas deformation of the Mg sub-lattice is seen to be functionally different from the other two. The rotation fields ω₁ for the three sub-lattices are plotted in Figure 6. It is observed that ω₁ has relatively small values in the Mg and Si sub-lattices. The largest ω₁value is 0.650 radian (i.e. 37.3°) in the O sub-lattice. The ω₁ field displays a dipolar structure in this sub-lattice, similar to the shear strain structure seen in Figure 5.

Figure 3. (colour online) Close-up showing the strain field E₂₂ for (a) O, (b) Mg and (c) Si sub-lattice.

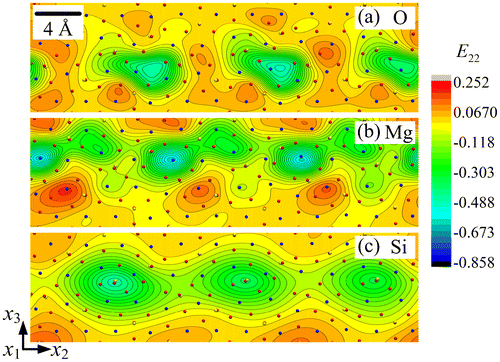
Figure 4. (colour online) Close-up showing the strain field E₃₃ for (a) O, (b) Mg and (c) Si sub-lattice.

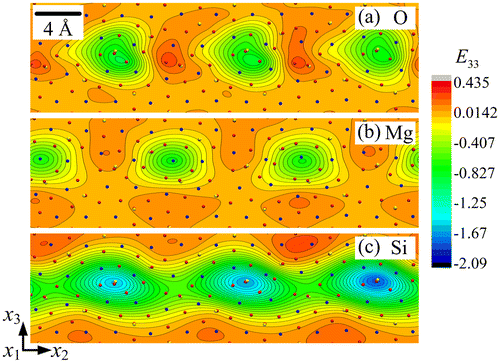
Figure 5. (colour online) Close-up showing the shear strain field E₂₃ for (a) O, (b) Mg and (c) Si sub-lattice.

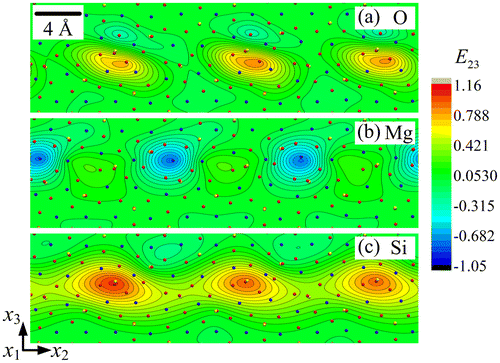
Figure 6. (colour online) Close-up showing the rotation field ω₁ for (a) O, (b) Mg and (c) Si sub-lattice.

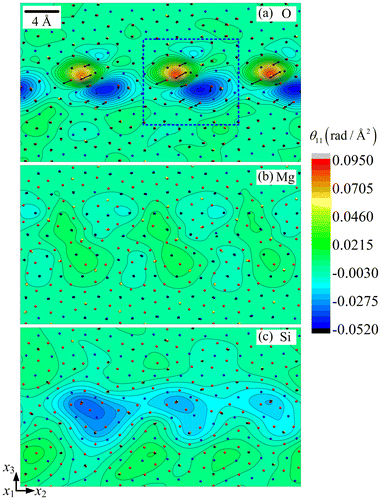
The disclination density θ₁₁ and dislocation densities (α₂₁, α₃₁) fields are displayed in Figure 7 for the three sub-lattices. The wedge disclination density θ₁₁ represents an elastic rotation discontinuity around the axis perpendicular to the figure and a defect line aligned with that same axis. The edge dislocation densities (α₂₁, α₃₁) render, respectively, horizontal and vertical Burgers vectors, for the same defect line direction perpendicular to the plane. In this figure, the disclination density is colour-coded and the dislocation densities are presented as the in-plane components of the Burgers vector field per unit surface (shown as arrows). The periodic dipolar arrangement of the disclinations in a thin 8 layer along the boundary is striking in the O sub-lattice, and is also present in the Si and Mg sub-lattices, but to a lesser degree. Note that the O and Si dipole arm lengths are both at angle with the symmetry line of the boundary. Similarly, the Burgers vectors are inclined with respect to the normal to the boundary. We checked that each disclination field is self-balanced, in the sense that its averaged value vanishes in the boundary layer. The θ₁₁ field in the Si sub-lattice is weaker than in the O sub-lattice by about one order of magnitude, but the dipolar arrangement follows rather closely that of the O sub-lattice (Figure 7(a) and (c)). It is even weaker and its arrangement is different in the Mg sub-lattice, where the dipole arm-lengths are nearly perpendicular to the symmetry line of the boundary, with each pole being halved in the two adjoining crystals. The intimate connections between the θ₁₁ density field in the O sub-lattice and the strain fields of the O and Si sub-lattices shown in Figures 3–5 are evidenced by a comparison of these figures with Figure 7(a). The dislocation density values (α₂₁, α₃₁) are smaller by an order of magnitude in the Si and Mg sub-lattices than in the O sub-lattice. Again, it can be seen that the dislocation distributions are confined to a thin 8 layer along the interface. The Burgers vector components relative to this dislocation distribution will be calculated and discussed in the next section, together with the relevant Frank vector components for the above disclination fields.

Figure 7. (colour online) Disclination density field θ₁₁ and Burgers vector fields for (a) O, (b) Mg and (c) Si sub-lattice. The arrows represent the local Burgers vector, whose components are the edge dislocation densities (α₂₁ and α₃₁) per unit surface.

4. Discussion

In this Section, we first compare the present results with the earlier approach [19], and then discuss the roles played by the O, Mg and Si sub-lattices and their dislocation–disclination fields in accommodating the rotational incompatibility associated with the investigated forsterite tilt boundary.

A disclination-based representation of the (0 1 1)/[1 0 0] tilt GB with misorientation 60.8° in forsterite has been previously built using a ‘top-down’ approach, where the disclination field was constructed from geometrical considerations on rotational incompatibility [19]. In this modelling scheme, the wedge disclination density spots were located on the vertices of the structural units, and the wedge disclinations were arranged in a zigzag configuration. The disclination density tensor component θ₁₁ ranged from –1.2 to 1.2 , with values two orders of magnitude larger than the present results. However, there is no pretence to uniqueness of this configuration, and there is no contradiction with the present results because the distribution of the disclination dipoles was much more localised within the structural units than in the present bottom-up approach starting from the atomic configuration. To verify the correctness of the present disclination and dislocation densities, the Frank and Burgers vector are now computed. The Frank vector is the angular closure defect obtained by integrating the incompatible elastic curvatures along a circuit C(6)

where S is the surface of unit normal delimited by C. In the present case, the Frank vector resulting from the distribution of the disclination density θ₁₁ over a surface S in the plane is(7)

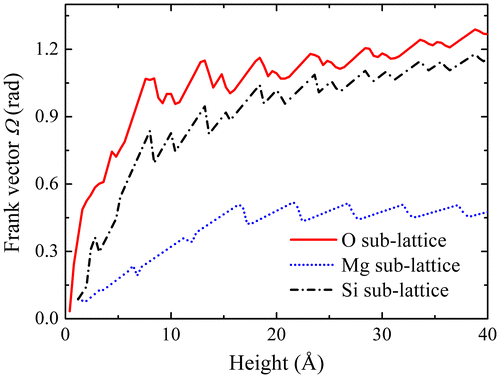
Clearly, the Frank vector has a dependence on the selection of circuit C. Consider the circuit delineated by the blue-dashed box in Figure 7. The length of the box in x₂ direction should correspond to the period of the lattice, but its height in the x₃ direction may be varied. The Frank vector components arising from the curvature field of the three sub-lattices can be obtained by performing the integration shown in Equation (7(1) ), and are plotted in Figure 8 as functions of the box height. They first increase but turn out to be relatively stable above 8 . For example, when the box height is 20 , the Frank vector component of the O sub-lattice is radian (i.e. 63.2°), close to the obtained in [19]. The components similarly obtained for the Mg and Si sub-lattices are 0.501 radian (i.e. 28.7°) and 1.047 radian (i.e. 59.6°), respectively. Note that, despite the smaller values of the disclination density field (see Figure 7), its more localised distribution is such that in the Si sub-lattice is roughly equal to the Frank vector component of the O sub-lattice. This result strongly suggests that the O and Si sub-lattices jointly account for the tilt angle across the boundary and accommodate the associated rotational incompatibility, with perhaps a slight residual misorientation for the Si sub-lattice, whereas the Mg sub-lattice has a different functionality. Since the overall Mg–Si–O lattice does satisfy the balance of momentum equations and periodic boundary conditions, whereas the Si–O sub-lattices primarily accommodate the rotational incompatibility arising from the crystal misorientation, we suggest that the Mg sub-lattice essentially contributes to complementary compatible elastic strain and curvature fields allowing fulfilment of the balance equations and satisfaction of the periodic boundary conditions.

Figure 8. (colour online) Values of Frank vectors as a function of the height of surface S.

In order to further verify this conjecture, let us compute the components of the Burgers vectors in the plane for the three sub-lattices. The Burgers vectors for a close circuit bounding a surface S is defined as:(8)

an expression involving both the dislocation and disclination density distributions. In the plane , Equation (8(A6) ) is(9)

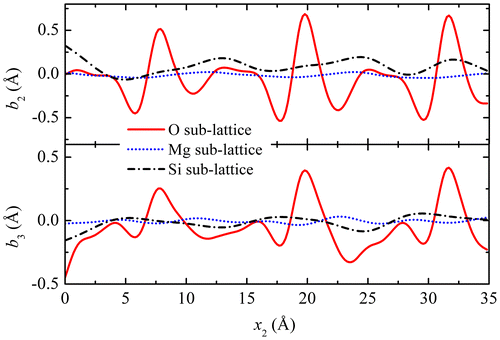
The Burgers vectors for the three sub-lattices were shown as arrows in Figure 7, and their components are displayed in Figure 9 as functions of the coordinates x₂, for x₃ = 0. It is seen that the main contribution to the Burgers vector arises from the O sub-lattice, with a secondary contribution coming from the Si sub-lattice, whereas the contribution of the Mg sub-lattice is much smaller. Integrated over a period along the boundary, both components b₂ and b₃ are positive in the O and Si sub-lattices, consistent with the inclination of the Burgers vectors shown in Figure 7(a), whereas they are close to zero in the Mg sub-lattice. Besides, the integrated b₃ normal component reaches about 1 nm, which is about what can be expected from a 60.8° tilt boundary in Frank’s relation.

Figure 9. (colour online) Components of the Burgers vectors in the plane for the three sub-lattices vs. coordinate x₂ along the boundary.

Hence, there is clear partition in the roles of the sub-lattices, in agreement with the above conjecture: the ‘skeleton’ O and Si sub-lattices and the incompatible strain and curvature fields associated with the dislocation and disclination fields in these sub-lattices are in charge of lattice incompatibility of the tilt boundary, whereas the Mg sub-lattice has an ‘accommodating’ role in the overall equilibrium by admitting complementary compatible elastic strain and rotation fields that offset the unbalanced incompatible strain and rotation fields.

5. Conclusion

The present paper presents a ‘bottom-up’ procedure to build a model for a tilt boundary in olivine as a periodic array of dislocations and disclinations dipoles, starting from the atomistic structure of the boundary. Applying the atomistic/continuum crossover technique [20] to the 60.8° forsterite tilt boundary provides new insights into the structure of the GB. It is shown on the basis of the dislocation and disclination fields found in the three O–Si–Mg sub-lattices and their contributions to the Frank and Burgers vectors, that the lattice incompatibility associated with the tilt angle is materialised by the incompatible distortion field of the O sub-lattice in the first place. The incompatible distortion field of the Si sub-lattice follows closely its O sub-lattice counterpart, as their Frank and Burgers vector components also suggest. The Mg sub-lattice behaves very differently from the other two sub-lattices. Its incompatible distortion field is very weak and is complemented by a compatible distortion field offsetting the unbalanced incompatible distortion of the O and Si fields, which allows fulfilling the balance of momentum and satisfying the periodic boundary conditions.

The present atomistic/continuum crossover techniques will be applied in forthcoming work to explore in details the structure of various boundaries in multi-element olivine, in terms of dislocation and disclination density fields. Beyond providing new insights into the structure and mechanical architecture of GBs, such field renditions of GBs at inter-atomic scale allow investigating GB mediated plasticity mechanisms in olivine, a material where dislocation glide lacks the independent slip systems needed to accommodate arbitrary loading paths [19]. Indeed, continuous renditions of GBs are not only able to account for essential features of GBs such as their structure and elastic energy but, introduced as part of the initial conditions in elasto-plastic continuum mechanics simulations, they can also be used as inputs to investigate the elasto-plastic properties of large-scale polycrystals [18].

Funding

This work was supported by funding from the European Research Council under the ERC [grant number 290424]; RheoMan and from the German Research Foundation (DFG) under [grant number HE2015/11-1].

Appendix 1.

The kinematics of the elasto-plastic incompatibility of crystal defects is briefly recalled in this section. Since compatible plastic processes are not envisioned in the present paper, the compatible measures of deformation involve only the elastic components.

A.1. Displacement gradient

A fixed Cartesian coordinate system is assumed to describe the changes in the shape, size and orientation of a simply connected continuous crystalline body containing defects. For each point, the Lagrange and Euler coordinates and label the positions of a material element in the reference and deformed state, respectively. is a function of , and the transformation gradient of is defined as the second-order tensor(A1)

The total displacement field describes the changes in position of matter. This field is assumed to be single valued and continuous, possibly between atoms and below inter-atomic distances, so matter is assumed to be able to transmit stresses and couple stresses at this scale. The displacement gradient, also referred to as the distortion tensor, is(A2)

where is the second order identity tensor and δ_ij is Kronecker delta(A3)

A.2. Strain, rotation and curvature tensors

Strain is a measure of the deformation of the body with respect to a reference configuration. In a small deformation approximation, the strain tensor is the symmetric part of the distortion ,(A4)

whereas the large-strain tensor , known as the Green-Lagrange strain tensor, is(A5)

If , the E_ij components reduce to the infinitesimal strain components, E_ij ≈ ε_ij.

The rotation tensor in a small displacement approximation is the skew-symmetric part of the distortion ,(A6)

and the associated rotation vector reads(A7)

where e_ijk is the alternating Levi-Civita tensor(A8)

The large-rotation vector is obtained by polar decomposition and then back-out transformation. From the polar decomposition theorem, can be written as , where is an orthogonal tensor representing a rotation, and is the right stretch tensor describing the deformations. The rotation matrix is obtained by the following three steps:

(1)	Calculate the right Cauchy-Green deformation tensor

(A9)

(2)	Compute the right stretch tensor . Firstly, transform the symmetric matrix to its principal orientation

(A10)

where the eigenvalues μ_i are associated with eigenvectors via(A11)

Secondly, take the square roots of the diagonal components μ_i and rotate back to the original orientation to get as(A12)

(3)	Multiply through by the inverse of to get the rotation matrix

(A13)

After the rotation matrix is obtained, a reverse transformation is performed to get the components of large-rotation vector [27](A14)

with . From the rotation vector , the curvature tensor can be defined as(A15)

A.3. Disclination and dislocation density tensors

In the absence of plasticity, the curvature tensor can be identified with its compatible elastic component . However, the elastic curvature tensor also comprises an incompatible part , which counter-balances the incompatible plastic curvature arising from the presence of crystal defects because continuity of the body is maintained. As a result, the elastic curvature tensor may not be curl-free, even if the total curvature tensor is compatible. This rotational incompatibility is conveniently described by the continuous disclination density tensor(A16)

deriving from the incompatible part of the elastic curvature. The same line of reasoning applies to the strain tensor, which results in defining Nye’s dislocation density tensor from the incompatible elastic strain field and curvature field through(A17)

In the finite strain assumption, the dislocation density tensor is obtained from the elastic transformation tensor through the relation(A18)