A review of hybrid renewable energies optimisation: design, methodologies, and criteria

ABSTRACT

Over the years, several achievements have been made in power generation and optimising hybrid renewable energy systems (HRES) to achieve nature conservation, achieve energy security, and reduce carbon emissions. However, there are many complexities in Renewable energy (RE) conversion, sizing, design, and implementation, that require optimisation techniques to achieve optimal results in terms of reliability, cost, and environmental protection over time. This paper presents an overview of research trends in Optimization methods in HRES which are classified into modern and conventional methods. These two classifications are further divided into control methods, Artificial intelligence, Iterative and mathematical operations. However, all mentioned techniques have inherent advantages and disadvantages which will be discussed in this survey. In addition, the review paper explored different types of research in computing intelligence (CI), an aspect of Artificial Intelligence (AI) that involves the development of nature-inspired algorithms for optimisation. Finally, general optimisation criteria, system sizing methods used in RES, Mathematical modelling of RES, and gaps for future work to achieve sustainability were also presented.

KEYWORDS:

• Optimization techniques
• hybrid renewable energy system (HRES)
• optimization criteria

1. Introduction

There has been a global upsurge in the amount of energy consumption due to the rapid increase in population, industrialisation, and transportation (IEA 2012). Besides, more than 80 percent of today’s world's energy supplies are from conventional energy resources (fossil fuel). Therefore, there is a need to deploy sustainable energy resources at the forefront of the global decarbonisation agenda due to their availability, equitable dissemination globally, minimal threat to the environment, and simplicity of onsite generation, in tackling the energy crisis (Paska, Biczel, and Kłos 2009). However, renewable energy is intermittent and depends on weather and climatic conditions. As a result, there is a need to combine two or more resources to form a hybrid system in which one strength complements the weakness of others to solve the problem of complexities in conversion, selection, design, and implementation. Optimisation of energy system components sizing is one of the critical challenges in RES developments in which cost, reliability, and environmental issues need to be considered to attain sustainability.

A good optimal hybrid system design should meet all the load requirements which should also lead to the minimisation of the overall system cost (Bhandari et al. 2014). Therefore, reducing emissions, overall system cost, excess electricity production, and unmet load are critically considered in sizing renewable energy components. Optimising renewable energy systems is a challenging task that requires of development of mathematical models for the components sizing and power management via appropriate techniques (Maleki and Rosen 2017) to address renewable energy intermittent challenges due to climate change and seasonal effects. Also, some of the challenges with these optimisation tools/techniques are premature convergence, poor efficiency, poor convergence speed/time, scalability issues, and poor accuracy, which can be overcome by parallelising /or hybridising two or more algorithms, adaptation/or modification of existing algorithm with specific parameter/or objectives (with difference dimension) on new benchmark function and application of multi-objective functions (Sharma and Kumar 2022). However, conventional, modern, or hybrid optimisation techniques can be deployed for optimal sizing and power management for successful HRES operations.

This review examines optimisation methodologies, modern computing tools in HRES optimisation, optimisation criteria factors considered for selecting HRES, combining diverse RE models along with their reliability measures, as well as the different software tools that are used with the modelling and optimisation of a functional HRES.

Furthermore, this paper has been able to bring into focus the different sections where challenges and loopholes exist in research processes as well as the regions where they exist. As a corrective protocol. It also suggests and discusses possible future patterns to be adopted in order to achieve an improved hybrid renewable energy system that is functional.

1.1. Objectives and methodology

To attain energy sustainability, balancing economics, technical, social, and environmental are necessary to raise the standard of living and reduce poverty. (Demirtas 2013). The principles guiding sustainability are carbon consumption reduction, biomimicry, critical natural preservation, cradle-cradle design, and energy security supply (Bishop, Amaratunga, and Rodriguez 2008; Li 2005) which can be obtained through the deployment of HRES. To ensure the impact of RE sources within the environmental limit; localisation, diversification (Lior 2010), and optimisation of energy resources as needed for system Reliability/sustainability.

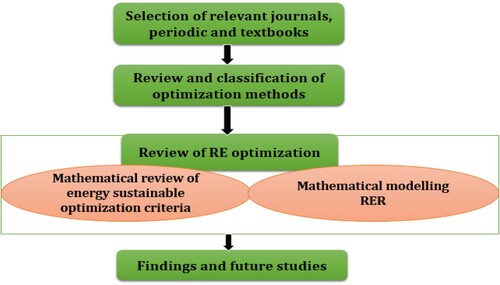
Literature was obtained from journals (mainly between the years 2010 to 2021 from google search/Elsevier database), periodic, and textbooks. Different methods and criteria were identified for HRES optimisation with their relevant merit and demerit. Economic, Environment, and Reliability criteria were spelled out with the mathematical design of Solar, Biomass, Hydropower, and Wind energy. A total number of Two hundred and nineteen relevant papers were reviewed with gaps for future studies. The summary of the method employed is shown in Figure 1.

Figure 1. Outline of the paper review.

2. The hybrid renewable energy system (HRES) optimization

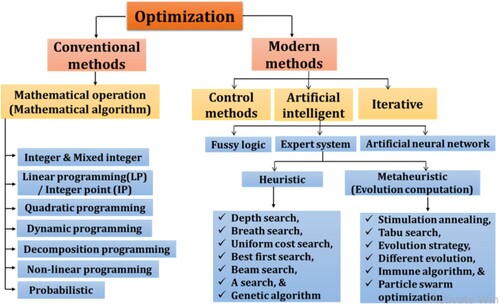
According to historical data, the first Hybrid power systems to be installed can be traced back to the year 1978 in – Papago, India, and Arizona in the United States of America (Bhandari et al. 2015). In recent times also, many green technologies or methods have been further developed and improved upon for extensive optimisation of HRES which gives better ways of obtaining the best result under given conditions (Rao 2009) to minimise undesirable costs, errors, and energy loss and maximise desirable events such as profit, efficiency, and reliability (Bansal 2005). Optimisation techniques are thereby classified into conventional and modern methods, as shown in Figure 2. Conventional optimisation methods are mathematically derived algorithms (i.e. differential Calculus), which are necessary for the development of the much-required optimum solution needed for a continuous differentiable functionality (Mahmoud and Hosseini 2016). Although this technique has a well-established theory and has been used for several renewable energy optimizations, it is characterised by long execution, convergence danger, and weak non-domination solution (Soliman and Mantawi 2010). Linear/ Interior point, Integer & Mixed-integer, Quadratic, Dynamic or Combinatorial, Decomposition, and Nonlinear are all examples of Conventional algorithms. Nonlinear optimisation techniques can be further classified into sequential quadratic programming (SQP), General Lagrangian method, Augmented Lagrangian method, Projected augmented Lagrangian, interior point method, and Successive linear programming (SLP) (Soliman and Mantawi 2010).

Figure 2. Classifications of optimisation techniques.

Modern optimisation methods are algorithms developed based on the behaviour and character of biological systems, neurobiological systems, molecular and the swarm of insects. Invariably, Artificial Intelligent (AI) algorithms can be classified as Expert Systems, Fuzzy, Artificial Neural Networks, and Hybrid algorithms. Furthermore, expert Systems can be sub-divided into Heuristic and Metaheuristic (Evolution Computation) (Gavrilas 2010; Lee and El-sharkawi 2008; Soliman and Mantawi 2010) as seen in Figure 2.

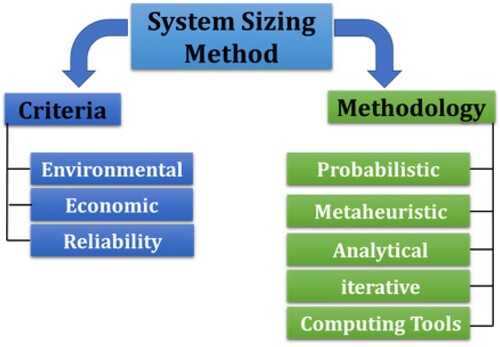
Amusat, Shearing, and Fraga (2016) identified two major methods of solving the renewable energy sizing problem based on the Literature. The first method is based on time-series data chronological simulation, while the second method is based on the probabilistic incorporated stochastic nature of renewable energy resources. Figure 3 shows the optimum sizing methodology and sizing criteria used for Renewable energy from the Literature.

Figure 3. Renewable energy system sizing methodology/optimum sizing criteria.

2.1. Optimum sizing methodology for renewable energy system

Referring to Figure 2, major methods employed in achieving optimal sizing of RE from literature are revealed in Figure 3.

2.2. Probabilistic method

Probability methods include the construction of an algorithm via random elements to improve system performance. It is, however, the most appropriate method that can be effectively adopted in finding the best solutions. A few performance indicators are used in sizing the components of the system under analysis. (Ganguly, Kalam, and Zayegh 2018). The probabilistic method may not be adopted as it cannot adequately represent the dynamic nature of the changes in performance within the hybrid system framework (Chauhan and Saini 2014; Kaabeche, Belhamel, and Ibtiouen 2011; Lian et al. 2019).

Probabilistic algorithms are classified into four (4) categories, namely: Monte Carlo, Las Vegas, Sherwood, and Numerical approximation algorithms (Brassard and Bratley 1989). Probabilistic methods have however been employed in sizing renewable energy. Some commercial computer tools for optimisation utilised one or two classes of the Probabilistic method mentioned above for reliability measures. In 2019, a Probabilistic model was developed by Rathore and Patidar (2019) to assess the reliability of standalone PSH/PV/wind microgrids. Their study modelled Wind & PV reliability units using forced outage rate (FOR) indices while the PSH reliability model on charging/discharge water rate. Comparative studies proved that the Analytical method is more time-efficient than the Monte Carlos Method, and PHS is also more reliable than battery system storage. Economics-constrained analysis was left out of the optimisation in their probabilistic models. Bracale et al. (2018) presented a probabilistic design of end-user equipment with renewable power generation and a battery system. Analytical techniques were used for battery optimisation, while Monte Carlo simulation was used for uncertainty load and Renewable energy resources. Probability density functions (PDF) were used for sizing considering uncertainty/random input variables while PDF of the load was normally distributed. The result showed that the battery energy storage system significantly reduces cost. The work was carried out with a single renewable energy source, while random variable inputs are recommended for future work. Arabali et al. (2014) analysed the stochastic performance assessment for wind-PV using autoregressive moving average and Monte Carlos Simulation to find the least cost combination that satisfies system reliability requirements. The study suggested demand-side management using load-shifting techniques to provide some flexibility to reduce the overall cost and mismatch in energy supply and demand from the stochastic hybrid system. Load shifting, in this case, means using higher energy-intensive appliances during peak sun hours or high wind speed.

Namanya and Gaunt (2013) established a probabilistic optimisation sizing method to improve the performance of the PV/Battery/Wind grid integration interconnection system. The grid connection model was based on capacity and failure rate with an on/off charge controller algorithm established with Monte Carlo simulation. The adequate confidence index (ACI) was used for reliability index simulation to optimise the size of battery capacities and cost. The algorithm was carried out using MATLAB with a successive combination of out stages hour confidence. A novel convolution technique using a probabilistic function for PV/Wind energy systems was presented in 2011 by Tina and Gagliano (2011). Probabilistic function and overlap were checked for clearness index and wind speed.

2.3. Computation method

Design, simulation, sensitivity analysis, and optimisation of HRES can be carried out using commercial computing tools such as HOGA, Homer Pro, Hybrid 2, HYBRID, MATLAB, LINDO, HYPORA, iHOGA, ARENA, Generic Algebraic modelling system (GAMS), Sim Pho Sys, SCADA, GRHYSO, H2RES, WDILOG2, Opt Quest, POOM (Barsoum and Petrus 2015; Edwin, Nair, and Joseph Sekhar 2022; Ekren and Ekren 2010; Jun et al. 2011; Kougias et al. 2016; Kwasnik, Elgqvist, and Anderson 2020; Mostafaeipour et al. 2019; Olatomiwa et al. 2015; Padrón et al. 2019; Perera et al. 2013; Rajoriya and Fernandez 2013; Ranjeva and Kulkarni 2012; Rezk et al. 2019; Atallah et al. 2020) and REopt (Kwasnik, Elgqvist, and Anderson 2020). Artificial Intelligent algorithms were implemented using MATLAB software (Edwin, Nair, and Joseph Sekhar 2022). System sizing, economical, technical, and feasibility studies have to be carried out using the above tools as followed.

Aghenta and Tariq Iqbal (2019) carried out a designed, dynamic model of diesel/PV standalone HRES and thermal modelling using Homer Pro software, MATLAB, and BEopt software respectively. Dynamic modelling for the study of power quality, harmonic, load impact, and others was observed via MATLAB, while HRES design and heat lost/ thermal modelling were studied using Homer Pro & BEopt software. The BEopt result shows the required energy consumption per year of the studied building to be 17485kWh/year. Salisu et al. (2019) studied the viability of a standalone Wind /Solar/Diesel generator hybrid system using HOMER Pro software. Cost of energy (COE), net present cost (NPC), renewable fraction (RF), greenhouse gas emission (GHG), and cost of operation as presented is $0.110/kWh, 98.3%, $1.01m, 2889.36kg/year and $ 4723, respectively. Hossen and Shezan (2019) conducted a feasibility study of PV/Wind/biomass/Battery off-grid HRES via RET Screen and HOMER Pro software. It was found that the hybrid system reduces CO_{2 –} related emissions by 31.9% with no increase in the investment cost as compared with other systems, and with 0.381$/kWh COE for the optimised HRES. Rousis et al. (2018) conducted a sensitivity analysis using HOMER Pro in the hybrid design of an isolated microgrid of PV-Diesel battery for residential application. The results show an inverse relationship between the diesel price and solar irradiance (an increase in diesel price increases the PV array and converter capacity).

Barrozo Budes, Valencia Ochoa, and Cardenas Escorcia (2017) presented an optimised size of HRES consisting of PV/Diesel/Battery/FC considering available location resources using HOMER Pro software. Twenty (20) scenarios were considered using the total annual cost (TAC). The first scenario, compared to others, presents the least LCOE of $ 0.191/kWh, $148901 total operating cost, an annual cost of $ 10714, and low CO₂ emission. The total operating cost, annual operating cost, and LCOE differences between the best and worst scenarios are 75%, 64%, and 76%, respectively. Ceran et al. (2017) also conducted an economic analysis of PV/Wind/Fuel cells with electrolyser and hydrogen energy storage. They selected available resources and load demand, 0.3kW wind turbine, 1 kW Solar panels, and 3kW fuel cell. The cost of electricity generated from the three configured scenarios was $ 0.287, $0.301, and $0.243, while their net present cost is $ 7962, $8359, and $6739, respectively. Ur Rehman et al. (2016) used HOMER for hybrid component selection, simulation, and economic analysis of Wind/Battery/Solar with diesel generator backup system for remote areas. The result shows that PV/Battery/Wind-turbine (100%) gives a COE of 0.733$/kWh compared to others. Also Khan et al. (2017) suggested an optimised technique to tackle the dynamics intensity of the hybrid renewable energy resources when configured Hybrid PV/Wind/Battery off-grid system via COE and NPC.

Yashwant and Gupta (2015) utilised Homer Pro software to design, simulate, and optimise PV/Diesel/Wind/Battery. The economic configuration contained 34% SPV and 66% wind with a lower net present cost of $100757, operating cost of $2334/yr, and energy cost of $0.502/KWh for the telecommunication base station. Singh, Baredar, and Gupta (2015) optimised HRES comprising fuel cell/ PV/ biomass gasification plants using HOMER Pro software to supply 101kWh/day. The result shows an optimised components size of 5kW each for Biomass gasification, Solar PV, and fuel cells with a COE of 15.064Rs/kWh and a TNPC of Rs. 51,89003. Ranaboldo et al. (2015) developed an HRES comprised of Wind/PV for an off-grid community using scenario algorithms for five (5) hours each, considering operation and maintenance costs (TLCC & LCOE) using Homer Pro. The LCOE obtained was 0.838$/KWh lower, 14% lower than the independent configuration, and 16.4% TLCC lower than the independent configuration. The sensitivity analysis and life span of 15 years are considered for the optimisation. Mahalakshmi and Latha (2015) presented an optimal comparative study of Grid alone, Biomass alone, and Hybrid PV/Biomass systems for a given location and load. They used ANN for Biomass feedstock optimisation, while economics and environmental analysis were conducted using HOMER Pro software. Biomass/PV HRES shows low GHG emissions with a relevant low LCOE of $ 0.111kWh. Hittinger et al. (2015) evaluated batteries in Micro-grid hybrid electricity systems using energy management system software EMS, which is like HOMER software, but with improved battery models in EMS. The study shows that temperature-related effects, variable efficiency (rate-based), and capacity fade operational modelling are essential aspects of a microgrid that significantly affect the optimal system design operation and LCOE. The study further shows that HOMER does not monitor capacity fade, which will help with periodical tracking when the batteries need replacement. It instead assumes that batteries operate at their original specification throughout the assigned lifetime, which underestimates the Levelized cost and, as a result, reduces battery cost by 20%. Ataei et al. (2015) carried out a technical/economic analysis on a standalone system based on NPC and COE to size HRES for a house with a load of 5.6kWh/day. HOMER software was used to simulate and prioritise feasible HRES. A system comprising of 3kW PV, 1kW inverter, 1kW wind turbine, and 1200AH battery with NPC of $21,132 and COE of $1.543/kWh is concluded to be cost-effective and reliable Okedu, Uhunmwangho, and Promise (2015), utilising available resources due to topography to develop an optimised hybrid system comprised of solar/ Hydro/ Biomass/ Battery. The best yield results with economic viability were presented using HOMER Pro software at the end of the work, among optimised configuration results were cash flow, and carbon emission result.

Esobinenwu and Omeje (2014) evaluated the PV/Microturbine /Diesel generator for a small village using Homer Pro Software for three Case scenarios. The second case scenario, which consists of PV/Microturbine alone, is cost-efficient and environmentally friendly compared to others with a total energy of 2,384,840kW/yr. Naik et al. (2014) proposed dynamic modelling and electronics power control interface for grid-connected Wind//PV HRES. DC-DC converters were implemented using a switch, diode, inductor, and filtering capacitor through the PI controller and grid-tied inverter/ converter. Simulation for three scenarios was presented in their study. Nazir et al. (2014) analysed the integration and optimisation of micro-hydro and photovoltaics systems using HOMER and MATLAB. After the simulation of three systems based on load profile and water availability, the result shows that the microgrid model with the highest capacity of micro-hydro produces the least COE and reduces CO₂ emissions. Again, the system has a high initial cost with increased RE penetration. The feasibility study of PV/wind/battery/diesel and diesel standalone system applications was examined using HOMER software by Abdilahi et al. (2014) and in the cause of the study, a feasible solution of PV/wind/battery/diesel hybrid system which have the lowest COE of 0.288USD/kWh was presented. In addition, a considerable non-harmful 10% annual capacity load shortage was modelled for the resident electrical stability test by the Author(s).

Using Homer Pro, Ould Bilal et al. (2013) optimised PV/Wind/diesel/Battery. Their optimisation objectives were the LCOE and CO₂. The result shows that LCOE AND CO₂ are inversely proportionate to various load profiles studied. Xu et al. (2013) proposed a complementary characteristics optimisation method for Solar/Wind HRES, power supply reliability, battery state of charge, grid injection fluctuation, and system cost. Their HRES grid integration was evaluated using LPSP, fluctuation rate, standard deviation, and a total annual cost (TAC) of the system in Homer software. A low-band filter was developed by the Author(s) for grid integration while Standalone HRES and grid-tied HRES are compared. The result shows grid-tied HRES to be more cost-effective and reliable than Standalone HRES.

Wind turbines, solar panels, converters, MPPT, and grid-tied inverters, were simulated by Harini, Ramaprabha, and Mathur (2012) using MATLAB. The design MPPT was implemented using an algorithm called incremental conductor to extract maximum power from Solar PV. Prakash, Ravikumar, and Gnanambal (2012) proposed hybrid renewable energy comprising Wind/Solar/Diesel engines with a Neural Network. MATLAB/Simulink was used for modelling, simulation, and control. Their method utilised a modified Elmma Neural Network and Radia bias function Network for wind turbine control and MPPT solar control. Adaramola, Oyewola, and Paul (2012) carried out a techno-economic assessment of an HRES comprised of wind turbine/Solar/Generator at Ibadan southwest Nigeria via HOMER Pro. Their result proved that combining renewable energy sources with the generator is more cost-effective than using the generator alone. However, the initial cost of installation of a renewable energy hybrid with a generator might be high. Kumaravel and Ashok (2012) presented a feasibility and cost analysis of Biomass/PV/Pico-Hydel HRES for a remote area using Table 1.

Table 1. Off-grid HRES configurations using HOMER Pro: a summary.

Study	System configuration	Computing tool	Application	Reference location
(Baker 2018) (Peffley and Pearce 2019) (Ma et al. 2015) (Delano et al. 2020) (Bekele and Tadesse 2012) (Kalinci, Hepbasli, and Dincer 2015) (Hossen and Shezan 2019) (Adaramola, Paul, and Oyewola 2014) (Abdilahi et al. 2014) (Rajkumar et al. 2011). (Kanase-Patil, Saini, and Sharma 2011)	PV-wind-battery PV-battery/Generator Hydro/pumped storage/PV PV/Diesel Generator/Battery Wind/PV/battery/diesel Hydro/PV/Wind/battery Wind/PV/hydrogen storage & wind only PV/wind/Biomass/ battery PV/diesel/battery PV-Wind-diesel-battery PV/Wind/battery Hydro/biogas: wood-based biomass gasifier/Rice husk-based gasifier/wind/PV Biogas/wood-based biomass gasifier/Rice husk-based gasifier/wind-PV	HOMER HOMER Single & double objective optimisation Genetic Algorithm HOMER HOMER HOMER HOMER RET screen & HOMER HOMER HOMER Artificial neural fuzzy inference system (ANFIS) Integrated RE optimisation model (IREOM)	Off-grid Off-grid Off-grid Off-grid Off-grid Off-grid Off-grid Off-grid Off-grid	Northern Cyprus Mediterranean Island United States China Benin Saudi Arabia Ethiopia Turkey Nigeria Somaliland Malaysia India

HOMER Pro. The least COE obtained is $ 0.164/kWh with daily solar radiation of 3.89kWh/m², 51.7 liters/secs hydro flow rate, and 0.692 biomass feedstock ton per day. The Author(s) concluded that Biomass HRES is suitable for rural areas.

Feasibility assessment and optimisation of PV/Wind/Battery stand-alone HRES were conducted by Paudel et al. (2011) using HOMER Pro and MATLAB. A mathematical equation was developed to optimise load configuration and loss of power supply probability (LPSP) from levelized unit electricity cost (LUCE) and compared with the simulation result from HOMER Pro software. The result proved that a system consisting of two numbers of 1KW wind turbine, 8.05KW PV module, and 112AH battery has a reliability of 99.9% with lower LUCE than others.

Katsigiannis, Georgilakis, and Karapidakis (2010) presented non-linear multi-objective optimisation comprised of Wind/PV/Diesel/Biodiesel/fuel cell/battery considering two scenarios using a Genetic algorithm (via HOMER Pro). Economic and GHG emission objective functions were set for each scenario with relevant constraints. A comparison between the two scenarios proved the scenario consisting of lead acid to be more economical and environmentally advantageous than the scenario with a hydrogen tank and fuel cell.

Selective effects of RE source, Renewable energy fraction (REF), and NPC were studied by (Dalton, Lockington, and Baldock 2009) via stand-alone/HOMER Pro software. The results shown from their study proved that an increase in RE source and REF is inverse proportional to NPC.

2.4. Iterative methods

The iteration optimisation technique solves the problem with successive approximations at each step. It is either a stationary or non-stationary algorithm. The iteration method has been effectively utilised to minimise cost through linearly changing parameter capacity/value components involved or through linear programming techniques. At the same time, reliability is evaluated using the probabilistic or chronicle approach (Lian et al. 2019). However, the iterative algorithm is considered inefficient for optimising swept area of the turbine, turbine height, the area of PV installations, and PV module angle, which have a more significant effect on cost.

Belmili et al. (2014) developed a simple user interface objective iterative programme for techno-economics analysis of PV/Wind energy systems considering LSPS and cost as the primary function to optimise storage and PV array capacity for the desired load. They introduced an NPC consisting of maintenance/replacement cost and international exchange rate variation often neglected in system sizing in the past. Ng, Lo, and Schober (2013) presented a resource allocation algorithm for hybrid renewable energy harvest, efficiency, and control of wireless communication using an iterative method at the base station. An iterative algorithm was used for resource (power) allocation for many carriers to balance system complexity and performance. The sub-online algorithm developed converges for all trials and optimises the system energy efficiency of the base station. Kaabeche, Belhamel, and Ibtiouen (2011) presented an iterative optimisation technique for component capacity sizing of Solar/Wind/Battery HRES considering the DPSP AND LUEC model. DPSP is used as an objective function in their design while Battery, PV, and wind capacities are considered sizing parameters. The system's efficiency is improved by storing excess energy in the form of hydrogen from the electrolyser.

2.5. Analytical methods

Analytical is obtained through a computation model, commercial computing software, or Numerical approximations component, in which system capacity is defined as a function of system feasibility (Ganguly, Kalam, and Zayegh 2018; Ng, Lo, and Schober 2013). In addition, it can accept long-term climatology data with short-time consumption and provides selective comparative information for decision-making for the best alternative’s economical/technical viable systems to be selected. However, the model cannot estimate the position-related mathematical equation coefficient (Khatib, Ibrahim, and Mohamed 2016; Lian et al. 2019; Luna-Rubio et al. 2012). Qayoom et al. (2012) presented novel analytical techniques comprising clearness index of the location, Lost of Load Probability, load demand, the unit cost of battery and PV for optima sizing of PV array area, battery capacity, and integration constant considering various load demands. The derived mathematical models are as follows. (1) $\mathrm{C}({\mathrm{C}}_{\mathrm{U},}\mathrm{A})=\alpha {\displaystyle \frac{\eta \mathrm{A}{\mathrm{G}}_{\mathrm{dm}}}{\mathrm{L}}+\beta {\displaystyle \frac{{\mathrm{C}}_{\mathrm{u}}}{\mathrm{L}}+{\mathrm{C}}_{\mathrm{u}}}}$(1) (2) ${\mathrm{A}}_{\mathrm{opt}}={\displaystyle \frac{\mathrm{l}}{2\mathrm{W}\left(\exp (\text{-}\mathrm{s}/2\mathrm{r})/\sqrt{4\mathrm{r}\beta /\alpha }\right)\mathrm{r}\eta {\mathrm{G}}_{\mathrm{dm}}}}$(2) (3) ${\mathrm{K}}_{\mathrm{opt}}={\displaystyle \frac{\mathrm{L}}{2\mathrm{W}\left(\exp (\mathrm{s}/2\mathrm{r})/\sqrt{4\mathrm{r}\beta /\alpha }\right)\mathrm{r}\eta \mathrm{G}{}_{\mathrm{gm}}}{\displaystyle \frac{\beta \mathrm{L}.\exp \left(2\mathrm{W}\left(\exp (\text{-}\mathrm{s}/2\mathrm{r})/\sqrt{4\mathrm{r}\beta /\alpha }\right)\mathrm{r}+\mathrm{s}/\mathrm{r}\right)}{\alpha \eta {\mathrm{G}}_{\mathrm{dm}}}}}$(3)

Where $C_u-Batterycapacity$, A – PV array Area, η – PV efficiently, $G_{dm}$-Daily monthly average incident Solar irradiation Wh/m2, L-Daily means energy demand, β – unit cost of battery storage($/Wh), $K_{opt}$ – Clearness index of the location for desired Loss of Load Probability.

Fantauzzi et al. (2017) proposed an analytical method for energy storage optimisation considering a load-based nodal calculus matrix formula for DC networks in renewable power generation. The Author(s) presented a constant approximation of voltage at all DC networks and a load flow linear approximation solution for power losses and storage optimisation. The two equations for those assumptions were tested and proved efficient for energy storage at varying load demands in the DC network. Bayram et al. (2017) presented an analytical method of system sizing in which energy storage systems are economically shared alongside a grid to meet customers’ demand load. The result shows that the storage-based end-user method, LOLP analysis, was used to optimise PV/Battery by Benavente-Araoz et al. (2017). State of Charge (SOC) profiles were computed in three scenarios to improve system design. However, less understanding of the SOC profile impact on the variation of the battery's life cycle was obtained because less effort was assigned to validate SOC profiles. Therefore, extensive work on the reliability assessment of the SOC profile and battery life cycle was recommended for future evaluation.

Amusat, Shearing, and Fraga (2016) investigated the effect of PV/ Solar thermal variability and PHES/AA-CAES/MTS storage. The non-linear model involving cost and reliability was developed for electrical, heat, and energy storage in these studies. The result shows that capital cost and system capacity are proportionate with declined demand satisfactory. Amusat et al. suggested that the trade-off between cost and reliability as observed in their work can be corrected by combining the multi-objective and stochastic Models.

Qayoom et al. (2012) presented an analytical model for the optimisation of PV standalone systems considering Solar array capacity, battery capacity, load demands, LOLP, cost, latitude, and clearness index. The result of the proposed model proved promising when compared with different analytical methods for sizing and reliability optimisation techniques in existence.

2.6. Artificial intelligence (AI) method

Artificial intelligence involves the science of mutating human behaviour in machines and the production of intelligent software. AI was coined in 1955 by John McCarthy (Manning 2020). It can make the decision automatically. Thinking based on stored data or experience and its operation can be supervised or unsupervised and can use multi-layer networks/hierarchical for continuous computation (Sinha and Chandel 2015). AI consists of an Expert system, Artificial Neural Network, and Fuzzy Logic, which can be split into Genetic Algorithm (GA), Particle Swarm Optimization(PSO), Simulated Algorithm(SA), Ant Algorithm(AA), Harmony Search (HS), Biogeography based optimisation (BBO), Gravitation search algorithm (GSA), Imperial competition algorithm (ICA), Tabu Search(TS), and Hybrid optimisation as used by the researcher in HRES optimisation (Chane, Gebru, and Khan 2021; Manning 2020; Naseh and Behdani 2021; Sinha and Chandel 2015). Kim, Song, and Han (2020) presented dynamic optimisation techniques based on the Markov decision process called reinforce learning to maximise the power output of the Trigen/Turbo hybrid generator inform of combining heat and power. Consequently, the hybrid generators’ efficiency improved by 3% by the optimisation algorithm, while more precise techniques are expected in the future.

Kiehbadroudinezhad et al. (2021) modelled, designed, and optimised three wind turbine configurations, solar, and battery for water desalination. Their results were obtained via a division algorithm considering different function's constraints, an improved genetic algorithm. Hybrid power optimisation of the renewable energy system was developed using a bee algorithm and neural architecture by Muthukumar and Balamurugan (2019). Their algorithm was trained and tested for various ranges of solar irradiance and wind velocities. Evaluation of the Thermal/Hydro/Wind storage hybrid system using Binary moth flame optimizations was presented by Arora, Kumar, and Kumar (2019). The optimal gain in the PI controller was attained by the Binary Moth flame optimisation modified sigmoid transformation algorithm which presents an alternative described meta-heuristic algorithm. Vinoth and Babu (2019) utilised the modified input LUO converter, and fuzzy logic MPPT to integrate the Wind/solar hybrid energy system to the grid using a PI controller to keep voltage and frequency in phase.

Kaabeche and Bakelli (2019) utilised four inspired natural algorithms (ALO, KH, GWO & JAYA) to minimise cost and storage technologies for energy storage (LA, Li-ion, and Ni-Cd Batteries). The sustainability of the system was carried out considering lifetime impact, cost of different batteries, and DOD on the unit cost of electricity (UCE). A comparison study shows the JAYA algorithm to be superior to others in terms of convergence, cost of Batteries (50% reduction), and reduction UCE by 30%, which pair Li-ion battery with LA battery in terms of cost. DOD of Ni-Cd and Li-ion were presented as 50% and 80%, respectively. PV/Wind/Ni-Cd and PV/Wind/LA are paired as most attractive in terms of the cost of UEC by the Author(S). Calado et al. (2019) optimised strategies for storage capacities and Hybrid Renewable energy system (off and grid-tied) dispatch for short-time and real-time operation with a new system architecture for PV/PSH/Wind/Battery/Diesel generators. They utilised a feed-forward neural network for short-time energy price forecast combined with energy storage technologies with a novel dispatched algorithm for cost reduction.

Firefly-based sizing algorithm (FASA) was presented by Abdul Aziz et al. (2017). They said algorithm was used for component sizing and reliability test (of LPSP) of a photovoltaic stand-alone system. The Firefly algorithm (FA) converged faster than GA, EP, and PSO to achieve an optimal result. In another related research conducted by Jain and Borkar (2020), fuel cell/diesel generator/electric vehicle/battery storage was used to support RE sources integration at various load levels. FA, GWO, and PSO were used to minimise the operation cost of the HRES microgrid in MATLAB software. The result proved FA superior to GWO and PSO in terms of cost reduction and convergence time. Ant Colony (ACO) and Particle swarm optimisation (PSO) were designed and validated by Abu et al. (2016) to improve the performance of the electric steering system for optimal operation. PSO with 3-dimensional search space for each particle is used for PID gain, while ACO is designed in a 3-different vector with an initial value of pheromone and search space representing ant regions. Using ACO and PSO algorithms, PID effectiveness was evaluated for steering turning power consumption. Turned controller of PID-ACO reduces power consumption of the motor by 76.87% while 75.22% for PID-PSO when tested on EPAS rig. In addition, PID – PSO and PID-ACO algorithms turned PID automatically. Vasanthavalli (2014) utilised a feedback propagation algorithm to optimise power quality via distributed static compensator (DSTATCOM) for harmonic control, load balancing, and Zero voltage regulation. The proposed control algorithm/DSTSTCOM is suitable for compensating for non-linear load and preventing an undershoot and overshoot of voltage during load variation. As with all ANN, training time and the number of hidden layers is often disadvantage of the present control algorithm. Sanchez et al. (2014) compared PSO and DE algorithms for economics analysis and optimal sizing of Wind/Fuel cell/PV HRES. Constraints and objectives were set with input parameters, although both algorithms’ optimal renewable energy systems met load demand. PSO algorithm converged at the initial condition, making it outshine DE in terms of cost and reliability. Tyagi and Kumar (2014) utilised data mining techniques for power optimisation in resource planning, parameter development, and decision making. The author(s) expatiates that data mining techniques can be attained through classification, outlier analysis, evolution analysis, and fuzzy set approaches. Gonçalves and Ramos (2012) show that ANN trained on configuration, economics, power simulator, and hydraulic is a suitable tool for the design of a suitable hybrid system for a Water scheme in respect of the available energy resources and optimisation of load (sink) to attain efficiency in 2012.

2.7. Meta-heuristic method

A meta-heuristic algorithm is a method that utilises one or two heuristic methods represented by the rule of thumb in solving a problem without exhausting the application procedure. It utilises appropriate solutions or nearby optimal solutions to find an exact optimal solution, not necessarily mathematic convergence proof to the optimal solution needed but computes faster than a conventional Algorithm (Bandaru and Deb 2016; Gavrilas 2010; Mahmoud and Hosseini 2016). Furthermore, the techniques are iterative but utilise stochastic operation in the searching process for candidate solutions modification through random sampling. This technique has been greatly used to optimise HRES extensively due to its effectiveness and accuracy (Hasancebi and Kazemzadeh Azad 2012). In addition, Meta-heuristics operators are either exploitation, exploration, or combination in search space (Hasancebi and Kazemzadeh Azad 2012), while exploitation involves the operator obtaining a solution from the previous iteration to intensify the search. Exploitation involves searching for the solution through diverse solutions in a global search. A meta-heuristic algorithm can either be trajectory or population-based with multiple interacting paths (Gonçalves and Ramos 2012) classified as single or multiple objectives. Most Artificial Intelligent is utilised as a single or Multi-objective Meta-heuristic algorithm.

Annual life cost and LPSP multi-objective function were minimised for optimal sizing of grid-tied PV/Wind/Battery/Biomass via an artificial cooperative algorithm by Pavankumar, Kollu, and Debnath (2021). A probabilistic approach was employed for time-series renewable energy sources and the required load, while ACS was modified to MOACS for renewable energy sizing. MOACS algorithm shows the lowest annual life cost (Rs 2,185,265.1) and unit cost of Rs 4.95983 compared to NSGA-II and IMOH algorithms. Samy, Elkhouly, and Barakat (2021) utilised (COE and LPSP) as a multi-objective PSO algorithm for mico-grid sizing of biomass/FC. In their design, biomass was used as a based generator, while biomass FC was a standby system when the biomass generator failed to meet the load demand. Two numbers of biomass generators, six numbers electrolysers, thirty-one numbers of fuel cells, and eighty-six numbers of hydrogen tanks were optimally sized with at least $231484 & $0.335/kW as NPC and COE respectively at 1.929% LPSP. Three scenarios were considered, including the probability of the system meeting the Load demand, over a generation, and demand. Habibollahzade, Gholamian, and Behzadi (2019) integrated biomass-based cathode/anode SOFCs/GT/SOECs for hydrogen and power production via multi-objective optimisation considering air, enriched air by oxygen, oxygen (O₂), and carbon dioxide (CO₂) gasification agents. Gasification agents were compared and analysed from different viewpoints ranging from exergoeconomic, exergy, and energy. Exergy efficiency Levelized emission and hydrogen rate of production are considered for multi-objective functions of CO₂ using GA for analysis and the result compared with other gasification agents mentioned above. The result proved the CO₂ agent to be more environmentally friendly with a high hydrogen production yield. SA, DA, DE, NSGA II, PSO, and ALO were used by Júnior et al. (2018) for emission-economic load dispatch (EELD). A comparison of the algorithms mentioned above was presented via multi-objective. Sensitivity analyses were carried out for ten scenarios while one system is taken one after another to determine the stability and system reliability of the whole system. SA gives the least emission value, while DE presents the least cost among the ten comparative units.

2.8. Graphical method

The graphical Method is a construction technique in which possible solutions (Minimum or Maximum optima results) are obtained by drawing simple graphs or contours for objectives and constraint functions. Graphical Methods can accommodate one or two variables for optimisation. From the literature, only Borowy and Salameh (1996) and Markvart (1996) have used graphic methods for renewable energy sizing. Markvart (1996) used a graphical method for optimal PV/Wind HRES considering monthly average wind and solar meteorology data with a simple condition in which the Cartesian Lane of variables $a_s$and $a_w$ were points on coordinate and proved that the system satisfy the required load demand as shown in equation (4). (4) $\mathrm{d}\le \mathrm{W}{\mathrm{a}}_{\mathrm{w}}+\mathrm{S}{\mathrm{a}}_{\mathrm{s}}$(4) where d – average daily demand, $a_w$ =  wind generator, $a_s$ – Solar array, W – wind energy measure perpendicular to wind direction, and S-solar energy.

Seasonal analysis was conducted by setting constraints and objective functions for sizing PV/Wind RES optimally from metrological data of a given location. The cost was considered the linear function of $a_w$ and $a_s$ as shown in equation (5). Economic analysis shows that PV/wind hybrid power systems are cheaper than PV or wind turbines alone. (5) $\mathrm{Hybrid}\mathrm{generator}\mathrm{cost}={\mathrm{C}}_{\mathrm{s}}{\mathrm{a}}_{\mathrm{s}}+{\mathrm{C}}_{\mathrm{w}}{\mathrm{a}}_{\mathrm{w}}$(5) where $C_s$ – Cost of Sola and $C_w$ – Cost of wind.

Borowy and Salameh (1996) proposed a method for determining the optimum size of the PV array and battery of PV/Wind HRES considering thirty (30) years of data. During the study, LPSP and the numbers of PV are considered non-linear functions of the number of batteries. In the end, the system cost function was defined and presented as shown in equation (6). (6) $\mathrm{C}=\propto {\mathrm{N}}_{\mathrm{pv}}+\beta {\mathrm{N}}_{\mathrm{batt}}+{\mathrm{C}}_{\mathrm{o}}$(6) where $\propto$ – Cost of Solar, C – The capital cost of the hybrid system $N_{pv}$-Numbers of Solar panels, $\beta$-Battery cost, $N_{batt}$-Numbers of batteries, $C_o$-total cost, including design and installations.

The plot of PV numbers against that of the battery gives the optimal size of tangency of 45 and 80, respectively. (7) ${\displaystyle \frac{\delta {\mathrm{N}}_{\mathrm{pv}}}{\delta {\mathrm{N}}_{\mathrm{batt}}}={\displaystyle \frac{\beta }{\alpha }}}$(7) Where $\beta /\alpha$ – curve in point s.

2.9. Hybrid method

The stochastic nature of renewable energy resources, the inadequacy of a single optimisation method available, and the conflict of optimisation parameters/objectives of HRES give rise to a combination of two or more techniques for economic and reliable optimisation of HRES. Therefore, the advantages and disadvantages of two or more algorithms (Chane, Gebru, and Khan 2021) are combined in Hybrid optimisation for optimal results in RE system economical sizing. The following are examples of Hybrid optimisation methods as applied to HRES (Table 2).

Table 2. Summary of key optimisation objective functions, constraints, methods, and findings in the HRES.

Objective functions	Constraints	System configurations	Finding	Optimisation method	References
$minCT=\sum _{k=1}^3{I}_k+P_{pwk}+O{M}_{pwk}+S_{pwk}$	LPSP	Solar(PV)/Wind	PSO was used to reduce the iterative complexity that rises in GA. PSO iteration proved better than GA operation.	AI	(Sasidhar and Kumar 2015)
$F=mim\sum _{i=1}^{n}RI+ACS+COE$	POWER	Solar(PV)/WIND/BATT/GEN	The COE can be reduced with an increase in RERs integration.	P	(Adefarati, Bansal, and Justo 2017)
$F^{obj}=max(F_{WDG}^{obj}-F_{DG}^{obj})$	LOAD SOC POWER BALANCE	Solar(PV)/WIND/BATT/GRID	Integration of RERs-DG into the conventional system will improve reliability and reduce cost.	P	(Adefarati and Bansal 2017)
$mmCC$ $mimEE$	System Capacity	Solar (PV)/ Solar thermal/ PHES/AA-CAES/MTS Storage	A stochastic/Multi-objective might be needed to correct identified trade-offs between cost and reliability.	A	(Amusat, Shearing, and Fraga 2016)
$F_1=mimLCOE$ $F_2=MIMLPSP$	Capacity	Hydro/PHS-PV	Effect of net head variation on the system	L	(Chaima et al. 2021)
$F=mimUEC$	LPSP	PV/Wind/Batteries (LA, Li-ion & Ni-Cd)	Comparative studies of ALO, JAYA, KH, and GWO were presented. The result thereby proved JAYA to be superior to others in terms of converging and cost reduction.	AI	(Kaabeche and Bakelli 2019)
$F=mim{C}^{tot}$	SOC SOH	PV/Batteries	Three steps in solving BESS optimal-capacity configuration with multiple batteries using MINLP models were presented.	L/NL	(Jiang, Kang, and Liu 2020)
$F=mim{C}^{tot}$	LPSP	PV/Wind/DG	ACO presents a relatively lower system annual cost of energy in the study.	AI	(Suhane et al. 2016)
$F=mim(TAC+LPSP+FuelCost)$	Generation Battery	PV/Wind/DG/Batt.	The optimal result was obtained when the penalty function was 1, LPSP$<4\text{\%}$ with the structure of $N_{WIND}=215$, $N_{batt}=1$, and $N_{DG}=8.$	H	(Cho, Chun, and Hong 2016)
$F=mim(cost+Polutiondemages)$	Fuel delivery Capacity. Power balance.	Gas engine	SA presents the least emission value of 1757.39$/hr while DE gives the least cost of installation of 1545.61$.	AI	(Júnior et al. 2018)
$F=mimTNPC$	LOLP Capacity	PV/Biogas/PH/Battery	The water cycle, month flame, and Genetic algorithms were used and compared. The result proved WCA to be a more effective intern of convergence, cost, and reliability.	AI	(Das, Singh, and Biswas 2019)
$F=TNPC=\sum NP{C}_K\ast N_K$	Capacity Battery	PV/Wind/ Battery	MILP, GAM, CPLEX Solver, and Homer Pro were combined as Hybrid optimisation methods for HRES optimal Sizing while Demand response programmes are utilised for optimal management & cost reduction	H	(Amrollahi and Bathaee 2017)
$F=mimTNPC$	LPSP	PV/Wind/battery	GS-PSO, MOPSO, and HOMER were used for optimal sizing and comparative study. GA-PSO result proved to be cost-efficient compared to the others at 2%, 5%, and 10% LPSP with LCOE of 0.508kWh at 7 & 10% deviation from other methods.	AI	(Ghorbani et al. 2018)

Where $CT$= $C^{tot}$-Total Cost $F_{WDG}^{obj}$ – Total cost of a power outage without RERs-DG

$CC$ – Capital cost $I_{}$-Investment cost

$EE$ – External energy $F_{DG}^{obj}$ – Total cost of power outages with RERs-DG

R-Replacement cost RI – Reliability index

UEC-unit electricity cos O&M – Operation & Maintenance Cost ACS – The annualised cost of System L – Linear programming $S_{pwk}$-Salvage $COE$-Cost of Electricity NL – Non-linear programing k – individual system $CC$ – Capital cost

$TNPC$ – Total Net Present Cost H – Hybrid Technique MINLP – Mixed integer Non-linear programming AI – Artificial Intelligent Technique CT-Computing tools

P – Probability Technique A – Analytical Technique

Human, van Schoor, and Uren (2019) developed and implemented a hybrid strength Pareto evolution /single objective genetic algorithm for sizing and power management of HRES in three locations. The author(s) compared the Strength of the Pareto evolution /genetic hybrid algorithm with the standard strength Pareto evolution algorithm written in C-code in a MATLAB environment. Their result shows that the Hybrid strength Pareto evolution /single objective genetic algorithm performs better than the latter in the area of efficiency and reliability, but analysis of their result rules insight needs to be investigated and re-presented.

Cho, Chun, and Hong (2016) presented the TLBO-CS algorithm for PV/Wind/DG/Battery HRES optimisation. The Author(s) used the teacher and student method of TLBO to search for a near solution globally which best student was selected using clonal selection techniques locally. The penalty function of TLBO-CS was considered for total annual cost while fuel cost and LPSP were satisfied. The best optimal result was obtained at LPSP $<$ 0.004. Leelaprasad, Anand, and Raju (2014) presented an hybrid adaptive particle swarm optimisation (APSO)/interior point method (IPM) for optimal power scheduling for baseload and cost objective function minimisation. APSO/IPM performed better than the other two-hybrid.

2.10. Linear programming (LP) methods

LP was developed in 1939 by Kantorovichin Leonid (Sinha and Chandel 2015) and applies to solving a problem in which constraints and objective functions are linear decision variables. It can be used for complex problems. Still, it is characterised by an unrealistic assumption that deterred its suitability except combining with other methods in a hybrid to attain maximum results as shown by Sundström and Binding (2010). Nevertheless, LP has been employed widely for HRES optimal sizing.

Chaima et al. (2021) selected linear optimisation to the optimised varied net head of the Hydropower plant and PHS-PV for day and night operation due to its short computation time. The research was implemented through multi-objective methods in which the PV(182MW) and PHS(86MW) plants achieved 99.8% reliability and added 53% power to the existing hydropower plant. Alamri, AlOwaifeer, and Meliopoulos (2020) presented MILP optimal sizing of HRES of PV/WIND/ battery. Probabilistic method (PCC) was used for reliability (LOLP, LOLE & EUE) integration of the system on ESS while variable generator (VG), Conventional generator (CG) and forced out stages are used as input. ESS was optimised as modified unit commitment economic dispatched. The penetrating level presented by CG and VG is 20% and 30%, respectively, to attain stability regarding ESS.

MINLT was implemented in GAMs for PV/Wind/Battery/DG HRES optimal sizing by Qari, Khosrogorji, and Torkaman (2019), and the output result compares with that of DHS and DSA. Hourly load and meteorology data with other technical parameters were fed in step to the algorithm to determine best-fit configurations. The system's annual cost was minimised, considering generating and battery constraints. MINLT demonstrated to be economically efficient as regards annual cost compared to the other two algorithms under study. Dawoud, Lin, and Okba (2018) showed that battery storage system needs constant tracking to ascertain their status for replacement within a few years; this raises the system cost. An LP optimisation model (General Algebraic Modelling system) of a hybrid off-grid energy system defines battery lifetime in years rather than cycles per time interval, leading to overestimating the optimal battery capacity. The model assumes a favourable operational condition throughout the battery's operational life, usually five years for lead-acid batteries (Huneke et al. 2012). Clack, Xie, and Macdonald (2015) developed two linear programming algorithms to optimise electrical power systems’ generation, transmission, and storage. The two algorithms were derived and compared on spatial resolution/geographic scale for load matching and cost minimisation. The Load matching optimisation performs better in speed and generation using variable energy sources but is less cost-efficient than cost-minimising optimisation. However, longer time-series data and higher resolution optimisation need to be incorporated into their work in the future. Optimisation of the charging behaviour of electric vehicles for the state of energy level and power balancing was carried out by Sundström and Binding (2010). The author(s) proposed linear and quadratic approximation optimisation charging schedules and compared them with non-linear/state-dependent algorithms. Their result shows that linear approximation applied to the charging schedule violates less battery boundary than quadratic approximation optimisation. Although linear and quadratic approximation algorithms are deterministic, additional work is required to validate the approach and address the stochastic nature of the system considering power grid constraints in transmission/distribution Table 3.

Table 3. Comparison of HRES optimisation tools/techniques.

Techniques/Tools	Strengths	Weakness	Ref
HOMER Pro Software	A quick way to get an objective solution from a single target objective	The initial properties of the linear equation model cannot be specified. The system is assumed to remain stationary throughout the study. It does not allow the user to naturally select the appropriate device. The effect of possible future battery charging/DOD growth is not taken into account. The solution is limited by the range of input parameters and cannot provide key value metrics if there are missed like modern optimisation algorithms. It cannot accept a control strategy like iHOGA.**It is less superior to Nature-inspired algorithms. Experienced criterion is required for the optimisation to converge to a good solution.	(Atallah et al. 2020; Chauhan and Saini 2014; Clack, Xie, and Macdonald 2015; Erdinc and Uzunoglu 2012; Kavadias and Triantafyllou 2021; Khare, Nema, and Baredar 2017; Okedu and Uhunmwangho 2014; Ramli et al. 2017; Saiprasad, Kalam, and Zayegh 2018; Zhou et al. 2010)
iHOGA	Ability to explicitly apply control strategy in HRES sizing.	Considered only single objective and Non-linear problems	(Saiprasad, Kalam, and Zayegh 2018)
Retscreen	Significantly reduces the costs associated with identifying and assessing potential energy projects compared to Homer Pro.	Compile manually in a workbook/Excel sheet	(Ramli et al. 2017)
Probabilistic	It is stochastic and can randomly determine the best solution from the available data.	It cannot adequately represent the dynamic nature of performance changes within a hybrid system. It is less efficient than the analytical method	(Chauhan and Saini 2014; Clack, Xie, and Macdonald 2015; Ganguly, Kalam, and Zayegh 2018; Kaabeche, Belhamel, and Ibtiouen 2011; Lian et al. 2019; Zhou et al. 2010)
Iterative	It is effective in obtaining minimised costs through linear variable parameters or linear programming techniques.	Considered inefficient for optimising swept area of the turbine, turbine height, the area of PV installations, and PV module angle, which have a more significant effect on cost.	(Chauhan and Saini 2014)
Analytical	It can accept long-term climatology data with short-time consumption and provides selective comparative information for decision-making for the best viable systems. The analytical method is more efficient than the Monte Carlos Method.	The model cannot estimate the position-related mathematical equation coefficient.	(Khatib, Ibrahim, and Mohamed 2016; Lian et al. 2019; Luna-Rubio et al. 2012)
Graphical	The simplest method of representing complex problems/situations involving too many mathematics equations.	It cannot accommodate more than two-dimensional problems. Due to the variable scale and difficulty in graphical interpretation, the accuracy of the solution is questionable. Difficulty in graphing non-linear, exponential, logarithmic, and trigonometric expressions. It is characterised by an unrealistic assumption that deterred its suitability except combining with other methods.	(Erdinc and Uzunoglu 2012; Rathore and Patidar 2019)
Linear Programming (LP)	It exhibits linearity between variables. It is characterised by good convergence and is less rigorous	It can be stuck in local search. It loses accuracy and certainty over time. It also failed to consider evolution and changes in variables.	(Birge and Louveaux 2011; Kavadias and Triantafyllou 2021; Khare, Nema, and Baredar 2017; Okedu and Uhunmwangho 2014; Ramli et al. 2017; Saiprasad, Kalam, and Zayegh 2018; Sinha and Chandel 2015)
Genetic algorithm (GA)	Ability to handle several parameters (integer, discrete, non-differential, and so on) simultaneously as multiple targets/objectives at the same time. The parallelism properties of GA allow multiple schemes to be implicitly evaluated at the same time, giving a greater chance of obtaining the optimal solution at each iteration. It can yield good results from several/different problem formations. GA outperformed HOMER Pro software and SA in terms of cost and environmental analysis.	Consume more time with an increase in the length of chromosomes. It takes more time and less computation effort than the Analytical method. It is only meant for local searching unlike other natured-inspired algorithms with both local and global search space.	(Birge and Louveaux 2011; Craenen et al. 2000; Hobson 1978; Iweh, Clarence, and Roger 2022; Momoh, El-Hawary, and Adapa 1999; Raju 2014; Riaz et al. 2022; Saiprasad, Kalam, and Zayegh 2018; Shorman and Pitchay 2015; Sultana et al. 2016)
Tabu Search (TS)	Ability to seek efficient and cost-effective solutions. It provides better local search capabilities than GA. Better than SA to get neighbourhood solutions.	Exploration can be trapped in local search due to its fixed size and static nature.	(Couman, de Klerk, and Jansen 2014; Qu 1986; Suresh, Muralidhar, and Kiranmayi 2020; Zuhaimy 2009)
Firefly Algorithm (FA)	Ability to deal with the multimodal problem. It performs more brilliantly than PSO.	It can be stuck in local search and has a relatively long convergence time.	(Hashmi et al. 2013; Lohrer 2013; Yang and Xingshi )
Simulated Annealing (SA)	Achieving optimal results is systematic and deterministic. Easy to programme. It is robust enough to handle the non-linear problem and various constraints. Flexibility and ability to switch from local search to global search.	Low performance with relatively long computational time.	(Busetti 2003; Skoonpong and Sirisumrannukul 2008)
Gravitation Search Algorithm (GSA)	It has two variable adjustable parameter settings (speed and mass). It has less memory than other nature-inspired algorithms. The algorithm is more suitable for non-linear problems and is more efficient than HS in analysing database functions.	It is complicated (complex). Gravitation constant (G) is difficult to appropriate. Convergence time is longer and if the initial population is not created correctly, there may be a convergence problem.	(Rather 2019; Sabri 2013; Systems and Sahoo 2014; Enikeeva et al.; Narimani et al. 2014)
Grey Wolf Optimiser (GWO)	Fewer parameters like GSA above and easy to implement.	Inability to exist local search due to slow convergence speed at the later end of the iteration. It is characterised by low precision/accuracy.	(Grey and Optimization 2022; Wang et al. 2020)
Harmony Search (HS)	Fewer turn-able control parameters are needed. An initial decision variable setting is not required. Require no derivative information. Better than K-means and GS in cluster problem analysis.	Slow and premature convergence. Poor limitation and adaptability search range.	(Dubey et al. 2021; Kumar, Chhabra, and Kumar 2012; Yusup et al. 2018)
Particle Swarm Algorithm (PSO)	Require fewer turn-able control parameters. Ability to perform parallel computation with high convergence speed. Ability to find the best global solution with high efficiency. Ability to solve complex problems.	Exhibit poor local search when dealing with the high-dimensional problem. It’s characterised by premature convergence.	(Systems and Sahoo 2014; Enikeeva et al.; Dubey et al. 2021; Gad 2022; Grey and Optimization 2022; Gupta and Srivastava 2020; Kumar, Chhabra, and Kumar 2012; Li, Du, and Nian 2014; Narimani et al. 2014; Search, Zhang, and Zhang 2020; Wang et al. 2020; Yusup et al. 2018)
Ant Colony Optimization (ACO)	Rapid discovery of good solutions because of positive feedback mechanisms. It exhibits parallelism. It can be easily customized and has the great advantage of being combined with another algorithm to get a powerful and highly reliable algorithm. It returns the global minimum with fewer iterations compared to PSO.	Improper selection of initial parameter values might lead to local search stagnation immature convergence and inability to reach an optimum solution. It can only handle discrete problems while continuous problems might pose a problem	(Abreu et al. 2011; Gupta and Srivastava 2020; Selvi and Tamilnadu 2010; Shehab, Khader, and Al-Betar 2017)
Cuckoo Search	Fewer turn-able control parameters are needed. It enhances by Levi's flight trait/character, which helps to converge at global optima solution. Strong random searching path and optimisation capacities. Strong affinity to form a hybridising with other algorithms.	It can be stuck in local search if initial parameters are not properly set. Slow convergence time	(Babukartik 2012; Liu et al. 2018; Shehab, Khader, and Al-Betar 2017; Shen et al. 2021)

3. Criteria for HRES optimization

HRES optimal sizing techniques involve combining energy resources, converting the resources using adequate technologies, and storing such energy to prevent wastage/system inadequacy economically with minimum acceptable security to meet required load demands without hampering the environment (Bhandari et al. 2015). Therefore, the metrics for HRES optimisation are economical, reliable, and environmental, as shown in the proceeding steps.

3.1. Economic criteria

Economic analysis is one of the major indicators for optimising energy at minimum cost and determining the visibility of the renewable energy project. Net present cost (NPC), Total annual cost (TAC), Levelized cost of electricity (LCOE), Net present Value (NPV), and, Life cycle cost (LCC) are economic criteria that exist in the literature (Emblemsvåg 2020; Ganguly, Kalam, and Zayegh 2018; Huneke et al. 2012; Nikolaidis, Chatzis, and Poullikkas 2019).

The LCOE is used for comparative competitiveness of renewable energy electricity generation. It is a measure of lifetime costs divided by energy produced by the plant. (7) $LCOE={\displaystyle \frac{TAC}{E_{TOTAL}}}$(7) (8) $TAC=ACC+AOMC+AR$(8) (9) $ACC=TCC\ast AF$(9) (10) $TCC=C{C}_K\ast n_K$(10) (11) $AOMC=C_{om}\ast ACC$(11) (12) $ARC=C_r\left({\displaystyle \frac{LC}{LT}-1}\right)\ast AF$(12) (13) $\mathrm{AF}={\displaystyle \frac{{\mathrm{i}}_{\mathrm{r}}\ast {(1+{\mathrm{i}}_{\mathrm{r}})}^{\mathrm{LC}}}{{(1+{\mathrm{i}}_{\mathrm{r}})}^{\mathrm{LC}}-1}}$(13) (14) $LCOE={\displaystyle \frac{\sum TES}{\sum TCC+AOMC+ARC}}$(14)

Where: TAC = total annualised cost, E_Total= Annual total electricity generated, AF = Amortization factor, TCC = Total capital cost, AOMC = Annual operating & maintenance cost, ARC = Annual replacement cost, ACC = Annual capital cost, C_r= Cost of replacement, LC = Lifetime of the whole system, ROI = Return on investment, CC = Capital cost, TES = Total electricity supply, ROI = Return on investment, LT = lifetime of an individual, C_o&m = operating and maintenance cost and n – number of quantity(Emblemsvåg 2020; Nguyen et al. 2020; Nikolaidis, Chatzis, and Poullikkas 2019)

LCC is a cost that encompasses a system from the cradle to the grave or incurred by a system over its lifetime. It can be evaluated using NPV and Levelized annual cost. (15) ${\mathrm{P}}_{\mathrm{v}}=\sum _{\mathrm{k}=1}^{\mathrm{t}}{\displaystyle \frac{{\mathrm{C}}_{\mathrm{t}}}{{(1+\mathrm{i})}^{\mathrm{t}}}}$(15) (16) $P_{VD}=(C+M{)}_{pv}+(C+M{)}_{wind}+(C+M{)}_{batt}+(C+M{)}_{Hydro}+(C+M{)}_{Biom}-D$(16) where $P_v$ – Present value without depreciation, $P_{VD}$ – Present value with depreciation, $C_t$-cost/year, $i$ – interest rate/year, M – maintenance cost, t – time of analysis, and D – depreciation present value. (Bhandari et al. 2015).

3.2. Reliability criteria

Power system reliability is the probability that a system will be performing the purpose of its design adequately for the intended operating period/time or the ability of the power system to supply the system load demand having reliable continuity and quality of power supply. Various studies have used several indices to measure system reliability, especially in the renewable energy system. This is due to its stochastic nature, which includes; Level of autonomy (LOA), Loss of load probability (LOLP), Levelized cost of energy (LCOE), loss of power supply probability (LPSP), and Expected Energy not supplied(EENS) (Khare, Nema, and Baredar 2016). LOLP occurs when the power system(s) load is more than its generation capacity (Huneke et al. 2012). Efstratiadis et al. (2014) defined the concept of system reliability in RE generation and assigned a complementary concept as the probability of failure, which is defined as$\alpha =P(X<x^{\ast })$, X = expresses performance of the random variable in the system such as energy production and x* the target value of the quantity which can be achieved at certain level $\alpha =P(X\ge x^{\ast })$ 99%, 97% and 95%.

The probability that HRES will perform its function as specified for a period under certain conditions is measured using reliability various indices. Some of these indices include Loss of Load expectant (LOLE), Loss of Load Duration (LOLD), Loss of Energy Probability (LOEP), System Performance Level (SPL), Deficiency of Power supply Probability (DPSP), Loss of Load frequency (LOLF), Lost of Load Risk(LOLR), Forced out rate (FOR), LOLP, LPSP, and EENS among others (Čepin 2011; Ganguly, Kalam, and Zayegh 2018; Shirvani et al. 2012).

LOLP happens when the system load demand is more than the available generating capacity and its value in the percentage of hours/days in a time frame that energy demand cannot be covered due to probability losses of generating plant (Sinha and Chandel 2015; Vijayamohanan Pillai 2015). However, LOLP expressed in time unit rather than percentage is LOLE. Therefore, LOLP and LOLE are interrelated. (17) ${\mathrm{E}}_{\mathrm{t}}={\rho }_{\mathrm{i}}{\mathrm{t}}_{\mathrm{i}}$(17) (18) $LOLP=\sum _{i=1}^n{\rho }_i{t}_i$(18) (19) $LOLP={\displaystyle \frac{LOLH}{8760}}$(19) (20) $LOLP=P[G_i<L_i]$(20) (21) $LOLH=\sum _{ij}\{{}_{1ifPea{k}_{loadij}\le G_{ij}}^{0ifPeak{}_{load}\le G_{ij}}\}$(21) where $E_t$-Power supply, ${\rho }_i$ – loss of capacity probability, $t_i$ – duration loss of capacity in %., G – Total power generation plant, i – hour, j – year. (Čepin 2011; Shirvani et al. 2012; Vijayamohanan Pillai 2015; Ascend Analytics; Li and Zio 2012; Milligan et al. 2017)

LSPS is defined using equation (22). (22) $LSPS={\displaystyle \frac{{\sum }_{i=1}^n{E}_i^{Def}}{{\sum }_{i=1}^n{E}_i^D}}$(22) where $E_i^{Def}$ – Energy deficit (KWh), $E_i^D$ – Energy demand (KWh). (Sinha and Chandel 2015)

EENS is a measure of energy security that denotes the amount of energy that is not supplied, at a period, to a given zone due to insufficient resources to meet such demand. (23) $EENS=C{a}_i\ast P{r}_I+t_i$(23) (24) $EENS=\sum _{i=1}^{N_t}{P}_i(G_i<L_I)\ast (L_i-G_i)$(24) (25) $\mathrm{If}LOLE=\sum _{i=1}^{N_t}{P}_i(G_i<L_i)$(25)

Then, (24) $EENS=LOLE\ast (L_i-G_i)$(24) where $C{a}_i$ – Capacity out stage(i), $Pr$ – Probability of capacity out stage i, t – Capacity (Paudel et al. 2011)out stage time I, $G_i$ – Total power generated at period, i – equally sized time step, $L_i$ – load demand at the time i, $N_t$ – total no of time steps. (Čepin 2011; Milligan et al. 2017).

Forced out rate (FOR) is a ratio of the failure rate to the total operating hour of a generating plant, and its equivalent is presented as the Equivalent forced outage rate (EFOR). (Mazumdar 1988; Shirvani et al. 2012) (25) $\mathrm{FOR}={\displaystyle \frac{\mathrm{Forces}\mathrm{outage}\mathrm{hours}}{\mathrm{In}\mathrm{service}\mathrm{hours}+\mathrm{Forced}\mathrm{outages}\mathrm{hours}}}$(25) (26) $\mathrm{EFOR}={\displaystyle \frac{\mathrm{Forces}\mathrm{outage}\mathrm{hours}+\mathrm{Equvalent}\mathrm{forced}\mathrm{outage}\mathrm{hour}}{\mathrm{In}\mathrm{service}\mathrm{hours}+\mathrm{Forces}\mathrm{outage}\mathrm{hours}}}$(26)

The reliability index is one of the important criteria to determine how healthy and dependable an HRES is. It is mathematically present in equation (27a and b) (Hobson 1978; Momoh, El-Hawary, and Adapa 1999). (27a) $\mathrm{RI}=1-{\displaystyle \frac{E_S}{E_{TD}}(27\mathrm{a})}$(27a) (27b) $E_{TD}=\sum _{t=1}^{T_S}{P}_{LOAD}{T}_{U_t}(27\mathrm{b})$(27b) Where $E_S\text{–}\mathrm{Energy}\mathrm{shortage}\mathrm{in}\mathrm{kWh}$, $E_{TD}-\mathrm{Total}\mathrm{Energy}\mathrm{demand}\mathrm{in}\mathrm{kWh}$, $P_{LOAD}-\mathrm{Load}\mathrm{demand}$, $T_{U_t}-\mathrm{Unavailable}\mathrm{power}-\mathrm{load}\mathrm{hour}$

Kanase-Patil, Saini, and Sharma (2011) evolved an HRES reliability model ensuring the minimum cost of energy at four different residential seasonal load profiles with a balanced technique by considering the EENS as a probabilistic criterion used in the model. The said model produced two optimum reliability criteria index results of 0.999 and 0.99 EIR, with relevant COE equivalent to 0.092USD/kWh and 0.087USD/kWh, respectively. However, the study stated that identifying the optimum configuration of HRES reliability depends on the site-specific conditions and seasonal load profiles. Ghaffari and Askarzadeh (2020) put forward a study on HRES optimisation comprised of PV/diesel generators/fuel cells using a cross-search algorithm approach. During the study, total net present cost minimisation TNPC was subjected to renewable energy portion and LPSP constraints. The result shows that both LPSP and TNPC are inversely proportional to each other, while the renewable energy portion and TNPC are proportionate to one another. Nevertheless, a compromise can be reached between increasing or decreasing either TNPC and/ or LPSP, respectively. Khare, Nema, and Baredar (2019) studied hybrid renewable energy reliability analysis of weather data and load profile using fault tree analysis. The result showed that system reliability is based on the monthly load profile. Moreover, real profit and confidence in renewable energy system supply require system reliability calculations for optimal operation.

3.3. Environmental criteria

Environmental footprint indicators such as carbon emission, land use, societal impact, and water consumption, among others, are essential for the deployment of the RE system (Ghaffari and Askarzadeh 2020). A robust evaluation of generating plant environmental footprint is CO₂ emission, and it can be quantified with respect to emission factor and fuel consumption as shown in equations (28) and (30). (28) $\mathrm{TEC}={\displaystyle \frac{\sum \mathrm{EF}{\mathrm{r}}_{\mathrm{C}}}{{\mathrm{r}}_{\mathrm{C}{\mathrm{O}}_2}}}$(28) (29) $EF=E_i\ast r_C$(29) (30) $C{O}_2(kg)=EF\ast \sum _{t=1}^{8760}fue{l}_{Consumption}(t)$(30)

Where $TEC$ – total emission cost($/g$C{O}_2$), E – load(kWh), $EF$ – emission factor, $fue{l}_{Consumption}$ – yearly fuel consumption, $C{O}_2$-Emission., $r_{C{O}_2}$ – indicator $GHG$ equivalent for each component, $r_C$ – the price of energy from renewable energy. (Evans, Strezov, and Evans 2009; Ghaffari and Askarzadeh 2020; Mokhtara et al. 2021; Nguyen et al. 2020).

3.4. Demand side management in hybrid renewable energy system

Any programme targeted to influence energy consumption characteristics is termed demand-side management. The programme must achieve its targeted objectives, such as reducing average electricity consumption rates, improving consumer satisfaction, and improving system reliability. Implementing effective demand-side management is crucial to achieving optimal operation of renewable energy-based microgrid systems, which is complicated by supply and load demand uncertainties. To avoid over the capacity of the plant as well as to reduce plant cost, demand side management(DSM) and demand response(DR) is essential in reliable operational design that might arise from a mismatch of power plant with demands (Parisio, Rikos, and Glielmo 2014).

DSM plays a major task in avoiding or shifting the peak load through DR which coordinates electricity use with the power system operation. The DR programme is a subcategory of DSM, often utilising techniques to induce consumers to reduce their energy consumption to limit peak demand. However, DR encourages consumers to increase their energy consumption during high production and low demand in renewable energy power plants (Siano 2014). Demand response measures directly or indirectly force energy consumption reduction for a short time in a critical situation like a direct load control (DLC) programme (Moura and de Almeida 2010). It is important to note that DR may limit customers’ comfort, but it desires to limit the downtime of the power plant system, which might expose customers to discomfort. An overview of demand response across continents by Paterakis, Erdinç, and Catalão (2017) showed that the increasing share of variable RE sources in the electricity grid mix intensifies the need to enhance flexibility in the system operations in order to accommodate any uncertainties of the power output that may jeopardise the security of supply. For this reason, DR is likely to be an essential resource to enhance flexibility and accommodate the increasing RES.

Energy loss possesses a significant challenge in isolated microgrids integrated with battery energy storage during charging and discharging cycles. As a result, the system efficiency decreases, prompting DSM to utilise the energy more efficiently. Demand-side management reduces the energy demand during off-peak sun hours by deferring or shifting some loads (demand response), hence reducing the charging, and discharging cycles of the system's battery. This approach reduces energy losses in the battery bank with a significant increase in overall system efficiency. The approach equally reduces the PV and battery capacity, respectively, which is further reflected in the capital cost reduction of the system (Singh 2017). A grid-connected PV system showed a stable grid network with maximum PV output at low load demand. This calls for a comprehensive analysis of economic options such as demand-side management, best dispatch strategy, storage system, automated control of PV output, and load shifting (Kumar et al. 2017). The study of optimal sizing and operation of a microgrid pumped storage system for an island community with deferrable loads considers demand response to improve the efficient use of variable renewable energy (Jing, Zhu, and Hu 2018).

Arabali et al. (2014) analysed the stochastic performance assessment for wind-PV using autoregressive moving average and Monte Carlos Simulation to find the least cost combination that satisfies system reliability requirements. The study suggested demand-side management using load-shifting techniques to provide some flexibility to reduce the overall cost and mismatch in energy supply and demand from the stochastic hybrid system. Load shifting, in this case, means using higher energy-intensive appliances during peak sun hours or high wind speed. Invariably intelligent energy management systems can be used to reduce/minimise battery aging costs and voltage fluctuations (Baloglu and Demir 2017).

5. Renewable energy system modeling

5.1. Wind power model

The fundamental mechanical equations governing wind energy conversion from a wind turbine are shown in equations (31) and (32). However, wind speed can harness power using wind turbine parameters as expressed in Equations (33) and (34). (31) ${\mathrm{P}}_{\mathrm{WT}}=\left\{\begin{array}{c}{\mathrm{P}}_{\mathrm{R}}\mathrm{if}{\mathrm{V}}_{\mathrm{s}}>{\mathrm{V}}_{\mathrm{r}}\mathrm{and}{\mathrm{V}}_{\mathrm{s}}<{\mathrm{V}}_{\mathrm{cut}\text{-}\mathrm{out}}\\ {\mathrm{V}}^3\left({\displaystyle \frac{{\mathrm{P}}_{\mathrm{R}}}{{\mathrm{V}}_{\mathrm{r}}^3\text{-}{\mathrm{V}}_{\mathrm{cut}\text{-}\mathrm{in}}^3}}\right)-\left({\displaystyle \frac{{\mathrm{V}}_{\mathrm{cut}\text{-}\mathrm{in}}^3}{{\mathrm{V}}_{\mathrm{r}}^3\text{-}{\mathrm{V}}_{\mathrm{cut}\text{-}\mathrm{in}}^3}}\right)\\ 0\mathrm{if}{\mathrm{V}}_{\mathrm{s}}<{\mathrm{V}}_{\mathrm{cut}\text{-}\mathrm{in}}\mathrm{or}{\mathrm{V}}_{\mathrm{s}}>{\mathrm{C}}_{\mathrm{cut}\text{-}\mathrm{out}}\end{array}\right\}$(31)

While wind turbine actual power ($P_{AWT}$) Is given as. (32) ${\mathrm{P}}_{\mathrm{AWT}}={\mathrm{P}}_{\mathrm{WT}}\ast {\mathrm{A}}_{\mathrm{WT}}\ast {\eta }_{\mathrm{WT}}$(32) where $P_R,V_r,V_s,V_{cut-out},$ $V_{cut-in}^3$, ${\eta }_{WT}$, $A_{WT}$ are power rated of the wind turbine, WT rated wind speed, study area wind speed, WT cut-out wind speed, cut-in wind speed of the WT, the efficiency of the wind turbine, and total swept area, respectively. (Baloglu and Demir 2017; Bhandari et al. 2014, 2015; Mokhtara et al. 2021; Mokheimer, Al-sharafi, and Habib 2015; Momoh, El-Hawary, and Adapa 1999; Sinha and Chandel 2015; Pavankumar, Kollu, and Debnath 2021)

Wind speed distribution can be attained by Weibull distribution. The probability density is given as- (33) ${\mathrm{f}}_{\mathrm{c}}={\displaystyle \frac{\mathrm{k}}{\mathrm{c}}\ast {\left({\displaystyle \frac{\mathrm{v}}{\mathrm{c}}}\right)}^{\mathrm{k}\text{-}1}\ast \exp \left[-{\left({\displaystyle \frac{\mathrm{v}}{\mathrm{c}}}\right)}^{\mathrm{k}}\right]}$(33) The average power output for every hour in a typical month for Wind energy can be calculated using equation (34) (34) ${\mathrm{P}}_{\mathrm{w}.\mathrm{av}}={\int }_0^{\mathrm{\infty }}{\mathrm{P}}_{\mathrm{WT}}\ast {\mathrm{f}}_{\mathrm{v}}\ast \mathrm{dv}$(34) where: $f_c$, $k$, $c$, $v$, $f_v$ and $P_{WT}$ are probability density function, shape factor, scale factor, wind speed, and electrical power output of the turbine.

5.2. Solar PV modelling

Photovoltaic (PV) cells are P-N junction semiconductor devices that convert sunlight (photons) to electricity (Bhandari et al. 2014). Its equivalent circuits are made up of a current source (photocurrent), one or two diode(s) parallel to the current source, an internal resistor to impede the flow of current, and a shunt resistor to express current leakages (Baba Kyari and Ya’u Muhammad 2019). PV models are classified as single-diode or double-diode models while the most commonly used model in history is single-diode (Rao 2009).

The current ($I$) supplied in the single diode model can be denoted as the function of output voltage$(V)$ as- (35) $\mathrm{I}(\mathrm{V})={\mathrm{I}}_{\mathrm{PH}}-{\mathrm{I}}_{\mathrm{O}}\left[\exp \left({\displaystyle \frac{\mathrm{V}+\mathrm{I}{\mathrm{R}}_{\mathrm{S}}}{\mathrm{d}}-1}\right)\right]\text{-}{\displaystyle \frac{\mathrm{V}+\mathrm{I}{\mathrm{R}}_{\mathrm{S}}}{{\mathrm{R}}_{\mathrm{P}}}}$(35) (36) ${\mathrm{P}}_{\mathrm{PH}}={\displaystyle \frac{\mathrm{G}}{{\mathrm{G}}_0}[{\mathrm{I}}_{\mathrm{PH}\text{-}\mathrm{STC}}+{\mathrm{C}}_{\mathrm{T}}(\mathrm{T}\text{-}298)]}$(36) (37) ${\mathrm{I}}_0={\mathrm{I}}_{0\text{-}\mathrm{STC}}{\left({\displaystyle \frac{\mathrm{T}}{298}}\right)}^3\left[\exp {\displaystyle \frac{\mathrm{q}{\mathrm{E}}_{\mathrm{g}}}{\mathrm{dK}}\left({\displaystyle \frac{1}{298}\text{-}{\displaystyle \frac{1}{\mathrm{T}}}}\right)}\right]$(37)

Diffuse and normal radiation are total radiation that is incident on PV cells with varying intensity of the sun relevant to its position and time of the year. Equation (38) shows the relationship between the trios. (Duffie, Beckman, and McGowan 1985) (38) ${\mathrm{I}}_{\mathrm{Tt}}={\mathrm{I}}_{\mathrm{n}}\ast {\mathrm{I}}_{\mathrm{n}}+{\mathrm{I}}_{\mathrm{d}}\ast {\mathrm{R}}_{\mathrm{d}}$(38)

PV hourly power output to the area of installation and total solar radiation on average day ‘j’ of the month (Bhandari et al. 2015; Duffie, Beckman, and McGowan 1985; Evans 1981; Habib et al. 1999) is given as. (39a) ${\mathrm{P}}_{\mathrm{PV}\text{-}\mathrm{hj}}={\mathrm{I}}_{\mathrm{Tt}\text{-}\mathrm{j}}\eta {\mathrm{A}}_{\mathrm{PV}}(39\mathrm{a})$(39a) were, (39b) $\eta ={\eta }_{\mathrm{m}}{\eta }_{\mathrm{pc}}{\mathrm{P}}_{\mathrm{f}}$(39b) (39c) ${\eta }_{\mathrm{m}}={\eta }_{\mathrm{r}}[1\text{-}\beta ({\mathrm{T}}_{\mathrm{c}}\text{-}{\mathrm{T}}_{\mathrm{r}})]$(39c) (39d) ${\mathrm{T}}_{\mathrm{c}}={\mathrm{T}}_{\mathrm{a}}+{\displaystyle \frac{\alpha \tau }{{\mathrm{U}}_{\mathrm{L}}}{\mathrm{I}}_{\mathrm{Tt}}}$(39d)

Then, (39e) ${\displaystyle \frac{{\mathrm{U}}_{\mathrm{L}}}{{\alpha }_{\tau }}={\displaystyle \frac{{\mathrm{I}}_{\mathrm{Tt}\text{-}\mathrm{NOCT}}}{(\mathrm{NOCT}\text{-}{\mathrm{T}}_{\mathrm{a}\text{-}\mathrm{NOCT}})}}}$(39e)

Open circuit voltage $({\mathrm{v}}_{0\mathrm{c}})$ with its relative maximum power$({\mathrm{P}}_{\mathrm{MAX}})$ the output of the single-diode Photovoltaic (PV) (Bhandari et al. 2014, 2015; Sun et al. 2020; Zhou, Yang, and Fang 2007) is presented as. (40) ${\mathrm{v}}_{0\mathrm{c}}={\displaystyle \frac{{\mathrm{V}}_{0\mathrm{C}}}{\mathrm{cKT}/\mathrm{q}}}$(40) (41) $\begin{array}{rl}{\mathrm{P}}_{\mathrm{MAX}}& ={\displaystyle \frac{{\mathrm{V}}_{0\mathrm{C}}/{\eta }_{\mathrm{MPP}}\mathrm{KT}/\mathrm{q}\text{-}\ln ({\mathrm{V}}_{0\mathrm{C}}/{\eta }_{\mathrm{MPP}}\mathrm{KT}/\mathrm{q}+0.72)}{1+{\mathrm{V}}_{0\mathrm{c}}/{\eta }_{\mathrm{MPP}}\mathrm{KT}/\mathrm{q}}\ast {\mathrm{I}}_{\mathrm{SCO}}{\left({\displaystyle \frac{\mathrm{G}}{{\mathrm{G}}_0}}\right)}^{\alpha }}\\ & \ast \left(1-{\displaystyle \frac{{\mathrm{R}}_{\mathrm{S}}}{{\mathrm{V}}_{0\mathrm{C}}/{\mathrm{I}}_{\mathrm{SC}}}}\right)\ast {\left({\displaystyle \frac{{\mathrm{T}}_0}{\mathrm{T}}}\right)}^{\gamma }\ast {\displaystyle \frac{{\mathrm{V}}_{0\mathrm{C}}}{1+\beta \ln \mathrm{G}/{\mathrm{G}}_0}}\end{array}$(41)

The total power output from the PV array in parallel and series is given as. (42) ${\mathrm{P}}_{\mathrm{PV}\text{-}\mathrm{array}}={\mathrm{N}}_{\mathrm{S}}\ast {\mathrm{N}}_{\mathrm{P}}\ast {\mathrm{P}}_{\mathrm{MAX}}\ast {\eta }_{\mathrm{MPP}}\ast {\eta }_{OTHERS}$(42) Were, $V$, $I$, $a$re Voltage and Current of the PV modules which varies with the availability of temperature and solar radiation, $I_0$ is diode reverse saturated current $I_{0-STC}$ is nominal saturated voltage, G – Available solar irradiation $G_O$-Nominal solar radiation (1000W/m²), $P_{PH}$-Photocurrent $d$-ideality factor, $C_T$-Cell circuit current temperature coefficient $R_S$ – series resistor, K-Boltzman constant. (1.38 × 10-23 J/K) $R_P$-parallel resistor, q-Electron charge (1.602 × 10-19 C) $E_g$-Energy gap of a semiconductor, $P_{pv-hj}$ – Hourly power output of PV (KW) $A_{pv}$ – PV area (m²), $I_{Tt-j}$-Toral solar energy radiation for j day $\eta$ – system efficiency, ${\eta }_m$-Module efficiency ${\eta }_{pc}$ – power conditioning efficiency, $P_f$ – power factor ${\eta }_r$-module reference efficiency, $T_r$-reference temperature $T_c$-monthly average temperature, $\beta$ – specific related dimensionless coefficient (0.058), $T_a$ – Instantaneous ambient temperature, $U_L$-coefficient of surrounding heat transfer{kW/m^2oC} ${\alpha }_{\tau }$-PV optical efficiency. $I_{Tt}$ – Total radiation $NOCT$ – Normal operating cell temp. $v_{0c}$-normalized open circuit voltage, $V_{0C}$ – Open circuit voltage T – PV module temperature (K), $\alpha$ – non-linear temp.-voltage effect. $P_{pv-array}$ – Power output from PV-array, $N_S$ – Numbers of series-connected modules, $N_P$-Number of parallel-connected PV modules ${\eta }_{MPP}$ = d = 95%, ${\eta }_{OTHERS}$ – factors with respect to losses (0.47%).

Weibull distribution using probability density for solar radiation distribution is shown in equation (43). (43) ${\mathrm{f}}_{\mathrm{S}}={\displaystyle \frac{\mathrm{k}}{\mathrm{c}}\ast {\left({\displaystyle \frac{\mathrm{I}}{\mathrm{c}}}\right)}^{\mathrm{k}\text{-}1}\ast \exp \left[-{\left({\displaystyle \frac{\mathrm{I}}{\mathrm{c}}}\right)}^{\mathrm{k}}\right]}$(43)

The average power output for every hour in a typical month for solar PV can be calculated using equation (44). (44) ${\mathrm{P}}_{\mathrm{PV}.\mathrm{av}}={\int }_0^{\mathrm{\infty }}{\mathrm{P}}_{\mathrm{WT}}\ast {\mathrm{f}}_{\mathrm{S}}\ast \mathrm{dv}$(44) where $f_s$, $k$, $c$, $v$, $f_v$ and $P_{WT}$ are probability density function of solar irradiation, shape factor, scale factor, solar radiation, probability density function, and electrical power output of the turbine.

5.3. Hydropower modeling

There is a linear and non-linear hydro-turbine model set with elastic and non-elastic column effects (Acakpovi, Hagan, and Xavier Fifatin 2014; Ramey and Skooglund 1970). Hydroelectric power (P) from the turbine considering the head and flow rate of the river is given in equation (46). The flow rate of a runoff hydropower system of a given catchment/watershed with (hourly, daily, and monthly) rainfall is given as. (45) ${\mathrm{Q}}_{\mathrm{SITE}}=\mathrm{K}\left[{\displaystyle \frac{{\mathrm{A}}_{\mathrm{SITE}}}{{\mathrm{A}}_{\mathrm{GAUGE}}}}\right]{\mathrm{Q}}_{\mathrm{GAUGE}}$(45)

Hydroelectric power ($P_{HE}$) generated by the turbine is given as. (46) ${\mathrm{P}}_{\mathrm{HE}}={\eta }_{\mathrm{Tt}}\ast \rho \ast \mathrm{gQH}$(46) (47) ${\eta }_{\mathrm{Tt}}(\lambda ,\mathrm{Q})=(3.33\mathrm{Q})\ast \left[{\displaystyle \frac{1}{2}\left({\displaystyle \frac{90}{{\lambda }_{\mathrm{i}}}+\mathrm{Q}+0.78}\right)\exp \left({\displaystyle \frac{-50}{{\lambda }_{\mathrm{i}}}}\right)}\right]$(47) (48) ${\lambda }_{\mathrm{i}}={\left[{\displaystyle \frac{1}{\lambda +0.089}-0.0035}\right]}^{-1}$(48) (49) $\lambda ={\displaystyle \frac{\mathrm{RA}\omega }{\mathrm{Q}}}$(49) where $Q_{SITE}$, $K$, $A_{GAUGE}$, $Q_{GAUGE}$, $A_{SITE},$ $\rho$, ${\eta }_{Tt}$, $g$, $Q$, $H$, R, A, $\omega$ are discharged at a site(m³/s), scaling function, gauge catchment area (m²), discharge at the gauge, power plant catchment area (m²), water density(1000kg/m³), turbine hydraulic efficiency, acceleration due to gravity (10ms-²), flow rate, head, the radius of the hydraulic turbine blade (m), swept area of the rotor(m²) and angular speed of rotor respectively (Acakpovi, Hagan, and Xavier Fifatin 2014; Bhandari et al. 2014; Márquez, Molina, and Pacas 2010; Ramey and Skooglund 1970).

5.4. Biomass model

Biomass gasification power output depends on the lower heating value of biofuel, and its gasifier efficiency is defined as shown in equation (50) (50) ${\eta }_{\mathrm{gasification}}={\displaystyle \frac{{\mathrm{M}}_{\mathrm{g}}\mathrm{LH}{\mathrm{V}}_{\mathrm{g}}}{{\mathrm{M}}_{\mathrm{b}}\mathrm{LH}{\mathrm{V}}_{\mathrm{bg}}}}$(50) where $M_g$, $M_b$, $LH{V}_g$, $LH{V}_{bg}$ are masses of gas generated by gasification, masses of biomass, the lower heating value of gas generated by gasifier, and lower heating value of biomass. (Balamurugan, Kumaravel, and Ashok 2011)

The power output of biomass generators $(P_{e-bg})$ is given by equation (51) (51) ${\mathrm{P}}_{\mathrm{e}\text{-}\mathrm{bg}}(\mathrm{t})={\eta }_{\mathrm{gasification}}\ast {\mathrm{Q}}_{\mathrm{bg}}\ast \mathrm{LH}{\mathrm{V}}_{\mathrm{bg}}$(51) (52) $\mathrm{LH}{\mathrm{V}}_{\mathrm{bg}}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{methane}}}{100}\ast \mathrm{LH}{\mathrm{V}}_{\mathrm{methane}}}$(52) Where ${\eta }_{gasification}$ is electrical conversion efficiency (25–40%)?, $Q_{bg}$ – flow consumption of biogas (m³/h), $LH{V}_{bg}$ – the measure of the volume of methane fraction in organic matter (36.3MJ/m³ or 10kEh/m³), $P_{methane}$ – the percentage of methane in the biomass.

The hourly Biomass gasifier energy output is expressed thus in equation (53). (53) ${\mathrm{Q}}_{\mathrm{bg}}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{W}\text{-}\mathrm{bg}}(\mathrm{t})}{{\eta }_{\mathrm{gasification}}\mathrm{LH}{\mathrm{V}}_{\mathrm{bg}}}}$(53) where $P_{W-bg}(t)$ – Biogas generator working. (Heydari and Askarzadeh 2016)

More so, annual electricity output ($P_{E-Annual}$) of biomass gasification in terms of capacity utilisation factor (CF) is given as. (54) $P_{E-Annual}=P_{BMG-R}\ast (8760\ast CF)$(54) Hourly energy output to the capacity utilisation factor is also given as (55) ${\mathrm{P}}_{\mathrm{E}\text{-}\mathrm{HR}}={\mathrm{P}}_{\mathrm{BMG}\text{-}\mathrm{R}}\ast {\eta }_{\mathrm{gasification}}$(55) where $P_{BMG-R}$ – The rated power output of a biogas electricity generator (Gupta, Saini, and Sharma 2010).

6. Scope for future work

Extensive work should be carried out on the industrial application of Fuel Cell/Hydrogen/ methanol fuel to decommission battery usage from HRES for Environmental Safety and cost minimisation. The result shows that fuel cell storage can be used instead of the generator to support the system because its capacity surpasses batteries and can prolong electricity supply when wind and solar are insufficient under windless weather, cloudy, and polar nights (Grigoriev et al. 2018).

Extensive work on the reliability assessment of the SOC profile and battery life cycle was recommended for future evaluation.

The tradeoff between PV/Solar Thermal and PHES/AACAS/MT storage using non-linear optimisation techniques should be corrected via a multi-objective and stochastic model.

More precise techniques should be expected in future work comprising Trigen/Turbo hybrid generator information of combining heat and power rather than reinforcing learning methods.

The study suggested demand-side management using load-shifting techniques to provide some flexibility to reduce the overall cost and mismatch in energy supply and demand from the stochastic hybrid system. Load shifting, in this case, means using higher energy-intensive appliances during peak sun hours or high wind speed.

Social acceptability and Environmental issues should not be left out in the design and optimisation of HRES as often done in most research work.

Energy demand and resource forecast should be a yardstick for sustainable energy transition, design, and deployment.

7. Conclusion

Efficiently utilising the best technological mix of RES can solve the LSPS, LOLP, LOLR, or LOLD, high operational and maintenance costs, social and environmental issues associated with HRES, including energy development problems. This study reviews multi-objective criterion and optimisation considerations important for the optimal configuration of hybrid renewables for sustainable energy development. Furthermore, integrating multi-objective criteria into modern computing tools such as artificial intelligence will alleviate complex optimisation problems with a better understanding of HRES. This survey also covers system design of Solar, Hydropower, Wind, and Biomass, and optimisation techniques as obtainable from previous research. Trade-offs between the economics, reliability, capacity, social and environmental optimal system designs are critical for optimal HRES performance and applications. In addition, modern computing techniques involving AI can solve complex optimisation issues if properly used for project specificity. Future research should identify AI optimisation methods specific to HRES, as it is the most effective method for solving optimisation problems.

Acknowledgements

Author Contributions: Conceptualization: E.A.O, S.G, and O.K.A.; Methodology and Assessment: S.G and E.A.O., research: O.K.A.; Drafting original draft: C.V.O and O.K.A.; Editing and proofreading: C.V.O and O.K.A.; Supervision: E.A.O and S.G. All authors have read and approved the published version of the manuscript and have no conflicts of interest.

Disclosure statement

No potential conflict of interest was reported by the author(s).