Mathematical modelling in the discourses of the KOM and PISA frameworks and teacher interviews

ABSTRACT

Mathematical modelling is emphasised in curricula worldwide. Since 2006, mathematical modelling has been considered a fundamental process in the mathematics subject in Norwegian upper secondary schools. This study aimed to identify tensions in the approaches to mathematical modelling expressed in teacher interviews (N = 4) and framework discourses (KOM and PISA) by four characteristics of communication (word use, routines, visual mediators and endorsed narratives). The tensions identified encompassed students’ abilities to make choices and decisions during modelling activities and connection to specific mathematical content or real-life situations. Teachers also questioned the relevance of mathematical modelling, even though the main reason for the implementation of mathematical modelling in education is to make school mathematics relevant for everyday life.

KEYWORDS:

• Mathematical modelling
• upper secondary school
• discourse analysis

Introduction

Although there is an increasing emphasis on mathematical modelling in education, the presence of modelling activities in day-to-day teaching is still limited (Blum & Pollak, 2018). The debate about how mathematical modelling should be handled in schools has been ongoing since the late 1960s (Julie & Mudaly, 2007). In many countries, modelling has been a part of mathematics curricula for decades. Since 2006, a Norwegian curriculum for upper secondary schools has described modelling as “a fundamental process in the subject, where the starting point is something that actually exists. This is described in mathematical terms through a formulated model, and the results are discussed in light of the original situation” (Norwegian Ministry of Education and Research, 2013, p. 2). Blum (2002) described a substantial gap between the ideals of educational debates about modelling and everyday teaching practices. However, there is still a gap when modelling has been a part of the curriculum for 30 years. This study aimed to provide insight into possible tensions in mathematical modelling approaches by comparing teachers’ descriptions of mathematical modelling with how modelling is described in frameworks written by scholars.

Mathematical modelling and frameworks

Niss and Blum (2020) defined two overarching reasons for including mathematical modelling as a significant component of learning at all levels of education. In simple terms, they formulated the first reason as mathematics for the sake of modelling, building on the fact that mathematics plays an important role in how individuals understand and interact with the world. Therefore, they argued that undertaking mathematical modelling should be a goal in mathematics education. The second reason is to “employ modelling as a means for something else, above all for supporting the learning of mathematics, by [e.g.] offering motivation for its study” (p. 28). Put simply, they labelled this reason modelling for the sake of mathematics. The reasons for modelling affect how modelling is implemented and which activities are performed in classrooms (Blum, 2015).

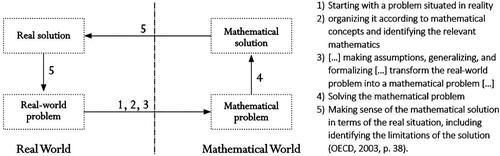
The 2006 Norwegian mathematics curriculum was inspired by the Danish framework of Niss and Jensen (2002) – Competencies and the Learning of Mathematics (KOM) (Botten, 2016) – which has been revisited in English (see Niss & Højgaard, 2019). The curriculum also included five basic interdisciplinary skills. According to Breakspear (2012), parallels can be drawn between such interdisciplinary mathematical skills and the Programme for International Student Assessment (PISA) framework's notion of mathematical literacy, which includes mathematical modelling (Organisation for Economic Co-operation and Development [OECD], 2003). Niss (2015), who was involved in developing both frameworks, presented the eight competencies in the KOM framework and discussed them concerning the PISA framework. In the KOM framework, modelling competence is two-sided. One side involves analysing and discussing the range and reliability of existing models – that is, de-mathematising the model to reveal hidden mathematics in society. The other side involves active model building; mathematics is used to deal with matters outside of mathematics itself (Niss & Jensen, 2002). The PISA 2003 framework focuses on the process of mathematisation, the active model building to which the KOM framework refers. In the PISA framework, this includes five processes (Figure 1) and is defined as “the fundamental process that students use to solve real-life problems” (OECD, 2003, p. 38). This cycle is also referred to as a modelling cycle (OECD, 2018; Stacey, 2015). Stillman (2015, p. 792) separated modelling from the applications of mathematics, stating that applications have “the direction (mathematics → reality) [see step 5 in Figure 1]. In mathematical modelling, the reverse direction (reality → mathematics) is the focus [steps 1, 2 and 3 in Figure 1]” (p. 792). The PISA 2012 framework indicates that often, “significant parts of the mathematical modelling cycle have been undertaken by others … many PISA items involve only parts of the modelling cycle” (OECD, 2013, p. 26). This is due to assessment tasks, which might not communicate the entire modelling process. Boaler (2001) found that students who were given open-ended tasks, including decision-making, obtained better results on the national examination and found school mathematics relevant for everyday life. According to Blum (2015), modelling is not a spectator sport but a cognitively demanding activity. These descriptions of mathematical modelling include complex cognitive processes, as described by Anderson et al. (2001) in processes of analysing, evaluating and creating. These are necessary when solving tasks for which students have not been taught a specific algorithm (Thompson, 2008). In contrast, less complex cognitive processes (e.g. remembering and applying) are involved when solving tasks by recalling information of well-known algorithms in contexts and situations likely familiar to students (Thompson, 2008). Intervention studies have shown that modelling helps students gain a deeper understanding of mathematical concepts (Zbiek & Conner, 2006) and facilitates the exploration, representation, formal construction and validation of mathematical results (Zapata-Grajales et al., 2018). Students become more self-directed as learners (Voss & Rickards, 2016) and see mathematics as relevant outside of school (Brown & Stillman, 2017).

Figure 1. Mathematisation cycle of the PISA 2003 framework (OECD, 2003, p. 38).

Knowledge in teaching mathematical modelling

Borromeo Ferri (2018) indicated four dimensions that should be considered when teaching mathematical modelling. One is the theoretical dimension, which comprises modelling cycles, the aims and perspectives of modelling and the types of modelling tasks (e.g. holistic tasks, which include all parts of a modelling process, and atomistic tasks, which include only parts of the modelling process). She emphasised that teachers must “understand the goals and aims of mathematical modelling, and how [to] use the modelling cycle as a multi-purpose learning instrument” (p. x). Conversely, Frejd (2012) investigated teachers’ conceptions of mathematical modelling in a Swedish upper secondary school and found that the teachers had little experience with modelling. In Turkey, Özdemir et al. (2017) studied 17 elementary teachers’ views on modelling applicability. The teachers saw modelling as relevant and reported using real-life problems and mathematics as tools to explain real-life situations. Not all teachers focused on the mathematisation process or saw modelling as an innovative approach or a process requiring thought. In several countries, such as Indonesia (Widyastuti & Wijaya, 2020), PISA-type problems are included in mathematics education as a response to not satisfying results on the PISA test. Japan also introduced a new national assessment that contained such problems. Ikeda (2015) discussed the results of a teacher questionnaire that assessed the emphasis teachers placed on real-world situations. Even after PISA-type problems were added to the national assessment, approximately 40% of teachers stated that they seldom taught the relationship between mathematics and real-world problems. This indicates that these PISA-type problems might not effectively confer the knowledge that students need “to use mathematics in the everyday aspect of their personal, civic and professional lives” (OECD, 2018, p. 43), as expressed in the latest PISA framework.

Theoretical framework of discourse analysis

Discourses can be investigated through four characteristics of communication: word use, visual mediators, routines and endorsed narratives (Morgan & Sfard, 2016). Mathematical vocabulary words can be understood as having explicit definitions, although they are used differently in colloquial discourses. Visual mediators are objects used to explain and communicate (e.g. algebraic ideographs, graphs and other visualisations). Mathematical routines are patterns of behaviour (e.g. following an algorithm when solving a mathematical task, or “set of rules that merely constrain the performer's actions” [Morgan & Sfard, 2016, p. 101]). Endorsed narratives refer to stories considered by the mathematical community as reliable descriptions of the mathematical universe. Narratives are continuously constructed (Morgan & Sfard, 2016). This study explores descriptions of mathematical modelling by identifying narratives.

Reification and alienation are two tightly related sub-processes of objectification, the “process in which a noun begins to be used as if it signified an extra discursive, self-sustained entity (object) independent of human agency” (Sfard, 2008, p. 300). Reification is the act of replacing sentences about processes and actions with propositions about states and objects. For example, “he was organising the problem situated in reality according to mathematical concepts, identifying the relevant mathematics and gradually trimming away reality through processes such as making assumptions, generalising and formalising, which promoted the mathematical features of the situation and transformed the real-world problem into a mathematical problem that faithfully presents the situation” can be reified as “he mathematised the real-world problem”. The phrase “mathematisation of the real-world problem” is introduced to simplify communication. Alienation means eliminating human subjects from sentences by using passive voice or employing the given noun as the grammatical subject. For example, alienation transforms “when he mathematised the real-world situation, he emphasised … ” to “the mathematisation of the situation pointed out that … ”. Mathematisation is now expressed as a noun, disguising the fact that it is caused by human action. When people objectify, they refer to a thing rather than a process. People objectify because they need to, and objectification increases the communicative and practical effectiveness of discourse (Sfard, 2008). If a discourse discusses an alienated and reified, and thus objectified, concept, the discourse has constructed a common understanding of the concept (Morgan & Sfard, 2016). However, objectification might hinder the understanding of mathematics as a human activity. Seeing processes as objects without human interaction might lead to the understanding of mathematical knowledge as absolute and contingent. Therefore, objectification can provide insight into the certainty of the approach to mathematical modelling in a discourse. For example, the phrasing “the interpretation” rather than “to interpret” may indicate that students are less free to interpret a mathematical answer themselves, insinuating a correct way of interpreting a mathematical answer. “To find the model” might communicate that there is one right answer, instead of using the term “modelling”, a process in which the aim is to represent a situation with mathematics to answer non-mathematical questions and evaluate and adjust a mathematical model.

Mathematical modelling has explicitly been a part of the curriculum in Norwegian upper secondary schools since 1994, where it was expressed that students “should be involved in the whole modelling process. They should be given practice in formulating the original problem in mathematical terms, choosing appropriate methods, solving the problem, and finally interpreting and evaluating the answer in the original situation” (Norwegian Ministry of Church, Education and Research, 1994, p. 5). This research provides insight into mathematical modelling approaches decades after they were implemented by investigating the following question:

What possible tensions in the approaches to mathematical modelling can be identified from a discourse analysis of relevant framework documents and interviews with four teachers?

Methods

Teacher discourse in the Norwegian context

Mathematical modelling has been one of the four main areas of a specific practical mathematics subject (2P) in Norwegian upper secondary schools since 2006. This subject is an alternative to theoretical mathematics for science education or mathematics for social science and economics. These students are 16 and 17 years old and in their second year of upper secondary school. To find teachers to interview, four schools in different towns and villages in two different counties were contacted at the beginning of the school year to determine who was teaching the specific course that year. The first teachers named by the four schools agreed to participate. Their teaching experience in mathematics varied from 4 to 20 years. When the interviewees’ own perspectives are emphasised, a semi-structured interview is suitable (Bryman, 2016) and therefore selected. The interview guide was formulated in five sections:

1. Background and experience in mathematical modelling from own schooling:

   • 1.1 Own education

   • 1.2 Years of experience as a teacher

   • 1.3 Modelling in own education

   • 1.4 Modelling experience in own schooling

2. Practical mathematics:

   • 2.1 Difference between 2P and other mathematics subjects

   • 2.2 What are the challenges in the teaching of 2P?

   • 2.3 What are the challenges for the students in 2P?

   • 2.4 What is practical mathematics?

   • 2.5 What have the students learned at the end of the year?

   • 2.6 What is the overall aim for the subject 2P as you see it?

3. Teaching mathematical modelling:

   • 3.1 Use of textbooks

   • 3.2 Are you focusing on the overall view of what modelling is? What do you emphasise?

   • 3.3 When do you include mathematical modelling in your teaching? Within a limited period or throughout the school year?

   • 3.4 What do the students use most of their time on when modelling?

   • 3.5 What are the challenges for the students when modelling?

   • 3.6 What does this mean that “modelling is a fundamental process of the subject”?

   • 3.7 How do you evaluate students’ mathematical competence?

   • 3.8 In your opinion, is the national exam testing modelling competence?

4. Definition of modelling:

   • 4.1 Where does your understanding of modelling originate from?

   • 4.2 What is, as you see it, the most crucial part of the modelling process?

   • 4.3 Would you say modelling differs from other content areas within mathematics? How?

   • 4.4 What must be involved in calling it mathematical modelling?

   • 4.5 Is modelling connected to problem-solving? How?

   • 4.6 Is modelling competence an important part of mathematics?

5. Evaluate the three tasks concerning mathematical modelling.

The three tasks differed in their depth of engagement in a real-world context and were included to let the teachers express their aims for teaching modelling and the description of the modelling process as well as their students’ routines.

Framework discourse

The framework discourse included the KOM section describing modelling competence, as well as the PISA 2003 section regarding mathematising. Jablonka and Bergsten (2010) determined the PISA framework to be a circular construction in which modelling is described as one of eight components of mathematical literacy; at the same time, it describes the processes of mathematising as the “main constitutive component” of mathematical literacy. This study includes only the description of mathematising, not the whole framework describing mathematical literacy. These frameworks were chosen because of their influence on the Norwegian curriculum and the PISA framework's worldwide influence.

Description of analysis

The analysis tool of Morgan and Sfard (2016) for written examination discourse was adapted for this study. This tool includes guiding questions and textual indicators suitable for identifying aspects within the four characteristics of communication with respect to mathematics. “Possibly in a slightly adapted form”, it is useful in other contexts, e.g. “comparisons between discourses in written and spoken forms within mathematics education” (Morgan & Sfard, 2016, p. 115). See the adapted form for this study in Table 1. The original authors categorised word use as specialised or non-specialised to the discourse of school mathematics; this was not done in this study. The original authors investigated the development of the discourse of mathematics examination tasks, including their logical complexity. In the present study, in which the notion of mathematical modelling was evaluated, mathematical complexity was less relevant; therefore, the guiding question concerning this was not included. Furthermore, instead of evaluating the specialised mathematical language used, this study evaluated the specialised language about the educational use of mathematical modelling, particularly concerning the theoretical component of teaching mathematical modelling. This component was also included within visual mediators, and a guiding question about a modelling cycle was added. A question about specific mathematical content was included within the characteristics of word use. The depth of engagement in a real-world context was already expressed in the original tool and seen as highly relevant in the evaluation of mathematical modelling. Although the original authors evaluated it directly on mathematical examination tasks, in this study, it was explored in the descriptions of mathematical modelling by frameworks and teachers. Tensions between the two discourses were identified as differences that could lead to contrary meanings. Relevant data relating to each of the four topics were collected from the frameworks and interview transcripts. Textual indicators were formulated and tested in the two discourses. They were reformulated, adjusted and ultimately expressed, as shown in Table 1. Relevant sections were marked for each textual indicator for each discourse. The text sections connected to each textual indicator were investigated through the guiding questions for each discourse and compared to identify tensions in modelling approaches. Differences in the answers to the guiding questions from the text sections in the two discourses were identified and written out for each of the four aspects of discourse (word use, visual mediators, routines and endorsed narratives). The differences were compared, and some overlapped and were related. From this process, five distinct tensions were identified. These are presented under four headings in the next section.

Table 1. Analytic tool, adjusted from Morgan and Sfard (2016).

	Aspects of discourse	Questions guiding the analysis	Textual indicators
Word use	Specialisation	To what extent is specialised language about educational mathematical modelling used?	Terms from the theory of educational mathematical modelling (e.g. mathematising), including different perspectives of mathematical modelling. Depth of engagement in a real-world context. Aim to solve a problem or create a mathematical model?
	Objectification of the discourse	To what extent does the discourse speak of properties of objects and the relationship between them rather than of processes?	Are, for example, properties of the modelling process depicted, or are models mentioned as objects?
		Is the mathematical modelling connected to specific mathematical content?	Which mathematical content is mentioned explicitly?
Visual mediator	The presence of multiple visual mediators	Is a modelling cycle included?	Visual mediator included in a framework or mentioned by teachers.
		To what extent does the discourse make use of specialised mathematical modes?	Refers to graphs, function expressions, tables, etc.
		How are multiple visual mediators incorporated into the discourse?	Are the mediators provided by students, teachers or textbooks?
	Transitions between visual mediators	What transformations need to be made between different modes?	Presence or demand of two or more modes of communication-equivalent information (e.g. both function expression and graph?)
		How are transformations indicated in the discourse?	Provided by a teacher or to be produced by students?
Routines	The types of action demanded of students	What areas of mathematics are involved?	Are the routines connected to special mathematics content?
		What are the characteristics of the routine procedures?	Are the students supposed to perform an algorithm, or do they have to engage in the situation at a different level?
Endorsed narratives	The origin of mathematical knowledge	What is the degree of alienation of the discourse?	Mathematical objects as agents in processes: Non-finite verb forms? Passive voice?
		To what extent is mathematics construed as involving material action or as atemporal objects and their properties?	Mathematical objects involved in material processes or relation/existential processes.
		To what extent is mathematics presented as a human activity?	Is mathematics expressed as useful and necessary knowledge? Is mathematical modelling included in mathematical knowledge?
	The status of mathematical knowledge as absolute or contingent	To what extent does the text indicate that decisions or choices are possible during mathematical activity?	Modifiers indicating a degree of certainty (may, can, will) Conditional clauses (if … or when …) Explicit decisions have been or need to be made

The fact that only four teachers were interviewed in this study might be considered a weakness. However, the aim was not to establish generalised truths about all teachers but to identify tensions related to the teaching of mathematical modelling, which has been present for several decades. Interviewing four different teachers from different schools and with different educational backgrounds and experiences provided the current study with rich data. Since the present study aimed to examine how individual teachers discussed teaching mathematical modelling, individual interviews were utilised instead of a group interview. The use of guiding questions and textual indicators reduced the possibility of bias in the analysis and made the results more reliable. Because of the space limit, some of the quotes may appear detached from the discourse when presented, but the arguments are represented by various quotes from multiple teachers to expose the identified tensions. When comparing frameworks and teacher discourses, one may expect the framework to be more precise, but general, in the descriptions of student activities. Prior to the interviews, the teachers only knew that the topic was mathematical modelling; therefore, there was no way for them to prepare. They were given the opportunity to talk openly during the interview, and the conversation occasionally became informal when the interviewer gave the teachers room to speak out. Therefore, one must be aware of the different characteristics of the two discourses when considering the present results. This study could have analysed the curriculum instead of the framework discourses. However, in the frameworks, there are also descriptions of the different aims, processes and example tasks. These are only vaguely presented in the curriculum. In addition, the PISA framework is well known in most countries, and including this framework makes it more accessible for readers.

Results

The tensions found across the aspects of discourse are presented and evaluated under the following four headlines.

Students’ opportunities to make their own decisions

Teachers used verbs in informal language as follows: “They have to make a function expression” (Teacher 2) and “to develop a mathematical model” (Teacher 1). Even if this language was not reified, they spoke of the objects “model” and “function expression”. When a teacher was asked how she introduced modelling, she said, “We have not yet used the term modelling, but we have talked about functions and the fact that mathematical models can be expressed as a function expression or a graph or a table” (Teacher 1). The teacher discourse was not objectified. The PISA framework was less reified when the processes in the cycle (Figure 1) were explained in a passive voice, thus alienated, showing a degree of objectification but still expressing the processes rather than objects. This may indicate a focus on students’ decisions in the frameworks. Here, the students’ tasks were presented as wide and open-ended. The KOM framework indicates that focusing only on certain parts of the modelling process in a given situation may be appropriate for helping students engage in situations. However, the aim is for students to perform all parts of the process themselves. When asked whether there was a focus on mathematical modelling throughout the year or in a limited period, Teacher 2 said that the students were not mature enough to work on overarching modelling tasks over time. Teachers expressed involvement in the modelling process; for example, students were given strict instructions when working on practical tasks, such as collecting empirical data. The students were given a table to fill out when collecting data (Teacher 4). Teacher 1 expressed that, when given an open task, “[the students] use too much time to find out what to do. So, I would guide them in the direction I had in mind. I wouldn't give them more than a couple of minutes before I gave them some keywords. You have a given amount of time […] How can we be efficient? Yes, I want them to do this and this”. The choices regarding the mathematisation of the situation were made by the teacher; the students did not organise the problem according to mathematical concepts or by identifying relevant mathematics. In other words, they did not make assumptions, generalise, formalise or transform the real-world problem into a mathematical problem. Stillman (2015) viewed the process of mathematisation as crucial to modelling and the interpretation of a mathematical result in the task context as the main direction for applying mathematics. According to Stillman (2015), what teachers referred to as modelling could instead be identified as the application of mathematics, which focuses on interpreting mathematical results, and not the process from a real-world situation to a mathematical model.

The teachers saw the following step-by-step procedures as an important part of school mathematics: “In all the mathematics subjects, they learn to proceed with given algorithms” (Teacher 3). The national examination was, according to this teacher, “an assessment of the students’ use of tools, GeoGebra®, if they have learned the step-by-step algorithms”. If the students knew how to perform regression analysis and interpret their answers, they would excel in the mathematical subject related to modelling on the national examination. One teacher's response to the open task (the last of the three tasks given in the interview) was as follows: “They had not managed to answer this. They would just … Tasks like this are never given. They are completely open, without connection to anything” (Teacher 2). This indicates that students were not challenged to approach problems without all the necessary information. The open modelling task allowed students to engage in the situation, decide which parameters from the real-world situation they would focus on and mathematise the situation based on their choices. They also had to decide which mathematical content and procedures to use to solve the task. However, this kind of task was not familiar to the teachers and students. The students learn both the how and when of a routine, as expressed by Sfard (2008). However, according to the teachers, they are not challenged to use creativity in modelling. The students’ mathematical knowledge was indicated as a reason for not being given open tasks: “In this group, where the students are not able to divide by 0.5, there is no time to … We need to focus on the basics” (Teacher 2). The teachers viewed open tasks as more challenging for the students than step-by-step procedures.

The framework discourse presented decision-making as crucial to modelling: “[Students] will attempt to work on their model of the problem situation, to adjust it, to establish regularities, to identify connections and to create a good mathematical argument” (OECD, 2003, p. 39). In the example problems in the KOM framework, modifiers indicate freedom of choice: “How could the floor area of a house look, if its area should be 120 m²?” (Niss & Jensen, 2002, p. 53). In contrast, most modifiers in the teacher discourse were connected to the teachers’ uncertainty when talking about mathematical modelling, not the students’ decision-making.

The first tension can be summarised as follows: even if the students’ choices of parameters to focus on, assumptions made, and selves identify relevant mathematics are in the frameworks expressed as crucial in the process of mathematising, this is not emphasised by the teachers; it is instead seen as a waste of time.

Connection of modelling to specific mathematical content and given procedures

The teachers connected modelling to the specific mathematical content of functions and figurate numbers. They referred to the textbook: “[A]ccording to the textbook, modelling is functions or the use of functions” (Teacher 4). Concerning visual mediators, the connection to the specific mathematical content of functions was also apparent. The students “get a table which they plot in GeoGebra® and get out a function … Most of the textbook tasks are like this” (Teacher 1). In contrast, specific mathematical content in the KOM framework can only be identified in modelling example tasks, such as those concerning probability, geometry, economy, statistics and given models expressed as functions. The PISA framework does not express any specific mathematical content connected to modelling. In the framework discourse, visual mediators were not related to specific mathematical content. Instead, they involved “[u]nderstanding the relationships between the language of the problem, and symbolic and formal language” (OECD, 2003, p. 39).

Transformations between mediators were also indicated as the “translation of objects, relation, questions and so on to a mathematical area” (Niss & Jensen, 2002, p. 52). These were used “to de-mathematise existing models, to decode and interpret elements”. The teachers were more concrete. They expected students to perform a transformation to “draw the function” (Teacher 2) when they were given a function expression or asked to “express a function formulated by two points, as an exponential function” (Teacher 1). In this instance, the model was already given in the text, and the students were asked to transform it into a function expression and graph it using GeoGebra®. Teacher 2 described the modelling process as “a variable for which you should make a function expression and draw”. The students performed this transformation in GeoGebra® when they plotted given data and used regression analysis to find a function expression and draw the function. The teachers referred to visual mediators as answers to mathematical exercises, but not as mediators in processes.

Routines were generally described in the framework discourse. Aspects of the reflecting and validating processes were formulated in the PISA framework as “[u]nderstanding the extent and limits of mathematical concepts, reflecting on mathematical arguments and explaining and justifying results, communicating the process and solution and critiquing the model and its limits” (OECD, 2003, p. 39). One teacher also described this in general terms – the students “have to identify which area of mathematics is relevant for the situation to be modelled” (Teacher 4). However, besides this statement, the routines referred to were related to the mathematical content area of functions: using GeoGebra® as a tool for regression analysis; drawing graphs; finding roots, maxima and minima and reading graphs. The identified tensions can be summarised as follows: first, in the teacher discourse, modelling is connected to the mathematical content of functions and given procedures; in the framework discourse, modelling is overarching and not connected to specific mathematical content. One part of the modelling process is to identify relevant mathematical content, and problems can be solved using different procedures. Second, in the teacher discourse, the focus was on less complex cognitive processes, while in the framework discourse, modelling is presented as cognitively demanding processes.

Relevant mathematics

The framework discourse expresses engagement in real-world contexts. The modelling competence in the KOM framework does not include mathematical problems that do not require the processing of elements from reality (Niss & Jensen, 2002, p. 53). In comparison, when asked about mathematical modelling, the teachers described it as “going further working with functions” (Teacher 1), “to make function expressions from given data” (Teacher 2), “figurate numbers and regression” (Teacher 3) and “mathematics in other contexts” (Teacher 4). This does not reveal the depth of engagement in real-life contexts. Teacher 3 confirmed that students had difficulty interpreting mathematical results: “[The students] are quite good at using GeoGebra® as a tool, plotting the data and get the right formula … but they have trouble understanding what it tells them”.

The development of the KOM framework was motivated by the “changes in culture and society … provoking changes in educational goals, content and assessment” (Niss & Jensen, 2002, p. 3). The competencies in the framework aim to make mathematics relevant for life and are thus perceived as necessary for children to develop as democratic citizens. This is similar to the first reason of Niss and Blum (2020) – mathematics for the sake of modelling – which states that modelling is important because it improves the skills necessary for everyday life.

While the framework discourse views mathematics as a human activity, the teachers perceived parts of mathematics as applicable: “As I see it, practical mathematics is mathematics that is relevant in everyday life” (Teacher 1), and “that is the idea of practical mathematics. It is mathematics that helps the students to master life” (Teacher 3). A teacher “hopes the students experience the importance of evaluating how different data are presented – that they see it as relevant. But it is challenging that they seldom read the news. They seldom see charts and such” (Teacher 3). The teachers did not believe that every part of mathematics was relevant: “I must say that these figurate numbers … You won't be needing this for anything else than such IQ tests in newspapers … So, I don't think modelling is the most central in practical mathematics in daily life” (Teacher 2). Teacher 3 expressed:

This might be like swearing in church, but mathematics is too big a part of education. I think most of the students will become decent human beings without knowing too much about it … I would have liked more relevant parts of mathematics to be included. When it comes to economy, loans and savings … to avoid getting cheated, whether it is Black Friday, or … But really, what I am most concerned about is if the students will pass their exams and manage to solve the tasks they are given.

This teacher was further asked if he experienced conflict between teaching for the examination and teaching for life in general. He answered:

Yes, actually there is. We are concerned about the educational flow. You feel that you are doing a bad job as a teacher if students fail the exam because you have emphasised other things. And that is what upper secondary is about, to give students a diploma. More than to facilitate evolvement of sensible, reflective and good human beings and such. That is rarely measured.

Another teacher also expressed the restrictions imposed by the national examination: “We could do practical stuff … But when they come to the exam they must know about straight lines” (Teacher 2). According to these two teachers, mathematics that is relevant for the national examination is not always relevant for daily life. Thus, students are not motivated because they do not see the relevance of the mathematics they are learning. As one teacher stated, “Students are asking, ‘Why are we learning this?’ It's for the tests and the exam” (Teacher 3). However, others said, “The idea of practical mathematics is mathematics that enables you to master a life in the society” (Teacher 4) and “We work on things that can be relevant for everyday life, or that we do practical stuff in the classroom. We do not do much of that” (Teacher 1). The tension identified here is this: even though the main reason the framework discourse includes mathematical modelling in education is to make school mathematics relevant for everyday life, the teachers considered mathematical modelling to be less relevant for their students.

Theoretical knowledge of mathematical modelling

The framework discourse uses specialised language within the field of mathematical modelling in education. The teachers used informal language and did not include theoretical terms. The framework discourse presents the modelling process as a cycle to explain and visualise the sub-processes, thus giving a meta-perspective of the modelling process. The teachers, however, did not refer to a visualisation of the modelling process. The framework discourse was partly reified; it discussed the properties of objects and the relationships between them. “Mathematisation first involves translating the problem from ‘reality’ into mathematics” (OECD, 2003, p. 39) expresses the process “to mathematise” as “mathematisation” (an object). The KOM framework expresses the properties of the object “active model building” by “a number of different elements” and the relationships between them. This is also expressed as an object, model building, but it is emphasised as an active process. The teachers used the subjects “student”, “I”, “you” and “they” in sentences with active voice. These subjects were “solving”, “drawing” and “using tools”, showing a small degree of alienation in the teacher discourse. Alienation is done when no rationalisation is necessary to make us certain of our choices (Sfard, 2008). Therefore, the teachers’ choice of words may reflect uncertainty about the preferable approach to mathematical modelling and the actions of the students while working on modelling. The teachers expressed that they had not been introduced to the theory of teaching mathematical modelling in their education. Their understanding originated from “the textbook and the curriculum” (Teacher 1). As an in-service teacher student, Teacher 2 had learned about modelling as finding a function from a given dataset in GeoGebra®. Teacher 3 said that he had not worked with mathematical modelling when he studied mathematics as an in-service teacher. Teacher 4 had modelled when studying science, but only through the textbook and curriculum for mathematics education. Some of the teachers also directly expressed uncertainty about the notion of mathematical modelling – “I am not that good at modelling, really, I’m not certain what is meant by it” (Teacher 3). All of the teachers indicated that mathematical modelling was not emphasised in their education.

In summary, the teachers were not familiar with aspects of theoretical knowledge concerning the teaching of modelling, even if these aspects are explicitly defined in the framework discourse. They were not familiar with modelling cycles, even if modelling competence is defined by such cycles.

Discussion

Objectification?

The modified analytical tool of Morgan and Sfard (2016) was used to identify different aspects of teaching and learning mathematical modelling. The frameworks use objectified language, alienated and partly reified, which “results in freeing the evolving narratives from the extension on time and from human agency” (Sfard, 2008, p. 51). However, the lack of reification when explaining the process of modelling – and focusing on the processes even if the language was objectified – underpins the need for human agency in the process of modelling in the frameworks. Here, objectification does not portray the objects as capable of independent thinking, as Sfard (2008) discussed.

In contrast, the language some of the teachers used when describing mathematical modelling was not objectified, but it could still communicate mathematical answers as capable of independent thinking; for example, if the aim of mathematical modelling is “using GeoGebra® as a tool, plotting the data and getting the right formula”, then the students are able to solve the tasks without really engaging in the situations. This may indicate that mathematical modelling requires only less complex cognitive processes, as described by Anderson et al. (2001). The routines that the teachers described and the fact that they did not provide opportunities for students to make their own choices substantiate this notion. The teachers often used the term “model” rather than “modelling”. A model was used synonymously with a mathematical function that was more concrete than the process of modelling expressed in the framework discourse. This also indicated that they had not developed an endorsed narrative involving the processes of mathematical modelling presented in the frameworks. The modified analysis tool was used as a lens to identify tensions by evaluating the use of words – whether the discourses were objectified, whether they communicated mathematical modelling as a process or as an object and what the teachers emphasised that contrasted with the framework discourse to explore the endorsed narratives concerning mathematical modelling.

Modelling for the sake of mathematics, mathematics for the sake of modelling, or … 

The tensions uncovered might indicate different goals of including mathematical modelling in mathematics education. In discussion about mathematics for the sake of modelling by Niss and Blum (2020), they argued that “mathematics ought to help students to come to grips with the world in which we live and to better master real-world situations stemming from everyday life” (p. 28). This reason for involving mathematical modelling in education requires the first steps of the modelling cycle, making decisions in the process of mathematising the real-world situation. Students who are given open tasks perceive school mathematics to be useful and relevant outside of school, unlike students who solve closed tasks, for which the aim is to solve the task in one correct way (Boaler, 2001). A teacher in the present study confirmed this, stating that open modelling tasks were more relevant to everyday life and that students see more of the usefulness of mathematics outside of school when they are challenged to make their own decisions, as in everyday situations. At the same time, the teachers argued that the textbook and examination did not view this as mathematical modelling. However, the PISA framework emphasises that assessment items do not represent the full-fledged notion of mathematical modelling. Thus, the examination tasks concerning mathematical modelling do not reflect all the steps of the modelling cycle frameworks. A study about PISA-type problems also found that teachers did not recognise these problems as emphasising the connection to real-life situations (Ikeda, 2015).

The process of modelling is complex and demanding (Blum, 2015). The framework discourse regarding this process uses objectified language, presenting students as involved in the processes. However, one teacher described students struggling to master the use of mathematics; he could not expect them to understand but focused on helping them solve tasks by learning the given procedures. Another teacher did not express the first part of the modelling cycle, “to find out what to do”, as an important part of the modelling process; it was instead expressed as problematic if the students used a lot of time to complete this step at the expense of working mathematically. This focus on mathematical content may reflect the other reason of Niss and Blum (2020) for implementing modelling in mathematics education – modelling for the sake of mathematics. This reason emphasises other aspects of the modelling process, and activities have priorities other than mathematics for the sake of modelling. Modelling tasks are assigned to involve students in specific mathematical content, such as the area of functions and the use of regression analysis in GeoGebra®. However, students still need to engage in real-world scenarios by making decisions, not only finding correct answers through given procedures, but modelling for the sake of mathematics includes learning mathematical content through the work of mathematical modelling. However, if students do not engage in real-life situations while working with mathematical modelling, they do not see the connection between mathematics and the real world. If the purpose of mathematical modelling is to perform given algorithms, then none of the reasons of Niss and Blum (2020) for including mathematical modelling in education are valid.

While the framework discourse describes an ideal situation in which students ask questions while working on their model, the teachers described a different type of student. They expressed challenges in motivating students to engage in learning. One teacher indicated that the overall aim of teaching was to help students pass the examination. If the aim is modelling for the sake of the exam, it will likely lead to completely different priorities and activities in the design and orchestration of mathematics teaching. Still, it is possible to give students open mathematical modelling tasks and simultaneously prepare them for the national examination, even if the examination consists of closed tasks (Boaler, 2001).

The teachers did not use specialised language from the research field of the educational use of mathematical modelling, such as the modelling cycle and aims for modelling. This was also true in previous studies from other countries. Frejd (2012) found that mathematical modelling was not a familiar term in Swedish teachers’ mathematics education. Even if modelling is included as a way to work with mathematics, the theoretical aspect behind teaching mathematical modelling is not necessarily emphasised. The theoretical aspects include knowledge of a) modelling cycles, to provide a meta-perspective of the process of modelling; b) aims and perspectives on mathematical modelling, to reflect upon the reasons for working with mathematical modelling and c) modelling tasks, to provide varied and adapted teaching methods of mathematical modelling that assign tasks focusing on different parts of the modelling cycle (Borromeo Ferri, 2018). In contrast, the teacher discourse described reasons for choosing certain tasks when teaching was connected to the national examination and textbooks, not related to the theoretical dimensions of teaching.

Earlier studies found that textbook tasks did not engage students in the first parts of the modelling process (Berget, 2022; Jessen & Kjeldsen, 2021). The same was found in this study: the teachers did not emphasise the first parts of the modelling process, even if this was the core of mathematical modelling, according to the framework discourse. The latest PISA framework expresses “using mathematical modelling as a lens onto the real world” (OECD, 2018, p. 18), and models are seen as abstractions of reality. Connected to digital tools, the PISA 2021 framework also expresses mathematical modelling as simulations and as “curvefitting and using the best fit curve to make predictions” (OECD, 2018, p. 36). This is how teachers expressed mathematical modelling as curvefitting. However, according to the PISA framework, it involves more than simply using digital tools for curvefitting and simulations (OECD, 2018). If mathematical modelling is reduced to this, teachers and students may struggle to identify the purpose of mathematical modelling – other than solving given mathematics tasks. Regression analysis might be a part of the processes, but other aspects should also be included in the teaching and learning of mathematical modelling to see the relevance of mathematics in everyday life.

Conclusion and recommendations

This discourse analysis of the frameworks and teacher interviews has shown five tensions in the approach to mathematical modelling. The first was a tension that had previously been identified in studies from other countries (e.g. Ng, 2018): teachers were not familiar with the theoretical knowledge about teaching mathematical modelling as presented in the frameworks – different aims, modelling cycles, types of tasks and perspectives – even though modelling has been explicitly included in the curriculum for approximately 30 years.

Second, what is expressed in the frameworks as the core of the modelling process – to engage in the real world and make decisions and assumptions – was not seen as important by the teachers. These processes are also not emphasised in the textbook tasks for this mathematics subject (Berget, 2022).

While the framework discourse presents mathematical modelling as overarching and not connected to any specific mathematical content, the teachers connected modelling to the content of functions. Furthermore, the teachers focused on less complex cognitive processes, to use given algorithms to find a given right answer, rather than the more complex cognitive processes of analysing, validating and creating mathematical models.

Finally, even if the main reason for including modelling in mathematics education is to help students connect math lessons to real-life scenarios and understand the relevance of mathematics, the teachers did not recognise mathematical modelling as relevant for the students’ everyday lives. This study implies that if mathematical modelling is to fulfil its goals stated in the research field, more open tasks should be included in the teaching to focus on students’ decision-making. Teachers should also develop their theoretical knowledge about teaching modelling to foster mathematical modelling competencies.

Disclosure statement

No potential conflict of interest was reported by the author(s).