How do school-related mathematical problems become relevant for prospective teachers in mathematics courses at university? A qualitative interview study

ABSTRACT

Prospective mathematics teachers often have to attend courses in academic mathematics. However, many struggle to see the connections between the course content and their future teaching, which is detrimental to learning motivation and success. Many universities try to address this with interventions focusing on the relevance of the mathematical learning opportunities. School-related mathematical problems (SRMPs), which highlight connections between school mathematics and academic mathematics, are a suggested intervention. Since SRMPs focus on the demands of the future profession, one would expect that students attribute high relevance to them. However, empirical results on this remain limited. To evaluate and enhance SRMPs, our study aims to elicit the criteria students use for assessing the relevance of SRMPs. We analysed ten qualitative interviews with prospective teachers. Our results show that similar criteria determine the perceived relevance in all cases. We discuss practical consequences for the design of school-related learning opportunities in teacher education.

KEYWORDS:

• Teacher education
• tertiary mathematics
• qualitative study

1. Introduction

Secondary teacher education in many countries traditionally contains a substantial amount of academic mathematics.¹ It is often implicitly assumed that prospective teachers can draw the connections to school mathematics they need for teaching on their own as long as they learn academic mathematics (so-called intellectual trickle-down hypothesis, see Wu, 2011). However, for more than 100 years it has been discussed that prospective teachers might not be able to draw these connections on their own. Felix Klein (1908) pointed out that prospective teachers experience a double discontinuity: Both at the beginning of their studies and at the entry to their career, they have difficulties seeing connections between the mathematical “worlds” they experience at school and university. As a result, teachers might barely be able to use the academic mathematical knowledge they acquired at university.

In line with Klein’s analysis, Hoth et al. (2020) found empirical evidence that school-related mathematical content knowledge is not automatically acquired with academic mathematical knowledge. Hence, empirical results do not seem to support the intellectual trickle-down hypothesis, and the double discontinuity remains a problem many students experience (Buchholz & Kaiser, 2013; Winsløw & Grønbæk, 2014).

Furthermore, qualitative studies show that many (prospective) teachers attribute little to no relevance to academic mathematics for their (future) teaching (Even, 2011; Wasserman et al., 2018; Zazkis & Leikin, 2010). Since low perceived relevance can negatively impact learning motivation and learning success (Frymier & Shulman, 1995), this can result in even greater difficulties for prospective teachers to see connections between academic mathematics and school mathematics. In contrast, higher perceived relevance can positively affect student effort (Guo et al., 2016) and academic achievement (Hulleman & Harackiewicz, 2009). Thus, successfully supporting prospective teachers to assign higher relevance to mathematical learning at university should affect the usability of their academic knowledge for teaching.

In the last few years, mathematical societies (e.g. CBMS, 2012), as well as universities, pointed to the need to support prospective teachers in drawing connections between the two mathematical “worlds” and the need to foster their perceived relevance of academic mathematics for teaching. Therefore, it is necessary to develop learning opportunities that address these connections and that students perceive as relevant. For example, there has been a rising number of “connection courses” in the US (Murray & Star, 2013). In Germany, many universities try to emphasise these connections within traditional academic mathematics courses by implementing “school-related mathematical problems”² (SRMPs): These problems highlight connections between school mathematics and academic mathematics. Thus, one assumes students perceive SRMPs as relevant. However, empirical results on the impact of SRMPs on the perceived relevance remain limited.

Therefore, we must ask to what extent SRMPs actually fulfil the intended goal of being perceived as relevant learning opportunities by students. If we know what exactly makes SRMPs relevant for students, lecturers can pursue targeted development of SRMPs, possibly leading to better learning outcomes. Therefore, our study aims to elicit the criteria students use to assess the relevance of SRMPs.

2. Theoretical background

2.1. Challenges associated with learning academic mathematics in secondary teacher education in Germany

We will briefly introduce the national context of our research to contextualise SRMPs. All secondary teacher education programmes in Germany are consecutive and span two phases: First, prospective teachers must undergo an academic education (typically 5 years) and earn a university degree in a teacher education study programme. The academic phase is followed by a post-academic practical phase of teacher training (typically 1.5 to 2 years), best described as paid training on the job.

Students must typically enrol in a specific teaching programme at the beginning of their studies (Terhart, 2021). Programmes leading to a teaching license at the upper secondary level are content-focused with low shares of pedagogy. Similar to the situation in other educational contexts (e.g. Canada, France, Israel, Tatto et al., 2010), the mathematics courses within these programmes aim to develop sound mathematical knowledge and uphold high academic expectations. Traditionally, German students on a teaching path take their courses with mathematics majors (Cortina & Thames, 2013; Gildehaus et al., 2021). Therefore, the practical challenge described in many countries (Tatto et al., 2010) remains: Prospective secondary teachers should learn academic mathematics to use this knowledge for their later teaching, even though the courses are not exclusively designed for them.

One suggestion to address this challenge is implementing school-related mathematical problems (SRMPs) in these courses so that prospective teachers receive profession-specific learning opportunities within the mathematics courses. However, as mentioned above, it is still unknown whether SRMPs are perceived as relevant by prospective teachers and hence can be considered as a way to support knowledge acquisition. Before we give an overview of previous research results on relevance perception, we will briefly discuss the cognitive objectives universities pursue with SRMPs – namely, the acquisition of knowledge about connections between school mathematics and academic mathematics.

2.2. Teachers’ professional knowledge of connections between academic mathematics and school mathematics

As outlined in the introduction, mathematics teachers may struggle using their academic mathematical knowledge for instruction if they do not know the connections between academic mathematics and the mathematics they teach in school. Klein (1908), for example, claimed more than 100 years ago that mathematics teachers need kind of an elementary mathematics from a higher standpoint. Over the last two decades, mathematics education scholars have developed several conceptualisations of professional knowledge regarding connections that build on Klein’s idea and offer a modern understandings of professional knowledge pertaining to connections between school mathematics and academic mathematics. We review the mathematical knowledge for teaching model (MKT, Ball et al., 2008; Ball & Bass, 2003) as an often cited model, and the model of school-related content knowledge (SRCK, Dreher et al., 2018), which explicitly addresses challenges associated with high mathematical expectations in secondary teacher education.

The MKT model was developed for primary mathematics teachers and conceptualises teachers’ professional content knowledge with three facets: common content knowledge (CCK), specialized content knowledge (SCK), and horizon content knowledge (HCK). CCK is described as the “mathematical knowledge and skills used in settings other than teaching” (Ball et al., 2008, p. 399) and is, therefore, a knowledge not exclusively used by teachers. In contrast, Ball et al. (2008) define SCK as “mathematical knowledge and skills unique to teaching” (p. 400). HCK, the third facet of the MKT model, was included “provisionally” (Ball et al., 2008, p. 405), addressing teachers’ need to know “how mathematical topics are related over […] the curriculum”. For example, a first-grade teacher needs to know what pupils will learn in grade three so that s/he can teach the required prerequisites.

Knowledge about connections between school mathematics and the underlying mathematical knowledge (CCK) can mainly be found in the SCK and HCK facets of the MKT model. However, several problems occur with this model when applied in the context of secondary mathematics teaching.

First, Speer et al. (2015), as well as Dreher et al. (2018), argued that the conceptualisations of SCK and CCK could not be smoothly transferred to the context of secondary mathematics teaching. Ball et al. (2008) claimed that for primary mathematics, the question of what might be common content knowledge (CCK) refers to the mathematical knowledge of an average adult. This definition is unsuitable for the context of secondary mathematics and the question of what might be CCK for secondary teachers might instead refer to the knowledge of people who (at least) studied academic mathematics at an undergraduate level (Speer et al., 2015). Furthermore, Speer et al. (2015) identified aspects of mathematical knowledge (e.g making sense of someone else’s mathematical ideas) that can be considered common for mathematicians but were considered as unique to teaching by Ball et al. (2008).

Second, as HCK was only included provisionally in the MKT model, it remained underdeveloped compared to CCK and SCK. Furthermore, it potentially overlaps with SCK and CCK since SCK is mathematical knowledge unique to teaching and CCK seems to be the complement. According to Wasserman (2018), this may explain why scholars had difficulties conceptualising HCK.

Third, scholars have struggled to empirically reproduce the theoretical differentiations within MKT. SCK was often highly correlated with pedagogical content knowledge (e.g. Hill, 2010; Hill, Dean, & Goffney, 2007) even though Ball et al. (2008) described SCK explicitly as part of teachers’ content knowledge rather than their pedagogical content knowledge.

Given these difficulties with the MKT model, Dreher et al. (2018) suggested school-related content knowledge (SRCK) as an alternative focusing on knowledge about connections between school mathematics and academic mathematics. SRCK was conceptualised as profession-specific content knowledge for secondary teachers anchored in academic mathematical knowledge and supporting teachers to use it for teaching (Dreher et al., 2018). SRCK synthesises Klein’s (1908) elementary mathematics from a higher standpoint and Ball’s and Bass’ (2003) specialized content knowledge and horizon content knowledge and incorporates the ideas to emphasise the connection to school mathematics in academic mathematics courses.

In detail, Dreher et al. (2018) conceptualised SRCK with three not necessarily exclusive facets corresponding to different types of connections between academic and school mathematics that are relevant for teachers: top-down, bottom-up, and curricular knowledge (see Figure 1). Top-down knowledge refers to connections drawn starting from academic mathematics. For example, knowledge of top-down connections is necessary if teachers consider how to introduce a certain mathematical concept and how to reduce it for teaching. For instance, from the viewpoint of academic mathematics, the real numbers $\mathbb{R}$ can be constructed from the rational numbers$\mathbb{Q}$ in different ways (topological closure, Cauchy-sequences, nested intervals, Dedekind cuts). The introduction of real numbers is part of secondary school mathematics, and teachers have to decide which of the abstract concepts they learnt at university is most helpful for introducing the concept of real numbers. A teacher with knowledge of top-down connections would be able to select the approach most accessible for teaching, like the idea of nested intervals defined by two rational sequences that yield arbitrary small intervals, and then reduce it further to its essentials for use in instruction. The idea of nested intervals can, for example, be illustrated by approximating the root of a non-square number (see Table 1). This can also be found in several schoolbooks (e.g. Jörgens et al., 2022; Lergenmüller & Schmidt, 2003). For further discussion of why the three other academic mathematical concepts are less suitable for school mathematics, see Dreher et al. (2018).

Figure 1. Conceptualisation of school-related content knowledge (adapted from Dreher et al., 2018, p. 330).

Graphical representation of the conceptualisation of school-related content knowledge (Dreher et al., 2018).

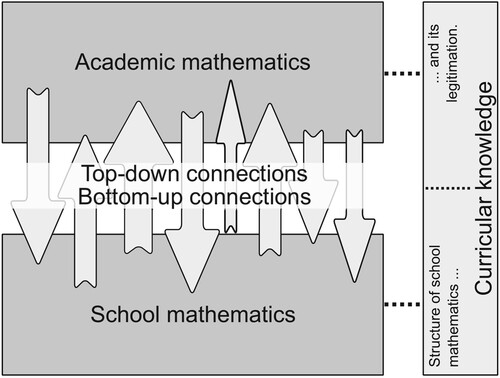
Table 1. Approximating $\sqrt{20}$ to illustrate the idea of nested intervals in school mathematics.

Step 1	$4^2=16<20$ and $5^2=25>20$	Therefore $4<\sqrt{20}<5$
Step 2	${4.4}^2=19.36<20$ and ${4.5}^2=20.25>20$	Therefore $4.4<\sqrt{20}<4.5$
Step 3	${4.47}^2=19,9809<20$ and ${4.48}^2=20.0704>20$	Therefore $4.47<\sqrt{20}<4.48$

In reverse, bottom-up connections are needed if elements of school mathematics are considered against the background of academic mathematics. An example of a typical task requiring knowledge about bottom-up connections would be deciding whether the way a certain textbook introduces a mathematical concept is “intellectually honest” (Bruner, 1960, p. 33). For example, a teacher would have to consider whether the textbook’s approach, e.g. for explaining why ${20}^{\frac{1}{2}}$ can be interpreted as $\sqrt{20}$, is essentially consistent with the academic concept, even if prepared for pupils of a certain age. In this case, the teacher should be able to evaluate the offer in regard to the underlying mathematical ideas (real numbers $\mathbb{R}$ extending rational numbers$\mathbb{Q}$ in a canonical way so that arithmetic operations, here exponentiating, extend canonically in fields). Another example of a situation where teachers need bottom-up knowledge is deciding whether an unexpected answer from a student contains a mathematically correct idea.

The third facet – curricular knowledge – contains knowledge of the structure of school mathematics and the underlying legitimation from the perspective of academic mathematics. For example, teachers need curricular knowledge to decide which ideas they may use to explain a mathematical concept (e.g. infinity) in a particular grade, considering which concepts are learnt earlier or which explanation might prepare for upcoming concepts.

Since SRCK describes knowledge about various connections between school mathematics and academic mathematics, it comprises knowledge about elements of both, school and academic mathematics. However, as profession-specific knowledge, SRCK differs from content knowledge conceptions for secondary teachers that comprise academic knowledge also needed by mathematicians, as explained above. Theoretically, SRCK is also different from another important aspect of professional knowledge, pedagogical content knowledge (PCK, e.g. Ball et al., 2008): In contrast to PCK, which is typically understood as knowledge about mathematical learning processes (e.g. typical pupil misconceptions, instructional representations), SRCK is a kind of pure content knowledge, focusing on content structures and not pupils’ cognition.

Several studies were conducted to gain evidence regarding the usability of the concept of SRCK for teacher research and training (e.g. Heinze et al., 2016; Jeschke et al., 2021). Heinze et al. (2016) could empirically separate SRCK from academic content knowledge and PCK in a study with prospective teachers, supporting its theoretical conceptualisation as a specific aspect of professional knowledge. A longitudinal study by Hoth et al. (2020) indicates that prospective teachers do not develop SRCK automatically when they learn academic mathematics. However, the acquisition of SRCK has not yet been investigated further and must remain outside this paper’s scope since we will focus on students’ relevance perception of SRCK-related learning opportunities. Instead of investigating the acquisition of SRCK, we use SRCK as a theoretical model that describes knowledge about connections between school mathematics and academic mathematics, which allows us to detail cognitive learning goals for secondary mathematics teacher education. Hence, we used SRCK to design matching learning opportunities to enhance the alignment between curriculum, instruction and assessment (so-called curriculum-instruction-assessment-triade, Pellegrino, 2010). We will discuss this in the following section, focusing on learning opportunities that pursue cognitive goals that can be described with the SRCK model and the relevance students attribute to them.

2.3. School-related mathematical problems and their perceived relevance – an intervention to address connections between school mathematics and academic mathematics

Academic mathematics courses in Germany typically consist of weekly lectures and additional tutorials based on mathematical problem-solving. Usually, all students (prospective teachers and other students of mathematics) solve the same problems. Traditional problems do not explicitly reference school mathematics, are not designed to address connections between school mathematics and academic mathematics, and usually ask for common mathematical practices like proving or inner-mathematical applications (e.g. see task analysis in Weber & Lindmeier, 2020). It was found that prospective teachers attribute less value to traditional problems than other students (Rach, 2023). Therefore, some universities started to use problems that address these connections to meet the specific aims of prospective teachers’ study programmes. We call these problems school-related mathematical problems (SRMPs).

SRMPs usually highlight connections between school mathematics and academic mathematics by addressing typical teacher tasks that occur in the classroom – like responding to pupils’ questions (see Figure 2, Subtask a) – or outside – like preparing a proof for class (see Figure 3). As we argued above, the cognitive goals of teaching innovations like the use of SRMPs fit with the theoretical conceptualisation of SRCK.

Figure 2. SRMP for a course in real analysis (adapted from Eichler & Isaev, 2017, p. 54). The problem is situated within school mathematics and asks for a teacher explanation (Subtask a). Subsequently, an academic proof is required (Subtask b, bottom-up connection).

Figure 3. SRMP for a course in real analysis (Weber et al., 2021, translated). It addresses the curricular facet of SRCK as it asks for different argumentations with respect to pupils’ grade (Subtask a) and reflects on gaps within school mathematics (Subtask b). Since the academic proof of $0.\overline{9}=1$ has to be adapted for the use in mathematics teaching, Subtask a) also addresses the top-down facet of SRCK.

When implementing these problems, lecturers typically decide to keep most of the traditional problems per week the same for all students (e.g. three of four problems) but gear some towards the different study programmes so that prospective teachers receive SRMPs as specific learning opportunities while the other students receive more of the traditional problems (e.g. in the US: Álvarez et al., 2020; in Germany: Bauer, 2013; Eichler & Isaev, 2017; Schadl et al., 2019).

Analysing sets of SRMPs from eight German universities, Weber and Lindmeier (2022) showed that SRMPs mainly differ in four characteristics: (1) addressed SRCK-facet(s) (none – one – more), (2) explicit reference to a teaching context (not existing – existing³), (3) required mathematical knowledge (school mathematics – academic mathematics – both), and (4) dominant mathematical practices (conventional mathematical⁴ – non-conventional).

It is still unclear whether prospective teachers perceive SRMPs as relevant learning opportunities and how SRMPs and their characteristics affect prospective teachers’ perception of the relevance of academic mathematics for their future teaching. Yet, research has shown that affective variables, like relevance perception, play an important role in students’ engagement and learning success (e. g. Dietrich et al., 2017; Rach, 2023). As stated above, knowing what exactly makes SRMPs relevant for prospective teachers would support lecturers in further developing their learning opportunities, which in turn may support student learning.

Rach (2023) showed that students’ perception of the importance of the learning content in different mathematical problems is relatively stable and does not significantly depend on the mathematical topic addressed in the problem. In contrast, the relevance perception seems to differ substantially between persons. In line with these results, Büdenbender-Kuklinski et al. (2022) found no significant differences between various mathematical contents when prospective teachers assessed their relevance. Furthermore, they found that prospective teachers attribute higher relevance to societal and vocational goals than to other individual goals, including intrinsic goals related to learning mathematics. Nevertheless, the future career was not the only reference frame prospective teachers used to assess relevance. Some students also wanted to develop as an individual and pursue their personal interests (Büdenbender-Kuklinski et al., 2022). This again highlights that students’ relevance assessments can be very different between individuals.

Since the future profession seems to be an important reference frame for prospective teachers, they likely assess SRMPs as relevant learning opportunities. However, currently the use of SRMPs is seldom investigated. Specifically, there seems to be no study on the perceived relevance of SRMPs. But there are few studies on the influence of SRMPs on the perceived relevance of academic mathematics. Schadl et al. (2019) found significant changes in students’ perceived relevance of academic mathematics for teaching at the beginning and end of a term in which they received SRMPs. However, significant changes were only found in one out of three cohorts. In a quasi-experimental design, Eichler and Isaev (2022) found an interaction effect of treatment and time: While the perceived relevance of academic mathematics for the teaching profession did not change significantly for prospective teachers who received SRMPs, a significant decline was found for the control group of students who only received traditional mathematical problems. Summarising, research on the contribution of SRMPs on the perceived relevance of academic mathematics for prospective teachers remains limited, and the few results are ambiguous. However, the studies only looked at the hypothesised effects of SRMP implementation on the perception of academic mathematics, not how the SRMPs themselves were perceived. Therefore, these studies are not informative regarding whether and how one may further develop SRMPs and their implementation.

Nevertheless, there are promising results for other approaches focusing on the connection between academic and school content knowledge in related subjects and projects: The ULTRA-project, for example, highlights connections between school mathematics and academic mathematics not via single SRMPs within a traditional course but via entire school-related seminars. Fukawa-Connelly et al. (2020) showed in their evaluation that such an intervention could promote the perceived relevance of academic mathematics for the understanding of school mathematics (comparable to the bottom-up and curricular facet of SRCK) and for explanations prospective teachers would give to pupils (comparable to the top-down facet of SRCK). Furthermore, Massolt and Borowski (2018) found that prospective teachers assess school-related physics problems as more relevant than regular physics problems if the content is distant to school physics.

Concerning the above-mentioned mixed results and the difficulty that studies mainly focused on the effects of SRMPs but not SRMPs themselves, it seems appropriate to first focus on the perceived relevance of SRMPs as specific learning opportunities themselves before going one step further investigating their potential impact on students’ perceived relevance of academic mathematics in general. Hence, the focus of this paper is the relevance perception of prospective teachers regarding SRMPs and underlying reasons, because the students’ relevance perception may influence whether SRMPs support indeed – as assumed according to the underlying SRCK model – their learning processes. Knowing what may students lead to perceive SRMPs as relevant is considered necessary for optimising SRMPs as well as furthering rigorous research on the impact of SRMPs on student learning.

2.4. Relevance perception

According to Priniski et al. (2018) relevance as a motivational construct can be defined as “a personally meaningful connection to the individual” (p. 12). They conceptualise relevance as a continuum with three sections of increasing personal meaningfulness: (1) personal association (connection to memory or experience), (2) personal usefulness (connection to personal goal), and (3) identification (part of one’s identity) (see Figure 4).

Figure 4. Conceptualisation of relevance along a continuum of personal meaningfulness (adapted from Priniski et al., 2018, p. 12).

Graphical illustration of the conceptualisation of relevance along the continuum of personal meaningfulness according to Priniski et al. (2018).

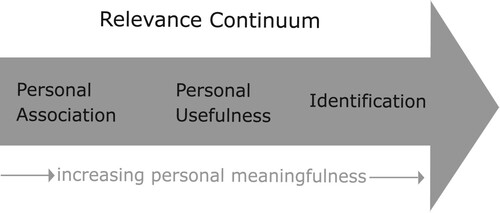
Different people can perceive a stimulus – the SRMPs can be regarded as such – as relevant in different ways and for different reasons. For instance, if a student works on the SRMP in Figure 2 and remembers that s/he also once had the impression that $0.\overline{9}$ “looks smaller than 1”, the student might experience a personal association with that problem. Another student might perceive the same SRMP as personally useful because s/he can practice giving explanations to pupils, which might be useful for the aspired profession. A third student might see the same SRMP as an opportunity to strengthen the own identity of being a prospective teacher since s/he can act like a teacher in the SRMP.

Priniski et al. (2018), as well as Eccles (2009), point out that an individual can assess the utility of a task relating to either short-term goals or long-term goals. For example, a student working on the SRMP in Figure 3 might find it useful to work out explanations that s/he might need later as a teacher (long-term goal). Or the same student could find the SRMP untimely because s/he does not think it will help her/him pass the next exam at university (short-term goal). Therefore, the perceived personal usefulness can differ from time to time depending on which goal is currently salient.

To sum up, the construct of relevance as personal meaningfulness allows conceptualising the perceived relevance of SRMPs by students as the result of an interaction of students with SRMPs. As illustrated, the students’ perceived relevance may be based on a variety of different, possibly implicit, criteria (e.g. familiarity, usefulness) referring to past, present, or expected future experiences. Based on the results of Rach (2023), as well as Büdenbender-Kuklinski et al. (2022), one can assume that these criteria do not differ substantially over time but between individuals.

2.5. Summary and research question

Many German universities adopted the idea of school-related mathematical problems (SRMPs) to support prospective secondary mathematics teachers in connecting school mathematics and academic mathematics and acquiring school-related content knowledge (SRCK). After universities have initially implemented these learning opportunities in teacher education, it is now necessary to investigate how students perceive them. In this study, we therefore focus on the relevance students attribute to SRMPs and investigate the following research question: Which criteria do prospective teachers use to assess the relevance of school-related mathematical problems?

Gaining deeper insight into what exactly makes SRMPs relevant for students provides opportunities to develop these learning opportunities further.

3. Methods

Since students might not be explicitly aware of the criteria they use, a qualitative interview study seemed advisable to elicit even criteria that students use implicitly. Furthermore, as previous research shows, some criteria could be very individual, so we used a qualitative approach suitable to elicit individual perspectives and conducted a material-based structured interview.

3.1. Participants

We interviewed N  =  10 (3 male, 7 female; age: 18–22 years) prospective secondary teachers that were second-term students at the Kiel University, Germany. We recruited the students through an open project call, and they volunteered to participate in the interviews. The interviews took place in the middle of the summer term of 2020, and all participants received a small expense allowance. Five of the students started their studies directly after graduating from school, and the other five one year after. Two students worked as assistant teachers for one year, whereas all other students had little (short internships, private lessons for struggling pupils) to no teaching experience.

The interviewed students had visited courses in linear algebra and real analysis in their first and second term together with mathematics majors, as all prospective teachers in this programme. All students had to solve four to five mathematical problems each week in each course and hand in their answers. Tutors (mostly advanced mathematics students) corrected the students’ answers and presented the correct answers during the weekly tutorials. The students had to achieve 50% of the points to be admitted to the course examination. For prospective teachers, one of the problems in each course per week was an SRMP.

3.2. Conception of the interviews

Due to the Covid19-pandemic, we conducted the interviews as video calls using a digital collaborative board.⁵ All ten interviews lasted between 45 and 60 min and were audio recorded and transcribed. The interviewer was an advanced student at the master’s level in the same teacher programme, who was neither engaged in the development of the SRMPs nor in any other part of the courses.

We used a manual to structure the interviews to ensure their comparability. All participants received the same questions, but the manual created room for individual opinions. As a warm-up and to orient participants towards their individual perceptions of relevance, we first asked the students to name what is especially important to them in their mathematics studies (open format, see Figure 5). The interview then focused on SRMPs, and participants could choose 2–3 statements of a given list of nine statements to describe what is most important to them regarding SRMPs (closed format, see Table 2).

Figure 5. The first question on the virtual board. We asked the students to write their responses in the three blank spaces.

Table 2. Statements students chose to describe what is most important to them in SRMPs.

Theoretical perspective (for the given statements S1–S9)	[Shorthand] statement (number of sort sequences aggregated across interviews)	Category according to the analysis (see Section 4)
Professional orientation	[S6] Through SRMPs, I gain different ways of thinking about the teaching profession. (3)	Alignment with the future profession; general
(Student generated)	[SG02b] SRMPs show a clear reference to teaching. (1)
	[SG07a] Demands on pupils are realistic in SRMPs. (1)
SRCK: bottom-up	[S3] SRMPs cultivate my ability to analyse pupils’ statements or assignments with a trained eye. (4)	Preparation for teacher tasks in classroom
SRCK: top-down	[S4] SRMPs cultivate my ability to prepare mathematical teaching content correctly (7)
(Student generated)	[SG06] In SRMPs, I learn how to present complex contents simply and correctly in the classroom. (1)
SRCK: curricular	[S5] SRMPs help me to better understand the structure of school mathematics. (4)	Preparation for teacher tasks/knowledge outside the classroom
Usability of academic mathematics	[S8] In contrast to previous learning opportunities, I learn professional knowledge through SRMPs that I will need and use later as a teacher. (2)
(Student generated)	[SG02a] Through SRMPs, I can enhance my mathematical background knowledge for teaching. (1)
	[SG03] SRMPs teach me to define neatly and thereby lay a foundation for teaching. (1)
	[SG08] Through SRMPs, I gain background information that helps me questioning school mathematics. (1)
	[SG10] In SRMPs, I learn properly substantiated mathematical background information (1)
SRCK: general	[S2] Trough SRMPs, I better recognise content interfaces between school and academic mathematics. (5)	Orientation towards academic mathematics for prospective teachers
Value of academic mathematics	[S7] SRMPs show me why learning academic mathematics is relevant in my studies. (2)
Interest in learning academic mathematics	[S1] SRMPs spark my interest in delving deeper into the subject matter. (0)	Affective/motivational aspects
Motivation for learning academic mathematics	[S9] SRMPs increase my current motivation for my studies. (2)
(Student generated)	[SG01] In SRMPs, I recognise the meaningfulness of the task. (1)
	[SG05] SRMPs allow for a variety of considerations. (1)
	[SG07b] SRMPs allow me to look at the content in a different way and offer a change from the other exercises. (1)
	[SG09] SRMPs provide clarity for me on the mathematical context (1)	Benefit for own mathematical learning

This part was meant to elicit criteria students use explicitly for assessing the relevance of SRMPs. The nine statements mirrored the theoretical perspectives of teacher knowledge (especially SRCK), profession-oriented teacher education programmes, as well as aspects of motivation and interest.

Five of these statements resulted from a pre-study conducted two months prior to the interviews. In a survey, all second-term prospective teachers were asked (among other things) to answer the question: “What is the most important thing you could learn in SRMPs?”. 48 students participated in the pre-study and 23 of them answered this question. For the interview study, we used these responses to formulate the statements S2, S4, S6, S7, and S8 (see Table 2, middle column) as potentially important aspects of SRMPs. Based on theoretical considerations, we added the statements S1 and S9 to mirror aspects of interest and motivation, and the statements S3 and S5 to picture all three facets of SRCK. Each of the nine statements can be read as a specific criterion that might lead students to evaluate a SRMP as relevant (or not), depending on whether the SRMP resonates with the statement or not.

The third part of the interviews was meant to validate the students’ responses from the earlier parts of the interview and, furthermore, to elicit criteria that are only available implicitly. Therefore, we used the repertory grid-method (e.g. Cohen et al., 2007) and asked the participants to sort six selected SRMPs along bipolar scales of agreement. Each participant completed 4–5 sort sequences according to different criteria. The interviewer asked the students to explain each sort sequence. The first criterion, which was used in all interviews, was relevance for you, leading to a global relevance score between 1 and 6 for each of the problems. Afterwards, the students sorted the problems along the individual statements that resulted from the first and second part of the interviews. This resulted in different numbers of sort sequences for each statement aggregated across interviews. Table 2 shows the statements the students used to sort the SRMPs and the underlying theoretical perspectives (first and middle column).⁶

Table 3 gives an overview on the SRMPs that we used during the interviews.⁷ All six problems were implemented during the participants’ first-term courses. We selected the set of problems specifically with respect to the courses and the components found by Weber and Lindmeier in a recent analysis of SRMPs (2022, see Section 2.3).

Table 3. Summary of the six SRMPs discussed during the interviews.

Problem	P1	P2	P3	P4	P5	P6
Related course	Linear algebra	Linear algebra	Real analysis	Linear algebra	Real analysis	Real analysis
Dominant SRCK-facet	Top-down	Top-down	Curricular	Bottom-up	Bottom-up	Curricular
Further SRCK-facet	–	–	Top-down	–	Top-down	–
Explicit reference to a teaching context	School (-book) assignment	Adequate response to pupils	Adequate response to pupils	Other reference to a teaching context	Approach/ definition as used in school mathematics	Approach/ definition as used in school mathematics
Required mathematical knowledge	School and academic	School and academic	School and academic	Academic	School and academic	Academic
Dominant mathematical practice	Non-conventio-nal	Non-conventio-nal	Conventio-nal	Conventio-nal	Conventional	Conventional

3.3. Data analysis

We used qualitative content analysis (see Cohen et al., 2007) – specifically a summarising content analysis by inductive category formation (Mayring, 2014) – to analyse the criteria students used to assess the relevance of SRMPs. We chose an inductive approach since, to our knowledge, no previous studies exist that could inform a deductive approach to code the criteria students use to assess the relevance of school-related learning opportunities.

The goal of a summarising content analysis is to reduce and abstract the interview material in a manner that the core aspects remain illustrated. The steps, according to Mayring (2014), include structuring the interview materials in units, extracting possible criteria, and reducing the findings through grouping across similar criteria, which results in a category system. This allows representing the richness of aspects raised by different individuals in the interviews in a coherent manner. One can also differentiate between aspects that seem more important and generalisable than others by simply counting the interviews raising a certain aspect.

When applying the method, we defined the recording unit as a whole interview, the context unit as one answer to an interview-question and the coding unit as single words. To account for the nature of the verbal materials, text passages could be coded with multiple categories. Two coders independently analysed all data. Each coder worked out a category system of criteria by coding the whole material and inductively grouping similar criteria. All resulting categories were illustrated using typical examples. Afterwards, both coders synthesised these systems into one consensus system. Since the systems were already quite similar, consensus was mainly to be negotiated on the naming of the categories. We established intercoder-reliability by checking whether both coders coded each category in the same transcripts. Cases with discrepancy were recoded consensually.

4. Results

We report the results starting with the global relevance score assigned by the participants to the given SRMPs (scale 1–6). As Table 4 shows, the students rated the problems differently, indicating that they did not necessarily assume SRMPs as relevant per se. Nevertheless, they perceived most problems as rather relevant, as most average scores were above 3.5. This first finding supports that the selected SRMPs are suited to further investigate the criteria which determined the perceived relevance.

Table 4. Rating of the SRMPs based on global relevance score (range 1–6).^a

Problem	P1	P2	P3	P4	P5	P6
Average score	4.5	2.8	4.2	4.2	4.0	3.6
N	10	10	10	9	10	9

^a Two students reported for one SRMP that they had not worked on it. Therefore, we removed the scoring of the two students for these problems from the analysis.

The qualitative analysis of the criteria that students used to assess the relevance of SRMPs in the ten interviews resulted in a system with seven main categories and 23 subcategories (see Table 5). We describe the system in detail in the following.

Table 5. Category system of relevance criteria students used during the interviews.^b

Category	Subcategory	Reference frame
A. Alignment with future profession; general	A1. Clear reference to a teaching context	Own school experience
	+ Visible
	− Not visible/assumed to be unrealistic
	A2. Importance of the content for teaching (+)
	A3. Preparation for future profession (unspecific) (+)	Future profession
	A4. Taking the perspective of a teacher (+)
	A5. Assumed applicability in future profession
	+ Applicability assumed
	− Applicability not assumed
B. Preparation for teacher tasks in classroom	B1. Reduction of abstract content to the essentials (+)
	B2. Explanations in general (+)
	B3. Development of adequate proofs with regard to pupils’ age (+)
	B4. Answering pupils’ advanced questions (+)
C. Preparation for teacher tasks/knowledge outside the classroom	C1. Good foundation of mathematical background knowledge (+)
	C2. Structure of the school curriculum (incl. implications for teaching) (+)
	C3. Reflection on pupils’ cognitions (+)
	C4. Reflection on classroom content (+)
	C5. Identification of gaps in school mathematics (+)
D. Orientation towards academic mathematics for prospective teachers	D1. Utility/relevance of academic mathematics for (prospective) teachers (+)
	D2. Connections and differences between school mathematics and academic mathematics (+)
E. Affective/ motivational aspects	E1. Personal value/usefulness
	+Visible
	− Not visible/devalued by teaching staff
	E2. Personal interest/fun	Personal preferences or aversions
	+Personal interest/fun addressed
	− Personal aversions addressed
	E3. Interest/fun from pupils’ perspective
	+ Interesting for pupils
	− Not interesting for pupils
F. Benefit for own mathematical learning	F1. Acquisition of (deeper) own understanding of subject matters (+)	Current studies
G. Structural/ organisational aspects	G1. Reference to the contents of the course (+)
	G2. (Admission to) course exam
	+ Points relevant for admission
	− Problems irrelevant for the exam
	G3. Level of difficulty; effort (-)

^b Subcategories in bold were mentioned in at least half of the interviews. Subcategories that are marked with (-) were only mentioned in a negative manner (impairing relevance), subcategories with (+) only in a positive manner. Sample quotations for each subcategory can be found in the supplement.

4.1. Alignment with the future profession; general

The first category summarises aspects that refer to the future profession as a teacher in general without giving specific examples of activities or content teachers might need to engage with.

One of the most frequently named criteria was a clear reference to a teaching context. This clear reference appears to be a fundamental criterion for the perceived relevance of SRMPs and resonates with many of the more specific subcategories of categories B and C.

Notably, the absence of a clear reference to teaching was used to state low relevance for problems. In this context, eight of the ten students rated a given reference as unrealistic because they were not introduced to the content when they were pupils (e.g. “And I’ve put problem three at ‘rather not relevant’. […] I’ve neither seen in grade six nor in upper secondary school that zero point nine repeating equals one. Accordingly, I didn’t really see the reference to a teaching context”⁸, S07 commenting on P3). This was by far the most important criterion that could inhibit the perceived relevance in our interviews.

Seven students considered the importance of the content for teaching as a factor for relevance. They assessed SRMPs that treat central school contents as more relevant. Most of the students explicitly referred to their own experience as a pupil in this context, whereas others referred to their future job.

The third subcategory is the preparation for the future profession (unspecific). This subcategory summarises all such statements that did not contain specific examples of activities or contents the students wanted to learn. Preparation for the future profession was a topic in all interviews, often in a highly differentiated manner (which is reflected in categories B–D). Hence, one can assume it is quite an important criterion for students’ perception of relevance. The prospective teachers clearly used their aspired future profession as a reference frame in this subcategory A3 and did not refer to their own school experience as pupils as they did in subcategory A1 and, partly, in A2.

The same holds for the subcategories A4 and A5. All interviewed students wanted to get an opportunity to take the perspective of a teacher. According to the interviews, this was achieved by SRMPs in which students could reconstruct or simulate typical teacher tasks, for example, when asked to construct mathematical problems for use in instruction.

Another criterion five students used was the assumed applicability of a content in the future profession as a teacher. Students rated problems more relevant when they could imagine themselves teaching the topic in school (“I am quite sure that I will introduce this topic at some point as a teacher. I can already see myself standing in front of a class and doing exactly that. Therefore, just exactly this type of problem with this topic, I think it fits perfectly here”, S06 commenting on P3). However, this criterion was also used as a negative argument for the uselessness of a problem as the following statement illustrates: “Well, then I don’t know, how much this will actually help me, if, in fact, I can’t use it in school” (S02 commenting on P4 which asks for an academic proof of a division rule).

4.2. Preparation for teacher tasks in the classroom

In contrast to the first category, statements in category B are on a very specific level and highlight the potential of SRMPs to prepare students for specific teacher tasks. Therefore, in this category students used their future profession and, especially, the tasks of teaching mathematics as a reference frame to assess the relevance of SRMPs.

Eight students gave examples of SRMPs in which they could learn how to reduce abstract content to its essentials so that it becomes accessible to pupils. They perceived the relevance of corresponding SRMPs as high. The students were aware that their reduction to the essentials had to be correct and specific (“Well, you had to again simplify the complex, you had from the lecture and then also still justify why it's the same, and I really liked that”, S09 commenting on P6). Therefore, the students demonstrated a sophisticated view that it is not only necessary to reduce abstract content for teaching but also to maintain the mathematical integrity (see top-down facet of SRCK).

Half of the students also liked SRMPs in which they could explain things in general. The statements that fell into this subcategory were vague compared to the previous subcategory, as students did not specify explaining and just labelled it as a fundamental teacher task. Some students offered direct comparisons to more traditional (not school-related) problems in this category (“So it's not just this rigid ‘yes, this is math and you must learn it now’, but it's really connected to the question of how I can explain this to a pupil”, S05).

Many of the discussed SRMPs asked students to develop proofs for a certain grade. Thus, all but one student mentioned the development of adequate proofs for pupils of certain ages as an important teacher task they could learn in SRMPs. This directly refers to the top-down facet of SRCK. The students appreciated that they got a better idea of what pupils can understand (“I find it a bit difficult to find proofs appropriate to the age of the pupils. I can’t even remember, what I did there back then. […] However, if you then find these proofs, then, of course, you can see very nicely the differences between the different grades or class levels and the university”, S03 commenting on P3).

Three students also mentioned that SRMPs are relevant for them because they prepare them to answer pupils’ advanced questions. In contrast to the previous subcategories, the focus in this subcategory is not on preparation for teacher tasks in everyday-situations, but on preparation for questions that go beyond the usual school curriculum and may be asked by high-performing pupils.

4.3. Preparation for teacher tasks/knowledge outside the classroom

The third category contains aspects and knowledge students named as relevant for mathematics teachers, although they might not be directly useful in classrooms yet may be part of pre- or post-instructional teacher work. Still, as in the previous category, students refer to the demands of their future jobs as teachers.

The first subcategory of category C is named good foundation of mathematical background knowledge. Eight of the interviewed students thought it relevant to know the academic background of mathematical content they will teach in school – even if pupils never asked for it (cf. subcategory B4). However, the students did not refer to broad mathematical background knowledge in general but made a clear reference to school mathematics (see subcategory A1).

Six students also mentioned that they like SRMPs in which they learn something about the structure of the school curriculum and its implications for teaching: “So you get a general idea, what is taught when, how can I incorporate and build on that. This is exciting for sure” (S01 commenting on P2 and P3). When talking about curricular aspects, many students directly referred to SRMPs designed to address the curricular facet of SRCK. Interestingly, the students did not only want to know what exactly is taught in school. Instead, they found it important to know what ideas they could use to introduce concepts or explain topics in different grades and how to build on these ideas in higher grades. Therefore, the students showed a sophisticated view on the importance of their knowledge about the school curriculum.

In addition, eight students said they wanted to learn what pupils of different ages can understand. Therefore, they liked SRMPs in which they could reflect on pupils’ cognitions (“So you can gain an understanding of what kind of comprehension I can expect from a pupil in a specific grade. That is quite enjoyable”, S10). In contrast to the previous subcategory, this subcategory does not focus on how things can be explained based on previous knowledge. Instead, the focus is shifted towards the cognitive prerequisites that pupils have at a certain age from a more general perspective.

Three more subcategories encompass aspects of preparation for teacher tasks/knowledge outside the classroom but were only named by a few students. Three students, for example, highlighted that they like SRMPs in which they could reflect on classroom content (e.g. a definition in a textbook) and question its formal correctness. Most of them directly referred to processes framed as bottom-up connections in the SRCK model, like checking a school definition or a pupil’s statement for its academic correctness.

Another aspect given by three students was that SRMPs helped them to identify gaps in school mathematics. Whilst the previous subcategory (C3) focused on minor shortfalls in school mathematics (e.g. a proposition that is given without formal proof), this subcategory highlights fundamental gaps that exist in the school curriculum and cannot be bridged within school mathematics (see the curricular facet of SRCK). For example, S04 commented on P3, “What I also liked is that this problem eventually shows that school proofs often cannot be done completely accurately – just with the knowledge they [pupils] have. And that academic mathematics helps out instead.”

4.4. Orientation towards academic mathematics for prospective teachers

The fourth category contains general aspects of the usefulness of studying academic mathematics as a prospective teacher. Hence, students still used their future profession as a reference frame in this category, which means that they focused on the usefulness for long-term goals.

For six participants, it was important to see the utility or relevance of academic mathematics for (prospective) teachers. The SRMPs could show reasons why it is important for prospective teachers to learn academic mathematics (“It’s very important that you recognise that there is a purpose in going to university. Because sometimes it actually is the case that, at first, one doesn’t really see what this has to do with school. And you can see quite well where you are in school right now. Sometimes you don’t even notice it and then see ‘ah we did that in this or that grade’ or so”, S03). The relevance of academic mathematics for teachers was specifically mentioned in connection with subcategories C4 (reflection on school contents) and C5 (identification of gaps in school mathematics). Students noticed that they could not answer all questions that arise from school mathematics within school mathematics: “So I think we had some questions from pupils as examples, and then we were supposed to refer to them somehow, to what extent that applies. And I found that in some cases, you couldn't have answered these questions with what you learned in school mathematics. And because of the academic mathematics that you have learned, you could have” (S04).

Seven students rated the relevance higher if they saw clear connections or differences between school mathematics and academic mathematics. Some students mentioned they were initially “a little shocked to see how different this [academic mathematics] is” (S09) and had difficulties – especially during the lectures – seeing the connections to their future work as teachers. SRMPs helped them to make these connections (“That you then realise, okay, I've done that before, but in a different way. That you link things together that you might not have done without the problems”, S05).

4.5. Affective/motivational aspects

The students also mentioned several affective and motivational aspects when rating the relevance of SRMPs. They used their future profession, as well as personal preferences or aversions, as a reference frame in this category.

Six students stated to rate the relevance of SRMPs higher if they could see a personal value or usefulness in them. This subcategory was mentioned in a positive and a negative manner. Students asked themselves, “What's the point?” (S01) and did not consider a problem relevant if they could not find a satisfying answer to that question. The personal value of an SRMP was also influenced by the appreciation the students experienced from the teaching staff (“But, in my opinion, this is still not enough. Because some assignment sheets have no SRMP or it is just a small part, a small sub-problem, which is, therefore, still so marginal. Along the lines of: Yes, you're doing a teaching degree, but actually the math studies are more important for now”, S05; “If we didn’t have enough time, it was always the SRMP that was dropped”, S04 commenting on the way tutors dealt with SRMPs in their tutorials).

Nine students assessed SRMPs based on personal interest/fun. Most of the comments were positive, but some students also mentioned personal aversions that made them dislike a certain problem (“Well, it probably isn’t bad, but I’m probably just not interested in it”, S01). Two students also considered the interest/fun in a topic from pupils’ perspective.

4.6. Benefit for own mathematical learning

In seven interviews, students mentioned that they acquired a (deeper) understanding of academic mathematics through the SRMPs. Notably, in this category, they did not reference their future profession but rather their current studies (short-term goals). They named several reasons that enabled deeper understanding: First, some students found SRMPs helpful to connect their prior knowledge to the newly learned academic mathematics. Second, in many SRMPs, students had to reduce academic mathematics to a basic level, which helped them to identify the essentials. Third, some students mentioned that SRMPs could show specific examples that help them better understand abstract definitions.

4.7. Structural/organisational aspects

The last category summarises statements that refer to structural or organisational aspects influencing the relevance assessments. The students used their current studies as a reference frame in this category. For example, half of the students liked SRMPs with a clear reference to the contents of the course (e.g. reference to a traditional (not school-related) problem) better, thereby supporting their own mathematical learning (see subcategory F1).

Five students noted the (admission to the) course exam as another important organisational aspect. On the one hand, some students appreciated that working on SRMPs typically made them earn more points than working on traditional problems. Therefore, they saw SRMPs as an opportunity which helped them gain admission to the exam. On the other hand, some students criticised SRMPs as not relevant for the exam itself, as it did not cover such types of problems. In these cases, the short-term goal of passing the exam conflicted with the long-term goal of getting prepared for the future profession.

A few students assessed some SRMPs as “just somehow too hard” (S04) or too extensive and, therefore, not relevant for their future teaching.

5. Summary and discussion

The main goal of our study was to investigate the relevance students attribute to school-related mathematical problems and to elicit the criteria prospective teachers use to assess the relevance. Our results show that students, on average, attribute high relevance to the SRMPs provided but also use multiple criteria to assess the relevance of SRMPs. Their perspectives hence indicate a wide and – to some extent – sophisticated view of what is important for their future profession. We found seven criteria that determine the perceived relevance of SRMPs and which were mentioned in different frequencies and combinations. Four of these criteria (categories A–D) clearly reference teaching, whereas the three other criteria (categories E–G) relate to less specific aspects. In the following, we will contextualise the identified criteria and ways they were mentioned within the research state to summarise important factors that made it easier or more difficult for students in this study to perceive SRMPs as relevant.

One basic criterion to assess relevance was the alignment with the future profession in general and, in particular, a clear reference to a teaching context. This aligns with results on school-related physical problems (Massolt & Borowski, 2018, 2020). Considering the result of an analysis of SRMPs by Weber and Lindmeier (2022), not all SRMPs fulfil this criterion yet. Remarkably, even if a problem showed a reference to a teaching context, many of the interviewed students did not think the reference to be realistic if they could not remember the content from their own experience as pupils (low personal association). This was the most important barrier to perceived relevance revealed during the interviews and has not been elicited in the studies on physical problems (Massolt & Borowski, 2018, 2020).

If SRMPs had a clear reference to a teaching context and students accepted it to be realistic, they rated the problem as more relevant if there were opportunities to take the perspective of a teacher (higher identification) and imagine situations in their future job in which they might use a problem’s content (higher personal usefulness). Regarding the alignment with the future profession, students differentiated between specific examples of teacher tasks in the classroom and teacher tasks/knowledge outside the classroom, mirroring a broad conception of the needed teacher competences. Both categories seemed to support identification and personal usefulness, which led to higher perceived relevance. Students mentioned all three facets of SRCK in these two categories and assessed them as relevant. These results are in line with the findings from the evaluation of the ULTRA-project where an intervention highlighting connections between school mathematics and academic mathematics had positive effects on the perceived relevance of academic mathematics (Fukawa-Connelly et al., 2020).

Another important criterion for assessing the relevance of SRMPs was the orientation towards academic mathematics for prospective teachers (personal usefulness). As students encountered SRMPs in the context of academic mathematics courses, it is not surprising that they applied this criterion. However, we would like to emphasise that, unlike criteria from most of the other categories, all students mentioning this criterion used it in a positive manner.

Apart from the relevance criteria that directly refer to teaching and the profession as a teacher, students mentioned three more categories that seem to be more general and do not only refer to SRMPs: affective and motivational aspects (personal association and personal usefulness), benefit for own mathematical learning (personal usefulness), and structural or organisational aspects (personal usefulness).

Our study has some limitations we must consider when interpreting the data. As with most qualitative interview studies, our study relies on a limited number of participants who were not randomly recruited but volunteered. This has to be considered when discussing the generalisability of the results. We used the number of students mentioning a category as one aspect to illustrate the degree of consensus between the interviewed students and individual differences respectively. Further studies could validate our results, for example, by presenting the relevance criteria to a larger sample of prospective teachers, asking them to rate each criterion as relevant or not on a Likert-scale. This would verify whether the criteria that most students in our sample found relevant correspond to the assessment of a representative sample of prospective teachers.

Another limitation is that we only interviewed students from one German university. This means that the results could depend on the way SRMPs were implemented in our context. We tried to address this issue by intentionally selecting the discussed SRMPs based on the criteria found in a sample from different universities (see Table 3) to display the variety of SRMPs valid for more than one university. Furthermore, first results of Isaev et al. (2022) indicate that students’ relevance perception does not develop fundamentally differently at different universities that use SRMPs. Nevertheless, our results need to be replicated in other contexts.

We must also discuss to what extent the statements we gave students as impulses to assess the SRMPs might have determined our results. As Table 2 shows, these statements can be mapped to the developed category system. Yet at the same time, we were able to elicit further criteria (e.g. benefit for own mathematical learning). Therefore, our methods have given not only opportunities to validate prompted criteria but also to elicit criteria that we did not expect in advance based on the theory or the pre-study.

Despite these limitations, our study yields novel insights into how prospective teachers perceive learning opportunities focusing on knowledge of connections between academic mathematics and school mathematics, a learning goal which is in this work modelled by the SRCK. These insights can serve as starting points for lecturers to pursue a targeted development of their learning opportunities with similar goals (see Section 6) to increase their perceived relevance. As motivational theories suggest, relevant problems support students’ engagement which in turn would be expected to support mathematical learning. It is important to keep in mind this study did not investigate whether these learning opportunities are effective for developing SRCK as it aimed to first close the research gap regarding how students perceive the learning opportunities. Similarly, the study is not informative regarding adjacent important questions, such as whether practising teachers have similar views on the relevance of the SRMPs.

6. Practical implications

The results of our study regarding the students’ perspectives on SRMPs offer practical consequences for the design of SRMPs and similar learning opportunities intended to foster SRCK to increase the probability that prospective teachers perceive them as relevant:

First, school-related learning opportunities need a very clear reference to a teaching context, so that prospective teachers perceive them as relevant (cf. Massolt & Borowski, 2018, 2020). Since students seem to verify the authenticity of a reference to a teaching context by matching it with their own experience as a pupil, it could be sufficient to use material perceived as familiar, like an extract from a schoolbook, to convince students of the authenticity of a reference.

Second, not surprisingly but still important, school-related learning opportunities should reference typical teacher tasks. Students especially appreciated SRMPs in which they had to accomplish or simulate such tasks, for example, reduce academic mathematics to its essentials. The value appears to result from simultaneously practising typical teacher tasks, learning something about the school curriculum, and challenging the own academic mathematical understanding. Similarly, Büdenbender-Kuklinski et al. (2022) found vocational aspects to be important for prospective teachers‘ relevance assessment.

Third, one must cautiously consider the structural and organisational conditions under which one implements school-related learning opportunities. On the one hand, attention has to be drawn to the manner in which school-related learning opportunities are discussed in the course. Only dealing with the SRMPs very marginally in the tutorials may impair the perception of relevance. On the other hand, to appreciate the learning of SRCK as goal of teacher education in academic mathematics courses, universities should acknowledge this in the course exams. In sum, the curriculum-instruction-assessment-triade (Pellegrino, 2010) should be kept in mind.

As discussed in Section 2.1, in Germany students must decide to become a teacher at the beginning of their studies, so universities use SRMPs in academic mathematics courses from the start. For other educational contexts, where students enrol in a teacher programme after a general mathematical education, SRMPs or other SRCK-focused learning opportunities may be alternatively implemented in self-standing seminars or courses (Fukawa-Connelly et al., 2020; Schadl et al., 2019). Our study is also informative regarding the design of such courses, as many of the criteria by which prospective teachers judge the relevance of school-related learning opportunities are likely to be similar, regardless of the structure of the SRCK-targeted intervention. In sum, three design principles are clearly supported by our findings for profession-specific learning opportunities targeting knowledge about connections between academic and school mathematics for prospective teachers:

1. Ensure that there can be little doubt regarding the reference to the teaching context, e.g. by incorporating authentic instructional materials or pupils’ work from school.

2. Prompt prospective teachers to experience, read up on, or reflect on the usefulness of mathematical knowledge for future professional demands, e.g. by asking them to solve teacher tasks using their mathematical knowledge or illustrate how others use mathematical knowledge to solve such tasks.

3. Ensure that the organisational and structural conditions do not impede the effect of school-related learning opportunities, e.g. by ensuring they are not devalued compared to non-school-related mathematical learning opportunities.

In summary, our study could elicit criteria likely to enhance prospective teachers’ perceived relevance as well as possible obstacles. Especially applying the theory of the relevance continuum (Priniski et al., 2018) helped understand how students form their relevance assessment. Therefore, our study revealed valuable aspects that can help improve learning opportunities for SRCK, especially the focused SRMPs, for prospective teachers in academic mathematics courses.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 We use the term “academic mathematics“ when referring to the knowledge of the discipline of mathematics in its scientific understanding.

2 The terminology is not consistent and other terms exist in Germany for similar types of problems (e.g. interface-problems, Bauer, 2013).

3 The study revealed different ways teaching was referenced in the analysed SRMPs. Explicit references to a teaching context included presenting snippets of schoolbooks or assignments, a pupil’s statement, an approach/ a definition as used in school mathematics, asking for an adequate response to pupils, a prosaic contextualisation, or another reference to a teaching context (Weber & Lindmeier, 2022). Not all SRMPs in this study made this explicit reference.

4 According to Rach et al. (2014), the conventional mathematical practices in academic mathematics courses are schematic application, extra-mathematical application, and proof. As universities implement SRMPs in mathematics courses, problems that require students to use other practices (e.g. visualising a formal concept for pupils) are termed non-conventional in this context.

5 The board (translated from German) can be found at https://padlet.com/bweber63/virtual–board-1u6ahv29zfiv4dhg.

6 The column on the far right maps these statements to the categories that were later extracted from the interviews (see Section 4).

7 The SRMPs can be found in the supplement.

8 All quotations from the interviews were translated from German as literally as possible.