The role of mathematical connections in object-level and meta-level learning: a potential lens for supporting pre-service teacher learning

ABSTRACT

The importance of mathematical connections in teaching mathematics is broadly acknowledged in the literature. Nevertheless, more research is needed to clarify how different types of mathematical connections manifest in classroom interactions and how they can support student learning. This article uses the commognitive framework to analyse 15 pre-service secondary teachers’ (PSTs’) discussions on mathematical connections that hypothetically could be made in a pattern generalisation task. The study seeks to explore the types of connections produced by the PSTs and to examine the potential opportunities for object-level and meta-level learning in algebra discourse. The findings are discussed in light of ongoing efforts to refine teachers’ pedagogical knowledge and practice regarding mathematical connections and to develop better pedagogical tools to communicate about mathematical connections.

KEYWORDS:

• Mathematical connections
• teaching practices
• commognition
• pre-service teachers

Introduction

Many researchers have recognised the importance of mathematical connections in the context of learning and teaching mathematics in K-12 school contexts (e.g., Carpenter et al., 2005; Evitts, 2004; Hiebert & Carpenter, 1992; Moschkovich et al., 1993; NCTM, 2000; Stein et al., 1996). Indeed, researchers, teacher educators, and policymakers agree that making connections between different mathematical topics, concepts, ideas, procedures, strategies, and representations is an important component of student mathematical thinking and understanding. Similar to other international standards (e.g., Australian Association of Mathematics Teachers, 2006; Perel, 2012), the Principles and Standards for School Mathematics in the National Council of Teachers of Mathematics (NCTM) stated that “when students connect mathematical ideas, their understanding is deeper and more lasting, and they come to view mathematics as a coherent whole” (NCTM, 2000, p. 4). Likewise, Hiebert and Carpenter (1992) suggested that conceptual understanding grows as connections among mathematical facts, procedures, and ideas become richer and more widespread.

Despite the recognised importance of mathematical connections, more research is needed regarding their exact definition, their manifestation in mathematics classrooms, and their specific role in supporting student learning (Evitts, 2004; Hatisaru, 2023; Mhlolo et al., 2012). Explicating the roles of mathematical connections, and how they manifest in classrooms, can particularly support PSTs as they learn about how to make connections during a lesson and how to engage students in making such connections (Rowland, 2013). Without understanding what constitutes a mathematical connection, how it manifests in classrooms, and how it can support student learning, PSTs may have more difficulty integrating such practice into their future teaching.

This article approaches mathematical connections from a commognitive perspective in order to describe and examine them operationally. In this context, the article describes how PSTs can learn about eliciting mathematical connections during lessons using a pedagogical tool that relies heavily on a theoretical lens for student learning. Such a tool has the potential to enable teachers to better understand how to elicit connections, why such connections are important, and how they can promote student mathematics' learning. The goal of this article is thus to explore the types of connections that PSTs refer to and how these connections can support student learning.

Mathematical connections

Mathematical connections, otherwise known as intra-mathematical connections, constitute the relationship between two or more mathematical ideas (Businskas, 2008; Hatisaru, 2023), often specified as “concepts, definitions, theorems, procedures, representations, and meanings” (García-García & Dolores-Flores, 2018, p. 229). To better illustrate the different types of connections and their characteristics, researchers have developed models for different categories of mathematical connections (e.g., Businskas, 2008; Eli et al., 2011; Hatisaru, 2023; Hatisaru et al., 2024; Rodríguez-Nieto et al., 2022). For example, the connection between the graph of a quadratic function and the equation $f(x)=a{x}^2+\mathrm{bx}+c$ exemplifies a connection between different representations (Businskas, 2008). The connection between the formula $S={\displaystyle \frac{a\cdot h}{2}}$ and its use in computing the areas of triangles is an example of a procedural connection in which “rules, algorithms or formulas are used to arrive at a result” (Rodríguez-Nieto et al., 2022, p. 4). Connections in which A is identified as a generalisation of B or, in contrast, B is a specific case of A, are known as part-whole connections (Rodríguez-Nieto et al., 2022). Making such connections is considered an important component in developing students’ conceptual understanding (Hiebert & Carpenter, 1992; Kilpatrick et al., 2001). Through their task selection, their teaching strategy, and their pedagogical knowledge and beliefs, teachers play a significant role in encouraging students to make mathematical connections (Eli et al., 2011; Low & Wong, 2021; Rowland et al., 2005; Swan, 2007).

PSTs’ knowledge and practice when helping students make connections

Ball et al. (2008) suggested that establishing mathematical connections is an essential component of PSTs’ pedagogical knowledge for mathematics teaching. These components include: “linking representations to underlying ideas and to other representations” and “connecting a topic being taught to topics from prior or future years” (p. 400). Askew et al. (1997) emphasised that effective teaching encompasses not only the enhancement of pedagogical knowledge towards making connections but also the development of beliefs and attitudes, which they named as connectionist orientation. Such an orientation involves teachers’ awareness of the connections between mathematical concepts that are established through dynamic teaching and learning interactions. Rowland (2013) and Rowland et al. (2005) sought to enhance such awareness of mathematical connections and to improve their accessibility and visibility in the context of PST learning. They developed an empirically based conceptual framework, known as the Knowledge Quartet, to inform PSTs’ reflective conversations on mathematics lessons. One dimension of this framework, “connection”, includes paying attention to connections between procedures and concepts made during the lesson and to conceptual appropriateness.

Other studies have designed practical tools that can help teachers develop a connectionist orientation. Among them are specific types of talk moves that teachers can use to help students make connections (Resnick et al., 2010; Sahin & Kulm, 2008) and different teaching strategies and lesson structures (e.g., launch-explore-discuss) that create a learning environment conducive to making connections (Lampert, 1990; Stein et al., 2008). Researchers have also explored the types of tasks that prioritise making mathematical connections (Eli et al., 2011; Stein & Smith, 1998). For instance, Hatisaru et al. (2024) showed how contextual algebra word problems with diverse solutions enable learners to make various mathematical connections, among them different representations, procedural, part-whole, and meaning connections. The “doing mathematics tasks” from the Task Framework developed by Stein et al. (1996) is another example of tasks that encourage learners to make connections. These tasks require students to explore the nature of mathematical concepts and connect them with the procedures they performed (Boston & Smith, 2009). Teachers participating in professional development programmes were exposed to such tasks and encouraged to implement them in their classrooms (Heyd-Metzuyanim et al., 2020; Tekkumru Kisa & Stein, 2015).

Some studies also highlight the effectiveness of card-sorting activities in encouraging learners to make connections (Koichu et al., 2016; Swan, 2007). During these activities, learners are given cards and asked to order, pair, classify or sort them in a way that makes sense. For example, participants are given cards that show different representations of mathematical objects—words, algebraic symbols, tables, graphs, and so on—and asked to match cards that show the same object. By interpreting, comparing, and grouping the cards, participants explicitly attend to the underlying concepts, helping them develop a connectionist orientation (Swan, 2011).

PSTs’ attention to mathematical meanings within connections

Eli et al. (2011) used a card-sorting activity to investigate the types of mathematical connections made by PSTs when they engaged in such an activity. Five types of connections were identified: categorial, procedural, characteristic/property, derivation, and curricular. The researchers suggested that the categories identified can serve as a pedagogical tool for PSTs to enhance their understanding of mathematical connections. The study underscored the significance of enabling PSTs to reflect on the different types of potential connections and their role in lessons, particularly those connections that focused on the underlying mathematical ideas and the relationship between concepts. One of the main findings of this study is that PSTs tended to establish procedural and categorical connections more than derivational or curricular connections. This means that PSTs tended to focus on the procedures performed and the features of categories rather than on the underlying mathematical ideas and on how concepts relate to, build upon or explain each other. These findings corroborate studies about teacher noticing, claiming that directing PSTs’ attention to the mathematical components of a task or a lesson—such as the main mathematical ideas embedded in a task or the relationship between different concepts students engage with—is a challenging endeavour (Sherin & Han, 2004; Star & Strickland, 2008). In the context of mathematical connection and as stated by Eli et al. (2011), developing effective tools for directing PSTs’ attention to the mathematical meanings within the connections is essential. However, these mathematical meanings and how they are manifested within connections are often subtle and challenging to identify.

The need to explicate the mathematical meanings in the context of mathematical connections was also stressed by Hatisaru et al. (2024), who examined the types of connections PSTs made while solving contextual algebra word problems. They noted that some important mathematical components related to the problem, such as modelling, using real life examples and context-related principles, were not adequately captured by the “meaning connections” category of the Extended Theory of Mathematical Connections theoretical framework that they used (Rodríguez-Nieto et al., 2023). Indeed, this category is marked by some degree of ambiguity surrounding the mathematical activity in which learners are engaged.¹

The Realisation Tree Mediator (RTM) has been identified as an effective tool for overcoming the obstacles described above by making the underlying mathematical ideas and meanings in a lesson or a task more explicit, available, and communicable (Weingarden & Heyd-Metzuyanim, 2024). The RTM can be used both as a research tool for identifying mathematical learning opportunities in classroom discussions and as a learning tool for teachers. The RTM, as elaborated in the following section, focuses on the mathematical content of the learning activity and, by using commognitive tools, it enables the explication of the mathematical meanings in an operationalised manner. Additionally, it describes which mathematical ideas are mentioned during classroom discussions and how these ideas can be connected. However, its potential, particularly in supporting teacher learning about eliciting mathematical connections, has not been fully explored. This article aims to explore this potential and examine how the RTM can be used as a pedagogical tool for developing teachers’ knowledge of mathematical connections. By using the RTM as a pedagogical tool for teachers, I propose a commognitive conceptualisation of mathematical connections and aim to explore which types of connections PSTs refer to and how these connections relate to mathematical meanings and student learning.

The realisation tree mediator (RTM)

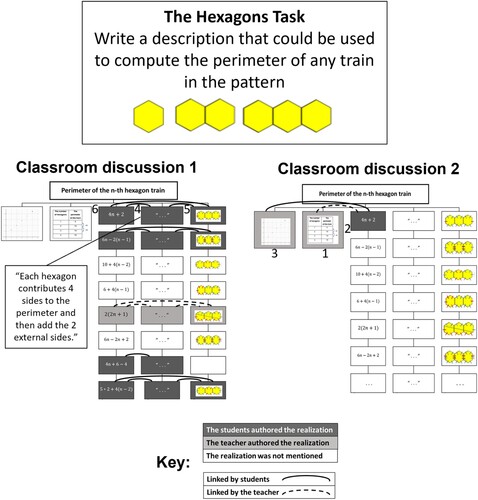
Drawing upon the commognitive perspective, the RTM (Weingarden & Heyd-Metzuyanim, 2024) visually describes a whole-classroom discussion (real or imaginary²) about a mathematical task, while directing PSTs’ attention to focus on the mathematical content at the core of the task, including mathematical connections (see Figure 1). The RTM incorporates the mathematical object at the core of the task (the top of the tree), the object’s different realisations³ (representations) in the form of various cells, and the links between these realisations (arcs). Figure 1 depicts two RTMs describing two classroom discussions in secondary schools focusing on the Hexagon Task, a popular pattern generalisation task (Ayalon et al., 2015; Warren & Cooper, 2008).

Figure 1. Two RTMs representing two classroom discussions around the Hexagon Task.

The different branches of the tree, the vertical columns in each RTM, include different types of realisations of the mathematical object: the graph of the function, table-of-values, algebraic expressions, verbal description and visual illustration. The coloured cells in the figure signify the realisations mentioned during the discussion according to who authored them (teacher: light colour, students: dark colour). The arcs indicate the connections made between realisations (teacher-authored: dashed arc; students-authored: continuous arc). The two classroom discussions included different types of realisations leading the participants to make different types of connections. The realisations mentioned in classroom discussion 2 included the table-of-values (see #1 in Figure 1) describing the perimeter of a train of $x$ hexagons (1 hexagon – 6 sides, 2 hexagons – 10 sides, etc.), the algebraic expression $4x+2$ (#2 in Figure 1), and the function graph (#3 in Figure 1). The connections between these realisations suggest that the lesson focused on linear functions (Weingarden et al., 2019).

In contrast, the realisations mentioned in classroom discussion 1 involved verbal descriptions of how the sides of the hexagons are counted (#4 in Figure 1), visual descriptions of the hexagon pattern (#5 in Figure 1) showing how the hexagons’ sides are counted, and algebraic expressions describing different routines for counting the hexagons’ sides (#6 in Figure 1). The connections between these realisations suggest that the lesson focused on identifying the pattern, generating a formal rule for describing the perimeter and justifying it by relying on the hexagon pattern (Weingarden et al., 2019).

The RTM has been shown to be a productive tool for directing PSTs’ attention to the mathematical aspects of teaching and for visually mapping the mathematical richness embedded in a task or a lesson (Weingarden & Heyd-Metzuyanim, 2023, 2024), a concern raised by researchers studying teacher noticing (e.g., Sherin & Han, 2004). Through visual mediation of mathematical connections around specific mathematical objects, the RTM can also serve as a valuable tool for addressing how mathematical connections are manifested in classroom discussions and how they relate to the mathematical object, another concern raised by several researchers studying mathematical connections (Evitts, 2004; Hatisaru, 2023; Hatisaru et al., 2024; Mhlolo et al., 2012).

In addition, the RTM is heavily grounded in the commognitive learning theory. Whereas other connection-oriented pedagogical tools that aim to enhance teachers’ practices (e.g., Stein et al., 2008), pedagogical knowledge and beliefs (e.g., Askew et al., 1997) often pay less attention to particular student learning processes, the RTM can direct more explicit attention to how mathematical connections can support student learning around particular mathematical objects. The study presented in this article aims to explore the types of connections referred to by PSTs when engaging with the RTM and to examine how their conversations around such connections are related to student learning processes. The commognitive theoretical perspective of object-level and meta-level learning is used to explore these potential student learning processes.

Theoretical perspective: object-level and meta-level learning

The term “commognition” combines “communication” and “cognition” in a theoretical framework that views thinking as a type of interpersonal communication (Sfard, 2008). This type of communication is defined as discourse and is characterised by special keywords, unique visual mediators, routines, and endorsed narratives. Participating in mathematical discourse entails producing narratives about mathematical objects (e.g. “$2+3=5$” or “the function $y=x$ is odd”). 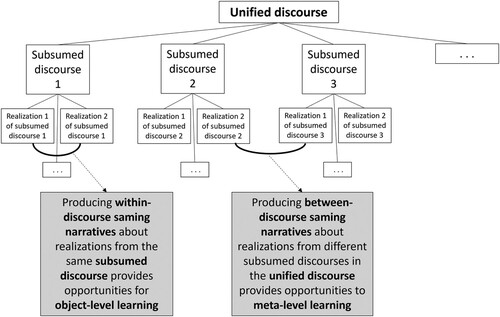Such mathematical objects as “half”, “4”, and “$y=x^2+4$” are produced by discourse and made up of different realisations. The mathematical object “half”, for example, can have different realisations: ½, 0.5, 50%, as well as visual realisations such as half a pie. Each of these realisations belongs to a different subsumed discourse (Sfard, 2008; Wallach, 2022) (e.g., decimals, percentages, numerator and denominator, or visual models such as bars or pies). Box II in Figure 2 depicts the subsumed discourses of fraction and the realisations belonging to these discourses.

Figure 2. The unified discourse of fraction, its subsumed discourses and narratives that relate to object-level and meta-level learning.

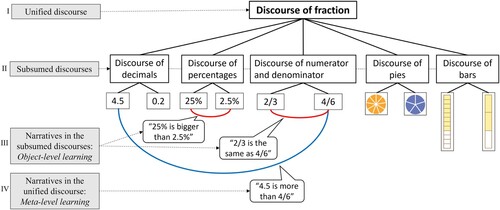
To gain proficiency with fractions, students must first become proficient in each of the subsumed discourses, including the production of narratives within these subsumed discourses (e.g. Box III in Figure 2). Producing such narratives in the subsumed discourses is described in terms of object-level learning. Ideally, these separate subsumed discourses will eventually coalesce into one unified discourse (Sfard, 2008; Wallach, 2022), such as the discourse of fraction in the above example (Box I in Figure 2). Participation in the unified discourse of fraction is characterised by producing narratives about realisations from different subsumed discourses (Box IV). This participation, which involves shifting from one subsumed discourse to another, is known as meta-level learning.

Thus, learning mathematics is a twofold process that involves developing proficiency in the various subsumed discourses (object-level learning) and in the unified discourse (meta-level learning). Such processes can also be seen in learning algebra. Similar to the unified discourse of fraction, the unified discourse of algebra also includes multiple subsumed discourses in which students communicate about patterns and relationships that are not limited to specific numerical values. At the object-level of learning algebra, students develop proficiency by producing narratives in the subsumed discourses. For example, in the discourse of visual realisations where students manipulate the sides of the hexagons (as can be seen in the visual branch in the RTMs in Figure 1), in the discourse of numbers where students produce narratives such as $4\cdot 1+2,4\cdot 2+2,4\cdot 3+2$, or in the discourse of algebraic expressions where the narratives are, for instance, $4n+2$ or $4(n-1)+6$. At the meta-level learning, students produce narratives in the unified discourse of algebra. They adopt one subsumed discourse and its meta-rules and shift to meta-rules in the unified discourse. This shifting provides students with opportunities to communicate about generalised patterns and relationships, constituting the core of the unified discourse of algebra.

Saming narratives (SNs) of different realisations

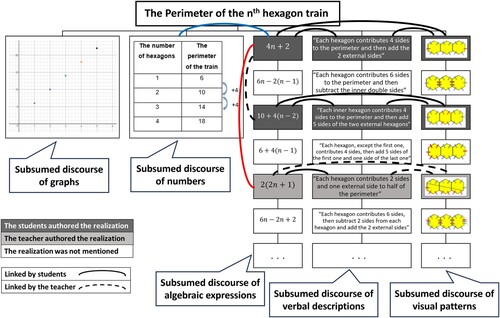
During object-level and meta-level learning, students begin referring to different realisations of a mathematical object as if they were the same. Sfard (2008) described this discursive process as saming, which involves assigning one signifier (giving one name) to a number of things that have not yet been considered as being the same. Weingarden and Heyd-Metzuyanim (2023) operationalised this discursive process by defining saming narratives (SNs) that “include the so-called translation between one realisation and another” (p. 100). According to Weingarden and Heyd-Metzuyanim, SNs “articulate the links between different realisations and the way by which the multiple realisations of a single object are equivalent” (p. 100). For example, consider the following SN (based on the Hexagon Task in Figure 1): I notice that in the first train, the perimeter is $4\cdot 1+2$, in the second train it is $4\cdot 2+2$, and in the third train it is $4\cdot 3+2$, so the perimeter of a train with n hexagon is $4n+2$. This SN articulates the link between the numerical realisation “$4\cdot 1+2,4\cdot 2+2,4\cdot 3+2,\dots$” and the algebraic realisation “$4n+2$”. The RTM was developed based on this conceptualisation in order to visualise these SNs and how they manifest in a classroom discussion (see Figure 3).

Figure 3. An example of an RTM depicting a classroom discussion based on the Hexagon Task.

Drawing upon the perspective of Sfard (2008) and the conceptualisation of Barnett (2022), Wallach (2022) differentiated between two types of SNs, suggesting that these types are strongly related to object-level and meta-level learning. The first type is within-discourse SNs, defined as SNs of two realisations from the same subsumed discourse. These SNs are related to object-level learning. For example, the red vertical arc in Figure 3 depicts a within-discourse SN articulating the translation between two algebraic realisations belonging to the subsumed discourse of algebraic expression: $2(2n+1)$ and $4n+2$. The second type is between-discourse SNs, defined as SNs of two realisations from different subsumed discourses. These SNs emerge from the unified discourse, involve shifting between subsumed discourses and, thus, are related to meta-level learning. For example, the blue horizontal arc in Figure 3 depicts a between-discourse SN articulating the translation between the numerical realisation and the algebraic realisation: $6,10,14,18$ and $4n+2$. Figure 4 summarises the theoretical concepts used in this article.

Figure 4. Summary of the theoretical concepts.

This article uses the conceptualisation of SNs to explore the types of mathematical connections PSTs refer to in their script writing while building RTMs for a pattern generalisation task and eliciting hypothetical student-teacher interactions. Additionally, the article explores the potential opportunities that the RTM, the types of SNs, and the conceptualisation of object-level and meta-level learning can offer PSTs for better understanding how different connections can support student learning. Two research questions guide this study:

1. Which SNs do PSTs refer to as they engage with the RTM?

2. How are object-level and meta-level learning characteristics reflected in the identified SNs that PSTs produce?

Method

Study context

The context of this study is a university-based advanced course for secondary mathematics PSTs titled “Advanced Workshop in Mathematics Teaching.” The PSTs who participated in this course were studying toward a teaching certificate in secondary school mathematics. Most were in their second (and last) year of studies. The one-semester course included thirteen 4-hour lessons. The aim of the course was to introduce PSTs to effective teaching practices, such as facilitating rich classroom discussions and encouraging student active participation. During the course, PSTs used the practices they learned while designing tasks, planning lessons, and enacting their planned lesson. Among the teaching practices that they had learned were the Five Practices introduced by Smith and Stein (2011). These practices focus on enabling students to struggle with a task that is cognitively demanding, facilitating a rich whole-classroom discussion connecting different mathematical ideas. Toward the end of the course, when the course instructors⁴ focused on teaching practices that can encourage students to make mathematical connections, they used the RTM. In what follows, I describe how the RTM was used during the course.

RTM workshop

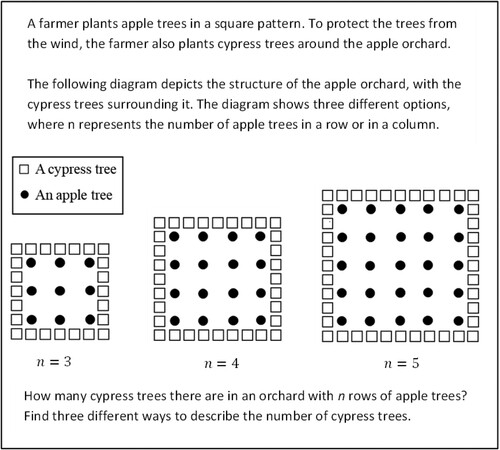
The four-part RTM workshop took place during the course and lasted four academic hours. The author of this article led the RTM workshop. It is important to note that the RTM workshop was not specifically designed for this course. It had already been implemented in other courses and contexts.⁵ In the first part, the PSTs participated as learners in a launch-explore-discuss lesson based on the Hexagon Task (Figure 1) in which they experienced the five practices in action. In the second part, the instructor introduced the RTM and the concepts of mathematical objects and realisations and explained that the mathematical object at the core of the task can be viewed as the answer to the following questions: What is this task about?; What are the main narratives that students are expected to produce while engaging with the task? The instructor further explained that the realisations of this object refer to the different ways such an object can be communicated in a lesson. The instructor then provided examples of narratives underlying the marked arcs in the RTM (SNs). In the third part, the PSTs discussed contrasting pairs of RTMs representing different classroom discussions (such as those appearing in Figure 1) while focusing on the connections made and the potential learning opportunities these connections could provide to students. The fourth part entailed an RTM-related assignment that involved a rich-realisation mathematical task, such as the Apple Orchard Task (Figure 5), which is at the core of this study. The PSTs were asked to solve the task, find as many solutions as possible, and build an empty RTM for the task. Then, using the RTM they built, they were asked to discuss the hypothetical implementation of this task in a classroom, contemplating potential learning opportunities and mathematical connections. The following section describes in detail the RTM-related assignment that was part of the course during which the data for this article was collected.

Figure 5. The Apple Orchard Task.

Data collection

The data collected for the study presented in this article were taken from the RTM-related assignment of 15 PSTs who participated in the RTM workshop in the fall of 2020 and agreed to have their data analysed for this study. Their RTM-related assignment focused on the Apple Orchard Task⁶ (Figure 5). The PSTs were asked to work in groups to (1) solve the task; (2) build an RTM for this task; (3) write two imaginary excerpts representing arcs in the RTM⁷; and (4) summarise the main mathematical ideas that can surface from the task, while referring to the RTM they created and the connections they produced. The 15 PSTs worked in five groups, such that the data include five RTMs, ten short imaginary excerpts of teacher-student interactions, and five lists of mathematical ideas.

Data analysis

I analysed the scripts written by the PSTs while focusing on what the PSTs recognised as the mathematical object at the core of the task, the SNs they referred to in their imaginary excerpts, the types of interconnected realisations in the SNs, and the type of learning (object-level or meta-level) reflected in the main mathematical ideas they wrote and in the RTMs they built.

The first analysis stage included identifying the SNs in the PSTs’ scripts.⁸ Overall, 26 SNs were identified. The second stage entailed detecting the types of interconnected realisations for each SN, the subsumed discourses to which these realisations belong, and the types of SNs. For example, consider the following SN: “I noticed that the two expressions $4+4(2n-1)$ and $8n$ are exactly the same. If we simplify them and use the distributive property, we get $4+4(2n-1)=4+8n-4=8n$”. The interconnected realisations are $4+4(2n-1)$ and $8n$: two algebraic realisations. Both realisations belong to the subsumed discourse of algebraic expressions. Hence, this SN was labelled as Algebraic-Algebraic and classified as a within-discourse SN.

In the third analysis stage, all the identified SNs were recorded in a table containing the SN types, their interconnected realisations, the mathematical objects and ideas indicated by the PSTs, and the RTM they created. The analysis included recognising the object-level and meta-level learning characteristics in their artifacts. These characteristics were identified based on the realisation types, the subsumed/unified discourse, and the SNs to which they implicitly referred.

Based on guidelines for assuring the quality of qualitative analysis from a constructivist perspective (Creswell & Miller, 2000), the study used the following procedure to ensure analysis trustworthiness (SNs, object-level and meta-level characteristics). First, an independent mathematics education researcher, who is familiar with the commognitive framework, read the analysis and posed critical questions. These critical questions focused on identifying the SNs from the PSTs’ scripts and determining whether the mathematical ideas indicated by the PSTs are related to the subsumed discourses or the unified discourse. In places where the mathematics education researcher found possible alternative interpretations, we discussed these alternatives, incorporated them into the analysis, and refined the consistency of the analysis method. For example, in some of the PSTs’ imaginary scripts, it was difficult to identify which narratives can be recognised as SNs. We were in a complete agreement about narratives that involved words like “it is the same as” or “similar to.” When the translation from one realisation to another was more implicit, however, we conducted more comprehensive discussions before reaching an agreement.

Findings

Object-level and meta-level learning around different mathematical objects

First, I describe the RTMs that the PSTs constructed based on the Apple Orchard Task.

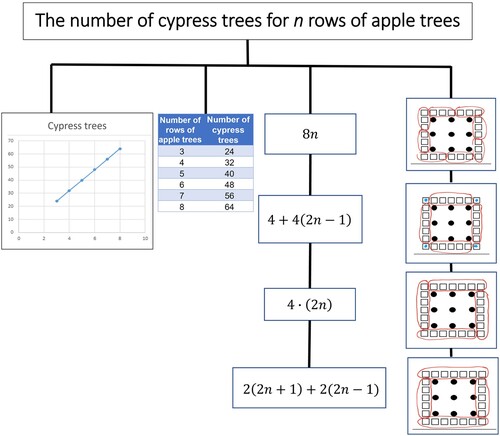
Overall, all five RTMs were similar and included four types of realisations appearing in the branches of the RTMs corresponding to four subsumed discourses (see Figures 6 and 7 as examples).

Figure 6. Group 4’s RTM.

Figure 7. Group 5’s RTM.

Table 1 depicts these subsumed discourses and shows how they relate to the Apple Orchard Task.

Table 1. The four subsumed discourses in the RTMs for the Apple Orchard Task.

Types of realisations/ subsumed discourses/ branches in the RTM	Graphic	Numeric	Algebraic	Visual
Realisations in the context of the task	Graph of the function of the number of cypress trees (y-axis) for each row of apple trees (x-axis)	A table-of-values showing the number of apple trees in each row (first column) and the number of cypress trees in each row (second column)	Algebraic expressions that algebraically describe the number of cypress trees for n rows of apple trees	The visual branch includes the images of the orchard trees and visualisation of the pattern according to which the cypress trees can be counted and generalised

Although the five RTMs shared a common structure and similar types of realisations in the branches, they differed in the PSTs’ choice of what to place at the top of the RTM (i.e., the PSTs’ perspective on the mathematical object at the core of the task). For example, whereas Group 5 (Figure 7) chose “algebraic expression” as the RTM heading, Group 4 (Figure 6) signified “the number of cypress trees for n rows of apple trees.”

Two of the five groups wrote “algebraic expressions” at the top of their trees, suggesting that they considered the focus of the task to be the production of an algebraic expression. Such a focus can be viewed in terms of allocating the task’s contribution and richness in the subsumed discourse of algebraic expressions, indicating object-level learning. In contrast, the PSTs in the other three groups chose to place the task’s potential in the unified discourse of algebra at the top of their trees, referring to generalisation of the number of cypress trees. This generalisation suggests meta-level learning that includes adopting one discourse and its metarules (e.g. numeric, visual) and shifting to the new metarules of the unified discourse of algebra. In the next section, I show how the SNs mentioned by the PSTs are related to object-level and meta-level learning characteristics.

Type I: between-discourse SNs related to meta-level learning

The first type of SNs is the between-discourse SNs. Such SNs, and the mathematical ideas the PSTs mentioned in relation to them, were found to be associated with meta-level learning. They involved shifting from discussing the images of orchard trees (visual subsumed discourse) to discussing numbers (numeric subsumed discourse) and then producing an algebraic expression (algebraic subsumed discourse) in order to identify the general principles (unified discourse of algebra). Three kinds of between-discourse SNs were found, describing SNs of realisations from different subsumed discourses: Visual-Numerical, Visual-Algebraic, and Numerical-Algebraic.

Visual-numerical and Numerical-Algebraic SNs

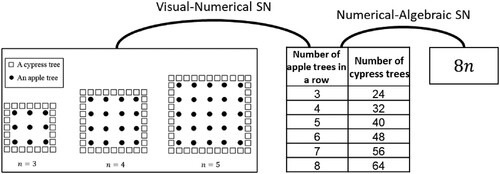
An example of Visual-Numerical and Numerical-Algebraic SNs can be seen in Group 1’s script. This imaginary script describes how the students translated the visual image of the orchard trees into a set of numbers (Visual-Numerical SN) and then generated an algebraic formula to represent the number of cypress trees in any row of apple trees (Numerical-Algebraic SN):

Student 1:

I see in the diagram that when n is 3, there are 24 cypress trees; when n is 4, there are 32 cypress trees; and when n is 5, there are 40 cypress trees.

Student 2:

Each time, 8 cypress trees are added, meaning that the pattern is … 

Student 3:

I know! The general principle is $8n$.

By the imaginary statement of Student 1, the PSTs first referred to the visual realisation (“I see in the diagram”) of the apple and cypress trees to create a numerical realisation, such as a table-of-values representing the relationship between 3 and 24, 4 and 32, and 5 and 40. By the statements of Students 2 and 3, the PSTs then referred to the algebraic realisation $8n$ generated from the numerical realisation (“Each time, 8 cypress trees are added, meaning that the pattern is […] $8n$”). Figure 8 depicts these two between-discourse SNs.

Figure 8. An example of Visual-Numerical and Numerical-Algebraic SNs.

Group 1 then generated another between-discourse Numerical-Algebraic SN (see Figure 9) while articulating the formula for the general term for an arithmetic sequence ($a_n=a_1+d(n-1)$) from the numerical realisation:

Teacher:

We found the table (see Figure 9), and you can see that the first value in our arithmetic sequence is 24, which is the first term ($a_1$), and we have a constant difference of 8. We multiply this difference by $n-3$ (because we start from an orchard with three rows). Then, we get the formula for the general term, which is $24+8(n-3)$.

These SNs are reflected in what Group 1 identified as the focus of the task. The group suggested that “translating the story so it could be represented in mathematical language” is one of the mathematical ideas embedded in the task. The opportunities that these SNs provide students for “translating the story” into “mathematical language” can be viewed as opportunities for meta-level learning. Group 1 “translated” the apple and cypress trees into numbers (table-of-values) and then translated these numbers into a general algebraic rule by identifying the pattern in the numbers (“each time, 8 cypress trees are added”) and by using the formula for the general term of an arithmetic sequence. As Group 1 sensed, the main idea of the task included “translation” from “story” to “mathematical language” or, as other groups described, “representing a phenomenon using an algebraic expression” and “finding the pattern and the general principle”. This main idea points to the necessity of shifting between discourses to produce narratives in the unified discourse, for example by shifting from talking about the image and the orchard trees (e.g. empty square, black circle, apple tree, cypress tree) to talking about numbers (e.g. 3, 24) or from talking about numbers to talking about patterns and general principles (e.g., $8n$).

Figure 9. Another example of Numerical-Algebraic SNs (the general term for an arithmetic sequence).

As evident from Group 1’s SNs, the algebraic expressions $8n$ and $24+8(n-3)$ were not directly related to the visual realisation of the orchard trees. The group used the visual image only to produce the numbers from which they generated the general rule, whereas they did not refer to how the general rule can be translated into the visual realisation of the orchard trees. This translation is evident in the Visual-Algebraic between-discourse SN that appeared in all the other groups’ scripts.

Visual-Algebraic SNs

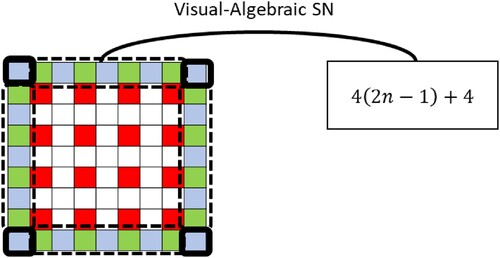
The Visual-Algebraic between-discourse SNs include translating the counting routines of the cypress trees into algebraic expressions. Figure 10 depicts an example of a Visual-Algebraic SN taken from Group 2.

Figure 10. An example of a Visual-Algebraic SN.

In Group 2’s imaginary script (Table 2), the teacher explained how the cypress trees can be counted and how the algebraic expression aligns with this counting routine.

Table 2. Group 2’s imaginary script –example of a Visual-Algebraic SN.⁹

	PSTs’ script (what the imaginary teacher said)	Algebraic realisation	Visual realisation
1	We will now try to see how many cypress trees are on one side of the apple trees’ orchard square.
2	For 3 apple trees, we will need 7 cypress trees on each side.
3	If we exclude the two cypress trees at the edges, we will need 5 cypress trees.
4	Similarly, for 4 apple trees, we will need 7 cypress trees on each side.
5	In the case of n apple trees in a row, we will need 2n-1 cypress trees on each side: for each apple tree, there is a cypress tree planted in front of it and diagonally from it until the last one in the row, where there is only a cypress tree in front of it.	$2n-1$ $\mathit{n}+\mathit{n}-1$ ↑ ↑
6	We will do this on the 4 sides and add the 4 cypress trees in the corners that we excluded.	$4(2n-1)+4$
7	Overall, this yields the algebraic expression $4\cdot (n+n-1)+4$ or $4\cdot (2n-1)+4$

Like the Numerical-Algebraic SNs, this type of SN also involves shifting between discourses and producing a narrative in the unified discourse of algebra. The discussion shifts from talking about the image of the orchard trees and how the cypress trees are located in relation to the apple trees (line 5: “For each apple tree, there is a cypress tree … in front of it and diagonally from it”) to talking about the pattern and how it can be generated for any number of cypress trees (line 5: “in the case of n apple trees in a row, we will need 2n-1 cypress trees on each side”). Such Visual-Algebraic SNs and the PSTs’ mathematical ideas in relation to these SNs show the opportunities for meta-level learning. The PSTs referred to “translation between verbal, algebraic, numerical, and visual representations,” “using multiple methods from different areas of mathematics,” and “connecting between the algebraic, verbal, and visual solutions.” Group 5, for example, suggested that one of the core mathematical ideas is “a function with a constant rate of change,” suggesting that the number of cypress trees for n rows of apple trees can be described as a linear function (8n). They explained that “in the case of the arrangement of the cypress trees described in the task, the number of cypress trees changes according to a single, continuous, and consistent pattern.” They referred to the visual realisations (“arrangement of the cypress trees”), noting that they can be represented by a “continuous and consistent pattern.” The shifting between discourses (visual, algebraic) is reflected in the between-discourse SNs (the arrangement of the trees and its translation to a consistent pattern), constituting narratives in the unified discourse. Such descriptions can be viewed as opportunities for meta-level learning.

Type II: within-discourse SNs related to object-level learning

Within-discourse SNs, which are realisations from the same subsumed discourse, constitute the second type of SNs. These SNs appeared in the data in two forms: Algebraic-Algebraic, where two algebraic expressions were samed, and Visual-Visual, where two counting routines were samed.

Algebraic-Algebraic SNs

An example of an Algebraic-Algebraic SN appeared in Group 5’s script, which focused on the comparison between $4n+4(n-1)+4$ and $2(2n+1)+2(2n-1)$. Table 3 describes this script.

Table 3. Group 5’s script describing an Algebraic-Algebraic SN.

Two expressions are shown on the board: $4n+4(n-1)+4$ $2(2n+1)+2(2n-1)$
1	Teacher:	There are two expressions here, and each of them is a solution to the problem. Do you see a connection between them?
2	Student:	Can I open the parentheses (use the distributive property)?
3	Teacher:	Try to think for a moment without doing anything
4	Student:	In both expressions, n appears twice. I also noticed that in the first expression there is a constant term (4), and in the second expression there is no constant term.
5	Teacher:	Let’s simplify each of these expressions to its simplest form
6	Student:	That’s not a problem. Each of them can be simplified to $8n$
7	Teacher:	So, what can we say now?
8	Student:	All the expressions are $8n$
9	Teacher:	Can you see a connection between the first two expressions?
10	Student:	They are equal

The object at the core of this script is the algebraic expression appearing in lines 1, 4, 5, 8, and 9. Upon simplifying these expressions to “the simplest form” (line 5), the imaginary students came to the conclusion that both expressions “are $8n$” (line 8) and “are equal” (line 10). This SN includes a translation from one expression to another by operating on the expressions themselves; i.e., simplifying them using the distributive property (e.g. $4n+4(n-1)+4)=4n+4n-4+4$) and combining like terms (e.g. $4n+4n-4+4=8n$).

This type of SN also appeared in Group 4’s scripts, where one of the imaginary students says:

I noticed that the two expressions that Emma and John suggested—$4+4(2n-1)$ and $8n-$are exactly the same. If we simplify them by opening the parentheses (using the distributive property), we get $4+4(2n-1)=4+8n-4=8n$.

As evident in the PSTs’ description of the main mathematical ideas, this type of SN focuses on the subsumed discourse of algebraic expressions and hints at object-level learning characteristics. Group 2, for example, suggested that one of the main ideas of the task is “presenting different algebraic expressions of the same object.” Group 5 indicated that the main mathematical idea focuses on the algebraic expressions that can be produced and that different expressions, “according to different interpretations,” can represent “the same object.” Not surprisingly, Groups 2 and 5 chose to position “algebraic expression” at the top of their RTMs, suggesting they were focusing on a subsumed discourse of algebraic expression.

Visual-Visual SNs

Another way of saming different algebraic expressions emerged in the scripts of Groups 2 and 3. Instead of comparing two algebraic expressions by operating on them, as suggested by Groups 4 and 5, they compared two algebraic expressions by saming their corresponding visual realisations. For example, Group 2 samed the two algebraic expressions, $4\cdot 2\cdot n$ and $4\cdot n\cdot 2$, by saming the visual realisations aligned with these expressions. Table 4 shows Group 2’s script.

Table 4. Group 2’s script describing a visual-visual SN.

1	Teacher:	Do you think there are connections between the different solutions for the number of cypress trees?
2	Student A:	It seems to me that there should be a relationship between $4\cdot 2\cdot n$ and $4\cdot n\cdot 2$. The expressions are very similar, so such a relationship is called for.
3	Student B:	Yes. $4\cdot 2\cdot n$ expresses two sequences [of cypress trees]. Each sequence is of the size of the number of apple trees in a row, n, on 4 sides, while $4\cdot n\cdot 2$ expresses n sequences of 2 cypress trees on 4 sides. You can take a cypress tree from any sequence of the 2 sequences in the first expression and create a pair of cypress trees in the second expression.
4	Teacher:	Excellent!

Group 2’s script begins with Student A describing the pursuit of an Algebraic-Algebraic SN to find a relationship between two algebraic expressions that “are very similar.” The script continues with Student B explaining how $4\cdot n\cdot 2$ can be translated to its visual counting routine (“$4\cdot 2\cdot n$ expresses 2 sequences of 2 cypress trees on 4 sides”). The script ends with Student B translating one counting routine to the other to justify the Algebraic-Algebraic SN. Table 5 shows the SNs involved in Group 2’s script.

Table 5. A visual-visual SN involving algebraic-algebraic and visual-algebraic SNs.

Student A: Algebraic-Algebraic SN		“The expressions are very similar, so such a relationship is called for”.
Student B: Visual-Algebraic SN		“$4\cdot n\cdot 2$ expresses n sequences of 2 cypress trees on 4 sides”
Student B: Visual-Visual SN		“You can take a cypress tree from any sequence of the 2 sequences in the first expression (visual realisation) and create a pair of cypress trees in the second expression (visual realisation).”
Conclusion		Showing the “relationship between $4\cdot 2\cdot n$ and $4\cdot n\cdot 2$.”

This Visual-Visual SN suggests that a cypress tree from each of the two sequences represented by the first expression ($4\cdot 2\cdot n$) can be paired to n couples, as it is represented by the second expression: $4\cdot n\cdot 2$. In contrast to Group 5’s Algebraic-Algebraic SN (Table 3), in this case, the equivalency between the algebraic expressions was not explained by operating on them. The PSTs could hypothetically use the commutative property to show that the algebraic expressions are equivalent (e.g. $2\cdot n=n\cdot 2$ and thus $4\cdot 2\cdot n$ is the same as $4\cdot n\cdot 2$). Instead, as Student B explained, they justified the equivalency by showing how the two counting routines representing the two algebraic expressions are the same.

In describing the main mathematical ideas of the task and explaining how these are incorporated with the resulting SNs, Group 2 indicated that the task enables “connecting between different algebraic expressions of the same object”, pointing to object-level learning characteristics, and facilitates “connecting between the visual, verbal and algebraic representations”, pointing to meta-level learning characteristics.

Discussion

This article demonstrates how PSTs can learn about eliciting mathematical connections during lessons while engaging with the RTM. In particular, the article examines which types of mathematical connections PSTs refer to and how such connections have the potential to provide students with opportunities for object-level and meta-level learning. The main goal of this article was to explore how different mathematical connections can be related to learning processes and to examine the potential use of this relationship in teacher learning contexts. The commognitive theory was used to explore the relationship between mathematical connections and how they can support student learning. Mathematical connections were conceptualised as SNs about two so-called different realisations of a mathematical object. Using this conceptualisation, I explored the types of SNs produced by PSTs while they considered imaginary classroom discussions around a pattern generalisation task (research question 1). Using the conceptualisation of object-level and meta-level learning, I showed how the identified SNs are related to object-level and meta-level learning processes (research question 2).

With respect to the first research question, the findings revealed different types of SNs, which I then categorised into two types: between-discourse SNs and within-discourse SNs. The between-discourse SNs include Visual-Numerical: translating the image (orchard) into numbers representing the items in the image (apple and cypress trees); Numerical-Algebraic: translating the pattern of the numbers representing the items into a general rule; and Visual-Algebraic: translating the image and the pattern in which the items can be counted into a general rule. The within-discourse SNs include Algebraic-Algebraic: translating one algebraic expression into another, and Visual-Visual: translating one visual pattern into another.

In the case of the second research question, analysis of the PSTs’ RTMs, their imaginary scripts, the SNs they produced and the main mathematical ideas they proposed revealed how different mathematical connections can be related to object-level and meta-level learning characteristics. The between-discourse SNs are related to meta-level learning characteristics. For example, while producing between-discourse SNs, the PSTs discussed ideas such as “representing a phenomenon,” “translating the story,” and “finding the pattern and the general principle.” All these ideas include shifting between subsumed discourses (e.g. numerical, visual) toward producing narratives in the unified discourse of algebra, suggesting opportunities for meta-level learning. The within-discourse SNs refer to object-level learning characteristics. For example, upon producing within-discourse SNs, the PSTs mentioned the idea of “presenting different algebraic expressions of the same object” highlighting opportunities to extend the subsumed discourse about algebraic expressions by presenting multiple equivalent algebraic expressions, thus suggesting opportunities for object-level learning.

Previous studies (Barnett, 2022; Sfard, 2008; Wallach, 2022) have described the association between SNs and object-level and meta-level learning suggesting that between-discourse SNs are associated with meta-level learning and within-discourse SNs are associated with object-level learning. These studies focused mainly on student learning and the development of student discourse. Recent studies have also examined the teaching actions and instructional activities that provide students opportunities for object-level and meta-level learning (Nachlieli & Elbaum-Cohen, 2021; Wallach et al., 2022) and encourage them to produce SNs (Weingarden & Heyd-Metzuyanim, 2023). The benefits of examining teaching and learning processes through the commognitive lens have been broadly acknowledged (Herbel-Eisenmann et al., 2017; Nardi et al., 2014; Sfard, 2012). One of the main strengths of commognition is that it provides an operationalised language for communicating about mathematics learning and teaching. This language and its embedded conceptual framework focus solely on the discourse itself, thus avoiding the use of so-called private entities related to the individual’s mind, such as concepts, groups of schemas, and mental networks. Still, little is known about how commognition helps support teacher learning. This study makes one small step toward this inquiry by showing that when PSTs learn how to encourage students to make connections, they tacitly refer to the characteristics of object-level and meta-level learning and the different types of SNs that support these learning types. The PSTs did not rely directly and explicitly on the commognitive-based conceptualisation while describing the main ideas of the task and the potential SNs. Nevertheless, this study shows that the characteristics of object-level and meta-level learning and the SNs that support each learning type may potentially emerge in PSTs’ conversations. This insight is clearly related to the fact that the PSTs elicited these connections while working with the RTM as a teaching mediator.

The RTM serves as a pedagogical tool for teachers as they learn how to encourage students to make connections by providing them with a visualisation of the mathematics (hypothetically) under discussion in the classroom. This visualisation can help resolve some of the concerns raised by researchers, including the need for a better understanding of how mathematical connections manifest in classrooms (Hatisaru, 2023; Mhlolo et al., 2012) and the need for directing teachers’ attention to the mathematical components of connections (Eli et al., 2011). Hatisaru et al. (2024) pointed to another significant concern by asking about the importance of connections in student learning processes:

Our investigation raised questions about whether it might be possible or useful to make qualitative determinations about the connections made by learners. Are all connections or types of connections equally valid or important, or are some connections more important or better than others. (p. 45)

By approaching mathematical connections through the commognitive theory, this article can provide some initial answers to such concerns. First, this study shows that it is possible to make qualitative determinations about connections. Within-discourse SNs that are produced in different subsumed discourses differ from between-discourse SNs produced in the unified discourse. They differ not only because they connect different types of realisations but also because they belong to different stages of student learning. Whereas within-discourse SNs support object-level learning, between-discourse SNs support meta-level learning, thus showing that mathematical connections are not equally valid. Both are important, but for different stages of learning and for different goals. Developing proficiency in subsumed discourses (e.g., algebraic expressions) includes producing within-discourse SNs, leading to object-level learning. In contrast, developing proficiency in the unified discourse (e.g., algebra) entails producing between-discourse SNs, leading to meta-level learning.

This article showed how the characteristics of object-level and meta-level learning can be reflected in PSTs’ conversations and in the SNs they produce as they engage with the RTM. The next step is to investigate whether explicitly introducing PSTs to commognitive-based conceptualisations is valuable. This will involve exploring the benefits that PSTs can derive from learning to teach using the conceptual framework of commognition and how teacher educators can effectively implement this. To this end, this operationalisation will need to be extended to different tasks and topics beyond the discourse of algebra. In addition to such theoretically related research directions, more practically oriented future studies can also be conducted. For example, examining how in-service teachers use the RTM to learn about ways to encourage students to make mathematical connections and examining the types of SNs that are referred to by in-service teachers as opposed to PSTs. Comparing in-service and pre-service teachers’ conversations can provide valuable insights into teachers’ varying perspectives regarding mathematical connections (Rowland, 2013). Another direction is to examine the benefits of PSTs’ imaginary scripts and the challenges they faced due to their lack of experience anticipating students’ responses in the classroom.

This article proposed exploring mathematical connections from the commognitive perspective. It illustrated different types of connections and how they can provide opportunities for object-level and meta-level learning. The proposed conceptualisation of mathematical connections, which combines an operationalisation of mathematical meanings with how they can be reflected in student learning processes, can potentially be used in teacher learning contexts. Teachers and teacher educators can refer to how each mathematical connection can support student learning at different learning stages and can point out what each connection contributes to students’ mathematical understanding. Doing so has the potential to help teachers encourage their students to make meaningful mathematical connections during lessons.

Acknowledgment

I would like to express my gratitude to Einat Heyd-Metzuyanim for the opportunity to collaborate in teaching the course. I would like to thank Miriam Wallach for her help with the analysis, her careful reading and her thoughtful critique. Additionally, I would like to thank the reviewers for their valuable feedback on earlier versions of this article.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 Hatisaru et al. refer to the definition of “meaning connections” offered by Rodríguez-Nieto et al. (2023): “(a) connections related to the meaning of a mathematical concept or definition and (b) connections related to different meanings of a mathematical concept that are useful for solving a given problem” (Hatisaru et al., 2024, p. 46).

2 The RTM was initially designed to assess classroom discussions (Weingarden et al., 2019). For this purpose, real classroom discussions were represented by visual images of realisation trees. These visual images, originally intended for assessing discussions, proved to be valuable as teaching representations for PST learning. Note that realisation trees can be beneficial for teacher learning even when they do not depict real lessons (Weingarden & Heyd-Metzuyanim, 2024).

3 As described later in the article, the RTM relies on the commognitive framework (Sfard, 2008). Sfard chose to use the term “realisation” instead of the commonly used term “representation” to highlight the notion that mathematical objects are simply a consequence of the discourse and not something that truly exists and should be represented.

4 Einat Heyd-Metzuyanim was the lecturer of the course. The author of this article was a teaching assistant in the course.

5 For more details about the workshop see Weingarden & Heyd-Metzuyanim, 2024.

6 The original task appeared in the PISA test, 2001. The task was modified as part of the TEAMS PD project (Heyd-Metzuyanim & Nachlieli, 2024; Heyd-Metzuyanim et al., 2020). The task involved another section that is beyond the scope of this article.

7 The PSTs were asked to write one excerpt representing a continuous arc (student-authored narrative) and one excerpt representing a dashed arc (teacher-authored narrative). For this article, no distinction was made between these two types of excerpts. In addition, the instructors asked the PSTs to propose hypothetical teaching situations instead of rehearsing teaching situations, e.g. to develop their thinking and exploration regarding potential mathematical connections that can be made in a discussion around a specific task. Similar to the practice of anticipating students” solutions in Stein et al. (2008), producing mathematical connections and hypothetical students-teacher interactions around such connections can help teachers encourage their students to make connections in other contexts and settings (e.g. tasks).

8 For more details and examples about how different SNs can be identified, see Weingarden and Heyd-Metzuyanim (2023).

9 The first column describes the original script produced by the PSTs. The visual and algebraic realisation columns did not appear in PSTs’ original scripts. They were added to help the reader follow the counting routine and understand how it relates to the algebraic realisation.