Connecting the threads: the role of multiplicative thinking in algebraic, geometrical, and statistical reasoning

ABSTRACT

Making connections within and between different aspects of mathematics is recognised as fundamental to learning mathematics with understanding. However, exactly what these connections are and how they serve the goal of learning mathematics is rarely made explicit in curriculum documents with the result that mathematics tends to be presented as a set of discrete, disconnected topics. Interest in establishing a more coherent approach to the teaching and learning of school mathematics has led to a focus on big ideas. That is, networks of related concepts, skills and ways of thinking that facilitate learning mathematics with understanding. Research on learning progressions has helped identify what these big ideas are and how they serve to build connections within and between different aspects of mathematics. This paper draws on research that provides an evidenced-based learning progression for multiplicative reasoning to illustrate the connective role of multiplicative thinking in the development of algebraic, geometrical, and statistical reasoning.

KEYWORDS:

• Csonnections
• multiplicative thinking
• mathematical reasoning

The nature and importance of connections

It is widely recognised that, where students have the opportunity to make connections within and between different aspects of mathematics and between mathematics and their lived lives, they are more likely to retain the mathematics they have learnt and apply it to new situations (e.g. Hiebert & Carpenter, 1992; National Research Council, 2001; Watson et al., 2013; van den Heuvel-Panhuizen, 2016). However, as “making connections is not something students need to know, it is something students need to do” (Boaler, 2002, p. 12, emphasis in the original), it is also recognised that for students to have these opportunities, their teachers need to have a deep, well-connected understanding of the mathematics they are teaching and how it develops over time (e.g. Askew, 2013; Chick & Stacey, 2013; Hurst, 2017; Ma, 1999; National Research Council, 2001; Siemon, 2022; Siemon et al., 2012).

Connections in mathematics education can be understood in many ways. As connections within and between different aspects of mathematics (e.g. Brophy, 2004; Businskas, 2008; Charles, 2005), as connections between prior knowledge and new learning (e.g. Askew, 2013; Eli et al., 2013; Gronow, 2021; Hiebert & Carpenter, 1992; Ma, 1999), or as connections between mathematics and a student's lived experience (e.g. Tout & Spithill, 2015; van den Heuvel-Panhuizen, 2016). Connections have also been described in terms of inferred mental structures such as schema (Tzur et al., 2013) and neurological networks (della Chiesa, 2013). In describing what they refer to as internal connections, Hiebert and Carpenter (1992) used the metaphor of a network “structured like a spider's web. The junctures or nodes can be thought of as pieces of represented information, and threads between them as the connections or relationships” (p. 67). This notion of connections as threads aligns with Eli et al.'s (2013) view of mathematical connections as “a link (or bridge) in which prior or new knowledge is used to establish or strengthen an understanding of relationship(s) among or between mathematical ideas, concepts, strands, or representations” (p. 122). It is this understanding of mathematical connections as threads or bridges that underpins our intentions here. That is, to demonstrate that the big idea of multiplicative thinking can be thought about as a thread connecting key aspects of algebraic, geometrical, and statistical reasoning.

In recent years, the need to “represent mathematics as a coherent and connected enterprise” (NCTM, 2000, p. 17) and the recognition that learning mathematics with understanding is related to the “quality and quantity of the connections that an idea has with existing ideas” (van de Walle et al., 2010, p. 24) has led to a focus on big ideas (Siemon, 2022). While there are various views on what constitutes a big idea, to the extent that big ideas can be understood as networks of related ideas, concepts, representations, relationships and/or procedures that “link numerous mathematical understandings into a coherent whole” (Charles, 2005, p. 10), they can also be considered as pointers to the connections that students need to make to learn mathematics with understanding.

A focus on big ideas in mathematics has been advocated as an important means of helping teachers develop a deeper understanding of mathematics and its interconnectedness (e.g. Askew, 2013; Brophy, 2004; Charles, 2005; Hurst & Hurrell, 2014; Siemon et al., 2006, 2012). While there are many big ideas in school mathematics (see Siemon, 2022), one of the most important in terms of supporting students’ achievement in mathematics is the big idea of multiplicative thinking (Askew et al., 2019; Siemon, 2019; Siemon et al., 2006). Until recently, this big idea was rarely, if ever, referred to explicitly in curriculum documents. As a result, it was not seen as a priority or recognised as having a critical underpinning role in school mathematics beyond the teaching and learning of fractions (Siemon, Banks, et al., 2018). This changed with the development of evidenced-based learning progressions for algebraic, geometrical, and statistical reasoning (Siemon, Callingham, et al., 2018) which pointed to a strong link between these progressions and a previously developed learning progression for multiplicative thinking (Siemon et al., 2006).

The purpose of this paper is not to revisit the development and validation of the respective learning progressions or the combined scale that was produced as a result of the relationships between these progressions, but to draw on the items used in the research on mathematical reasoning to demonstrate and amplify the critical connecting role of multiplicative thinking in school mathematics more generally. Before proceeding however, it is necessary to clarify what we mean by mathematical reasoning, multiplicative thinking, and multiplicative reasoning.

Mathematical reasoning has been described as the “capacity for logical thought, reflection, explanation, and justification” (National Research Council, 2001, p. 5) that can be observed across all areas of mathematics and across all stages of schooling. For the purposes of research, this broad understanding tends to be linked to specific aspects of mathematics, for example, algebraic reasoning (Kaput, 2008), geometrical reasoning (Battista, 2007), spatial reasoning (Lowrie et al., 2019), and statistical reasoning (Watson & Callingham, 2017). In these contexts, thinking and reasoning tend to be used as synonyms, even though thinking is a more general process that may or may not be either conscious or logical. This is not always the case for multiplicative reasoning where the use is variable. For instance, mathematical reasoning is generally used in the context of research on rational number and proportional reasoning (e.g. Harel & Confrey, 1994; Hodgen et al., 2014; Thompson & Saldanha, 2003). However, Askew et al. (2019) used this term to refer to the “kinds of reasoning required in situations underpinned by a multiplicative (i.e. a multiplication- or division-based) structure” (n. p.) in the early years of primary school. On the other hand, Lamon (1999) referred to multiplicative thinking in terms of relative thinking where, for example, students are able to “understand change in two perspectives: actual growth and growth compared to present length” (p. 13). Described more generally as unitising (the ability to construct a reference unit or unit whole) and norming (reinterpreting a situation in terms of that unit), Lamon regards this capacity as “the first and most basic perspective that students need to adopt before they reason proportionally” (p. 13).

We are using the term multiplicative thinking to recognise that rational number reasoning and proportional reasoning are underpinned by earlier understandings related to fair shares, in particular, recognising that as the number of shares increase the size of each share decreases (Lamon, 1999), the use of processes such as doubling and halving, and an awareness of multiplicative structure (e.g. recognising place value parts as composites of composites and using the properties of multiplicative operations).

Multiplicative thinking

Vergnaud (1983) posited the notion of a multiplicative conceptual field to capture the complexity inherent in problems involving relationships between different quantities (e.g. grapes cost $8.95 a kilogram, what is the cost of half a kilogram?), as opposed to problems involving the aggregation or disaggregation of similar quantities (e.g. Sarah has saved $148, her brother has saved $166, how much have they saved together or how much more has her brother saved than Sarah?). One way of distinguishing between the two types of situations is to consider that the first involves a covariation between two or more measure spaces, while the second typically involves understanding a single measure space in terms of part-part-whole relations.

This difference is partially captured in Steffe's (1994) description of a multiplicative situation as one where “it is necessary to coordinate two composite units in such a way that one of the composite units is distributed over the elements of the other composite unit” (p. 19) (e.g. 12 strawberry plants per row, 7 rows, how many strawberry plants altogether?). While this describes many of the situations introduced to children in the early years of schooling, it does not cover the situation where the numbers involved are not sets but variables as in the grapes problem above.

From our perspective, multiplicative thinking involves recognising and working with invariant relationships between quantities which can be implicit as in the strawberry plant problem or explicit as in the grapes problem. Although some aspects of multiplicative thinking are available to young children (e.g. one-to-many correspondence and sharing equally), multiplicative thinking is substantially more complex than additive thinking and may take many years to achieve (Lamon, 2007; Vergnaud, 1983). This is because multiplicative thinking is also concerned with processes such as replicating, splitting, shrinking, enlarging, and exponentiating, which are fundamentally more complex than the more obvious processes of aggregation and disaggregation associated with additive thinking (Siemon, 2013).

For the purposes of the research that is drawn on here, multiplicative thinking was described in terms of the ability to:

• work flexibly and efficiently with whole numbers, fractions, decimals, and percents;

• recognise and solve a range of problems involving multiplication or division including those involving proportional reasoning; and

• explain solution strategies in a variety of ways (e.g. words, diagrams, symbolic expressions and/or algorithms) (Siemon et al., 2006).

However, as many of the multiplicative situations encountered by students in the primary and middle years of schooling can and are solved additively (i.e. by repeatedly adding or subtracting equal groups), it was necessary to distinguish between the multiplicative structure of the situation and the strategies that might be used in its solution. As a result, a response was regarded as indicative of multiplicative thinking where it was evident that the solution strategy and/or explanation had in some way attended to the multiplicative structure of the situation rather than repeated addition/subtraction.

The research

This paper aims to provide empirical evidence of the links between multiplicative thinking and algebraic, geometrical and statistical reasoning. Apart from being a core focus of middle years mathematics curriculum in Australia (Australian Curriculum, Assessment & Reporting Authority (ACARA), 2018) and overseas, the three domains were chosen as there was evidence to suggest that Australian teachers at this level were largely unaware of the critical underpinning role of multiplicative thinking in developing a deep, well-connected understanding of the key ideas and processes within and between these domains (Siemon, 2019).

The research draws on four large-scale data sets. One from a design-based study on multiplicative thinking (Siemon et al., 2006) and three from a study that explored the development of algebraic, geometrical and statistical reasoning in the middle years of schooling (Siemon & Callingham, 2019). Just over 3200 Years 4 to 8 students from six school clusters (a secondary school and at least three local primary schools, two in Victoria and one in Tasmania) were involved in the first study, the Scaffolding Numeracy in the Middle Years (SNMY) project. The more recent study, the Reframing Mathematical Futures (RMFII) project, involved 3500 Years 7 to 10 students from 32 secondary schools from all Australian states and territories bar the Australian Capital Territory.

The two projects used a similar approach in that hypothetical learning progressions for each area (i.e. multiplicative thinking and the three mathematical reasoning domains) were derived from the relevant research literature and used to inform the design of rich assessment tasks and partial credit scoring rubrics that in turn could be used to test and revise the hypothesised learning progressions through successive iterations of assessment and Rasch analyses (Bond & Fox, 2015; Rasch, 1960). The tasks were consistent with curriculum expectations below, at, and above the year levels concerned, and in almost all cases required students to explain or justify their thinking. A key feature of Rasch analysis is that it measures item difficulty (rubric scores) and student performance on the same scale using a common unit, the logit (the logarithm of the odds of success). This allows item difficulties at the same or similar points on the scale to be scrutinised to identify what students, who score at that level of the scale, are able to do across a range of items. The ordered list of item difficulties also allows researchers to identify points on the scale that mark qualitative shifts in students’ thinking as the items get increasingly more difficult. As a result of this analysis, the ordered list of item difficulties is divided into a relatively small number of hierarchically organised, qualitatively different zones or levels, and it is this that forms the learning progression. That is an “empirically derived, connected, and ordered set of behaviours through which learners variously proceed towards the attainment of a particular goal” (Callingham & Siemon, 2021, p. 3).

A more detailed account of the use of Rasch modelling for the purposes of this study is included below. It suffices to say here that, for the two projects referred to above, this approach resulted in four evidenced-based learning progressions, one for multiplicative thinking in 2006 (Siemon et al., 2006) and three (i.e. one each) for the three mathematical reasoning domains in 2018 (Callingham et al., 2019; Day et al., 2019; Seah & Horne, 2019 ). In this study, the term scale is used to describe the output from Rasch analysis (i.e. the ordered list of item difficulties) and learning progression is used to describe the final, zone-based product.

A detailed consideration of the zones across the four learning progressions, in terms of what students were able to do at comparable points on the respective progressions, indicated a strong relationship between multiplicative thinking and mathematical reasoning. To test the extent of this relationship, the RMFII research team turned their attention to the possibility of developing a combined scale for multiplicative reasoning by testing relevant tasks from each domain against one another.

The technical processes involved in developing the combined scale for multiplicative reasoning, established by combining the learning progressions for mathematical reasoning and multiplicative thinking, have been reported elsewhere (Callingham & Siemon, 2021). In this paper we present a detailed analysis of some of the tasks used to develop the combined scale to illustrate the connecting role of multiplicative thinking in the development of algebraic, geometrical, and statistical reasoning.

The tasks

To explicate the connections between multiplicative thinking and mathematical reasoning, it is necessary to say something more about the tasks themselves and the basis of their relationship to the combined scale. As indicated above, the tasks consisted of one or more items accompanied by an associated scoring rubric based on an anticipated hierarchy of increasing quality or response. The codes were constructed to indicate the reasoning domain (first letter) and task (three or four letters), for example, SCLIM refers to the statistical reasoning Climate Change task. This was followed by a number or letter to indicate the particular item (e.g. SCLIM2 indicates the second item of the Climate Change task). The different levels of response were coded from 0 (no response or a totally irrelevant response) to the highest level for that rubric, usually 2 or 3 but occasionally 4 or 5. The codes provided a way for teachers to score their students’ work by matching each student's response to the descriptor. Figures 1, 3, and 5 below show the rubrics associated with illustrative tasks from each of the three mathematical reasoning domains.

The rubrics thus provided a series of task-steps (Watson & Callingham, 2003) that defined the point at which a response moved from one level of competence to another. The task-steps were not equally spaced and the distance between them provided an indication of how difficult it was for students to progress to the next level of competence. For example, SCLIM2.1 represents a score of 1 while SCLIM2.2 represents a score of 2 on this item.

The codes for each student were entered into a spreadsheet and combined to form a large data set. Because each set of assessment tasks given to students contained several tasks that were common across several assessment forms, the data could be analysed using Rasch approaches (Bond & Fox, 2015). Rasch analysis provides a “difficulty” estimate for each code in logits, the unit of Rasch measurement, and these task-steps are ordered along a scale from lowest to highest difficulty. This produces an interval level scale for the underlying construct.

To provide an initial basis for discussion, the ordered difficulties from the Rasch analysis were examined for shifts in difficulty that might mark a shift in cognitive demands. This resulted in eight “chunks” (potential zones) that were then discussed by the project team. The initial focus was on the boundaries between chunks to identify any items close to the boundary that fitted better in the chunk above or below. Once the placement of boundaries was identified, the rubric descriptors of all the items in a chunk were considered and common elements and demands across all domains were described with reference to the rubrics across the domains (e.g. see Table 1).

Table 1. Zone descriptions for the Combined Multiplicative Reasoning Scale.

Zone 1	Can perform some routine straightforward mathematical tasks. Little/no evidence of mathematical reasoning.
Zone 2	Demonstrates emerging reasoning, which may/may not be correct. Tends to rely on familiar language, situations, or visual cues, often attending to just one aspect.
Zone 3	Recognises straightforward relationships and beginning to justify solutions. Tends to rely on additive approaches or reasoning based on relevant observations but ignores one or more important aspects.
Zone 4	Notices and uses some appropriate relationships but explanations are limited. Beginning to coordinate some aspects of the situation in familiar situations. Starting to use multiplicative approaches but tends to rely on additive explanations in complex or unfamiliar situations.
Zone 5	Reasons using visualisation and multiple representations and demonstrates evidence of multiplicative thinking in familiar situations. Coordinates several aspects of the task as a basis for justification, including some relational aspects in known situations.
Zone 6	Constructs plausible arguments using appropriate language to explain or justify. Beginning to use symbolic arguments, recognise relevance of proportion and/or use deductive reasoning in familiar situations. In complex or unfamiliar situations may revert to non-proportional arguments.
Zone 7	Recognises necessary and sufficient conditions or uses relevant aspects of the task to explain or justify. Coordinates multiple representations and uses symbolic arguments and deductive reasoning to justify conclusions and support generalisations. Recognises causal relationships. Evidence of proportional reasoning.
Zone 8	Uses necessary and sufficient conditions as a basis for reasoning. Develops and tests conjectures and makes and defends generalisations. Uses proportional reasoning, coordinates and integrates all relevant information to draw evidence-based decisions and conclusions. Interprets complex situations, coordinating visual, symbolic, and linguistic information to provide multi-step arguments relevant to context.

In this way, the empirically derived scale for multiplicative reasoning was divided into eight zones. This was not arrived at by researchers allocating rubrics to zones, rather the codes contained within each zone as a result of the Rasch analysis gave meaning to the zone. At times, codes appeared in higher or lower zones than might have been expected. It was then necessary to try to explain why the difficulty was high or low by examining the underlying mathematical structures. The zones within which exemplar rubric codes appeared are illustrated in Figures 1–5 below. The final outcome was an eight-zone hierarchy describing multiplicative reasoning summarised in Table 1.

The evidence

As indicated earlier, we do not intend to explore the Combined Multiplicative Reasoning Scale in any detail as it is still a work in progress. Its development is summarised here as it provides the empirical basis for the connecting role of multiplicative thinking in the development of algebraic, geometrical, and statistical reasoning. It is beyond the scope of the paper to include the full ordered list of coded responses for the combined scale or even the ordered list of responses for the three Zones we will consider. As a result, the evidence for the connecting role of multiplicative thinking will be presented using one or more representative tasks and their associated scoring rubrics from each reasoning domain (statistical reasoning, geometrical reasoning and algebraic reasoning). Tasks from Zones 3, 5 and 7 of the combined scale will be used as it is these Zones that most clearly illustrate the shift in multiplicative thinking from little/no evidence, in Zone 3, to an emerging understanding in Zone 5 before becoming more established in Zone 7.

Multiplicative thinking in statistical reasoning

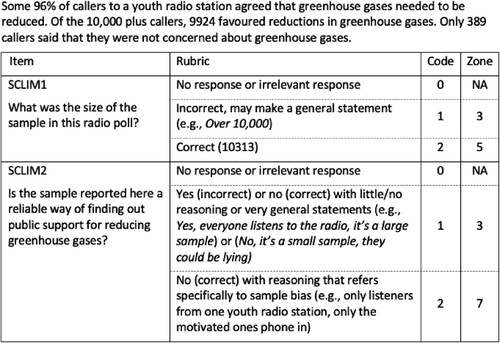
In the domain of statistics, the ability to think multiplicatively is critical. Take, for example, the concept of a sample. Understanding the concept requires the population to be defined. Then decisions are needed about the nature and size of the sample. A random and representative sample inherently demands proportional reasoning and a flexible approach to choosing the sample. Balancing the population characteristics against the sample size and its representative nature makes use of the relationship between the two quantities of population and sample. Students were presented with a task in the context of climate change (SCLIM) (Figure 1).

Figure 1. Climate Change Task with associated rubrics and zone locations.

The Climate Change Task appears relatively straightforward, but a Code 1 response appears at Zone 3 of the Combined Multiplicative Reasoning Scale, indicating that it is more complex than it appears. This problem requires students to have some background understanding of the context (a radio survey), the nature of a survey, and the recognition that the responses form a sample. Although the correct answer to SCLIM1 uses addition, the underlying structure is multiplicative, inherent in the wording asking about the size of the sample. Students obtaining a Code 1 to SCLIM2, demonstrate a simple understanding of sample as a concept. A sophisticated response to SCLIM2 appears in Zone 7, indicating that students understand the nature of a sample that is representative of a population. This reasoning draws on an underlying multiplicative structure of the relationship between population and sample (the whole and the part). Unless that multiplicative relationship is understood by students, they will not be able to reach sophisticated levels of response.

This structural relationship is evident in other statistical contexts. The Mr Robinson Task (Figure 2) was based on a newspaper article about the relationship between heart disease and car usage (SM8GR, SM8QU). Students were asked to draw a representation of the association and then ask questions about the research reported.

Figure 2. Mr Robinson task with associated rubrics and zone locations.

The Zone 3 (Code 1) responses for both questions indicate that students have some knowledge about graphs and sampling, but little or no understanding of the relationship between the variables. By Zone 5 (Code 2, SM8GR) responses indicate an understanding of trends and variables but students are still unable to put these together in a meaningful way or represent the relationship clearly. It is not until Zone 7 (Code 3, SM8GR and Code 2, SM8QU) that the underlying multiplicative structure can be represented or considered in more than a descriptive way, for example, in a bivariate graph or by asking questions outside the information presented.

The two tasks (SCLIM and SM8GR/SM8QU) exemplify the subtle interaction between multiplicative thinking and statistical reasoning. The contextual nature of statistical reasoning, however, tends to make the application of multiplicative thinking more difficult than in straightforward number situations.

Multiplicative thinking in geometrical reasoning

At first glance, geometry may have little to do with multiplicative thinking. However, geometry provides students with opportunities to visualise two- and three-dimensional shapes and objects, engage in spatial reasoning, and recognise and work with proportional reasoning in practical situations (e.g. scale diagrams, maps). Geometry is also intrinsically linked to measurement concepts, the units of which embody multiplicative relationships (e.g. square metres, cubic centimetres, kilometres/hour).

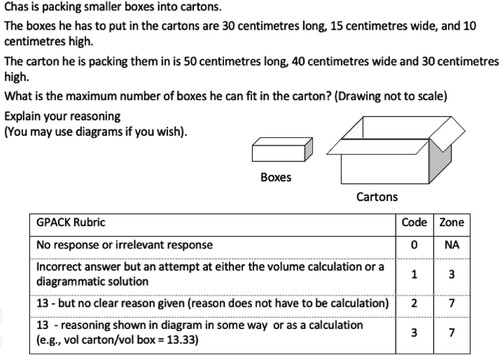
Multiplicative thinking requires more than a recall of basic facts and the ability to perform calculations involving multiplication and/or division. Access to visual images of multiplicative situations is fundamental to the development of multiplicative thinking (Sullivan et al., 2001) as is the ability to mentally switch between different concepts and processes and coordinate the relationships between multiple pieces of information. Geometry tasks that are challenging but accessible can provide opportunities for students to draw on their visualisation skills to connect key aspects of geometry, measurement and number. In this case, even though the majority of the geometrical reasoning tasks reflected curriculum expectations at this level, students found many of the tasks difficult. The results showed that the difference between task-steps varied considerably with some located many Zones apart on the ordered list of coded responses while others were located within the same Zone. As a consequence, to illustrate the role of multiplicative thinking in geometrical reasoning, we will consider the Packing Boxes Task (GPACK) shown in Figure 3 and two items from the Beverage Company Task (GBEV5 and GBEV6) shown in Figure 4.

Figure 3. Packing Task (GPACK) with associated rubrics and zone locations.

Figure 4. The Beverage Company Task with associated rubrics and zone locations.

In the GPACK task, the length of the box is the same as the height of the carton, so can be solved by dividing the volume of the carton by the volume of the box, a calculation that is relatively straightforward if it is set up to facilitate the use of factors and cancellation (i.e. 40/3). Hence, it illustrates the importance of being able to visualise the situation in order to work with the underlying multiplicative structure. For example, recognising that the length of the box and the height of the carton are both 30 cm invites a visual image of a box being rotated to align its 30 cm length with the height of the carton, its 15 cm width with the 40 cm width of the carton, and its 10 cm height with the 50 cm length of the carton. This also leads to a relatively straightforward calculation (2 rows of 5 boxes along the front of the box with room for another three at the back of the box). However, the very low success rate on this task (8.3%) suggests that neither of these strategies were widely available to the 432 students who attempted this task.

While some students were able to make a start (Code 1), the Zone 3 location of this Code indicates that students were unable to coordinate the necessary aspects of the situation and/or manage the calculations involved. The Zone 7 (Codes 2 and 3) responses indicate that, irrespective of whether or not an explanation was provided, students need to be able to coordinate all necessary aspects of the task (i.e. the length, width and height of the various containers and the concept of volume) and manage the calculations involved to arrive at a successful outcome. This task was extremely difficult for the majority of students, suggesting that something more than visualising the situation or being able to carry out the necessary calculations is involved. It appears that a disposition to notice multiplicative relationships (e.g. factors) and work with the underlying multiplicative and spatial structures (i.e. volume) is a necessary aspect of geometrical thinking.

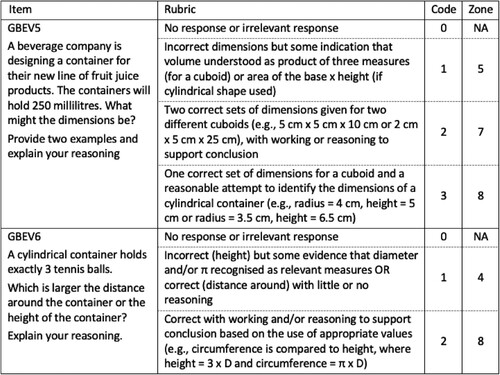
To solve the two items from the Beverage Company Task (GBEV5/GBEV6) (Figure 4) successfully requires a robust understanding of the measurement concepts involved (i.e. capacity, area and volume), an appreciation of the relevant measurement units and the relationships between them, and a capacity to coordinate and carry out the processes involved accurately. Both items require an appreciation of the underlying multiplicative structure and the coordination of multiple pieces of information.

The Zone 5 (Code 1) responses for GBEV5 (see Figure 4) indicate some appreciation of the relevance of volume but not necessarily an awareness of the multiplicative relationship between the units of capacity and volume that is needed to arrive at a reasonable set of dimensions. The Zone 7 (Code 2) responses to this task indicate an awareness of the underlying multiplicative structure of the problem and an ability to work efficiently with the numbers involved and provide a logical explanation. The apparent reluctance to consider the possibility of a cylindrical container suggests there may be an issue with calculating the area of circles and/or the use of π.

GBEV6 requires the capacity to visualise a cylindrical container that holds three tennis balls exactly and recognise the role of the diameter in comparing the height to the distance around the container. While a diagram of a cylinder was included with the task, no dimensions were provided, which required the students to work with the relationships involved at a general level. As a result, it is perhaps not surprising that a Code 2 response is located at Zone 8.

The Zone 4 (Code 1) responses to GBEV6 are very similar to the Zone 3 (Code 1) responses to GPACK in that they both indicate a partial awareness of the underlying multiplicative structure (i.e. a comparison of linear measure in GBEV6 and the determination of volume in GPACK) and an inability to carry out the necessary calculations. However, the Code 1 responses to GBEV6 are consistent with Zone 4 where students are beginning to coordinate some aspects of the situation (e.g. recognising relevance of diameter in the comparison).

Multiplicative thinking in algebraic reasoning

One of the strongest connections to multiplicative thinking was observed when the research team were working on the evidenced-based learning progression for algebraic reasoning. For instance, at Zone 5 of this scale, students “use multiplicative reasoning in simple situations, … [they] recognise and represent simple functional representations” (Day et al., 2019, p. 143), while at Zone 7 they coordinate “multiplicative thinking and the associated language to notice algebraic structure” (p. 144). The following item from the Relations Task, ARELS (Figure 5), demonstrates the critical importance of attending to the underlying multiplicative structure in recognising the relationships between the variables and numbers involved.

Figure 5. Relations Task item with associated rubrics and zone locations.

Although factors are introduced in the curriculum at Year 4, only 13% of the 269 secondary students who attempted this task were successful, suggesting that students are not given opportunities to coordinate the use of factors in equivalence situations. That is, although students may be able to identify factors and products, they may not have been exposed to the way factors behave across the equals sign. This observation connects with a similar observation made in relation to GPACK above where there was evidence to suggest that students failed to notice the role of factors in facilitating computation. This lack of relational thinking and the ability to coordinate more than a single process does not begin to emerge until Zone 5 of the Combined Multiplicative Reasoning Scale whereas by Zone 7 students are able to coordinate several processes and recognise the multiplicative relationships that exist.

Another task that shows the critical connection between multiplicative thinking and algebraic reasoning is the Real Graphs Task (ARLG) shown in Figure 6 which requires students to match graphical representations to relatively familiar situations.

Figure 6. Real Graphs Task.

In each case, Codes of 0, 1, and 2 are used to distinguish between little/no response (0), a correct response with little/no reasoning or an incorrect response with a plausible explanation that ignores one or more aspects (1), and a correct response with an appropriate explanation (2). In terms of the combined scale for Multiplicative Reasoning, a Code 2 response to ARLG1 (situation E) is located at Zone 3, a Code 2 response for ARLG3 (situation A) is located in Zone 5, and a Code 2 response to ARLG4 (situation D) is located in Zone 7.

While this range of Codes reflects the relative difficulties of items a, c and d, it also provides windows into students’ thinking that would not be evident independently of the scale. For example, a Code 2 response to ARLG1 might suggest that the student is attending to the nature of the multiplicative situation involved but its location in Zone 3 suggests that this is not the case. Rather, it suggests that students are choosing situation E because the shape of the graph resembles the movement of the javelin through the air. This interpretation is supported by the fact that situation F was a common incorrect choice for ARLG1. A Code 2 response to ARLG3 requires that students attend to the inverse relationship between the height of the candle and the constant rate of burning. This is consistent with Zone 5 where students typically demonstrate evidence of multiplicative thinking in familiar situations. The location of a Code 2 response to ARLG4 in Zone 7 reflects the increased difficulty involved in recognising an exponential relationship in a less familiar situation (i.e. radioactivity as opposed to repeated acts of paper folding, the situation corresponding to the graph shown in ARLG2).

The Real Graphs Task is similar to the statistical reasoning Mr Robinson Task (SM8GR) reported earlier in Figure 2 in that it requires students to recognise a quantitative relationship between two variables expressed graphically. In both cases, students had to engage with the situation to discern the nature of the multiplicative relationship (i.e. linear or non-linear) and relate that to an appropriate representation. Interpreting multiplicative relationships relative to context in graphs such these, and in the Mr Robinson Task item SM8QU, illustrate how multiplicative thinking can be seen as a thread connecting different aspects of mathematical reasoning, in these cases, algebraic and statistical reasoning.

The critical role of multiplicative thinking

The critical role of multiplicative thinking in the progression from naïve to more sophisticated levels of mathematical reasoning is illustrated by the relative proportion of responses by Code and Zone for each of the tasks presented above. This is an important application of the empirically derived scale for Multiplicative Reasoning as it shows just how critical this relationship is and points to what is needed to improve mathematics learning outcomes more generally (i.e. beyond the domains of rational number and proportional reasoning). As indicated above, the results are from the third and fourth rounds of assessment in the RMFII project that were used to create the combined scale for multiplicative reasoning (Callingham & Siemon, 2021). A range of different assessment forms were used across the two rounds, as a result the numbers of students attempting any one task varied. Where a task was used in both rounds the results have been combined. Students were drawn from Years 7 to 10 with the majority in Year 8 from the 32 project schools. A condition of funding was that the schools were selected from lower socio-economic areas.

Although the tasks were consistent with the Australian mathematics curriculum at the Year levels concerned and an effort was made to set the tasks in familiar contexts, many of the mathematical reasoning tasks proved difficult for the students concerned. This is illustrated in the proportion of Code 0 responses (i.e. little/no response or incorrect) for each of the tasks/items referred to above (see Table 2).

Table 2. Proportion of Code 0 responses to reasoning tasks considered.

Reasoning Task	Item	N	Little/no/incorrect response (%)
Climate Change	SCLIM1	496	45.2
	SCLIM2		37.7
Mr Robinson	SM8GR	372	43.8
	SM8QU		53.8
Packing Boxes	GPACK	432	46.8
The Beverage Company	GBEV5	162	44.4
	GBEV6		27.8
Relations	ARELS	269	50.9
Real Graphs	ARLGR3	466	41.0
	ARLGR4		52.6

One of the reasons for the high level of Code 0 responses is that many of the algebraic and statistical reasoning tasks required a deeper understanding of multiplication and division than repeated addition to appreciate what was involved in the situation (e.g. proportionality) and a need to explain their thinking. In addition, the overall low levels of response to the geometrical reasoning tasks suggest that the students involved had limited experience of geometry and the application of measurement ideas to solve realistic problems involving three-dimensional objects. The proportion of Code 0 responses to GBEV6 (27.8%) compared to the other tasks suggests students felt more confident about making a start, even if they could not carry it through to a solution.

Responses at Zone 3 of the Multiplicative Reasoning scale can be seen in Code 1 responses to SCLIM1, SCLIM2, SM8GR, SM8QU, and GPACK and Code 2 responses to ARLGR1. In each case, the responses suggest students are able to make a start on the problem in a way that suggests some appreciation of what is involved in the situation but tend not to notice one or more important aspects of the problem, particularly where this requires some awareness of, or disposition to notice, multiplicative relationships. For example, the failure to take into account the number of callers who were not concerned about greenhouse gases (SCLIM1) suggests that the notion of a sample as a proportion of a population may not be understood or noticed. In SM8GR and GPACK, the multiplicative relationship may be partially recognised, but students are unable to progress this through to a solution. The querying of the sampling method in SM8QU suggests an intuitive sense of proportion but little or no appreciation of the relationship between the variables. Similarly, the Code 2 response to ARLGR1 appears to be based on the shape of the graph rather than an understanding of the relationship between the variables. The much higher proportion of Code 2 responses to this task (65%) compared to the proportion of Code 1 responses to the remaining tasks, which indicate some level of multiplicative awareness (i.e. from 27% for SCLIM to 49% for SCLIM2), tend to support this observation.

Responses at Zone 5 of the Multiplicative Reasoning scale can be seen in Code 2 responses to SCLIM1, SCLIM2, and ARLGR3 and in Code 1 responses to GBEV5, ARELS7 and ARLGR4. These responses suggest that while students are able to coordinate one or more relevant aspects of familiar situations (e.g. SCLIM1, ARLGR3), they find it difficult to describe or represent relationships between two or more variables in more complex situations (e.g. SCLIM2, ARLG4). The Zone 5 responses to GBEV5 and ARELS7 suggest some appreciation of the underlying multiplicative structure, but an inability to coordinate the necessary aspects of the situation (i.e. the relationships between the dimensions of the box and the container in GPACK and the relationship between 14 and 2 in ARELS7). These responses suggest that what is needed, but missing here, is an alertness to numbers and the relationships between them.

Responses at Zone 7 of the Combined Multiplicative Reasoning Scale can be seen in Code 2 responses to SCLIM2, SM8QU, GBEV5, ARELS7 and ARLG4, in Codes 2 and 3 responses to GPACK, and in Code 3 responses to SM8GR. These responses indicate an ability to recognise and work with proportionality (e.g. notice the possibility of sample bias in SCLIM2) and coordinate multiple aspects of the multiplicative situation in ways that lead to a correct solution (e.g. GPACK, GBEV5, ARELS7). The responses at this Zone also indicate a capacity to recognise multiplicative relationships between variables in less familiar contexts (e.g. choose and justify situation D in ARLG4, represent relationship in SM8GR, and question causality in SM8QU).

The Zone 7 location of Code 2 responses to GPACK (i.e. correct, 13 boxes, without a clear reason) is another example where the scale provides windows into students’ thinking that may not be obvious from a consideration of the responses alone. For instance, although no explanation is provided, it is difficult to imagine arriving at 13 boxes without some form of calculation and/or spatial visualisation of the situation. The co-location of Codes 2 and 3 for this task suggests that something like this may have taken place but for various reasons (e.g. diagram too difficult to draw, calculations too difficult to represent), an explanation was not forthcoming.

The critical role of multiplicative thinking in the development and application of mathematical reasoning is starkly illustrated by the proportion of Zone 7 responses to the reasoning tasks considered here (see Table 3). With the exception of GBEV5 (two correct sets of dimensions for two cuboids with a volume of 250 cm³), considerably less than 20% of the responses to each task are indicative of the thinking identified at Zone 7 of the Multiplicative Reasoning scale. This is a matter of concern given current and emerging curriculum expectations at this level of schooling (e.g. Organisation for Economic Co-operation and Development (OECD), 2022).

Table 3. Proportion of Zone 7 responses to reasoning tasks considered.

Reasoning Task	Item	N	Zone 7 Code	Proportion (%)
Climate Change	SCLIM2	496	2	13.7
Mr Robinson	SM8GR	372	3	11.0
	SM8QU		2	12.1
Packing Boxes	GPACK	432	2 & 3	9.7
The Beverage Company	GBEV5	162	2	36.4
Relations	ARELS	269	2	13.4
Real Graphs	ARLGR4	466	2	16.1

Discussion

Multiplicative thinking has long been recognised as a necessary foundation for school mathematics in the middle years and beyond (e.g. Harel & Confrey, 1994; Siemon et al., 2006; Vergnaud, 1983). While clearly relevant to all further work involving rational numbers and proportional reasoning (Brown et al., 2010), the responses considered above, together with their location on the Combined Multiplicative Reasoning Scale, demonstrate the critical role of multiplicative thinking in the development of mathematical reasoning more generally. The Australian Curriculum (ACARA, 2022) described mathematical reasoning in terms of an “increasingly sophisticated capacity for logical thought and actions” (n. p), indicative instances of which are then provided. However, what the increasingly sophisticated responses in the Combined Multiplicative Reasoning Scale show is that the capacity for logical thoughts and actions is dependent on a deep understanding of the relevant content and that this understanding largely determines what information is attended to, what representations are employed, what strategies and procedures are used and the extent to which the whole process is managed and reflected upon. This level of understanding aligns with Skemp's relational understanding which others have described in terms of structural thinking, or the capacity to see the general in the particular (Mason et al., 2009; Vale et al., 2011). For example, recognising the relevance of the multiplicative inverse in situations like ARELS7 could be described as structural thinking. A situation might be described as having a multiplicative structure if it requires a comparison of measures (e.g. GPACK) or involves proportion (e.g. SM8GR), or embodies a multiplicative relationship if it involves an invariant relationship between quantities (e.g. ARLG), proportion (e.g. SM8GR) or equivalence (e.g. ARELS7).

What the Combined Mathematical Reasoning Scale and the above analysis also show is that students who can identify and work with multiplicative structures and relationships are able to access mathematical reasoning at a more sophisticated level than those who cannot. This has important implications for teaching and learning. For instance, one of the discriminating elements in the scale is the ability to attend to all relevant aspects of the situation. While this undoubtedly depends on the extent to which students understand the content in the way described above, it is also something that many have recognised can and should be taught in conjunction with content (e.g. Gronow et al., 2022; Ministry of Education, 2018; Schoenfeld, 2022). However, as Mason et al. (2009) pointed out, such teaching needs to be focused on the underlying structures and relationships rather than the surface features of the task. It also needs to focus on developing a productive disposition to look for patterns and relationships, explore different representations, reflect on one's actions and decisions. Watson and Mason (2006) provided a number of tasks than can be used to develop an understanding of mathematical structure and increase the likelihood of noticing all relevant information in a task.

Another aspect that appears to facilitate the use of multiplicative thinking and support mathematical reasoning is the capacity to visualise or represent situations in multiple ways (e.g. GPACK, GBEV6). Visualisation has long been recognised as an important component in building mathematical understanding (e.g. Davis, 1992; Nardi, 2014). However, it is only relatively recently that researchers have examined the efficacy of spatial training on mathematics achievement (e.g. Lowrie & Logan, 2018; Lowrie et al., 2019) or spatialised approaches to the teaching of topics that have proved difficult to master (e.g. Cutting, 2021; Harris et al., 2023). The results of these studies are consistent with the findings of the Combined Multiplicative Reasoning Scale and suggest a much greater focus is needed on the development of spatial reasoning skills as a way of connecting procedural and conceptual knowledge in the way envisaged by Skemp and increasing awareness of mathematical structures and relationships in the way envisaged by Mason and his colleagues.

As indicated above, the very low proportion of student responses at Zone 7 of the Combined Multiplicative Reasoning Scale is a cause of concern particularly as the increased emphasis on mathematical reasoning worldwide by the OECD (2022) has prompted a number of countries to revise their mathematics curricula (e.g. ACARA, 2022; Department of Education, 2021; National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010). The consequence is that, without a deep and well-connected understanding of the structures and relationships that underpin school mathematics in the middle years, many students will be denied the opportunity to develop the levels of mathematical reasoning needed to participate in the burgeoning fields of science, technology, engineering, and mathematics.

Stacey (2010) called for a description of a “developmental path in mathematical reasoning across the grades, that would give teachers, textbook authors and curriculum writers a sense of what type of reasoning they can expect and encourage at each year level and in what directions students’ reasoning should be developed” (p. 19). We believe the empirically derived combined scale for Multiplicative Reasoning, examples of which are presented here, makes a major contribution in this regard. The advantage to teachers is that using the scale, and the Zone descriptors, can uncover subtleties in students’ thinking that might otherwise be overlooked or misinterpreted. This was shown above in a Code 2 response to ARLG1, which appeared in Zone 3 rather than one of the higher Zones and the Zone 7 location of Codes 2 and 3 for GPACK. What these responses point to is that there is more to the combined scale than multiplicative thinking. In other words, while multiplicative thinking is an important thread connecting the different domains of mathematical reasoning, it needs to be regarded as a necessary but insufficient aspect of what is involved in the development of mathematical reasoning more generally. It is beyond the scope of this paper to elaborate further but the zone descriptions for multiplicative reasoning shown in Table 1 point to a number of other aspects that might warrant investigation as potential connecting threads. One of these is spatial reasoning (i.e. the ability to visualise, manipulate and reflect on spatial objects in the “mind's eye”). Glimpses of the possible role of spatial reasoning as a connecting thread are evident in the Packing and Beveridge tasks above, as well as in Real Graphs. Another aspect worthy of further investigation is an awareness of pattern and structure which supports going beyond the superficial aspects of a situation to consider all of the elements involved and the relationships between them. Glimpses of this as a potential connecting thread, can be seen in the Climate Change and Relations tasks and it is evident more generally in the upper level zone descriptions shown in Table 1.

While the combined scale of Multiplicative Reasoning has enabled us to update and extend the SNMY formative assessment resources for multiplicative thinking¹, our next step in this process is to use the combined scale to tease out just what more is needed to support the development of mathematical reasoning beyond access to multiplicative thinking and to represent this in a form that is useful to teachers.

Conclusions

This paper used the ordered difficulties from an empirically derived scale for Multiplicative Reasoning to illustrate the important connecting role of multiplicative thinking in building a deep, well-connected understanding of mathematics in three key areas of the middle years mathematics curriculum. Six of the reasoning tasks used in the development of the combined scale together with their associated rubrics and respective locations on the scale were used to demonstrate how and to what extent multiplicative thinking underpins these important aspects of the curriculum at this level. Access to multiplicative thinking has long been recognised as critical for success in school mathematics in the middle years. The research reported here and the research from which it is drawn demonstrate that this access cannot be taken for granted. To ensure middle year students have the capacities and depth of knowledge needed to participate fully and successfully in school mathematics, teachers need to be supported to become much more aware of what is involved in the development of multiplicative thinking and how it serves to connect key aspects of the middle school mathematics curricula.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The RMFII project was funded by the Australian Department of Education under the auspices of the Australian Mathematics and Science Partnership Program from 2015 to 2018. The views expressed herein are those of the authors.

Notes

1 See http://www.mathseducation.org.au/online-resources/growing-mathematically/