Numerical simulation of deployable ultra-thin composite shell structures for space applications and comparison with experiments

Abstract

In the present article, the geometrical nonlinear behavior of deployable booms undergoing large displacements and rotations is investigated. The triangular rollable and collapsible boom made of fiber-reinforced composite materials is considered along with a metallic tape spring. The mathematical model makes use of higher-order 1D structural theories based on the Carrera unified formulation, which allows the description of moderate nonlinearities to deep post-buckling mechanics of ultra-thin shells in a hierarchical and scalable manner. Particular attention is focused on the study of equilibrium paths of the booms subjected to coiling bending. Dedicated experimental tests reveal the validity of the proposed finite element approach, whereas the investigation of different lamination sequences offer a valuable perspective for possible future designs.

Keywords:

• Deployable structures
• ultra-thin shells
• layer-wise models
• tape springs
• finite element method

1. Introduction

Nowadays applications of robotic space explorations are always more sophisticated. In fact, spacecraft require even more technological advances to fulfill higher energetic power requirements. This has represented a challenge for engineers and scientific researchers and, since a very low ratio of the mass of the spacecraft to the one of the instrumentation is needed for the propulsion efficiency, solutions for deployable and ultra-lightweight structures are requested. In this context, flexible structures, able to be packaged during the take-off phase and to be deployed once in space, became very attractive thanks to their higher specific power (W/kg) and lower specific packaging volume (W/m³). The main technological issues are related to the manufacturing process of deployable, to pack them into a small volume that fits into the fairing of the launcher and to in-orbit deploy these ultra-lightweight structures [1]. Briefly, deployable and ultra-thin booms consist of structure with the capabilities of flattening and coiling around a cylinder. Then, while passively deploying, they release the elastic strain energy that was stored during the furling phase. Deployable booms found a large number of applications such as for telescopes [2], photovoltaic surfaces [3, 4], antennas [1], solar sails and arrays [4–6] and advanced aircraft structures [7]. The main advantages of deployable structures, compared to classical rigid ones, are listed below:

1. reduced volume during launch allowing large systems design;

2. notable gain in terms of requirements of dimensional stability in the launch phase;

3. strong inertia and mass reduction.

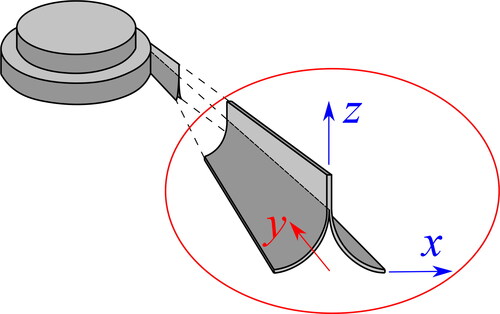
An example of a deployable boom is represented by the Storable Tubular Extendable Member (STEM) [8–10]. Briefly, a single strip forms a circular cross-section, during the deployment phase. This solution has the advantages of easy fabrication and packaging, but the drawback of a significant height once packaged. A good design for deployable booms is represented by the collapsible tubular mast (CTM). This very thin composite shell structure consists of a two omega-shaped closed cross-section. The section ensures large stiffness, giving high dimensional stability and enabling the boom to be coiled in a small area. This type of boom was first adopted during the Viking 1 and 2 [11] robotic explorations, which goal was to collect samples of the soil on the Mars surface. On that occasion, a thin metal sheet was used for the manufacturing of the CTMs. Afterwards, several studies on the adoption of composite materials were conducted in the 1970s regarding the adoption of carbon fiber reinforced plastic. However, the first usage of composite CTMs dates back after 15 years, and they were employed under the European Space Agency umbrella [12]. In addition to these first designs of deployable booms, Murphey and Banik [13] invented the Triangular Rollable And Collapsible (TRAC), developed by the Air Force Research Laboratory. Its cross-section gives to TRAC larger bending stiffness (around 10 and 34 times more than CTM and STEM booms, respectively) and packaging efficiency compared to CTM, STEM [14] and bi-STEM booms [15] solutions. It consists of two circular domains made of tape-spring that are attached along the common edge (web). Figure 1 shows an example of the TRAC boom. Moreover, the curved flanges of the TRAC require smaller strain energy than previous booms, giving the possibility of the employment of thicker materials. Metallic TRAC booms was used for the deployment of the solar sails Planetary Society’s LightSail-1 [16], LightSail-2 [17] and NASA’s NanoSail-D [18, 19]. More recently, it has been found that metallic TRAC suffers from thermal gradients, inducing large deflections when the two flanges undergo large thermal gradients, for instance, in solar sails applications [20]. For this reason, several studies were carried out about composite TRAC booms. Murphey and Banis [13] stated that the best stacking sequence to match thermal requirements and to prevent the bifurcation of the flanges in the rolled configuration is [0° tape, 45° weave, 0° tape] for each circular boom flange, where 0° is the longitudinal direction of the deployable structure.

Figure 1. Deployment phase of a TRAC.

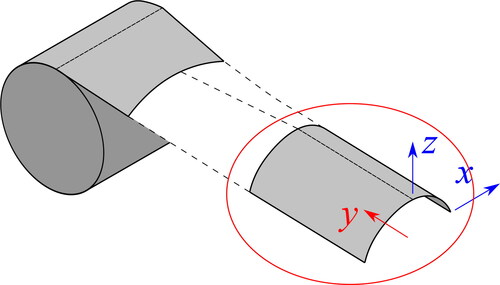
Another type of boom structure is represented by the tape-springs. They have the advantage of a low cost and easy adoption. But such steel curved thin shells offer a very simple idea with elastic behavior and the capability to be easily packaged. Tape-springs are widely adopted for a large number of applications, including high-resolution deployable telescope [21] and the deployment of collapsible rib-tensioned surface [22] and rigid-panels [23]. In the aforementioned applications, tape-springs are used as self-locking hinges. Another way to use it is based on the coiling of the strip instead of folding with the same principle as industrial tape-measure like the deployment cassette of bi-STEM [24].

Consider a TRAC boom as shown in Figure 1. It is first stowed around a cylindrical hub and then deployed into the configuration with two curved flanges and one common web. During its deployment phase, three different regions can be highlighted:

• Coiled region, where the boom is furled around a cylindrical hub depicted in Figure 1;

• Ploy region, where the deployable structure is being uncoiled but has not reached its stable form yet. It is shown by dashed lines in Figure 1;

• Uncoiled region, where the structure is completely deployed and stable.

The same domains can be highlighted in a tape-spring, as depicted in Figure 2.

Figure 2. Deployment phase of a tape-spring.

In this article, both TRAC and tape spring coilable booms are analyzed and their geometrical nonlinear behavior is investigated. In particular, the performances of ultra-thin composite TRAC booms loaded in bending are analyzed, aiming to study their buckling behavior under pure bending. This kind of applications shares characteristics with other types of thin-walled beams, such as T-shaped beams, where local buckling phenomena within the web and a global lateral-torsional buckling mode appear [25]. These collapsible longerons are prone to suffering instabilities and failure mechanisms as a consequence of the large displacements and rotations happening in the coiling and deployment phase. In fact, during both the coiling phase and in the deployed configuration, due to the nature of the cross-section, which is open and thin-walled, TRAC booms show complex nonlinear behavior [26]. Moreover, the localized buckling, which was observed to be the first buckling mode when the booms are loaded under pure bending [26, 27], may induce localized material failure [28, 29]. In this context, the availability of appropriate mathematical models for the accurate prediction of the stiffness properties as well as the stress state within deployable longerons is of paramount importance for design and verification. The finite element method (FEM) can be used to develop reliable mathematical models for this kind of structure. For instance, Banik and Murphey [6] accurately predicted the behavior of thick booms (around 1 mm) using nonlinear finite elements (FEs). An optimization procedure of the cross-section of ultra-thin booms (less than 100 μm), with the aim of reducing the effects of a shape imperfection during the boom collapsing, was conducted by Bessa and Pellegrino [30].

Predicting stiffness and stress distribution accurately in both linear and nonlinear regimes is of great importance for design and verification. However, modern FEs show time-consuming procedures for this kind of analysis and it was demonstrated by Pagani et al. [31] that the first-order shear deformation theories and von Kármán strain approximations, which is the theory often used by commercial softwares, is not effective when dealing with moderate and large rotations of thin structures. In order to develop a model able to accurately predict the stiffness and stress distribution in the geometrical nonlinear regime, the Carrera unified formulation (CUF) [32, 33] is used in this article. CUF makes use of arbitrary expansion functions to evaluate the three-dimensional displacement field, starting from the unknowns evaluated by the FEM. In this way, the stiffness matrix and the related FE arrays, can be written in a unified form by the so-called “fundamental nuclei.” Those nuclei represent the basic building block that can be expanded according to the adopted expansion functions. Consequently, the user can a priori choose the structural theory to be adopted for the selected analysis. CUF was employed for geometrical nonlinear analyses in the pioneering works by Pagani and Carrera for the static analysis of isotropic [34] and composite [35] beams. Recently, this formulation was extended for the analysis of plates [36] and shells [37, 38] and for the analysis of TRAC and tape spring [39, 40]. In this article, the CUF capabilities to evaluate the 3D stress field even in a far nonlinear regime is exploited for the analysis of isotropic tape-spring and composite TRAC booms.

This article is organized as follows: (i) Section 2 described the proposed one-dimensional model of the deployable booms using CUF. The derivation of the nonlinear governing equations is briefly explained; (ii) Section 3 reports the obtained results for the geometrical nonlinear analysis of composite TRAC booms and isotropic tape-spring. Those results are compared to the available experimental solutions. Finally, the main conclusions are drawn.

2. One-dimensional numerical model of coilable booms

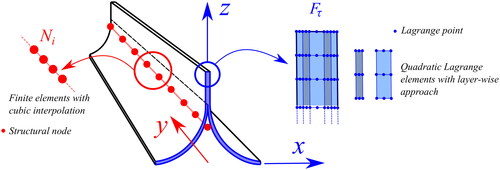
A Cartesian reference system is used, so that the y direction is placed in the deployment direction, and the x, z identify the cross-sectional domain. In order to develop the numerical model of the booms, this research work makes use of the CUF. CUF allows to generate one-dimensional (1D) FEs able to capture any cross-section deformation through the implementation of expansion functions. Namely, according to CUF, the three-dimensional (3D) displacement field can be written in the following unified manner (1) $$\begin{array}{c}\mathbf{u}(x,y,z)=F_{\tau }(x,z){\mathbf{u}}_{\tau }(y),\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\tau =1,2,\dots .,M\hfill \end{array}$$(1) where $\mathbf{u}(x,y,z)$ is the displacement vector, whose components are expressed in the general reference system (x, y, z) of Figures 1 and 2, $F_{\tau }$ represent the cross-sectional functions depending on the x, z coordinate, τ is the sum index and M is the number of terms of the expansion in the cross-section plane assumed for the displacements. In the case Lagrange expansion is used to approximate the cross-section, every layer can be approximated as an independent entity, leading to the layer-wise approach, which has been demonstrate to produce accurate results (see [41]). For the sake of brevity, Lagrange expansions are not detailed in this work, but interested readers may refer to [42] for further information.

2.1. FE approximation

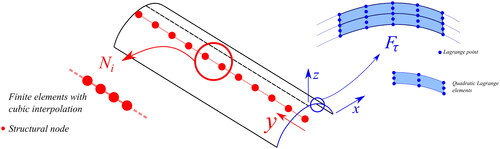
The FEM is adopted to discretize the structure along the y axis. Thus, the generalized displacement vector ${\mathbf{u}}_s(y)$ is approximated as follows: (2) $$\begin{array}{c}{\mathbf{u}}_{\tau }(y)=N_i(y){\mathbf{u}}_{\tau i}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}i=1,2,\dots ,N_n\hfill \end{array}$$(2) where $N_i(y)$ stands for the ith one-dimensional shape function, ${\mathbf{u}}_{\tau i}$ is the vector of the FE nodal parameters, i indicates summation and N_n is the number of the FE nodes per element. An exhaustive review of the shape functions N_i is given by Bathe [43] and by Carrera et al. [32, 33]. In this work, a cubic interpolation is assumed. Basically, four nodes FEs (B4) are employed to discretize the 1D structure along the y axis. Figures 3 and 4 show the one-dimensional model of TRAC and tape-spring, respectively.

Figure 3. One-dimensional model of the TRAC.

Figure 4. One-dimensional model of the tape-spring.

2.2. Constitutive and geometrical relations

The 3D stress, $\mathit{\sigma },$ and strain, $\mathit{ϵ},$ components are introduced in the following, with a vectorial notation: (3) $$\mathit{\sigma }={\left\{\begin{array}{cccccc}{\sigma }_{xx}& {\sigma }_{yy}& {\sigma }_{zz}& {\sigma }_{xz}& {\sigma }_{yz}& {\sigma }_{xy}\end{array}\right\}}^T,\hspace{1em}\mathit{ϵ}={\left\{\begin{array}{cccccc}{ϵ}_{xx}& {ϵ}_{yy}& {ϵ}_{zz}& {ϵ}_{xz}& {ϵ}_{yz}& {ϵ}_{xy}\end{array}\right\}}^T$$(3)

Thus, the geometrical relations take the following form: (4) $$\begin{array}{c}\mathit{ϵ}=\mathbf{bu}\hfill \end{array}$$(4) where b is the matrix of the differential operators. Interested readers can find the expression of b in [32, 33].In this work, we consider each layer to be made of linear elastic monoclinic material. Consequently, the constitutive equations at layer level hold (5) $$\mathit{\sigma }=\mathbf{C}\mathit{ϵ},$$(5) where and $\mathbf{C}$ is the material elastic matrix. For the sake of brevity, the complete expressions of the components of $\mathbf{C}$ matrix are not given here, but can be found in many reference texts, such as [44].

2.3. Nonlinear governing equations

In this work, the principle of virtual work is recalled for the derivation of the FE governing equations, which, for a generic structure, can be expressed as: (6) $$\delta L_{\text{int}}=\delta L_{\text{ext}}$$(6) where $\delta L_{\text{int}}$ is the virtual variation of the work of the internal loads (i.e. the strain energy) and $\delta L_{\text{ext}}$ is the virtual variation of the work of the external loads.The first term of Eq. (6)(6) $$\delta L_{\text{int}}=\delta L_{\text{ext}}$$(6) can be written as as: (7) $$\delta L_{\text{int}}={\int }_V\delta {\mathit{ϵ}}^T\mathit{\sigma }\mathrm{d}V$$(7) where V is the volume of the body. Introducing the geometrical (Eq. 4(4) $$\begin{array}{c}\mathit{ϵ}=\mathbf{bu}\hfill \end{array}$$(4) ) and contitutive relations (Eq. 5(5) $$\mathit{\sigma }=\mathbf{C}\mathit{ϵ},$$(5) ) into Eq. (7)(7) $$\delta L_{\text{int}}={\int }_V\delta {\mathit{ϵ}}^T\mathit{\sigma }\mathrm{d}V$$(7) , it takes the following form: (8) $$\delta L_{\text{int}}=\delta {\mathbf{q}}_{sj}^T{\mathbf{K}}_S^{\mathit{\text{ijτs}}}{\mathbf{q}}_{\tau i}$$(8)

The argument of the integral of the Eq. (8)(8) $$\delta L_{\text{int}}=\delta {\mathbf{q}}_{sj}^T{\mathbf{K}}_S^{\mathit{\text{ijτs}}}{\mathbf{q}}_{\tau i}$$(8) represents the so called secant stiffness matrix ${\mathbf{K}}_S^{\mathit{\text{ijτs}}}.$ The complete form of the secant stiffness matrix ${\mathbf{K}}_S^{\mathit{\text{ijτs}}}$ is omitted here for the sake of brevity, but can be found in [34, 45].

The right term of Eq. (6)(6) $$\delta L_{\text{int}}=\delta L_{\text{ext}}$$(6) , omitting some mathematical steps that can be found in Carrera et al. [32], can be written as: (9) $$\delta L_{\text{ext}}=\delta {\mathbf{q}}_{sj}^T{\mathbf{p}}_{sj}$$(9) so that Eq. (6)(6) $$\delta L_{\text{int}}=\delta L_{\text{ext}}$$(6) becomes: (10) $${\mathbf{K}}_S^{\mathit{\text{ijτs}}}{\mathbf{q}}_{\tau i}-{\mathbf{p}}_{sj}=0$$(10) Equation (10)(10) $${\mathbf{K}}_S^{\mathit{\text{ijτs}}}{\mathbf{q}}_{\tau i}-{\mathbf{p}}_{sj}=0$$(10) can be arbitrarily expanded to reach any desired theory, from low- to higher-order ones, by choosing the values for $\tau ,s=1,2,\dots ,M$ and $i,j=1,2,\dots ,p+1,$ to give: (11) $${\mathbf{K}}_S\mathbf{q}-\mathbf{p}=0$$(11) where ${\mathbf{K}}_S,$ q and p are the global, assembled FE arrays of the final structure.

Equation (11)(11) $${\mathbf{K}}_S\mathbf{q}-\mathbf{p}=0$$(11) represents a nonlinear algebraic system of equation for which an iterative method is needed. We employ here the same procedure detailed in the work by Pagani and Carrera [35], where a Newton–Raphson scheme is used by making use of a path following constraint. The main steps of the procedure is explained in this work. This procedure demands for the linearization of the nonlinear governing equations. As a result, we need to introduce the so-called tangent stiffness matrix ${\mathbf{K}}_T=\frac{\mathrm{d}({\mathbf{K}}_S\mathbf{q}-\mathbf{p})}{\mathrm{d}\mathbf{q}}.$ The explicit form of ${\mathbf{K}}_T$ is not given here, but it is derived in a unified form in [35]. The resultant system of equations introduces a load-scaling parameter which is taken as a variable, so an additional equation is needed for its resolution. In this work, it is represented by an opportune arc-length path-following constraint. More detail about the arc-length method adopted can be found in the works by Carrera [46] and Crisfield [47, 48].

3. Numerical results

Numerical results deal with the geometrical nonlinear static analysis of the TRAC boom and a tape-spring. For both cases, the obtained solutions are compared with experimental ones. Moreover, the case of different fiber orientations of the TRAC material is investigated.

3.1. TRAC

First analysis regards a typical TRAC boom employed in aerospace applications. Figure 5 describes the geometry and the stacking sequence of the structure where t represents the thickness of the curved flange and it is equal to 80 μm, r is its curvature radius equal to 12.7 mm, ϑ is the sweep angle equal to 90°, the flat vertical web h is 8 mm long and total length L of the TRAC is equal to 570 mm. The displayed stacking sequence reveals three layers for the curved flange and seven layers for the flat web, and the properties of the implemented material are reported in Table 1, where CF represents a unidirectional carbon fiber pre-preg tape with epoxy resin and GFPW stands for E-glass fabric glass fiber plain weave pre-preg with epoxy resin.

Figure 5. Geometry and stacking sequence of the composite TRAC subjected to positive and negative moments M_x. The blue color indicates the CF layers, the red color indicates the CFPW material.

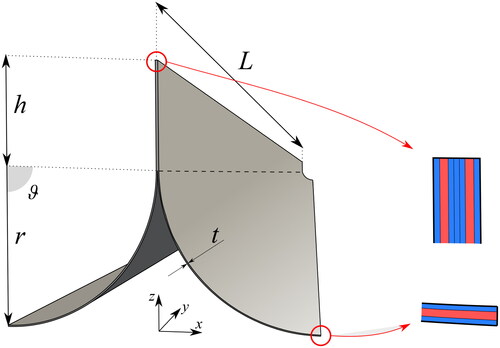
Table 1. Material properties of the composite TRAC.

	E1	E2	G12	ν12	t${}_{\text{layer}}$
	(GPa)	(GPa)	(GPa)	(-)	(μm)
CF	128	6.5	7.6	0.35	30
GFPW	23.8	23.8	3.3	0.17	25

Figure 6 shows the geometrical nonlinear results obtained with simply supported boundary conditions and applied moments around x axis on both sides. The obtained equilibrium curve is reported against the experimental results. The experiment setup for the bending test experiments is detailed in [40]. Briefly, the rotations at the ends of the TRAC are independently controlled by the testing machine. The TRAC can shorthen, since only one end is constrained in the longitudinal direction. End rotations are measured by calibrated camera. The accuracy of the proposed methodology is evident. Important equilibrium states of the equilibrium curve are represented by “A” and “C” for negative and positive moments, respectively. These equilibrium states correspond to the buckling (localized or global) phenomena occurring to the structure.

Figure 6. Nonlinear static solution for the composite TRAC subjected to positive and negative moments M_x.

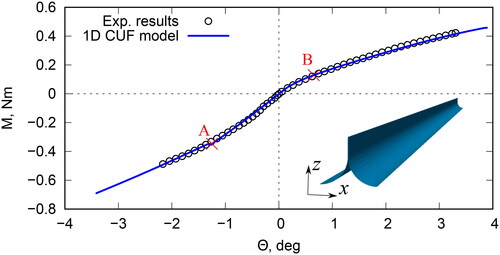
For a better understanding of the situation, relevant deformed configurations are reported. As far as the negative moment M_x is concerned, Figure 7 shows the deformed configurations of the point “A” of Figure 6, where the localized buckling phenomena occurs. In particular, Figure 6(a) reports the numerical solution, whereas the Figure 6(b) shows the localized buckling detected by the experimental test. Clearly, the numerical simulation is perfectly in agreement with the available experiment test.

Figure 7. Nonlinear equilibrium states correspondent to the point “A” of Figure 6 for the composite TRAC subjected to a negative moment M_x. Numerical (a) vs. experimental (b) solutions (elaborated from Ref. [49]).

About positive moment M_x, the global buckling phenomena is highlighted in Figure 8(a). As for the previous case, the numerical simulation is able to describe the post-buckling of the composite boom, reproducing the global web waviness from the experimental results, shown in Figure 8(b).

Figure 8. Nonlinear equilibrium states correspondent to the point “B” of Figure 6 for the composite TRAC subjected to a positive moment M_x. Numerical (a) vs. experimental (b) solutions (elaborated from Ref. [49]).

In addition, two additional stacking sequence are considered, changing the orientation of the CF layers, so that $[\pm {45}_{\text{GFWP}}/{45}_{\text{CF}}/\pm {45}_{\text{GFWP}}]$ and $[\pm {45}_{\text{GFWP}}/{90}_{\text{CF}}/\pm {45}_{\text{GFWP}}]$ are analyzed. The results from the geometrical nonlinear simulation are reported in Figure 9 and the evaluated buckling-like phenomena are highlighted with circles of the same color as the considered stacking sequence.

Figure 9. Nonlinear static solution for the composite TRAC subjected to positive and negative moments M_x considering the $[\pm {45}_{\text{GFWP}}/{45}_{\text{CF}}/\pm {45}_{\text{GFWP}}]$ and $[\pm {45}_{\text{GFWP}}/{90}_{\text{CF}}/\pm {45}_{\text{GFWP}}]$ stacking sequences.

The post-buckling deformed configurations are reported in Figures 10 and 11. Clearly, localized buckling are detected when negative moments are applied, whereas a global web waviness is detected with positive moments.

Figure 10. Nonlinear equilibrium states correspondent to the buckling of the $[\pm {45}_{\text{GFWP}}/{45}_{\text{CF}}/\pm {45}_{\text{GFWP}}]$ TRAC subjected to negative (a) and positive (b) moments M_x. The equilibrium states correspond to the red circled of the Figure 9.

Figure 11. Nonlinear equilibrium states correspondent to the buckling of the $[\pm {45}_{\text{GFWP}}/{90}_{\text{CF}}/\pm {45}_{\text{GFWP}}]$ TRAC subjected to negative (a) and positive (b) moments M_x. The equilibrium states correspond to the gray circled of the Figure 9.

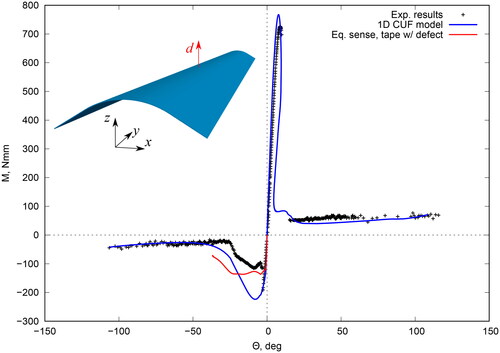
3.2. Metallic tape spring

The second analysis case deals with a metallic tape-spring. The geometric characteristics are depicted in Figure 12. The structure has a curvature radius R equal to 12.3 mm, curvature angle ϑ equal to 62°, length of the flat domains l equals 6.1 mm, total length L is 170 mm and the thickness t is 0.114 mm. The considered tape is made with isotropic steel with Young modulus E $=$ 210,000 MPa and Poisson’s modulus ν equal to 0.3.

Figure 12. Geometry of the isotropic tape.

The obtained numerical results are compared with those from experimental tests. Figure 13 shows the 170 mm sample that is the subject of this study. The sample was opportunely obtained from a commercial tape-spring. Testing was done using the Fischer’s machine [50], which makes use of two rotation control dials to apply moment at the free ends of the samples. Note that one side of the machine is fixed, while the other end is allowed to translate.

Figure 13. A 170 mm sample of commercial tape-spring. Figure elaborated from Ref. [39].

This structure is loaded with positive and negative moments at its ends, whereas simply supported boundary conditions are employed to numerically reproduce the experimental setup. The numerical geometrical nonlinear solution is reported in Figure 14. Clearly an overall match between the numerical solution and the experimental results is demonstrated, especially for positive moments.

Figure 14. Nonlinear static solution for the isotropic tape subjected to positive and negative moments M_x.

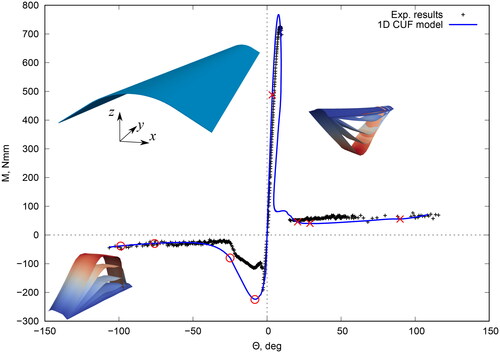
Some relevant deformed numerical and experimental configurations are reported hereafter. Figure 15 shows the deformed configurations correspondent to the red crosses of Figure 14. Clearly, the numerical deformations are in a perfect agreement with the experiments.

Figure 15. Nonlinear equilibrium states correspondent to crosses of Figure 14 for the isotropic tape subjected to a positive moment M_x. Numerical (a) vs. experimental (b) solutions, elaborated from Ref. [39].

Finally, the deformed configurations correspondent to the circles of the Figure 14 are reported in Figure 16. Clearly, there is a mismatch between numerical simulation and experimental results, both in terms of nonlinear static curve and deformed configurations. In fact, by looking at Figure 16(b,d), it is clear that the structure is not perfectly symmetric, and an imperfection is present within the structure.

Figure 16. Nonlinear equilibrium states correspondent to circles of Figure 14 for the isotropic tape subjected to a positive moment M_x. Numerical (a) vs. experimental (b) solutions, elaborated from Ref. [39].

To account for this aspect, another numerical simulation is performed, including a defect load as depicted in Figure 17.

Figure 17. Nonlinear static solution for the isotropic tape using a defect load.

The numerical results are closer to the experimental ones, as also highlighted by the deformed configurations in Figure 18.

Figure 18. Nonlinear equilibrium states correspondent to crosses of Figure 14 for the isotropic tape subjected to a positive moment M_x, using a defect load for the numerical simulations. Experimental figures elaborated from Ref. [39].

4. Conclusions

This work has explored the use of the CUF for the simulations of the geometrical nonlinear analysis of composite TRAC and isotropic tape-spring booms. The use of CUF is justified due to its hierarchical nature. In fact, it allows to expresses the governing equations in terms of fundamental nuclei, which are invariant of the theory approximation order and both the efficiency and the accuracy of the analysis can be opportunely tuned. The efficacy of the proposed method in describing near and far post-buckling mechanics of the booms is demonstrated via dedicated experiments. The model is able to foresee limit loads and steady-state moments. Conversely, it has been shown that the structure is very sensitive to geometry defects in the case of equal sense moment for both considered booms. From this standpoint, a dedicated sensitivity analysis by CUF will be performed. Moreover, a different stacking sequence for the composite materials of the TRAC longerons is considered and the results offer interesting points for possible future designs, in terms of critical applied moments which induce localized and global buckling phenomena.

Acknowledgments

The authors acknowledge the Space Structures Laboratory at California Institute of Technology, USA, for providing the experimental data and Prof. Sergio Pellegrino and Dr. Armanj Hasanyan for the fruitful discussions.

Disclosure statement

No potential competing interest was reported by the authors.

Additional information

Funding

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 850437).