Dynamic analysis of chevron structures in liquid crystal cells

ABSTRACT

If a surface stabilized ferroelectric liquid crystal cell is cooled from the smectic-A to the smectic-C phase its layers thin causing V-shaped (chevron like) defects to form. These create an energy barrier that can prevent switching between equilibrium patterns. We examine a gradient flow for a mesoscopic Chen-Lubensky energy that allows the order parameter to vanish, so that the energy barrier does not diverge if the layer thickness becomes small. The liquid crystal can evolve during switching in such a way that the layers are allowed to melt and heal near the chevron tip in the process.

KEYWORDS:

• Smectic-C
• liquid crystals
• chevron

1. Introduction

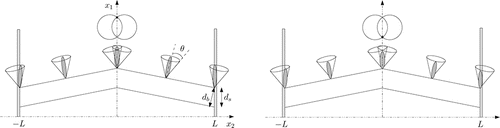
In surface stabilized ferroelectric liquid crystal [SSFLC] cells smectic layers usually deform into a characteristic chevron pattern [1, 2]. The chevron structure (see Fig. 1) is believed to arise due to the mismatch between the natural smectic layer thickness and the periodicity imposed by the layer pinning at the surface in the smectic-A phase, where this surface memory effect has been confirmed experimentally [3]. In the past, several theoretical models have been presented to describe the director and layer structure in smectic-C chevron cells. This work has been motivated by a potential use of [SSFLC] cells in display devices. The original model was put forward by Clark and co-workers [1, 4]. Theirs is a macroscopic description where the molecular alignment varies slowly across each chevron arm, restricted so that the molecules lie on the arm’s smectic-C cone. The chevron tip is idealized to have zero thickness; the smectic layers form a sharp bend at the tip so that their normal is discontinuous there. A key assumption in their model is the continuity of the equilibrium director pattern across the cell. Assuming the cone angle is larger than the layer tilt, these conditions lead to two out-of-plane states determined by the intersection of the cones from each side of the tip. This means that chevron cells exhibit two stable director states between which the cell can be switched by the application of an external electric field. An important reason to model surface stabilized cells is to describe the switching dynamics between these stable director states. The model of Clark et al. has been extended to include continuity of the biaxial ordering at the chevron tip ^{Figure 1}[5].

Figure 1. Switching in a Chevron Structure.

The development of models to describe ferroelectric switching has a number of difficulties. These are largely due to the contrasting length scales associated with the chevron arms and tip. The macroscopic models such as the one described above require that the director at the chevron tip leaves the cones from the adjacent arms during the switching process. The models account for this by allowing the director to be discontinuous at the tip during the transition and an ad hoc energy barrier is included in the free energy penalizing the director’s jump across the tip. (See Maclennan et al. [6, 7], Ulrich and Elston [8], and Brown et al. [9]).

A number of models of the chevron structure have been reported which take into account continuous layer bending at the chevron tip and the director rotation on the cone [10–15]. These models however, enforce specific couplings between the molecular cone angle from the smectic layer tilt angle that permit a continuous pattern near the tip but are also ad hoc.

In this paper we use a Chen-Lubensky model to characterize the director and layer structure of surface stabilized smectic-C cells in an external electric field. This approach has been developed in the papers Kralj and Sluckin [16], Vaupotĭc et al. [17, 18], Hazelwood and Sluckin [19], and Cheng and Phillips [20]. We build on these works here. The advantage of this phenomenological model over others is that the formation of chevrons and the nature of the director pattern near the chevron tip follow from energetic considerations as opposed to features that are directly inserted into the model. In [20], the smectic layer thickness is introduced as a small parameter and the static model of Clark et al. described above is captured as a singular limit having smectic layers with a sharp chevron tip and its two out-of-plane equilibrium director patterns. In this work we consider a more complete Chen-Lubensky model that allows the smectic layers to melt near the chevron tip under the application of a finite electric field allowing for the switching from one state, tending to the other assuming gradient flow dynamics. Our contribution here is that we establish existence and uniqueness results for the gradient flow problem. Many open questions for this model remain to be explored. For example once the switching occurs, the model allows the smectic layers to reform near the chevron tip. Just how robust this regeneration is remains an open question. This is an important point since the studies of Willis et al. [21] showed that there should be no significant change in smectic layer thickness or chevron layer structure under typical director switching conditions.

2. Model

We consider a cross section of an SSFLC cell of width 2L and place the origin of the axes at the midpoint of the lower cell aperture. The domain is then written as {(x₁, x₂); −L < x₂ < L}.

To model a smectic phase, we need two types of ordering, orientational and positional. The former is described by a unit vector n that indicates the average local orientation of the rod-shaped molecules, called the nematic director field. The latter is described by a complex-valued order parameter, Ψ, whose amplitude indicates the degree of smectic ordering and whose phase indicates the position of the smectic layer. If |Ψ| = 0, then the phase is completely nematic. For a smectic phase, |Ψ| > 0, with |Ψ| ⩾ 1 for well-structured smectic layers.

An essential parameter in our analysis is the wave number q, which equals 2π/d_b, where d_b is the layer thickness in the bulk smectic-C phase. In a realistic model, d_b is very small (typically L/d_b is in the range 300–400 [17]), so one eventually would like to study the limiting problem letting q → ∞. For the present work, q is assumed to be a large number. Let d_s denote the layer thickness at the surface. This is a spacing inherited from the material initially being cooled from the smectic-A phase. We use the parameter to measure the mismatch between the different layer thicknesses. Lastly, let θ denote the bulk tilt angle of the molecules from the layer normal in the smectic-C phase.

We base our model on a covariant form of the Landau-de Gennes free energy, introduced by Chen & Lubensky [22]. The density for our free energy consists of three parts, nematic, smectic and electrostatic

The nematic density, f_N(n), measures the uniformity of n and we take it to be the one-constant approximation of the Oseen-Frank energy density, where K > 0. The smectic part, , measures the uniformity of the layer structure and is a variation of the Chen-Lubensky energy density. We split this energy density into two components, F(n, Ψ) and G(|Ψ|²). The first component is the elastic energy density, The second component we call the smectic penalization density, D is the covariant derivative, D = ∇ − iqcos θn with its parallel component (to n) D_‖ = (n · D)n and perpendicular component (to n) D_⊥. The parameter constants a_⊥, a_‖, c_‖, c_⊥, g are positive and determined by the material. Lastly, we write the electrostatic part, f_E(n, Ψ) = −P · E, where is the spontaneous polarization field and E = (0, E, 0) is the applied electric field directed across the cell.

Due to the periodicity of Ψ, we are able to reduce our model to be one-dimensional. Specifically, we write where ψ is complex-valued. Expressing periodicity in this form was used by Kralj and Sluckin [16], wherein to enforce the smectic density wave in the x₁ direction, Ψ was written in the form such that η > 0 was assumed to be a constant and x₁ = g(x₂) was the graph of a uniformly smectic layer in their setting. The same idea was also used in [20]. Our approach, however, is different in that it aims to explain the whole process through the model without invoking any ad hoc energy terms added later. Particularly, we want the system to allow for phase changes in certain areas if that is less costly in an energetic sense (by melting, for instance). The tool to do that is to keep the complex-valued order parameter in a general form, allowing ψ to vanish.

We consider the admissible set where such that . The boundary conditions enforce uniform smectic layers at the cell surfaces and for simplicity there are no boundary conditions on the director. We rewrite the smectic energy by integrating by parts and taking into account the boundary conditions to get an integrand that is bounded below. We then carry out the dimension reduction with our variable denoted by x rather than x₂. Within the above admissible set, our total free energy (per unit length with respect to x₁) becomes (2.1)

Remark 2.1.

We have added a regularizing factor , with ρ a small positive constant, to aid with the analysis. We will let ρ → 0 later.

3. Static analysis

To set up for the dynamic analysis, we highlight the quantities that are bounded uniformly (in q). We are able to find well-prepared initial data, specifically we can construct a family of possible initial configurations. One such example is and where g′(x₂) = −btanh (qx₂)/tanh (qL).

Lemma 3.1.

For q sufficiently large, there exists (n⁰, ψ⁰) ∈ X such that , where C₀ is independent of q.

Our dynamic analysis is based on energy minimization, so we only consider the states (n, ψ) ∈ X with . Throughout this paper it is assumed that the constants appearing in (2.1(2.1) ), with the exceptions of 0 ⩽ ρ < 1 and q ⩾ 1 are fixed. We use C₁ to denote a constant in our estimates such that is independent of the quantities ρ, states (n, ψ) for which and all q sufficiently large Since the energy for our initial data is uniformly bounded, we can deduce using Sobolev’s embedding theorem in 1-dim that |ψ| and at later times are uniformly bounded as well. We also prove a Modica-Mortola type estimate.

Lemma 3.2.

For q sufficiently large, on [ − L, L], where C₁ is independent of q.

This specific boundedness, in fact, has an important physical implication for our system: the coupling between n and |ψ| weakens for a sufficiently large q.

Proof.

Note ψ ∈ C¹[ − L, L] and we seek a specific bound in terms of q. We write {x: |ψ(x)| > 0, −L < x < L} as a countable union of disjoint intervals Since on , it is enough to prove on each interval (a_j, b_j) for a constant C₁ independent of The plan is to prove the real and imaginary parts of are bounded.

We first note that since we have It follows that where C₁ and M₁ are independent of q for q ⩾ 1. Fix Using the fact that the initial energy is bounded, and after carrying out some algebraic manipulations, we get (3.1) Consider the set where M is such that . On E, we have (3.2) and (3.3) We now utilize the equality Knowing that and that we conclude that (3.4) Adding Inequalities (3.3(3.3) ) and (3.4(3.4) ), noting that the second inequality above is a Modica-Mortola type estimate.

If Φ is such that Φ′(y) = [y² − 2M]⁺, then . If − L < a_j < b_j < L then |ψ(a_j)| = |ψ(b_j)| = 0 and it follows that |ψ(x)|′ = 0 for some x ∈ (a_j, b_j). If either a_j = −L or b_j = L then it follows from the boundary conditions that |ψ|′ = 0 at that point. In either case it follows that is uniformly bounded independent of q and j on (a_j, b_j). A similar reasoning can be applied to the imaginary part to get the conclusion.

One last static result we present is the existence of minimizers.

Theorem 3.3.

For q sufficiently large, there exists (m, ξ) ∈ X such that

Proof.

By coercivity and initial boundedness of the energy (2.1(2.1) ), we can guarantee the existence of a subsequence (n_j, ψ_j) that converges weakly to (m, ξ) in H¹ × H³. Weak convergence, however, is not enough due to the nonlinearity of the terms. We invoke a Sobolev embedding theorem to deduce that {n_j} and {ψ′_j} are uniformly bounded in C^{0, 1/2}( − L, L), followed by Arzelà-Ascoli theorem to get uniform convergence to m and ξ′ respectively. By convergence proved thus far and lower semicontinuity of the L²-norm, proving that is a minimizer.

4. Dynamic analysis

4.1. Method of Rothe

We begin the dynamic analysis of a chevron structure under an applied electric field by constructing a discretized-in-time gradient flow. We follow the Method of Rothe [23], through which we construct an approximate elliptic-type problem. Convergence of the approximate solution to the continuous solution is the main goal of our analysis. An advantage of this approach is that it not only exploits the variational feature of the problem, but also accommodates for its nonlinearity, as will be seen later.

Let (n⁰, ψ⁰) ∈ X be any initial data (which we showed exist in lemma 3.1). Consider any time period [0, T] and let τ > 0 be any step size in t. Choose the number of steps M such that Mτ > T. Minimize: where , with the given initial values, on [0, τ]. We know that such a minimizer exists by theorem 3.3. Denote the minimizer by (n¹, ψ¹). Use the minimizer (n¹, ψ¹) as the initial values for the second time step [τ, 2τ] and minimize the new energy functional J¹(n, ψ). Repeating the process, we get a sequence of minimizing problems and a family of minimizers (n^m, ψ^m), m = 0, 1, …, M.

These minimizers satisfy Euler-Lagrange equations as well as an energy dissipation inequality. Specifically, the minimizer (n^m₁, n₂^m, n^m₃, ψ^m) satisfies the following four equations over the time interval ((m − 1)τ, mτ] - see details of the derivation in Appendix A, (4.1) (4.2) (4.3) and (4.4) where (u₁, u₂, u₃, φ) are the test functions such that (u₁, u₂, u₃) ∈ H¹( − L, L), φ ∈ H³( − L, L) with

The elastic part of the smectic free energy density from (2.1(2.1) ) is We have used the notation for and the fact that for a complex number z. However, in the fourth equation, for F_ψ where F = a₁|g₁|² + a₂|g₂|² + a₃|g₃|² means . In addition, δ_τn₁ is the difference quotient defined by .

Lemma 4.1.

(Energy Dissipation) (4.5)

Proof.

Let m be an integer such that 1 ⩽ m ⩽ M where Mτ > T. Since (n^m, ψ^m) is a minimizer of J^m(n, ψ), we have Adding the (m − 1)^st difference quotient to both sides of the above inequality, With , we get Adding the (m − 2)^nd difference quotient to both sides of the above inequality and iterating, we deduce the desired inequality.

Set Ω = ( − L, L). To extend the Euler-Lagrange equations to Ω_T = ( − L, L) × (0, T), we construct piecewise constant (in t) functions, for instance, for n₁; and similarly for the other components. For piecewise constant test functions, we multiply the first Euler-Lagrange equation (4.1(4.1) ) by τ and add up the equations as m spans 1 to M. As the integrand is independent of t, we get: (4.6) We define the Sobolev-Bochner space H^{k, 1}(Ω_T) by Since our piecewise constant functions fail to belong to such a Sobolev space, we construct piecewise linear (in t) functions , for instance, ; and similarly for the other components.

Lemma 4.2.

is uniformly bounded in H^{1, 1}(Ω_T) for any τ. Similarly, and are uniformly bounded in is bounded in H^{2, 1}(Ω_T), and is bounded in H^{3, 1}(Ω_T) for any τ.

Proof.

We have where that last inequality is true by (4.5(4.5) ). From the well-prepared initial data, we get the uniform bound. In a similar way, we can prove is uniformly bounded.

Since is uniformly bounded in H^{1, 1}(Ω_T), there is a subsequence, still denoted by which converges strongly to some n₁ in L²(Ω_T). Also, by weak compactness of Sobolev spaces we can find a subsequence, converging weakly to n₁ in H^{1, 1}(Ω_T). Similarly, we can prove strong convergence of , , , and ; and weak convergence in the corresponding Sobolev-Bochner spaces.

In the analysis of the discrete gradient flow, it is more convenient to work with the piecewise constant approximations than with the piecewise linear approximations and since the two have the same asymptotic behavior, we use (n^τ₁, n₂^τ, n^τ₃, ψ^τ) from now on.

4.2. Convergence of the discrete gradient flow

Due to the high nonlinearity of the discrete system, the above convergence of subsequences is not enough to prove convergence of the discrete gradient flow. It turns out that we need higher regularity, which is achieved through the following three major steps that are carried out for q sufficiently large.

Step I. Local Regularity. We utilize the Euler-Lagrange equations themselves, and replace the test functions by convenient ones. For instance, in equation (4.6(4.6) ), we let u₁ = Δ_{− h}[(Δ_hn^τ₁)ϕ²] for a small h > 0, where ϕ ∈ C^∞₀( − L, L) is a cut-off function s.t. 0 ⩽ ϕ ⩽ 1 and (4.7) From the resulting equation, we are able to deduce an estimate on in terms of the initial energy bound and small multiples of the integral itself (See Appendix B). We repeat the process for the remaining Euler-Lagrange equations, as the equations are coupled, and get the following estimate Letting h → 0, We are able to remove the dependence on ρ in the final estimate (See Appendix B) to get the following theorem.

Theorem 4.3.

(4.8) where Ω′_T = (L − η, L + η) × [0, T].

Step II. Higher Local Regularity. Due to the nature of the local regularity achieved thus far, we are not able to attain the convergence required. We therefore prove higher local regularity by following a similar method. Specifically, the test function in the first equation is now replaced by u₁ = Δ_{− h}[(Δ_hn^τ′₁)ϕ²]′ for a small h > 0 and with the same cut-off function as before. The difference here is that we require more of the initial conditions on n (See Appendix C). We complete the estimates by removing the dependence on ρ, as before, to get the following result.

Theorem 4.4.

Under the assumption that is initially bounded, we have (4.9)

To be able to extend the estimates to the full domain, we need to get rid of the regularization term at this stage. The regularity results, (4.8(4.8) ) and (4.9(4.9) ), are set up in a way that allows for this, due to their independence of ρ. However, to recover the Euler-Lagrange equations when we let ρ → 0, more should be done (See Appendix D). Specifically, the fourth Euler-Lagrange equation recovered is (4.10)

Step III. Regularity up to the Boundary.

Theorem 4.5.

(4.11)

Proof.

Our analysis will deal with the right boundary point x = L, the left boundary point is analogous. Since |ψ^τ|²(L, t) = 1 and ∫^L_{− L}(|ψ^τ(x, t)|²′)²dx ⩽ C₁ uniformly in t, we can assume that |ψ^τ|² > 1/2 over (L − λ, L) for some λ > 0. Fix . In the following, we let R_j denote a sum of terms that are integrable over (L − λ, L′) and whose square integrals are bounded by a constant and small multiples of ∫^L′_{L − λ}|n₁^τ′′|² dx, ∫^L′_{L − λ}|n₂^τ′′|² dx, ∫^L′_{L − λ}|n₃^τ′′|² dx and ∫^L′_{L − λ}|ψ^τ′^′′|² dx. And let S_j denote a sum of terms such as |δ_τn₁|, |δ_τn₂|, |δ_τn₃|, |δ_τψ| and their integrals over (L − λ, L).

We replace the test function in (4.10(4.10) ) by where ζ is a compactly supported smooth function over [0, T] × (L − λ, L). The higher estimates (4.9(4.9) ), together with integration by parts, allow us to write the Euler-Lagrange equation (4.10(4.10) ) in explicit form, (4.12) Now we go back to the first three weak Euler-Lagrange equations, write them in explicit form, and deduce the following estimate: (4.13) We also go back to the weak equation (4.10(4.10) ), integrate by parts, and write the explicit equation. We replace ψ^τ|ψ^τ|²⁽⁶⁾ by (ψ^τ|ψ^τ|²⁽⁵⁾)′ − ψ^τ′|ψ^τ|²⁽⁵⁾, plug equation (4.12(4.12) ) into (4.10(4.10) ), and then take anti-derivatives to get the estimate (4.14) Provided q is sufficiently large we have ε small and can insert inequality (4.13(4.13) ) into the above to get (4.15) So [e^{− Cx}∫^x_{L − λ}|ψ^τ′^′′|]′ ⩽ e^{− Cx}|R₄| + e^{− Cx}|S₄|. Integrating from L − λ to L′, we get an estimate on ∫^L′_{L − λ}|ψ^τ′^′′|, which we use to bound the integral on the right-hand side of (4.15(4.15) ). We square the resulting inequality, as well as (4.13(4.13) ), and integrate both from L − λ to L′. The result is the following inequality (4.16) where crucially is independent L′. Integrating from 0 to T, and since the resulting right-hand side is bounded by (4.5(4.5) ), we can let L′↑L to conclude that (4.17) Going back to (4.12(4.12) ), it is now easy to see that ∫^T₀∫_{L − λ}^L||ψ^τ|²⁽⁵⁾|² dxdt ⩽ C. Note that we gain one more order of regularity for |ψ^τ|² through this method.

4.3. Existence

With the higher regularity bound (4.11(4.11) ) thus obtained, we define the solution set X_sol then state and prove the existence theorem. Let

Theorem 4.6.

Given . We can find so that, if q > q₀ and for some initial data (n⁰, ψ⁰) ∈ X with n⁰′′ ∈ L²(Ω′), there exists a solution (n(x, t), ψ(x, t)) ∈ X_sol to the time-dependent Euler-Lagrange equations: (4.18) (4.19) (4.20) (4.21) for any such that φ( ·, t) ∈ H²₀( − L, L) with for almost every 0 < t < T.

Proof.

Let (n^τ, ψ^τ) be a discrete gradient flow. Write equation (4.6(4.6) ) as where U^τ₁ and V^τ₁ are nonlinear functions of n^τ₁, n^τ₂, n^τ₃, ψ^τ and their derivatives. Knowing that n^τ₁ → n₁ and δ_τn₁⇀∂_tn₁ in L²(Ω_T), with nn_t = 0 since |n| = 1, It remains to prove that U^τ₁⇀U₁ and V^τ₁⇀V₁ in L²(Ω_T). In fact, it suffices to prove that U^τ₁, V^τ₁ are bounded in L²(Ω_T) and U^τ₁ → U₁, V^τ₁ → V₁ in L¹(Ω_T). To show how this can be achieved, we consider a typical nonlinear term, Cn^τ₂′ψ^τψ^τ′′. Before estimating this, note that it follows from (4.5(4.5) ) and the coercivity of that uniformly in τ. Applying Nirenberg’s interpolation inequality [24], we can see that where the last inequality is true by (4.11(4.11) ). This proves L²-boundedness. To prove L¹-convergence, we utilize Nirenberg’s interpolation inequality and higher regularity again to improve the convergence of subsequences. {n^τ₁} is Cauchy and {n^τ₁′′} is bounded in L²(Ω_T) so {n^τ₁′} is Cauchy in L²(Ω_T), hence convergent to n′₁. Similarly, we obtain ψ^τ′′ → ψ′^′′ in L²(Ω_T). We have and So

The higher convergence obtained in the proof of theorem 4.6, along with energy dissipation statement (4.5(4.5) ), result in the following energy inequality.

Corollary 4.7.

(4.22)

4.4. Uniqueness

Now that we established the existence of a continuous gradient flow, we prove uniqueness of the solution independent of the choice of minimizing sequence and the time discretization.

Theorem 4.8.

Given . We can find so that, if q > q₁ and for some initial data (n⁰, ψ⁰) ∈ X, then there exists at most one solution (n(x, t), ψ(x, t)) ∈ X_sol to the time-dependent Euler-Lagrange equations, (4.18(4.18) ), (4.19(4.19) ), (4.20(4.20) ), and (4.21(4.21) ), satisfying the energy inequality (4.22(4.22) ).

Proof.

We consider two solutions (n, ψ) and of the weak Euler-Lagrange equations with the same initial data (n⁰, ψ⁰) and that satisfy the energy inequality. We take the difference between the corresponding Euler-Lagrange equations and highlight the terms we need. Replace u₁(x, t) by v₁(x, t)χ_{(t − δ, t + δ)} for each t ∈ [0, T] then let δ → 0. By the Lebesgue Differentiation Theorem, we get for a.e. t ∈ [0, T]: Letting , We want to estimate the right-hand side, so we consider one of the terms, Note that |ψ| and are uniformly bounded independent of q, in the first and third terms above. We repeat the process for the remaining equations and add up the final estimates to get, for q sufficiently large, where As a consequence of the global estimates (4.11(4.11) ), η(t) is integrable over [0, T]. By the differential form of Grönwall’s inequality, we conclude that Consequently,

5. Conclusions

Our analysis of the switching dynamics of chiral smectic-C falls within the Landau-de Gennes theory. It also serves as an example of investigating defects using geometric flows, particularly in problems arising in Materials Science. We build our mathematical model upon the free energy introduced by Chen and Lubensky [22]. This energy is closely related to the work of Vaupotič, Kralj, Čopič and Sluckin in [17], and Shalaginov, Hazelwood and Sluckin in [25]. The main difference is that |ψ| = 1 is assumed throughout their analyses. While this does not present a major obstacle in the statics, it results in a high energy barrier to overcome in the dynamics. The construction and an analysis of the gradient flow under the assumption |ψ| = 1 was done by Cheng in [26]. In the present work, we use a full complex-valued order parameter allowing the smectic structure to relax, which leads to a well-posed flow problem for a realistic energy barrier.

Funding

Research supported by NSF grant DMS-1412840.

Appendices

A.

Derivation of the weak Euler-Lagrange equations

Write the Energy Functional as where , and .

We take the first variation of J(n, ψ) with respect to n and ψ respectively. Let (u, φ) be test functions where with .

Let ε₀ > 0. For every ε ∈ [ − ε₀, ε₀], define Since |n_ε| = 1, n_ε belongs to the same space as n. Write n_ε = n + εP(n)u + o(ε) where P(n) = I − n⊗n is a projection tensor. We have: The components of are: Similarly, we have The components of are: , with components , with components Note that we use to denote the derivative of F with respect to n₁, and we calculate it using the fact that For instance,

Adding the components of the above variations, we get the first 3 Euler-Lagrange Equations in weak form, (4.1(4.1) ), (4.2(4.2) ) and (4.3(4.3) ).

For the fourth Euler-Lagrange equation, we note that the energy has the general form ∫a₁|g₁|² + a₂|g₂|² + ⋅⋅⋅ + a_k|g_k|² dx where g₁, g₂,… and g_k are linear in ψ, ψ′, ψ′′. We’ll take for example f(ψ) = ∫a₁|b₁ψ|² + a₂|b₂ψ|² dx. Then where φ is a test function. Proceeding in a similar way as in deriving the first three equations, we add the different variations to get Note that are not derivatives but notation for expressions that are sums of terms like respectively.

B.

Proof of L²-local estimates (4.8(4.8) )

We replace the test function in (4.6(4.6) ) by Δ_{− h}[(Δ_hn₁)ϕ²] for a small h > 0 with ϕ as in (4.7(4.7) ). We drop the superscript τ for convenience throughout this proof. Using the fact that ∫fΔ_{− h}g dx = −∫Δ_hfg dx and rearranging the terms, (B.1) We want to estimate the right-hand side by a constant or a small multiple of the left-hand side. We highlight a few terms, the remaining terms are approximated in a similar fashion. Recall that |n| = 1 and |ψ| ⩽ C₁, where C₁ is independent of q. where we have used Young’s inequality for conjugate Hölder exponents and the energy dissipation property (4.5(4.5) ). where we have used the fact that for f ∈ H¹(Ω), .

We estimate Δ_hF_n′1, . Going back to equation (B.1(B.1) ), we estimate all the right-hand side terms and deduce (B.2) where C₁ is independent of q and η.

For the fourth Euler-Lagrange equation, we use the test function φ = Δ_{− h}[Δ_hψϕ²]. with ϕ being the same cut-off function. knowing that remaining terms.

We write and isolate the terms we want to estimate. (B.3) As before, we want to estimate the right-hand side by a constant or a small multiple of the left-hand side. We highlight only a few terms. Recall that .

One term we consider, where . Another term we consider, where remaining terms. A third term we consider, Note that the constant on the right-hand side is dependent on ρ.

Going back to equation (B.3(B.3) ), we estimate all the terms and deduce However, Therefore, (B.4) We add the two estimates (B.2(B.2) ) and (B.4(B.4) ), along with the corresponding ones for n₂ and n₃, Choosing ε sufficiently small, and for q sufficiently large, and since ϕ = 1 on ( − L + η, L − η), Letting h → 0, we deduce that n′′₁, n′′₂, n′′₃, ψ′^′′, |ψ|²⁽⁴⁾, ψ⁽⁴⁾ ∈ L²(( − L + η, L − η) × [0, T]). To remove the dependence on ρ, we repeat all the estimates replacing difference quotients by derivatives. For instance, We proceed as before and arrive to which leads to (4.8(4.8) ).

C.

Time-quotient reasoning in higher estimates

To prove higher local regularity, we repeat a similar process as in Appendix B. Here we just highlight where the extra condition, that is initially bounded, arises from. For that we consider only one piece of the Euler-Lagrange equation, after replacing the test function by u = Δ_{− h}[Δ_hn′ϕ²]′. Using the fact that we write Using the fact that we write We can prove that to get the following estimate (C.5) As can be seen from (C.5(C.5) ), in order to get an estimate using the Euler-Lagrange equations with the terms and , among others, on the left-hand side, we need to be initially bounded.

D.

Recovering Euler-Lagrange equations when ρ → 0

Recall the energy functional where we consider (n, ψ) = (n^{k, ρ}, ψ^{k, ρ}) that minimizes J^ρ. We want to let ρ → 0, assuming that the time step k is fixed. From the interior estimates (4.8(4.8) ) we have that n^{k, ρ} → n^{k, 0} in and ψ^{k, ρ} → ψ^{k, 0} in H²( − L′, L′) for each L′ < L. We want to prove that n^{k, ρ} → n^{k, 0} in and ψ^{k, ρ} → ψ^{k, 0} in H²( − L, L).

From the lower semi-continuity of the integrals with respect to these sequences we have

We first show that this is in fact an equality by constructing test functions (n_ϵ, ψ_ϵ). Fix r > 0 so that 2 > |ψ^{k, 0}| > 1/2 on ( − L, −L + r)∪(L − r, L). Set On ( − L, −L + r)∪(L − r, L) we write ψ^{k, 0}(x) = |ψ^{k, 0}|e^iΘ(x). Since Θ(x) ∈ H³(L − r, L′)∩H²( − L + r, L), we can find Θ_ϵ ∈ H³(L − r, L) so that Θ_ϵ(L − r) = Θ(L − r), Θ′_ϵ(L − r) = Θ′(L − r), Θ′′_ϵ(L − r) = Θ′′(L − r), Θ_ϵ(L) = Θ(L), Θ′_ϵ(L) = Θ′(L) and so that Θ_ϵ(x) → Θ(x) in H²(L − r, L). We carry out the corresponding construction on ( − L, −L + r). We set on ( − L, −L + r)∪(L − r, L).

We find that ψ_ϵ(x) ∈ H³( − L, L), ψ_ϵ → ψ^{k, 0} in H²( − L, L) as ϵ → 0 with ψ_ϵ having the correct boundary conditions at x₂ = ±L. This renders (n_ϵ, ψ_ϵ) a comparison function for each ϵ, ρ > 0 for J^ρ.

We now choose, for each ϵ > 0, a ρ(ϵ) > 0 and small so that Then we have Thus It follows that each of the integrals making up J^ρ converge to their counterpart in J⁰. Therefore ∫^L_{− L}|(n^{k, ρ})′|² dx → ∫_{− L}^L|(n^{k, 0})′|² dx which implies that n^{k, ρ} → n^{k, 0} in H¹( − L, L).

Expanding the first two terms in out we get where ∫^L_{− L}I(ρ) dx → 0 and ∫^L_{− L}II(ρ) dx → ∫_{− L}^LII(0) dx as ρ → 0. Here we are using the properties that II(ρ) is at most linear in (ψ^{k, ρ})′′ and n^{k, ρ} → n^{k, 0} in H¹( − L, L). Since the integral of this expression converges to the corresponding integral in J⁰ we get Due to this, ψ^{k, ρ} → ψ^{k, 0} in H²( − L, L).

Finally using the strong convergence for ψ^{k, ρ} and n^{k, ρ} we can show that one recovers the Euler-Lagrange equations (4.1(4.1) ), (4.2(4.2) ), (4.3(4.3) ) with (u₁(x, kτ), u₂(x, kτ), u₃(x, kτ)) ∈ H¹( − L, L) upon letting ρ → 0.