Highly Efficient 3D-Printed Graphene Strain Sensors Using Fused Deposition Modeling with Filament Deposition Techniques

ABSTRACT

Graphene is a two-dimensional (2D) material known for its exceptional strength and high electrical conductivity, making it an ideal substance for resistive strain sensors. Recently, fused deposition modeling (FDM) in three-dimensional (3D) printing has gained attractiveness as a promising process due to its ability to produce 3D structured strain sensors by layer-by-layer melting and depositing conductive polymer composites. To ensure reliable strain sensors, comprehending how sensor properties change based on strain direction is crucial. In this study, graphene-based sensors with different slicing angles were successfully fabricated using FDM, enabling systematic study of the effect of strain angles on the performance of graphene-based sensors. The alignment of graphene filaments relative to the direction of applied strain was found to impact the gauge factor (GF) and other important sensor parameters. Our results showed that the 45° pattern exhibited higher sensitivity and stability compared to the 180° pattern, while the GF was greater for the 180° pattern. Additionally, we demonstrated high reliability and linearity through 1000 bending tests. The findings of this study will contribute to the growing body of research on FDM-fabricated graphene-based strain sensors.

摘要

石墨烯是一种二维（2D）材料，以其优异的强度和高电导率而闻名，是电阻应变传感器的理想材料. 最近，三维（3D）打印中的熔融沉积建模（FDM）由于其能够通过逐层熔融和沉积导电聚合物复合材料来生产3D结构应变传感器，因此作为一种有前途的工艺而备受关注. 为了确保可靠的应变传感器，了解传感器特性如何根据应变方向变化至关重要. 在这项研究中，使用FDM成功地制备了具有不同切片角度的石墨烯基传感器，从而能够系统研究应变角对石墨烯基传感性能的影响. 发现石墨烯细丝相对于施加应变方向的排列会影响规范因子（GF）和其他重要的传感器参数. 我们的结果表明，与180°模式相比，45°模式表现出更高的灵敏度和稳定性，而180°模式的GF更高. 此外，我们通过1000次弯曲试验证明了高可靠性和线性. 这项研究的发现将有助于FDM制造的石墨烯基应变传感器的研究.

KEYWORDS:

• Graphene
• filament deposition
• electrode
• strain sensor
• wearables

关键词:

• 石墨烯
• 细丝沉积
• 电极
• 应变传感器
• 可穿戴设备

Introduction

A strain sensor, defined as a device for measuring the deformation of a material subjected to applied stress, is widely used for various applications, including structural health monitoring (Kang et al. 2006), industrial machinery (Seyedin et al. 2020), biomedical engineering (Lorussi et al. 2005), automotive engineering (Garcia-Pozuelo et al. 2017), agriculture (Liqiang, Sun, and Yebo 2023), and robotics (Cheng et al. 2019; Ha et al. 2023). Among the various types of sensors, resistive strain sensors are generally preferred particularly for wearable electronics, structural health monitoring system of constructions, and robotic and biomedical devices because they are relatively inexpensive, easy to install, and have high sensitivity to strain (Kim, Qaiser, and Hwang 2023; Myeongjong et al. 2021; Xue et al. 2020, 2023; Yan et al. 2021; Milić et al. 2023). The mechanism of a strain sensor with a crack is based on the change in resistance of the material in the bridge as the crack opens or closes (Amjadi et al. 2016; Souri et al. 2020; Ha et al. 2023; Wang et al. 2014; Milić et al. 2023). When the sensor is subjected to tensile strain, the crack opens, leading to an increase in the resistance of the material in the bridge (Amjadi et al. 2016; Wang et al. 2014; Hwang et al. 2022). Conversely, when the sensor is subjected to compressive strain, the crack closes, which causes the resistance of the material in the bridge to decrease (Amjadi et al. 2016; Wang et al. 2014). These types of sensors are sensitive but also fragile and brittle because of the cracks in the materials of thin films (Guo et al. 2019).

Recently, fused deposition modeling (FDM) three-dimensional (3D) printing has become attractive as a promising process to produce 3D structured strain sensors by melting and depositing conductive polymer composites layer by layer (Li et al. 2022; Maurizi et al. 2019). The composites generally include various conductive fillers such as carbon nanotubes (Kim, Seob Choi, and Yim 2022; Kim et al. 2019; Park et al. 2019), carbon fibers (Li et al. 2022; Nyiranzeyimana et al. 2022), graphene (Choi, Joo Shin, and Hee Lee 2022; Larraza et al. 2021; Qian et al. 2022), graphite (Georgopoulou, Sebastian, and Clemens 2020; Maurizi et al. 2019; Munasinghe et al. 2019), and carbon black (Lian et al. 2022; Zhang et al. 2022). In particular, graphene is a two-dimensional (2D) material that is extremely strong and has high electrical conductivity, making it an ideal material for strain sensors (Chun, Choi, and Park 2017; Ji-Huan and Abd Elazem 2022; Wang et al. 2014). FDM printing allows the production of sensors in a cost-effective manner, as it is a relatively simple and inexpensive process (Ahmed, Nauman, and Muhammad Khan 2021; Choi, Joo Shin, and Hee Lee 2022; Yizong et al. 2022). With the advantages, FDM-printed graphene-based composites were integrated into various structures and explored for the application to strain sensors (Aga et al. 2021; Ahmed, Nauman, and Muhammad Khan 2021; Choi, Joo Shin, and Hee Lee 2022; Tao et al. 2017; Yizong et al. 2022). For example, Tao et al. demonstrated graphene-based strain sensors using the FDM method (Tao et al. 2017). They incorporated graphene with Ecoflex to create stable and stretchable composites, which exhibited a Gauge Factor (GF) of 268 within a strain range of 100%. In the work by Choi et al., 3D-printed auxetic structures were showcased using the FDM method. They coated 3D-printed thermoplastic polyurethane (TPU) with graphene to form strain sensors (Choi, Joo Shin, and Hee Lee 2022). The researchers investigated sensor performance in relation to the number of graphene coating layers. The results revealed that sensors with a dense graphene layer exhibited higher reliability. Additionally, Aga et al. developed graphene-based film-type strain sensors using the FDM technique (Aga et al. 2021). They directly printed graphene inks containing terpineol, graphite, and ethyl cellulose using FDM, followed by a subsequent laser sintering process. The researchers made a direct comparison of strain sensor performance with commercially available foil strain sensors. Interestingly, the FDM-printed graphene sensors displayed a higher GF of 3.58 compared to the GF of commercial sensors.

Gauge factor (GF), sensitivity, stability, reliability, and linearity are the main parameters determining the performance of resistive strain sensors (Amjadi et al. 2016; Souri et al. 2020; Wang et al. 2014). The performance of strain sensors mentioned earlier is significantly impacted by the direction in which the strain is applied (Liao et al. 2017; Na et al. 2022, Na et al. 2022; Shintake et al. 2018; Yan et al. 2021). Given that strain can be exerted on these sensors from various angles, comprehending how sensor properties change based on strain direction becomes crucial for creating reliable resistive strain sensors (Amjadi et al. 2016; Liao et al. 2017; Na et al. 2022; Shintake et al. 2018; Souri et al. 2020; Wang et al. 2014; Yan et al. 2021). While previous studies have demonstrated commendable sensor performance in graphene-based strain sensors produced via FDM methods (Aga et al. 2021; Ahmed, Nauman, and Muhammad Khan 2021; Choi, Joo Shin, and Hee Lee 2022; Tao et al. 2017; Yizong et al. 2022), there has been a notable absence of investigations into how filament alignment influences the performance of graphene-based strain sensors manufactured using the FDM technique. Crafting electrodes with different alignments using FDM presents challenges as it necessitates employing a well-calibrated extrusion system and appropriate slicer settings in the printing process to manage filament alignment (Cheng-Yu et al. 2021; Georgopoulou, Vanderborght, and Clemens 2021; Li et al. 2022; Liu et al. 2021). Thus, despite the technique’s significance, there has been limited research on producing strain sensors with diverse directions of graphene filaments and comprehending their impact on strain sensor performance.

In this work, a highly efficient strain sensor was fabricated with a graphene-based polymer composite using the A detailed exploration of the influence of slicing angle on such sensor characteristics is conducted; slicing angle is a factor that has largely been overlooked in previous studies despite its potential significant impact on sensor performance. Thus, two directions, namely, 180° and 45° patterns according to the graphene filament deposition method, were compared and analyzed, facilitating a comprehensive investigation of the differential effects of these patterns on performance factors such as sensor sensitivity, GF, stability, and reliability. The resistive sensors with 180° and 45° patterns showed different GFs of 58 and 32 and sensitivities of 0.08 and 0.12 V/με, respectively. The linearity of both patterned samples was over 90%. To interpret this result, crack-based computational fluid dynamics (CFD) simulation was performed regarding the required force, and the results were analyzed. In addition, high stability was validated through 1000 bending tests, and pressure measurement according to the top, side, and twist characteristics of the 3D strain sensor was conducted. The findings of this work will significantly contribute to the understanding of the intricate interplay between 3D printing parameters and sensor performance, which represents a pioneering contribution to the field of sensor technology and 3D printing.

Experiment

Materials and sample preparation

[Table 1 near here] For the preparation of 3D-printed strain sensors, graphene-filled polylactic acid filaments with a diameter of 1.75 mm were obtained from Blackmagic 3D company. The FDM-based sensors were fabricated using an Ender-3Pro 3D printer with a print volume of 220 × 220 × 250 mm. STL files were generated using Fusion 360 software and further prepared for printing using Creality Slicer version 4.8. Dog-bone-shaped tensile specimens were printed with a width, length, and thickness of 5, 200, and 2 mm, respectively. To ensure consistent sample characteristics and minimize the effects of temperature changes during fabrication, each specimen was printed individually on the central bed area; the printing parameters are listed in Table 1. The deposition angle of the graphene filament was varied between two conditions: 180° parallel to the deposition direction and 45° in a zigzag stacked pattern. Five layers were deposited on each specimen, with all other variables kept constant to isolate the effect of the deposition angle.

Table 1. Printing parameters for FDM-printed 3D graphene strain sensor.

Parameters	Value
Nozzle diameter	0.4 mm
Designed layer thickness	2 mm
Number of printing counters (layer number)	5
Printing speed	10 mm/s
Nozzle temperature	220°C
Bed temperature	50°C

Characterization

Micrographs were obtained using an optical microscope (Eclipse LV100ND/LV100NDA, Seoul, Korea). The tensile properties of the 3D-printed strain sensors were evaluated using a universal testing machine (Instron 5943, Norwood). The strain-sensing performance of the printed samples was quantified through measurements of the output voltage and current using an electrometer (Keithley 2450). The applied force was monitored during tensile and compression measurements using a force sensor.

Result and discussion

Figure 1 illustrates the schematic structure of the FDM 3D printer, comprising a nozzle head, three-axis moving platform, and heating bed, utilized in this study. The graphene filament is inserted into the nozzle head and extruded through a nozzle that is heated to a specified temperature. During the printing process, the filament is deposited on the heating bed according to a predefined pattern. Figures 1(b,c) present 3D modeled images of the strain sensor design, with parallel axial (180°) and diagonal (45°) filaments, respectively. The images in Figures 1b1 and 1c2 depict the implementation of the design using an FDM printer, where the central portion of the sensor is designed to detect mechanical deformation and the ends of both heads are clamped into holders to measure electrical changes. The microscope images in Figures 1b2 and 1c3 show the alignment direction of the filament on the central part of the fabricated sensor, which was used to analyze the sensitivity to deformation.

Figure 1. (a) schematic of FDM-printed graphene strain sensor. 3D modeling of dog-bone-shaped strain sensor with parallel (b) and zigzag (c) direction of filament deposition. FDM-based graphene strain sensor printed, with microscope images for parallel (b1 and b2) and zigzag-patterned strain sensors (c1 and c2).

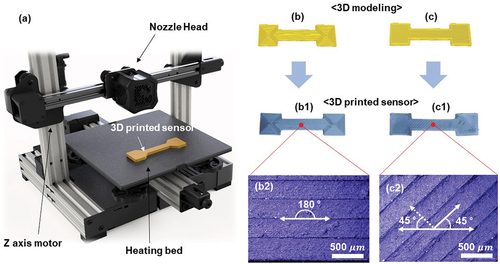
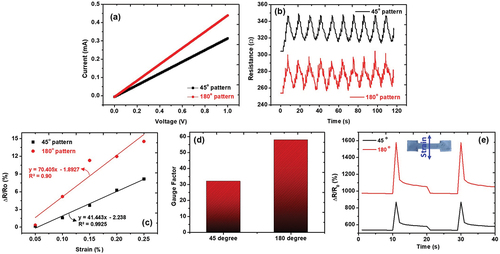
Two strain sensors with identical widths (5 mm) and lengths (200 mm) were fabricated with different thicknesses—2.0 mm for the 180° design and 2.2 mm for the 45° design – as shown in Figures 1b1 and 1c1, respectively. The difference in thickness despite the same 3D model design was attributed to the ease of forming a dense structure in the parallel deposition method as evidenced by the I – V curve results. Figure 2a displays the I – V curves of the printed sensors at a varying voltage gradient from 0 to 1 V, showing an increase in current output with an increase in the applied voltage. Both strain sensors demonstrated uniform conductivity according to Ohm’s law, which is crucial for obtaining accurate sensitivity as the resistive sensors comprise electrodes. Notably, the parallel-design sensor with a lower thickness tended to exhibit higher current output, which could be attributed to the aforementioned denser graphene structure. The results presented in Figure 2b illustrate the sensing performance of the composite strain sensor under tension with applied strains ranging from 0.05% to 0.25%. Strain value is calculated by ε =ΔL/L₀, where ε, ΔL and L₀ are the applied strain, the change in length and the initial length of the electrodes. The strains were incrementally applied in five steps with an interval of 0.05% in a second, which was followed by a recovery process. We employed a bending machine to generate flexural strain within the samples. This apparatus functions by securely securing the sample at both ends and gradually applying force. As the force is incrementally raised, the sample experiences both bending and stretching deformations, resulting in the development of strain within the material. It’s worth noting that our equipment underwent meticulous calibration to ensure precise control of strain levels, specifically within the range of 0.05% to 0.25%. The strain-dependent response was observed to exhibit a monotonic increase with increasing applied strain. The 180° sensor showed more sophisticated step-type sensing with lower precision and higher amplitude compared to the 45° sensor. The sensitivity of the sensors was calculated through regression analysis as shown in Figure 2c, which reveals that the 180° pattern has lower sensitivity (R² = 0.90) compared to the 45° pattern (R² = 0.99). The GF, calculated as [GF = (ΔR/R₀)/ε], was found to be 32 and 58 for the 45° and 180° patterns, respectively. These values are over 20 times higher than those typically found for commercial strain sensors (GF = 2) (Shuang et al. 2020). The linearities of both sensors with the different pattern angles were similar (>90%). These results imply that the alignment of the filament relative to the direction of the applied strain can affect the GF. When the filament is aligned parallel to the applied strain, it generally results in a lower GF compared to an orthogonally aligned filament. This difference is attributed to the fact that the interfacial strength between the cross-sectional layers is higher than the bonding strength in the continuously connected cross sections in the orthogonal direction (Li et al. 2022). However, the results obtained indicated the opposite trend, suggesting that the magnitude of the change in internal cracks caused by the internal bonding strength is not always dependent on the deposition direction. The interfacial strength between the cross-sectional layers was higher than the bonding strength in the continuously connected cross sections in the orthogonal direction. This suggests that the magnitude of the change in internal cracks caused by the internal bonding strength is not always dependent on the deposition direction. The interfacial strength plays a critical role in determining how well a strain sensor can transfer mechanical stress from one layer to another (Zhao et al. 2020). If the interfacial strength is poor, stress may be concentrated at certain points, leading to cracking or failure of the sensor. However, if the interfacial strength is high, stress can be distributed more evenly across all layers, resulting in better sensitivity and higher GF. Therefore, the optimization of interfacial strength is an important factor for designing and fabricating strain sensors. Figure 2e demonstrates the contrasting sensing reactions of the 3D printed samples deposited at 45° and 180° angles when exposed to equivalent lateral strain. The samples underwent two cycles of straining, each at a magnitude of 0.25% strain in a lateral direction, as illustrated in the inset of Figure 2e. The application of this force results in a noticeable shift in resistance, indicating the strain encountered by the material. This strain, in turn, generates an upward drag or reactive force, which the sensor converts into a change in resistance. Notably, the 180° sample displays a more significant modification in its resistance compared to the 45° sample. This behavior implies that the vertically stacked 180° sample could potentially encounter an increased vertical drag when subjected to the same applied strain. The relative magnitudes of these resistance variations offer insights into the material’s sensitivity and its capacity to transform mechanical forces into electrical signals. As the force is potentially eliminated or reduced, both samples appear to return to a state of balance, evident from the stabilization of their respective resistance levels. This observation underscores the significance of sensor orientation in determining its response characteristics to external mechanical stimuli.

Figure 2. (a) I – V curves of the printed sensors for 45° and 180° patterns at a varying voltage gradient from 0 to 1 V. (b) sensing performance of the composite strain sensor under tension with applied strains ranging from 0.05% to 0.25%. (c) sensitivity of the sensors calculated through regression analysis. (d) calculation of gauge factor for 45° and 180° patterns. (e) response of the 45° and 180° patterns to equivalent lateral forces with different pressures for two times.

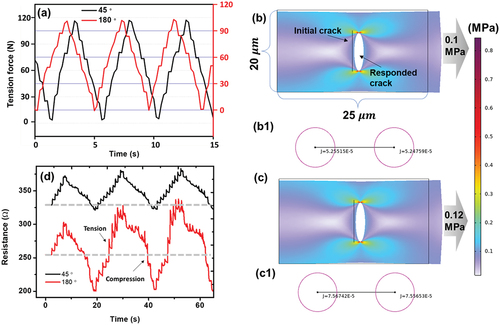
The response force to a specific applied strain of 0.25% was measured and compared to understand the phenomenon as illustrated in Figure 3a. The 45° pattern required a force of approximately 120 N, while the 180° pattern required approximately 100 N. This result indicates that the zigzag shape in the 45° pattern has a stronger bonding force, leading to a lower degree of crack deformation. To examine this phenomenon using a crack-based standard sensor, a CFD simulation was conducted in COMSOL Multiphysics 6.1 as shown in Figure 3b. The simulation modeled cracks within a rectangular solid under tension forces of 0.1 and 0.12 MPa, which reflected the measured force, and was aimed at assessing the energy required to alter the crack in response to the tension in the same sensor. The initial crack prior to the application of tension and the cracks formed under tension are referred to as the “responded cracks.” The energy release rate at the crack tip was calculated using the J-integral:

Figure 3. (a) response force to a specific applied strain of 0.25%. CFD-based simulation of cracks within a rectangular solid under a tension force of (b) 0.1 and (c) 0.12 MPa. (d) response of the 45° and 180° patterns under the same tensile and compressive strains of 0.25% in five steps.

$J=\underset{\mathrm{\Gamma }}{\overset{\hspace{0.17em}}{\int }}Wsm\cdot e1-\left(\sigma \cdot m\right)\cdot \left(\mathrm{\nabla }u\cdot e1\right)dl$,(1) (Griffith and Ingram Taylor 1921)

where Ws is the strain energy density, e1 is the unit direction vector of the crack, m is the unit vector normal to the integration path, σ is the Cauchy stress tensor, and u is the displacement vector.

The simulation visually depicts the initiation of cracks, which are challenging to observe in experimental studies using the energy J-integral. When different tension forces were applied, the responded crack appeared along the direction of the initial crack, as shown in Figures 3a-c. The energy release rate of the responded crack was calculated to be 5.25 and 7.56 for tension forces of 0.1 (Figure 3b) and 0.12 MPa (Figure 3c), respectively. The value of J was found to be proportional to the applied tension, as illustrated in Figure 3b1, c1). Because J represents the difference between the work applied by an external force (tensile force in this case) and the energy used by the crack at the crack tip when subjected to the external force, the larger the size of the generated crack, the larger is the value of J. This implies that more energy is consumed to generate the crack under a force of 0.12 MPa. This simulation result confirms that tension force and crack change are proportional in the same sample. Therefore, the 45° pattern, which exhibited low sensitivity despite the relatively high force required to achieve the same strain value, did not generate cracks significantly because of its structurally strong bonding force. Figure 3d provides experimental evidence to support these findings. When identical tensile and compressive strains of 0.25% were applied in five steps, the 45° pattern was stable but showed low sensitivity, while the 180° pattern was relatively unstable but showed high sensitivity. This may also be attributed to the higher bonding strength of the internal structure for the 45° pattern.

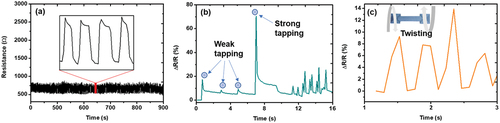
To assess the response repeatability and durability with respect to the zigzag printed pattern, the sensor was subjected to repeated stretching and release cycles. Figure 4a displays the changes in resistance of the sensors, indicating a fully recoverable electrical resistance without hysteresis at a 0.25% stretching rate for 1000 cycles. Figures 4b and cpresent experimental results showing the various usage examples of the 3D resistive strain sensor. A biological concept similar to a resistive-type strain sensor in 3D form is that of mechanoreceptors (Barth 2004, 2019). Mechanoreceptors are specialized sensory cells that respond to physical stimuli such as pressure, tension, and stretching and convert them into electrical signals that can be processed by the nervous system. They are found throughout the body, including the skin, joints, and organs, and are essential for our sense of touch, proprioception (awareness of body position), and control of movement. Similar to a resistive-type strain sensor, mechanoreceptors sense and respond to changes in mechanical strain and can provide information about the force and direction of that strain. A 3D structured resistive strain sensor has several advantages over the 2D type in terms of mimicking the function of mechanoreceptors in the human body. One of its main advantages is its sensitivity to pressure even when it is applied to the upper layer. Figure 4b illustrates the sensitivity characteristics of the 3D structured resistive strain sensor when it is subjected to different pressures applied to the upper layer with relatively strong and weak stresses, resulting in distinguishable responses. This sensitivity is due to the 3D structure of the sensor, which allows it to respond to pressure from multiple directions. By contrast, the 2D-type sensor is limited in its sensitivity to touch owing to the formation of a thin film on the substrate, which restricts its ability to detect pressure from different angles. In addition, the 3D structured resistive strain sensor provides a more accurate representation of the complex and multidirectional pressure-sensing capabilities of mechanoreceptors in the human body. Further, Figure 4c illustrates the sensitivity of the sensor to twist-type hybrid strain rather than just tension and compression. The peak response to torsional motion ranged from 8% to 14% of ΔR/R0, which was approximately 1/7 of the tap peak value (70%).

Figure 4. (a) fully recoverable electrical resistance without hysteresis at a 0.25% stretching rate for 1000 cycles. (b) sensitive responses of the 3D-printed graphene strain sensor for different tapping stresses. (c) sensing performance under twisting stresses.

Conclusion

In this work, a highly efficient strain sensor was fabricated through a graphene-based FDM 3D printing process. The results of printing electrodes in two different directions with the graphene filament deposition method were compared and analyzed. When stacking was parallel to the printing direction (180°), the sensitivity was higher than that of the sensors printed in a zigzag pattern (45°). However, the stability and reliability tended to be lower because the resistive force of the sensor printed at 45° was greater under the same strain. To interpret this observation, crack simulation was performed according to the force, and the results were consistent with the experimental force measurement results. The measured GF values were 58 and 32 for the 180° and 45° patterns, respectively, and the linearity was over 90%. In addition, high stability was validated through 1000 bending tests. By applying the 3D-printed strain gauge, the pressure was measured according to the top, side, and twist characteristics of the 3D strain sensor, and the response curve showed that it could be applied to wearables.

Highlights

• A highly efficient strain sensor was fabricated using FDM-based 3D printing of graphene filaments.

• Two different printing methods designed with parallel axial (180°) and diagonal (45°) filaments were compared.

• The 3D-printed strain sensor was used for pressure measurement and showed promising results for wearable applications.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) (No. NRF-2021R1A2C1011248). This research was supported by the Chung-Ang University Graduate Research Scholarship in 2022.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The work was supported by the National Research Foundation of Korea [2021R1A2C1011248]. This research was supported by the Chung-Ang University Graduate Research Scholarship in 2022.