Rheological properties of Indian coffee plum (Flacourtia jangomas) pulp in steady and dynamic shear at different temperatures

ABSTRACT

Indian coffee plum (Flacourtia jangomas) is an underutilized fruit with many great nutritional and medicinal value generally available in the northeastern part of India. Although rheological study of different fruit pulps have been studied till now, however no such study has been undertaken on Indian coffee plum. The present study was aimed to evaluate the steady-state shear and viscoelastic rheological properties of Flacourtia jangomas (F. jangomas) pulp as function of temperature in the range 20 to 80°C using dynamic oscillatory viscometry, as well as applicability of Cox-Merz rule. Under steady-state shear tests, the shear stress versus shear rate data were adequately fitted to the Bingham model (R² = 1) for too low shear rate (0.1to 1.0 s⁻¹) and Power law model (R² > 0.83) for moderate shear rate (1.0 to 100 s⁻¹). Oscillatory shear data of the fruit pulp showed weak gel behavior where loss modulus exceeded the value of storage modulus. The power modified Cox-Merz rule was tested for all temperature and found applicable for lower temperatures. These results could be beneficial for future studies on food properties and industries.

KEYWORDS:

• Viscosity
• rheology
• viscoelasticity
• cox-Merz rule
• indian coffee plum

Practical applications

F. jangomas fruit is an underutilized, wild, tropical fruit having vast applications both in the field of medicine and food industries. The rheological properties of the fruit (steady shear properties and dynamic shear properties) will be of great help in developing equipment and processing techniques required for its processing of different pulp-based products while also increasing its acceptability with the consumers. Moreover, the understanding of the rheological properties is necessary for prediction of different parameters like heat and mass transfer coefficient for development of product along with packaging and storage techniques. The result obtained from this study will greatly help food processing companies in developing the pulp-based products of F. jangomas.

Introduction

Flacourtia jangomas (Lour.) Raeush. more familiar as Indian coffee plum is an tropical, semi-wild, and indigenous medicinal fruit grown widely in the South-eastern and Eastern part of Asia (Barbhuiya et al., 2020; Dutta and Borah, 2017). It belongs to the Salicaceae family having sour to astringent taste and is 100% edible. Various traditionally produced jams, jellies and pickles are made from this fruit but it is yet to be produced on a large industry scale. The fruit extracts, the plant leaves and roots also have medicinal characteristics. It can be used as antibiotic, antioxidant, analgesic and antidiarrheal medicine (Talukder et al., 2012). The leaves and stem can be used as antidiabetic medicine and helps in treatment of Diabetes mellitus which effects a large proportion of population in the world (Singh and Singh, 2010), though further research is required in this field. Thus, it is very important to know about the physical and chemical properties of the fruit for industrial process to be technically and economically feasible (Rifna et al., 2019). Rheological properties come under the physical properties of the fruit. Rheology is quite important in the development of processed food, quality control measures, design and operation of process equipment, sensory evaluation, and high-quality product development (Ahmed and Ramaswamy, 2006). Rheological properties help in understanding the flow behavior of the fruit pulp using various flow parameters like shear stress, shear rate, shear rate–viscosity. Both the steady shear and dynamic shear properties are found out (Ahmed and Ramaswamy, 2007). The processing temperature greatly effects the rheological properties of the food product. Therefore, it is quite necessary to find out the rheological properties of the fruit as a function of temperature (Ahmed et al., 2007).

With the increase in demand of indigenous and exotics product in the market specially in the food sector, it is necessary to know about the processing properties of fruit which will not only help in development of new product but also will boost the economy of the region through commercialization of various underutilized but abundant fruit (Murakonda and Dwivedi). Although many rheological studies have been done on various exotic fruits available throughout the world but no work on rheological characterization has been done on the F. jangomas fruit.

The present work has explored the steady state shear and dynamic shear properties of F. jangomas pulp (FJP) and the effect of temperature on the rheological properties of the fruit pulp.

Materials and methods

F. jangomas were procured from the local market of Silchar, Cachar District, Assam, India, in August 2019. Then the fruits were transported immediately to the laboratory to perform the experiments within 72 hours. The fruits were washed with normal water to remove the dust and unwanted foreign matters. The moisture content of good quality fruits having uniform size and shape was measured by using the hot air oven method at 105 ± 1°C following AOAC method 925.10 (AOAC, 1990) and found to be 68 ± 5%. The fruits were pulped before the rheological measurements were taken. Digital refractometer (Milwaukee, MA 871) was used to determine the Total Soluble Solids (TSS) of the fruit in ^oBrix and found to be 10.4 ± 0.1 ^oBrix. All experiments were done in the Food Process Engineering Department, NIT, Rourkela.

Rheological measurements

A controlled stress (σ) rheometer (AR 2000ex, TA Instrument, USA) attached with a computer-controlled software (TRIOS software) was used to study the rheological behavior of the fruit pulp. A 40 mm diameter parallel plate geometry was used with a gap of 1 mm. The gap was determined by gap independency procedure as described by (Tonon et al., 2009).

The instrument was supplemented with Peltier temperature control system and the temperature was controlled precisely and monitored. The rheological properties were evaluated from 20 to 80°C with incremental steps of 20°C. Geometry material thermal expansion was considered in order to guarantee the gap dimension. A small quantity (approximately 1 ml) of the sample was placed on the round bottom plate of the rheometer. At higher temperatures (60°C and 80°C) a solvent trap was used to minimize the evaporation from the product.

Viscoelastic properties

Dynamic oscillatory tests were carried out between 0.01 and 100 Pa at a frequency of 1 Hz. The oscillatory stress sweeps was selected to determine the products’ linear visco-elastic range. Then the frequency sweep measurements were carried out at 1.0 Pa and the oscillatory frequency (ω) was varied from 0.01 to 50 Hz. The oscillation stress was selected based on linear part of the visco-elastic range. The storage modulus (G’, a measure of elastic property), complex viscosity (η*) and loss modulus (G”, a measure of viscous property) and phase angle (tan δ, ratio of loss modulus to storage modulus) were thus obtained from the software.

Steady-state shear properties

For steady state flow measurements, the experiments were carried out in the shear rate range of 0.01 to 100 s⁻¹. To avoid thixotropy the samples were subjected to a shearing rate at 300 s⁻¹ for 5 minutes (Data not mentioned)(Augusto et al., 2012). In order to maintain the steady state condition a two-cycle programmed protocol was followed by changing shear from 0.1 to 100 s⁻¹ in 5 minutes and back to 0 s⁻¹ in next 5 minutes (Ahmed et al., 2007). Rheological parameters (shear stress, apparent viscosity, and shear rate) were obtained directly from the TRIOS software. Among various rheological models namely Newtonian, Bingham, Power law and Herschel- Bulkley the best fit model was selected based on R² value.(Augusto et al., 2012)

Applicability of the Cox-Merz Rule

The Cox-Merz empirical rule equation (1)(1) ${\eta }_a(\gamma )=\eta \ast \left(\omega \right){\left|\gamma \right.}_{=\omega }$(1) states the relation between apparent viscosity (η_a = σ/$\gamma$) at a specific shear rate ($\gamma$) and complex viscosity (η*) at a specific oscillatory frequency (ω) when $\gamma$= ω (Augusto et al., 2012). When this rule is valid either oscillatory or steady-state shear experiments can be carried out to determine the rheological properties of the food which are useful due to limitation in each kind of experiment (Augusto et al., 2012; Gunasekaran and Ak, 2000).

Thus, the results obtained from the dynamic and steady state analysis can be used for evaluation of the Cox-Merz rule applicability:

(1) ${\eta }_a(\gamma )=\eta \ast \left(\omega \right){\left|\gamma \right.}_{=\omega }$(1)

Results and discussions

Shear stress-shear rate model

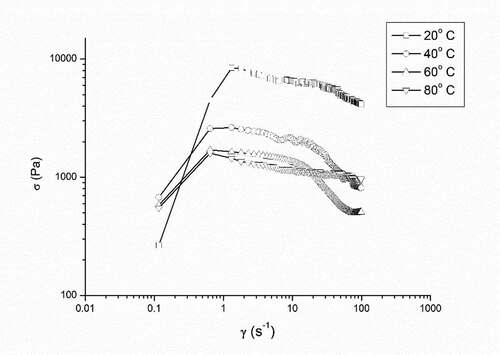
The flow behavior of FJP was analyzed at 20, 40, 60, and 80 °C and the shear stress versus the shear rate data at each experimental condition were tested for various rheological models (Power, Newtonian, Bingham, Herschel Buckley). It was observed that the FJP data have distinct two parts (Part A and Part B), the former having too low shear rate (0.1to 1.0 s⁻¹) and the latter having moderate shear rate (1.0 to 100 s⁻¹) are shown in Figure 1. It was found that Bingham model fitted adequately for part A and properly described the flow properties of FJC at temperature ranging from (20–80) ^oC with highest coefficient of determination (R²) and Power law model described well the data for part B.

Figure 1. Flow curves of FJP at 20 ^o C, 40 ^o C, 60 ^o C, 80 ° C

The Bingham and Power law model are represented as

(2) $\sigma ={\sigma }_{{ }^{\circ }}+K\gamma$(2)

(3) $\sigma =K{\gamma }^n$(3)

Where $\sigma$ is shear stress in (Pa) and $\gamma$ is the shear rate in (1/s). The parameters that characterize the flow behavior are consistency coefficient (K), flow behavior index (n)(dimensionless) and the yield stress (${\sigma }_{{ }^{\circ }}$). Both the Bingham model and Power law model parameters are presented in Table 1.

Table 1. Parameter values for Bingham model and power law model of FJP

Model	Temperature (^o C)	K (Pa.s^n)	n	R^2	Yield Stress (Pa)
Part A
Bingham	20	18609	-	1.0	207.469
Bingham	40	2998.87	-	1.0	298.65
Bingham	60	1751.64	-	1.0	321.19
Bingham	80	1685.24	-	1.0	268.134
Part B
Power law	20	9587.39	0.166	0.90	-
Power law	40	3402.06	0.271	0.83	-
Power law	60	2267.14	0.313	0.83	-
Power law	80	1434.47	0.088	0.91	-

Bingham Model

Bingham model states that the material should have very high yield stress value and upon application of heat the yield stress should decrease causing the material to flow. From the above experiment data one can say that FJP had a tendency to remain rigid when the magnitude of shear stress is smaller than yield stress. FJP samples show high yield stress due to high interaction between the internal particles of the samples which resist its deformation. When the stress applied is below the yield stress, the material behaves like an elastic material; above the yield stress the material starts flowing, like a viscous liquid (Bayod et al., 2007). Yield stress is a very essential control parameter of process industries, especially for comparing the product properties made on separate production lines (Ahmed, 2004). Yield Stress is important for the optimal design various thermal processing units in food processing industries (Steffe, 1996). The typical characteristic of multiphase materials is the presence of yield stress (Augusto et al., 2012; Gunasekaran and Ak, 2000) as fruit pulps and juices, consists of various insoluble components in a water solution (serum, containing sugars, minerals, proteins, and soluble polysaccharides). The data obtained from the experiment showed a good reasonable fitting for Part A on Bingham model with R² .

It was observed that, the yield stress value of the FJP samples slightly increases with increases in temperature till 60° C after that it decreases at 80°C while the consistency coefficient (K) decreased with increase in temperature which meant a decrease in the apparent viscosity with increase in temperature of the FJP sample.

Power law model

For approximation of the viscosity data, power law is one of the most widely used models. The reason behind this is that the rheological behavior of the food is represented simply by straight line (Steffe, 1996). According to power law model the shear stress versus shear rate data are described by two parameters (K and n). The fluid has shear-thinning behavior or pseudoplastic if the value of n is less than 1, the fluid is dilatant if the value of n is more than 1 and for n equals to 1 the fluid has a Newtonian behavior.

The values of the shear stress and shear rate are fitted into equation (4)(4) ${log}_{10}\sigma ={log}_{10}K+n{log}_{10}\gamma$(4) to obtained the value of the parameters,

(4) ${log}_{10}\sigma ={log}_{10}K+n{log}_{10}\gamma$(4)

The results obtained from the data showed reasonably good fitting to Power law model for part B with R² 0.83 to 0.91. The flow behavior index (n) tends to increase with increasing temperature (20 to 60 ^oC) showing that the FJP tends to become closer to Newtonian fluid. The FJP showed shear thinning behavior as the value of n < 1 for all samples. Most of the non-Newtonian foods exhibits shear-thinning behavior including pomelo juice (Keshani et al., 2012), orange juice, grape juice (Chuah et al., 2008; Hernandez et al., 1995; Kaya and Belibaǧlı, 2002), siriguela pulp (Augusto et al., 2012), araca pulp (Haminiuk et al., 2006), guava pulp (Harnanan et al., 2001) etc.

Figure 1 shows the flow curves of the FJP samples at 20, 40, 60, 80 ° C. The marked points denote the mean values of the data of the rheogram. Irregularities in the shear stress data were found which was the result of the increase in temperature. Some examples related to temperature increase are gelation to form pectin gels, softening of cheese or chocolate due to melting of fat, meat and egg products become firm due to protein denaturation and thickening of solutions from starch gelatinization (Haminiuk et al., 2006; Steffe, 1996).

Unlike many studies found on the rheological behavior of fruit pulps, in this present study, the FJP was no subjected to any processing centrifugation, sifting, or homogenization to keep the pulp properties as close possible as it is found in a fresh fruit. Mostly before analyzing steady state shear properties the fruit pulps are subjected to processes to obtain a homogenous pulp as showed by araçá (Psidium cattleianum sabine) (Haminiuk et al., 2006) and açai (Euterpe oleraceae Mart.) (Tonon et al., 2009). The processing adopted by these authors may promote changes in rheological behavior.

Dynamic Rheological properties

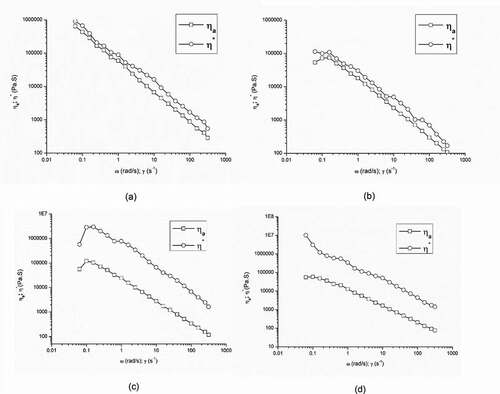
Frequency sweep

The dynamic rheological properties of FJP were analyzed by storage modulus (G^/) and loss modulus (G^//) as a function of frequency Figure 2(a, b). G^//and G^/were obtained at different temperatures (20, 40, 60, 80 ^o C). Both Moduli were slightly dependant on the frequency where the G^/exceeded G^//at the frequency range of 0.01–50 Hz. For 20 ° C, G^/increased from 39271.8 Pa to 83751.8 Pa whereas G^//increased from 13850 to 33773 Pa. These data showed that the FJP samples behaved like a gel and can be classified as a weak gel (MA Andy Rao, 2010) as observed with tomato products (Valencia et al., 2002) and yellow potato puree (Fasina et al., 2003). This behavior is due to the chemical structure of the FJP, especially the high pectin content of F. jangomas and other polysaccharides present in the fruit matrix. For 40 ° C, G^/and G^//values increased from 3273.53 Pa to 32516.2 Pa and 924.386 Pa to 7416.96 Pa, respectively; for 60 ^o C G^/and G^//values increase 3492.83 Pa to 23403.1 Pa and 137.985 Pa to 4741.1 Pa, respectively, and for 80 ° C the G^/and G^//values increases from 3354.99 Pa to 36344.8 and 1056.36 to 9283.0 Pa respectively. From the G^/, G^//- ω curve it can be seen that there was a progressive decrease in G^/, G^//values with increase in temperature, and this behavior is observed in other food product like acai pulp (Tonon et al., 2009), baby foods (Ahmed and Ramaswamy, 2006) and cheddar cheese (Rosenberg et al., 1995). However, an unusual behavior at 80 ° C was observed where both the moduli were higher than 60 ^o C, which could be explained by partial sample drying due to long experiment time or due to gelation attributed to pectin content in the fruit (Rosenberg et al., 1995).

Figure 2. Effect of temperature on dynamic rheological behavior of FJP at 20, 40, 60, 80 ° C (a) storage modulus(G^/) – ω graph (b) loss modulus (G^//) – ω graph (c) damping factor- ω graph

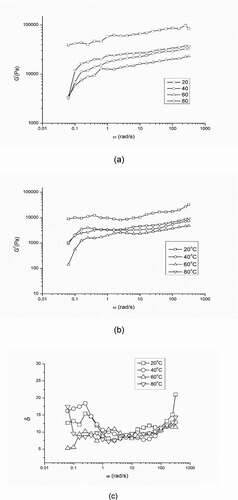
These data showed that the FJP was thermally stable at different temperature range; internal structure changes were low in the temperature range analyzed (Barbieri et al., 2018). The thermal stability of FJP also suggested that there could be various applications in the bakery industry, such as jam and fruit filling, which involve heating of the sample. Moreover, the FJP is also suitable for pasteurization, which is usually done at 60–90° C to inhibit the growth of microorganism including extending the shelf life (Barbieri et al., 2018).

At higher frequencies, the FJP became more rigid which could be attributed to the fact that some degree of relaxation is required for the rearrangement of proteins and carbohydrates. The caramel acts like a fluid at lower frequencies as they have adequate time to rearrange themselves. In contrast, at higher frequencies, the molecules cannot rearrange themselves within the short time resulting in a rigid structure (Ahmed et al., 2006).

Tangent of phase angle δ is defined as the ratio of G^//and G^/is termed as loss factor or damping factor. For ideal elastic behavior, δ = 0°, i.e., no viscous portion is present in the sample whereas for ideal viscous behavior, δ = 90°. i.e., no elastic portion in the sample. At temperatures 20, 40, 80°C, δ ranged from 7.26° to 20.96°. However, at 60°C, δ ranged from 5.51°-12.48°, supporting a higher viscous nature. Sharp changes in G^/, G^//and δ at 60°C again indicates the possible initiation of gelatinization and thermal transition of the FJP sample (Ahmed and Ramaswamy, 2006). A curve showing δ vs ω is illustrated in the graph 2(c).

A simple mathematical model was used to illustrate the rheological properties of the FJP. A power law type equation was used for the calculation of dynamic rheological properties of FJP

Linear regressions of ln ($G{ }^{\mathrm{\prime }}$), ln ($G{ }^{\mathrm{\prime }\mathrm{\prime }})$and ln ($\omega$) were calculated at different temperature and the magnitudes of slope and intercept were calculated with the help of these equations (5)(5) $G{ }^{\mathrm{\prime }}=K{ }^{\mathrm{\prime }}(\omega {)}^{n{ }^{\mathrm{\prime }}}$(5) and equation (6)(6) $G{ }^{\mathrm{\prime }\mathrm{\prime }}=K{ }^{\mathrm{\prime }\mathrm{\prime }}{\left(\omega \right)}^{n{ }^{\mathrm{\prime }\mathrm{\prime }}}$(6)

(5) $G{ }^{\mathrm{\prime }}=K{ }^{\mathrm{\prime }}(\omega {)}^{n{ }^{\mathrm{\prime }}}$(5)

(6) $G{ }^{\mathrm{\prime }\mathrm{\prime }}=K{ }^{\mathrm{\prime }\mathrm{\prime }}{\left(\omega \right)}^{n{ }^{\mathrm{\prime }\mathrm{\prime }}}$(6)

Here K^/, K^//and n^/, n^//are the regression coefficients. The value of the parameters was provided in Table 2 for different temperatures with the R² values.

Table 2. Power model parameters values for loss modulus (G^/) and storage modulus (G^//) of FJP

		G^/			G^//
Temperature (^o C)	K^/(Pa.s^n)	n^/	R^2	K^//(Pa.s^n)	n^//	R^2
20	52573.07	0.102	0.95	10376.05	0.096	0.82
40	13634.61	0.139	0.81	2964.35	0.126	0.75
60	10175.34	0.165	0.88	1384.17	0.185	0.81
80	17797.08	0.159	0.74	2982	0.163	0.90

From Table 2, it is clear that the G^/-ω and G^//- ω data fitted reasonably well (R^2.>0.75) according to the power-law for the FJP sample. From the values, it was evident that the FJP showed more solid-like property where the magnitude of K^/is greater than K^//. Although the effect of temperature on K and n were not systematic.

(Ahmed and Ramaswamy, 2006) reported that in true gels, ln (G^/), ln (G^//) vs ln (ω) have zero slopes, while for weak gels, those plots have positive slopes and G^/showed higher values than G^//with respect to ω, while the n value decreased in a trend resembling shear thinning in flow model. From the data, it is clear that the FJP showed more solid characteristics than viscous characteristics. This study showed that storage modulus(G^/) and loss modulus(G^//) play a significant role in determining the rheological characteristics of the FJP sample studied and is dependant not only on the temperature range but also on the product itself.

Effect of temperature on rheological characteristics of FJP

The effect of temperature on the apparent viscosity of FJP at a constant shear rate of 10 s⁻¹ was adequately explained by the Arrhenius equation (M. Rao and Tattiyakul, 1999), where the apparent viscosity decreases in an exponential function with temperature.

(7) ${\eta }^{\ast }={\eta }_0{e}^{\left(\frac{Ea}{RT}\right)}$(7)

Where η* is complex viscosity; η₀ is pre-exponential factor; E_a is activation energy (kJ mol⁻¹); R is the universal gas constant (JK⁻¹ mol⁻¹); T is temperature(K)

The Arrhenius model provided a good representation of the effect of temperature on the apparent viscosity. The activation energy (E_a) of the whole FJP sample was 19.34 KJ mol⁻¹ with an R² value of 80.21. These values were found to be consistent with that of previous works done on orange juice (Vitali and Rao, 1984), araca pulp (Haminiuk et al., 2006), siriguela pulp (Augusto et al., 2012), tamarind juice (Ahmed et al., 2007). According to (Steffe, 1996), higher E_a value denotes a rapid change in the viscosity in a food system with an increase in temperature. However, the activation energy of FJP was higher than the other fruits described in the literature, which indicated that the increase in temperature has fewer effects on the internal structure as compared to other fruits.

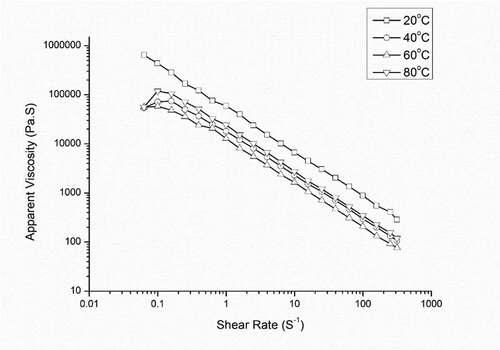
Apparent viscosity and shear rate model

The apparent viscosity of the FJP was estimated by modifying the power-law model, as shown in equation 8(8) ${log}_{10}\tau ={log}_{10}K+n{log}_{10}\gamma$(8) (Haminiuk et al., 2006).

(8) ${log}_{10}\tau ={log}_{10}K+n{log}_{10}\gamma$(8)

Dividing the equation by log₁₀ γ, the resulting equation becomes

(9) $\eta =\frac{k}{\gamma }+n$(9)

The plot of apparent viscosity as calculated from equation (9)(9) $\eta =\frac{k}{\gamma }+n$(9) with the shear rate is shown in Figure 3. The apparent viscosity and shear rate were inversely proportional, i.e. the apparent viscosity decrease with increase in shear rate. (Haminiuk et al., 2006) and (Ahmed et al., 2007) also found this characteristic while studying the rheological properties of araca pulp and tamarind juice, respectively. This decrease in viscosity can be explained by the increase in intermolecular distance due to thermal expansion because of the increase in temperature. The viscosity kept on decreasing with increase in temperature up to 40°C; However, at 60 °C, there was an increase in the apparent viscosity which could also be attributed to the possible starch gelatinization in the FJP sample. (Haminiuk et al., 2006) also reported the same behavior while studying the whole araca pulp.

Figure 3. Apparent viscosity vs shear rate graph for FJP at 20 ^o C, 40 ^o C, 60 ^o C, 80 ° C

Cox-Merz Rule

While evaluating the applicability of Cox-Merz rule, it was not possible to use it in its original form. Generally, in food products, the complex viscosity is always higher than the apparent viscosity (Augusto et al., 2012). The Cox-Merz rule has been verified experimentally for several polymer solutions and polysaccharide dispersions; however, in a complex system such as food products, it is required to modify the original equation (M Anandha Rao et al., 2005). The non-applicability of Cox-Merz rule for complex dispersion is mainly due to the strain applied to the sample (Ahmed and Ramaswamy, 2006), presence of high-density entanglement, the internal molecular bonds or complex structure (Augusto et al., 2012). Therefore, the FJP sample shows different rheological properties from those of the polymer solutions and polysaccharide dispersions and are more similar to structured systems (Ahmed and Ramaswamy, 2006).

The oscillatory and the steady-state shear rheological properties of food materials made to correlate with each other by modifying the Cox-Merz rule according to the equation given by (M Anandha Rao et al., 2005) which is

(10) $\beta .[{\eta }_a(\gamma ){]}^{\alpha }={\eta }^{\ast }\left(\omega \right){|}_{\dot{\gamma }=\omega }$(10)

Equation 8(8) ${log}_{10}\tau ={log}_{10}K+n{log}_{10}\gamma$(8) is the power modification of the original equation as is used for the analysis of various food materials. Table 3 shows the parameters of the modified Cox-Merz rule.

Table 3. Parameter values of modified Cox-Merz equation for FJP

Temperature (^o C)	β	α	R^2
20	0.220	0.955	0.98
40	0.930	0.868	0.97
60	10.683	1.120	0.97
80	14.746	1.054	0.99

From Table 3, it can be observed that the power-law parameters are significantly affected by the temperature.

In the modified Cox-Merz rule, the β is the difference between the complex viscosity and apparent viscosity, whereas α is associated with the behavior difference (Augusto et al., 2012). The parameter β increased with increase in temperature. The small value of β confirmed that the apparent viscosity and complex viscosity value were close, which can also be seen in Figure 4. Power law parameters β and α established the Cox Merz rule at 20 ° C and 40 ^o C but did not fit at higher temperatures.

Figure 4. Effect of temperature on apparent viscosity and complex viscosity of FJP at temperature (a) 20 ^o C (b) 40 ^o C (c) 60 ° C (d) 80 ° C

Conclusions

The steady and dynamic shear characteristics of the FJP with temperature as its function in the range 20–80°C a showed shear-thinning behavior. The steady-state shear properties of FJP showed both low shear rate and moderate shear rate as such, both the Bingham model and power model were used, and its parameters were modeled as a function of temperature. The activation energy was 19.34 KJ mol⁻¹ which was found to be consistent with other literatures. In dynamic shear properties, power model was selected to evaluate the loss modulus (G^/) and the storage modulus (G^//) as a function of temperature. The G^/value exceeded the G^//value at a fixed ω range. The data showed abnormalities at specific temperatures making the dependence of temperature on the magnitude of the parameters difficult to evaluate. High pectic content and soluble solids present in the solution was assumed to be one of the reasons for this behavior. The modified Cox Merz rule was found to be applicable at lower temperatures but failed at higher temperatures of the FJP sample. The results presented the rheological properties of Indian coffee plum pulp which displayed quite different rheological characteristics as compared to other fruit pulps due to its unique chemical composition.