Drying of Cataloglu Apricots: The Effect of Sodium Metabisulfite Solution on Drying Kinetics, Diffusion Coefficient, and Color Parameters

ABSTRACT

The effect of temperature and pre-treatment on drying kinetics and color parameters of apricot was investigated. The apricots were dried at 50, 60, 70, and 80°C and constant air velocity of 2.0 m/s in cabinet dryer. Sodium metabisulfite solution (8%, w/w) was applied to 10 min prior to drying process. It was observed that both the drying temperature and the pre-treatment affected the drying and color parameters. The drying times of pre-treated samples were 6.49–20% shorter than those of control samples. To select the most appropriate thin-layer drying model for drying treatments, 10 mathematical drying models were fitted to the experimental data. Midilli & Kucuk model satisfactorily described the drying kinetics of SMB and control apricots. Effective moisture diffusivity ranged from 6.85 × 10⁻¹⁰ to 2.10 × 10⁻⁹ m²/s for control, between 7.83 × 10⁻¹⁰ and 2.49 × 10⁻⁹ m²/s for SMB samples calculated using the Fick’s second law. Activation energy was estimated by using an Arrhenius type equation and found to be 34.25 kJ/mol and 35.39 kJ/mol control and SMB samples, respectively.

KEYWORDS:

• Apricot
• color
• drying
• effective moisture diffusivity
• mathematical modeling

Introduction

Apricot (Prunus armeniaca L.) is classified under the Prunus species of Prunaidea subfamily of the Rosaceae family of the Rosales group. Apricots can be used as fresh, dried, or processed fruit. According to FAO (FAO, 2017), the World’s apricot annual production in 2016 is approximately 3881204 tons and Turkey is the first with 730000 tons of apricot production. About 21.79% of the World apricot harvest areas are in Turkey. In 2016, 3881204 tons of apricots were produced in 508014 hectares in the world and 730,000 tons of apricots were produced in Turkey in 123805 hectares. Fifty percent of the fresh and 90–95% of dried apricots of Turkey is produced in Malatya region. In Malatya region, 6.2 million apricot trees yield approximately 250–400 and 50–100 thousand tons of fresh and dried apricots annually, respectively (Gokbulut and Karabulut, 2012). The most widely produced two types of apricots are Hacihaliloglu and Cataloglu in Malatya region, dry matter rate is around 30%. The world average of this value is around 15–20%. It is suitable for drying because of its high dry matter content. Therefore, 90% of the apricots in Malatya are evaluated by drying. Turkey is the leading producer and provides about 75% of the world’s dried apricots (Inserra et al., 2017).

Apricot is a climacteric fruit with a very short storage life of food preservation and is very important in terms of food security and unsuitable for the production and maintenance of product quality and nutritional value method can create a loss for choice. Drying is one of the most used process in preserving the food stability and is a complicated process with simultaneous heat and mass transfer accompanied by physicochemical transformations. Drying occurs because of vaporization of liquid by supplying heat to wet feedstock. Based on the mechanisms of heat transfer, drying is categorized into direct (convection), indirect or contact (conduction), radiant (radiation) and dielectric or microwave (radio frequency) drying (Sahni and Chaudhuri, 2012). Open air-sun drying is the most common drying method for fruits and vegetables in the world and Turkey. However, this drying technique has some disadvantages like the slowness of the process, the exposure to environmental contamination, and the hand labor requirement. Furthermore, direct exposure to solar radiation results in desired color changes. There is also quality of the dried products may be lowered significantly. Therefore, using solar and hot air dryers, which are far more rapid, providing uniformity and hygiene, are inevitable for industrial food drying processes (Doymaz, 2004; Karabulut et al., 2007).

Convective drying of food products is extensively employed as a preservation technique. During the convective drying of solids, two processes occur simultaneously, namely: transfer of energy from the surrounding environment; and transfer of moisture from within the solid (McMinn and Magee, 1999). To reduce the influence of unwanted reactions and drying to make it more effective to increase the quality of the final product is recommended for some pre-treatment process. Chemical and physical pretreatments were suggested by several authors to improve the drying rate of whole fruits with waxy skins, e.g., grapes, plums, peach, cherries, apricots, gooseberry, blueberries, and hawthorn fruit (Doymaz, 2004; Bingol et al., 2012; Kingsly et al., 2007; Vásquez-Parra et al., Mahmutoglu et al., 1996; Senadeera et al., 2014; JafariNaeimi et al., 2016).

Sulfur dioxide is used widely in the food industry for different purposes. It is used for preventing color degradation (the Maillard reaction inhibitor), as antioxidants (oxygen scavengers) and the antimicrobial during the drying process and storage. There are several compounds used in the food industry from which the water-soluble sulfite anion SO₃^2- is derived: Sulfur dioxide, sodium sulfite, and potassium and sodium salts of bisulfite and metabisulphate (Alvarez and Boye, 2012). The pretreatments and heat are applied to help to reduce the resistance to water diffusion by showing a synergistic effect. In Turkey, apricots are pre-treated with water-soluble sulfite salts (such as potassium metabisulphite (K₂S₂O₅) and sodium metabisulphite (Na₂S₂O₅)) which are commonly burned in the presence of elemental sulfur oxygen to produce sulfur dioxide gas. While maximum sulfur levels vary by country, with dry apricot, Turkey, and Germany in 2000 mg/kg given permission Italian 600 mg/kg is allowed.

Various drying methods of apricot are presented in the literature, such as sun drying (Gogus et al., 2007; Karabulut et al., 2007; Togrul and Pehlivan, 2004), convective drying (Doymaz, 2004; Garcia-Martinez et al., 2013; Ihns et al., 2011), infrared drying (Kayran and Doymaz, 2017) and combine drying (radiation and convection) (Albanese et al., 2013; Horuz et al., 2017; Izli, 2016). However, there is no information in literature about hot-air drying of Cataloglu apricot variety. The main objectives of this study were to investigate the effect of drying temperature and pretreatment affected on drying time, drying rate, and product color, fit the experimental data to 10 thin-layer drying models, and to calculate the effective moisture diffusivity and activation energy.

Materials and Methods

Sample Preparation

Cataloglu apricot (Prunus armeniaca L.) samples were obtained from a producer from Malatya region. The fruits were collected according to the characteristics of the ripe maturity, uniform size, color and texture. Before drying process, the samples are divided into two lots before use. One lot of apricots was pretreated with solution of sodium metabisulfite (8% Na₂H₂SO₅) at 20°C for 10 min (SMB code). The other lot was untreated (Control code).

The dry matter and initial moisture contents of the fresh apricots were determined according to using AOAC method 934.06 (AOAC, 1990). Triplicate samples were used for the determination of moisture content and the average values were reported as 2.98 kg water/kg dry matter (dry basis). The pH was determined by using pH meter (Inolab/Level) and acidity (% citric acid) was determined according to Cemeroglu (2007). Ash were analyzed according to TS 1128 ISO 763.

Experimental Set-up

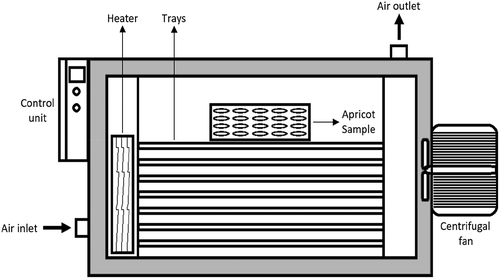
Apricot samples were dried as a single layer in a cabinet type dryer (APV & PASILAC, England), which is shown in Figure 1. It was constructed from stainless steel sheets formed as a rectangular tunnel of dimensions 0.54 × 1.4 × 1.02 m. The dryer was started 30 min before the experiments in order to reach steady-state. About 200 g of the raw product, spread as a thin layer, was loaded onto the drying tray of size 0.3 × 0.3 m. Moisture loss in the samples with initial load of 85 ± 0.2 g and was measured with a digital balance (Mettler-Toledo AG, Grefensee, Switzerland, model BB3000) with accuracy of 0.1 g and recorded at 30 min intervals. Drying was stopped when the moisture content of samples were approximately 0.29 kg water/kg dry matter (d.b.). The dried product was cooled and packed in low-density polyethylene bags that were heat-sealed. The experiments were triplicated and average values of the moisture content were used for drawing the drying curves. Drying data was analyzed using two-way analysis of variance at p < 0.5.

Figure 1. Experimental setup for the drying experimental studies

Mathematical Modeling

The data derived from drying of apricot were fitted with 10 thin-layer drying models (Table 1) typically used for the modeling of drying curves. The moisture ratio (MR) of apricots during drying experiments was calculated by using the following equation (1)(1) $MR=\frac{M_t-M_e}{M_o-M_e}$(1) :

(1) $MR=\frac{M_t-M_e}{M_o-M_e}$(1)

Table 1. Thin-layer drying models used for apricot drying

Model name	Model^1)	Reference
Lewis	$MR=aexp(-kt)$	Roberts et al. (2008)
Henderson & Pabis	$MR=aexp(-kt)+c$	Henderson and Pabis (1961)
Logarithmic	$MR=aexp(-kt)+(1-a)exp(-gt)$	Wang et al. (2017)
Verma et al.	$MR=a+bt+c{t}^2$	Ihns et al. (2011)
Parabolic	$MR=1+at+b{t}^2$	Sharma and Prasad (2004)
Wang & Singh	$MR=aexp(-k{t}^n)+bt$	Izli et al. (2014)
Page	$MR=exp\left(-{\left(\frac{t}{b}\right)}^a\right)$	Tiwari et al. (2018)
Midilli & Kucuk	$MR=exp\left(-\left(\frac{at}{1+bt}\right)\right)$	Midilli and Kucuk (2003)
Weibull	$MR=exp(-k{t}^n)$	Corzo et al. (2008)
Aghbashlo et al.	$MR=exp\left(-\left(\frac{at}{1+bt}\right)\right)$	Aghbashlo et al. (2009)

a, b, c, g, k, k₀, k₁, n: empirical constants and coefficients in drying models

Where M_t, M₀ and M_e are moisture content at any time, initial moisture content, equilibrium moisture content (kg water/kg dry matter), MR is the moisture ratio, M₀ is the initial moisture (kg water/kg dry matter), M_e is the equilibrium moisture (kg water/kg dry matter) and t is drying time (min). The equilibrium moisture content (M_e) is relatively small compared with M₀, especially for long drying time, which was assumed to be zero. So MR can be simplified to MR = M_t/M₀ (Faal et al., 2015).

The drying rate (DR) was calculated using Eq. (2)(2) $DR=\frac{M_t-M_{t+\mathrm{\Delta }t}}{\mathrm{\Delta }t}$(2) :

(2) $DR=\frac{M_t-M_{t+\mathrm{\Delta }t}}{\mathrm{\Delta }t}$(2)

Where M_t+Δt is moisture content at t+ Δt (kg water/kg dm), and t is time (min).

Data Analysis

Data were analyzed using Statistica 8.0.550 (StatSoft Inc., Tulsa, OK, USA) software package. The parameters of models were estimated using a non-linear regression procedure based on the Levenberg-Marquardt algorithm. The fitting quality of the experimental data to all models was evaluated using the coefficient of determination (R²), mean relative percent error (P), reduced chi-square (χ²), and root mean square error (RMSE). The P, χ² and RMSE were calculated from the following formulas:

(3) $P=\frac{100}{N}\sum Ni=1\frac{\left|M{R}_{\exp ,i}-M{R}_{pre,i}\right|}{M{R}_{\exp ,i}}$(3)

(4) ${\chi }^2=\frac{\sum _{i=1}^N{\left(M{R}_{exp,i}-M{R}_{pre,i}\right)}^2}{N-z}$(4)

(5) $RMSE={\left[\frac{1}{N}\sum _{i=1}^N{(M{R}_{pre,i}-M{R}_{exp,i})}^2\right]}^{1/2}$(5)

where MR_exp,i and MR_pre,i are experimental and predicted dimensionless moisture ratios, respectively, N is number of observations, and z is number of constants. The best model was chosen based on the following three criteria: The highest value of R² and the least values of P, χ², and RMSE (Fahloul et al., 2009).

Determination of Effective Moisture Diffusivity

It is generally assumed that the mechanism of moisture migration during thin-layer drying of food materials is characterized by diffusion as described by Fick’s second law of diffusion:

(6) $\frac{\mathrm{\partial }M}{\mathrm{\partial }t}=\mathrm{\nabla }\left[D_{eff}(\mathrm{\nabla }M)\right]$(6)

The analytical solution of Fick’s second law (Eq. 6)(6) $\frac{\mathrm{\partial }M}{\mathrm{\partial }t}=\mathrm{\nabla }\left[D_{eff}(\mathrm{\nabla }M)\right]$(6) unsteady state diffusion in a spherical coordinates with the assumptions of moisture migration being by diffusion, negligible shrinkage, constant effective diffusivity and temperature during the drying process is given as follows (Crank, 1975):

(7) $MR=\frac{6}{{\pi }^2}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}exp\left(-n^2{\pi }^2\frac{D_{eff}t}{r^2}\right)$(7)

For long drying periods, Eq. (7)(7) $MR=\frac{6}{{\pi }^2}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}exp\left(-n^2{\pi }^2\frac{D_{eff}t}{r^2}\right)$(7) can be further simplified to only the first term of the series. Thus, Eq. (7)(7) $MR=\frac{6}{{\pi }^2}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}exp\left(-n^2{\pi }^2\frac{D_{eff}t}{r^2}\right)$(7) is written in a logarithmic form as follows:

(8) $ln(MR)=ln\left(\frac{6}{{\pi }^2}\right)-\left(\frac{{\pi }^2{D}_{eff}t}{r^2}\right)$(8)

The effective moisture diffusivity is obtained by plotting the experimental drying data in terms of ln (MR) versus time (min). From Eq. (8(8) $ln(MR)=ln\left(\frac{6}{{\pi }^2}\right)-\left(\frac{{\pi }^2{D}_{eff}t}{r^2}\right)$(8) ), a plot of ln MR versus time gives a straight line with a slope of (K), in which:

(9) $K=\frac{{\pi }^2{D}_{eff}}{r^2}$(9)

Computation of Activation Energy

The relationship between the effective moisture diffusivity and drying temperature was described using the Arrhenius-type equation:

(10) ${\mathrm{D}}_{\mathrm{e}\mathrm{f}\mathrm{f}}=5.155\times {10}^{-4}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{4291.7}{T+273.15}\right)(R^2=0.9354)$(10)

Here D₀ is the pre-exponential factor (m²/s), E_a is the activation energy (kJ/mol), R is the universal gas constant (8.314 kJ/(mol×K)), and T is drying air temperature (°C).

Color

The color attributes of fresh and dried apricot samples in terms of L, a, and b values were measured using a CR-400 colorimeter (Konica Minolta Co, Osaka, Japan), which was calibrated with a white standard board. Total color change (ΔE) and chrome (C) were calculated by using Eqs. (11)(11) ${\mathrm{D}}_{\mathrm{e}\mathrm{f}\mathrm{f}}=3.401\times {10}^{-4}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{4214.6}{T+273.15}\right)(R^2=0.9707)$(11) and (12(12) $MR=\frac{M_t-M_e}{M_o-M_e}$(12) ), respectively.

(11) ${\mathrm{D}}_{\mathrm{e}\mathrm{f}\mathrm{f}}=3.401\times {10}^{-4}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{4214.6}{T+273.15}\right)(R^2=0.9707)$(11)

(12) $MR=\frac{M_t-M_e}{M_o-M_e}$(12)

The samples were placed in a standard light. L, a, and b values separately represent brightness to darkness, redness (+) to greenness (−), and yellowness (+) to blueness (−). Four replications were performed.

Results and Discussion

Physicochemical Characterization

The average initial moisture of fresh samples was determined as 2.98 kg water/kg dry matter (d.b.). The values of pH and titratable acidity were found to be 4.20 and 0.34, respectively. Similar results have been obtained by Haciseferogullari et al. (2007). They found that the pH and acidity contents of various apricot varieties in the Malatya region were established between 4.16–5.23 and 0.17–0.79 (% malic acid), respectively. Akin et al. (2008) reported that the ash content, titratable acidity (citric acid) and pH of Cataloglu variety were 0.74%, 0.1% and 5.51, respectively.

Drying Curves

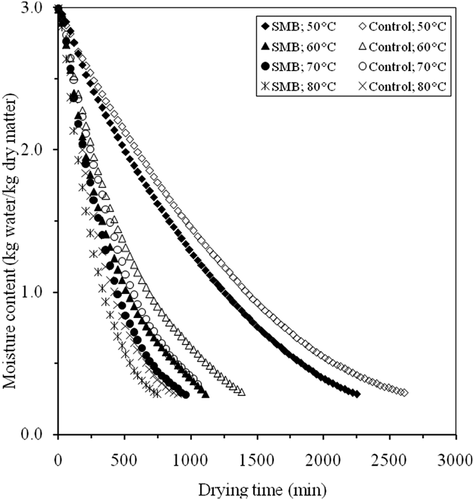
The effect of temperature on drying curves of the apricot during drying is shown in Figure 2. The drying curves are typical to ones for similar fruits. The moisture content decreased exponentially with elapsed duration of drying and decreased faster at higher temperature levels in all cases, as expected. The results showed that drying time decreased greatly when the temperature increased. The pretreated samples with SMB solution were dried faster than the control samples, confirming that the pretreatment-reduced resistance to moisture movement and thus increased drying rate. The drying time required reaching the final moisture content of control samples were 2610, 1380, 1050, and 840 min and SMB samples 2220, 1110, 930, and 720 min at the drying temperature of 50, 60, 70, and 80°C, respectively. The average drying rate of control and pretreated samples increased 3.10 and 3.08 times, respectively, as temperature increased from 50 to 80°C. This is due to the increasing energy of the water molecules at increased temperature, which can escape easier and faster. The decrease in drying time with an increase in the air temperature has been reported by some authors. Also, the pretreated samples with SMB solution showed a shortening of drying time between 11.43% and 19.56% compared to control samples according to drying temperatures. These results are in agreement with the earlier observations (Karabulut et al., 2007; Togrul and Pehlivan, 2004).

Figure 2. Drying curves of apricot at different temperature

Drying Rate

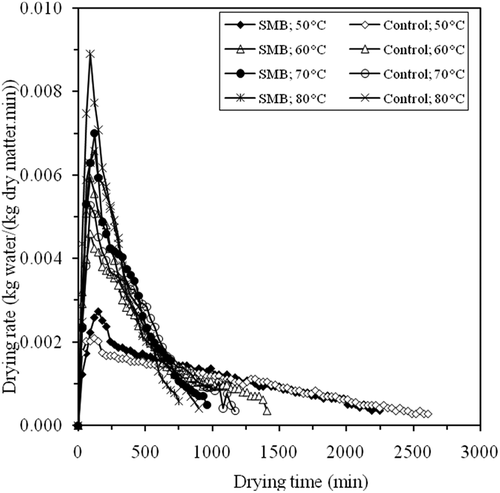
Figure 3 exhibits the variation of drying rate as a function of time. A constant drying rate period was not observed in all cases. The drying of apricot occurs in the falling drying rate period, and a continuous decrease of the drying rate decreasing moisture content can be seen. This indicated that diffusion was the dominant mechanism for removing of water from apricot halves. Similar results were also observed by some authors (Faal et al., 2015; Horuz et al., 2017; Stegou-Sagia and Fragkou, 2018). In Figure 3, the increase of drying rate is observed with the increase of air temperature. This means, at high temperatures the heat and mass transfer is higher and the water loss is more excessive. The drying rate was higher in the initial operation and then decreased during the drying process to reduce the moisture content in the samples. The results were consistent with observations made by different authors on apricot drying (Horuz et al., 2017; Mirzaee et al., 2009).

Figure 3. Drying rate vs. time for apricots pretreated and without treatment

Evaluation of the Models

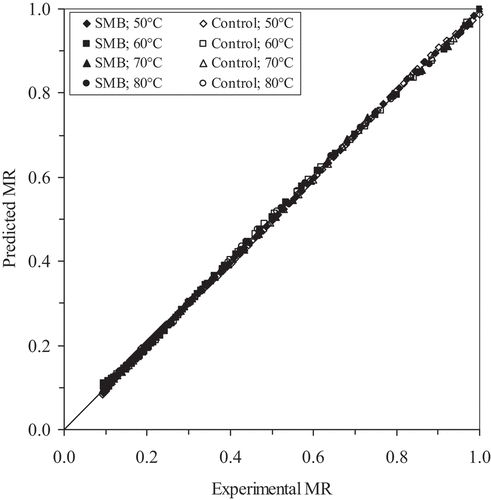
The moisture content data obtained at different temperatures were converted into the MR and fitted to ten thin-layer drying models listed in Table 1. Performance of the models were evaluated in terms of R², P, χ² and RMSE, which represent the coefficient of determination, mean relative percent error, reduced chi-square and the root mean square error of non-linear regression analysis, respectively. The higher the R², lower the P, χ² and RMSE, the better is the goodness of fit. Tables 2 and 3 show that among the selected models, the Midilli & Kucuk model gave the highest R² with an average value of 0.9996 and the lowest P, χ², and RMSE with average values of 1.3075, 0.000026, and 0.026025, respectively, considering all the treatments. Therefore, the Midilli & Kucuk model was selected as a suitable drying model to represent the drying behavior of apricot in hot-air dryer within the experimental range. In Figure 4 the predicted MR versus experimental MR is given for the Midilli & Kucuk model. Since the data plotted is very near the straight line, it can be said that experimental data and predicated data are in good agreement.

Table 2. Statistical results obtained from the selected drying models for SMB samples

T (^oC)	Model	R^2	P	x^2	RMSE
50	Lewis	0.9911	9.7146	0.000635	0.195522
	Henderson & Pabis	0.9943	7.6206	0.000406	0.151029
	Logarithmic	0.9998	1.0468	0.000013	0.024500
	Verma et al.	0.9997	0.9735	0.000016	0.022580
	Page	0.9984	3.5909	0.000110	0.078563
	Midilli & Kucuk	0.9998	1.1056	0.000014	0.026446
	Parabolic	0.9994	1.4132	0.000038	0.041488
	Wang & Singh	0.9993	1.8464	0.000047	0.049881
	Weibull	0.9984	3.5909	0.000110	0.078563
	Aghbashlo et al.	0.9997	0.8757	0.000017	0.027636
60	Lewis	0.9983	2.1044	0.000116	0.046760
	Henderson & Pabis	0.9990	2.4235	0.000069	0.044024
	Logarithmic	0.9992	1.8663	0.000055	0.032928
	Verma et al.	0.9992	2.5240	0.000055	0.039739
	Page	0.9985	2.6615	0.000104	0.050437
	Midilli & Kucuk	0.9994	2.2038	0.000048	0.033490
	Parabolic	0.9948	6.7371	0.000386	0.101760
	Wang & Singh	0.9944	7.3435	0.000408	0.104586
	Weibull	0.9985	2.6615	0.000104	0.050437
	Aghbashlo et al.	0.9983	2.2697	0.000118	0.048553
70	Lewis	0.9924	6.7761	0.000610	0.117345
	Henderson & Pabis	0.9973	3.1783	0.000220	0.061133
	Logarithmic	0.9980	3.6340	0.000172	0.055551
	Verma et al.	0.9995	1.8534	0.000035	0.027628
	Page	0.9988	3.2888	0.000098	0.040818
	Midilli & Kucuk	0.9997	0.6863	0.000029	0.019731
	Parabolic	0.9986	3.7145	0.000119	0.051358
	Wang & Singh	0.9982	3.1944	0.000148	0.048517
	Weibull	0.9988	3.2888	0.000098	0.040818
	Aghbashlo et al.	0.9968	4.8268	0.000265	0.069919
80	Lewis	0.9951	4.1504	0.000398	0.071818
	Henderson & Pabis	0.9981	2.3315	0.000157	0.040566
	Logarithmic	0.9982	2.7305	0.000157	0.041799
	Verma et al.	0.9997	1.6680	0.000018	0.013852
	Page	0.9984	3.5104	0.000131	0.041846
	Midilli & Kucuk	0.9996	1.1535	0.000032	0.020224
	Parabolic	0.9973	5.2638	0.000234	0.064594
	Wang & Singh	0.9973	5.0165	0.000228	0.062792
	Weibull	0.9984	3.5105	0.000132	0.041846
	Aghbashlo et al.	0.9969	4.1221	0.000261	0.057026

Table 3. Statistical results obtained from the selected drying models for control samples

T (^oC)	Model	R^2	P	x^2	RMSE
50	Lewis	0.9901	10.2404	0.000708	0.227239
	Henderson & Pabis	0.9935	7.9953	0.000472	0.183742
	Logarithmic	0.9993	2.5550	0.000046	0.054788
	Verma et al.	0.9994	2.4176	0.000040	0.048702
	Page	0.9988	2.7478	0.000087	0.074530
	Midilli & Kucuk	0.9997	1.5905	0.000023	0.038139
	Parabolic	0.9999	0.3214	0.000003	0.012011
	Wang & Singh	0.9998	0.5889	0.000009	0.021323
	Weibull	0.9988	2.7478	0.000087	0.074530
	Aghbashlo et al.	0.9998	1.2837	0.000011	0.026567
60	Lewis	0.9992	1.8648	0.000054	0.036195
	Henderson & Pabis	0.9996	1.6514	0.000027	0.030034
	Logarithmic	0.9996	1.6520	0.000028	0.030030
	Verma et al.	0.9993	1.5856	0.000048	0.036272
	Page	0.9994	1.6715	0.000039	0.034986
	Midilli & Kucuk	0.9996	1.6001	0.000028	0.029947
	Parabolic	0.9955	5.9364	0.000321	0.105574
	Wang & Singh	0.9944	7.0136	0.000380	0.115797
	Weibull	0.9994	1.6715	0.000039	0.034986
	Aghbashlo et al.	0.9993	1.6245	0.000047	0.036499
70	Lewis	0.9931	6.7151	0.000535	0.127040
	Henderson & Pabis	0.9975	3.3907	0.000199	0.068221
	Logarithmic	0.9984	2.9757	0.000127	0.054959
	Verma et al.	0.9997	1.1920	0.000024	0.023788
	Page	0.9993	2.4109	0.000050	0.034661
	Midilli & Kucuk	0.9998	0.9005	0.000015	0.019622
	Parabolic	0.9990	3.2506	0.000078	0.045779
	Wang & Singh	0.9988	2.9412	0.000095	0.047325
	Weibull	0.9993	2.4109	0.000050	0.034661
	Aghbashlo et al.	0.9977	3.9403	0.000178	0.068381
80	Lewis	0.9915	6.5631	0.000695	0.111643
	Henderson & Pabis	0.9971	2.8777	0.000246	0.055814
	Logarithmic	0.9976	3.2086	0.000208	0.05427
	Verma et al.	0.9998	1.1434	0.000100	0.011923
	Page	0.9984	3.7515	0.000130	0.049703
	Midilli & Kucuk	0.9997	1.2204	0.000025	0.020604
	Parabolic	0.9980	4.3337	0.000173	0.060231
	Wang & Singh	0.9974	3.7000	0.000220	0.061349
	Weibull	0.9984	3.7515	0.000130	0.049703
	Aghbashlo et al.	0.9960	4.9583	0.000342	0.077758

Figure 4. Experimental and predicted moisture ratio from the Midilli & Kucuk model distributions of apricots at different temperature

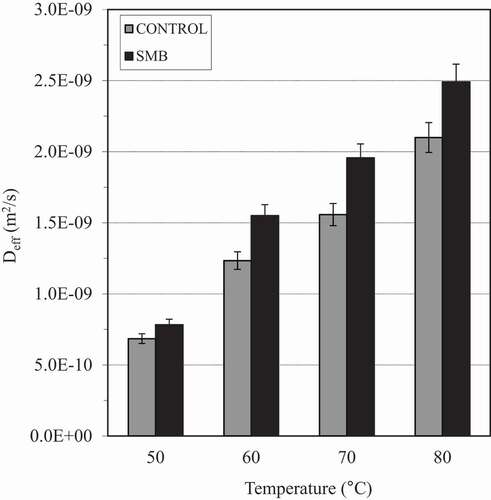
Effective Moisture Diffusivity

The effective moisture diffusivity (D_eff) values of apricot samples calculated from Eq. (9(9) $K=\frac{{\pi }^2{D}_{eff}}{r^2}$(9) ), are given in Figure 5 and ranged from 6.85 × 10⁻¹⁰ to 2.49 × 10⁻⁹ m²/s. It can be seen that D_eff values increased greatly with increasing air temperature. A similar result of the influence of drying temperature on moisture diffusivity during air drying has been found in apricot, peach, and plum (Doymaz, 2004; Goyal et al., 2007; Kingsly et al., 2007). The experimental results demonstrate the importance of the pretreatment in reducing the mass transfer resistance of the apricot skin. A similar effect of pretreatment has been found in the other drying studies for apricot (Doymaz, 2004; Mahmutoglu et al., 1996). Drying at 80°C has the highest value of effective moisture diffusivity and the lowest value was obtained for 50°C. Several investigations, carried out on apricots under similar temperature and velocity conditions showed D_eff values to lie between 4.86 and 8.32 × 10⁻⁹ m²/s for apricots (Togrul and Pehlivan, 2003), 2.49–5.74 × 10⁻⁹ m²/s (Ubeyitogullari and Cekmecelioglu, 2016); 1.70–1.15 × 10⁻⁹ m²/s (Mirzaee et al., 2009), and 0.83–1.38 × 10⁻⁹ m²/s (Xiao et al., 2010). Generally, the values of effective moisture diffusivity fall within the range of 10⁻¹² to 10⁻⁸ for all agricultural and food products (Zogzas et al., 1996).

Figure 5. Effective moisture diffusivity versus temperature

Activation Energy

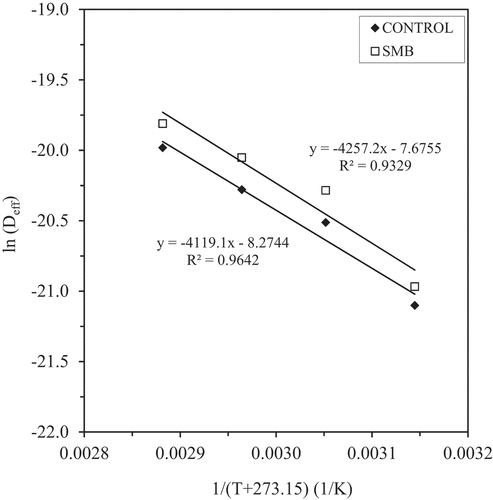
The activation energy can be determined from the slope of Arrhenius plot, ln (D_eff) versus 1/(T + 273.15) (Eq. 10)(10) ${\mathrm{D}}_{\mathrm{e}\mathrm{f}\mathrm{f}}=5.155\times {10}^{-4}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{4291.7}{T+273.15}\right)(R^2=0.9354)$(10) . The ln (D_eff) as a function of air temperature is plotted in Figure 6. The slope of the line is (-E_a/R) and the intercept equals to ln (D₀). The results show a linear relationship due to Arrhenius type dependence. Eqs. (13(13) $DR=\frac{M_t-M_{t+\mathrm{\Delta }t}}{\mathrm{\Delta }t}$(13) and 14(14) $MR=exp(-kt)$(14) ) shows the effect of temperature on D_eff of samples with the following coefficients:

Figure 6. Arrhenius-type relationship between effective moisture diffusivity and temperature

For SMB samples:

(13) $DR=\frac{M_t-M_{t+\mathrm{\Delta }t}}{\mathrm{\Delta }t}$(13)

For control samples:

(14) $MR=exp(-kt)$(14)

It was estimated that the values of activation energy (E_a) were 34.24 and 35.39 kJ/mol, with an Arrhenius factor (D₀) of 2.549 × 10⁻⁴ m²/s and 4.640 × 10⁻⁴ m²/s control and SMB samples, respectively. Similar studies are available in the literature. The activation energy was determined as 29.35–33.78 kJ/mol for temperatures of 40–80°C and air velocity of 1–2 m/s for apricot drying in the study of Mirzaee et al. (2009). Bon et al. (2007) reported activation energies ranged at 32.8–46.3 kJ/mol for the temperature range of 50–90°C during apricot drying. Ubeyitogullari and Cekmecioglu (2016) found that activation energy is 40.52 kJ/mol for the temperature range of 60–80°C.

Color Evaluation

Color is an important parameter related to the quality of the product and criteria to consumers of dried fruits. The average values for the color parameters of fresh apricots were as follows: L = 61.75, a = 9.08, and b = 34.47. The color parameters of fresh and dried samples are presented in Table 4. The color values of all dried samples are less than the fresh samples. As the drying temperature increased from 50°C to 70°C, the L, a, and b values of the dried samples were increased. In contrast, a decrease in the L, a and b values of the dried samples at 80°C was recorded.

Table 4. The color values of the fresh and dried samples at different temperatures

Code	T (°C)	L	a	b	ΔE	C
Fresh	-	61.75±3.01	9.08±0.424	34.47±1.68	-	35.65±1.67
Control	50	36.31±1.65	8.13±0.39	1.67±0.07	41.52±1.95	8.30±0.38
	60	37.03±1.69	9.23±0.44	3.14±0.11	39.91±1.89	9.75±0.44
	70	38.03±1.77	9.56±0.46	3.36±0.14	39.12±1.85	10.13±0.47
	80	37.29±1.71	9.27±0.45	3.19±0.12	39.71±1.81	9.80±0.45
SMB	50	41.29±1.99	11.59±0.54	9.39±0.43	32.46±1.47	14.92±0.70
	60	45.23±2.11	11.78±0.56	15.88±1.02	25.02±1.19	19.77±0.94
	70	46.65±2.22	11.91±0.58	16.40±1.13	23.72±1.17	20.27±0.97
	80	43.66±2.05	11.87±0.57	14.38±0.95	27.18±1.32	18.65±0.88

It can be seen that the entire-dried apricots had lower values of L than the fresh samples. The L values which show brightness of product were ranged between 41.29 and 46.65 for SMB samples, and 36.31 and 38.03 for control samples. The lowest L values were obtained at 50°C dried SMB and control apricots. As can be clearly seen from Table 4, a values increased as the drying temperature increased. On the other hand, the creation of brown pigments in the effect of non-enzymatic processes (Maillard reaction) during drying process might play an important role in the production of red color (Vega-Galvez et al., 2009). The values of b were increased with increasing of drying temperature, indicating dried samples with pre-treated SMB solution at high temperature were yellower.

The chroma is measure of chromaticity (C), which denotes the purity or saturation of the color. The chroma (C) values showed an increase during drying process. Chroma (C) values varied from 14.92 to 20.27 and 8.30 to 10.13 for SMB and control samples, respectively. Total color change (ΔE) gives the result of the change in color values. When the drying temperature increases from 50 to 80°C, ΔE was decreased from 32.46 to 27.18, and 41.52 to 39.71 for SMB and control samples, respectively.

Conclusions

In this study, the drying characteristics of apricot were investigated in cabinet dryer at different temperatures. Constant rate period was not observed and drying carried on in falling rate period. The drying and color characteristics were significantly influenced by temperature and pretreatment. The drying time decreased with the increase of temperature. To explain the drying behavior of apricot, 10 thin-layer drying models were applied. The Midilli & Kucuk model gave the best results and showed good agreement with experimental data obtained from the experiments for SMB and control samples. The effective moisture diffusivity was computed from Fick’s second law, the values of which varied between 6.85 × 10⁻¹⁰ m²/s and 2.15 × 10⁻⁹ m²/s for control and 7.82 × 10⁻¹⁰ m²/s and 2.51 × 10⁻⁹ m²/s for SMB samples. With the increase of temperature, the effective moisture diffusivity increased. Activation energy was estimated by an Arrhenius type equation and found to 35.04 kJ/mol and 35.68 kJ/mol for control and SMB samples, respectively.

Disclosure statement

The authors declare that they have no conflict of interest.