Evaluating School Priorities for Equal Opportunity in Admission to Schools

ABSTRACT

Schools’ priorities in student selection constitute the basis for fairness in school admissions. We study the case where schools are active strategic players that rank their applicants in terms of priorities. A methodological framework is developed to examine the impact of the variation in the admission settings on the equality of opportunity in access to high-quality schools. The school’s priorities are formulated following a Multi-Attribute Decision Analysis (MADA) approach with several scenarios including geographic, family, academic, and socioeconomic variables. The matching is simulated using student preferences, multiple assignment algorithms, varying school capacities, and changing priority profiles. The Human Opportunity Index (HOI) logistic regression approach is used to examine how far from, or how close the admission is to being an equitable assignment, i.e., one that gives equal opportunities to children with different backgrounds. The analysis is based on choice admission data from a large specialized (magnet) middle school program in Florida. The results suggest that how the school priority is designed slightly affects the equality of opportunity. The second impact is due to the algorithm used to perform the selection. The availability of places in high-quality schools has a big impact and is tightly correlated with the parents’ satisfaction with their most preferred school choices.

KEYWORDS:

• School choice
• school admission
• school priorities
• school preferences
• inequality of opportunity (IOP)
• human opportunity index (HOI)
• policy simulation
• magnet schools
• Florida

Introduction

In recent decades, several countries worldwide have introduced policies to make it easier for parents to choose the school of their preference. In OECD countries, opportunities for school choice in public education have expanded at both primary and secondary levels (OECD, Education at a Glance, 2018). School choice refers to educational policies that intend to give families more choices so they can find schools that best fit their children’s needs and desires. For instance, in the Netherlands, most schools are open to everybody, and all citizens have the constitutional right to choose a school of any denomination (Gramberg, 1998). In school choice, students express preferences over what schools they would like to attend, ranking them by personal preferences, and schools define a priority ordering over the set of students that apply for admission. A set of rules determines the final allocation.

School choice provides educational opportunities in such a way that all students could have access to all schools. One important goal of school choice is to provide all students (particularly those in poorer neighborhoods) with a fair chance of attending a good school (Kloosterman & Troyan, 2017). Since basic education is a public social good, it entails universal accessibility (Merry & Arum, 2018). Nevertheless, school choice can be restricted in different ways. Depending on the form of school choice that parents select and the administrative designs of programs that schools offer, public school choice may exacerbate or ameliorate inequality (Riel, Parcel, Mickelson, & Smith, 2018). A rich body of research has emphasized equity concerns revealing that disadvantaged families may be less able to exercise choice, leading to greater social, cultural, and ethnic segregation in the school system (Hastings, Kane, & Staiger, 2009; Musset, 2012).

Equality of opportunity is based on the idea of giving people equal opportunity early in life, whatever their socioeconomic background, so that everybody has the same chance to be successful (Roemer, 1998). This paper uses the Human Opportunity Index (HOI) methodology to analyze Inequality of Opportunity (IOP) in accessing good quality education for young students. We measure how far or close the admission stands from being an equitable assignment, i.e., one that gives equal opportunities for children with different backgrounds. When this principle is applied to school admission, it is expected that the opportunity to get admission to good quality education is not influenced by children’s circumstances such as gender, parental education, race, nationality, or religion.

An assignment is equitable when all available school places are fairly distributed among all applicants, i.e., none of the socioeconomic groups defined by the circumstances are disproportionally represented. The coverage rate indicates what fraction of the population has access to the opportunity. HOI is a combined measure that reflects the overall level of coverage of the service and the disparities in the distribution among the circumstance groups by detecting the vulnerable groups, those whose coverage rates are below the overall coverage rate of the service.

The assignment problems arising in school choice are typically many-to-one: a school can admit many applicants, but each applicant wishes to be assigned to one school (Pathak & Sethuraman, 2010a). Although some school choice settings are one-sided matching problems in which only students’ preferences are considered, we study the case where schools are also active strategic players that rank their applicants in terms of priorities. This kind of assignment has been studied as a two-sided matching problem (Abdulkadiroğlu, Pathak, & Roth, 2005).

Schools’ priorities over students constitute the basis for fairness considerations (Kesten & Ünver, 2015). A school’s priority ordering is a ranking of students based on observed characteristics of the students, or other criteria, such as geographic proximity to the school, having a sibling already at the school, or performance on standardized test scores.

School admission procedures are central to determining access to high-quality schools. In the US, seats at good or popular public schools are often scarce and in great demand. High-quality schools are frequently located in more affluent areas. Thus, low-income families might be excluded. Most low-income students and students of color in the US who live in poor and segregated neighborhoods “do not have access to high-quality schools simply because of where they live” (USCCR, 2010). Given residential segregation and the geographically-based criteria used for assignments, admissions are likely inequitable.

The literature has shown that selective admissions can make a source of greater inequality and stratification in a school system (OECD, 2015). Selection decisions involve choosing from among a pool of applicants, several of whom more or less satisfy the school priority criteria. According to OECD (Education at a Glance, 2018), selective admission criteria are used by 12 out of 30 OECD countries at the primary level, and 17 out of 30 OECD countries at the lower secondary level. In the United States, academic diversity, class size, and income diversity are standard admission criteria (OECD, Education at a Glance, 2018). Geographical allocation, e.g., the proximity of the family home to the school, catchment areas, or neighborhood assignments, are the main criteria used to assign children to schools. Selection based on ability is determinant in 10 out of 30 OECD countries.

There are equity concerns about administration arrangements, the procedures, and the management of the admission process. Evidence from New York high schools points out that “when schools face strong accountability pressure, schools might respond strategically to weakly regulated choice systems” (Jennings, 2010); they compete in an educational marketplace seeking higher-achieving students who will enhance their test scores, even though the schools are forbidden from screening applicants on academic characteristics.

Similarly, evidence from the UK indicates that, when the schools are responsible for their admissions, they use a variety of oversubscription criteria that could be socially selective; “they act on their self-interest by ‘selecting in’ or ‘creaming’ particular pupils and ‘selecting out’ others,” for instance, based on ability, or aptitude in a subject area, or by using interviews (Basteck, Klaus, & Kübler, 2018; Coldron, Willis, & Wolstenholme, 2009; Noden, Anne & Audrey, et al., 2014; West, 2006; West, Hind, & Pennell, 2004).

A systematic procedure that selects a matching for each school choice problem is known as a “student assignment mechanism.” Recent surveys of the choice literature show that the design of the student assignment mechanisms, particularly the study of the properties of the allocation algorithms, has gathered significant attention (Abdulkadiroğlu, 2013; Kojima & Troyan, 2011; Pathak, 2017; Sönmez & Ünver, 2009). In contrast, there is a lack of a rigorous understanding of the role that school priorities over students play in the assignment (Abdulkadiroglu et al., 2017). The question of how to design the school priorities used by the allocation mechanism is a crucial design question that has been mostly overlooked. However, it has turned out to be as important (if not more so) as the assignment algorithms and remains an open issue (Kloosterman & Troyan, 2017; Pathak, 2017).

In this paper, to contribute to filling this gap, we study a school choice model in which admission can be redesigned by performing simulations. Our analysis aims to examine the impact of the variation in the admissions settings on the equality of opportunity in access to high-quality schools. To achieve the objective, this paper addresses the following research questions:

1. What is the level of equality of opportunity in access to high-quality schools under different school priorities?

2. What is the level of equality of opportunity in access to high-quality schools under different assignment algorithms?

3. What is the level of equality of opportunity in access to high-quality schools under different capacity constraints?

4. How well does each admission setting satisfy the parents’ preferences for ranked schools?

The remainder of the paper is as follows. The following section summarizes some relevant literature. Section three describes the case study’s context. Section four covers the materials and methods, including the data available, descriptive statistics, and the empirical strategy to perform the analysis. Section five presents the results and section six the conclusions.

Related literature

Two different strands of literature are reviewed: first, policy simulations that change the admission settings aiming at social integration; second, alternative ways to assign school priorities, and the implications of the fairness of the assignment.

The first set of studies analyzes how policy interventions influence school choice opportunities by targeting integration and desegregation efforts. Böhlmark, Holmlund, and Lindahl (2016) conducted an exploratory study to understand the increased school segregation in Sweden by exploiting a policy change that introduced generalized school choice. After analyzing parental choice, neighborhood segregation, and cream-skimming, they find evidence that neighborhood segregation is the primary determinant of school segregation. (Koedel, Betts, Rice, & Zau, 2009) use choice application data from San Diego, US, to examine the integrating and segregating effects on students, by test scores, parental education levels, and language status using exposure indexes. They find that both the magnet and the voluntary ethnic enrollment program have strong integration effects in the district, while the open-enrollment program increases segregation in the district along most dimensions. Using school data from the secondary schools in Amsterdam, (Oosterbeek, Sóvágó, & Klaauw, 2019) examine how specific interventions influence school segregation. Their experiments simulate the effect of four alternative policies: affirmative action, stricter ability tracking, variations of the assignment mechanisms, and relocation of schools. They find that school segregation by ethnic/social groups is mainly due to ability tracking and preference heterogeneity. They conclude that segregation can be reduced when using affirmative action policies in the form of minority quotas. (Glazerman & Dotter, 2017) use data from Washington DC, ranked order models, and an algorithm that gives advantage to an applicant when schools are oversubscribed. Their simulations suggest that it is possible to reduce segregation and increase enrollment in high-performing schools by relaxing capacity constraints.

The second strand of studies focuses on how school priorities are used to achieve fairness in admission. (Kessel & Olmez, 2018) experimented with Swedish choice data and mixed logit models to estimate household preferences. They evaluate three alternative ways to assign priority to oversubscribed primary schools – proximity, lottery, and affirmative action. Using the Duncan index, school segregation is measured by foreign background and parental education. They find that segregation effects across schools can be decreased when proximity-based priorities are abandoned. (Merry & Arum, 2018) study how the selection of students can be best structured to achieve more equitable outcomes. They propose an equity framework for assessing the fairness of school selection based on three criteria: the intended aims of the selection, the appropriateness of the organizational process, and accountability measures regarding outcomes. They test the framework in one of New York’s specialized schools. They conclude that the selection based on a standardized entrance exam is problematic since it relies on one single indicator; considering multiple indicators such as talent, motivation, effort, and multiple forms of assessment might help achieve more equitable ends. Using data from Boston public schools, (Dur, Kominers, Pathak, & Sönmez, 2018) study admission policies in which applicants can be admitted via multiple routes, dealing with reserved slots for specific groups (e.g., racial minorities or neighborhood applicants). Their work also deals with changes in the magnitude of the open and reserved seats. They note that the admission policy must account for the order of precedence in which reserve and open seats are processed; the effect is comparable to adjusting reserve sizes. (Cantillon, 2009, 2017) follows the market design approach to design school priorities for Brussels public schools. Four political objectives are analyzed: respect for parents’ preferences, equity among children, promotion of social diversity, and incentives for parents’ investment in children’s education. An example involving two incompatible objectives (equity and parents’ investment) is analyzed to evaluate precedence, and a procedure to implement the priority based on deferred acceptance is proposed.

We expect differences in the design of our simulations, compared with previous work, to bring further insights into the impact and relevance of priorities in market design for school choice. In the future, these insights might help guide the design, development, and implementation of an effective public admission policy aimed at equalizing opportunity for access to high-quality education.

Context

This section describes the context of our study, a centralized middle school magnet program in Florida. First, it explains the segregation context in Florida and the school district. Next, it describes the choice options available in Florida.

The roots of segregation in Florida

The empirical setting takes place in the School District of Hillsborough County (SDHC), the eighth largest school district in the US, which serves the city of Tampa, Florida, and its metropolitan area.

The history of school choice in SDHC is usually linked to discrimination and segregation, dating back to 1958. Dual systems of Education (one for White students and another for Blacks) were common in Florida (FL) and other southern states in the US prior to 1954. During the past 50 years, Brown vs. Board of Education (Supreme Court Of The United States, 2004) and other nationwide school desegregation lawsuits have shaped debates and strategies aimed at equalizing educational opportunities. Since then, following the US Supreme Court decisions, several county-wide comprehensive school desegregation plans have been developed, SDHC pioneering most efforts in FL (Kimmel, 1992). The plans during the 1960s and 1970s consisted of using race as a factor in student assignment, closing historically all-Black schools, desegregating teachers and principals, extensive busing of Black children to achieve racial balance, and creating magnet schools to diversify school populations (Days, 1992; Kimmel, 1992; Orfield & Eaton, 1996; Shircliffe, 2002).

In the 1990s and 2000s, several districts in Florida, including SDHC, earned the “unitary status” from the courts, moving from mandatory to voluntary desegregation plans, and race-based policies for student assignment were no longer a legal option (Borman et al., 2004). Florida’s schools became increasingly more segregated during these decades despite desegregation efforts, particularly in the largest urban districts (Eitle & Eitle, 2003; Stretesky & Lynch, 2002). In the 2010s and 2020s, the focus shifted from concerns about racial segregation to an emphasis on equalizing the funding of education (implementing Florida’s Accountability Act) to reduce inequalities both in opportunities and achievement for all students (Borman et al., 2004).

SDHC’s long experience with public school choice, the pressures imposed by facing a large influx of immigration, and the historical efforts to introduce measures designed to promote racial and socioeconomic integration (Borman et al., 2004; Shircliffe, 2002), make the district a particularly interesting site for performing policy simulations that aim at equalizing opportunity in access to high-quality education.

School choice in Florida

In the US, public schools are free of charge, and parents send their kids to the school assigned in the attendance zone, according to the place they reside in. Every student in the county at any level (grades PK to 12) is guaranteed a spot in an assigned public neighborhood school close to the place of residency. The most common form of school choice may be in choosing where to live based on the neighborhood public schools available. Additionally, some school districts offer school choice plans that promise to enlarge access to schools beyond residential boundaries.

In Florida, school choice consists of an array of options, including private schools (religious or nonsectarian), other public schools (open choice, magnet schools, charter schools, career academies, virtual schools), scholarship programs, and home schools, among others, with particularities adjusted to each location (FDOE, 2002). Open choice, magnet, and charter schools are the most popular forms of public school choice available in SDHC. Students may attend any public school outside their attendance zone district in an Open choice plan policy. Charter schools are popular and among the fastest-growing school options in the US; they are independent public schools of choice that exercise increased autonomy in return for stronger accountability (academic and fiscal). Magnet schools started as a way to promote desegregation, foster racially and socio-economically diverse student enrollments, and reduce minority group isolation in public schools (Smrekar & Honey, 2015). We exclude open choice and charter schools from the study and focus only on Magnet schools. Magnet schools enroll students from a wide array of neighborhoods across a school district and are often located in minority or low-income neighborhoods. Each magnet school has a specialization, or a curricular theme, such as math/sciences, humanities, and fine arts, designed to appeal to families across racial and social class boundaries.

Participation in school choice options is entirely voluntary. Families who wish to participate in one of the district choice options need to submit an application to gain access to public magnet schools and open enrollment programs outside of their neighborhood school but within the same school district. The admission mechanism at SDHC is centralized and includes all magnet middle schools (6^th, 7^th, 8^th) in the school district for children aged 11–13 years old.

Parental choice is constrained by capacity in the high-demand schools. Like most urban school districts in the US, SDHC operates magnet programs that are popular and therefore oversubscribed. In case of oversubscription, computerized lotteries are used to allocate the available spots. The district school board determines the priority criteria at SDHC, and these criteria are applied homogeneously to all the schools in the district. At SDHC, most magnet programs offer free transportation to all students. The choice admission mechanism consists of the main round and additional rounds that assign applicants who are unassigned after the previous round. Our study uses data from the first round, as it contains the first attempt made by families to get access to the desired schools.

Materials and methods

This section describes the data and methodology used for the analysis of the case study and then explains how we use the parental preferences and school ranking for students in order to perform the matching and subsequent simulations.

Data sources

Our analysis is based on admission data for magnet middle schools for the 2015–2016 academic year, provided by SDHC. The geocoded applications are the student choices for schools containing secure and anonymized records, including location and demographic details. School-level data from SDHC describe the school program’s characteristics and geographic boundaries of school service areas. This dataset was enriched with statistics obtained from the US Department of Education’s National Center for Education Statistics (NCES) from the Common Core of Data (CCD) (NCES and U.S., 2014–15). It contains the schools’ demographics, enrollment levels, and socioeconomic composition, extracted using the Elementary/Secondary Information System (ElSi).

School quality metrics are collected by the Florida Department of Education (FDOE) for the year 2014–2015. School quality is measured by the school grades, a metric to measure the performance of a school. School grades are designated annually, based on student outcomes on statewide standardized assessments, with the letters A to F, letter A being the highest level of quality. See (FDOE, 2018) for details on the calculations. In this study, schools are coded as “high-quality” when they are ranked with A or B scores, and “poor-quality” when the schools are ranked with C, D, or F scores. The code, “any-quality,” refers to all schools.

Descriptive statistics

SDHC is the eighth largest school district in the US, with about 207,000 students enrolled in about 279 K-12 public schools. School choice programs are pretty popular; more than 50,000 students are enrolled in one of the school choice programs. Magnet schools are the most popular option among the choice alternatives offered by SDHC. They served 8.5% of the total school district population, with 17,700 enrolled students in 2015–2016. All families are asked to rank order up to three middle magnet schools with unfilled seats in each round. Several families rank multiple schools: 48% of them rank three schools, 30% rank two schools, and 22% rank only one school.

Table 1 presents the racial/ethnic mix of the entire school district enrolled population, the magnet middle schools, and the student applications received for this year 2015–2016, first presented in (Prieto, Aguero-Valverde, Zarrate-Cardenas, & Van Maarseveen, 2018) and replicated here for clarity. In all schools at SDHC, the student population is distributed as follows: 21% of the students are Black, 36% are White, 35% are Hispanic, and 8% are from other races/ethnicities. The population enrolled in magnet middle schools is distributed as follows. 34% of the students are Black, 27% are White, 29% are Hispanic, and 10% of students are from other races/ethnicities. This distribution closely mimics that of the application pool.

Table 1. SDHC middle magnet program enrolled population and applications by race/ethnicity for the 2015–2016 academic year.

ID	School	Program	FDOE	Total enrolled	Enrolled population				Total all ranked	All ranked applications
			Theme	population	BLA	WHI	HIS	XOT	applications	BLA	WHI	HIS	XOT
S1	Stewart	Math/Science/Technology	MAT	857	34%	24%	35%	7%	1,011	27%	33%	27%	13%
S2	Dowdell	Environmental Studies	OTH	613	28%	19%	49%	4%	283	27%	36%	29%	8%
S3	Sligh	Health Professions	OTH	648	76%	4%	16%	4%	339	38%	32%	18%	12%
S4	Franklin (Boys) Magnet	Boys Preparatory Academy	OTH	419	42%	26%	24%	8%	480	44%	25%	23%	8%
S5	Ferrell (Girls) Magnet	Girls Preparatory Academy	OTH	405	42%	24%	26%	8%	581	43%	28%	19%	10%
S6	Orange Grove Magnet	Visual/Performing/Arts	ART	562	31%	33%	30%	6%	1,008	46%	26%	20%	8%
S7	Progress Village	Visual/Performing/Comm. Arts	ART	865	29%	36%	28%	7%	861	32%	31%	28%	9%
S8	Roland Park K-8 Magnet	International Baccalaureate	IB	763	28%	29%	27%	16%	563	22%	33%	24%	21%
S9	Rampello Downtown K-8	Cultural Arts & Humanities	OTH	766	32%	34%	29%	5%	210	37%	30%	25%	8%
S10	Walker Magnet	International Baccalaureate	IB	900	12%	42%	31%	15%	764	13%	23%	42%	22%
S11	Williams	International Baccalaureate	IB	798	29%	23%	19%	29%	779	33%	18%	22%	27%
S12	Young Magnet	Creative Science Center	MAT	561	52%	13%	30%	5%	919	48%	25%	18%	9%
Total magnet middle schools				8,157	2,816	2,171	2,355	815	7,798	2,692	1,911	2,141	1,054
					34%	27%	29%	10%		34%	25%	27%	14%
Total SDHC enrolled population				207,469	44,402	74,336	71,971	16,760
					21%	36%	35%	8%

Note: FDOE Theme Specialty: MAT (Sciences/Math), ART (Performing Arts), IB (International Baccalaureate), OTH (Other Theme Specialty);

Race/Ethnicity: BLA (Black), WHI (White), HIS (Hispanic), XOT (Other Race/Ethnicity).

Table 2 shows the list of SDHC magnet middle schools and their main characteristics, including 6712 ranked choices made by 3231 applicants to grade 6 at twelve magnet middle school programs. Most of the school programs (9 out of 12) are high performance (A score). Half of the schools are Title-I schools, i.e., schools with high fractions of economically disadvantaged students. 60% of applicants are eligible for free/reduced price (FRL) meals. The last column displays the actual capacity of each school, i.e., the number of available seats to be assigned for grade 6. This number was derived from the genuine offers for admission sent by SDHC to applicants for this academic year.

Table 2. SDHC magnet middle school program characteristics and applications to Grade 6 for the 2015–2016 academic year.

School Program				School enrolled population		Applications to Grade 6
ID	School	FDOE School grade	Title-I school	Total school students	Free/ Reduced Lunch	All ranked applications Grade 6		Ranked first applications Grade 6		Seats Available Grade 6
S1	Stewart	A	YES	857	70%	875	13%	369	11%	351	13%
S2	Dowdell	C	YES	613	92%	240	4%	61	2%	100	4%
S3	Sligh	F	YES	648	95%	291	4%	74	2%	81	3%
S4	Franklin (Boys) Magnet	A	YES	419	68%	405	6%	203	6%	239	9%
S5	Ferrell (Girls) Magnet	A	YES	405	74%	509	8%	247	8%	293	11%
S6	Orange Grove Magnet	A	NO	562	48%	832	12%	365	11%	211	8%
S7	Progress Village	A	NO	865	55%	742	11%	414	13%	348	13%
S8	Roland Park K-8 Magnet	A	NO	763	42%	478	7%	195	6%	44	2%
S9	Rampello Downtown K-8	A	NO	766	45%	178	3%	61	2%	55	2%
S10	Walker Magnet	A	NO	900	38%	690	10%	550	17%	424	16%
S11	Williams	A	NO	798	38%	687	10%	452	14%	359	13%
S12	Young Magnet	C	YES	561	88%	785	12%	240	7%	211	8%
	Total			8,157	60%	6,712	100%	3,231	100%	2,716	100%

Note: FRL = Free/reduced price meals.

FDOE School Grading Scale: A = 62% of points or greater, B = 54% to 61% of points, C = 41% to 53% of points, D = 32% to 40% of points, F = 31% of points or less;

Table 3 shows descriptive statistics of the applications to grade 6. Most variables are treated as binary (yes/no), showing the percentage of applicants who belong to the group (yes). There is a good representation of all races/ethnicities, with 27% of Black, 28% of Hispanic, 30% of Whites, and only 14% of other races. 51% of applicants are female; 29% of applicants have siblings; 6% of applicants have a parent who is an employee of SDHC; 58% of applicants are eligible for FRL meals; 74% of applicants speak English at home; almost all applicants (98%) live in an urban area, and 56% are currently assigned to a disadvantaged (Title-I) neighborhood school.

Table 3. Descriptive statistics for SDHC magnet middle applications to grade 6 for the 2015–2016 academic year.

ID	School	Ranked First Applicants	Race/Ethnicity				ESE	FEM	SIB	EMP	LUN	ENG	URB	TIT
			BLA	HIS	XOT	WHI
S1	Stewart	369	20%	40%	10%	30%	41%	20%	23%	5%	67%	64%	97%	67%
S2	Dowdell	61	25%	39%	3%	33%	28%	51%	28%	0%	80%	72%	97%	84%
S3	Sligh	74	31%	42%	11%	16%	32%	69%	15%	0%	78%	54%	100%	74%
S4	Franklin (Boys) Magnet	203	34%	33%	5%	28%	36%	0%	21%	8%	68%	80%	98%	67%
S5	Ferrell (Girls) Magnet	247	40%	31%	6%	23%	27%	100%	23%	4%	73%	79%	100%	77%
S6	Orange Grove Magnet	365	42%	27%	7%	24%	35%	73%	30%	5%	72%	81%	100%	72%
S7	Progress Village	414	26%	30%	10%	34%	28%	71%	27%	8%	59%	81%	98%	59%
S8	Roland Park K-8 Magnet	195	14%	42%	12%	32%	40%	47%	41%	7%	53%	64%	99%	56%
S9	Rampello Downtown K-8	61	28%	36%	3%	33%	33%	51%	49%	8%	59%	80%	98%	54%
S10	Walker Magnet	550	8%	22%	22%	48%	42%	48%	30%	8%	31%	77%	98%	18%
S11	Williams	452	25%	14%	37%	24%	55%	49%	32%	6%	37%	65%	98%	41%
S12	Young Magnet	240	55%	20%	7%	18%	35%	35%	31%	4%	83%	78%	98%	80%
	Total	3,231	27%	28%	14%	30%	38%	51%	29%	6%	58%	74%	98%	56%

Note: Applicant’s race/ethnicity: BLA: Black, HIS: Hispanic, XOT: Other race, WHI: White; ESE: Applicant is eligible for ESE (special education services); FEM: Applicant is female; SIB: Applicant has siblings; ENG: the English language is spoken at home; EMP: Applicant’s parent is an employee of SDHC; LUN: Applicant is eligible to free/reduced price (FRL) meals; URB: Applicant’s home located in an urban area; TIT: Applicant is assigned to a disadvantaged (Title-I) neighborhood school;

Simulation strategy

The simulation strategy is set so that the school district designs the school choice plan to decide which students they want to admit. The input data for the simulations are the real student applications for grade 6 for all magnet middle schools for the academic year 2015–2016.

We simulate student assignments under different sets of priorities, rules, and conditions to better comprehend how school seat supply translates into sorting applicants under various school choice plans. The setting in the admission is altered in multiple ways, as follows: 1) varying school priorities by offering higher chances of admission to certain groups of applicants based on their circumstances; 2) performing the matching – between students’ preferences and schools’ priorities – with different assignment algorithms; and 3) by increasing or shrinking the schools’ capacity, i.e., the number of school seats available for allocation. We perform the simulations considering any-quality schools and compare them when considering only schools of high quality.

The simulations aim to guide the selection of the best school choice plan. This selection is a multiobjective continuous decision problem characterized by an infinite number of feasible alternatives. Multiobjective Decision Support Systems (MODSS) can play a role in understanding such kinds of complex problems (Janssen, 1992). We rely on discrete evaluation methods by selecting an appropriate finite subset from all possible alternatives.

The premise is that schools can design a school choice plan that leads to an “equitable assignment”, i.e., an assignment that gives equal opportunities for children with different family backgrounds. The use of simulations was chosen to explore the potential consequences of changing the admission priorities, rules, and conditions to enable the assessment and comparison of alternative allocations. This kind of approach has been envisioned by (Steinitz, 2012) and applied previously in multiple geo-computational simulation case studies. See for instance (Martin van Maarseveen & Flacke, 2019; Perez-Molina, Sliuzas, & Flacke, 2019).

The results of the simulations provide insights that guide the design of such a choice plan. We use a decision support system to structure the decision process. In Simon’s terminology (Simon, 1962), the focus of this study is on the quality of the decision process (procedural rationality) rather than on the quality of the final decision (substantial rationality). Therefore the overall objective of decision support is defined as an improvement of the decision procedure.

Methodological framework

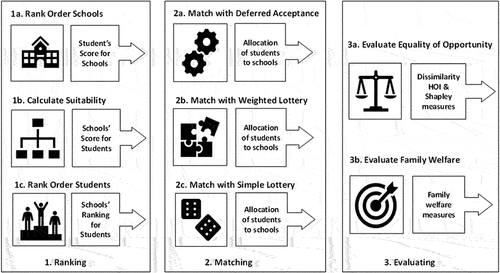
The methodology demonstrates how to simulate student allocation to schools by combining students’ preferences for schools, and schools’ priorities for students. The sequence of methodology steps is shown in Figure 1: ranking, matching, and evaluating. In the following sections, each step is elaborated on in more detail.

Figure 1. Sketch of the simulation strategy.

The first step is student ranking. A routine calculates the student suitability scores and the rank order of all applicants for each school is obtained. The variation happens in the way that school priorities are determined.

The second step is matching. Simulations for admission to all the schools are performed. The variation happens in the school capacities and the algorithm used for allocation. The algorithm varies between the weighted lottery approach, the simple lottery approach, and the deferred acceptance algorithm.

The third step is evaluating. The measure of the IOP for each allocation is calculated, along with a measure of how well the allocation satisfies the students’ preferences for the ranked schools.

Step 1: ranking

This step aims to define the main structure of the decision support system. To organize the decision problem, we follow the Multi-Attribute Decision Analysis (MADA) hierarchical structure adapted from (Malczewski, 1999), and apply it to the student allocation decision problem (Malczewski & Jackson, 2000). The hierarchical structure consists of several levels that go from the general to the more specific (Malczewski & Rinner, 2015): The top level is the ultimate goal. The goal might be defined in terms of specific objectives which are defined at lower levels. At the lowest level of the hierarchy are all the evaluation criteria. They are quantitative indicators to measure the level of achievement of the objectives.

We name a school´s “priority profile” to the formula that generates the suitability score for a given scenario, i.e. a specific combination of some decision criteria and their relevance or relative importance over the other criteria. The schools’ priorities assigned to the decision criteria are denoted in terms of criterion weights, $w_k$, $0\le w_k\le$ $1$, and ${\sum }^{w_k}=1.$ Less important criteria obtain smaller weights. The combination rule allows for obtaining the final suitability score of the applicants for each school and scenario. The score is calculated using the Weighted Linear Combination (WLC) approach (Malczewski & Rinner, 2015) as follows,

$V\left(A_i\right)=\sum _{k=1}^n{w}_{k}v\left(a_{ik}\right)$

Where $V\left(A_i\right)$ is the overall suitability score of the i-th applicant; $w_k$ are the criterion weights for the k-th criterion; and $v\left(a_{ik}\right)$ is the normalized value of the i-th applicant with respect to the k-th criterion.

MCDA requires transforming the evaluation criteria to comparable units. We use “Norm,” a Stata module to normalize variables (Ansari, 2013), and apply the min-max ($mmx)$ normalization technique. The normalized score values range from a specified minimum of 0 (less desirable) to a maximum value of 1 (most desirable). Variables that represent cost, (e.g. distance), are inversed using $1-mmx$.

Once the suitability scores are calculated, each school generates the priority order (the ranking), by ordering from high to low the suitability scores of each of the applicants to the school. Higher suitability scores generate higher ranks. Ties are resolved by a random number assigned to each applicant.

Step 2: matching

We consider a many-to-one matching model consisting of schools (that seek to match multiple applicants) and applicants (who seek to match with a single school). The task of the matching algorithm is to select $x$ out of $n$ applicants, given the preference order expressed by the students and the priority order expressed by the schools. The list of possible matching algorithms is very long and there exist criteria that an algorithm should satisfy (Abdulkadiroglu & Sönmez, 2003). The most common assignment mechanisms include neighborhood assignment, choice-based assignment, test-based assignment, and random assignment (Allen, Burgess, & McKenna, 2013). See Agarwal and Somaini (Agarwal & Somaini, 2018) for a partial list of mechanisms in use around the world.

In our experimental setting, the two-side matching happens in three different ways, namely the deferred acceptance algorithm (DFA), the weighted lottery approach (LOT), and the simple lottery approach (SLA). See details of each approach below. All matching algorithms assume that there are many schools in the school district and each student applies to up to three schools, each of them with some strict priority. For both lotteries, the student rank was considered in the implementation of the algorithm, similar to the procedure used by the school district in the case study, to offer the best parent satisfaction possible.

The simulated allocations are done initially with the same capacities for each school as in the original choice data set. In a set of simulations, this restriction is relaxed. The algorithm needs to control for all the schools’ capacities: each time an applicant is selected for a given school, the number of places in this school is updated.

Deferred Acceptance Algorithm (DFA)

The DFA, initially proposed by (Gale & Shapley, 1962), had been adapted for matching mechanisms and implemented in multiple school choice systems around the world (Abdulkadiroglu, Pathak, & Roth, 2009; Roth, 2008). We use the school-proposing version, i.e. schools make proposals of available seats to students, in the order of each school’s priority list (obtained from step 1).

The conceptual understanding of the DFA is simple: when an applicant is selected by a school, the assignment is provisional (deferred). His chances for the other schools are still active. If an applicant is lucky to be selected by more than one school, the algorithm checks the applicant’s ranking of the schools, and always gives him the option of higher preference (among the offers received). The applicant’s acceptance of an offer is not final until the very end. The other (provisional) matches are deleted, and capacities in the rejected schools are restored.

Simple Lottery Approach (SLA)

Lotteries are perceived as a “fair and transparent way to distribute school places and promote equal access to educational opportunities” (Stasz & Von Stolk, 2007). A fair lottery generates several outcomes, all of them with equal probability. Numerous school choice programs use randomly-assigned priorities, e.g. Beijing (He, 2015), Amsterdam (Haan, Gautier, Hessel, Bas van der, 2015), and New York (Abdulkadiroğlu et al., 2005).

In a single lottery mechanism, a single random ordering of the applicants is drawn; any ties (at any school) are broken somehow, for instance favoring a student whose lottery number is lower. In contrast, multiple lottery mechanisms allow each school to conduct its lottery (Pathak & Sethuraman, 2010b). In our experimental setting, we draw a single lottery mechanism, since it has been demonstrated to be more favorable in terms of family welfare (Abdulkadiroğlu et al., 2005).

Weighted Lottery Approach (LOT)

A weighted lottery uses an algorithm to increase the odds for a certain type of student, such as those from low-income families or English-language learners. The input for this allocation is the number of points (suitability score) assigned to each applicant for each school (in step 1), which is used as the weight for the lottery. Conceptually, those applicants with a higher number of points will get more “tickets” for the lottery, and hence will have more chances to be accepted. However, having more points (and lottery tickets) does not guarantee admission.

The task of the algorithm is to randomly select $k$ out of $n$ applicants, such that the probability of an applicant being chosen is proportional to the weight. The allocations are final; once an applicant is selected for one of the schools, his remaining applications for the other schools are deleted.

Step 3: evaluating

The impact of the variation of the school choice plan is evaluated in two ways. From the demand side, the family welfare is calculated, i.e. the amount of satisfaction produced by the assignment. From the supply side, we calculate the amount of inequality of opportunity produced by the assignment.

Measuring family welfare

The measure of the family welfare in each of the scenarios is calculated using the school choice rank metric, proposed by (Shi, 2015). This metric is the rank of school choice obtained. For instance, being admitted to a first-choice school corresponds to the choice rank 1, being admitted to a second-choice school corresponds to choice rank 2, etc. If the applicant was not assigned, then the metric is undefined. We summarize the rank obtained by all the applicants and calculate the percentage of admission by rank for all the grade 6 magnet middle schools.

Measuring equality of opportunity

We draw from the Human Opportunity Index (HOI) framework presented in (Barros, Ricardo, Molinas Vega, Saavedra, Jaime, 2009; Paes, Molinas Vega, & Saavedra, 2010). HOI is a measure developed by researchers at the World Bank to track society’s advances toward basic opportunities for all. HOI measures progress toward universal coverage of basic opportunities as well as equitable provision of those opportunities, in a single indicator (World Bank, 2012).

A basic opportunity is a key service or minimum living condition that is necessary to succeed in life, and society wants everybody to have. For instance, vaccination, access to running water, and adequate learning. Circumstances are defined as personal or family, or the community characteristics over which a person has no direct control, and cannot be held accountable for, such as gender, location, ethnicity, or race (World Bank, 2012). The coverage rate expresses information on what fraction of the population has access to the opportunity. A society that has achieved universal coverage would score 100, universal deprivation would score zero (World Bank, 2012). The Penalty (P) measures unequal access across circumstance groups. It is estimated by taking into account the differences between the coverage rate of each circumstance group and the overall coverage rate. The Dissimilarity index (D) measures whether the access to the opportunity is allocated equitably, comparing the probability of access of the different circumstance groups. The D-index measures the share of the total number of seats allocated to children in the schools that need to be reallocated between circumstance groups in order to ensure equality of opportunities (Paes, Molinas Vega, & Saavedra, 2008). The target value for D-index is zero, obtained when access to the opportunity is independent of the circumstances.

We study the opportunity to get an offer for admission to both a school of any quality and a school of high quality by using the regression approach. The procedure consists of running the logistic regression model to estimate, at an individual level, the relationship between access to any/high-quality education (binary dependent variable) and the applicant’s circumstances (independent variables). Taking the coefficient estimates, the HOI module computes, for each applicant, the predicted probability of access to the educational service.

Assume that there is a random sample of the population of children with information on whether child $i$ has or doesn’t have access to any/high-quality education ($I_i=1$ if the child has access, and $I_i=0$ otherwise) and there is a vector of variables indicating his/her circumstances (e.g., gender, race/ethnicity, location, etc.), $X_i=X_{1i},X_{2i},\dots ,X_{mi}$. All children having the same set of circumstances are said to be of the same group type. Circumstance groups whose coverage rates are below the overall coverage rate are called vulnerable groups.

The HOI methodology applied for admission to schools for this case study has been previously analyzed elsewhere (Prieto, Flacke, Aguero-Valverde, & Van Maarseveen, 2018). However, for clarity, we replicate the procedure in this section. The inequality measures are calculated following six steps (Azevedo, Franco, Rubiano, Hoyos, 2010), as presented in Table 4.

Table 4. Steps for calculations of the inequality measures.

Step 1: estimate a logistic regression model on whether a child $i$ has access to high-quality education, as a function of his or her personal $m$ circumstances, using the maximum likelihood method.

$Ln\left(\frac{P(I=1|x_1,\dots ,x_m)}{1-P(I=1|x_1,\dots ,x_m)}\right)=\sum _{k=1}^m{\beta }_k\left(X_k\right)$

From the estimation of this logistic regression, the coefficient estimates ${\hat{\beta }}_k$ are obtained.

Step 2: obtain for each child, the predicted probability of access to high-quality education ${\hat{p}}_i,$ based on the predicted relationship ${\hat{\beta }}_k$ and the vector of their circumstances $X_{ki}$.

${\hat{p}}_i=\frac{exp\left({\hat{\beta }}_0+{\sum }_{k=1}^m{X}_{ki}{\hat{\beta }}_k\right)}{1+exp\left({\hat{\beta }}_0+{\sum }_{k=1}^m{X}_{ki}{\hat{\beta }}_k\right)}$

Step 3: obtain the overall coverage rate for the service C. The coverage rate shows what fraction of the population has access to high-quality education. $C=\sum _{i=1}^n{w}_i{\hat{p}}_i,$

where $n$ is the total population, and $w_i=1/n$ or some sampling weights.

Step 4: the Dissimilarity Index (D-Index) $\hat{D},$ is calculated,

$\hat{D}=\frac{1}{2C}\sum _{i=1}^n{w}_i\left|{\hat{p}}_i-C\right|$

Step 5: obtain the penalty $P$ for inequality. $P$ refers to access to the service that was allocated unfairly. $P=C\times \hat{D}$

Step 6: calculate the HOI, discounting the penalty for improperly allocated opportunities from the overall coverage rate ($C$). $HOI=C-P$

The HOI module (Azevedo, Franco, Rubiano, Hoyos, 2010) in Stata Version 14.2. was used for the estimations. Only the applications to the student’s most preferred option were included in the model estimation. Although the dataset contains data for the 6^th, 7^th and 8^th grades, applications for grade 6 were chosen for the simulations, given that it is the starting year for middle school and therefore the capacity (number of free slots) of the schools is higher.

Selection of decision variables for the case study

We study the heterogeneity in access across groups based on circumstances. For details on the circumstances used in the analysis and for the maps with the geographic distribution of the applications, please refer to (Prieto, Aguero-Valverde, Zarrate-Cardenas, & Van Maarseveen, 2018, 2018). Some of the characteristics selected for this analysis have the potential problem that they may be influenced by individual behavior rather than by circumstances pre-determined at birth. However, they have been included in the analysis because they are exogenous to the child applicant, and therefore they must be understood as characteristics that are beyond the control of a student of this age (11–13 years old).

Table 5 shows the set of dimensions, objectives, and decision variables defined for the simulations. This list is a subset of the circumstances. The selection is based on literature review and expert advice and is constrained by the data availability. Note that the result of the suitability analysis is influenced by the criteria selected.

Table 5. The link between school choice policy, dimensions, objectives, and decision variables chosen for the simulations.

Dimension	Objective	Id	Decision variable	Variable type
Geography	Minimize school transportation costs	GEO	Distance from applicant’s home to school	Continuous
Family and Community	Facilitate school logistics for parents	SIB	Sibling attending a school	Binary
		EMP	The parent is an employee from the school district	Binary
Socioeconomic Diversity	Foster social cohesion and social mobility	FRL	The applicant is eligible for free/reduced price (FRL) meals	Binary
		BLA	The applicant is of Black race/ethnicity	Binary
Academic Quality	Maximize expected academic excellence	TIT	The applicant is assigned (by default) to a disadvantaged (Title-I) neighborhood school	Binary

An objective function is identified for each dimension, indicating what the school district seeks to optimize. In the geography dimension, the objective is to minimize transportation costs. The variable is the distance from the applicant’s home to school, measured in miles and calculated using the road network. The family and community dimension aims at facilitating school logistics for parents. It is measured with two variables: whether the applicant has a sibling attending the school and whether the parent is an employee from the school district. The socioeconomic diversity dimension aims to foster social cohesion and social mobility. It is characterized by two variables, the poverty level of the applicant and his race/ethnicity. Applicants who qualify for the free and reduced-price meals (FRL) program are considered low-income; this variable is used as a proxy for the student’s socioeconomic status (SES). Race/ethnicity was encoded as a dichotomous variable, coded one if the applicant is of Black race and zero if the applicant is of any other race/ethnicity. The last dimension, academic quality, aims to maximize expected academic excellence. A feasible metric is to consider the applicant’s current default school assignment. We consider whether the child is residing in an attendance area with high numbers of economically disadvantaged students (assigned by default to a Title-I school) who are failing, or most at risk of failing, to meet state student academic achievement standards.

Table 6 shows the value weights used for the simulations. These examples represent a diverse, but not an exhaustive selection of possible weighting options. The term “scenario” refers to each value weighting configuration. Each scenario is run with a given focus that happens in four different ways: geography, academics, family, and socioeconomics; and one scenario with no focus (equal weights to all variables).

Table 6. Criterion weighting used in the scenarios.

	GEOGRAPHY	ACADEMICS	FAMILY		SOCIOECONOMICS
Scenario #	GEO	TIT	SIB	EMP	BLA	FRL	FOCUS
1	0.750	0.083	0.042	0.042	0.042	0.042	Geography
2	0.083	0.750	0.042	0.042	0.042	0.042	Academics
3	0.083	0.083	0.375	0.375	0.042	0.042	Family
4	0.083	0.083	0.042	0.042	0.375	0.375	Socioeconomics
5	0.250	0.250	0.125	0.125	0.125	0.125	Equal weight
6	0.000	0.000	0.000	0.000	0.500	0.500	Socioeconomics
7	0.410	0.160	0.050	0.260	0.020	0.100	Geography
8	0.290	0.240	0.040	0.100	0.140	0.190	Geography

Notes: GEO: Distance from applicant’s home to school; TIT: Applicant is assigned to a disadvantaged (Title-I) neighborhood school; SIB: Sibling already attending a school; EMP: Parent is an employee of the school district; BLA: Applicant is of Black race/ethnicity;

FRL: Applicant is eligible for free/reduced price meals

That is, we deliberately influenced the applicant’s admission chances based on his/her circumstances, and we observed the impact of this variation. For instance, scenario 3 has a family focus; applicants with siblings, and those whose parent is an employee of the school district are favored; they get higher suitability scores, get higher rank-order from the schools, and hence priority in admission. There are four more scenarios, namely 9, 10, 11, and 12, without weights (hence not shown in Table 6). They are used for SLA, with entirely random allocations.

The last column identifies a focus for each scenario; for instance, scenarios 1, 7, and 8 focus on geography. For scenarios 1–6, there was no explicit method used for estimation of the criterion weights; scenarios 7 and 8 use the stepwise method of ranking preferences (Voogd, 1982); scenario 7 was carried out using the Expected Value Method (EVM) (Janssen, 1992); scenario 8 was carried out with Ranked Sum Weight (RSW) (Malczewski & Rinner, 2015).

Results

In the sections that follow each research question is responded to, based on the setting offered in Table 7. A large number of simulations were run in each case, however, due to space limitations only a few scenarios are exhibited as examples, to illustrate the behavior that was observed at a large scale.

Table 7. Settings used for the simulations performed to answer the research questions.

Simulation	Focus	Algorithm	Capacity
1. Variations in school priorities	Varying school priorities	DFA	100%
2. Variations in assignment algorithms	Geography	DFA, LOT, SLA	100%
3. Variations in capacity	Socioeconomics/equal	DFA	25% – 175%
4. Measuring family welfare	Socioeconomics	DFA	25% – 175%

Each scenario creates an alternative future that is evaluated by the overall level of Inequality of Opportunity (IOP). The HOI captures two elements: the level of coverage of the service considered, and how unequally it is distributed across groups of children defined by a mix of variables that capture their circumstances, such as socioeconomic level, and the language spoken at home. The measurement of success in the design of the choice plan is given by how close the allocation scenario is to the target values of the Coverage (C = 100), the Dissimilarity Index (D-index = 0), the Penalty (P = 0), and the Human Opportunity Index (HOI = 100).

Variations in school priorities

Research question 1: What is the level of equality of opportunity in access to high-quality schools under different priority profiles?

We look at the school district’s performance in the two opportunities (access to a school of any-quality vs. high-quality) separately for eight different scenarios. The variations in priority profiles seek to determine the impact in the HOI metrics when varying the weights applied in the priority profile for the selection of the applicants. To answer the research question, the simulations for admission were run with the deferred acceptance algorithm (DFA) and the initial (real) capacity (100%) used in the 2015–2016 academic year for grade 6. Table 8 summarizes the HOI metrics for eight scenarios. A summary finding is that for all the scenarios, a specific weight does not have (or hardly has) any impact on the value of HOI. Details follow.

Table 8. HOI for the opportunity in access to schools, with variations in school priority profiles.

		Access to a School of Any-Quality				Access to a School of High-Quality
Scenario	Focus	HOI	D-index	Penalty	Coverage	HOI	D-index	Penalty	Coverage
1	Geography	62.8	14.0	10.3	73.1	56.0	11.8	7.5	63.5
2	Academics	64.8	14.6	11.1	75.8	58.0	11.4	7.4	65.5
3	Family	63.9	15.3	11.6	75.5	57.5	11.9	7.8	65.3
4	Socioeconomics	64.7	14.8	11.3	75.9	58.3	11.0	7.2	65.6
5	Equal Weight	64.6	14.7	11.1	75.8	57.9	11.4	7.4	65.4
6	Socioeconomics	64.2	14.4	10.8	75.0	58.1	10.4	6.7	64.8
7	Geography	64.4	14.4	10.9	75.2	57.5	11.5	7.5	65.0
8	Geography	64.2	14.8	11.2	75.3	57.5	11.5	7.5	65.0

Notes: Algorithms: DFA=Deferred Acceptance Algorithm; LOT=Weighted Lottery Approach; SLA= Simple Lottery Approach. These simulations were run using only DFA, multiple focus in the priorities, and 100% capacity. HOI= Human Opportunity Index; D-Index: Dissimilarity Index; IOP= Inequality of Opportunity

First, we analyze the IOP separately to access schools of any-quality (left-hand columns) and high-quality (right-hand columns). In both cases, there are little or no variations in the HOI metrics when changing the weights given to a variable for a specified algorithm and holding a fixed capacity, with minor differences of only 1 or 2 points in the HOI indexes in all cases.

The number of allocated seats in the simulations is quantified and compared between circumstance groups. Large between-group differences in seats allocated to some circumstance groups produce large D-indexes and high penalties, hence lower HOI and henceforth high IOP. Since the scenarios in our simulations have purposely favored a group of applicants, the metrics reflect this IOP with a high D-index number in all cases, no matter which circumstance group was preferred. For instance, in scenario 3 for any-quality schools, applicants who have a sibling or a working parent at the school are allocated first. The created IOP is evidenced by a D-index of 14.0. The D-index indicates the proportion of this circumstance group (sibling and employee) that would need to move in order to create a uniform population distribution. Note another instance, in scenario 4, poor and Black applicants are allocated first. Again, the D-indices are similar (14.8). The D-index represents the percentage of this circumstance group (poor and Black) that would need to transfer in order to create a uniform population distribution. The index does not reveal the favored circumstance group that caused the D-index to be unequal. Thus, this is somehow misleading.

Second, we compare the metrics among the two opportunities (any-quality vs. high-quality education) shown in Table 8. There is a noteworthy difference of about 10 points in the service coverage, explained by the lower number of high-quality schools, hence fewer opportunities are available. In contrast, the D-index and penalty have slight variations of about 3 points. The lower coverage highly impacts the HOI metrics; the dissimilarities seem to remain high when evaluating higher-quality educational services.

Third, we keep a given focus -using geography as an example- and analyze differences in the weighing methods (last two rows), namely the expected value method and the ranked sum method, as revealed in scenarios 7 and 8. Similarly to the previous scenarios, there are little or no variations in the metrics when changing the weighting methods while maintaining the same focus.

Variations in assignment algorithms

Research question 2: What is the level of equality of opportunity in access to high-quality schools under different assignment algorithms?

We look at SDHC’s performance in the two opportunities separately, for several scenarios and under variations in the assignment algorithms. The variations seek to find out what is the impact in the HOI metrics when changing the matching method used for the applicants’ selection. The HOI metrics for the opportunity in access to a school of any-quality (left-hand columns) and high-quality (right-hand columns) are exposed in Table 9.

Table 9. HOI for the opportunity in access to schools, with variations in assignment algorithms.

		Access to a School of Any-Quality				Access to a School of High-Quality
Scenario	Algorithm	HOI	D-index	Penalty	Coverage	HOI	D-index	Penalty	Coverage
1	DFA	62.8	14.0	10.3	73.1	56.0	11.8	7.5	63.5
7	DFA	64.4	14.4	10.9	75.2	57.5	11.5	7.5	65.0
8	DFA	64.2	14.8	11.2	75.3	57.5	11.5	7.5	65.0
1	LOT	76.8	1.9	1.5	78.3	67.3	1.8	1.2	68.5
7	LOT	75.7	3.5	2.7	78.4	67.1	2.2	1.5	68.6
8	LOT	74.5	5.2	4.1	78.6	66.3	3.3	2.2	68.6
9	SLA	76.6	2.1	1.7	78.2	65.5	4.0	2.7	68.3
10	SLA	77.6	1.7	1.3	78.9	65.5	4.2	2.9	68.4
11	SLA	76.5	2.2	1.7	78.1	64.8	4.4	3.0	67.8

Notes: These simulations were run using all the available algorithms, and 100% capacity.

Scenarios 1, 7 and 8 have a focus on geography, applicants who live close to school are prioritized for admission.

Algorithms: DFA=Deferred Acceptance Algorithm; LOT=Weighted Lottery Approach; SLA= Simple Lottery Approach.

HOI= Human Opportunity Index; D-Index: Dissimilarity Index; IOP= Inequality of Opportunity

The simulations are performed for three different assignment algorithms, namely Deferred Acceptance Algorithm (DFA); Weighted Lottery Approach (LOT); and Simple Lottery Approach (SLA). All the algorithms are run using one single focus (Geography) and the initial (real) capacity, with 100% of the available seats assigned in the 2015–2016 academic year for grade 6th. Recall from the criteria weightings in Table 6 that for scenarios 1, 7, and 8, we deliberately upgraded the applicant’s admission chances based on his/her circumstance of living close to the school.

The HOI metrics are similar for the different scenarios for a given algorithm, and the differences between the two opportunities are also congruent with those analyzed in the previous research question, therefore we analyze only access to high-quality schools (right-hand columns), and refer to scenario 7 to analyze the results for DFA and LOT (middle row in bold in each group); we then contrast it against SLA for various runs (scenarios 9, 10, 11), which were run with a completely random assignment, to highlight the differences.

For the three algorithms, the coverages are alike, and they stay relatively high. There is only a slight variation of 3 points in the coverage when comparing DFA (65.0) against the two lotteries (LOT is 68.6; SLA is 68.4). This is due to the smaller number of seats allocated by DFA for some schools. When there are no more students on the school’s priority list, DFA will skip this school, and in the end, a few seats are not allocated. In contrast, the two lotteries assign all the seats available.

The difference becomes tougher when looking at the D-Indexes of the three algorithms. The D-Indexes vary from 11.5 (DFA), and diminish dramatically to 2.2 (LOT) and 4.2 (SLA). The higher values of the D-Index for DFA indicate that the achieved coverage rates are more unequally distributed among circumstance groups. The assignment process populates schools with a D-Index of 11.5 under DFA. In other words, 11.5% of applicants would have to be reallocated between circumstance groups to achieve perfect balance. The D-Index, closer to the target value of zero for LOT and SLA, indicates that the access to the opportunity is independent of the applicant’s circumstances. Similar behavior is echoed by the penalties.

The results allow concluding that both of the lotteries seem to deliver more equality of opportunity in access to schools of high quality, than deferred acceptance. The impact in the HOI metrics given the variations in the algorithm is lower under both lotteries than under DFA. This behavior can be explained due to the random component (probabilistic selection) prevailing in both lotteries, which diminishes the effect of the applied school priorities in LOT, and SLA, leveraging the chances of every child, no matter his/her circumstances. The impact shown by DFA is higher, as expected, since its allocation is deterministic; it allows to capture directly the inequality created by the weight applied to in the priority profiles.

Variations in school capacity

Research question 3: What is the level of equality of opportunity in access to high-quality schools under different capacity constraints?

We look at the school district’s performance in the two opportunities separately, for two different scenarios, and under variations in the number of available seats in the schools. The variations seek to find out what is the impact in the HOI metrics when shrinking or augmenting the schools’ capacity.

The initial (real) capacity is set as a reference, with 100% of the available seats assigned in the 2015–2016 academic year for grade 6. The shrinking starts with 25%, 50%, and 75% of the initial capacity. The enlargement happens with 125%, 150%, and 175% of the initial capacity. Cutting the enrollment down to 25% of capacity is probably not feasible in real-life situations, however this reduction is shown to illustrate the high impact observed with such a significant constraint. The simulations for the admission are performed using the DFA algorithm, given its deterministic behavior, hence a higher correctness in the results’ interpretation. The HOI metrics for the opportunity in access to a school of any-quality (left-hand columns) and high-quality (right-hand columns) are presented in Table 10.

Table 10. HOI for the opportunity in access to schools, with variations in capacity constraints.

		Access to a School of Any-Quality				Access to a School of High-Quality
Scenario	Capacity	HOI	D-index	Penalty	Coverage	HOI	D-index	Penalty	Coverage
5	25%	5.3	68.3	11.5	16.8	5.4	62.2	8.9	14.3
5	50%	19.0	47.1	16.9	35.9	17.7	42.1	12.9	30.6
5	75%	38.4	31.5	17.6	56.0	35.1	27.3	13.2	48.3
5	100%	64.6	14.7	11.1	75.8	57.9	11.4	7.4	65.4
5	125%	86.5	4.1	3.7	90.2	77.2	1.8	1.4	78.6
5	150%	92.4	2.1	2.0	94.3	81.2	1.8	1.5	82.7
5	175%	95.2	1.2	1.2	96.3	82.5	2.6	2.2	84.7
6	25%	4.4	68.5	9.6	14.1	4.0	67.2	8.2	12.3
6	50%	19.5	41.8	14.0	33.4	16.9	40.8	11.6	28.6
6	75%	38.2	29.7	16.2	54.4	34.7	25.9	12.1	46.9
6	100%	64.2	14.4	10.8	75.0	58.1	10.4	6.7	64.8
6	125%	86.9	4.0	3.7	90.5	77.1	2.3	1.8	78.9
6	150%	92.1	2.4	2.3	94.4	80.7	2.5	2.1	82.8
6	175%	94.9	1.5	1.5	96.3	82.2	3.0	2.5	84.7

Algorithms: DFA = Deferred Acceptance Algorithm; LOT = Weighted Lottery Approach; SLA = Simple Lottery Approach. These simulations were run using only DFA and several variations in school capacity.

Scenario 5 assigns an equal weighting to all the variables, while scenario 6 focuses on socioeconomic variables.

HOI= Human Opportunity Index; D-Index: Dissimilarity Index; IOP= Inequality of Opportunity

Recall from the criteria weightings in Table 6 that scenario 5 assigns an equal weighting to all the variables while scenario 6 focuses on socioeconomic variables. The behavior is similar for the two scenarios, therefore we refer to scenario 6 to analyze the results. In scenario 6, the applicant’s admission chances are deliberately influenced, based on his/her circumstances of being of Black race/ethnic, and being eligible to free/reduced price (FRL) meals. We call this circumstance group of applicants, “socially-vulnerable.” We also refer to access to high-quality schools in the analysis below.

The picture which emerges is very different when looking at access to magnet middle schools under different capacity constraints. In summary, IOP appears to work in wide-ranging synchronization with the school capacities. Schools with shrunken capacities face massive constraints to achieve IOP. Schools with enlarged capacities allow admission of a larger number and more diverse set of students, and hence all the HOI indicators perform soundly, close to the target values (as expected).

The HOI reflects two elements: the first element is the level of coverage of the educational service. The coverage rate indicates what fraction of the population has access to the opportunity. When the school capacity grows, more chances for admission arise, hence the coverage can be increased, and the opposite is also true. The second element refers to how equally the educational service is distributed across groups of children, defined by a combination of variables that capture their circumstances. When the school’s capacity is augmented, there are also more chances for fair distribution of the resources. This impact can be observed better when the school capacity is highly shrunken. For instance, if each school only has four available seats, and all of them are assigned to only socially vulnerable applicants (black and poor), as in scenario 6, then the distribution of places is vastly inequitable. This is captured by extremely high D-indexes and extremely low HOI indexes.

Comparing real capacity (100%) with an increase in the capacity of only 25% (to reach 125%), the indices show giant improvements of about 15 points in coverage (64.8 to 78.9), and almost 20 points in the HOI index (58.1 to 77.1). The Penalty and D-index both decline and reach ideal values close to zero. When capacity is further enlarged (up to 175%), the indicators are further upgraded, reaching near to optimal values, for HOI (82.5), close to universal coverage (84.7), low penalty (2.5), and low D-index (3.0). Note that the maximum coverage cannot reach as far as 100, and it is reached at 84.7 because the schools’ quality is mixed (3 out of 12 schools are low quality).

The situation gets reversed as soon as the number of available seats are limited. When capacity is extremely reduced (up to 25%), the HOI reflects values close to universal deprivation with a tremendously low HOI of 4.0, low coverage of 12.3, and huge IOP in access across groups (D-Index of 67.2). Under very high capacity constraints the IOP is high, the school district falls short of achieving satisfactory HOIs, and the achieved coverage rates are extremely unequally distributed among circumstance groups. The small number of seats are allocated only to the highly privileged circumstance groups. This behavior in the HOI metrics is as expected; the fewer opportunities are available, the harder to achieve equality of opportunity.

Measuring family welfare

Research question 4: How well does each admission setting satisfy the parents’ preferences for ranked schools?

We first look at the measure of the family welfare in the two opportunities separately, for a single scenario, scenario 6 (socio economic focus), and under variations in the number of available seats in the schools. The examination seeks to find out what is the impact on family welfare when shrinking or augmenting the schools’ capacities.

This metric chosen is the rank of school choice obtained in the simulated allocation. Recall from step 3 in the methodological framework that choice rank 1 means that the applicant was offered a place in the first choice (most preferred school), etc. Table 11 shows the summary of the applications accepted by choice rank. The results for any-quality and high-quality are similar, therefore we state the results for the latter (see the right-hand columns).

Table 11. Measuring family welfare for the opportunity to have access to a school.

			Access to a School of Any-Quality				Access to a School of High Quality
Scenario	Capacity	Algorithm	Ranked Third	Ranked Second	Ranked First	Total	Ranked Third	Ranked Second	Ranked First	Total
6	25%	DFA	10%	23%	67%	680	9%	23%	68%	582
6	50%	DFA	6%	15%	79%	1,362	6%	15%	79%	1,165
6	75%	DFA	3%	11%	86%	2,036	3%	10%	87%	1,742
6	100%	DFA	2%	8%	90%	2,680	2%	8%	91%	2,306
6	125%	DFA	0%	5%	95%	3,070	0%	5%	95%	2,678
6	150%	DFA	0%	3%	97%	3,145	0%	3%	97%	2,762
6	175%	DFA	0%	2%	98%	3,175	0%	2%	98%	2,794
1	100%	LOT	1%	6%	93%	2,716	1%	4%	95%	2,324
2	100%	LOT	1%	6%	93%	2,716	1%	4%	95%	2,324
3	100%	LOT	1%	6%	94%	2,716	1%	4%	96%	2,324
4	100%	LOT	1%	5%	94%	2,716	1%	3%	96%	2,324
5	100%	LOT	1%	7%	93%	2,716	1%	4%	95%	2,324
6	100%	LOT	1%	4%	95%	2,716	1%	2%	96%	2,324
7	100%	LOT	0%	6%	93%	2,716	0%	4%	95%	2,324
8	100%	LOT	1%	6%	94%	2,716	1%	4%	95%	2,324
9	100%	SLA	1%	6%	93%	2,716	1%	4%	95%	2,324
10	100%	SLA	2%	5%	94%	2,716	1%	3%	95%	2,324
11	100%	SLA	1%	6%	93%	2,716	1%	4%	94%	2,324
12	100%	SLA	1%	6%	93%	2,716	1%	4%	95%	2,324
1	100%	DFA	4%	9%	87%	2,716	3%	8%	88%	2,324
2	100%	DFA	2%	7%	91%	2,686	2%	7%	92%	2,309
3	100%	DFA	2%	7%	91%	2,691	2%	7%	91%	2,311
4	100%	DFA	2%	7%	92%	2,670	1%	6%	92%	2,297
5	100%	DFA	2%	7%	91%	2,686	2%	7%	92%	2,309
6	100%	DFA	2%	8%	90%	2,680	2%	8%	91%	2,306
7	100%	DFA	3%	7%	90%	2,702	2%	6%	78%	2,702
8	100%	DFA	2%	8%	91%	2,680	1%	6%	78%	2,680

Notes: Algorithms: DFA=Deferred Acceptance Algorithm; LOT=Weighted Lottery Approach; SLA= Simple Lottery Approach. Focus in the Scenarios: 1,7,8: Geography; 2: Academics; 3: Family; 4,6: Socioeconomics; 5: Equal weight.

Scenarios 9, 10, 11,12 were run with SLA, with no weights in the criteria; it is a completely random assignment.

HOI= Human Opportunity Index; D-Index: Dissimilarity Index; IOP= Inequality of Opportunity.

Results are aligned with the logic of the college-proposing DFA algorithm. Applicants are allocated following the school’s priority order: when the applicant receives multiple offers, preference is given to the applicant’s first-choice school, then to the second choice, and lastly to the third choice. In all cases, the percentage of allocated applicants ranked first is the largest, starting from 68% and ending at 98%; allocations to second-ranked choices follow, ranging from 23% down to 2%; and lastly, allocations to the third rank are the smallest, ranging from 9% down to 0%. The upper part of Table 11 shows that family welfare works in alignment with changes in capacity.

When the capacity is reduced to 25%, only 68% of families get their most desired ranked school, 23% get their second-ranked option, and 9% get their third-ranked school. At 100% (real) capacity, the panorama looks sound; by now, already 91% of families get their first ranked option, 8% get their second ranked, and only 2% get their third-ranked choice. At 125% expansion of capacity, the algorithm can provide higher well-being, granting the families’ most desired choices: the family welfare reaches 95% for the first rank, and 5% for the second rank. These results seem to indicate that under DFA there is no need to further expand capacity to provide higher levels of family welfare.

Note that when the availability of the seats is increased (125% to 175%), the total number of seats allocated remains almost constant. This happens because the number of received applications is still a constraint (there are more seats, but not enough applicants). In summary, family welfare is impacted in agreement with the available capacity, however, reducing the number of seats has a larger impact than increasing them. The amount of expansion has to be calculated according to the number of applications.

Similar results were obtained for all the other scenarios when using DFA, LOT and SLA, and run with 100% (real) capacity, as shown in the lower part of Table 11. The parents’ welfare is not compromised in the simulations with LOT and SLA because the applicant’s ranking was considered when sorting applicants in the allocation algorithms, mimicking the way SDHC operates. Therefore, the family welfare stays sound and stable, according to the given capacities. However, when this functionality is relaxed, then LOT and SLA go down, and family welfare gets very low values. The results of these changes are as expected and are not presented, due to space restrictions.

Discussion

In 1954, the United States Supreme Court ruled in Brown v. Board of Education (Supreme Court Of The United States, 2004) that, when the opportunity of an education is provided by the state, it “is a right which must be available to all on equal terms.” Yet, more than sixty years later, public schools in the US remain strongly segregated by class and by race, mainly due to neighborhood assignment practices, de facto residential segregation, profoundly unequal funding practices, and the scarcity of high-quality educational opportunities at the primary and secondary level (USCCR, 2010). Access to good schools is mainly limited to families who can afford to live in wealthy neighborhoods, or those who can get access to tuition or scholarships to attend private schools. Therefore, low-income and minority students are educated in lower-performing schools, compared to White and more advantaged peers (Reardon, 2016).

Given the scarcity of high-quality educational opportunities through public K-12 institutions, a central question arises: how educational opportunities should be distributed? And more precisely, can this distribution be equitable? We evaluate equality of opportunity in access to high-quality education offered by magnet schools in a large school district in Florida. We perform several simulations to investigate how the chances of admission for a child can be increased or reduced, by considering alternative scenarios that change the setting of the admission. We then evaluate the impact of admission changes by analyzing the allocation using the Human Opportunity Index (HOI) regression approach. HOI indicates how far or close the results of each scenario are from being an “equitable assignment,” i.e. an assignment that gives equal opportunities for children with different family backgrounds. We also measure the impact of the changes in family welfare, measured with the choice rank obtained in the allocation.

From among all the simulations performed with grade 6 of magnet middle schools at SDHC, the variation in school capacity is the element that most strongly impacts the HOI indexes. The constraints imposed on the number of seats available have a huge impact on the equality of opportunity that could be achieved. A 125% expansion of capacity would be enough to get an increase of about 20 points in the HOI metrics. This implies that one possible way to improve the access rate to opportunity at SDHC is to implement policies that increase the coverage rate of high-quality educational services. The second impact is due to the algorithm used to perform the selection. Both of the lottery systems seem to deliver more equality of opportunity in access to schools of high quality than does deferred acceptance. A lottery selection favors no applicant, and hence it is highly linked with large HOI metrics, and higher equality of opportunity for everyone. The third impact is due to the weighting used in the criteria used to select the applicants; the weighting has a rather small or no apparent impact on the HOI metrics at a given capacity. Family welfare summarizes the rank of school choice obtained in the simulated allocation. It is impacted by the algorithm used and the school capacity. When using Deferred Acceptance (DFA), parental satisfaction performs well at real (100%) capacity. It is highly impacted when the capacity is reduced, but only slightly impacted when expanding the capacity. Parents’ satisfaction increases in an analogous way, taking full advantage of the exceeding capacity. When running the matching with both lotteries, the family welfare gets slightly compromised when the applicant’s ranking for schools is accounted for in the logic.

The HOI metrics should be read cautiously and we must discuss the limitations of this work. First, the study excludes families who do not exercise choice. Families have their neighborhood school assigned by default, and the application to choice programs is optional. Consequently, the results cannot be generalized to all the families in the school district. Second, the study focuses only on magnet schools at the middle level. Although Charter schools and open choice are popular school choice options in SDHC, they were excluded from the study given the particularities of the options, as were the variations in student and school preferences at different levels (elementary, middle and high schools), which deserve separate treatment. Third, these data predate the COVID-19 pandemic, and parental school choice patterns may have shifted since then. Fourth, there are important omitted variables in the estimation. Most significantly, variables related to the applicant’s academic ability were not considered, so we could not model the impact related to this circumstance. Academic ability is mostly used in high school admission at SDHC. Fifth, the study assumes that families rank their true preferences, which are used as input for the simulations. Selection in SDHC is done by a computer lottery, which makes it infeasible for parents to be strategic about their choices (Prieto, Aguero-Valverde, Zarrate-Cardenas, & Van Maarseveen., 2018). Sixth, perhaps the most important limitation, the decision variables used to alter the school priorities consist of one continuous dimension and five binary ones. Although binary data is simpler to read, its usage is limited due to less data variability, loss of power to detect differences, and less sensitivity to change. Fifth, the HOI metrics per se do not reveal which are the unequal circumstances that contribute to IOP. The circumstance groups are formed based on combinations of variables, and such a technique makes it tough to discover what is going on. If instead of defining the groups based on ten variables, we would repeat this exercise using only three variables, then the HOI indexes would change – they still account for between-group differences, the source of inequality is associated with the variables considered, and it is still hard to discover what is happening with the HOI metrics per se. To counter this limitation, the HOI metrics should be analyzed along with the regression coefficients and probabilities, and the Shapley decomposition. We completed this analysis, but due to space restrictions, the outcomes are not presented.

The focus of this research is about equality and not equity. Equality in education asserts that every student is given the same resources or opportunities, and should have the same access to high-quality education, regardless of their background, circumstances, and abilities. On the other hand, equity recognizes that each student has different needs and talents, and allocates the exact resources and opportunities needed to reach an equal outcome. For instance, if an applicant with learning disabilities (LD) applies for school admission and his/her grades and standardized test scores are low as a result of this disability, an equality admission policy would give an LD applicant the same chances as any other applicant. In contrast, an equity admission policy would prioritize an LD applicant by increasing the chances of admission, by intentionally allocating him/her to a high-quality special education school, and assigning tailored resources which account for his/her limitations (i.e. offering extra effort to compensate for the disability) so that he/she can succeed in learning. We have not yet explored this dimension.

A natural continuation of this effort would be to do simulations focused on equity. Educational opportunities should aim at promoting the welfare of the least advantaged groups. Following affirmative action practices, which reserve preferential treatment for historically disadvantaged groups, a possible approach could be to carry out a longitudinal study to analyze over a long time period who had access to quality education and to identify the underrepresented groups. Based on this outcome, following the methodological framework proposed in this study, make the selection more unequal, by giving preferential treatment in admission to these historically under-represented groups. Finally, evaluate the effects of these policy changes, not in the admission group, but instead in the (new, simulated) school population, when the new incoming population of students is incorporated. This knowledge might be valuable for decision-makers in the design of an admission policy that has equity – instead of equality – as the primary objective.

Disclosure statement

No potential conflict of interest was reported by the author(s).