A Decomposition Approach to Distributed Control of Dynamic Deformable Mirrors

Abstract

Deformable mirrors with spatially invariant dynamic response can be considered as part of the class of decomposable systems. Such systems can be thought of as the interconnection of a number of identical subsystems, and they can be used to model certain classes of large scale systems. We show in this article that the technique allows the design of a distributed ℋ₂ controller for a deformable mirror of any size, with a computational cost that does not increase with the size of the mirror. The method shows a performance close to that of the centralized ℋ₂ optimal controller in a simulation example, which is about two times better (in terms of ℋ₂ norm) than the performance of a decentralized PI controller, with additional notches to suppress the high resonance frequencies of the deformable mirror.

Keywords:

• adaptive optics
• biharmonic operator
• decomposable systems
• distributed control
• thin plate PDE
• ℋ₂ optimal control

NOMENCLATURE

⊗	=	Kronecker product
Δ	=	smallest distance between actuators
γ	=	optimization parameter in LMI
λ	=	wavelength
	=	maximal/minimal/average eigenvalue
η	=	relative material damping
ζ	=	relative actuator damping
A	=	surface area
A •	=	state-transition matrix indexed by •
B •	=	input to state matrix indexed by •
C •	=	state to output matrix indexed by •
D	=	mirror diameter
D •	=	input to output matrix indexed by •
E	=	Young's modulus
𝒢	=	finite difference operator
ℋ2	=	class of causal operators that are bounded in 2-norm
I	=	moment of inertia
I N	=	identity matrix of size N × N
N	=	number of actuators
𝒫 N	=	pattern matrix of size N × N
ℝ	=	set of real numbers
S 1/2	=	shift operator along principal axis s 1/2
T s	=	sampling time
X, Y	=	decision variables in LMI
H i , J i , P i	=	decision variables in LMI
Fi , Li	=	decision variables in LMI
Qi , Ri , Wi	=	decision variables in LMI
ℤ	=	set of positive and negative integers
a	=	parameter of AR turbulence model
c	=	actuator stiffness
d	=	actuator damping
d k	=	wavefront phase distortion at time index k
f i	=	force supplied by actuator i
f k	=	vector stacking of actuator forces at time index k
h	=	plate thickness
i, j	=	indices refering to spatial dimensions
k	=	index refering to discrete time instants
p	=	actuator pressure
r 0	=	outer-scale of turbulence
s 1, s 2	=	principal axes in hexagonal grid
t	=	time instant
u k	=	control input at time index k
v k	=	measurement noise at time index k
w	=	deflection of the mirror
w k	=	vector stacking of mirror deflections at time index k
x	=	coordinate along x − axis
x k	=	state of state-space model at time index k
y	=	coordinate along y − axis
z k	=	residual phase at time index k

1. INTRODUCTION

Because of the turbulent nature of the atmosphere, light from distant stars and planets is distorted before being received by ground-based telescopes. The strength of the turbulence is usually quantified by the Fried parameter r ₀, which is the coherence length of the turbulence, i.e., the phase of the wavefront can be assumed to be flat over a distance of r ₀. The value of r ₀ depends on the observation conditions, and is typically in the order of 20–60 cm such that for telescopes with diameter D > r ₀ the angular resolution will not improve, unless the influence of the turbulence is compensated for. For this reason, adaptive optics systems that compensate for the aberrations of the wavefront are standard in ground-based telescope systems. For a good introduction to adaptive optics systems in astronomical observation, we refer to Roddier (1999), and for the application in vision science we refer to e.g., Hampson (2008).

In adaptive optics systems, a deformable mirror is controlled to counteract the spatially-distributed wavefront distortion with a spatial resolution equivalent to r ₀. Hence, the number of actuators scales with (D/r ₀)², which will be in the order of 10⁴-10⁵ for extremely large telescopes with diameters D > 30 m.

Because atmospheric turbulence is a dynamic phenomenon, the adaptive optics system needs to be sufficiently fast, and sampling times even below 0.5 ms may be necessary. With these high sampling frequencies, the deformable mirror in adaptive optics systems cannot be considered as a static system, since high frequency resonance modes can be excited as well, see e.g., Miller and Grocott (1999).

This article addresses the problem of efficiently controlling large scale adaptive optics systems with high spatial and temporal bandwidths. In the literature, much attention has been paid to the problem of efficient wavefront reconstruction and prediction, but the control of large scale dynamic deformable mirrors has not been addressed in much detail. In Miller and Grocott (1999), the dynamic control of large scale deformable mirrors has been addressed, under the assumption that the mirror dynamics can be described by circulant matrices, such that the system can be fully decoupled. In Andersen et al. (2006), a decoupling controller in a series with a decentralized controller is designed, but no guarantee of stability and optimality has been given. In Kulkarni et al. (2003), a distributed control approach has been applied to the control of a deformable mirror. This approach is comparable with the approach presented here, but is derived under the assumption that the mirror is of infinite dimension. This assumption is not needed for the approach presented here.

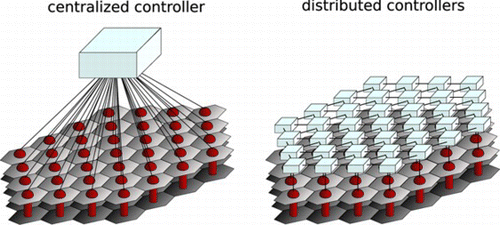
In this article, we also follow a decoupling approach, as in Miller and Grocott (1999) and Andersen et al. (2006), but we do not limit to systems described by circulant matrices. The proposed approach considers systems that are contained in the much broader class of decomposable system, which was introduced in Massioni and Verhaegen (2009), and for which a performance-based method for distributed control synthesis has been given. A distributed controller, as in Kulkarni et al. (2003), consists of a series of parallel low complexity controllers, where each of the low complexity controllers communicates with some of its neighbors (Figure 1). Distributed controllers can be implemented much more efficiently than a centralized controller because their complexity scales linearly with the number of control channels, whereas the complexity of (unstructured) centralized controllers scales up in a quadratic fashion. In Massioni et al. (2009), we have shown that static deformable mirrors with spatially invariant influence functions for all actuators are contained in the class of decomposable systems. In this article, we extend the results in Massioni et al. (2009) to dynamic deformable mirrors.

Figure 1 Centralized and distributed control. (Figure is provided in color online.).

Another result of this study is that if the function describing the cross-coupling has a certain regularity (or spatial invariance), then it is possible to obtain a distributed controller that consists of identical modules and that is proven to work for mirrors of any size. This would allow the implementation of such controllers in a truly modular fashion, as local computational units connected to each other, which achieve their performance goals regardless of the size of the mirror. The proof is obtained thanks to considerations on the spectrum of the matrices describing the actuator cross-coupling; under this perspective, the purpose of this article is similar to the one of Fax and Murray (2004) and Massioni and Verhaegen (2008), which presented methods allowing the synthesis of controllers for vehicle formations of any size, on the basis of the spectral properties of graph Laplacian matrices.

The article is organized as follows. Section 2 introduces adaptive optics and shows that dynamic deformable mirror can be considered as decomposable systems. Section 3 explains the theoretical background used in this article and it introduces the distributed control methods, showing a possible way of application to the distributed control of dynamic deformable mirrors. Section 4 presents a reasoning that allows the development of distributed controllers for mirrors of any size, with a constant computational cost. Numerical results are given in Section 5, and finally the conclusions are drawn in Section 6.

We denote by ℝ the field of real numbers, and by ℝ ^n×m the set of real n × m matrices. Let ⊗ indicate the Kronecker product, I _n the identity matrix of order n, and let j be the imaginary unit. The notation A≻0 indicates that all the eigenvalues of the Hermitian matrix A are strictly positive, and the bullet • denotes a symbol that is either not relevant or clear from the context.

2. DYNAMIC DEFORMABLE MIRRORS

Deformable mirrors are typically made of a thin reflective membrane or plate that can be shaped by means of an array of linear actuators, e.g., piezoceramic or electromagnetic as seen in Hamelinck et al. (2005). In Massioni et al. (2009), we considered deformable mirrors with a static Gaussian-shaped influence function. Here, we will assume that the deflection w(x, y, t) of the mirror can be described by the thin plate partial differential equation.

where ∇⁴ = (partialdiff⁴/partialdiffx ⁴ + 2partialdiff⁴/partialdiffx ²partialdiffy ² + partialdiff⁴/partialdiffy ⁴) the biharmonic operator, E the Young's modulus, I = h ³/12 the moment of inertia, η a material damping parameter, ρ the density, h the thickness of the plate, and p(x, y, t) the pressure excerted by the actuators (Timoshenko and Woinowsky-Krieger, 1959). The actuators are distributed over a spatial grid with equidistant spacing. In this article, we consider the case of a hexagonal pattern, which is common for deformable mirrors. However, the method can also be applied for other grids provided they have equidistant spacing. Each actuator consists of a parallel connection of a spring with stiffness c, a damper with damping constant d = ζc, and a force f _i that can be controlled, where i refers to the index of the actuator (Figure 2). See Hamelinck et al. (2005), for a similar deformable mirror configuration. Here, we assume that the stiffness and damping ratio of all actuators are equal.

Figure 2 A deformable mirror with a thin plate membrane suspended by springs with stiffness c and dampers with damping d = ζc, and controlled by force actuators.

The distance Δ between the actuators is considered to be small, such that the finite-difference discretization of Eq. (1) over the hexagonal grid of the actuators yields a sufficiently accurate model. The finite-difference approximation of the biharmonic operator over the hexagonal grid with unit distance between two neighboring points is given by Southwell (1946)

where S ₁ and S ₂ are the unit shift operators along the two principal axis s ₁ and s ₂ of the hexagonal grid, as indicated in Figure 3.

Figure 3 Infinite hexagonal grid, schematized as ℤ².

Then, if w(i, j, t) and f(i, j, t) are the displacement and force, respectively, at the point with discrete index (i, j), the finite-difference discretization of Eq. (1) interconnected with the actuators results in the following finite-difference equation.

where is the surface area of one element corresponding with one actuator. In the following, we will assume that w(i, j, t) = 0 for the grid points (i, j) outside the dimensions of the deformable mirror. This assumption corresponds with the clamped boundary condition. Other boundary conditions may be taken into account as well, though the spectral analysis in Section 4 may need some adjustment.

The deformable mirror described by Eq. (3) can be written as an interconnection of a series of equal and small size subsystems. The interconnection pattern is determined by the finite-difference operator Eq. (2). The next section will show how for this type of systems, which will be called decomposable systems, efficient and structured controllers can be derived. To show how Eq. (3) can be written as a decomposable system, we rewrite it in the following state-space form.

where [wdot] = partialdiffw/partialdifft and , and we have used and I = h ³/12. With some abuse of notation, we denote the vector stacking of the values w(i, j, t), f(i, j, t) and the (local) state x(i, j, t) = [w(i, j, t) [wdot](i, j, t)] ^T at, say N grid points (i, j) within the dimensions of deformable mirror, by w(t) ∈ ℝ ^N , f(t) ∈ ℝ ^N , and x(t) ∈ ℝ^2N . Then, the (global) deformable mirror model can be written as

where

and 𝒫 _N is a (sparse) pattern matrix, where the non-zero elements on each row are the coefficients of the operator 𝒢(S ₁, S ₂) in Eq. (2) and defines the coupling between subelements. Then, discretization w.r.t. time using a forward Euler discretization and a sampling time T _s yields the following discrete time system.

where w _k  = w(kT _s ), f _k , and x _k are defined similarly, and A _a  = I ₂ + T _s A _{a, c} , A _b  = T _s A _{b, c} , , , and C _a  = C _{a, c} .

In adaptive optics, the objective is to determine the controls u _k  = f _k of the deformable mirror, such that phase disturbances in the light beam reflected by the mirror are compensated. The deformable mirror generates an optical path difference of 2w _k , such that the phase shift of (4π/λ)w _k is obtained, where λ is the wavelength of the light beam. The phase disturbance will be modeled by a first order auto-regressive (AR) model.

where |a| ≤1 and v _k is a zero-mean stationary white noise process with unit covariance matrix. Then, the residual phase aberration is given by z _k  = (4π/λ)w _k  + d _k , and is given by the output of the following (integrated) state-space model.

where

We assume that the residual wavefront is measured or reconstructed from wavefront sensor measurements (Roddier, 1999). In optical imaging, the objective is to maximize the Strehl ratio, which, for small phase aberrations, is approximately equivalent to minimizing the mean square value of z _k as shown in Born and Wolf (1999), which is the same as minimizing ℋ₂ norm of the transfer function between the distortion v and the residual phase z in Eqs. (11) and (12).

3. DISTRIBUTED CONTROL OF DECOMPOSABLE SYSTEMS

The state-space models Eqs. (6)–(9), (11) and (12), are special cases of the class of decomposable systems. Before presenting the formal definition of such systems, we can say that these systems can be interpreted as the result of the interconnection of N identical subsystems of order l. The interconnection follows a pattern that is described by a pattern matrix 𝒫 _N ∈ ℝ ^N×N ; a sparse pattern matrix accounts for a limited interaction among the subsystems, that for example, can only influence a few neighboring elements. Some examples of systems that are included in this category can be found in vehicle formation control problems by Fax and Murray (2004), article machines by Stewart et al. (2003), and adaptive optics as is made clear in this article.

Definition 1 (Decomposable systems)

Let us consider the Nl-th order linear dynamical system described by:

where x ∈ ℝ ^Nl is the state, u ∈ ℝ ^{Nm _u} is the control input, w ∈ ℝ ^{Nm _w} is the disturbance, y ∈ ℝ ^{Nr _y} is the measured output, and z ∈ ℝ ^{Nr _z} is the performance output. We call such systems decomposable systems if and only if there exists a state-space realization that can be parameterized as

where 𝒫 _N ∈ ℝ ^N×N is a diagonalizable matrix (𝒫 _N  = Z ⁻¹ΛZ, where Λ is the diagonal matrix containing the eigenvalues), which we call pattern matrix. If the pattern matrix 𝒫 _N is symmetric, then we call the system a symmetric decomposable system (and the eigenvalues of 𝒫 _N are all real).

These systems have an interesting property that allows them to be decomposed into a set of N independent modal subsystems; hence the name. This property and its consequences for control design have been already explained in detail in Massioni and Verhaegen (2009). We invite interested readers to look into this reference for more insight. However, we summarize the main result that is used here.

Theorem 2 (Adapted from Massioni and Verhaegen, 2009)

Consider a discrete time symmetric decomposable system (Definition 1), with B _{u, b}  = 0, C _{y, b}  = 0, D _{zu, b}  = 0, and D _{yw, b}  = 0 (i.e., ℬ _u , 𝒞 _y , 𝒟 _zu , and 𝒟 _yw have only the block-diagonal part). A sufficient condition for the existence of a decomposable dynamic output feedback controller as in

that yields a ‖T _wz ‖_ℋ2  < γ is that the following coupled LMI constraints in

Eq. (16) have a feasible solution. The decision variables are X, Y, S, , , J _i , F _i , R _i , W _i , L _i , and Q _i for i = 1, 2. The matrices in bold font such as L _i , Q _i , A _i , etc., are shorthand notation for the following: , , etc., with and the maximum and minimum eigenvalue of 𝒫 _N , respectively; λ_av is the average of the eigenvalues, that can be easily computed as the trace of the pattern matrix divided by N (the trace is the sum of the eigenvalues). The state space matrices of the controller can be retrieved from the decision variables through the following relations.

Notice that the LMIs provide a sufficient condition only, so the method provides only suboptimal ℋ₂ controllers. Further, note that the structure of the controller Eq. (15) has the similar structure as the model of the system, Eqs. (11) and (12). Hence, when 𝒫 _N is a sparse matrix the controller will have a similar sparsity structure.

We notice that the parameters influenced by the pattern matrix are only its spectral properties, namely , , and λ_av. The value of λ_av can be determined by the trace of 𝒫 _N divided by N. Because the diagonal elements of 𝒫 _N are all given by , as follows from Eq. (2), independent of N. In the next section, we show how we can derive an upper bound for the maximum eigenvalue and a lower bound for the minimal eigenvalue of 𝒫 _N . Then, it can be shown (Massioni and Verhaegen, 2009) that the solution of the LMIs Eq. (16) for these upper and lower bounds for the maximum and minimum eigenvalues, also satisfies the LMIs for the actual maximum and minimum eigenvalues. So the solution obtained with the bounds of the eigenvalues would be applicable to all pattern matrices 𝒫 _N where N ≥ 1, and thus for any size N of the deformable mirror. This result is based on the fact that the spectrum of 𝒫 _N is constrained to be in a fixed interval Böttcher and Grudsky (2005, 245). The object of the next section is to provide a simple, self-contained proof for this statement.

4. SPECTRA OF INFLUENCE MATRICES

4.1. The Infinite Dimensional Case

In this section, we will show that the spectrum of all pattern matrices coming from the same spatially finite-difference operator (as in Eq. (2)) is bounded. In order to do so, we will first evaluate the spectrum of the pattern matrix (or better, operator) in the infinite case (N → ∞) by making use of the theory of spatially invariant systems by Bamieh et al. (2002), and then relate this result to finite truncations.

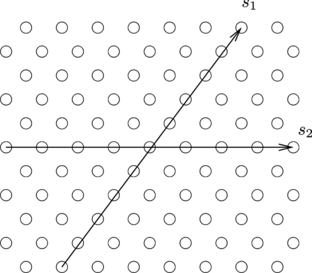
In the infinite case the finite-difference operator Eq. (2) is defined as a function on an infinite 2-D hexagonal grid (Figure 3). Recall, s ₁ and s ₂ are two directions or coordinates, then the deflection of the mirror w(i, j, t) for a fixed time instant t can be considered as a real functions of these coordinates (x = x(s ₁, s ₂): ℤ² ↦ ℝ).

We define for two functions x and y of this kind an inner product rule.

and a norm,

We define as ℒ₂ the set of the functions whose norm is finite, and we restrict our attention to functions in this set. Let us consider the operators mapping ℒ₂ to ℒ₂. The finite-difference operator Eq. (2) is such an operator that maps signals in ℒ₂ to ℒ₂. Consider the expression,

Because of the operator 𝒢 given by Eq. (2) contains terms with for (i, j) different from zero, there is a cross-coupling in Eq. (20). This cross-coupling, however, can be diagonalized by means of a Fourier transform Rudin (1962) in two dimensions. Let , , and be the 2-D Fourier transforms of x(s ₁, s ₂), y(s ₁, s ₂), and 𝒢(S ₁, S ₂), respectively, then Eq. (20) can be rewritten in the Fourier domain as

where z ₁ and z ₂ are complex numbers on the unit circle. Note, that is formally equivalent to 𝒢 with S ₁ and S ₂ replaced by z ₁ and z ₂, such that by using Eq. (2) we can write as

where we have made use of the fact that z ₁ and z ₂ are on the unit circle, such that z + z ⁻¹ = 2Re(z) for z = z ₁, z ₂.

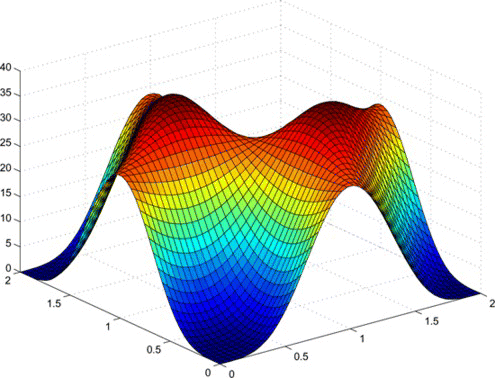
Hence, the spectrum of 𝒢 is given by the interval whose bounds are the lower and upper value of the (continuous) function with z ₁ = e ^{j θ ₁} , z ₂ = e ^{j θ ₂} , and θ ₁, θ ₂ ∈ [0, 2π]. Gridding and plotting the function as seen in Figure 4, we find global maximum and minimum that allows stating that the spectrum is given by the interval [0, 36]. Thus, the smallest upper bound for is given by 36 and the highest lower bound for is given by 0. Note, that the average eigenvalue for all N, is slightly larger than half the upper bound of the maximum eigenvalue .

Figure 4 Spectrum of the operator 𝒢. (Figure is provided in color online.).

4.2. From Infinite to Finite

We now consider finite influence matrices that can be considered as truncations of the operators, and we try to relate the spectrum of the former to the one of the latter. In order to do so, we first state some properties of the operator 𝒢. Here, we assume 𝒢 is given by the general form

Note, that Eq. (2) is a special case of Eq. (23).

Lemma 3 (Properties of 𝒢)

	𝒢 is self-adjoint: ⟨x, 𝒢y⟩ = ⟨𝒢x, y⟩ ∀ x, y ∈ ℒ2
	𝒢 is translation invariant: (S 1𝒢)x = 𝒢(S 1 x), (S 2𝒢)x = 𝒢(S 2 x) ∀ x ∈ ℒ2
	𝒢 is bounded if exists and is a finite number.

Proof

	From Eqs. (20) and (18): as ζ depends only on the distance, then we have that . Recognizing that: this proves this part of the lemma.
	From Eq. (20): proving immediately what is stated.
	It is immediate to see that for any x ∈ ℒ2, it holds that ‖𝒢x‖ ≤I ζ‖x‖.

Theorem 4

For any arbitrary bounded self-adjoint operator ℱ, the following,

are spectral points, and the spectrum is contained in the interval (Rudin, 1977).

Theorem 5

Consider a finite subset 𝔾 ⊂ ℤ², and the functions g: 𝔾 → ℝ. Let us define the embedding operator x _g mapping functions of 𝔾 to functions of ℤ².

Let us also define the restriction operator mapping functions of ℤ² to 𝔾,

Notice that the restriction operator is the adjoint of the embedding operator. We define as G the linear function mapping the space of the real functions in 𝔾 to itself as follows.

Notice, that g corresponds to a vector in ℝ ^k , where k is the number of elements in 𝔾, and that G corresponds to the finite pattern matrix previously defined, mapping the space of vectors ℝ ^k into itself. Then it holds that,

Proof

We only show that , the rest of the theorem can be similarly proven. From Theorem 4 we have that,

where we exploited the fact that the set of x ∈ {x _g g: ‖g‖ = 1} is a subset of all the x: ‖x‖ = 1.

The concept expressed in Theorem 5 can be summarized as follows. The maximum and minimum values of the spectrum of a linear, bounded, self-adjoint (symmetric) operator are bounds for the spectrum of any finite-linear operator (matrix) resulting from a truncation. This means that the upper and lower bounds of the spectrum of the operator are also upper and lower bounds for any finite-pattern matrix stemming from the same spatially invariant influence function. So, by choosing these bounds for and for the optimization problem in Eq. (16), we can find a suboptimal ℋ₂ controller that is applicable to any mirror with the same finite-difference operator, regardless of size and shape.

5. SIMULATION RESULTS

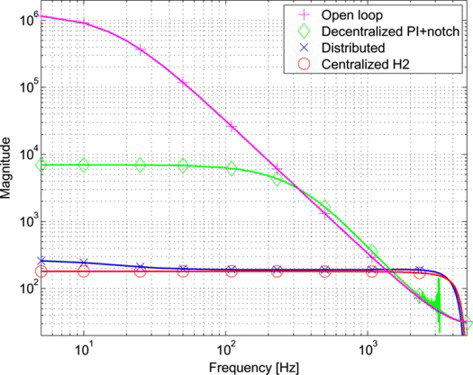
Simulations have been performed with an aluminum membrane mirror with Young's modulus E = 69 GPa, density ρ = 2.7·10³ kg, and thickness h = 10⁻⁶ m, actuated by 127 force actuators positioned on a hexagonal grid of seven rings with an inter-actuator distance of Δ = 3·10⁻³ m. The springs in parallel to the force actuators have a stiffness of c = 30 N/m. The material and the actuator damping ratios are η = ζ = 10⁻⁴. The measured output is the residual phase z collocated with the actuator positions. The system is discretized using a sampling time of T _s  = 10⁻⁴ s. The disturbance is modeled by a first order AR process as in Eq. (10), with a = 0.99. At low frequencies, the stiffness c = 30 N/m of the springs is dominant and the system is approximately diagonal. At the frequencies above 3 kHz the structural vibrations due to the elasticity of the membrane are dominant, resulting in resonances as can be seen from Figure 5.

Figure 5 Magnitude of the transfer between the first actuator and sensor of the deformable mirror plant, the loop gain, and the PI +notch controller. (Figure is provided in color online.).

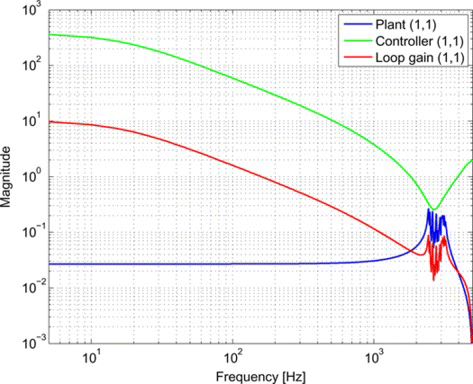
A distributed controller minimizing the ℋ₂ norm between v and z has been computed by solving the LMI problem Eq. (16). For comparison, the centralized ℋ₂ optimal controller has been computed and a diagonal PI controller with a pole at 0.99 and a notch at 3.5·10³ Hz has been tuned close to optimality (Figure 5). The notch has been added to suppress the high frequency resonances due to the elasticity of the membrane.

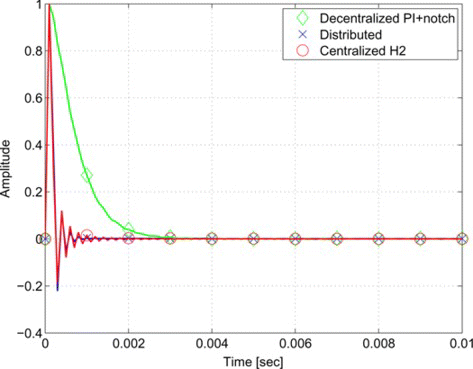
Table 1 gives the resulting ℋ₂ norms. It can be seen that the performance obtained by the distributed controller is very close to the performance obtained by the ℋ₂ optimal centralized solution; whereas, the decentralized PI +notch controller results in a rather conservative performance.

Table 1. ℋ₂ performance from disturbance w to output y with various control methods

Method	ℋ2 norm
Open-loop	50.8
Decentralized PI +notch	24.1
Distributed	12.4
Centralized ℋ2	12.3

Figure 6 shows the mean squared error spectral density of the output z as a response to v being a zero-mean white noise process with unit covariance, i.e., the frequency distribution of the ℋ₂ norm. We observe that the decentralized PI controller shows resonant behavior at the high frequencies, whereas the distributed and the centralized ℋ₂ optimal controller provide a well damped closed loop. Figure 7 shows the closed loop impulse responses from the first disturbance input to the first output obtained by the various controllers.

Figure 6 Spectral density of the mean square error with unit-covariance zero-mean white noise as input. (Figure is provided in color online.).

Figure 7 Impulse response of the first disturbance input to the first output. (Figure is provided in color online.).

6. CONCLUSIONS

We have shown that a deformable mirror, described by the thin plate partial differential equation, is a decomposable system under the assumption that the spatial derivatives can be approximated by finite-differencing. The decomposable system describing the deformable mirror consists of a series of identical subsystems which are interconnected only with neighboring subsystems in a way described by a sparse pattern matrix. A controller has been designed that has the same decomposable structure as the system, such that its implementation can be efficiently distributed over a number of interconnected parallel processors. Simulations have shown that almost no performance is sacrificed in comparison with the ℋ₂ optimal performance.

Future developments of the research will see the application of the method on an adaptive optics breadboard, and the possibility of applications of the methods to the problem of wavefront reconstruction and the use of spatial correlation in turbulence data will be investigated as well.

ACKNOWLEDGMENT

This research is supported by the MicroNed programme, an initiative of the Dutch Government.