Modeling of Pull-In Instability of Nano/Micromirrors Under the Combined Effect of Capillary and Casimir Forces

Abstract

In the current article the effect of the Casimir force on the static behavior and pull-in characteristics of nano/micromirrors under capillary force is investigated. At the first, the dimensionless equation governing the static behavior of nano/micromirrors is obtained. The dependency of the critical tilting angle on the physical and geometrical parameters of the nano/micromirror and its supporting torsional beams is investigated. It is found that the Casimir effect can considerably reduce the pull-in instability limits of the nano/micromirror. It is also found that rotation angle of the mirror under capillary force highly depends on the Casimir force applied to the mirror. Finally the analytical tool Homotopy Perturbation Method (HPM) is utilized for prediction of the mirror's behavior under combined capillary and Casimir forces. It is observed that a sixth order perturbation approximation accurately predicts the rotation angle and stability limits of the mirror. Results of this article can be used for successful fabrication of nano/micromirrors using the wet etching process where capillary force plays a major role in the system.

Keywords:

• capillary force
• Casimir force
• HPM
• nano/micromirror
• pull-in

NOMENCLATURE

A wet	=	wet area of the plate
c	=	speed of light
F cap	=	capillary force
F Cas	=	Casimir force
G	=	shear modulus of elasticity of the beam's material
h	=	initial distance between the mirror and the substrate
I p	=	momentum of inertia of the beams cross section
l	=	length of each torsion beam
L	=	length of mirror
P cap	=	capillary pressure
r	=	width of the torsion beams cross section
s	=	length of the torsion beams cross section
U	=	potential strain energy of the torsion beams
U tot	=	interfacial energy
V	=	potential energy of applied loads
W	=	width of mirror
W e	=	work done by external forces
Greek Letters	=
γ	=	surface energy of the liquid
γ LA	=	liquid-air interfacial tensions
γ SA	=	solid -air interfacial tensions
γ SL	=	solid-liquid interfacial tensions
∏	=	total potential energy of the system
θ	=	tilting angle of the mirror
θ c	=	contact angle
Θ	=	dimensionless tilting angle of the mirror

1. INTRODUCTION

The technology of MEMS devices has experienced a lot of progress recently. Their low manufacturing cost, batch production, light weight, small size, durability, low energy consumption, and compatibility with integrated circuits, makes them extremely attractive (Maluf and Williams 1999; Younis 2004). Successful MEMS devices rely not only on well developed fabrication technologies, but also on the knowledge of device behavior, based on which a favorable structure of the device can be forged (Chao et al. 2006). The important role of MEMS devices in optical systems initiate the development of a new class of MEMS called MicroOptoElectroMechanical Systems (MOEMS). MOEMS mainly include micromirrors and torsional micro-actuators. These devices have found a variety of applications such as digital micromirror devices (DMD) (Hornbeck 1991), optical switches (Ford et al. 1999), micro scanning mirrors (Bai et al. 2007; Dickensheets and Kino 1998), optical cross connects (Zavracky et al. 1997), and etc.

The existence of a liquid bridge between two objects results in the forming of capillary force (Wei and Zhao 2007). The existence of capillary force even in low relative humidity is observed experimentally (Zwol et al. 2008). Parallel plate MEMS actuators are conventionally fabricated by forming a layer of a plate or beam material on the top of a sacrificial layer of another material and wet etching the sacrificial layer. In this process, capillary force can be easily formed and in the case of poor design, the structure will collapse and adhere to the substrate. So investigating the effect of capillary force on micromirrors is extremely important in their design and fabrication.

Many researchers investigated the effect of capillary force on MEMS devices. Mastrangelo and Hsu (1993) studied the stability and adhesion of thin micromechanical structures under capillary force, theoretically and experimentally. Moeenfard et al. (2010) studied the effect of capillary force on the static pull-in instability of fully clamped micromirrors. The effects of capillary force on the static and dynamic behaviors of atomic force microscopes (AFM) are widely assessed (Zitzler et al. 2002; Li and Peng 2006; Jang et al. 2004). Recently, the instability of torsional MEMS/NEMS micro-actuators under capillary force was investigated by Guo et al. (2009).

When the size of a structure is sufficiently small, Casimir and van der Waals forces play an important role and in the case of poor design, can lead to the collapse of the structure. VdW force is the interaction force between neutral atoms and it differs from covalent and ionic bondings in that it is caused by correlations in the fluctuating polarizations of nearby particles (Xie 2009). Casimir force is understood as the longer distances range analog of the vdW force, resulting from the propagation of retarded electromagnetic waves, whose distance ranges from a few nanometers up to a few micrometers (Gusso and Delben 2007). An important feature of the Casimir effect is that even though it is quantum in nature, it predicts a force between macroscopic bodies (Bordag et al. 2001). This makes the Casimir force relevant in N/MEMS (Zhao et al. 2003).

Zhao et al. (2003) discussed the Casimir force induced adhesion in MEMS. Tahami et al. (2009) discussed Pull-in Phenomena and Dynamic Response of a Capacitive Nano-beam Switch by considering Casimir effect. Casimir effect on the pull-in parameters of nanometer switches has been studied by Lin and Zhao (2005a). They (Lin and Zhao 2005b) also studied Nonlinear behavior of nano-scale electrostatic actuators with Casimir force. Ramezani et al. (2007; 2008) investigated the two point boundary value problem of the deflection of nano-cantilever subjected to Casimir and electrostatic forces using analytical and numerical methods to obtain the instability point of the nanobeam. Modeling and simulation of electrostatically actuated nano-switches under the effect of Casimir forces have been studied by Mojahedi et al. (2009). Sirvent et al. (2009) theoretically studied pull-in control in capacitive microswitches actuated by Casimir forces using external magnetic fields. Effect of the Casimir force on the static deflection and stiction of membrane strips in MEMS have been studied by Serry et al. (1998). Guo and Zhao (2004) discussed the effect of Casimir force on the pull-in of electrostatic torsional actuators. But statical behavior and pull-in of single sided nano/micromirrors under effect of capillary and Casimir forces has not been investigated. So in this article, the combined effect of Casimir and capillary forces on the tilting angle and stability of torsional nano/micromirror is studied. In this study, HPM is used as a perturbational based analytical tool.

Perturbation methods have been used to analytically solve the nonlinear problems in MEMS. Younis and Nayfeh (2003) investigate the response of a resonant microbeam to an electric actuation using the multiple-scale perturbation method. Abdel-Rahman and Nayfeh (2003) used the same method to model secondary resonances in electrically actuated microbeams. Since perturbation methods are based upon the assumption that there is a small parameter in the equations, they have some limitations in problems without involvement of small parameters. In order to overcome this limitation a new perturbational based method, namely Homotopy Perturbation Method (HPM) was developed by He (2000). His new method takes full advantages of the traditional perturbation methods and homotopy technique. Homotopy perturbation method has also been used for solving the nonlinear problems encountered in N/MEMS. For example, Moeenfard et al. (2011) used HPM to model the nonlinear vibrational behavior of Timoshenko micobeams. Mojahedi et al. (2010) applied the HPM method to simulate the static response of nano-switches to electrostatic actuation and intermolecular surface forces. But so far no analytic solution has been presented to model the behavior of nano/micromirrors.

In the current article, the equations governing the static behavior of rectangular nano/micromirrors are obtained using the minimum potential energy principle. Then pull-in parameters of nano/micromirrors under the effect of Casimir and capillary forces are investigated. At the end, the tilting angle of a nano/micromirror under Casimir and capillary forces is calculated both numerically and analytically using HPM.

2. THEORETICAL MODEL

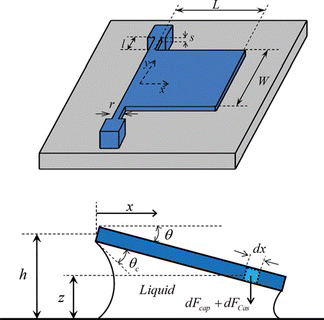
The contact angle θ _c for a liquid drop shown in Figure 1 a is determined by the balance among the liquid-air (LA), solid–air (SA), and solid-liquid (SL) interfacial tensions, which are denoted by γ _LA , γ _SA and γ _SL , respectively (Guo et al. 2009). At the equilibrium state, Young's equation (Knospe and Nezamoddini 2009) is satisfied as follows.

Figure 1 (a) Contact angle of a droplet at a solid-liquid interface (b) Liquid bridge between two parallel plates (color figure available online).

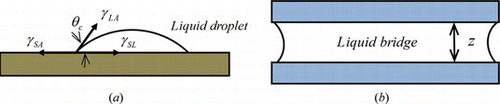
At the equilibrium state, the energy of the system shown in Figure 1 b is (Fortes 1982):

where U _tot is the interfacial energy, A _wet is the wet area of the plate, C is a constant and γ = γ _LA is the surface energy of the liquid. Since the volume of the liquid shown in Figure 1 b, v = z A _wet is constant, it can be easily concluded that:

The capillary force can be obtained from the interfacial energy as follows.

As a result, the capillary pressure underneath the plate is

Using the obtained equation for capillary pressure, the capillary force applied to the differential surface element of the micromirror shown in Figure 2 is

where h is the initial distance between the mirror and the substrate and θ is the tilting angle of the mirror.

Figure 2 Schematic view of a nano/micromirror (color figure available online).

Furthermore the differential Casimir force applied to a differential surface element of the mirror shown in Figure 2 is (Liu et al. 2010):

where c is speed of light, ℏ is Plank's constant divided by 2π and W is width of mirror as illustrated in Figure 2.

The minimum total potential energy principle (Rao 2007) is utilized here to obtain equilibrium equation and to investigate the stability of the equilibrium points. The total potential energy of the system can be divided into two parts: the potential strain energy of the torsion beams and the potential energy of applied loads which is equal to the minus of work done by external forces.

where ∏ is the total potential energy of the system, U is the potential strain energy of the torsion beams, V is the potential energy of applied loads and W _e is the work done by external forces. In equilibrium points, variation of the total potential energy of the system is zero.

The potential strain energy of system can be calculated as:

where (Huang 2004)

In this equation, G is the shear modulus of elasticity of the beam's material, l is length of each torsion beam and I _p is the polar momentum of inertia of the beams cross section which can be calculated using equation (12) (Huang 2004).

where r and s are the width and length of the torsion beams cross section respectively as illustrated in Figure 2.

The variation of U would be as

The total external work done on nano/micromirror to rotate it from angle θ to angle θ + δθ can be calculated as follows.

where L is length of mirror as illustrated in Figure 2. Since , the tilting angle is small, and sin θ can be closely approximated by θ. For simplification purpose, the following dimensionless variable is introduced.

where is the maximum physically possible rotation angle of the mirror.

At equilibrium points, equation (9) must be satisfied. So by performing the integration in equation (14), the equilibrium equation is obtained as follows.

where η and λ are called instability numbers and are defined as equations (17) and (18) respectively.

Performing the second variation operator on equation (8) and using equilibrium equation yields:

According to minimum total potential energy principle an equilibrium point is stable when δ²∏ > 0 and is unstable when δ²∏ < 0 (Gambhir 2004). So the stability condition is reduced to:

Finding η from equation (16) and substituting it in equation (20) leads to:

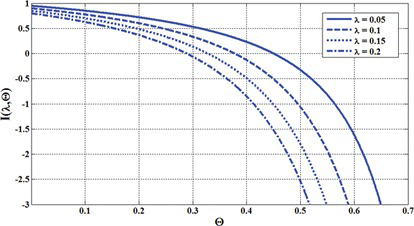
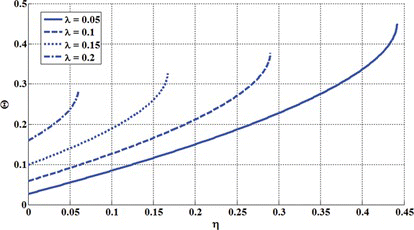
Figure 3 shows the function I(λ, Θ) versus Θ at some values of λ.

Figure 3 Function I (λ,Θ) versus Θ (color figure available online).

An equilibrium point is stable if I(λ, Θ) > 0 and unstable if I(λ, Θ) < 0. It is observed that at certain value of Θ called Θ _P , which relates to the pull-in state, I(λ, Θ) becomes zero. When Θ < Θ _P , I(λ, Θ) would be positive and the resulting equilibrium point is stable and when Θ > Θ _P , I(λ, Θ) would be negative and the resulting equilibrium point is unstable.

At the pull-in state, in addition to the equilibrium equations, the following equation is also satisfied.

Equations (16) and (22) can be solved simultaneously for finding η and λ at the pull-in. The results are as follows.

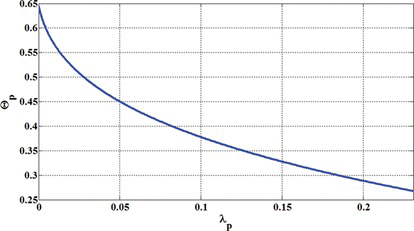
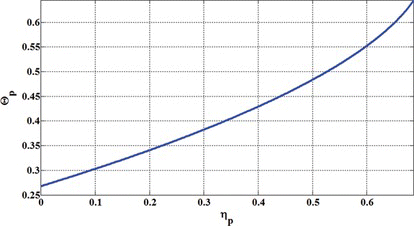
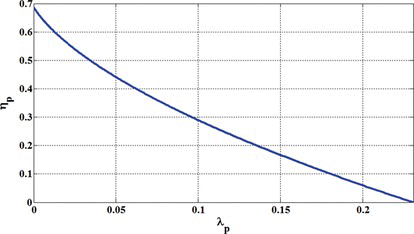
In equations (23) and (24), λ _P , η _P and Θ _P are the values of λ, η and Θ at pull-in, respectively. Figures 4 and 5 shows the values of pull-in angle versus λ _P and η _P , respectively. It is observed that with increasing the value of λ _P the pull-in angle of the mirror is reduced, while with increasing the η _P , the pull-in angle of the mirror is increased.

Figure 4 Pull-in angle of mirror versus λ_p (color figure available online).

Figure 5 Pull-in angle of mirror versus η_P (color figure available online).

By eliminating Θ _P between equations (23) and (24), η _P can be obtained versus λ _P as plotted in Figure 6. It is observed that by increasing the dimensionless Casimir force applied to the mirror λ _P , the mirror resistance to the capillary force is reduced and pull-in occurs at lower values of η. In fact this figure shows that Casimir force can significantly reduce the maximum allowable value for η and as a result, the stability limits of the nano/micromirror are reduced. In addition it can be concluded that even in the absence of capillary force, Casimir force can lead to the occurrence of pull-in. So, in order to have a successful and stable design for nano/micromirrors fabricated using wet etching process where capillary force plays a major role, the inequalities given in equation (25) have to be satisfied.

Figure 6 η_P versus λ_P (color figure available online).

In order to investigate the mirror's behavior under combined capillary and Casimir loading, the dimensionless rotation angle has been plotted versus η in Figure 7.

Figure 7 Stable equilibrium angle versus η (color figure available online).

It is observed that by increasing the value of η the rotation angle of the nano/micromirror is increased, but the maximum value of η at pull-in, highly depends on the value of λ and it is verified that by increasing λ, the maximum allowable value for λ is reduced. Furthermore it is concluded that at a constant η, larger values of λ would lead to larger values for stable equilibrium angle.

3. ANALYTICAL SOLUTION OF EQUILIBRIUM EQUATIONS

In this section, we try to find the value of the rotation angle of the nano/micromirror analytically in terms of η and λ. For this purpose, the analytical tool, HPM is utilized.

The linear part of equation (16) can be found by using Taylor series expansion of the equilibrium equation (16) as follows.

where L(Θ, η, λ) is the linear part of equation (16). Obviously the nonlinear part of equilibrium equation is obtained by subtracting L(Θ, η, λ) from equation (16).

Now, the homotopy form is constructed as follows.

In equation (28), is the homotopy form and P is an embedding parameter which serves as perturbation parameter. When P = 1, the homotopy form would be the same as the equilibrium equation and when P = 0, homotopy form would be the linear part of equilibrium equation. The value of the dimensionless rotation angle Θ can also be expanded in terms of the embedded parameter P as follows.

Substituting equation (29) into homotopy form yields:

The Taylor series expansion of right hand side of equation (30) in terms of P would be as

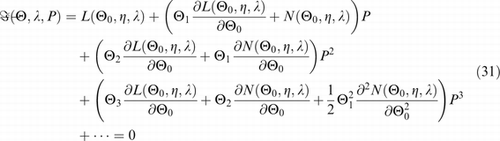
Since the homotopy form must be unified with zero, the coefficients of all powers of P must be zero. This, leads to the following equations.

With solving equations (32) to (35), the parameters Θ _i 0 ≤ i ≤ 3 are found as follows.

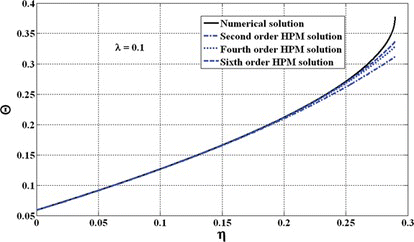
The value of Θ can be found by substituting Θ _i 0 ≤ i ≤ 3 and P = 1 in equation (29). In Figure 8 the results of the numerical simulations is compared with those of analytical HPM results for the special case of λ = 0.1. It is observed that HPM closely approximates the rotation angle of the mirror. Obviously increasing the order of perturbation approximation would lead to more precise results, but increasing the order of the perturbation approximation more than 6 will not improve the accuracy of the obtained response significantly. As a result, a sixth order perturbation approximation used in HPM can precisely predict the nano/micromirror behaviour under the combined effects of capillary and Casimir force.

Figure 8 Estimation of nano/micromirror's rotation angle using HPM (color figure available online).

4. CONCLUSION

The dimensionless equilibrium equation of the nano/micromirror under capillary force was obtained considering Casimir force. The dependency of the critical tilting angle on the instability numbers defined in the article was investigated. Results show that neglecting the Casimir effect on the static equilibrium of nano/micromirrors under capillary force may lead to considerable error in predicting stability limits of the mirror and can lead to an unstable design.

It was observed that rotation angle of the mirror due to capillary force highly depends on the Casimir effect applied to the mirror. HPM was utilized to analytically predict the rotation angle and stability limits of the nano/micromirrors. It was found that a sixth order perturbation approximation can accurately estimate the rotation angle of the mirror due to capillary and Casimir loading. The presented results in this article can be used for stable design and fabrication of nano/micromirrors using wet etching process where the gap between the mirror and the underneath substrate is less than a few micrometers and as a result, both capillary and Casimir forces have significant effects on the system.