High-resolution data assimilation through stochastic subgrid tensor and parameter estimation from 4DEnVar

Abstract

In this paper, we explore a dynamical formulation allowing to assimilate high-resolution data in a large-scale fluid flow model. This large-scale formulation relies on a random modelling of the small-scale velocity component and allows to take into account the scale discrepancy between the dynamics and the observations. It introduces a subgrid stress tensor that naturally emerges from a modified Reynolds transport theorem adapted to this stochastic representation of the flow. This principle is used within a stochastic shallow water model coupled with an 4DEnVar assimilation technique to estimate both the flow initial conditions and the inhomogeneous time-varying subgrid parameters. The performance of this modelling has been assessed numerically with both synthetic and real-world data. Our strategy has shown to be very effective in providing a more relevant prior/posterior ensemble in terms of the dispersion compared to other tests using the standard shallow water equations with no subgrid parameterization or with simple eddy viscosity models. We also compared two localization techniques. The results indicate the localized covariance approach is more suitable to deal with the scale discrepancy-related errors.

Keywords:

• uncertainty quantification
• 4DEnVar
• parameter estimation

1. Introduction

The numerical simulation of all the scales of geophysical fluid flows up to the smallest dissipation scales remains nowadays completely intractable due to the dimension of the problem to handle (which scales as the cube of the Reynolds number). For atmospheric flows, for instance, the spatial scales range from several millimetres to thousands of kilometres. The temporal scale is also huge and goes from decades to seconds. Many of the physical processes related to the submeso-scale and micro-scale of the geophysical systems are left unresolved. However, due to non-linear interactions between scales, it is important to understand the actions of those unresolved components to take them into account in a large-scale representation of the dynamics.

For several years, there has been a growing interest in modelling the unresolved processes through random terms. In that respect, the simplest method consists in introducing random forcing terms into the flow dynamics equations (Leith, 1990; Mason and Thomson, 1992; Buizza et al., 1999; Shutts, 2005; Slingo and Palmer, 2011). This kind of methods is often coupled to the usual subgrid-scale (SGS) parameterization used in deterministic large-scale approaches where the statistically averaged flow on a coarse grid is solved directly and the effects of the small unresolved scale on the large resolved scales are modelled thereafter. Those models of the Reynolds stress reflect primarily the dissipation due to turbulence while stochastic subgrid closure terms have been proposed to model also the energy backscattering from small to large scales (Frederiksen et al., 2013).

Another way of considering the stochastic nature of the neglected scales is to study directly the governing differential equations driven by stochastic processes. To that end, a stochastic dynamics modelling is proposed in Mémin (2014). In this approach, which constitutes the fundamental cornerstone to this article, the author proposed to introduce the stochasticity from the very beginning in the dynamics physical derivation.

The basic idea is built on the assumption that the Lagrangian fluid particle displacement results from a smooth velocity component and a fast oscillating stochastic velocity component uncorrelated in time,(1)

with denoting the flow map at time t, the smooth fluid particles’ velocity corresponding to the sought ‘large-scale’ solution and a d-dimensional Wiener increment (). The term represents the fast-changing fluctuation associated to turbulence; it has a much lower time scale than , the smooth component. Both and require to be solved or modelled. Stochastic calculus principles provide then the rules to derive the expressions describing the evolution of functions of such flows.

Large-scale models are usually assessed and calibrated by comparing simulated results and data. Opposite to the sparse heterogeneous network of in situ measurements, satellite image data exhibit a spatial resolution that is finer than the resolved scales at which the state variables are solved through a filtered dynamics. This still increasing scale discrepancy due to the rapid technological progress of satellite sensors advocates the set-up of methods enabling to calibrate the numerical flow model from high-resolution data. The data assimilation (DA) approach can indeed serve this purpose. Note that image data assimilation is a research topic drawing more and more attention since the last decades and several strategies have been proposed to deal with these difficulties (Papadakis and Mémin, 2008; Corpetti et al., 2009; Cuzol and Mémin, 2009; Titaud et al., 2010; Beyou et al., 2013; Huot et al., 2013; Bereziat and Herlin, 2015; Chabot et al., 2015).

Traditionally, data assimilation techniques are widely used to recover as exactly as possible the initial condition given a dynamics model, a certain span of time called assimilation window and some observations across this window (Talagrand, 1997). The initial condition is crucial for Numerical Weather Prediction (NWP) systems but the inference of the models’ parameters is also tractable through the data assimilation process. In a broader sense, the assimilation technique discussed in this article can be viewed as a learning process of a dynamic model on the basis of the observations available by adjusting the model’s parameters.

Data assimilation techniques are classically categorized into two groups. The first group, referred to as variational assimilation techniques, is formulated from the optimal control theory and variational calculus (Lions, 1971; Le Dimet and Talagrand, 1986). The second group of ‘ensemble methods’ originates from Monte Carlo Bayesian filtering principles (Gordon et al., 1993; Evensen, 1994). The parameter estimation problem can also be divided in the same spirit into those two groups.

In the former approach, the estimation consists in considering the unknown parameters as a control parameter as proposed by Navon (1998). Consequently, the objective of the variational system is to find the optimal initial condition and the associated optimal parameters for which a system trajectory fits best the available observations. Several works in this vein can be found in Cacuci et al. (2013), Navon (1998), Zhu and Navon (1999), Pulido and Thuburn (2005).

The latter approach is a direct extension of standard ensemble Kalman filter methods. Within this framework, one can choose freely the specific ensemble filtering schemes in terms of specific applications Zupanski and Zupanski (2006), Tong and Xue (2008), Yang and Delsole (2009), Bocquet and Sakov (2013b), Ruiz et al. (2013), Tandeo et al. (2014), Sawada et al. (2015).

In this article, we propose to use an ensemble-based variational scheme which gathers the advantages of both the variational assimilation schemes and the ensemble-based sequential methods (Yang et al., 2015). In addition to the obvious opportunity of not requiring any adjoint dynamical models, ensemble-based schemes provide other benefits, especially when considering stochastic dynamics. As a matter of fact, ensemble prediction systems are becoming more and more crucial in meteorology and oceanography. In that respect, under-dispersion of the ensemble greatly jeopardizes forecasting quality (Slingo and Palmer, 2011). Such underestimation of the ensemble spread is usually related to the unawareness of the uncertainties associated with the dynamic system. Recent studies show that the quality of the ensemble spread can be significantly improved by not only perturbing the initial condition but also some parameters related to the dynamics (Wei et al., 2013; Yang et al., 2015). Those facts advocate the set-up of physically relevant stochastic dynamical models coupling the random production terms and the dissipation term.

Within this paper, we focus on the specification through high-resolution image data assimilation of the dynamics model uncertainties. A fully justified argument on the derivation of the stochastic fluid flow dynamics is not the main purpose here. This framework is briefly reviewed in Section 2; then, we introduce on this basis the stochastic shallow water system. In Section 3, we investigate methods for estimating a central object called the quadratic variation tensor from the data. Model and experimental settings, results and discussions with some concluding remarks are provided in the following sections.

2. Stochastic modelling

Analogously to the standard deterministic case, the derivation procedure from the physical conservation laws of the Navier–Stokes equations is based primarily on the Reynolds transport theorem (RTT). In our context, the RTT consists of a stochastic expression of the rate of change of a given quantity (mass, momentum and energy) in a material volume. A comprehensive derivation process of this theorem (Mémin, 2014) is presented in Appendix 1 for reader convenience.

Applied to scalar function, q, the expression of the RTT within a volume transported by a stochastic flow (1(1) ) with an incompressible small-scale velocity component () is given by:(2)

This modified RTT involves the time increment of function q (the differential of q at a fixed point) instead of the time derivative. A diffusion operator emerges also naturally. For clarity’s sake, this term is designated as ‘subgrid stress tensor’ following the protocols of large eddies simulation (LES). However, its construction is quite different. It is not based on Boussinesq’s eddy viscosity assumption nor on any structural turbulence models (Sagaut, 2006) but arises from stochastic calculus rules. It expresses the mixing process exerted by the fast oscillating velocity component. This diffusion term is directly related to the small-scale component through the variance tensor, , defined from the diagonal of the uncertainty covariance:

The variance tensor corresponds to an eddy viscosity term (with units in ).

A corrective advection term, , appears also in the stochastic RTT formulation. This correction expresses the influence of the small scales inhomogeneity on the large ones. A drift is engendered from the regions associated with maximal variance (maximal turbulent kinetic energy – TKE) towards the area of minimum variance (e.g. minimal TKE). For homogeneous noise (i.e. within a homogeneous turbulence assumption), the variance tensor is constant and this corrective advection does not come into play.

Through this modified RTT, stochastic versions of the mass and momentum conservation equations can be (almost) directly derived. Incompressibility conditions can for instance be immediately deduced from the RTT applied to and the flow jacobian (J):(3)

Together with the incompressibility of the random term, the incompressibility condition reads thus:(4)

Imposing, a priori, an incompressibility condition to the large-scale component, , simplifies the previous constraint as:(5)

Note that for a homogeneous unresolved velocity, the last condition is naturally satisfied since this unresolved velocity component is associated with a constant variance tensor, . It should be stressed that condition (4(4) ) corresponds to a weaker form of the incompressibility constraint in the sense that it does not impose an incompressibility condition to the large-scale component but only to the effective drift. It has the advantage not to include a cumbersome condition on the variance tensor.

In the following section, we will briefly present how this principle can be applied to derive a stochastic expression of the shallow water equations. Those expressions are derived from the application of the stochastic RTT to the linear momentum conservation principle. Interested readers may consult (Mémin, 2014) for a thorough development or (Resseguier et al., in press-a, in press-b, in press-c) for the derivation and the analysis of general geophysical flow models and their quasigeostrophic approximations.

2.1. The stochastic 2D non-linear shallow water model

Considering the usual assumptions underlying the constitution of the shallow water model: the depth is shallow compared to the horizontal dimension, the friction forces and the vertical shear on the velocity horizontal components can be neglected, the external force is only due to gravity, we get the following 2D momentum equations for the horizontal velocity components (where superscript ‘h’ stands for the horizontal coordinates)(6) (7) (8)

The last equation arises from a balance of the advected Brownian term and the random pressure, , associated to the random small-scale component. This equation stems from a separation principle between the smooth terms and the Brownian terms. It can be noted that in those equations the noise components are assumed to depend only on the horizontal components. Thus, the diffusion tensor as well as the variance tensor does not depend on depth. These equations are complemented by the three incompressibility constraints (5(5) ). The noise component (and its related variance tensor) as well as the horizontal velocity component can be interpreted as depth-averaged components of the 3D velocity and uncertainty components, respectively. Integrating the incompressibility constraints () and () along the depth from the bottom to the surface , we get from the effective drift expression (7(7) ):

and

We may have noticed that for () we recover the traditional balance between the divergence of the horizontal averaged velocity components and the vertical motions at the interfaces. In the same way as in the traditional setting, considering the difference of the kinematic boundary conditions at the surface and the still bottom, and introducing the previous relation for the depth variable, , the shallow water continuity equation reads:(9)

It should be remarked that this continuity equation involves the horizontal components of the (divergence free) effective advection term: . The term plays the role of an additional forcing condition that ensues from the small-scale inhomogeneity. For smooth enough fluctuation variances, this forcing is negligible.

Introducing the hydrostatic balance (which is well respected in the shallow water model due to a negligible vertical acceleration), the pressure (after depth integration and with a boundary condition provided by the atmospheric pressure at the water–air interface) and its gradient reads, respectively,(10)

We get hence the following horizontal linear momentum conservation equation:(11)

It is important to outline that the free surface acts here as a random forcing term on the momentum equations. It is driven by the stochastic evolution of the height variable (9(9) ). For a deterministic height evolution such as the one associated to the mean depth evolution conditionally to a deterministic velocity field, the momentum equation would provide the velocity fields attached precisely to this particular (mean) instance of the evolving free surface.

The uncertainty formalism allows us to obtain the 2D shallow water equation in the form of (9(9) , 8(8) ). It can be observed that the dissipative terms emerged both in the continuity equation and in the momentum conservation equation. It is similar in spirit to the eddy viscosity assumption used in LES and Reynold average numerical simulation (RANS). Nevertheless, our subgrid-scale model takes its origin in the stochastic representation of the uncertainty associated to the model itself. No extra assumption is needed. However, their similarities indeed bring us another perspective for the interpretation of the subgrid-scale effect. For instance, it can be shown (Mémin, 2014) that setting the variance tensor as:(12)

with the eddy viscosity coefficient(13)

corresponds, for smooth enough rate of strain tensor norm, to the famous Smagorinsky (1963) subgrid model.

2.2. Conservative form

The conservative form of shallow water equations is usually more useful when implementing the finite volume method. It can be inferred directly by combining Equations (8(8) ) and (9(9) ). Alternatively, one can deduce such a form by integrating Equation (9(9) ) along the depth from the bottom to the surface . Finally, we have, (note we dropped in the following the subscript h for sake of clarity; all the vectorial variables and spatial derivative operators represent planar vectors and derivations w.r.t. horizontal components, respectively)(14)

As previously indicated, if the focus is only on the ensemble average depth evolution (denoted by ) or if the noise is assumed to live on iso-height surfaces (i.e ) , the above equation greatly simplifies as it boils down to a deterministic system: (15a) (15b)

This system, as opposed to the usual deterministic Shallow water model, still includes additional subgrid terms that depend on the variance of the small-scale random component.

2.3. 1D stochastic shallow water equation

The tests shown in the next sections are carried out with a 1D stochastic shallow water equation since it is less time-consuming but remains representative of the considered dynamics. The 1D stochastic shallow water system simply reads, (16a) (16b) and the mean depth and its associated horizontal fields satisfy, (17a) (17b)

As stated before, one of the main motivations of our approach is to propose methods for the assimilation of fine resolution image data. An interesting idea consists thus in estimating the diagonal quadratic variation tensor, , or to model the (plain) diffusion tensor, , from the statistical variations of small-scale velocity measurements extracted from image data (Heitz et al., 2010).

In the following experiments, we will restrain our interests to the horizontal mean flow fields described in Equations (17) and (15). However, the use of the full stochastic model with the noise forcing terms is also a possible alternative (Miller et al., 1999) that will be explored in a future study for data assimilation methods expressed in a stochastic filtering context.

3. Estimation of the quadratic variation tensor from data

3.1. Estimation by explicit formulation

Several immediate and simple strategies can be used to define the variance tensor. As detailed previously, an explicit form of this tensor can be given so as to recover classical subgrid models. However, the specific statistical nature of this tensor allows us to specify a variety of empirical forms for this tensor (Kadri Harouna and Mémin, 2016). For instance, it can be defined from local velocity covariances matrices estimated on local spatial or temporal neighbourhood. The previous estimation methods are easy to implement, but constitute only rough approximations as they rely either on the resolved components or on the flow velocity measurements, which are in practice large-scale observations (Heitz et al., 2010). A more accurate way of estimating the parameters is through a data assimilation process.

3.2. Estimation through data assimilation process

Data assimilation techniques consist in estimating the evolution of a given state variable, denoted , by associating measurements, , of this system with a dynamics model. The evolution model will be denoted in a general way as(18) (19)

It involves a non-autonomous differential operator – usually non-linear – that depends in our case on the variance tensor, . The second equation defines the initial state, , which is assumed to be known up to a zero Gaussian noise, , of covariance . The integration of the initial forecast guess, , is called the forecast trajectory, . It is usually fixed from a previous assimilation result on an anterior temporal window. Note that depending on the context, is also referred as the background. The observations, , and the state variable are linked together through an observation operator (20)

The error, , between the measurements and the state is assumed to be a zero mean Gaussian random field with a covariance tensor, . This noise is assumed to be uncorrelated from the state variable.

Optimal parameter can be found through data assimilation techniques along with the system state. The strategies are formulated as the minimization with respect to control variables (here the initial condition and the variance tensor) of an energy functional encoding a distance between the data and a state variable trajectory with low values of the parameters norm. In our approach, we express the cost function in an incremental form (Courtier et al., 1994), with a Mahalanobis norm where is an inverse covariance matrix and (f, g) is the inner product:(21)

The initial analysis filed (denoted by subscript a) is related to the increments to be sought through(22)

The innovation vector is defined as:(23)

where is the flow map (viewed here as a function of the initial condition and of the initial parameters). In addition the increment, is driven by the tangent linear model linearized around the current trajectory ,

We are interested in applying a particular DA method, namely a group of ensemble variational schemes (4DEnVar), to our state/parameter estimation problem. 4DEnVar (Liu et al., 2008; Buehner et al., 2010) features a 4D ensemble-based covariance field in a variational system. The strategy described here is a direct extension of the scheme discussed in Yang et al. (2015). The extension of 4DEnVar for parameter estimation is done by the so-called augmented state vector technique. If we assume that the parameter variables are random variables, then the extension of state space-based methods to parameter space is straightforward by encapsulating the parameters. The state augmentation technique has shown to be effective in diverse applications (Tong and Xue, 2008; Kang et al., 2011; Sawada et al., 2015; Simon et al., 2015). The parameter estimation is also related to the estimation of model error from ensemble-based approach. The model error can take simple forms of model bias (Dee, 2005; Baek et al., 2006) or functional forms through parameterization.

3.2.1. Augmented 4DEnVar algorithm

The constitution of a corresponding joint estimation algorithm is illustrated below within an augmented state context. First, we need to define as the initial augmented state vector where p is the degree of freedom of . In an incremental framework, we are looking for defined by . The cost function in terms of the augmented state increment vector reads:(24)

where the symbol denotes the augmented version of the tangent linear model or the tangent observation model, respectively. Firstly, the extended tangent linear model operator is composed of the parameter evolution model as well as the tangent linear dynamic model operator . Secondly, in a fully and directly observable case, the observation operator corresponds to the identity matrix. In our case, the validity of hinges on the quality of the analysis trajectory driven by the model; therefore, rather than to simply fit to the noisy empirically observed values with few samples, we will assume that is non-observable. Let us note that a prior information on the variance tensor is included in the background regulation term. The observation operator or its linear tangent expression takes the form of .

The augmented state ensemble, denoted by , is obtained by perturbing the background ; N is the number of ensemble members. We defined the ensemble anomaly matrix as,(25)

where the operator takes the ensemble mean and the jth perturbed ensemble member is noted . The background covariance is approximated by the ensemble anomaly matrix:(26)

where the sub-matrices and correspond to the auto-covariance matrix and contains the cross-covariance between the state and the parameter. As suggested by several studies, a localization procedure enables to robustify the construction of ensemble-based covariance to sampling errors. Due to the parameters’ spatial structure, it is necessary to introduce similar localization to the parameter-related covariances. In this study, we have tested two different localization techniques referred to as ‘localized covariance’ and ‘local analysis’, respectively. The former relies on a Schur product between the global covariance matrix and an isotropic correlation function,(27)

to filter out the long range spatial correlations. The spatial correlation matrix is defined from a polynomial approximation of a Gaussian function with compact support and a hard cut-off (Gaspari and Cohn, 1999). Same values of the cut-off distance are adopted for all . The latter consist in bounding – or localizing – directly the region of influence of a given observation on the grid to a restricted area.

The 4DEnVar consists in applying a change of variable with the square root of the error covariance matrix, by setting , where is the control weight vector and is the square root of calculated through a spectral decomposition (Buehner, 2005) or simply in the case of no localization. We can define the following scheme: .

The control variable transformation is also relevant as a preconditioning technique. The cost function in terms of control variable reads,(28)

where The contains a set of samples based on an expression of the ensemble integrated in time. Note that for the Schur product-based localization of this empirical matrix, we implemented rather than (which comes to consider a time invariant localization).

In order to handle high non-linearity either related to the model or the observations, many authors advocated the use of an iterative approach (Gu and Oliver, 2007; Kalnay and Yang, 2010; Sakov et al., 2012; Bocquet and Sakov, 2013a). The algorithm in Yang et al. (2015) is characterized by an iterative resampling strategy of the prior ensemble and an update of the ensemble sensitivity matrix within the increment minimization steps. It adopts the form of a Gauss–Newton scheme with nested loops that show the relevance of this approach, in particular in the case of a badly known background information and incomplete observations. In our current problem, with the background information bounded by the coarse resolution and the absence of observed parameter fields, it is indeed appropriate to introduce such iterative approach. Here, the iterative update concerns two parts: on the one hand, the innovation vector of the current outer loop is updated by the analysis trajectory based on the analysis state of the previous outer loop driven by the non-linear model; on the other hand, the ensemble anomaly matrix is updated through the posterior ensemble fields. The ensemble update can either be derived from the posterior ensemble built on perturbed observations or by a direct transformation of the prior perturbations.

3.2.1.1. Perturbed observation with global analysis

In the first approach, at the kth outer loop iteration, a parallel realization of minimization with regard to each member of the initial ensemble is conducted,(29)

where denotes the jth innovation vector calculated from perturbed observation field and denotes the control weight matrix. Finally, the updated initial ensemble field and its perturbation matrix read:(30)

3.2.1.2. Ensemble transformation with local analysis

The square root transformation approach corresponds to a mean preserving transformation as used in Ensemble Transform Kalman filter (ETKF). The updated background ensemble anomaly matrix reads,(31)

The transformation matrix is the square root of inverse Hessian.¹

The arbitrary orthogonal matrix is used to centre the posterior ensemble on the updated initial condition/analysis. In this approach, a single minimization process with respect to the background state is sufficient since the ensemble does not need to be updated explicitly. Finally, the updated initial ensemble fields are,(32)

where corresponds to the updated augmented vector,(33)

Since the minimization is done in the ensemble space, we use here the local analysis approach. This computationally efficient approach proposed in Ott et al. (2004) and Hunt et al. (2007) consists to lead the analysis step through an EnKF procedure in a local spatial region. The minimization and the error covariance update steps are done around each grid point considering the flow representation and the observations within a region of small size. Within the local domain, observation error is gradually increased when further away from the analysis grid point (Greybush et al., 2011). Note that the ensemble forecast step must be done globally with the full non-linear dynamic model.

3.2.1.3. Deterministic global analysis

We also tested another strategy capable of generating global deterministic ensemble anomaly matrix without perturbing the observations. This formulation is close in spirit with the DEnKF method proposed in Sakov and Oke (2008). In this approach, the posterior ensemble is obtained using half of the Kalman gain therefore preventing the level of posterior error from underestimation in the context of unperturbated observations. Here, we use the same format for the analysis ensemble which can be found in Fairbairn et al. (2013):(34)

Let us note that the iterative schemes described above are also used in the ensemble cycling procedure to move from one assimilation window to the next.

3.2.2. Parameter evolution and uncertainties

It is essential to realize that the parameters involved in geophysical models can be global or local in time and/or space. The parameters are generally time-dependent and their values may change when a new observation occurs. However, in this work, we will make the assumption that the parameters exhibit only slow temporal variation compared to the model state variation. In DA approaches, it is even custom to assume a constant value of parameters during the assimilation window. This consists in forecasting the analysis state, at the end of the ith assimilation window, to the beginning of the i+1th cycle with the optimum parameter :(35)

and to propagate the parameters using a persistent model,(36)

However, this persistent model can be a source of instability to the model integration with limited ensemble numbers. Gottwald and Majda (2013) explained this instability by the contribution of the unrealistic large covariance terms. In order to damp the rapid temporal change of model parameter, we set,(37)

where is the optimizer obtained at the ith cycle and is a damping coefficient that needs be tuned in order to maximize the ensemble spread while not causing filter divergence based on trial-and-error principle.

In the framework of the augmented state technique, the parameters are treated as random variables. So their distribution must be set implicitly or explicitly. In our case, we can use the estimators proposed in Section 3.1 as prior values. The errors associated with those prior values of are assumed to be centred Gaussian fields, with variance given by an uncertainty representation of the Smagorinsky model:(38)

note is defined as variation of high-resolution velocity on local spatial region, , centred on the coarse grid points indexed by k.

3.2.3. Ensemble inflation

Ensemble methods typically require an explicit variance inflation scheme in order to maintain a relevant ensemble spread. Although such scheme is widely used in practice by either additive or multiplicative inflation formulations, it reflects a lack of knowledge on how to address properly the model errors responsible for the maintenance of the ensemble spread.

Here, we adopt the multiplicative inflation (Anderson and Anderson, 1999) by multiplying the ensemble anomaly matrix with a tunable factor ranging from (1.0, 1.3) for each cycle. This strategy is applied to the standard model as a reference run but not to the stochastic model because one advantage of our stochastic model is to provide an inflation-free DA scheme. More precisely, our combined approach discussed in Sections 2 and 3.2 can be seen as an implicit inflation scheme where the corresponding scale discrepancy errors are dealt by the stochastic dynamics.

However, as shown in next section, the ensemble transformation approach with local analysis is particularly unable to produce sufficient ensemble spread leading to the filter divergence. To tackle such bad behaviour, we employed a relaxation scheme in which part of the posterior ensemble perturbation is relaxed back to the prior perturbations (Zhang et al., 2004).(39)

with . This approach is similar to the conditional covariance inflation method used in Aksoy et al. (2006).

3.2.4. Parameter estimation effect

It can be emphasized that although the estimation of the initial condition and the parameter proceed simultaneously, the estimation process of the initial condition is nevertheless not directly related to the auxiliary covariance terms () partly associated to the parameter . The , however, interferes in the quality of the analysis trajectory in two ways: firstly, it explicitly manifests itself on the model integration in the form of the estimated parameter ; secondly, it implicitly affects the analysis state through the ensemble spread from which the propagation of the ensemble perturbation matrix is calculated. Depending on the context, either of the two factors can exhibit large impact to the result (Koyama and Watanabe, 2010; Ruiz and Pulido, 2015). Note that in our ensemble-based 4DVar approach, the parameter is not only related to the forecast analysis cycling process, but also can affect the ensemble fields generated between two consecutive outer loops.

Figure 1. RMSE comparison in terms of free surface height (a) and velocity (b) between various configurations. PO: Perturbed observation. LC: Localized covariance approach. Standard model: no subgrid tensor parameterization. N: number of ensemble member.

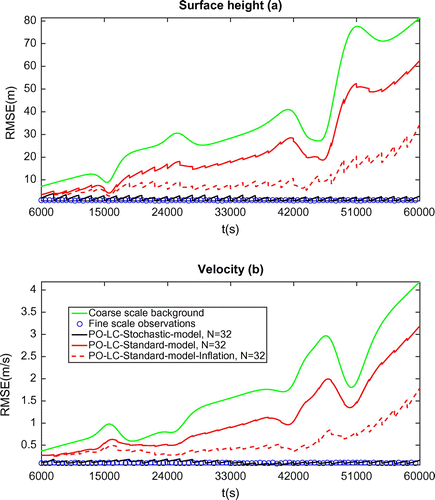
Figure 2. RMSE comparison in terms of free surface height (a) and velocity (b) between various configurations of 4DEnVar. PO: Perturbed observation. LC: Localized covariance approach. Standard model: no subgrid tensor parameterization. N: number of ensemble member. 6 DA cycle phase:  s. Forecast phase:  s.

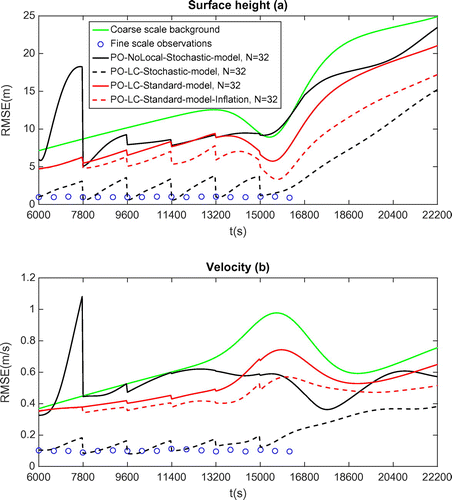
Figure 3. Ensemble spread in terms of free surface height (a) and velocity (b): standard model (circle) with ensemble in function of initial states; standard model (triangle) with ensemble in function of initial states but with multiplicative inflation technique; subgrid model (square) with ensemble in function of initial parameters.

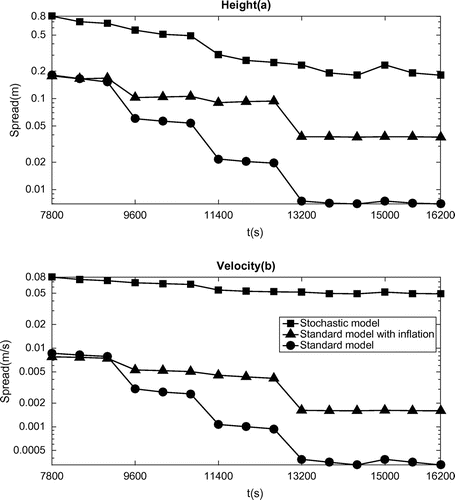
Figure 4. RMSE comparison in terms of free surface height (a) and velocity (b) between various subgrid model configurations in Table 1 of stochastic shallow water model (17). The meaning of different is shown in Table 1.

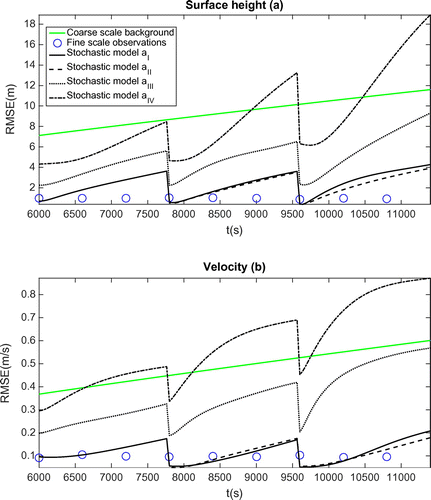
Figure 5. The RMSE of height comparison in the 1st and 2nd cycle as a function of Cut-off distance (LC, localized covariance) or local domain size (LA, local analysis).

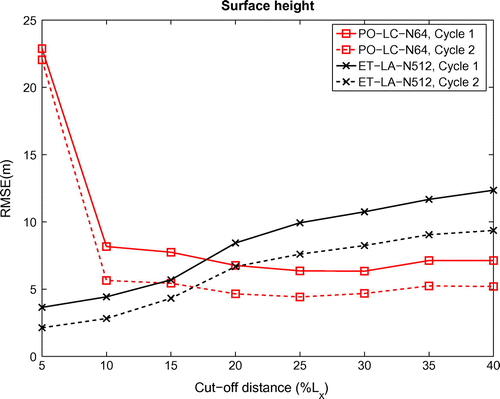
Figure 6. RMSE comparison in terms of free surface height (a) and lengthwise velocity (b) between various configurations of 4DEnVar. ET, ensemble transform. PO, perturbed observation. DE, deterministic ensemble. LC, localized covariance. LA, local analysis. ET-LA-N128-Stochastic (solid line) case with shows ensemble ‘blow up’; ET-LA-N128-Stochastic (dashed line) with shows ensemble collapse; ET-LA-N512-Stochastic (dotted line) used ensemble relaxation inflation technique for state ensemble; PO-LC-N64-Standard used standard model and multiplicative inflation technique for state ensemble.

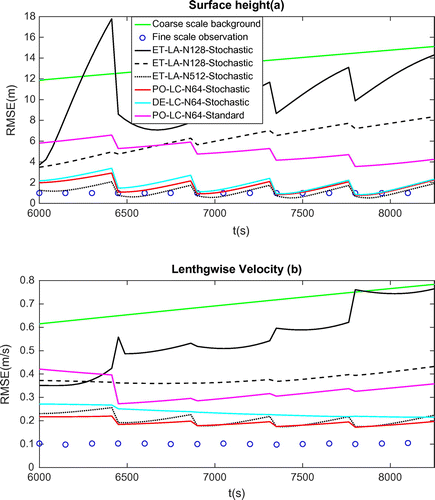
Figure 7. Power spectral density of ensemble anomalies for the forecast ensemble (a), the analysis ensemble by LC (b) and LA (c).

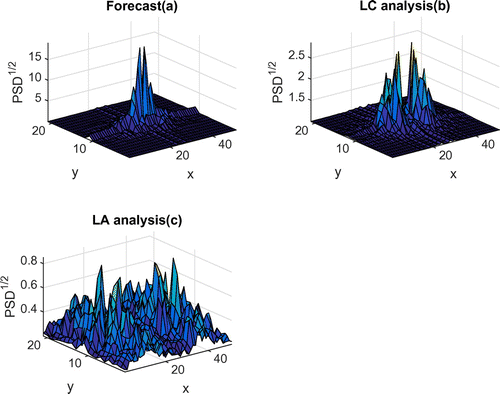
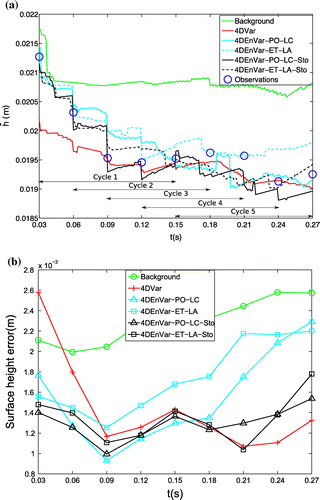
Figure 8. Comparison of various configurations of 4DEnVar w.r.t. (a) Mean surface height of the wave crest region as a function of time and (b) The RMSE against observation at observation time. 4DVar, 4DEnVar-PO-LC and 4DEnVar-ET-LA are tested with the standard model; 4DEnVar-PO-LC-Sto and 4DEnVar-ET-LA-Sto are tested with the stochastic model. LC, localized covariance. PO, perturbed observation. LA, local analysis. ET, ensemble transformation.

Figure 9. Ensemble Spread in terms of free surface height (a) and lengthwise velocity (b) for: standard model cycle 1 and cycle 5 (circle with solid/dashed line); stochastic model cycle 1 and cycle 5 (square with solid/dashed line).

3.2.5. Parameter identifiability

Before we carry out the experiments, it is important to assess the parameter identifiability. This is especially pertinent in our case as the quadratic variation tensor is non-observable. This concept, following the definition in Navon (1998), can be viewed as a criteria to decide whether or not the parameter of interest can be inferred from the data. With an ensemble-based method, an efficient way of examining the parameter identifiability consists in calculating the correlation coefficient (Tong and Xue, 2008).(40)

A strong correlation suggests that any changes in the parameter space will heavily affect the state space through the cross-covariance part of the error covariance matrix and vice versa.

4. Model and experimental settings

In order to evaluate the methods proposed, we have first carried out experiments on a one-dimensional stochastic shallow water model (Equations (17)) with synthetic data. We extended then this procedure on a 2D stochastic shallow water model (Equations (15)) with both synthetic and real image data.

4.1. Model numerical scheme

The systems studied here concentrate on the large-scale evolution of an average depth. We note that the subgrid-scale model associated with the quadratic tensor emerges both in the continuity equation and the momentum conservation equation. The finite volume method is directly applicable to these equations (Bradford and Sanders, 2002). Indeed, the numerical flux formulation of the new subgrid-scale terms is analogous to the viscous terms.

4.2. Experimental settings

Several experiments have been conducted to evaluate the performance of the stochastic model. We first tested the 1D stochastic shallow water equation. The 1D domain is of length km with the initial surface height h(x, 0).(41)

where  m, is the Coriolis parameter, and g are the gravity accelerations. Let us remark that though the Coriolis force is not described in the original formulation for sake of clarity, it can be added without any difficulty to the model (see Resseguier et al., in press-a, in press-b, in press-c). An additional noise is considered with as its amplitude. And is a random Gaussian covariance field computed as the spectral methods discussed in Evensen (2003) (with de-correlation length equals to 20%L). The initial velocity field is inferred from the geostrophic relation. The true state used to construct the finer observation is obtained by integrating the standard shallow water equation with the initial condition (40(40) ) on 401 grid points. The coarse resolution background state with the same initial condition is simulated with the stochastic model on only 101 grid points. The time step is set to 37.5 s for the true state model and to 150 s for the coarse resolution model in order to satisfy the different CFL conditions. The synthetic observation is extracted from the true state every 600 s by adding i.i.d Gaussian noise to the true state. Each assimilation window is set as 1800 s therefore containing three observations. In order to maintain the balance of state variables for ensemble fields, the analysis started at 6000 s.

For the 2D case, a very similar set-up is implemented. The length of the domain is the same as in 1D case. The width is km. The initial height surface is a 2D field with the extra error term as a 2D random Gaussian field. The background state resolution is and the observation resolution is . The time step is set to 10 s for the true state model and to 50 s for the coarse resolution model.The synthetic observations are sampled every 150 s from the true state. Each assimilation window is set as 450 s therefore also containing three observations.

For both cases, we tested the cycling windows strategies in order to adapt the temporal variation of parameters. Here, the parameter values change at the beginning of every assimilation window. In terms of the iterative scheme, we found it necessary to introduce similar parameter evolution model between two outer loops. For the 1D case, we firstly carried out a run of 30 assimilation windows in order to show the stability of the scheme. Then, we adopted six windows along with a forecast stage whose duration equals three assimilation windows to show the details of error growth in the first few cycles. Similarly, five windows are chosen for the 2D case. Note that in these synthetic cases, the coarse grid nodes of the background state coincide with those of fine synthetic observations.

Finally, we applied this stochastic model to those Kinect-captured images. Kinect is a depth sensor developed by Microsoft as the motion sensing input device for game consoles. Those images related to the work of Combes et al. (2015) are captured by a Kinect sensor to reflect the evolution of a unidirectional wave generated by an initial free surface height difference on a grid of  pixels. The flow is bounded in a rectangle flat tank of size . The flow surface was located between 680 and 780 mm from the device. When the attenuation coefficient of the liquid is larger than , the Kinect sensor displays a mean measurement error of 0.5 mm with standard deviations of about 0.5 mm for both flat and sinus-like surfaces. The sensor captures successfully sinus-like varying elevations with spatial periods smaller than 20 mm and amplitudes smaller than 2 mm. However, these raw data suffer large areas of missing information. Therefore, the same image pre-processing as in Yang et al. (2015) has been done in order to fix the issues related to the observation errors’ spatial distribution and the background state. For the observation errors: in terms of a point located in the unobserved region, the observation error is set to be dependent on the distance. The longer the distance, the larger the error. The observation error is bounded by a maximal value of 60% of the height difference . Within the observed region, we set the observation error homogeneously to the instrument error . The simulation is executed on a rectangle grids mapped on the same domain. In this case, the initial background was completely unknown; hence, it was set to a filtered observation with interpolated values on the missing data regions at the initial time. Since the initial background quality is bad, the system is designed to assimilate repeatedly the first few observations in order to obtain a faster ’spin-up’. So we chose five overlapping assimilation windows over nine observations with each window containing five observations.

In all cases, the observation error covariance matrix is assumed to be diagonal and all the observations are local in the sense that all the observations are taken at a certain spatial location. We employed different strategies to construct the ensemble in the synthetic case and in the real case. For the synthetic cases, as there is no explicit initial error associated with the background, the ensemble was initialized as a function of the parameters. And the prior parameters are determined from an empirical estimation of the variance tensor on local spatio-temporal regions, , centred on the coarse grid points indexed by k (42)

where is the characteristic time step used to regularize the unit of and denotes the spatial-temporal mean. The error uncertainty is computed by Equation (37(37) ). For the real cases, parameters are perturbed in addition to the initial state Gaussian perturbations to initialize the ensemble. Since no velocity observation is available at the initial time, the parameter initial observation is given by the initial ensemble variance:(43)

4.3. Comparison criterion

With a reference state available in both synthetic cases, we used the Root Mean Square Error (RMSE) to measure the differences between the values predicted by a model or an estimator and the reference value. Such RMSE is defined through norm:(44)

In the 2D synthetic case, we check the lengthwise velocity besides the surface height. The lengthwise velocity is the primary velocity component along . In the real image case, since there is no ground truth, we compare the background/analysis at discrete time levels against the observations as well as the surface height profile obtained by different methods.

5. Results and discussions

5.1. 1D case results, synthetic observations

As for the 1D experiment, the spatial mean of the correlation coefficient calculated from Equation (39(39) ) is and . Such an order of magnitude of the correlation coefficient ensures the identifiability of through the state variables.

A 30 pure assimilation cycles’ test has been performed for the 4DEnVar schemes with perturbed observations and localized covariance. In order to evaluate the robustness of the proposed scheme and the effectiveness of the stochastic model, we carried out one test with the model under uncertainty (with suffix ‘stochastic-model’) and two tests on the ‘standard-model’ in which no subgrid parameterization is introduced and the ensemble is generated by perturbing the initial condition state with the uncertainties computed a few time steps after the starting of the experiment. The two tests on the ‘standard-model’ differ on whether or not the ensemble multiplicative inflation technique discussed in Section 3.2.3 is used or not. Figure 1 shows the RMSE evolution in the course of the 30 cycles (here we use PO prefix denoting perturbed observations and LC prefix denoting localized covariance). The results are clearly in favour of our proposed inflation-free uncertainty model. The ensemble inflation technique improved to a certain extent the result but further improvement can hardly be obtained by simply enlarging the inflation coefficient since this causes numerical instability for the standard model.

The RMSE curves plotted in Fig. 2 represent the results obtained by the different assimilation configurations mentioned in Section 3.2. After a six windows cycling of assimilation procedure, we run a forecast stage, whose duration equals the length of three assimilation windows. We have discussed in Section 3.2.4 about the two different sources of the parameter estimation effect. The purpose of a prevision stage is to study only the effect upon the numerical integration using the prescribed stochastic model. In terms of the performance with the model under uncertainty, we have found that with no damping in parameter evolution model, insufficient number of ensemble members () lead to model blow-up characterized by unrealistic model variables’ values. This is not shown in Fig. 2 since it makes the figure scale unreadable. By introducing adequate damping factor which attenuates the change rate of variance tensor , the black curve displayed in Fig. 2 only experiences a strong divergence in the first cycle, while this behaviour is dampened at later cycles. The analysis trajectories across the assimilation stage show that increasing the ensemble size allows achieving a considerable improvement in the analysis quality in terms of the initial condition and indirectly of the parameters. We also find that the localization technique with optimally tuned localization scales enables improving the result for ensemble of small dimension. Note that compared to a localization procedure, increasing the ensemble size do not improve significantly the analysis performance. In fact, the RMSE curve using 512 sampling numbers and no localization scheme was very close to the one with only 32 members. Therefore, it has not been included in the figure for sake of readability.

In terms of the forecast stage (starting from 15,000 in Fig. 2), the forecast trajectories associated with better analysis states from the last cycle yield less error and distinct error growth schematic compared to the background. Conversely, the error evolutions with the standard model (with or without inflation) coincide closely with the one of the background. This reflected the power of the subgrid modelling in producing more relevant analysis state. Nevertheless, a similar divergence can be found in all the forecast trajectories. This behaviour indicates that the effect of the parameters here is only slightly significant with respect to forecast. This seems to indicate that the strategy consisting to keep the variance tensor constant along the assimilation window (and therefore for the whole forecast) does not provide a slower slope of the error growth at long terms. Its assimilation performance enables nevertheless to get forecast results of much better quality. Choosing a time-dependent variance tensor may lead to better result for long-term forecasting.

Eventually, we conjectured that the effectiveness of the corresponding methods is actually related to the ensemble spread. The ensemble spread curves shown in Fig. 3 correspond to three identical experiment set-ups (No localization scheme with same sampling numbers) but with the state driven by the stochastic model and the standard model with or without inflation scheme, respectively. Note that the first cycle is not shown here since during this cycle the ensemble spread is dominated by arbitrary noise. We observed that the ensemble spread for stochastic model is significantly larger than the spreads associated with the standard model (with or without inflation). The spread curve of the standard model without inflation not only decreases faster but also collapses nearly 100% after the fourth cycle. The inflation technique does increase the ensemble spread but its power is intrinsically limited by the model stability. On the other hand, we observed that the ensemble spread of the stochastic model also decreases but is still maintained at a rather high level across the sliding windows. A relatively high-level ensemble spread explains why the forecast state is corrected effectively at the beginning of each cycle in terms of the RMSE curve (e.g. the black dotted line in Fig. 2); similarly, a collapsed ensemble related to the standard model loses gradually the ability of improving the forecast state.

We have also conducted a study on the different terms composing the subgrid model in Equations (17). The configuration of different cases is shown in Table 1. The RMSE evolution along three cycles is illustrated in Fig. 4. We can conclude that the stochastic shallow water model works equally well with the case (complete terms presented) and the case (no term associated with the gradient of in the momentum equation). Case does not take account of the terms associated with the gradient of in both mass and momentum conservation equations. The initial analysis resulting from this case is relatively bad compared to the previous two cases, which indicates the relevance of the missing modelling part of the continuity equation in generating larger ensemble spread. Case assumes a similar form as the Smagorinsky-like eddy viscosity model described in the previous section without any subgrid term in the continuity equation. Besides the significantly lower quality of initial analysis state, the evolution of RMSE diverges faster and to a greater extent compared to other three counterparts. This test suggests that the subgrid modelling term presented in the continuity equation is crucial to keep an accurate representation of the small-scale uncertainty constituting a more balanced ensemble spread between the height and the velocity fields. Note that case is the default case for all the other tests conducted in this article.

Table 1. Different combination of the terms composing the subgrid model.

	Momentum equation	Continuity equation
		None

5.2. 2D case results, synthetic observations and real data

Under the 2D experimental set-up, due to the sizable degrees of freedom of the system, the localization-free paradigm basically does not work anymore. So here we focus on the comparison of two localization techniques: localized covariance (LC) and local analysis (LA). Sakov and Bertino (2011) have shown the similarities of the two types of localization schemes within the framework of EnKF under some restricted conditions. In our practice, other factors interfere so that the similarity of the two different localization schemes may break down. One of factors is the effectiveness of the minimization scheme since our localization techniques are constructed on a variational basis. The background error statistics as well as the relevance of the initial ensemble also contribute to the inequality. Another important factor is the ensemble update schemes used in combination with LC or LA technique. We use perturbed observation scheme (PO)with LC and ensemble transform scheme (ET) in conjunction with LA. In order to separate the two factors (the ensemble update scheme and the localization scheme), we employed another scheme (Section 3.2.1.3) using global covariance localization and a deterministic ensemble update approach (denoted as DE-LC) without perturbing the observations. All those have been run for the 2D stochastic large-scale dynamics described in Equations (15a(15a) ) and (15b(15b) ).

To be able to diagnose the performances, the first step is to study the sensitivities of localization scales. The localization scale is termed as cut-off distance in terms of LC and local domain size in terms of LA, respectively. Figure 5 shows the mean of RMSE of height per cycle against different localization scales. We observed that the LC approach tolerates a larger scale while the LA approach clearly is more in favour of a smaller scale. Although the average RMSE monotonically increased in function of the local domain size when using LA, the local domain size smaller than contains only several grid points which results in numerical instability. Eventually, we chose 20% as the cut-off distance for LC and 10% as the local domain size for LA.

The RMSE results regarding the 2D Synthetic Results are shown in Fig. 6. In terms of the group of three LC scheme, the error evolution of the localized covariance (LC) cases with stochastic model indicated consistent sensible results. The result of a PO-LC test using the standard shallow water model and multiplicative inflation technique shows relatively higher error and a diverged velocity RMSE from the 2nd cycle compared to those associated to the stochastic model using LC scheme. Between two ensemble update schemes using LC and the stochastic subgrid modelling, the DE scheme yields comparable result in height field but slightly worse result in velocity field. In terms of ET-LA scheme, as shown by the black solid line in Fig. 6, a similar catastrophic filter divergence to the 1D case can be found in the first cycle with underdamped parameter model. We can conclude that the damping parameter model is essential to the first cycle for the parameters estimated in the first cycle are badly constrained. After optimally tuning the value of , we can see that the analysis state for LA approach (the black dashed line in Fig. 6) is corrected at the 1st cycle and its trajectory does not diverge anymore. However, the analysis across later cycles is characterized by a monotonically increasing error caused by the collapsing of ensemble spread. Because when the ensemble spread is too small, the state variables will conform to the background and the observation will barely exert any effect. Parameter ensemble collapsing is a common problem encountered by many studies of parameter estimation in an augmented state vector framework (Aksoy et al., 2006; Simon et al., 2015). Regarding our test, firstly, after the 1st cycle, the estimated parameters have to be severely tampered before they can be used to evolve the analysis ensemble to the beginning of the 2nd cycle (therefore formulating the forecast ensemble). This damping process is a source of loss of signal in the ensemble parameter fields. Secondly, during the assimilation process, the variances of both the state variables and the parameters are naturally decreased. We concluded that the reason why the ensemble fields deteriorate in LA is linked to the form of calculating the ensemble anomaly fields in local domains. Since the noise that we are trying to characterize in this paper is mainly due to the non-consistent spatial and temporal sampling numerical steps, consequently, using a transformation matrix of small dimension can lead to excessive small-scale variations and eliminate the longer correlations since it restricts the directions of the variations of increments in the ensemble space. To verify this, we plot the ensemble anomalies’ PSD (power spectral density) in terms of height with respect to the forecast ensemble, the analysis ensemble of LC and LA, respectively, for the 1st cycle in Fig. 7. We observed that after integrating the stochastic model for some time, the forecast ensemble is clearly dominated by few leading modes. The analysis ensemble yielded by LC preserves considerably the spectral form while the magnitude associated with each mode decreases. The result clearly reveals why the LC approach is more robust even with a relative small ensemble size. However, the computational cost associated with LC approach of 64 members ensemble is already considerably high. The analysis ensemble produced by LA, on the contrary, spreads the energy over much more modes. These small-scales energy variations are then very likely smoothed out by the diffusive subgrid model.

In order to make LA work better, we adopt the relaxation methods discussed in Section 3.2.3 in which is tuned as 0.9 for state ensemble. As shown by the black dotted line in Fig. 6, the LA approach with relatively large ensemble generates sensible analysis comparable with the LC experiments.

One possible fix besides this relaxation method is to use left multiplication ensemble transformation schemes which are in the state vector space. Note that this scheme is both compatible with LC and LA. However, the left-multiplied form will require the minimization process to be done in state vector space which is more computationally demanding. Another possible approach would be to introduce a static full-rank B and to apply a 3DVar-FGAT in order to add more directions in the incremental field which is not solely covered by the ensemble B as suggested in Gustafsson and Bojarova (2014). This will in fact add a hybrid taste in our EnVar scheme, which constitutes an interesting perspective for advanced study. From the perspective of image data, it is also beneficial to introduce correlation into the observation error covariance matrix (Chabot et al., 2015). This remains another interesting outlook for future work.

In terms of the real image data depicting the free surface height of a laboratory tank, Fig. 8(a) shows the evolution of the mean surface height of the wave crest region using different methods. We particularly chose to focus on this region as the flow is dominated by a single wave. Figure 8(b) shows the RMSE between background/analysis state and the observation at discrete observation times. Note the analysis trajectories denoted by 4DVar, 4DEnVar-PO-LC and 4DEnVar-ET-LA are the same as in Fig. 8 in Yang et al. (2015), which are produced by the standard model without any subgrid parameterizations. No ensemble inflation technique is used in this test. Basically, the group of 4DEnVar outperforms the 4DVar in terms of the surface height at the beginning of the assimilation window. We observed an underestimation of the surface height for 4DVar in Fig. 8(a), while the group of 4DEnVar follows quite well the first two observations. The analysis trajectories generated by EnVar schemes with stochastic models (with Sto suffix) show a slight improvement between the third and the sixth observations. Their trajectories started to attenuate in the last cycle compared to their counterpart using standard model. This local phenomenon is again validated in the global RMSE results of Fig. 8(b). We can observe that the RMSE values regarding the stochastic models between the third and the sixth observations are consistent with the 4DVar case. Lower RMSE associated with stochastic models are also found in the last cycle (black symbols vs. cyan symbols). We recalled in this experiment that the initial background state is unknown, which makes the numerical performance of the model highly unstable. Hence, the parameterization procedure can only tolerate a relatively low magnitude of the variance tensor, which cannot induce significant ensemble perturbations. All in all, the stochastic version has been found more stable than the other schemes.

We have also plotted the ensemble spread vs. time in Fig. 9. As in the synthetic case, the ensemble spread associated with subgrid model is larger than those of the standard model for the whole assimilation windows. However, the difference of ensemble spread between the two models is less evident compared to the synthetic case, which indicates the perturbed initial states are mainly responsible for generating relevant background error estimations, especially for the later cycles. This behaviour also sheds light on the divergence of the analysis trajectory.

6. Concluding remarks

In this paper, we started by presenting shortly the principle of the stochastic fluid dynamics proposed in Mémin (2014), which offers us a way to reinterpret the so-called subgrid stress models used in CFD for many years. In this framework, the subgrid models are theoretically sound as they are directly related to the small-scale uncertainty components and inferred from physical conservation laws. They are therefore not prone to theassumptions underlying the eddy viscosity models (to list few of them: filter permutation with differentiation, specific shape of the dissipation, isotropic turbulence, diffusion alignment with the rate of strain proper directions).

Then, we have focused on the numerical evaluation of the stochastic model with a coherent scheme 4DEnVar proposed in Yang et al. (2015). The idea is this: since we argue that the subgrid-scale stress term attached to the uncertainties plays an essential role in formulating the effects of the uncertainties on the resolved scales, we can indeed try to estimate these effects through high-resolution data by a parametrization of the associated terms. In our 4DEnVar scheme, the unknown augmented initial vector is adjusted to fit the 4D observations simultaneously. Besides, due to its cycling and iterative ensemble update strategy, we are able to fully utilize the 4D Ensemble in order to meet the needs of dealing with bad background and incomplete observations.

The numerical results have been encouraging. Using the stochastic shallow water model with synthetic data-sets, the 4DEnVar scheme is tested to compensate the gap between the coarse resolution background state and fine resolution observations. The results clearly indicated the pertinence of the quantification of the unknown small-scale physical processes or numerical artefacts. We have a much better analysis state in global quality in terms of spatial errors; and the error growth tendency of the analysis trajectory with the estimated subgrid-scale stress parameters is distinct from other cases driven by the standard model (with/without inflation), which suggests that more relevant information from the observation can be extracted and contribute to the formulation of a more correct and coherent analysis state. Such an improvement is largely due to two related subjects. The stochastic model introduced more relevant ensemble spread growth and avoided the common catastrophe of ensemble collapse due to the insufficient ensemble spread. The ensemble-based DA scheme therefore benefited from these 4D ensembles in formulating the necessary components (innovation vector, ensemble anomaly matrix, etc.), and consequently generated more accurate analysis states and parameter fields for the stochastic model. It is important to note that the subgrid-scale stress term appearing in the stochastic model, although only labelled as resolution-related, can actually embrace broader types of errors as long as these errors can be inferred from the discrepancies between the dynamics and the high-resolution data.

The numerical results are also discussed in detail with two localization techniques. In ensemble-based methods, localization is useful not only in removing the unrealistic correlation, but also in enlarging the control space to a space with greater degree of freedom. With 2D synthetic or real case, using localization is obligatory. The localized covariance approach is proved to be more robust in the sense that the posterior ensemble produced by such scheme not only kept its magnitude, but also maintained to a large extent its energy spectral form. The spectral form is important in terms of our experimental set-ups since it prevented the small-scale energy variations from diffusing by the stochastic model, which is exactly the case with the local analysis scheme. The results revealed by the real data case are less convincing due to the numerical instabilities associated with the variance tensor. The analysis trajectory only showed a slight improvement with a more stable behaviour in the analysis. More work needs to be done in order to provide a better initial background, which eventually allows generating a more pertinent prior ensemble. Employing the full stochastic model with the noise term constitutes an interesting perspective for this path.

Our results suggested that the two localization techniques both suffered some limitations in their current forms. In the localized covariance approach, the posterior ensemble can only be sought through an ensemble analysis, which is computational demanding. The local analysis, although much cheaper and easy to implement, has shown some difficulties in bridging the gap between the local and the global representations. Following works will investigate new localization schemes that do not have the above restrictions. One way to improve the posterior ensemble efficiency and accuracy is to construct the estimation scheme on adjoint models. By introducing the adjoint models, the optimization is done in the state space rather than the ensemble space. Although maintaining and computing an adjoint model are cumbersome and time-consuming, using a state space formulation allows to express the left transformation of the prior ensemble to the posterior ensemble (Bocquet, 2015). In this form, the ensemble transformation takes the form of EAKF (Anderson, 2001; Sakov and Bertino, 2011). In the future, we are planning to adopt a similar strategy with complex data-sets. Since the scheme is formulated on variational base, the transition is straightforward. Adding a static full-rank B and applying a 3DVar-FGAT (Gustafsson and Bojarova, 2014) can also be beneficial to the posterior ensemble quality as more directions are permitted to grow in the incremental field. This path constitutes another promising direction to follow.

Acknowledgements

We thank three anonymous reviewers for their insightful comments and suggestions that helped improving the manuscript.

Additional information

Funding

The author Yin Yang acknowledges the support of RTRA STAE Foundation grant RTRA-STAE/2014/P/AVENUE/03.

Notes

No potential conflict of interest was reported by the authors.

1 Note that the relationship between the Hessian and the covariance matrix holds rigorously in a linear sense; in a non-linear scenario, this relationship is only an approximation. As the minimization algorithm LBFGS relies on an approximation of the inverse Hessian matrix , we can use this byproduct to evaluate Equation (30(30) ).

3 Formally, it is a cylindrical -Wiener process (see Da Prato and Zabczyk (1992) for more information on infinite dimensional Wiener process and cylindrical -Wiener process).

Appendix 1

Stochastic Reynolds transport theorem

We derive in this appendix the expression of the Reynolds transport theorem for the drift plus noise decomposition: In a Lagrangian stochastic picture, the infinitesimal displacement associated to a trajectory of a particle is noted:(A1)

The random field involved in this equation is defined for all points of the fluid domain, through the kernel associated to the diffusion operator (A2)

This operator is assumed to be of finite norm for any orthonormal basis of the associated Hilbert space and to have a null boundary condition on the domain frontier:(A3)

Function denotes a d-dimensional Brownian function³ and the resulting d-dimensional random field, , is a centred vectorial Gaussian function correlated in space and uncorrelated in time with covariance tensor:

We observe that those random fields have a (mean) bounded norm: , where the trace of the covariance tensor is given for any basis of as . In the following, we will note the diagonal of the covariance tensor as: . Tensor, , that will be referred to as the variance tensor

is by definition a symmetric positive definite matrix at all spatial points, . This quantity corresponds to the time derivative of the so-called quadratic variation process:

The notation stands for the quadratic cross-variation process of f and g. This central object of Stochastic Calculus can be interpreted as the covariance along time of the increments of f and g. The quadratic variation process is briefly presented in Appendix 2.

The drift term, , of Lagrangian expression (A1(A1) ) represents the ‘smooth’ – differentiable – part of the flow, whereas the random part,(A4)

figures the small-scale velocity component associated to a much thinner time scale. This component is modelled as a delta-correlated random field in time as it represents a highly non-regular process at the resolved time scale. In this work, we assume that this small-scale random component is incompressible and therefore associated to a divergence-free diffusion tensor: . This assumption, which obviously does not prevent the drift component (and therefore the whole field) to be compressible, leads to much simpler modelling and remains realistic for the models considered in this study.

Let us consider now a spatially regular enough scalar function of compact support, transported by the stochastic flow (A1(A1) ) and that vanishes outside volume and on its boundary . As this function is assumed to be transported by the stochastic flow, it constitutes a stochastic process defined from its initial time value g:

We will assume that both functions have bounded spatial gradients. Besides, the initial function vanishes outside the initial volume and on its boundary. Let us point out that in this construction, function cannot be a deterministic function. As a matter of fact, if it was the case, its differential would be given by a standard Ito formula(A5)

which here cancels as is transported by the flow. A separation between the slow deterministic terms and the fast Brownian term would yield a null uncertainty or a specific uncertainty orthogonal to . This would lead us back to the deterministic case, which is not the general goal followed here.

As is a random function, the differential of involves the composition of two stochastic processes. Its evaluation requires the use of a generalized Ito formula usually referred in the literature to as the Ito–Wentzell formula (Kunita, 1990, see Theorem 3.3.1). This extended Ito formula incorporates in the same way as the classical Ito formula a quadratic variation term related to process but also co-variation terms between and the gradient of the random function . Its expression is in our case given by(A6)

It can be immediately checked that for a deterministic function, the standard Ito formula is recovered since the co-variations terms between and cancel.

It follows from A6(A6) that for a fixed grid point, function is solution of a stochastic differential equation of the form(A7)

where the Brownian term must compensate the Brownian term of (A6(A6) ). The quadratic variation term involved in (A6(A6) ) is given through (Appendix 2) as(A8)

and the covariation term reads(A9)

In these expressions, (resp. ) designates the kernel associated to operator (resp. ). Now identifying first the Brownian term and next the deterministic terms of equations (A6(A6) ) and (A7(A7) ), we infer

and finally get(A10) (A11)

This differential at a fixed point, , defines the equivalent in the deterministic case of the material derivative of a function transported by the flow. The differential of the integral over a material volume of the product is given by(A12)

where the first line comes from and the second one from the integration by part formula of two Ito processes. Hence, from (A11(A11) ), this differential is

Introducing , the (formal) adjoint of the operator in the space with Dirichlet boundary conditions, this expression can be written as

With the complete expression of (remarking that the second right-hand term of A12(A12) is self-adjoint) and if , where stands for the characteristic function, we get the sought form of this differential:(A13)

Appendix 2

Quadratic variation and covariation

We recall here the notion of quadratic variation and co-variation, which play a central role in stochastic calculus. We will here restrict ourselves to standard Ito processes: quadratic variation and co-variation correspond, respectively, to the variance and covariance of the process increments along time. The quadratic co-variation process denoted as , (respectively the quadratic variation for ) is defined as the limit in probability over a partition of [0, t] with , and a partition spacing , noted as and such that when :

For Brownian motion, these covariations can be easily computed and are given by the following rules , , where h is a deterministic function and B a scalar Brownian motion.