A decadal inversion of CO₂ using the Global Eulerian–Lagrangian Coupled Atmospheric model (GELCA): sensitivity to the ground-based observation network

Abstract

We present an assimilation system for atmospheric carbon dioxide (CO₂) using a Global Eulerian–Lagrangian Coupled Atmospheric model (GELCA), and demonstrate its capability to capture the observed atmospheric CO₂ mixing ratios and to estimate CO₂ fluxes. With the efficient data handling scheme in GELCA, our system assimilates non-smoothed CO₂ data from observational data products such as the Observation Package (ObsPack) data products as constraints on surface fluxes. We conducted sensitivity tests to examine the impact of the site selections and the prior uncertainty settings of observation on the inversion results. For these sensitivity tests, we made five different site/data selections from the ObsPack product. In all cases, the time series of the global net CO₂ flux to the atmosphere stayed close to values calculated from the growth rate of the observed global mean atmospheric CO₂ mixing ratio. At regional scales, estimated seasonal CO₂ fluxes were altered, depending on the CO₂ data selected for assimilation. Uncertainty reductions were determined at the regional scale and compared among cases. As measures of the model–data mismatch, we used the model–data bias, root-mean-square error, and the linear correlation. For most observation sites, the model–data mismatch was reasonably small. Regarding regional flux estimates, tropical Asia was one of the regions that showed a significant impact from the observation network settings. We found that the surface fluxes in tropical Asia were the most sensitive to the use of aircraft measurements over the Pacific, and the seasonal cycle agreed better with the results of bottom-up studies when the aircraft measurements were assimilated. These results confirm the importance of these aircraft observations, especially for constraining surface fluxes in the tropics.

Keywords:

• carbon cycle
• top-down approach
• flux estimation
• carbon dioxide
• inversion
• coupled model
• tropical Asia

1. Introduction

Carbon dioxide (CO₂) is a major greenhouse gas and the most important contributor to anthropogenic climate change. Before the industrial revolution, the atmospheric CO₂ exchange with natural carbon reservoirs (land and ocean) was largely in balance, in the absence of human influences. However, the combustion of fossil fuels (coal, natural gas and oil), as well as certain industrial processes and land-use changes, has considerably increased since the pre-industrial era. The current level of CO₂ in the atmosphere has increased by nearly 40% compared to the level in the pre-industrial era (Conway and Tans, 2014). Currently, about half of the extra CO₂ that modern human activities have released into the atmosphere has been absorbed by the land biosphere and oceans (Ciais et al., 2010a). Although global land and ocean carbon sinks increase with rising atmospheric CO₂, the Intergovernmental Panel on Climate Change Fifth Assessment Report stated with high confidence that global warming will reduce the sinks and partially counterbalance the equilibrium. It is thus urgent to understand the current status and trends of CO₂ exchange between land, ocean, and atmosphere so that the potential impacts of ongoing global climate change on the carbon cycle can be assessed.

Inverse modelling is one approach to quantifying the spatiotemporal distribution of sources and sinks at the Earth’s surface; this approach starts from a set of atmospheric mixing ratio observations by using an atmospheric transport model and sophisticated statistical inversion schemes (Ciais et al., 2010b). Global Eulerian models have been used extensively for global CO₂ inversion (e.g. Gurney et al. (2004) and references therein). Initially, Eulerian models with low spatial resolution (starting from 10° × 10° in the 1980s) were able to reproduce the seasonal cycle of global atmospheric CO₂ mixing ratios reasonably well. At that time, observational network was much less abundant and most observations were made at weekly to monthly intervals. In 1996, the GLOBALVIEW-CO₂ data product was provided by the US National Oceanic and Atmospheric Administration (NOAA) Earth System Research Laboratory (ESRL) (http://www.esrl.noaa.gov/gmd/ccgg/globalview/). This data product contains extended records of CO₂ with a regular temporal distribution, derived from high-precision atmospheric measurements such as those from the World Data Centre for Greenhouse Gases (http://ds.data.jma.go.jp/gmd/wdcgg/introduction.html) of the World Meteorological Organization Global Atmospheric Watch program and the Carbon Dioxide Information and Analysis Center (CDIAC; http://cdiac.esd.ornl.gov). The observational records in GLOBALVIEW products are free of temporal gaps and have been extensively used by many carbon cycle models. Recently, spatial observational coverage has been expanding as more vertical profiles and better horizontal coverage become available from aircraft and satellite measurements, and measurement frequency has been getting higher as more continuous measurements are being made at surface stations, including tower sites (Bruhwiler et al., 2011; Saeki et al., 2013; Houweling et al., 2015). Models have been developed that are able to handle the higher frequency but irregular data-sets, and such models have started to use actual data for inversion (e.g. Rodenbeck et al., 2003; Chevallier et al., 2010; Chevallier et al., 2011). NOAA ESRL released a new set of observation data products in 2012 as a successor to GLOBALVIEW, called Observation Package (ObsPack) data products (Masarie et al., 2014).

To derive regional surface flux information, high-frequency observations that represent hourly to synoptic variations are particularly useful. Nevertheless, simulating fine spatial and temporal CO₂ variability in the vicinity of variable sources and sinks is quite challenging. Global Eulerian models with high spatial resolution have a high computational cost. One way of obtaining higher resolution flux estimates within a region of interest is to use a ‘zoomed’ or ‘nested’ atmospheric transport model (Peters et al., 2005; Peylin et al., 2005). The idea of coupling two different types of models for global and regional modelling for inversion was introduced by Rodenbeck et al. (2009), and Trusilova et al. (2010) implemented this idea as a coupled system consisting of TM3, a global Eulerian atmospheric transport model and the Stochastic Time-Inverted Lagrangian Transport (STILT) regional Lagrangian model. Rigby et al. (2011) implemented a global inverse model with zoom over several regions resolved with a regional Lagrangian transport model NAME. Lagrangian particle dispersion models (LPDMs) are an effective tool for simulating observations at high spatial and temporal resolutions (Lin, 2012). Lagrangian models have minimal numerical diffusion, which is inherent in Eulerian models. LPDMs have been coupled with numerical weather prediction (NWP) models and used extensively in air-pollution dispersion modelling (Uliasz, 1993). Recently, coupled LPDM/NWP models, such as the coupled Weather Research and Forecasting-Stochastic Time-Inverted Lagrangian Transport (WRF-STILT) model, have been used for a wide range of applications, including surface flux estimates by carbon cycle studies (Gerbig et al., 2003; Gourdji et al., 2010; Nehrkorn et al., 2010; Pillai et al., 2011).

Ganshin et al. (2012) developed the Global Eulerian–Lagrangian Coupled Atmospheric model (GELCA) based on a framework introduced by Koyama et al. (2011). GELCA combines two transport models: The National Institute for Environmental Studies-Transport Model (NIES-TM) version 8.1i (Maksyutov et al., 2008; Belikov et al., 2013), a Eulerian global transport model, is coupled with FLEXPART version 8.0 (Stohl et al., 2005), a LPDM. The global background mixing ratio field generated by NIES-TM is used as time-variant boundary conditions for FLEXPART, which performs backward simulations from each receptor point (observation location). GELCA has demonstrated better performance in resolving short-timescale variations compared with NIES-TM only (Koyama et al., 2011; Ganshin et al., 2012).

In this paper, we introduce a global CO₂ inverse system using GELCA and we evaluate the performance of the GELCA inverse modelling system in estimating decadal global monthly CO₂ flux distributions. As constraining observation data, we used an ObsPack data product, which includes actual data (whereas GLOBALVIEW contains only processed data), to take full advantage of the coupled modelling approach, which can effectively make use of measurements reflecting CO₂ exchange along a local path or footprint as well as measurements representing hemispheric-scale background air. We examine the sensitivity of the inverse system to the data selection by comparing inversion results among five different subsets of the ObsPack data product.

2. GELCA inverse modelling system

2.1. GELCA coupled atmospheric model

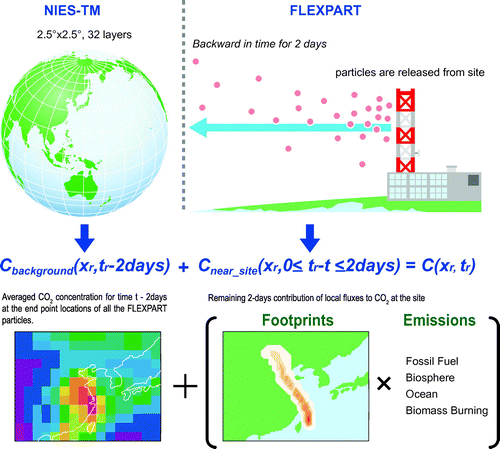
A schematic diagram of the GELCA inverse modelling framework is shown in Fig. 1. We implemented the coupling at temporal boundaries instead of spatial boundaries. Two-day backward-transported particles modelled by FLEXPART were combined at the end points with the background CO₂ levels 2 days prior to the observations simulated by NIES-TM. The mixing ratio at the receptor location x_r at time t_r can be expressed as the sum of near-site contributions calculated by FLEXPART and the background contributions calculated by NIES-TM.(1)

Fig. 1. Schematic diagram of GELCA inverse modelling framework.

FLEXPART simulates the backward transport of 10,000 particles released from each receptor point (observation location). is calculated by integrating the sensitivity of CO₂ mixing ratio to the surface fluxes (footprint) along 2-day trajectory paths of all particles. is the average of the CO₂ mixing ratios at the time of coupling simulated by NIES-TM, weighted by the number of the end points of the back-trajectories contained in each model grid cell. Detailed description about the Eulerian–Lagrangian coupling is given in Ganshin et al. (2012).

The duration of the backward calculations was set to two days to be consistent with the timescale of particles leaving the mixed layer (Gloor et al., 2001). Note that coupling with a Lagrangian model might not result in a significant improvement, compared with use of a pure Eulerian model, for remote sites, because numerical diffusion has a significant impact on the simulated mixing ratios at the receptor only if there are inhomogeneous sources or sinks near (less than about two days upwind of) the receptor. Supplementary Figure 1 shows the examples of footprints in winter and summer for one of the observational data-sets used in this study, from which we point out the following features. Firstly, the distribution of observation sites mostly determines the footprint coverage, making North America and Europe fairly well covered compared to other regions. Secondly, the footprint coverage varies significantly with the wind as well. In general, the coverage widens in winter compared to summer due to the stronger winds during winter in middle and high latitudes. The wind direction is important as well. For example, in East Asia, in winter, the wind blows dominantly from the Siberian High towards the Pacific Ocean, whereas it blows dominantly from the Pacific High towards the continent in summer. Since most observation sites are located around the east side of the continent, more surface flux signal can be captured from the continental East Asia in winter than in summer (Supplementary Figure 1).

The meteorological fields driving both models were taken from the Japan Meteorological Agency Climate Data Assimilation System (Onogi et al., 2007), which has a regular horizontal resolution of 1.25° × 1.25°, 40 hybrid sigma-pressure vertical model levels, and a temporal resolution of 6 h. Planetary boundary layer height data were obtained from the European Centre for Medium-Range Weather Forecasts Interim Reanalysis data-set (Dee et al., 2011).

2.2. Inversion scheme

For long-lived trace gases such as CO₂, the assumption that atmospheric mixing ratios respond linearly to changes in emissions holds well. Under the assumption of linearity, the relationship between a vector of observed values (z) and that of sources and sinks (s) can be expressed in matrix form as(2)

where H is a matrix of the sensitivities of observations to changes in emissions or initial conditions and v represents the model–data mismatch error, which includes both observational and model errors. The sensitivity of the observations to emission fields can be decomposed into two parts for the coupled model:(3)

The term H_{near_site} represents the sensitivity of the observations at a particular site to emissions surrounding the site as calculated by FLEXPART. The term H_background represents the sensitivities to background emissions (i.e. the impact of emissions beyond the immediate vicinity of the site), which are estimated by NIES-TM.

Using the Bayesian approach, the measure of the fit between modelled source strengths s and observed values z is expressed as a cost function J(s), assuming that s, z, and their uncertainties can be described as Gaussian probability density functions:(4)

where s_p is the vector of the prior source strength, R is the observation error covariance matrix and Q is the prior source strength error covariance matrix. The prior covariance structure describes the uncertainties of each regional flux, and the correlation in space of the regional fluxes. In the current study, we assumed a diagonal prior covariance matrix, which means that estimated fluxes were assumed to show no correlation. At the minimum of , the posterior source strength vector s and the posterior covariance matrix Q′ are expressed as(5) (6)

where the Kalman gain matrix is (7)

In a batch mode inversion, all non-observed parameters are estimated using all available observations simultaneously at each solution step. When the number of observations and source regions increases, the matrix of basis functions H becomes very large, and the computational cost becomes very large. To avoid this large computational cost, we employed the fixed-lag Kalman Smoother optimization technique (Bruhwiler et al., 2005) to minimize J(s) in Equation (4(4) ) rather than a full-matrix batch mode inversion. In this technique, only a subset of the transport information is kept at each time step, because most of the signal from source regions decays within a few months to half a year. The time window of the transport information kept is called the lag length. We used a lag length of three months based on the results of the numerical experiments performed by Maksyutov et al. (2009) on the influence of various time windows. The detailed description about the fixed-lag Kalman smoother applied for atmospheric inversion is given in Bruhwiler et al. (2005).

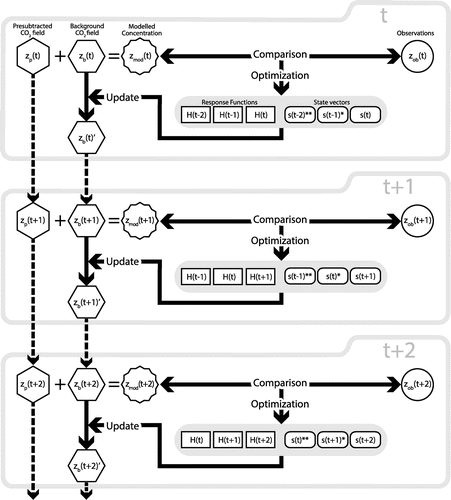
The inversion process employed in this study is illustrated in Fig. 2. The modelled CO₂ concentrations z_mod are sum of the background concentrations z_b and the presubtracted concentrations z_p calculated by GELCA. The calculation of z_b is started from the initial CO₂ mixing ratio 3D field based on an ensemble of forward simulation results by six different transport models: Gap-filled and Ensemble Climatology Mean (Saito et al., 2011). Details about the prior fluxes used to calculate z_p are given in the next section. In each inversion cycle, the modelled concentrations are compared to observations z_ob and the state vector s is optimized with a 3-month window. With the response functions prepared by GELCA, posterior fluxes from step t are calculated from the optimized state vector, and incorporated into the background concentration for step t + 1.

Fig. 2. Illustration of the inversion process employed in this study. The t indicates the time step on monthly basis. The modelled CO₂ concentrations z_mod are sum of the background concentrations z_b and the presubtracted concentrations z_p calculated by GELCA. In each inversion cycle, the modelled concentrations are compared to observations z_ob and the state vector s is optimized within a 3-month window. Optimized fluxes are incorporated into the background concentration () before calculating for the next time step. The number of asterisks in the upper right of s shows how many times a set of monthly fluxes has been optimized previously from past cycles. The prime in the upper right of z_b means that the z_b has been updated. The dashed arrows mean monthly calculations by GELCA.

In the inversion process, we applied a criteria to filter outliers from data-sets. We deselected data points for which the model–data mismatch exceeded three times of the annual value of the residual standard deviation (RSD) around the smooth-fit curve of the measurements at each site. These data-filtering criteria worked much more effectively in keeping as many data while filtering obvious outliers than eliminating data points with a larger model–data mismatch than a certain fixed value because the filtering condition is nicely adjusted according to the normal variability of CO₂ records at each site.

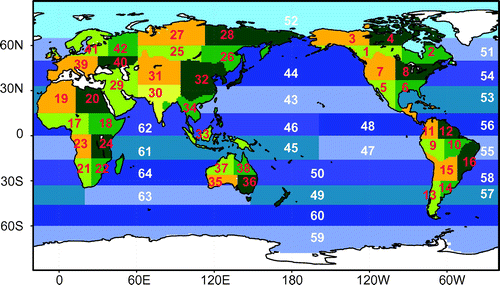
The calculation period was from January 2001 to December 2011. The first year was considered to be a spin-up period. Fluxes were solved monthly for 64 regions: 42 land regions and 22 ocean regions (Fig. 3).

Fig. 3. Definitions of the 64 regions used in the inversion.

2.3. Prior CO₂ flux estimates and their uncertainties

As prior CO₂ fluxes, we used daily terrestrial biosphere fluxes, monthly oceanic fluxes, monthly fossil fuel CO₂ emissions, and monthly biomass-burning emissions. The spatial resolution of all prior fluxes used in this study was 1° latitude × 1° longitude. The fluxes from the biosphere, the oceans, and fossil fuel burning were developed for the NIES Level 4 data product of the Greenhouse gas Observing SATellite (GOSAT) project; detailed descriptions are available in Maksyutov et al. (2013).

For daily CO₂ exchange between the terrestrial biosphere and the atmosphere, Net Ecosystem Production (NEP) of the Vegetation Integrative SImulator for Trace gases (VISIT) process-based biosphere model was used (Ito, 2010). The physiological parameters of the VISIT model were optimized by the method described by Saito et al. (2014).

The monthly ocean-atmosphere CO₂ exchange was calculated by an ocean pCO₂ data assimilation system (Valsala and Maksyutov, 2010) based on an ocean offline tracer transport model (OTTM) (Valsala et al., 2008). The OTTM was coupled to a simple biogeochemical model that synthesizes the surface ocean pCO₂ and air-sea CO₂ flux by a variational assimilation method.

Fossil fuel emissions, which were imposed in forward and inverse calculations, were obtained from the Open-source Data Inventory of Anthropogenic CO₂ (ODIAC) emission data-set (Oda and Maksyutov, 2011); emission estimates were based on CDIAC the country-level estimates (~2008) and to the year 2008 emissions were projected up to 2011 by using data from the British Petroleum Statistical Review of World Energy (British Petroleum, 2012). The emissions data-set used in this study are available from the NIES web site (http://db.cger.nies.go.jp/data-set/ODIAC/).

Prior estimates of CO₂ emissions from biomass burning were taken from the Global Fire Emissions Database version 3.1 (Giglio et al., 2010; van der Werf et al., 2010).

The prior flux uncertainty for land regions and oceanic regions were prescribed as the mean standard deviation of the monthly NEE calculated by VISIT for the past 30 years (1979–2009) and the mean standard deviation of the oceanic flux assimilated by OTTM for the period 2001–09.

2.4. Atmospheric CO₂ observational data

In this study, the global atmospheric CO₂ data are from the package version obspack_co2_1_PROTOTYPE_v1.0.3_2013-01-29, hereafter called the ObsPack product, which includes actual CO₂ measurement data from multiple observation platforms, including towers, aircraft, and ships, contributed by 22 laboratories from around the world. Quality control of data in the ObsPack products is left to the data providers, which means that the criteria for data selection are not uniform across each product. Most of the data are provided by the data providers as ‘representative of site,’ indicating that the data have been selected to represent large, well-mixed air masses. When there was more than one laboratory conducting the same type of measurements during the same time period at a given site, we chose only one (priority was given to NOAA). For tower sites, which provide data from multiple sampling altitudes, we used only data from the highest level as representative of the boundary layer mixing ratio. The programmable flask package, an automated grab sampler (Turnbull et al., 2012), was categorized as a flask sampler in this study. The details of each measurement technique are available elsewhere (e.g. Gomez-Pelaez and Ramos, 2011; Stephens et al., 2011). All sites used in this study are listed in Table 1.

Table 1. Observational sites used in this study, including the model–data mismatch results for the control case inversion. Check marks in the last four columns show whether the site is used in the indicated case.

Code	Site name	Lab.	Platform, Sampling^1		Lat.^2	Long.^2	Altitude (m)^2	Bias (ppm)	RMSE (ppm)	Correlation coefficient R	CT	NF	SEL^3	NA^3
ABP	Arembepe, Bahia	NOAA	g	f	12.76^°S	38.16°W	6	−0.34	0.41	0.980	✔		✔	✔
ALT	Alert, Nunavut	NOAA	g	f	82.45^°N	62.51^°W	205	−0.22	0.69	0.997	✔	✔	✔	✔
		EC	g	i	82.45^°N	62.51^°W	210				✔		✔	✔
AMT	Argyle, Maine	NOAA	g	p	45.03^°N	68.68^°W	157	0.37	3.72	0.928	✔		✔	✔
		NOAA	t	i	45.03^°N	68.68^°W	160				✔		✔	✔
ASC	Ascension Island	NOAA	g	f	7.97^°S	14.40^°W	90	−0.29	0.50	0.997	✔	✔	✔	✔
ASK	Assekrem	NOAA	g	f	23.26^°N	5.63^°E	1847	−0.05	0.52	0.997	✔	✔	✔	✔
AZR	Terceira Island, Azores	NOAA	g	f	38.77^°N	27.38^°W	24	0.24	1.18	0.985	✔	✔	✔	✔
BAL	Baltic Sea	NOAA	g	f	55.35^°N	17.22^°E	28	−1.86	3.72	0.926	✔	✔	✔	✔
BAO	Boulder Atmospheric Observatory, Colorado	NOAA	g	p	40.05^°N	105.00^°W	1584	−1.51	3.28	0.783	✔	✔	✔	✔
		NOAA	t	i	40.05^°N	105.00^°W	1884				✔		✔^a	✔^a
BGI	Bradgate, Iowa	NOAA	a	p	42.82^°N	94.41^°W	600–8100	−0.76–0.09	0.52–3.87	0.879–0.968			✔
BGU	Begur	LSCE	g	f	41.97^°N	3.23^°E	13	−1.01	3.24	0.926			✔	✔
BHD	Baring Head Station	NOAA	g	f	41.41^°S	174.87^°E	95	−0.27	0.52	0.995	✔	✔	✔	✔
BKT	Bukit Kototabang	NOAA	g	f	0.20^°S	100.32^°E	850	3.54	3.12	0.813	✔	✔	✔	✔
BME	St. Davids Head, Bermuda	NOAA	g	f	32.37^°N	64.65^°W	17	0.22	1.19	0.982	✔	✔	✔	✔
BMW	Tudor Hill, Bermuda	NOAA	g	f	32.26^°N	64.88^°W	60	0.15	1.06	0.991	✔	✔	✔	✔
BNE	Beaver Crossing, Nebraska	NOAA	a	p	40.8^°N	97.18^°W	600–8200	−0.68–−0.11	0.67–3.50	0.868–0.990			✔
BRA	Bratt’s Lake Saskatchewan	EC	g	i	51.2^°N	104.7^°W	630	−0.03	3.15	0.908			✔	✔
BRW	Barrow, Alaska	NOAA	g	f	71.32^°N	156.61^°W	28	−0.28	0.81	0.995	✔	✔	✔	✔
		NOAA	g	i	71.32^°N	156.61^°W	28				✔		✔	✔
BSC	Black Sea, Constanta	NOAA	g	f	44.18^°N	28.66^°E	5	−5.24	5.17	0.889	✔	✔
CAR	Briggsdale, Colorado	NOAA	a	p	40.37^°N	104.3^°W	1800–11,900	−0.11–0.22	0.64–1.07	0.989–0.996			✔
CBA	Cold Bay, Alaska	NOAA	g	f	55.21^°N	162.72^°W	25	−0.51	1.07	0.991	✔	✔	✔	✔
CDL	Candle Lake, Saskatchewan	EC	g	i	53.99^°N	105.12^°W	630	−0.14	2.57	0.957	✔		✔	✔
CFA	Cape Ferguson, Queensland	CSIRO	g	f	19.28^°S	147.06^°E	5	−0.28	0.72	0.993	✔		✔	✔
CGO	Cape Grim, Tasmania	NOAA	g	f	40.68^°S	144.69^°E	164	−0.14	0.20	0.999	✔	✔	✔	✔
CHM	Chibougamau, Quebec	EC	g	i	49.68^°N	74.3^°W	423	0.04	2.16	0.953			✔	✔
CHR	Christmas Island	NOAA	g	f	1.70^°N	157.15^°W	5	−0.27	0.30	0.998	✔	✔	✔	✔
CIB	Centro de Investigacion de la Baja Atmosfera	NOAA	g	f	41.81^°N	4.93^°W	850	−0.80	2.74	0.863		✔	✔	✔
CMA	Cape May, New Jersey	NOAA	a	p	38.83^°N	74.31^°W	300–8200	−0.25–−0.07	0.71–3.68	0.894–0.988			✔
CON	CONTRAIL	NIES/MRI	a	f			3500–12,200	−0.54–−0.14	0.43–0.76	0.987–0.996			✔
CPS	Chapais, Quebec	EC	g	i	49.82^°N	74.98^°W	387	0.08	1.59	0.884			✔	✔
CPT	Cape Point	NOAA	g	f	34.35^°S	18.49^°E	260	−0.04	0.30	0.999		✔	✔	✔
		SAWS	g	i	34.35^°S	18.49^°E	260						✔	✔
CRI	Cape Rama	CSIRO	g	f	15.08^°N	73.83^°E	66	−0.53	1.80	0.981			✔	✔
CRZ	Crozet Island	NOAA	g	f	46.43^°S	51.85^°E	202	−0.22	0.26	0.999	✔	✔	✔	✔
CYA	Casey, Antarctica	CSIRO	g	f	66.28^°S	110.52^°E	55	−0.24	0.21	0.999	✔		✔	✔
DND	Dahlen, North Dakota	NOAA	a	p	47.5^°N	99.24^°W	500–8100	−0.39–−0.16	0.66–1.86	0.960–0.990			✔
DRP	Drake Passage	NOAA	s	f	59.0^°S	64.49^°W	10	−0.19	0.29	0.997			✔	✔
EGB	Egbert, Ontario	EC	g	i	44.23^°N	79.78^°W	251	−0.20	5.04	0.904	✔		✔	✔
EIC	Easter Island	NOAA	g	f	27.16^°S	109.43^°W	55	0.32	0.74	0.994	✔	✔	✔	✔
ESP	Estevan Point, British Columbia	CSIRO	g	f	49.38^°N	126.54^°W	47	−0.41	1.46	0.962			✔	✔
		EC	g	i	49.38^°N	126.54^°W	47						✔	✔
		NOAA	a	p	49.38^°N	126.54^°W	100–5800	−0.43–−0.13	0.88–1.36	0.981–0.991			✔
EST	Esther, Alberta	EC	g	i	51.66^°N	110.21^°W	710	−0.01	3.23	0.913			✔	✔
ETL	East Trout Lake, Saskatchewan	EC	g	i	54.35^°N	104.98^°W	597	−0.31	2.04	0.961	✔		✔	✔
		NOAA	a	p	54.35^°N	104.98^°W	600–7800	−0.35–0.01	0.94–1.77	0.963–0.981			✔
FIK	Finokalia, Crete	LSCE	g	f	35.34^°N	25.67^°E	150	−0.09	1.85	0.948			✔	✔
FNS	North Sea Platform (F3)	RUG	g	i	54.85^°N	4.73^°E	46	−1.25	1.64	0.956			✔	✔
FSD	Fraserdale	EC	g	i	49.88^°N	81.57^°W	250	0.30	2.91	0.955	✔		✔	✔
FTL	Fortaleza	NOAA	a	p	3.52^°S	38.28^°W	100–4300	−0.39–0.02	0.45–0.80	0.209–0.973			✔
FWI	Fairchild, Wisconsin	NOAA	a	p	44.66^°N	90.96^°W	600–8100	−0.49–0.79	0.59–3.05	0.909–0.969			✔
GMI	Mariana Islands	NOAA	g	f	13.39^°N	144.66^°E	6	−0.11	0.58	0.997	✔	✔	✔	✔
HAA	Molokai Island, Hawaii	NOAA	a	p	21.23^°N	158.95^°W	300–8100	−0.16–0.27	0.39–0.66	0.988–0.995			✔
HBA	Halley Station, Antarctica	NOAA	g	f	75.61^°S	26.21^°W	35	−0.12	0.20	0.999	✔	✔	✔	✔
HDP	Hidden Peak (Snowbird), Utah	NCAR	g	i	40.56^°N	111.65^°W	3369	0.00	1.29	0.966			✔	✔
HEI	Heidelberg	UHEI-IUP	g	i	49.42 N	8.68^°E	146	−4.37	8.17	0.855
HFM	Harvard Forest, Massachusetts	NOAA	a	p	42.54^°N	72.17^°W	600–8100	−0.21–0.22	0.66–2.43	0.959–0.991			✔
HIL	Homer, Illinois	NOAA	a	p	40.07^°N	87.91^°W	600–8100	−0.24–−0.17	0.72–2.98	0.926–0.992			✔
HPB	Hohenpeissenberg	NOAA	g	f	47.80^°N	11.02^°E	990	2.96	5.03	0.854	✔	✔	✔	✔
HUN	Hegyhatsal	NOAA	g	f	46.95^°N	16.65^°E	344	0.27	5.28	0.910	✔	✔	✔	✔
		HMS	t	i	46.95^°N	16.65^°E	363						✔	✔
ICE	Storhofdi, Vestmannaeyjar	NOAA	g	f	63.40^°N	20.29^°W	100	−0.40	0.81	0.995	✔	✔	✔	✔
IZO	Izana, Tenerife, Canary Islands	NOAA	g	f	28.31^°N	16.50^°W	2378	−0.16	0.69	0.995		✔	✔	✔
		AEMET	g	i	28.31^°N	16.50^°W	2381						✔	✔
JFJ	Jungfraujoch	KUP	g	i	46.55^°N	7.98^°E	3580	−0.05	1.92	0.940			✔	✔
KEY	Key Biscayne, Florida	NOAA	g	f	25.67^°N	80.16^°W	6	0.07	0.82	0.993	✔	✔	✔	✔
KUM	Cape Kumukahi, Hawaii	NOAA	g	f	19.52^°N	154.82^°W	8	−0.34	0.77	0.994	✔	✔	✔	✔
KZD	Sary Taukum	NOAA	g	f	44.08^°N	76.87^°E	595	−1.46	2.50	0.946	✔	✔	✔	✔
KZM	Plateau Assy	NOAA	g	f	43.25^°N	77.88^°E	2524	0.59	1.62	0.97	✔	✔	✔	✔
LEF	Park Falls, Wisconsin	NOAA	g	p	45.95^°N	90.27^°W	715	−0.05	3.29	0.939	✔		✔	✔
		NOAA	t	i	45.95^°N	90.27^°W	868				✔		✔^a	✔^a
		NOAA	a	p	45.95^°N	90.27^°W	600–4000	−0.29–0.53	1.11–3.63	0.927–0.985			✔
LJO	La Jolla, California	SIO	g	f	32.9^°N	117.3^°W	20	0.70	0.78	0.993			✔	✔
LLB	Lac La Biche, Alberta	NOAA	g	f	54.95^°N	112.45^°W	546	−0.38	4.03	0.912		✔	✔	✔
		EC	g	i	54.95^°N	112.45^°W	550				✔		✔	✔
LMP	Lampedusa	NOAA	g	f	35.52^°N	12.62^°E	50	−0.41	1.52	0.941	✔	✔	✔	✔
LPO	Ile Grande	LSCE	g	f	48.8^°N	3.58^°W	20	−0.43	2.35	0.93			✔	✔
LUT	Lutjewad, Netherlands	RUG	g	i	53.4^°N	6.35^°E	61	−3.11	5.40	0.81			✔	✔
MAA	Mawson Station, Antarctica	CSIRO	g	f	67.62^°S	62.87^°E	42	−0.27	0.24	0.999	✔		✔	✔
MEX	High Altitude Global Climate Observation Center	NOAA	g	f	18.98^°N	97.31^°W	4469	0.38	1.15	0.937		✔	✔	✔
MHD	Mace Head, County Galway	NOAA	g	f	53.33^°N	9.90^°W	26	−0.17	0.95	0.993	✔	✔	✔	✔
MID	Sand Island, Midway	NOAA	g	f	28.21^°N	177.38^°W	11	0.18	0.80	0.994	✔	✔	✔	✔
MKN	Mt. Kenya	NOAA	g	f	0.06^°S	37.30^°E	3649	0.61	1.78	0.939	✔	✔	✔	✔
MLO	Mauna Loa, Hawaii	NOAA	g	f	19.54^°N	155.58^°W	3402	−0.14	0.49	0.997	✔	✔	✔	✔
		NOAA	g	i	19.54^°N	155.58^°W	3437				✔		✔	✔
MNM	Minamitorishima	JMA	g	i	24.28^°N	153.98^°E	28	−0.07	0.66	0.996			✔	✔
MQA	Macquarie Island	CSIRO	g	f	54.48^°S	158.97^°E	13	−0.18	0.31	0.999	✔		✔	✔
NAT	Maxaranguape	NOAA	g	f	5.51^°S	35.26^°W	20	−0.38	0.80	0.792		✔	✔	✔
NHA	Worcester, Massachusetts	NOAA	a	p	42.95^°N	70.63^°W	200–8000	−0.52–0.14	0.80–2.67	0.947–0.990			✔
NMB	Gobabeb	NOAA	g	f	23.58^°S	15.03^°E	461	−0.31	0.56	0.991	✔	✔	✔	✔
NWR	Niwot Ridge, Colorado	NOAA	g	f	40.05^°N	105.59^°W	3526	0.10	1.16	0.980	✔	✔	✔	✔
		NCAR	g	i	40.05^°N	105.59^°W	3528				✔		✔	✔
OBN	Obninsk	NOAA	g	f	55.11^°N	36.60^°E	484	−0.35	2.54	0.956	✔		✔	✔
OIL	Oglesby, Illinois	NOAA	a	p	41.28^°N	88.94^°W	500–8100	−0.11–0.36	0.65–3.17	0.874–0.964			✔
ORL	Orleans	LSCE	a	f	47.83^°N	2.5^°E	200–6000	−0.26–0.82	0.97–4.08	0.882–0.986			✔
OTA	Otway, Victoria	CSIRO	g	f	38.52^°S	142.82^°E	50	−0.44	0.32	0.992			✔	✔
OXK	Ochsenkopf	NOAA	g	f	50.03^°N	11.81^°E	1185	0.03	3.84	0.889	✔	✔	✔	✔
PAL	Pallas-Sammaltunturi, GAW Station	NOAA	g	f	67.97^°N	24.12^°E	565	−0.31	2.03	0.973	✔	✔	✔	✔
		FMI	g	i	67.97^°N	24.12^°E	565						✔	✔
PDM	Pic Du Midi	LSCE	g	f	42.94^°N	0.14^°E	2877	−0.45	1.73	0.971			✔	✔
PFA	Poker Flat, Alaska	NOAA	a	p	65.07^°N	147.29^°W	100–7600	−0.35–0.01	0.73–0.97	0.990–0.995			✔
POC	Pacific Ocean	NOAA	s	f			20	−0.36–0.30	0.31–0.55	0.994–0.998	✔	✔	✔	✔
PSA	Palmer Station, Antarctica	NOAA	g	f	64.92^°S	64.00^°W	15	−0.16	0.27	0.999	✔	✔	✔	✔
PTA	Point Arena, California	NOAA	g	f	38.95^°N	123.74^°W	22	−2.47	2.93	0.93	✔	✔	✔	✔
RBA	Roof Butte, Arizona	NCAR	g	i	36.46^°N	109.10^°W	3004	0.04	1.13	0.928			✔	✔
RPB	Ragged Point	NOAA	g	f	13.16^°N	59.43^°W	20	−0.08	0.42	0.998	✔	✔	✔	✔
RTA	Rarotonga	NOAA	a	p	21.25^°S	159.83^°W	15–6500	−0.30–0.12	0.36–0.51	0.998–0.999			✔
RYO	Ryori	JMA	g	i	39.03^°N	141.82^°E	280	−0.47	1.65	0.977			✔	✔
SAN	Santarem	NOAA	a	p	2.85^°S	54.95^°W	100–5200	−0.54–0.66	0.47–2.16	0.935–0.996			✔
		IPEN	a	f	2.85^°S	54.95^°W	100–4400						✔
SCA	Charleston, South Carolina	NOAA	a	p	32.77^°N	79.55^°W	200–13,300	−0.39–−0.14	0.56–2.81	0.912–0.994			✔
SCT	Beech Island, South Carolina	NOAA	g	p	33.41^°N	81.83^°W	420	−0.31	3.90	0.850			✔	✔
		NOAA	t	i	33.41^°N	81.83^°W	420				✔		✔	✔^a
SEY	Mahe Island	NOAA	g	f	4.68^°S	55.53^°E	3	−0.18	0.57	0.996	✔	✔	✔	✔
SGP	Southern Great Plains, Oklahoma	NOAA	g	f	36.61^°N	97.49^°W	374	0.24	3.35	0.913	✔	✔	✔	✔
		LBNL	g	i	36.61^°N	97.49^°W	374				✔		✔	✔
		NOAA	a	p	36.61^°N	97.49^°W	200–13,000	−0.34–−0.03	0.75–3.29	0.849–0.984			✔
SHM	Shemya Island, Alaska	NOAA	g	f	52.71^°N	174.13^°E	28	−0.55	1.05	0.992	✔	✔	✔	✔
SIS	Shetland Islands	CSIRO	g	f	60.09^°N	1.25^°W	30	0.11	0.73	0.986	✔		✔	✔
SMO	Tutuila	NOAA	g	f	14.25^°S	170.56^°W	47	−0.16	0.31	0.999	✔	✔	✔	✔
		NOAA	g	i	14.25^°S	170.56^°W	60				✔		✔	✔
SNP	Shenandoah National Park	NOAA	t	i	38.62^°N	78.35^°W	1025	−0.35	2.61	0.926	✔		✔^n	✔^n
SPL	Storm Peak Laboratory (Desert Research Institute)	NCAR	g	i	40.45^°N	106.73^°W	3219	−0.52	1.59	0.949	✔		✔	✔
SPO	South Pole, Antarctica	NOAA	g	f	89.98^°S	24.80^°W	2821	−0.15	0.12	1.000	✔	✔	✔	✔
		NOAA	g	i	89.98^°S	24.80^°W	2821				✔		✔	✔
STM	Ocean Station M	NOAA	g	f	66.00^°N	2.00^°E	7	−0.08	0.95	0.991	✔	✔	✔	✔
STR	Sutro Tower, San Francisco, California	NOAA	g	p	37.76^°N	122.45^°W	486	−1.97	4.86	0.721	✔		✔	✔
SUM	Summit	NOAA	g	f	72.60^°N	38.42^°W	3215	−0.08	0.84	0.994	✔	✔	✔	✔
SYO	Syowa Station, Antarctica	NOAA	g	f	69.00^°S	39.58^°E	11	−0.23	0.18	1.000	✔	✔	✔	✔
		NIPR	g	i	69.00^°S	39.58^°E	21						✔	✔
TAP	Tae-ahn Peninsula	NOAA	g	f	36.74^°N	126.13^°E	16	−1.47	2.65	0.953	✔	✔	✔	✔
TDF	Tierra Del Fuego, Ushuaia	NOAA	g	f	54.85^°S	68.31^°W	32	−0.29	0.46	0.997	✔	✔	✔	✔
TGC	Sinton, Texas	NOAA	a	p	27.73^°N	96.86^°W	200–8100	−0.29–−0.08	0.54–1.85	0.950–0.995			✔
THD	Trinidad Head, California	NOAA	g	f	41.05^°N	124.15^°W	112	−1.24	2.4	0.934	✔	✔	✔	✔
		NOAA	a	p	41.05^°N	124.15^°W	200–8100	−0.30–0.16	0.60–1.02	0.987–0.992			✔
TOT	Toronto, Ontario	EC	g	i	43.78^°N	79.47^°W	218	−2.24	2.91	0.961
TRN	Trainou	LSCE	t	i	47.97^°N	2.11^°E	311	1.25	4.46	0.886			✔	✔
ULB	Ulaanbaatar	NOAA	a	p	47.4^°N	106.0^°E	1500–6000	–0.12–0.36	0.11–1.18	0.975–0.980			✔
UTA	Wendover, Utah	NOAA	g	f	39.90^°N	113.72^°W	1332	0.08	1.76	0.969	✔	✔	✔	✔
UUM	Ulaan Uul	NOAA	g	f	44.45^°N	111.10^°E	1012	−0.71	2.12	0.967	✔	✔	✔	✔
WBI	West Branch, Iowa	NOAA	g	p	41.72^°N	91.35^°W	621	−0.28	4.04	0.887	✔		✔	✔
		NOAA	t	i	41.72^°N	91.35^°W	621				✔		✔^a	✔^a
		NOAA	a	p	41.72^°N	91.35^°W	600–8200	−0.13–−0.03	0.64–2.77	0.915–0.991			✔
WGC	Walnut Grove, California	NOAA	g	p	38.27^°N	121.49^°W	91	−0.99	4.35	0.721	✔		✔	✔
		NOAA	t	i	38.27^°N	121.49^°W	483				✔		✔^a	✔^a
WIS	WIS Station, Negev Desert	NOAA	g	f	30.86^°N	34.78^°E	482	−0.25	1.73	0.973	✔	✔	✔	✔
WKT	Moody, Texas	NOAA	g	p	31.31^°N	97.33^°W	708	0.16	2.88	0.895	✔		✔	✔
		NOAA	t	i	31.31^°N	97.33^°W	708				✔		✔^a	✔^a
WLG	Mt. Waliguan	NOAA	g	f	36.29^°N	100.90^°E	3815	−0.33	1.10	0.987	✔	✔	✔	✔
WSA	Sable Island, Nova Scotia	EC	g	i	43.93^°N	60.02^°W	30	−0.46	2.27	0.955	✔		✔	✔
YON	Yonagunijima	JMA	g	i	24.47^°N	123.02^°E	50	−0.48	1.44	0.98			✔	✔
ZEP	Ny-Alesund, Svalbard	NOAA	g	f	78.91^°N	11.89^°E	479	−0.02	0.86	0.995	✔	✔	✔	✔

¹ Platform and sampling method: g, surface; a, aircraft; t, tower; s, shipboard; f, flask; i, continuous; p, programmable flask package (Turnbull et al., 2012; considered a flask sampling method in this study).

² These parameters may change over time; only the most current information is listed in the table.

³ Temporal data selection applied in Case SEL and Case NA: a, only afternoon mean was used; n, only night-time mean was used.

The mean annual values of RSD were used as elements of the data mismatch error covariance matrix. The RSD for corresponding sites are provided in the obspack_co2_1_GLOBALVIEW-CO2_2013_v1.0.3_2013-05-24 product (GLOBALVIEW-CO2, 2013). For the sites that are not included in the GLOBALVIEW product, we used the average RSD values of all other sites over a latitudinal zone of 20° and an altitudinal level of 1 km. These RSD values were also used in data filtering described in Section 2.2. The minimum uncertainty value was set to 0.25 ppm.

In this study, we conducted sensitivity tests for different cases, each consisting of different site/data selections and observation uncertainties, to determine the impact of the observation settings on the inversion results. We prepared five cases, a control case data-set and four different subsets of the control case. The control case used all of the sites listed in Table 1, whereas the other four cases included only selected sites (indicated by checkmarks in the four right-hand columns of the table). The number of sites and types of data used in each case are shown in Table 2. A total of 154 sites were used in the control case, including 35 continuous measurement sites and 27 aircraft sites. Among 35 continuous sites, data from 29 sites were pretreated to give the ‘afternoon mean’ and ‘night-time mean’ that is the average value of 12–16LT and 2–5LT, respectively. We used both afternoon and night-time means in the control case. We used only data collected at 00:00 UTC and 12:00 UTC values when continuous data were provided at an hourly time step, which was the case for 3 JMA sites (MNM, RYO, and YON in Table 1). Since these sites are ‘marine boundary’ sites, we considered diurnal cycles were not significant. Among 27 aircraft sites, 26 are vertical profiles at certain locations except CONTRAIL (CON; Comprehensive Observation Network for Trace gases by Airliner) (Machida et al., 2008; Matsueda et al., 2015) of which we used data from a specific sampling mode ASE (Automatic Air Sampling Equipment) that sampled at certain latitudes during the level flight along a nearly fixed route between Narita and Sydney/Brisbane. For CON, we aggregated the data by 5 latitude bin between 30N and 25S, whereas for other aircraft sites, we aggregated the data by vertical bins. The interval of the vertical bins varied from 0.5 to 2 km, mostly following the interval used for the corresponding site in the GLOBALVIEW product, 2013.

Table 2. Types of observation sites used in each case.

Case	Total	Surface flask	Surface in situ	Tower	Shipboard	Aircraft
Control case	154	82	33	10	2	27
Case CT	90	67	14	8	1	0
Case NF	61	60	0	0	1	0
Case SEL	151	81	31	10	2	27
Case NA	124	81	31	10	2	0

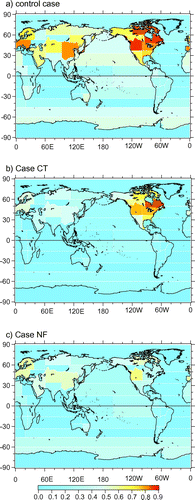
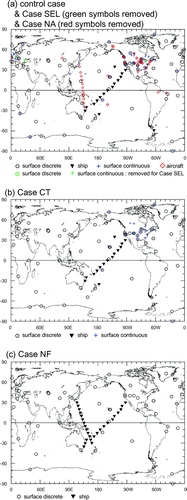
Case CT used 90 surface sites, including 22 continuous measurement sites and a shipboard site but no aircraft sites. This case was named Case CT because the selected sites are those used by CarbonTracker North America (CT2011_oi), a CO₂ measurement and modelling system developed by NOAA (Peters et al., 2007). For Case CT, a prior observation uncertainty was assigned to each observation site according to the categories defined by Peters et al. (2005); these uncertainties ranged between 0.75 ppm (marine boundary layer) and 7.5 ppm (difficult sites). Case NF used 61 surface flask sites in the NOAA ESRL Cooperative Global Air Sampling Network (Dlugokencky et al., 2013); it included no continuous-measurement or aircraft sites. The case NF was named meaning ‘case NOAA Flasks’. In this study, a sensitivity test was first conducted using the control case, Case CT, and Case NF. The observation locations of these three cases are shown in Fig. 4. Case SEL and Case NA were then defined on the basis of the inversion results obtained in the first sensitivity test. For Case SEL, three sites that showed large model–data mismatch values were removed from the control case. The name SEL means that the ‘data selection’ is applied. For Case NA, all aircraft data were removed from Case SEL. NA stands for ‘no aircraft data’. Details of these two cases are explained in Sections 3.5 and 3.6.

Fig. 4. Map showing the observation site locations of the different site selection cases: (a) control case (all symbols), Case SEL (green symbols removed), and Case NA (red symbols removed); (b) Case CT and (c) Case NF. Symbol shapes indicate the type of sampling: ○, surface discrete; +, surface continuous; ▾, ship; ♢, aircraft.

3. Results and discussion

3.1. Global budget/trend

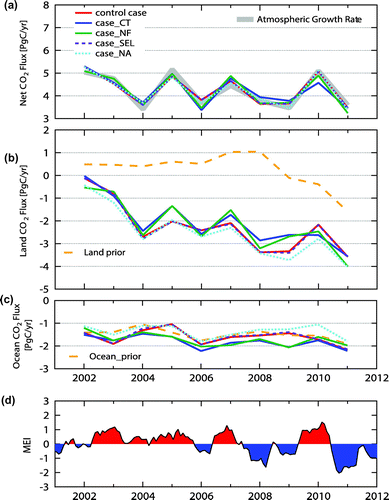
Decadal time series of the annual CO₂ fluxes estimated by inversion using the five different observation data-sets (five cases) described in Section 2.4 are shown in Fig. 5. The global net fluxes into the atmosphere are also plotted against the global atmospheric CO₂ growth rate derived directly from the observed CO₂ (Dlugokencky and Tans, 2014) for comparison. The time series of the global net fluxes agreed well among the five cases and were generally consistent with the time series of the observed growth rate with respect to both year-to-year variations and annual mean values (Fig. 5(a)). The interannual variability of the net fluxes appeared to be strongly correlated with the variability in the land CO₂ flux, shown in Fig. 5(b). The large interannual fluctuations of the land flux correspond to El Niño-Southern Oscillation (ENSO) phases (Fig. 5(d)). High growth rates of the CO₂ mixing ratio in 2003, 2005, 2007 and 2010 were likely due to reduced CO₂ uptake by land during El Niño phases (Jones et al., 2001; Knorr et al., 2007; Mabuchi, 2013). The low land CO₂ uptake in 2002 is considered to be due to global dry condition during the period (Knorr et al., 2007). The interannual variations of the estimated land flux is in phase with the ensemble results of nine dynamic global vegetation models (Le Quéré et al., 2013) and with the atmospheric inversion results of an ensemble of 11 transport models (Peylin et al., 2013) and 7 transport models in which GELCA is included as well (Thompson et al., 2016). The increasing tendency of the land CO₂ sink in the early 2000s (Fig. 5(b)) was also reported by Peylin et al. (2013). The effect of ENSO events on the ocean CO₂ flux (Fig. 5(c)) is not clear. In an intercomparison study of the air-sea CO₂ flux in the Pacific Ocean (Ishii et al., 2014), an association of interannual variation in the tropics with ENSO events was suggested by diagnostic models and ocean general circulation models, but it was not clear in the results of atmospheric inversions. Since global interannual variability of land fluxes is generally larger than that of oceanic fluxes, it is more challenging for atmospheric inversions to resolve the global interannual variations of oceanic fluxes without interference from larger atmospheric CO₂ fluctuations mainly caused by land fluxes.

Fig. 5. Comparison of global annual mean posterior fluxes: (a) net, (b) land biosphere, and (c) ocean. (d) Multivariate ENSO Index (MEI) (Wolter and Timlin, 1993) for 2002–2011. Positive fluxes indicate emission and negative fluxes indicate uptake. In (a), the global annual mean atmospheric CO₂ growth rate is shown with net fluxes. The CO₂ growth rate in ppm are converted to the emission rates in Pg of carbon with a conversion factor of 2.12 PgC ppm⁻¹ via simple molecular weight considerations. In (b) and (c), the global annual mean prior fluxes for land biosphere and ocean are shown, respectively.

3.2. Regional flux distributions

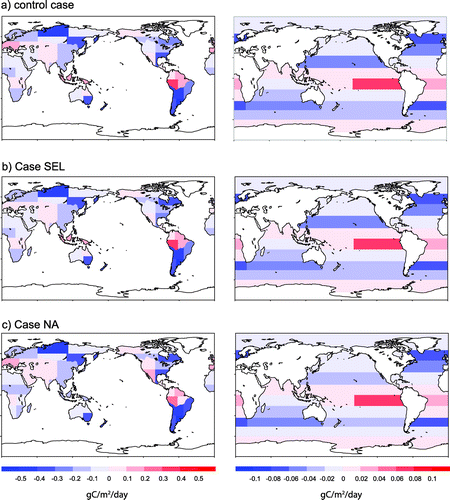
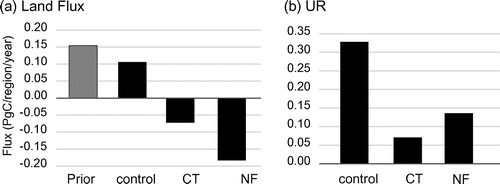
The spatial distributions of the decadal mean CO₂ fluxes during 2002–2011 of the control case, Case CT, and Case NF are shown in Fig. 6. Although the global net fluxes agreed well among these three cases, at regional scales, we can see differences in the estimated CO₂ fluxes among them due to the different observational data used in each case. The three inversion results share some features in common, such as increased uptake in temperate South America and boreal Eurasia and increased emissions in tropical South America and south-western Europe, compared to the prior fluxes. These regions, except for south-western Europe, are poorly constrained. The results for tropical Asia (Region 33) are interesting. The decadal mean CO₂ flux from this region was positive (emission) in the control case, but negative (uptake) in both Case CT and Case NF. Considering that the prior flux in this region is positive, the observational constraints of Case CT and Case NF changed the flux to negative. In the control case, which had more observational constraints than the other two cases, the flux was estimated to be positive. The reason for this difference is discussed in Section 3.6.

Fig. 6. Decadal mean (2002–11) spatial distributions of posterior fluxes for (a–c) land and (e–g) ocean regions: (a, e) control case, (b, f) Case CT, (c, g) Case NF. Prior fluxes from the (d) land biosphere and (h) ocean. Positive fluxes indicate emission and negative fluxes indicate uptake.

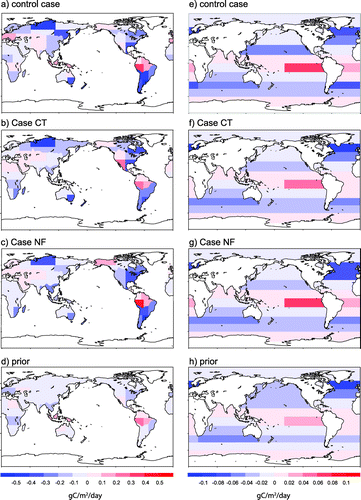
Table 3 shows the number of data used in the inversion in these three cases. The control case used twice as many observational data as Case CT and six times as many as Case NF. Just on the basis of the number of observations, the control case would be expected to constrain the regional flux estimation much better. However, not only does the effectiveness of the inversion depend on the amount of observational data, but it also depends strongly on the spatial (and temporal) coverage of the observation sites. We evaluate the effectiveness of the inversion using two indicators, the uncertainty reduction (UR) and the model–data mismatch, in the following sections.

Table 3. The number of data used in the inversion, mean bias, root-mean-square error (RMSE), and correlation coefficient (R): (a) control case, Case CT, and Case NF; and (b) control case, Case SEL, and Case NA.

Case	Number of data	Bias (ppm)	RMSE (ppm)	R
(a)
Control case	171,641	0.21	1.34	0.962
Case CT	78,821	0.25	1.66	0.958
Case NF	28,578	0.23	1.07	0.974
(b)
Control case	171,641	0.21	1.34	0.962
Case SEL	156,549	0.18	1.29	0.963
Case NA	115,082	0.20	1.53	0.958

3.3. Uncertainty reduction

UR is a measure commonly used to evaluate the effectiveness of observational constraints in different regions. UR is defined as the relative difference between the prior and posterior flux uncertainty:

where and are the quadratic means of the posterior standard deviation and the prior standard deviation, respectively. By definition, the more the posterior error is reduced relative to the prior error, the closer to 1 UR becomes, which means that more information from observations is provided to the inversion. Figure 7 shows the UR calculated for each region in each of the three cases. UR is higher in land regions in the northern mid-high latitudes, where observations are the most abundant in the framework of the current surface observation network, whereas UR is lower in the poorly covered tropical Northern Hemisphere and the whole Southern Hemisphere. The global pattern of the UR distribution is consistent with the UR distributions reported by Chevallier et al. (2010), who conducted an inversion at both grid scale (3.75° × 2.5° longitude × latitude) and regional scale (22 Transcom3 regions distributed worldwide).

Fig. 7. Uncertainty reductions by region: (a) control case, (b) Case CT, and (c) Case NF.

The control case showed higher UR than Case NF and Case CT in all regions, and the difference was significant in East Asia and southern Europe, where the control case had better data coverage. Case CT had strong constraints in North America, which is the target of the CarbonTracker North America project (Fig. 7(b)). Outside of North America, however, Case CT had slightly lower URs than Case NF. Considering that most of the stations included in Case NF were also in Case CT, this UR difference may be due to the relatively larger prior observation uncertainty values assigned to sites outside North America, which resulted in the constraints in Case CT being weaker than those in Case NF.

The UR became more sensitive to the exact location of each observational station as the spatial scale became finer. For example, the Transcom3 ‘Europe’ region is, as a whole, relatively well covered by observations, but in our land mask in which the Transcom3 ‘Europe’ is divided into four sub-regions, Western Europe (regions 39 and 41) is well constrained with denser observation coverage, whereas Eastern Europe (regions 40 and 42) is barely constrained owing to fewer observation sites. Therefore, the high UR in Transcom3 ‘Europe’ is due mainly to the denser observation network in Western Europe.

3.4. Model–data mismatch

The model–data mismatch is another measure used to evaluate the effectiveness of inversion results. We compared the forward simulation results using the optimized fluxes with observed CO₂ mixing ratios at the observation sites and calculated three measures of the model–data mismatch: the model–data bias, the root-mean-square error (RMSE), and the linear correlation. The model–data bias is a systematic mismatch between observations and model (model minus observations) throughout the observation period. The RMSE is an aggregated form of the residuals (the difference between simulated values and observed values). The correlation indicates the strength and direction of the linear relationship between model output and observed values. These three measures of the model–data mismatch calculated for each observation site in the control case are shown in Table 1, and the averaged values for all sites used in each case are shown in Table 3.

Table 3(a) compares these measures among the control case, Case CT, and Case NF. In the control case, the global mean bias of 0.21 ppm was the smallest of the three cases. The mean RMSE was ±1.34 ppm for the control case, ±1.66 ppm for Case CT, and ±1.07 ppm for Case NF. The differences in RMSE may reflect the fraction of continuous data in each data-set, because the RMSE is affected by the higher variability of continuous data compared with flask data. The mean correlation coefficient R was 0.962, 0.958, and 0.974 for the control case, Case CT, and Case NF, respectively. The model–data correlations were high for all cases, indicating overall good performance of the GELCA inversion system.

The bias and RMSE for each site in the three cases are shown in Fig. 8. The observations were not well reproduced by the model at sites that showed high values of both bias and RMSE. Nine sites in the control case showed a bias larger than ±1 ppm: Heidelberg (HEI), Toronto (TOT), Bukit Kototabang (BKT), Black Sea (BSC), Lutjewad (LUT), Sutro Tower (STR), Hohenpeissenberg (HPB), Baltic Sea (BAL), and Point Arena (PTA). We investigated the reasons for the discrepancies between observations and simulations at these sites. Among these nine sites, three were probably strongly influenced by a local CO₂ flux such as urban emissions (HEI and TOT) or forest uptake (BKT). For sites located in cities or downwind of urban areas, the model often failed to reproduce sporadic sharp peaks in the observations. Continuous measurements inside urban areas (HEI and TOT) resulted in a significantly negative bias compared to background sites. LUT and STR often captured a high CO₂ plume transported from urban areas of The Netherlands and San Francisco, respectively. In the case of BSC, the observational behaviour has apparently been changing. The prominent seasonal cycle seen in the early 2000s gradually disappeared, and the frequency of significantly high mixing ratios increased in the late 2000s. These changes might reflect a change of either the surrounding environment (possibly increasing CO₂ sources) or the measurement system. When both the topography near a site and nearby source or sink distributions are complicated, the model tends to express a higher mismatch, as in the cases of HPB, BAL, and PTA.

Fig. 8. Model–data mismatch for observation sites after inversion: (a) control case, (b) Case CT, (c) Case NF. The colour and size of the coloured circles indicate the bias and the RMSE, respectively. The size of the open circles indicates the prior uncertainty value.

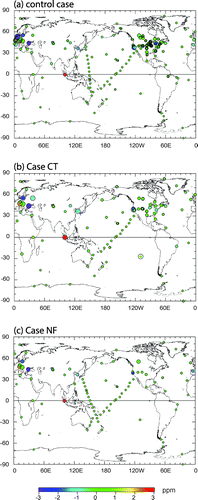
GELCA showed significantly better performance compared to NIES-TM for the site that require finer resolution than 2.5° grid of NIES-TM. For example, two European tower sites Ochsenkopf (OXK; 50.0°N, 11.8°E) and Pic du Midi (PDM; 42.9°N, 0.1°E) are located close to the border of the model grids in which the topography is rather complicated (on the top of mountain). Since NIES-TM cannot resolve the topographical change within a grid, the forward simulation doesn’t fit observation well. On the other hand, GELCA handles the simulation in the vicinity of the observation sites with FLEXPART, resulting in much better fit at these difficult sites. The observed and simulated CO₂ time series for OXK and PDM are shown in Supplementary Figure 2. The performance of GELCA depends on site-specific conditions (e.g. source and sink distributions in the vicinity and topographic features), and should be further investigated in future studies.

3.5. Data selection to reduce observational noise

Based on the results reported in Section 3.4, we designed a new subset called Case SEL to minimize noise from observations. To avoid strong local influences, data from BSC, HEI, and TOT were excluded from Case SEL. We also applied temporal data selection to seven continuous sites located near source or sink areas. Only afternoon averages were used from the tower sites Boulder Atmospheric Observatory (BAO), Moody (WKT), Beech Island (SCT), Park Falls (LEF), West Branch (WBI), and Walnut Grove (WGC), and the Pallas-Sammaltunturi (PAL) surface site (PAL), to exclude local extreme values in the stable boundary layer at night. In contrast, only night-time averages were used from a mountain site, Shenandoah National Park (SNP; 1008 m above sea level) to minimize the bias from local sources or sinks. Temporal data selection has been used in previous studies carried out since the TransCom Continuous experiment (Peters et al., 2007; Law et al., 2008; Patra et al., 2008; Chevallier et al., 2010).

Figure 9(b) shows the inversion results for Case SEL. The decrease in biospheric emissions from southwestern Europe (region 39) compared to the control case is the most prominent feature, whereas the impact of Case SEL was not significant in south-eastern Europe (region 40). The decadal mean decrease of biospheric emissions was 0.076 ± 0.024 PgC/region/year in north-western Europe, and 0.040 ± 0.026 PgC/region/year in south-western Europe; both values correspond to a 41% change from the estimated regional fluxes in the control case. This result indicates that HEI, BSC and PAL significantly affected the inversion results for Western Europe. Estimation of finely distributed anthropogenic and natural sources and sinks in Western Europe may need higher spatial and temporal resolution of both prior fluxes and transport simulation. In contrast, in North America, there was no significant difference between the control case and Case SEL. This result shows that the temporal data selection of continuous tower observations and the removal of TOT did not significantly affect the flux estimation in North America.

Fig. 9. Comparison of decadal mean (2002–2011) spatial distributions of posterior fluxes for the land biosphere (left panels) and ocean (right panels): (a) control case, (b) Case SEL, (c) Case NA. Positive fluxes indicate emission and negative fluxes indicate uptake.

3.6. Effect of aircraft observations on flux estimates in tropical Asia

Here we discuss the large difference in terrestrial biosphere fluxes from tropical Asia (region 33) among the prior and three posterior fluxes described in Section 3.2. The decadal mean flux and UR for this region in the control case, Case CT, and Case NF are shown in Fig. 10. In tropical Asia, only one observation site, BKT in Indonesia, was used in this study (Fig. 4). We set the observation uncertainty for BKT to 2.8 ppm for the control case and Case NF; this value is derived from the RSD values of the data record at site BKT in the ObsPack GLOBALVIEW product. For Case CT, the observation uncertainty for BKT was set to 7.5 ppm, which is the maximum uncertainty in the CarbonTracker model, because of its relatively large model–data mismatch (Peters et al., 2005). The higher UR for Case NF than Case CT (Fig. 10) can be explained by the smaller prior uncertainty assigned to BKT as well as by additional constraints from the Western Pacific Cruise (WPC; shipboard observations in the western Pacific Ocean; Fig. 4(c)) during 2004, which may have detected flux signals from tropical Asia.

Fig. 10. (a) Prior and posterior land fluxes and (b) uncertainty reduction (UR) in tropical Asia (Region 33) in the control case, Case CT, and Case NF. Positive fluxes indicate emission and negative fluxes indicate uptake.

As shown in Fig. 8, BKT showed the largest positive bias among all sites used in this study. A similar large positive bias for BKT has been found by many other atmospheric inversion studies as well (e.g. CarbonTracker Team, 2014). The flask sampling at BKT is conducted on a weekly basis, usually around 14:00 LT, when the CO₂ hourly average mixing ratio reaches its minimum value (Nahas, 2012). Because the observation site is surrounded by a tropical rainforest, the samples may be more representative of the daily minimum mixing ratio, which reflects uptake by local vegetation, than of the daytime large-scale boundary condition. Thus, the net CO₂ uptake in tropical Asia in Case CT and Case NF may be largely due to the BKT observations.

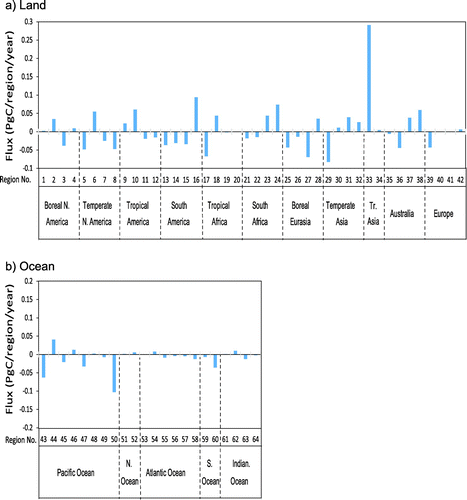
In contrast to Case CT and Case NF, the control case yielded net CO₂ emissions in tropical Asia even though it used BKT data. The UR of the control case was higher not only in tropical Asia but also in the overall tropical southern Pacific Ocean, compared to Case NF and Case CT. This spatial distribution difference of UR suggests that net CO₂ emissions in tropical Asia in the control case might result from the observational constraints in the tropical southern Pacific Ocean, which were used only in the control case. These observational constraints are aircraft data such as Rarotonga (RTA; 21.25°S, 159.83°W) and CON, which were included only in the control case. Therefore, we hypothesize that the aircraft data affected the inverted flux for the tropical Asia region in the control case. The measurement periods of RTA and CON are 2001–2011 and 2001–2009, respectively. The frequencies of both observations are biweekly on average.

To test this hypothesis, we conducted another sensitivity test by removing all aircraft observations from the control case. Without aircraft data, the decadal mean regional flux in tropical Asia became negative (Fig. 9(c)). This result supports our hypothesis that the aircraft data strongly constrained the CO₂ flux estimate in this region. However, the differences did not appear to be significant in the oceans and other land regions. To check the sensitivity to aircraft data in detail, differences between decadal mean regional fluxes estimated with (Fig. 9(a)) and without (Fig. 9(c)) aircraft data are shown in Fig. 11. The flux difference in tropical Asia (region 33 in Fig. 11(a)) stands out among the regions. Among oceanic regions, the largest flux difference was found in South Pacific north (region 50 in Fig. 11(b)). This sensitivity analysis indicates that tropical Asia and its neighbouring ocean regions are the areas most sensitive to the aircraft data used in the inversion.

Fig. 11. Differences between estimated annual mean regional CO₂ fluxes from the (a) land biosphere and (b) ocean derived with and without aircraft observations (control case – Case NA) during 2002–11. The numbered regions are shown in Fig. 3. Positive fluxes indicate emission and negative fluxes indicate uptake.

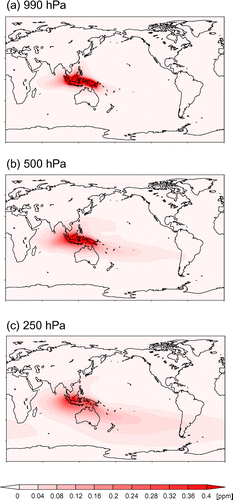
To investigate how surface fluxes from tropical Asia are transported, we calculated the distribution of atmospheric CO₂ at three vertical levels, approximately 990, 500, and 250 hPa, from monthly, pulse emission from the region (annual mean is shown in Fig. 12). We kept a constant CO₂ source (spatially distributed according to the multiple year mean of NEP from VISIT) in tropical Asia, and the transport model tracked its mixing ratios over the course of a month. The results shown in Fig. 12 indicate that the signal from surface fluxes in tropical Asia could be detected by aircraft observations in the mid/upper troposphere through vertical convection and the consequent rapid horizontal transport in the free troposphere. This active convection in tropical Asia as part of the Walker circulation must be a key process connecting surface fluxes and aircraft observations.

Fig. 12. Annually averaged atmospheric CO₂ distributions at (a) 990 hPa, (b) 500 hPa, (c) 250 hPa, calculated from monthly pulsed emission from tropical Asia (Region 33) in 2008.

We next examined the impact of the aircraft data on the seasonality of terrestrial biospheric fluxes from tropical Asia. The decadal mean seasonal cycle derived from the inversion using the aircraft data (control case) and the inversion without using the aircraft data (Case NA) are plotted with the prior flux in Fig. 13. The flux estimates in Case NA became significantly negative (sink) compared with the prior fluxes, whereas the seasonal estimates were mostly positive (source) in the control case. This might be due to the increased effect of the negative bias from BKT observation when we don’t use aircraft measurements. A major difference in the estimated fluxes between the control case and Case NA was found during two periods: May–June and November–January. During May–June, the estimated flux was almost zero in the control case, whereas Case NA estimated a sink. During November–January, the control case estimated large emissions, but Case NA estimated much lower emissions in November–December and even uptake in January. Niwa et al. (2012) have also pointed out CO₂ emissions in tropical Asia during October–January in their atmospheric inversion for the period 2006–2008 using CONTRAIL data that were enhanced compared to an estimate made by using only ground-based data (GLOBALVIEW-CO₂). Niwa et al. (2012) used CONTRAIL CME (Continuous CO₂ Measuring Equipment) data, which were binned and monthly averaged after smoothing and gap-filling, and the inversion was conducted with the NICAM-TM (Nonhydrostatic Icosahedral Atmospheric Model-based Transport Model). We used only CONTRAIL ASE data without preprocessing, and we conducted the decadal inversion by GELCA. The decadal inversion results in this study confirmed the strong impact of aircraft data on surface flux estimates in tropical Asia.

Fig. 13. Monthly mean land biosphere posterior fluxes (control case – red; Case NA – green) and prior fluxes (VISIT – gray), averaged over 2002–11. Positive fluxes indicate emission and negative fluxes indicate uptake.

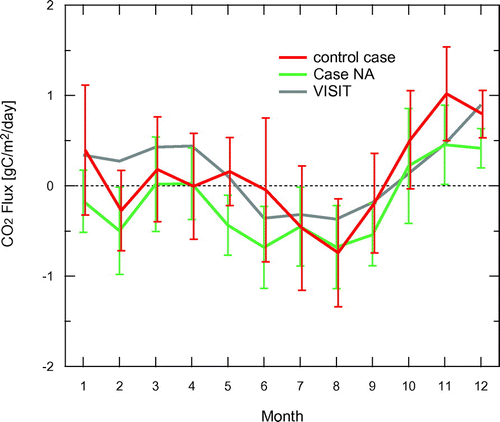
To further evaluate the seasonality of the estimated fluxes for tropical Asia, we compared our results with bottom-up studies. Among the limited number of bottom-up studies in this region, the seasonal cycle of NEP was estimated by continuous CO₂ flux measurements using the eddy covariance technique in tropical peat swamp forests in Central Kalimantan (Hirano et al., 2007, 2012). These estimates suggest that the CO₂ flux is positive during the rainy season (November–April) and the late dry season (August–October), whereas it is nearly neutral or slightly negative during the early dry season (May–July). The neutral flux in the early dry season and higher emissions during the early rainy season were also seen in the seasonal cycle of the control case (Fig. 13). The seasonal cycle of the control case agrees better with the results from the bottom-up study than Case NA. This result indicates that the inversion with aircraft data captures well the seasonal signals of the regional land biosphere. Both our inversion results and those of the top-down study by Niwa et al. (2012) agree better with independent bottom-up studies when aircraft data are included; thus, aircraft observations play a key role in constraining CO₂ flux estimates in tropical Asia.

4. Summary and conclusions

We presented an assimilation system for atmospheric CO₂ using GELCA, and we demonstrated its ability to capture observed atmospheric CO₂ mixing ratios and to estimate CO₂ fluxes. In this study, to take full advantage of the data handling efficiency of GELCA, we used non-smoothed observational data from ObsPack as constraints. ObsPack includes various types of direct atmospheric CO₂ measurements, continuous tower measurements, and aircraft measurements, provided by a large number of laboratories around the world.

We conducted sensitivity studies to examine the impact of the observation network setting on the inversion results and to optimize the site/data selection to minimize noise while optimizing the signal from the extensive observation data-set. We selected five different sets of sites/data from ObsPack: (1) comprehensive data-set (control case); (2) data selection conformed to the CarbonTracker North America project (Case CT); (3) data selection conformed to the NOAA ESRL Cooperative Global Air Sampling Network (Case NF); (4) data selection according to the model–data mismatch of the inversion results of the control case (Case SEL); and (5) Case SEL without aircraft sites (Case NA).

For all cases, the time series of the global net flux to the atmosphere were similar to that of the fluxes calculated from the growth rate of the observed global mean atmospheric CO₂ mixing ratio. At regional scales, estimated seasonal CO₂ fluxes were altered by the selection of assimilated CO₂ data. UR was derived at regional scale and compared among cases. In all regions, UR was higher in the control case than it was in Case CT and Case NF. Case CT showed considerably higher UR in North America, whereas outside of North America, Case NF showed slightly higher UR than Case CT. We employed three measures of model–data mismatch between the forward simulation results using the posterior fluxes and the observed CO₂ mixing ratios: the model–data bias, RMSE, and the linear correlation. For most observation sites, the model–data mismatch was reasonably small (global mean bias, 0.21 ± 0.03 ppm; mean RMSE, 1.38 ± 0.23 ppm; correlation coefficient R > 0.9 for 91% of all used sites). There were some sites with a larger model–data mismatch, caused mostly by local conditions.

Surface fluxes in tropical Asia were found to be the most sensitive to the use of aircraft measurements in the inversion. The seasonal cycle agreed better with the results from bottom-up studies when aircraft measurements were used. These results confirm the importance of aircraft observations, especially in constraining surface fluxes in the tropics.

Overall, we found GELCA to be capable of handling various types of observations provided in ObsPack, and its performance in reproducing observed concentrations was good, with reasonably small model–data mismatches. The sensitivity studies indicated that the reduction of uncertainty in CO₂ flux estimation could be improved by expanding the observation network. In particular, the study results highlighted the impact of aircraft measurements over the Pacific on surface flux estimation in tropical Asia. This study evaluated the basic performance of GELCA as an assimilation tool for top-down CO₂ flux estimation. Studies are now underway, for example, to integrate more observations (e.g. satellite data) into GELCA and to analyse certain regional carbon flux estimations. Our future plans include optimization of GELCA’s settings (e.g. the duration of backward simulation by FLEXPART, temporal/spatial resolutions, and preprocessing of certain types of data) according to the specific aims of an investigation.

Disclosure statement

No potential conflict of interest was reported by the authors.

Funding

R. Zhuravlev is supported by Russian Science Foundation (grant No. 15-17-10024). T. Oda is supported by NASA Carbon Cycle Science program [grant number NNX14AM76G].

Supplemental data

Supplemental data for this article can be accessed http://dx.doi.org/10.1080/16000889.2017.1291158.

Acknowledgements

The authors are indebted to the data providers of the ObsPack product (obspack_co2_PROTOTYPE_v1.0.3_2013_01-29). The providers are listed below with their funding agencies and/or funded projects if applicable: P. Steele, P. Krummel, and M. van der Schoot (Commonwealth Scientific and Industrial Research Organisation (CSIRO), Australia); L. Gatti and A. Martinewski (Instituto de Pesquisas Energéticas e Nucleares (IPEN), Brazil); D. Worthy (Environment Canada (EC), Canada); J. Hatakka and T. Aalto (Finnish Meteorological Institute (FMI), Finland); M. Ramonet, M. Delmotte, M. Schmidt, and P. Ciais (Laboratoire des Sciences du Climat et de l’Environnement – UMR8212 CEA-CNRS-UVSQ (LSCE), France); J.A. Morgui (University of Barcelona (UB), Spain); N. Mihalopoulos (University of Crete (UOC), Greece); F. Gheusi (University of Toulouse, France); G. Bentz (LPO Station Ornithologique de l’Ile Grande, France), I. Levin and S. Hammer (University of Heidelberg, Institut für Umweltphysik (UHEI-IUP), Germany); L. Haszpra (Hungarian Meteorological Service (HMS), Hungary); A. Takizawa (Japan Meteorological Agency (JMA), Japan); T. Machida (National Institute for Environmental Studies (NIES), Japan); H. Matsueda and Y. Sawa (Meteorological Research Institute (MRI), Japan); S. Morimoto, T. Nakazawa, and S. Aoki (National Institute of Polar Research (NIPR) and Tohoku University, Japan); H. Meijer (University of Groningen, Centre for Isotope Research (RUG), the Netherlands); E. Brunke, E. Scheel and C. Labushagne (South African Weather Service (SAWS), South Africa); R. Ramos (Izaña Atmospheric Research Center, Meteorological State Agency of Spain (AEMET), Spain); M. Leuenberger (University of Bern, Physics Institute, Climate and Environmental Physics (KUP), Switzerland); S. Wofsy (Harvard University (HU), United States); S. Biraud and M. Torn (Lawrence Berkeley National Laboratory (LBNL), United States); K. Masarie, A. Andrews, E. Dlugokencky, C. Sweeney, P. Tans and K. Thoning (Global Monitoring Division (NOAA), United States), the aircraft measurements for the National Oceanic and Atmospheric Administration (NOAA) Global Greenhouse Gas Reference Network have been funded by the NOAA North American Carbon Program; B. Stephens (National Center For Atmospheric Research (NCAR), United States), the RACCOON network CO₂ concentration measurements have been supported by NSF (EAR-0321918), NOAA (NA09OAR4310064) and DOE (DE-SC0010624 and DE-SC001625); and R. Keeling (Scripps Institution of Oceanography (SIO), United States). The authors also thank Drs Akihiko Ito and Kazuo Mabuchi at NIES for helpful discussions.