ABSTRACT
This paper deals with general fuzzy two-term controllers of Takagi-Sugeno (TS) type. Analytical structures and properties of general fuzzy PI/PD controllers are investigated with a modified rule base. The rule base contains three rules which effectively reduce the number of tuning parameters of the controllers. The fuzzy two-term controller uses at least three triangular or trapezoidal fuzzy sets on each input variable, algebraic product/minimum t-norm, bounded sum/maximum t-co-norm, and Centre of Gravity (CoG) defuzzification strategy. Four new models of TS type fuzzy controllers are proposed. The general fuzzy PI/PD controller with modified TS rule base is analogous to a variable gain (nonlinear) PI/PD controller. The gain either varies or remains constant in different regions of the input plane. The gain variations of the controller and the stability analysis of closed-loop control system with any one of the proposed models in the loop have been investigated. The applicability of the proposed controllers is shown with the help of examples.
1. Introduction
Fuzzy logic control (FLC) tries to emulate human-like thinking and processes natural language. It applies to plants of higher order with or without time delays, complex and ill-defined systems without precise mathematical models, and systems with nonlinearities and uncertainties. Zadeh [Citation1] introduced the framework to deal with these types of systems where IF-THEN statements described the fuzzy control strategy. In the literature, two kinds of linguistic descriptions of fuzzy control rules are available, namely Mamdani [Citation2] type and Takagi-Sugeno (TS) [Citation3] type. They differ only in the rule consequent part; fuzzy sets are used in Mamdani type, whereas linear functions of input variables are used in TS type. Mamdani type rule base is linguistically intuitive, while the TS rule base is interpolative. An overview of fuzzy systems and their applications can be found in [Citation4]. Some recent developments on the applications of computational intelligence in modelling and control are presented in [Citation5]. FLC is one of the most attractive control strategies which utilises the qualitative knowledge of the process to design a controller.
Stability has been a major concern for the fuzzy control engineers. Extensive research has been done on the stability analysis of fuzzy control systems. A sufficient condition which guarantees the stability of TS type fuzzy systems was obtained in terms of Lyapunov's direct method by Tanaka and Sugeno [Citation6]. Wang et al. [Citation7] developed a design methodology for the stabilisation of nonlinear systems based on TS fuzzy model and parallel distributed compensation design. New stability conditions were proposed in [Citation8] for the closed-loop TS fuzzy control systems based on the analysis of fuzzy control systems with standard fuzzy partition (SFP) inputs. Absolute stability analysis of a class of TS fuzzy control systems was studied by transforming it into a multi-variable Lure type system by Fuh [Citation9]. Based on Lyapunov's direct method, a new stable and convergent technique was presented in [Citation10] for iterative feedback tuning of TS PI controllers for discrete-time input affine SISO systems. Sufficient conditions in terms of a single parameter minimisation problem were proposed [Citation11] for local stability analysis of continuous-time TS systems using Lyapunov's theory and Linear Matrix Inequalities techniques. A sufficient condition for BIBO stability of nonlinear feedback systems containing Takagi-Sugeno-Kang (TSK) fuzzy PI/PD controllers was derived in [Citation12] using the Small Gain theorem. The Small Gain theorem was used to establish a sufficient condition in [Citation13] for global BIBO stability of nonlinear systems controlled by Mamdani type fuzzy PI controllers.
Mathematical modelling of fuzzy controllers has been an active area of research since 1993. Mathematical models of fuzzy controllers help in establishing stability conditions for feedback systems that contain fuzzy controllers in the loops, obtaining optimal values of fuzzy controller parameters, and investigating computational and memory requirements for implementing the controller. Mathematical models of fuzzy controllers depend on various factors such as membership function, t-norm, t-co-norm, rule base, and defuzzification strategy. Fuzzy controllers do not have a single fixed model since different combinations of these factors yield different models. Looking at the historical perspectives of mathematical modelling of fuzzy controllers, Ying [Citation14] proposed four different models for the simplest fuzzy proportional-integral controller of Mamdani type. An analytical structure of Mamdani type fuzzy PI controller was derived [Citation15] using multiple fuzzy sets for inputs and output, linear control rules, and Mamdani inference. It was shown that the fuzzy controller is the sum of a two-dimensional multilevel relay and a local nonlinear PI controller. Ying introduced simplified linear control rules [Citation16,Citation17] for TS fuzzy PI/PD controllers. Moreover, the explicit structures of TS fuzzy PI/PD controllers were derived, and the properties of the resulting structures were investigated. Subsequently, Ding et al. [Citation18] have developed TS fuzzy PI and PD controllers that use at least three input fuzzy sets with triangular or trapezoidal membership functions, minimum t-norm, and CoG defuzzifier. Mohan and Reddy [Citation19] have proposed a general TS fuzzy PI/PD controller using the same number (at least three) of input fuzzy sets, minimum t-norm, bounded sum t-co-norm, modified fuzzy rule base to reduce the number of tunable parameters of the controller, and the same universe of discourse for both the inputs. Raj and Mohan [Citation20] have developed the simplest TS fuzzy PI/PD controllers using two input fuzzy sets and modified rule base which comprises only two rules.
Some other related works on fuzzy controllers were also reported. For nonlinear SISO systems, a proportional integral control law was developed [Citation21] based on the Lyapunov's theory to eliminate chattering. A supervisory control system was proposed [Citation22] for variable speed wind turbine using the second-order sliding mode approach. A fuzzy logic control system was designed [Citation23] for Liu-Chen four-scroll chaotic system using TS models. Some methods for the analysis, design, and control of chaotic and hyper-chaotic systems can be found in [Citation24,Citation25].
In this paper, four new classes of general TS fuzzy controllers are proposed. The analytical structures of the proposed controllers are investigated. These controllers use at least three triangular or trapezoidal input fuzzy sets, modified rule base, algebraic product/minimum t-norm, bounded sum/maximum t-co-norm, and CoG defuzzifier. The strength of TS fuzzy controllers lies in the tunable controller parameters. These parameters in the consequent part can be adjusted to achieve the required control, but as the number of rules increases, it becomes difficult to tune these parameters. The models proposed in this paper are superior to those existing in the literature as the number of tunable parameters has been reduced by modifying the rule base. The rule base consists of three rules having three different linear models in the consequent parts and six tunable parameters. It is shown that the gains are
nonlinear functions of input variables. In the literature, same Universe of Discourse (UoD) has been considered for both the inputs and
. To fully
utilise the nonlinear characteristic of the fuzzy controller, we consider different UoDs for the inputs. Small Gain theorem is used to derive the stability condition for ensuring the stability of a feedback system that contains one of the proposed fuzzy controllers in the loop. Simulation results are presented to demonstrate the superiority of the proposed fuzzy controllers over the linear controller.
The remaining paper is arranged as follows: the configuration of the general fuzzy controllers is discussed in Section 2. In Section 3, the analytical structures and properties of the controllers are derived. Section 4 deals with the stability analysis of fuzzy control systems. Section 5 deals with the simulation studies. The conclusion is presented in the last section.
2. Configuration of General TS PI/PD Controllers
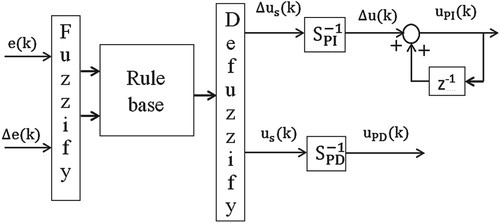
In this section, principle design components of general TS PI/PD controllers are presented. Figure shows the block diagram of a typical closed-loop control system. The inputs of the TS PI/PD controllers are error and change of error
. These are defined as
(1)
(2) where
and
are, respectively, the reference command and process output at
instant. Figure shows the block diagram of a typical TS PI/PD controller.
and
represent the scaled outputs of fuzzy PI and fuzzy PD controllers, respectively, and in general they are nonlinear functions of the inputs. The nonlinear function depends on the configuration of the fuzzy controller.
and
are the scaling factors for control outputs of fuzzy PI and fuzzy PD controllers, respectively.
2.0.0.1 Fuzzification
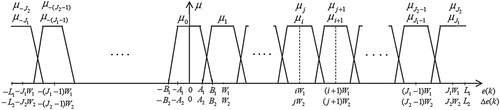
The error and change of error are fuzzified by and
fuzzy sets, respectively, with trapezoidal membership functions. Assuming
number of fuzzy sets on negative
(
), one fuzzy set for near zero
(
), and
number of fuzzy sets on positive
(
), we have
and
with
. Figure shows the input fuzzy sets with their trapezoidal membership functions where
and
are the lower and upper sides of trapezoidal membership function over
, respectively. For
, the trapezoid reduces to a triangle. Uniform distribution of fuzzy sets is considered over
for
and over
for
, where
and
are the design parameters. The central value
of the first fuzzy set on
is given by
. The mathematical description of
and
fuzzy sets on
and
, respectively, is given by
The description of positive and negative
fuzzy sets on
is as follows:
where
and
.
Also,
2.0.0.2 Rule Base
control rules are required to cover
possible combinations of input fuzzy sets. The fuzzy controller under consideration employs the following modified form of TS fuzzy rules:
: IF
is
AND
is
THEN
: IF (
is
AND
is
) OR (
is
AND
is
) THEN
: IF
is
AND
is
THEN
In the rules, the resultant membership grades are obtained using the algebraic product and minimum t-norms (AND operators). These t-norms are defined as
In the case of rule 2, bounded sum and maximum t-co-norms (OR operators) are used to join the two premise parts. If the premise parts generate membership grades
and
, then the resulting membership grades using bounded sum and maximum t-co-norms are defined as
Using all combinations of triangular norms and co-norms, four different classes of fuzzy controllers are defined as given in Table .
Table 1. Classes of fuzzy controllers.
2.0.0.3 Defuzzification
The overall output is defuzzified by the CoG defuzzification method. It is given by
(3) The output of the fuzzy PI controller is given by
(4) For fuzzy PD control,
is replaced by
in Equation (Equation3
(3) ).
3. Analytical Structures and Properties of General TS PI/PD Controllers
In this section, the models of the general TS PI/PD controller are derived. The input–output structural relationship of the PI controller takes the following form:
(5) where
,
, and
and
are defined as the gains of the fuzzy controller. On comparing with the expression of linear PI controller,
(6) we can say that
is (nonlinear) variable integral gain and
,
is (nonlinear) variable proportional gain. The expressions for these gains have been derived explicitly for the general TS PI/PD controller here.
When and
are within
and
, respectively, then at any sampling instant k, the input variables must satisfy
and
. In this case, the input plane is divided into 12 regions as shown in (a) of Figure . In each region, the premise parts of the rule base have been evaluated for all four classes of controllers and are given in Tables . The analytical structure has been computed using the outcomes of the rules premise parts in Tables , and the corresponding gains are tabulated in Tables . The expressions of
and
in Tables are given by
Figure 4. Division of input plane: (a) when both and
and (b) when
is outside
or
is outside
or both
and
are outside
.
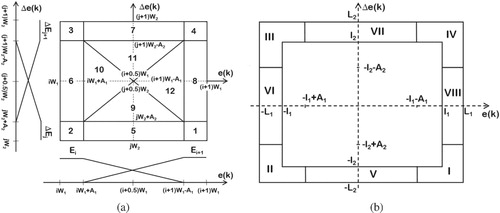
Table 2. Outcomes of algebraic product and bounded sum operations (Class 1).
Table 3. Outcomes of algebraic product and maximum operations (Class 2).
Table 4. Outcomes of minimum and bounded sum operations (Class 3).
Table 5. Outcomes of minimum and maximum operations (Class 4).
Table 6. Outcomes of AND and OR operations for all four classes of controllers.
Table 7. Expressions of gains of Class 1 controller.
Table 8. Expressions of gains of Class 2 controller.
Table 9. Expressions of gains of Class 3 controller.
Table 10. Expressions of gains of Class 4 controller.
Similarly, when (or
) lies outside
(or
), the input plane is divided into eight regions as shown in (b) of Figure . The resultant membership functions of the premise parts of the rule base are given in Table . The analytical structures have also been computed in the eight regions and the corresponding gains are given in Table . The values of the coefficients
and
are given in Table . From Tables , it is evident that the gains
and
are nonlinear functions of the input variables
and
. So, TS fuzzy controller under investigation is a variable (nonlinear) gain controller.
Table 11. Expression of gains of all classes of controllers in outer regions.
Table 12. Coefficients  ,
,  and
and  .
.
Note: For triangular membership functions is substituted, i.e. the input regions
1–8 do not exist and hence the models of fuzzy controllers are modified accordingly.
To study the gain variation and output of the TS fuzzy controller, three-dimensional plots of and
have been shown in Figures and for Class 1 controller. Without the loss of generality, we have used the values of
,
, and
. The values of the controller parameters are selected as:
,
,
,
,
, and
for Figure and
,
,
,
,
, and
for Figure . Different characteristics of the gain can be obtained by varying the controller parameters. Similarly, the three-dimensional plot of
can also be shown.
Figure 5. Three-dimensional plots for Class 1 controller: (a) variable proportional gain and (b) control effort
when
,
,
,
,
, and
.
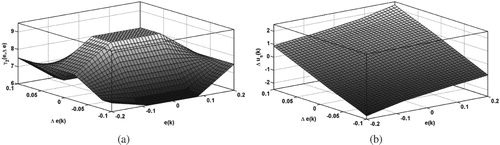
Figure 6. Three-dimensional plots for Class 1 controller: (a) variable proportional gain and (b) control effort
when
,
,
,
,
, and
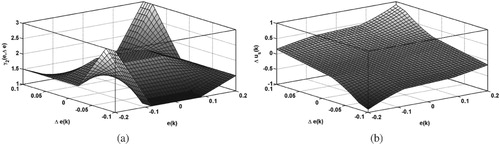
From the plots, some properties of the gains have been observed and are stated as follows:
When
the gains become
(7) for Class 1 and Class 3 controllers, and
(8) for Class 2 and Class 4 controllers.
The gains
and
are nonlinear functions of the input variables
and
.
The fuzzy controller becomes a linear controller if and only if
and
.
The gains
and
depend on the parameters of the rule consequent.
and
satisfy the following inequalities:
(9) The inequalities in Equation (Equation9
(9) ) show that the maximum value of gain is the parameter with the largest value, whereas the minimum value of gain is the parameter with the smallest value in the rules consequent parts.
4. Stability Analysis
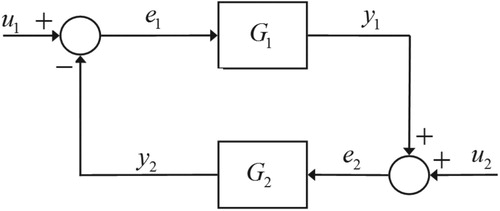
Based on the explicit structure of the TS fuzzy controller, the BIBO stability of the TS fuzzy control system has been presented in this section. The overall feedback control system is shown in Figure . Following equations describe the feedback control system:
Considering as TS fuzzy controller and
as any nonlinear plant, and using Small Gain theorem, we can state that
, i.e. the product of gains of
and
must be less than 1. Also for any bounded input pair
, the output pair
must be bounded.
At any time instant k, the inputs of the TS fuzzy controller satisfy and
. From Equation (Equation5
(5) ), we have
where
is the maximum magnitude of the error signal, defined as
From Equation (Equation9
(9) ) , we have
;
where and
Therefore,
(10) Considering
as any nonlinear plant and defining the norm of the plant as
(11) where
and
are any two control signals in the set
,
and
are outputs of plant
for control signals
and
, respectively. The norm of
is the gain of the nonlinear plant under consideration. Using the Small Gain theorem, the sufficient condition for the BIBO stability of the feedback control system is given in the following theorem.
Theorem 4.1
The sufficient condition for the BIBO stability of the feedback control system in the whole input space, defined by for all values of i and j, can be stated as
(12) for
and
where, max() operator chooses the maximum value from a set of values for all i and j.
Proof.
Applying the Small Gain theorem [Citation26] to the feedback control system in Figure , we have where
is TS fuzzy controller and
is any linear/nonlinear plant.
is nothing but the maximum value of
term in Equation (Equation10
(10) ) where
and
, and
is defined in Equation (Equation11
(11) ). Hence,
.
5. Simulations
In this section, we demonstrate the applicability of the proposed controllers. Two examples of nonlinear systems are considered, and the simulation results are presented. The analytical structure of the fuzzy controllers, derived in Section 3, are implemented to achieve the control objectives in each example. To tune the parameters of the fuzzy controller, genetic algorithm (GA)-based optimisation is employed. The steps of optimisation algorithm are as follows:
Step 1: First tune linear PI or PD controller to obtain the best possible response. For this one may use either conventional controller design techniques or GA-based optimisation technique. Thus the controller parameters ,
or
are obtained.
Step 2: From step 1, note down the UoDs of error and change of error
.
Step 3: Next, we need to tune the parameters of fuzzy PI or PD controller. The parameters to be tuned are ,
,
,
,
,
,
,
,
,
,
,
,
,
(assuming
), and
or
. Thus the number of tuning parameters is 15. This is done using GA-based optimisation technique. The above 15 parameters constitute the string of GA. One possible string of GA is:
,
; some arbitrary values of
,
,
and
such that
and
;
,
and
are some arbitrary values around
, and
,
and
are some arbitrary values around
(assuming PI controller);
or
= 1. In this manner, a few more strings can be generated by the GA toolbox as we set the lower and upper limits of each parameter on arbitrary manner to decide the possible parameter search space in which the search for new population always takes place. The number of strings, decided arbitrarily, decides the population size n. The GA also requires some more information like fitness function f, crossover probability
, and mutation probability
. The GA toolbox has some default values for n,
and
and we use the same to proceed with optimisation. The fitness function is related to the cost function as
where
(13) which is to be minimised where q and r are positive real.
Step 4: In case the GA does not converge, we need to redefine the search space, and
, and proceed with optimisation once again as discussed in step 3. This process continues until the algorithm converges.
In the simulations, we have considered trapezoidal membership functions ( and
),
,
, and the least number of fuzzy sets for both the inputs
and
i.e.
.
Example 5.1
We consider a series DC motor [Citation27], whose speed is to be maintained at 100 rad/s using PI controller. The mathematical model of series DC motor is given by
(14) where ω is the speed to be controlled, v is the input voltage, i is the current,
is the load torque, J is the moment of inertia of the motor, D is the viscous friction coefficient,
is the motor torque constant,
is the field inductance, and
,
, where
and
are the armature inductance and resistance, respectively, and
is the field resistance. The parameters used for simulation are given in Table .
Table 13. Series DC motor: list of parameters.
The fuzzy and linear PI controllers are designed to maintain the speed at 100 rad/s by choosing optimal parameters. The parameters are optimised using the GA. The cost function is selected as in Equation (Equation13(13) ) with q=r=1, and
. The number of parameters to be optimised is found to be 11 for fuzzy PI controller and 2 for linear PI controller. The values of the parameters are given in Table . The system is considered to be in a relaxed state initially, so that the initial conditions become zero, i.e.
and
.
Table 14. Parameters of linear PI and fuzzy PI controllers.
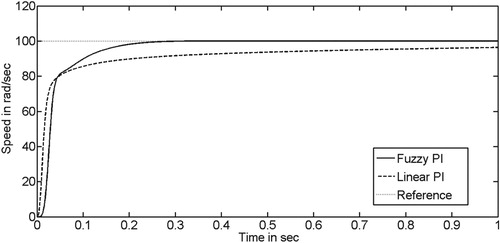
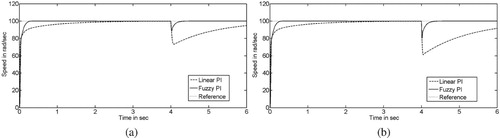
The output responses with the fuzzy and linear PI controllers are shown in Figure . The time-domain performance data of the fuzzy and linear PI controllers has been enlisted in Table . The simulation results clearly show the advantage of the general fuzzy PI controller over the linear PI controller. The sampling period T =0.001 s is considered for simulation.
Table 15. Time-domain performance data.
Next, the performance of the fuzzy controller in the presence of disturbance has been studied. Two cases are considered (i) load torque, , and (ii) load torque,
. In both the cases, we have found that the disturbance rejection is faster in the case of fuzzy PI controller. The simulation results are shown in Figure .
Figure 9. Step responses of series DC motor with fuzzy PI (class 1) and linear PI controllers in the presence of load torque (a) load torque, , and (b) load torque,
Example 5.2
This example deals with the design of fuzzy PD controller to control the robot arm [Citation28]. The differential equation representing the model of the robot arm is given by
(15)
A single fuzzy PD controller and a single linear PD controller have been designed to tackle two different scenarios: (Case I) ref = 0, = 0.5 and
= 1; (Case II) ref = 0.5,
= 0 and
= 1, where ref is
,
and
are the initial conditions. The initial conditions can take other values as well. The sampling time period is considered as T = 0.001 s. An optimal controller has been designed using GA. The cost function is selected as in Equation (Equation13
(13) ) with q=1, r=0.1, and
. The number of parameters to be optimised is found to be 11 for fuzzy PD controller and 2 for linear PD controller. The values of the parameters are given in Table .
Table 16. Parameters of linear PD and fuzzy PD controllers
The output responses with fuzzy PD controller and linear PD controller for two different set points are shown in Figure . It is evident from the responses that fuzzy PD controller is far superior to its linear counterpart.
Figure 10. Step responses of robot arm with fuzzy PD (class 1) and linear PD controllers (a) Case I (b) Case II.
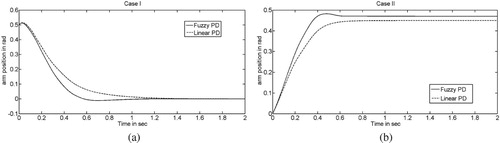
From the simulation results, see Figure (b), it can be seen that there is some steady-state error in the plant response since the PD controller affects the transient response and not the steady-state response. Still, the response of fuzzy PD controller is far better than that of linear PD controller.
6. Discussions and Conclusions
We have developed models of four different classes of general Takagi-Sugeno fuzzy PI/PD controller using modified rule base, algebraic product/minimum t-norm, bounded sum/maximum t-co-norm, CoG defuzzifier, unequal number (at least three) of fuzzy sets on the inputs, and different UoDs for the inputs. The greatest advantage of the proposed approach is that it has only parameters to tune in comparison to
parameters in [Citation18]. Tuning becomes relatively easier as the number of parameters in the rule consequent reduces. The proposed models are equally applicable to triangular membership functions case (
) where
and
in the model expressions. The model expression reveals that the developed fuzzy controller is a nonlinear PI/PD controller with variable gains. The bounds on gain variation are found, and the three-dimensional plots of gain provide an insight into the nature of gain variation. A sufficient condition for BIBO stability of the feedback control system having one of the proposed models in the loop is established.
This work can further be extended to fuzzy Two-Input Two-Output (TITO) PI/PD controllers which will bridge the gap between SISO and MIMO systems. In this paper, we have demonstrated the performance of fuzzy controller models through simulation study on two nonlinear plants. We have not, however, addressed real-time implementation issues of fuzzy controller models in the context of controlling some laboratory benchmark systems. This is currently under progress.
Acknowledgements
The authors are thankful to the Editors and anonymous reviewers for their constructive and valuable suggestions for improving this paper. Peer review under responsibility of Fuzzy Information and Engineering Branch of the Operations Research Society in China.
Disclosure statement
No potential conflict of interest was reported by the authors.
References
- Zadeh LA. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans Syst Man Cybern SMC-. 1973;3(1):28–44. doi: 10.1109/TSMC.1973.5408575
- Mamdani EH. Application of fuzzy algorithms for control of simple dynamic plant. Proc Inst Electr Eng. 1974;121(12):1585–1588. doi: 10.1049/piee.1974.0328
- Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern SMC-. 1985;15(1):116–132. doi: 10.1109/TSMC.1985.6313399
- Azar AT. Overview of Type-2 fuzzy logic systems. Int J Fuzzy Syst Appl. 2012;2(4):1–28. doi: 10.4018/ijfsa.2012100101
- Azar AT, Vaidyanathan S. Computational intelligence applications in modeling and control. Berlin: Springer-Verlag; 2015. (Studies in Computational Intelligence; vol. 575).
- Tanaka K, Sugeno M. Stability analysis and design of fuzzy control systems. Fuzzy Sets Syst. 1992;45(2):135–156. doi: 10.1016/0165-0114(92)90113-I
- Wang HO, Tanaka K, Griffin MF. An approach to fuzzy control of nonlinear systems: stability and design issues. IEEE Trans Fuzzy Syst. 1996;4(1):14–23. doi: 10.1109/91.481841
- Xiu ZH, Ren G. Stability analysis and systematic design of Takagi-Sugeno fuzzy control systems. Fuzzy Sets Syst. 2005;151(1):119–138. doi: 10.1016/j.fss.2004.04.008
- Fuh CC. Absolute stability analysis for a class of Takagi-Sugeno fuzzy control systems. Int J Syst Sci. 2008;39(5):477–486. doi: 10.1080/00207720701832606
- Precup RE, Radac MB, Tomescu ML, et al. Stable and convergent iterative feedback tuning of fuzzy controllers for discrete-time SISO systems. Expert Syst Appl. 2013;40(1):188–199. doi: 10.1016/j.eswa.2012.07.023
- Lee DH, Joo YH, Tak MH. Local stability analysis of continuous-time Takagi-Sugeno fuzzy systems: a fuzzy Lyapunov function approach. Inf Sci. 2014;257:163–175. doi: 10.1016/j.ins.2013.08.036
- Choi OK, Kim J, Kim J, et al. BIBO stability analysis of TSK fuzzy PI/PD control systems. Intell Autom & Soft Comput. 2015;21(4):645–658. doi: 10.1080/10798587.2015.1015243
- Chen G, Ying H. BIBO stability of nonlinear fuzzy PI control systems. J Intell & Fuzzy Syst. 1997;5(3):245–256.
- Ying H. The simplest fuzzy controllers using different inference methods are different nonlinear proportional-integral controllers with variable gains. Automatica. 1993;29(6):1579–1589. doi: 10.1016/0005-1098(93)90025-O
- Ying H. Analytical structure of a fuzzy controller with linear control rules. Inf Sci. 1994;81(3 & 4):213–227. doi: 10.1016/0020-0255(94)90098-1
- Ying H. The Takagi-Sugeno fuzzy controllers using the simplified linear control rules are nonlinear variable gain controllers. Automatica. 1998;34(2):157–167. doi: 10.1016/S0005-1098(97)00173-8
- Ying H. Constructing nonlinear variable gain controllers via the Takagi-Sugeno fuzzy control. IEEE Trans Fuzzy Syst. 1998;6(2):226–234. doi: 10.1109/91.669021
- Ding Y, Ying H, Shao S. Typical Takagi-Sugeno PI and PD fuzzy controllers: analytical structures and stability analysis. Inf Sci. 2003;151:245–262. doi: 10.1016/S0020-0255(02)00302-X
- Mohan BM, Reddy JM. Mathematical model of a Takagi-Sugeno PI/PD controller. International Conference on Industrial and Information Systems (ICIIS) IEEE; 2010, p. 620–625.
- Raj R, Mohan BM. Modeling and analysis of the simplest fuzzy PI/PD controllers of Takagi-Sugeno type. IFAC-Paper Online. 2016;49(1):537–542. doi: 10.1016/j.ifacol.2016.03.110
- Ho HF, Wong YK, Rad AB. Adaptive fuzzy sliding mode control with chattering elimination for nonlinear SISO systems. Simul Model Pract Theory. 2009;17(7):1199–1210. doi: 10.1016/j.simpat.2009.04.004
- Billel M, Dib D, Azar AT. A second-order sliding mode and fuzzy logic control to optimal energy management in PMSG wind turbine with battery storage. Neural Comput Appl. 2016;28(6):1417–1434.
- Vaidyanathan S, Azar AT. Takagi-Sugeno fuzzy logic controller for Liu-Chen four-scroll chaotic system. Int J Intell Eng Inform. 2016;4(2):135–150.
- Boulkroune A, Bouzeriba A, Bouden T, et al. Fuzzy adaptive synchronization of uncertain fractional-order chaotic systems, Advances in Chaos Theory and Intelligent Control. Berlin: Springer-Verlag; 2016. (Studies in Fuzziness and Soft Computing; vol. 337).
- Boulkroune A, Hamel S, Azar AT. Fuzzy control-based function synchronization of unknown chaotic systems with dead-zone input, Advances in Chaos Theory and Intelligent Control. Berlin: Springer-Verlag; 2016. (Studies in Fuzziness and Soft Computing; vol. 337).
- Khalil HK. Nonlinear Systems. 3rd ed. Upper Saddle River (NJ): Prentice Hall; 2002.
- Mehta S, Chiasson J. Nonlinear control of a series DC motor: theory and experiment. IEEE Trans Ind Electron. 1998;45(1):134–141. doi: 10.1109/41.661314
- Obaid ZA, Sulaiman N, Marhaban MH, et al. Analysis and performance evaluation of PD-like fuzzy logic controller design based on MATLAB and FPGA. IAENG Int J Comput Sci. 2010;37(2