On m-Polar Interval-valued Fuzzy Graph and its Application

Abstract

In this paper, the concept of the $m$-polar fuzzy graph ($m$-PFG) and interval-valued fuzzy graph (IVFG) is integrated and introduced an unprecedented kind of fuzzy graph designated as $m$-polar interval-valued fuzzy graph ($m$-PIVFG). Complement of the $m$-PIVFG is defined and the failure of this definition in some cases are highlighted. Various examples are cited and then redefined the notation of complement such that it applies to all $m$-PIVFGs. The other algebraic properties such as isomorphism, weak isomorphism, co-weak isomorphism of the $m$-PIVFG are investigated. Moreover, some basic results on the isomorphic property of $m$-PIVFG are proved. Finally, an application of $m$-PIVFG is explored.

Abbreviations: The following abbreviations are employed in this study: FS: Fuzzy set; FG: Fuzzy graph; IVFS: Interval-valued fuzzy sets; IVFG: Interval-valued fuzzy graph; $m$-PFS: $m$-polar fuzzy sets; $m$-PFG: $m$-polar fuzzy graph; $m$-PIVFS: $m$-polar interval-valued fuzzy sets; $m$-PIVFG: $m$-polar interval-valued fuzzy graph.

KEYWORDS:

• $m$-polar fuzzy graph
• interval-valued fuzzy graph
• $m$-polar interval valued fuzzy graph
• complement of $m$-polar interval valued fuzzy graph
• isomorphic $m$-polar interval valued fuzzy graph

1. Introduction

A graph is a mathematical structure used to represent pairwise relations between objects. It is defined as an ordered pair $G=\left(V,E\right)$ consisting of a set of vertices, designated as $V$ and a set of edges, denoted by $E$. When there is a vagueness either in vertices or in edges or in both then a fuzzy model is needed to describe a fuzzy graph. With the Konigsberg bridge problem, the graph theory was started in 1735. The concept was first introduced by Swiss Mathematician Euler in 1736. Then, Euler studied and incorporated a structure that solves the Konigsberg bridge problem which is also known as a Eulerian graph. Thereafter, the complete and bipartite graphs were proposed by Mobius in 1840. Recently, applications of graph theory are mostly promoted to the areas of computer networks, electrical networks, coding theory, operational research, architecture, data mining, etc.

Observing the vast application of graph theory motivated to explain fuzzy graph which is a non-empty set $V$ together with a fuzzy set and a fuzzy relation. In 1973, Kauffman [1] defined fuzzy graph depending on the idea of fuzzy set introduced by Zadeh [2]. In 1975, Rosenfeld [3] first proposed another definition of the Fuzzy graph which is a generalization of Euler's Graph theory. He also elaborated definition of fuzzy vertex, fuzzy edges and several fuzzy concepts such as cycles, paths, connectedness, etc. The idea of isomorphism, weak isomorphism, co-weak isomorphism between fuzzy graphs was introduced by Bhutani [4] in 1989. The extension of the concept of fuzzy set and the idea of bipolar fuzzy sets were given in 1994 by Zhang [5, 6]. Several properties of fuzzy graphs and hypergraphs were discussed by Mordeson and Nair [7–9] in 2000.

IVFG was defined by Hongmei and Lianhua [10] in 2009 and some operations on this were studied by Akram and Dudek [11] in 2011. Complete fuzzy graph was defined by Hawary [12]. He also studied three new operations on it. Nagoorgani and Malarvizhu [13, 14] studied isomorphic properties on fuzzy graphs and also defined the self-complementary fuzzy graphs. The extension of bipolar fuzzy set and the idea of $m$-polar fuzzy sets ($m$-PFS) were introduced by Chen et al. [15] in 2014. Samanta and Pal [16–19] investigated on fuzzy tolerance graph, fuzzy threshold graph, fuzzy $k$-competition graphs, $p$-competition fuzzy graphs and also fuzzy planar graphs. Some properties of isomorphism and complement on IVFG were studied by Talebi and Rashmanlou [20]. Later, Ghorai and Pal [21, 22] described various properties on $m$-PFGs. They examined isomorphic properties on $m$-PFG. Different types of research on generalized fuzzy graphs were discussed on [23–31]. The main contribution of this study is as follows:

• Concept of $m$-PIVFGs and complement of $m$-PIVFGs are introduced with examples.

• The definitions of classic and non-classic $m$-PIVFG related to complement of that are also discussed.

• Definition of isomorphic, weak isomorphic and co-weak isomorphic $m$-PIVFG are explained.

• Results based on isomorphic properties of $m$-PFGs are discussed.

• A case study based on $m$-PIVFG is explained.

The rest of the paper is arranged as follows: Section 1 describes the historical backgrounds of Fuzzy graphs. Section 2 provides some basic ideas of the $m$-PFGs, IVFGs with some examples. In Section 3, $m$-PIVFG is defined and supported with examples. Complete $m$-PIVFG and strong $m$-PIVFG are also investigated with suitable examples. Section 4 provides the definition of a complement of an $m$-PIVFG. This section is based on a description of the complement of an $m$-PIVFG and some improvements over this definition. In section 5 various types of isomorphic property of $m$-PIVFGs are described with examples. Some propositions and theorems related to this property are also discussed. Section 6 provides the application of an $m$-PIVFG in decision-making problems. Section 7 is based on a summary of this article.

2. Preliminaries

In this part, some definitions related to $m$-PFG are defined and demonstrated with the help of examples. The basic definition of IVFG is also discussed in this part, followed by an example for demonstration.

A fuzzy set is a set whose elements have degrees of membership. Fuzzy sets were introduced by Zadeh [2] in 1965 as an extension of the classical notion of the set. A fuzzy set $A$ is a pair $\left(S,m\right)$ where $S$ is a set and $m:S\to \left[0,1\right]$ is a membership function. Throughout this article, $G^{\ast }$ is a crisp graph, and $G$ is a fuzzy graph.

Proof

DEFINITION 2.1

([15]) An $m$-PFS (or a [0,1]^m-set) on a set $X$ is a mapping $A:X\to [0,1{]}^m$. The set of all $m$-PFS on $X$ is denoted by $m\left(X\right)$.

Proof

DEFINITION 2.2

[32] Let $A$ be an $m$-PFS on $X$. An $m$-polar fuzzy relation on $A$ is an $m$-PFS $B$ of $X\times X$ such that $B\left(x,y\right)\le min\left\{A\left(x\right),A\left(y\right)\right\}$ $\mathrm{\forall }x,y\in X$ i.e. for each $i=1,2,\dots ,m$ and $\mathrm{\forall }x,y\in X$ $p_i\circ B\left(x,y\right)\le min\left\{p_i\circ A\left(x\right),p_i\circ A\left(y\right)\right\}$.

Proof

DEFINITION 2.3

[32] An $m$-PFG of a crisp graph $G^{\ast }=\left(V,E\right)$ is a pair $G=\left(A,B\right)$ where $A:V\to [0,1{]}^m$ is an $m$-PFS in $V$ and $B:V\times V\to [0,1{]}^m$ is an $m$-PFS in $V\times V$ such that for each $i=1,2,\dots ,m$; $p_i\circ B\left(xy\right)\le min\left\{p_i\circ A\left(x\right),p_i\circ A\left(y\right)\right\}$ $\mathrm{\forall }xy\in V\times V$ and $B\left(xy\right)=0$ $\mathrm{\forall }xy\in \left(V\times V\right)-E$, where $0=\left(0,0,\dots ,0\right)$ is the smallest element in $[0,1{]}^m$. $A$ is called the $m$-polar fuzzy vertex set of $G$ and $B$ is called the $m$-polar fuzzy edge set of $G$.

Proof

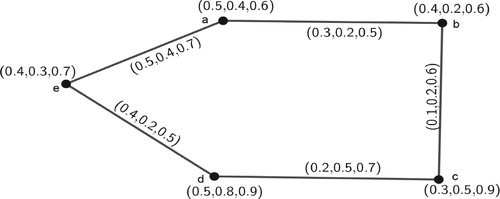
Example 1

The following Figure 1 is an example of an $m$-PFG. Let $G^{\ast }=\left(V,E\right)$ be a crisp graph where $V=\left\{a,b,c,d,e\right\}$ and $E=\left\{ab,bc,cd,ae,de\right\}$. Let $p_i\circ V$ be an $m$-PFS on $V$ and let $p_i\circ E$ be an $m$-PFS on $E$ defined by Tables 1 and 2, respectively:

Figure 1. 3-PFG.

Table 1. $m$-PFS on $V$.

	$a$	$b$	$c$	$d$	$e$
$p_1\circ V$	$0.5$	0.4	0.3	0.5	0.4
$p_2\circ V$	$0.4$	0.2	0.5	0.8	0.3
$p_3\circ V$	$0.7$	0.6	0.9	0.9	0.7

Table 2. $m$-PFS on $E$_.

	$ab$	$bc$	$cd$	$de$	$ae$
$p_1\circ E$	$0.3$	0.1	0.2	0.4	0.3
$p_2\circ E$	$0.2$	0.2	0.5	0.2	0.1
$p_3\circ E$	$0.5$	0.6	0.7	0.5	0.5

Proof

DEFINITION 2.4

[33] An IVFS $A$ on $V$ is defined as $A=\left\{\left(x,\left[{\mu }_A^l\left(x\right),{\mu }_A^u\left(x\right)\right]\right):x\in V\right\}$, where ${\mu }_A^l\left(x\right)$ and ${\mu }_A^u\left(x\right)$ are fuzzy subsets on $V$ such that ${\mu }_A^l\left(x\right)\le {\mu }_A^u\left(x\right)$, $\mathrm{\forall }x\in V$. Based on this set a graph called IVFG is defined.

Proof

DEFINITION 2.5

[10] By an IVFG of a crisp graph $G^{\ast }=\left(V,E\right)$ we mean $G=\left(A,B\right)$, where $A=\left[{\mu }_A^l\left(x\right),{\mu }_A^u\left(x\right)\right]$ is an IVFS on $V$ and $B=\left[{\mu }_B^l\left(xy\right),{\mu }_B^u\left(xy\right)\right]$ is an IVFS on $E$, such that ${\mu }_B^l\left(xy\right)\le min\left\{{\mu }_A^l\left(x\right),{\mu }_A^l\left(y\right)\right\}$, ${\mu }_B^u\left(xy\right)\le min\left\{{\mu }_A^u\left(x\right),{\mu }_A^u\left(y\right)\right\}$ $\mathrm{\forall }xy\in E$.

Lots of works have been done on this graph [34–38].

Proof

Example 2

The following Figure 2 is an example of IVFG. Let $G^{\ast }=\left(V,E\right)$ be a crisp graph where $V=\left\{a,b,d,e\right\}$ and $E=\left\{ab,ae,de\right\}$. Let A be an IVFS on $V$ and let B be an IVFS on $E$ defined by Tables 3 and 4, respectively:

In the following section the $m$-PIVFG, a combination of IVFG and $m$-PFG is defined.

Figure 2. An IVFG.

Table 3. IVFS on $V$_.

	$a$	$b$	$d$	$e$
${\mu }_A^l$	$0.2$	0.2	0.5	0.3
${\mu }_A^u$	$0.4$	0.3	0.7	0.5

Table 4. IVFS on $E$.

	$ab$	$de$	$ae$
${\mu }_B^l$	$0.2$	0.3	0.2
${\mu }_B^u$	$0.3$	0.4	0.4

3. $m$-polar Interval-valued Fuzzy Graph ($m$-PIVFG)

Herein, $m$-PFG and IVFG are combined and the concept of $m$-PIVFG is introduced and demonstrated with examples. Also, in this part we described complete $m$-PIVFG with appropriate examples and strong $m$-PIVFG, illustrated with examples.

Proof

DEFINITION 3.1

An $m$-PIVFG of a graph $G^{\ast }=\left(V,E\right)$ is a pair $G=\left(V,A,B\right)$ consists of a non-empty set $V$ together with pair of interval-valued function $A:V\to [0,1{]}^m$ is an $m$-PFS in $V$ and $B:V\times V\to [0,1{]}^m$ and $\mu :V\times V\to [0,1{]}^m$ for each $i=1,2,\dots ,m$; $p_i\circ {\mu }_A\left(x\right)=\left[p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^u\left(x\right)\right]$, $0\le {\mu }_A^l\left(x\right)\le {\mu }_A^u\left(x\right)\le 1$ and $p_i\circ {\mu }_B\left(xy\right)=\left[p_i\circ {\mu }_B^l\left(xy\right),p_i\circ {\mu }_B^u\left(xy\right)\right]$, $0\le {\mu }_B^l\left(xy\right)\le {\mu }_B^u\left(xy\right)\le 1$ and for each $i=1,2,\dots ,m$, the interval number of vertex $x$ and of the edge $xy$ in $G$ respectively satisfying $p_i\circ {\mu }_B^l\left(xy\right)\le p_i\circ min\left\{{\mu }_A^l\left(x\right),{\mu }_A^l\left(y\right)\right\}$, $p_i\circ {\mu }_B^u\left(xy\right)\le p_i\circ min\left\{{\mu }_A^u\left(x\right),{\mu }_A^u\left(y\right)\right\}$, $\mathrm{\forall }x,y\in V$.

Now, we give an example of $m$-PIVFG:(See Figure 3).

Figure 3. A $3$-PIVFG.

Proof

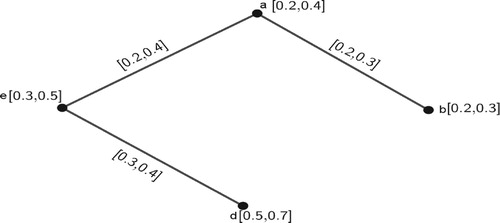
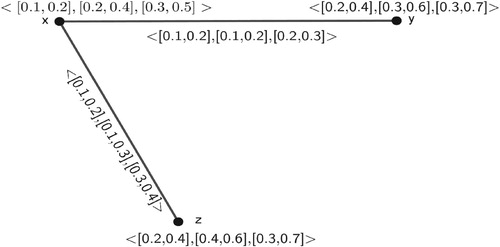
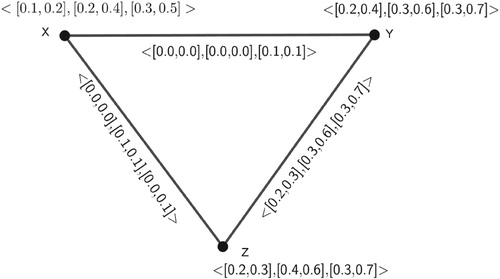
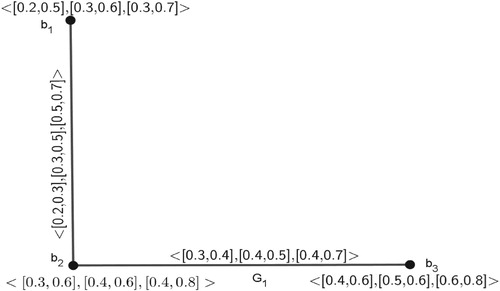
Example 3

Let us consider a $3$-PIVFG $G=\left(V,A,B\right)$, where $\begin{array}{rl}A& =\left(\frac{u}{⟨\left[0.3,0.5\right],\left[0.2,0.4\right],\left[0.5,0.8\right]⟩},\frac{v}{⟨\left[0.3,0.6\right],\left[0.5,0.6\right],\left[0.2,0.5\right]⟩},\right.\\ & \left.\frac{w}{⟨\left[0.7,0.8\right],\left[0.4,0.6\right],\left[0.1,0.5\right]⟩}\right)\\ andB& =\left(\frac{uv}{⟨\left[0.3,0.5\right],\left[0.2,0.4\right],\left[0.2,0.5\right]⟩},\frac{vw}{⟨\left[0.3,0.6\right],\left[0.4,0.6\right],\left[0.1,0.5\right]⟩},\right.\\ & \left.\frac{wu}{⟨\left[0.3,0.5\right],\left[0.2,0.4\right],\left[0.1,0.5\right]⟩}\right)\end{array}$

Proof

DEFINITION 3.2

An $m$-PIVFG $G=\left(V,A,B\right)$ of $G^{\ast }=\left(V,E\right)$ is said to be complete if $p_i\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}$ and $p_i\circ {\mu }_B^u\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$ for every pair of vertices $x,y\in V$ and for each $i=1,2,\dots ,m$.

Proof

Example 4

Let us consider Example 3, here, $p_1\circ {\mu }_B^l\left(uv\right)=0.3=\text{min}\left\{p_1\circ {\mu }_A^l\left(u\right),p_1\circ {\mu }_A^l\left(v\right)\right\}=\left\{0.3,0.3\right\}$ $p_1\circ {\mu }_B^u\left(uv\right)=0.5=\text{min}\left\{p_1\circ {\mu }_A^u\left(u\right),p_1\circ {\mu }_A^u\left(v\right)\right\}=\left\{0.5,0.6\right\}$ $p_2\circ {\mu }_B^l\left(uv\right)=0.2=\text{min}\left\{p_2\circ {\mu }_A^l\left(u\right),p_2\circ {\mu }_A^l\left(v\right)\right\}=\left\{0.2,0.5\right\}$ $p_2\circ {\mu }_B^u\left(uv\right)=0.4=\text{min}\left\{p_2\circ {\mu }_A^u\left(u\right),p_2\circ {\mu }_A^u\left(v\right)\right\}=\left\{0.4,0.6\right\}$ $p_3\circ {\mu }_B^l\left(uv\right)=0.2=\text{min}\left\{p_3\circ {\mu }_A^l\left(u\right),p_3\circ {\mu }_A^l\left(v\right)\right\}=\left\{0.5,0.2\right\}$ $p_3\circ {\mu }_B^u\left(uv\right)=0.5=\text{min}\left\{p_3\circ {\mu }_A^u\left(u\right),p_3\circ {\mu }_A^u\left(v\right)\right\}=\left\{0.8,0.5\right\}$ Similarly, we get the edges vw and wu. Hence, the graph G is complete, since for all the pair of vertices $x,y\in V$ the conditions $p_i\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}$ and $p_i\circ {\mu }_B^u\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$ hold.

But, for the graph of Figure 4 is not complete. Here, $\begin{array}{rl}A& =\left(\frac{u}{⟨\left[0.3,0.6\right],\left[0.1,0.4\right],\left[0.5,0.8\right]⟩},\frac{v}{⟨\left[0.1,1.0\right],\left[0.2,0.3\right],\left[0.2,0.5\right]⟩},\right.\\ & \left.\frac{w}{⟨\left[0.7,0.8\right],\left[0.2,0.3\right],\left[0.1,0.5\right]⟩}\right)\\ \text{and }B& =\left(\frac{uv}{⟨\left[0.3,0.5\right],\left[0.2,0.4\right],\left[0.2,0.5\right]⟩},\frac{wu}{⟨\left[0.3,0.5\right]\left[0.2,0.4\right],\left[0.1,0.5\right]⟩}\right)\end{array}$ This is not complete $m$-PIVFG. From the definition of $m$-PIVFG, there must be an edge between vertices v and w with $\mu \left(vw\right)=⟨\left[0.1,0.8\right],\left[0.2,0.3\right],\left[0.1,0.5\right]⟩$ . But there is no edge ‘vw’ that ‘s' why the graph is not complete.

Figure 4. A $3$-PIVFG $G$ which is not complete.

Proof

DEFINITION 3.3

An $m$-PIVFG $G=\left(V,A,B\right)$ of $G^{\ast }=\left(V,E\right)$ is said to be strong $m$-PIVFG if $p_i\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}$ and $p_i\circ {\mu }_B^u\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$ for all the edges $xy\in E$ and for each $i=1,2,\dots ,m$.

Above described example is an example of a strong $m$-PIVFG. Already, we have discussed that Figure 4 is not complete.

4 Complement of an $m$-PIVFG

In this present section, first, the complement of $m$-PIVFG with suitable examples are defined. Then the limitations of the definitions are observed with the help of some examples. After that new modified definition for the complement is developed and is verified with examples.

Proof

DEFINITION 4.1

Let $G=\left(V,A,B\right)$ of $G^{\ast }=\left(V,E\right)$ be an $m$-PIVFG. The complement of $G$ is an $m$-PIVFG $\overline{G}=\left(\overline{A},\overline{B}\right)$, where $p_i\circ {\mu }_{\overline{B}}\left(xy\right)=\left[p_i\circ {\mu }_{\overline{B}}^l\left(xy\right),p_i\circ {\mu }_{\overline{B}}^u\left(xy\right)\right]$, $p_i\circ {\mu }_{\overline{B}}^l\left(xy\right)=min\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)$, and $p_i\circ {\mu }_{\overline{B}}^u\left(xy\right)=min\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right)$ for each $i=1,2,\dots ,m$ and for every $x,y\in V$.

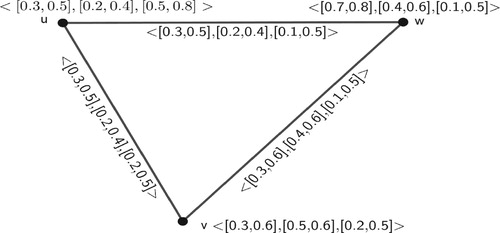
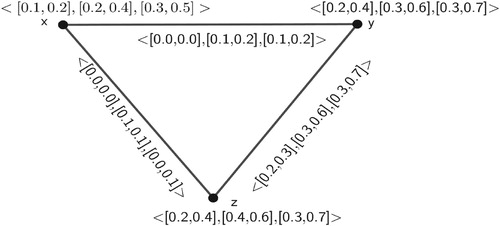
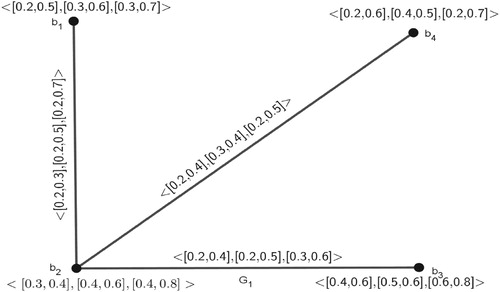
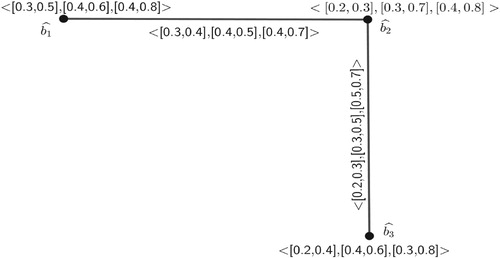
Example 5 The following Figure 5 is an example of an $m$-PIVFG while Figure 6 represents its complement. Let us consider a $3$-PIVFG $G=\left(V,A,B\right)$, where $\begin{array}{rl}A& =\left(\frac{x}{⟨\left[0.1,0.2\right],\left[0.2,0.4\right],\left[0.3,0.5\right]⟩},\frac{y}{⟨\left[0.2,0.4\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\right.\\ & \left.\frac{z}{⟨\left[0.2,0.4\right],\left[0.4,0.6\right],\left[0.3,0.7\right]⟩}\right)\\ andB& =\left(\frac{xy}{⟨\left[0.1,0.2\right],\left[0.1,0.2\right],\left[0.2,0.3\right]⟩},\frac{xz}{⟨\left[0.1,0.2\right],\left[0.1,0.3\right],\left[0.3,0.4\right]⟩}\right).\end{array}$ The complement $\overline{G}$ of $G$ is $\begin{array}{rl}\overline{A}& =\left(\frac{x}{⟨\left[0.1,0.2\right],\left[0.2,0.4\right],\left[0.3,0.5\right]⟩},\frac{y}{⟨\left[0.2,0.4\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\right.\\ & \left.\frac{z}{⟨\left[0.2,0.4\right],\left[0.4,0.6\right],\left[0.3,0.7\right]⟩}\right)\\ p_1\circ {\mu }_{\overline{B}}^l\left(xy\right)& =\text{min}\left\{p_1\circ {\mu }_A^l\left(x\right),p_1\circ {\mu }_A^l\left(y\right)\right\}-p_1\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{0.1,0.2\right\}-0.1=0.0\\ p_1\circ {\mu }_{\overline{B}}^u\left(xy\right)& =\text{min}\left\{p_1\circ {\mu }_A^u\left(x\right),p_1\circ {\mu }_A^u\left(y\right)\right\}-p_1\circ {\mu }_B^u\left(xy\right)=\text{min}\left\{0.2,0.4\right\}-0.2=0.0\\ p_2\circ {\mu }_{\overline{B}}^l\left(xy\right)& =\text{min}\left\{p_2\circ {\mu }_A^l\left(x\right),p_2\circ {\mu }_A^l\left(y\right)\right\}-p_2\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{0.2,0.3\right\}-0.1=0.1\\ p_2\circ {\mu }_{\overline{B}}^u\left(xy\right)& =\text{min}\{p_2\circ {\mu }_A^u(x),p_2\circ {\mu }_A^u(y\}-p_2\circ {\mu }_B^u(xy)=\text{min}\{0.4,0.6\}-0.2=0.2\\ p_3\circ {\mu }_{\overline{B}}^l\left(xy\right)& =\text{min}\left\{p_3\circ {\mu }_A^l\left(x\right),p_3\circ {\mu }_A^l\left(y\right)\right\}-p_3\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{0.3,0.3\right\}-0.2=0.1\\ p_3\circ {\mu }_{\overline{B}}^u\left(xy\right)& =\text{min}\left\{p_3\circ {\mu }_A^u\left(x\right),p_3\circ {\mu }_A^u\left(y\right)\right\}-p_3\circ {\mu }_B^u\left(xy\right)=\text{min}\left\{0.5,0.7\right\}-0.3=0.2\end{array}$ Similarly for others, Thus, we get $\begin{array}{rl}\overline{B}& =\left(\frac{xy}{⟨\left[0.1,0.2\right],\left[0.1,0.2\right],\left[0.2,0.3\right]⟩},\frac{yz}{⟨\left[0.2,0.3\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\right.\\ & \left.\frac{zx}{⟨\left[0.0,0.0\right],\left[0.1,0.1\right],\left[0.0,0.1\right]⟩}\right).\end{array}$ Construction of complements we just stated by the above definition fails for some $m$-PIVFG. For further illustration, we consider the examples as follows.

Figure 5. A 3-PIVFG.

Figure 6. The complement of the 3-PIVFG of Figure 5.

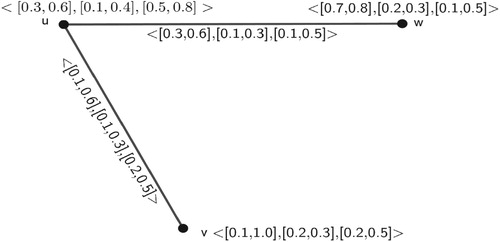
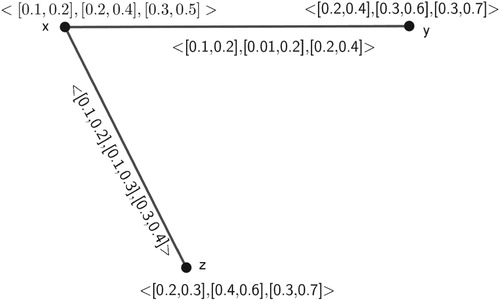
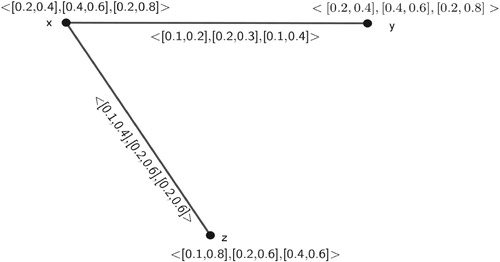
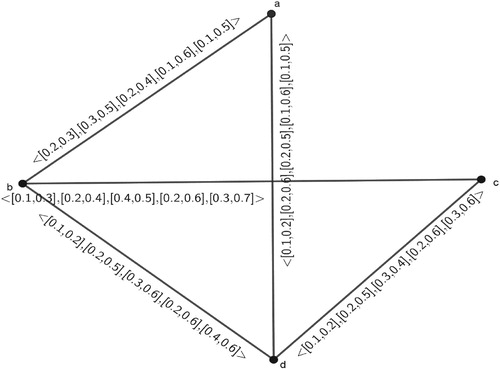
Example 6 Let us consider a $3$-PIVFG $G\left(V,A,B\right)$ of $G^{\ast }\left(V,E\right)$ (See Figure 7), $\begin{array}{rl}A& =\left(\frac{x}{⟨\left[0.1,0.2\right],\left[0.2,0.4\right],\left[0.3,0.5\right]⟩},\frac{y}{⟨\left[0.2,0.4\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\right.\\ & \left.\frac{z}{⟨\left[0.2,0.3\right],\left[0.4,0.6\right],\left[0.3,0.7\right]⟩}\right)\\ \text{and }B& =\left(\frac{xy}{⟨\left[0.1,0.2\right],\left[0.01,0.2\right],\left[0.2,0.4\right]⟩},\frac{xz}{⟨\left[0.2,0.3\right],\left[0.4,0.6\right],\left[0.3,0.7\right]⟩}\right)\end{array}$ The complement $\overline{G}$ (Figure 8) of $G$ is $\begin{array}{rl}\overline{A}& =<\left(\frac{x}{⟨\left[0.1,0.2\right],\left[0.2,0.4\right],\left[0.3,0.5\right]⟩},\frac{y}{⟨\left[0.2,0.4\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\right.\\ & \left.\frac{z}{⟨\left[0.2,0.3\right],\left[0.4,0.6\right],\left[0.3,0.7\right]⟩}\right)\\ \overline{B}& =<\left(\frac{xy}{⟨\left[0.0,0.0\right],\left[0.19,0.0\right],\left[0.1,0.1\right]⟩},\frac{yz}{⟨\left[0.2,0.3\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\right.\\ & \left.\frac{zx}{⟨\left[0.0,0.0\right],\left[0.1,0.1\right],\left[0.0,0.1\right]⟩}\right)\end{array}$

Here for i=2, $p_2\circ {\mu }_B^l\left(xy\right)=0.19$ and $p_2\circ {\mu }_B^u\left(xy\right)=0.0$, $p_2\circ {\mu }_B\left(xy\right)=\left[0.19,0.0\right]$, which is not an interval. So, we can't construct this type of $m$-PIVFG.

Figure 7. A 3-PIVFG.

Figure 8. Complement of the 3-PIVFG of Figure 7.

Keeping in mind the limitations of definition 9 as demonstrated by example 5, we propose a new definition of the complement of $m$-PIVFG which is well defined given below.

Proof

DEFINITION 4.2

Let $G=\left(V,A,B\right)$ be an $m$-PIVFG. Also let $A^{\mathrm{\prime }}$ and $B^{\mathrm{\prime }}$ represent $\text{min}\{p_i\circ {\mu }_A^l(x),p_i\circ {\mu }_A^l(y\left)\right\}-p_i\circ {\mu }_B^l\left(xy\right)$ and $\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right)$, respectively. The complement $\overline{G}=\left(V,\overline{A},\overline{B}\right)$ of $G$ is also an $m$-PIVFG, where $\begin{array}{rl}{p}_i\circ {\mu }_{\overline{B}}\left(xy\right)& =\left[p_i\circ {\mu }_{\overline{B}}^l\left(xy\right),p_i\circ {\mu }_{\overline{B}}^u\left(xy\right)\right]\\ & =\left\{\begin{array}{l}min\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}\\ -p_i\circ {\mu }_B^l\left(xy\right),min\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right);& if{A}^{\mathrm{\prime }}\le B^{\mathrm{\prime }}\\ \text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}\\ -p_i\circ {\mu }_B^u\left(xy\right),\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right);& if{A}^{\mathrm{\prime }}>B^{\mathrm{\prime }}\end{array}\right.\end{array}$ for each $i=1,2,\dots ,m$ and for every $x,y\in V$.

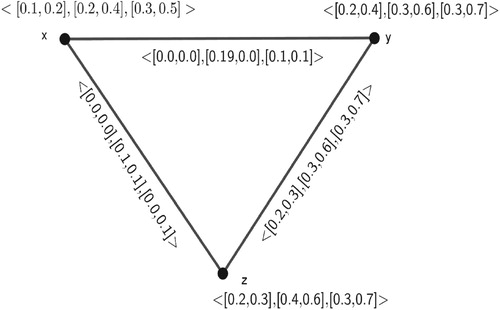
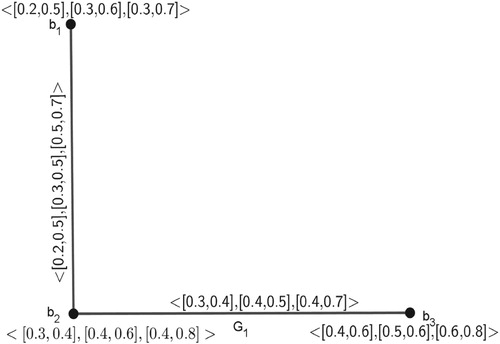
Example 7 For the above considered $3$-PIVFG $G=\left(V,A,B\right)$, modified $\overline{G}$ will be (Figure 9) $\begin{array}{rl}\overline{A}& =\left(\frac{x}{⟨[0.1,0.2],[0.2,0.4],[0.3,0.5]⟩},\frac{y}{⟨[0.2,0.4],[0.3,0.6],[0.3,0.7]⟩},\frac{x}{[0.2,0.3],[0.4,0.6],[0.3,0.7]}\right)\\ \overline{B}& =\left(\frac{xy}{⟨[0.0,0.0],[0.0,0.0],[0.1,0.1]⟩},\frac{yx}{⟨[0.2,0.3],[0.3,0.6],[0.3,0.7]⟩},\frac{zx}{[0.0,0.0],[0.1,0.1],[0.0,0.1]}\right)\end{array}$

Proof

DEFINITION 4.3

An $m$-PIVFG $G=\left(V,A,B\right)$ of a crisp graph $G^{\ast }\left(V,E\right)$ is called $classic$ $m$-PIVFG if all its $m$-pole of all its edge satisfy the condition $\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)\le \text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right)$ for each $i=1,2,\dots ,m$ and for every $x,y\in V$.

Figure 9. Modified $\overline{G}$.

Proof

DEFINITION 4.4

Let $G=\left(V,A,B\right)$ be an $m$-PIVFG of a crisp graph $G^{\ast }=\left(V,E\right)$. Then the edge $xy$ in $G$ satisfying $\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)\le \text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right)$, for each $i=1,2,\dots ,m$ and for every $x,y\in V$ are called perfect edges and all other edges $xy$ for which $min\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)\ge min\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right)$, are called imperfect edges $\mathrm{\forall }i=1,2,\dots ,m$.

Proposition 1:

All the edges of an $m$-PIVFG are perfect iff $m$-PIVFG is classic.

Proof Let us consider an $m$-PIVFG is classic. Then, $\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)\le \text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right)$, for each $i=1,2,\dots ,m$ and for every $x,y\in V$, i.e. for each edge this condition satisfies. Hence all of the edges are perfect. The proof of the converse part is straight forward.

In the next section, we study various types of isomorphic property of $m$-PIVFG with proper examples. Thereafter, we describe some propositions and theorems of $m$-PIVFG with the proofs.

5. Isomorphic $m$-PIVFG

Proof

Definition 5.1

Let $G_1=\left(V_1,A_1,B_1\right)$ of $G_1^{\ast }=\left(V_1,E_1\right)$ and $G_2=\left(V_2,A_2,B_2\right)$ of $G_2^{\ast }=\left(V_2,E_2\right)$ be two $m-PIVFGs$. A homomorphism $\phi :G_1\to G_2$ is a mapping $\phi :V_1\to V_2$ satisfying the following conditions,

1. 1. $p_i\circ {\mu }_{A_1}^l\left(x\right)\le p_i\circ {\mu }_{A_2}^l\left(\phi \left(x\right)\right)$, $p_i\circ {\mu }_{A_1}^u\left(x\right)\le p_i\circ {\mu }_{A_2}^u\left(\phi \left(x\right)\right)$, $\mathrm{\forall }x\in V_1$ and for each $i=1,2,\dots ,m$.

2. 2. $p_i\circ {\mu }_{B_1}^l\left(xy\right)\le p_i\circ {\mu }_{B_2}^l\left(\phi \left(x\right)\phi \left(y\right)\right)$, $p_i\circ {\mu }_{B_1}^u\left(xy\right)\le p_i\circ {\mu }_{B_2}^u\left(\phi \left(x\right)\phi \left(y\right)\right)$, $\mathrm{\forall }xy\in E_1$ and for each $i=1,2,\dots ,m$.

Example 8 Here for any two $3$-PIVFG, $\begin{array}{rl}{G}_1& =\left(V_1,A_1,B_1\right):A_1=\left(\frac{v_1}{⟨\left[0.2,0.3\right],\left[0.4,0.8\right],\left[0.5,0.7\right]⟩},\frac{v_2}{<\left[0.2,0.4\right],\left[0.3,0.9\right],\left[0.4,0.8\right]}\right),\\ B_1& =\left(\frac{v_1{v}_2}{⟨\left[0.2,0.3\right],\left[0.3,0.7\right],\left[0.3,0.7\right]⟩}\right)\end{array}$ and $\begin{array}{rl}{G}_2& =\left(V_2,A_2,B_2\right):A_2=\left(\frac{{\hat{v}}_1}{⟨\left[0.2,0.4\right],\left[0.4,0.9\right],\left[0.6,0.8\right]⟩},\frac{{\hat{v}}_2}{⟨\left[0.2,0.4\right],\left[0.4,0.7\right],\left[0.5,0.9\right]⟩}\right),\\ B_2& =\left(\frac{{\hat{v}}_1{\hat{v}}_2}{⟨\left[0.2,0.4\right],\left[0.3,0.7\right],\left[0.4,0.8\right]⟩}\right)\end{array}$

Consider a mapping $\phi :V_1\to V_2$, here, $p_i\circ {\mu }_{A_2}^l\left(\phi \left(v_1\right)\right)=p_i\circ {\mu }_{A_2}^l\left(\widehat{v_1}\right)$, $p_i\circ {\mu }_{A_2}^u\left(\phi \left(v_1\right)\right)=p_i\circ {\mu }_{A_2}^u\left(\widehat{v_1}\right)$ $\mathrm{\forall }{v}_1\in V$, $p_i\circ {\mu }_{A_1}^l\left(v_1\right)\le p_i\circ {\mu }_{A_2}^l\left(\phi \left(v_1\right)\right)$, $p_i\circ {\mu }_{A_1}^u\left(v_1\right)\le p_i\circ {\mu }_{A_2}^u\left(\phi \left(v_1\right)\right)$, and also $p_i\circ {\mu }_{B_1}^l\left(v_1{v}_2\right)\le p_i\circ {\mu }_{B_2}^l\left(\phi \left(v_1\right)\phi \left(v_2\right)\right)$, $p_i\circ {\mu }_{B_1}^u\left(v_1{v}_2\right)\le p_i\circ {\mu }_{B_2}^u\left(\phi \left(v_1\right)\phi \left(v_2\right)\right)$ for $v_1{v}_2\in E_1$ and $i=1,2,\dots ,m$. Since all the conditions of homomorphism are hold therefore, there exists a homomorphism $\phi :G_1\to G_2$ (See Figures 10 and 11).

Proof

DEFINITION 5.2

Let $G_1=\left(V_1,A_1,B_1\right)$ of $G_1^{\ast }=\left(V_1,E_1\right)$ and $G_2=\left(V_2,A_2,B_2\right)$ of $G_2^{\ast }=\left(V_2,E_2\right)$ be two $m$-PIVFG. An isomorphism $\phi :G_1\to G_2$ is a bijective mapping $\phi :V_1\to V_2$ satisfying the following conditions,

1. $p_i\circ {\mu }_{A_1}^l\left(x\right)=p_i\circ {\mu }_{A_2}^l\left(\phi \left(x\right)\right)$, $p_i\circ {\mu }_{A_1}^u\left(x\right)=p_i\circ {\mu }_{A_2}^u\left(\phi \left(x\right)\right)$, $\mathrm{\forall }x\in V_1$ and

2. $p_i\circ {\mu }_{B_1}^l\left(xy\right)=p_i\circ {\mu }_{B_2}^l\left(\phi \left(x\right)\phi \left(y\right)\right)$, $p_i\circ {\mu }_{B_1}^u\left(xy\right)=p_i\circ {\mu }_{B_2}^u\left(\phi \left(x\right)\phi \left(y\right)\right)$, $\mathrm{\forall }xy\in E_1$ and for each $i=1,,2,\dots ,m$.

The following $m$-PIVFG depicted in Figures 12 and 13 show that there exists an isomorphism between them by the help of Definition 14.

Figure 10. A $3$-PIVFG $G_1\left(V_1,A_1,B_1\right)$.

Figure 11. A $3$-PIVFG $G_2\left(V_2,A_2,B_2\right)$.

Figure 12. A $3$-PIVFG $G_1$

Figure 13. A $3$-PIVFG $G_2$.

Example 9 For any two $3$-PIVFG $G_1=\left(V_1,A_1,B_1\right)$ $\begin{array}{rl}{A}_1& =\left(\frac{b_1}{⟨\left[0.2,0.5\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\frac{b_2}{⟨\left[0.3,0.4\right],\left[0.4,0.6\right],\left[0.4,0.8\right]⟩},\right.\\ & \left.\frac{b_3}{⟨\left[0.4,0.6\right],\left[0.5,0.6\right],\left[0.6,0.8\right]⟩},\frac{b_4}{⟨\left[0.2,0.6\right],\left[0.4,0.5\right],\left[0.2,0.7\right]⟩}\right)\\ B_1& =\left(\frac{b_1{b}_2}{⟨\left[0.2,0.3\right],\left[0.2,0.5\right],\left[0.2,0.7\right]⟩},\frac{b_2{b}_3}{⟨\left[0.2,0.4\right],\left[0.2,0.5\right],\left[0.3,0.6\right]⟩},\right.\\ & \left.\frac{b_2{b}_4}{⟨\left[0.2,0.4\right],\left[0.3,0.4\right],\left[0.2,0.5\right]⟩}\right)\end{array}$ and $G_2=\left(V_2,A_2,B_2\right)$ $\begin{array}{rl}{A}_2& =\left(\frac{{\hat{b}}_1}{⟨\left[0.3,0.4\right],\left[0.4,0.6\right],\left[0.4,0.8\right]⟩},\frac{{\hat{b}}_2}{⟨\left[0.4,0.6\right],\left[0.5,0.6\right],\left[0.6,0.8\right]⟩},\right.\\ & \left.\frac{{\hat{b}}_3}{⟨\left[0.2,0.6\right],\left[0.4,0.5\right],\left[0.2,0.7\right]⟩},\frac{{\hat{b}}_4}{⟨\left[0.2,0.5\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩}\right)\\ B_2& =\left(\frac{{\hat{b}}_1{\hat{b}}_2}{⟨\left[0.4,0.6\right],\left[0.3,0.4\right],\left[0.2,0.5\right]⟩},\frac{{\hat{b}}_1{\hat{b}}_4}{⟨\left[0.2,0.4\right],\left[0.2,0.5\right],\left[0.3,0.6\right]⟩},\right.\\ & \left.\frac{{\hat{b}}_3{\hat{b}}_4}{⟨\left[0.2,0.6\right],\left[0.4,0.5\right],\left[0.2,0.7\right]⟩}\right)\end{array}$ We consider a homomorphism (See Figures 12 and 13) $\phi :G_1\to G_2$ where the mapping $\phi :V_1\to V_2$ satisfies the following criteria, $p_i\circ {\mu }_{A_1}^l\left(b_1\right)=p_i\circ {\mu }_{A_2}^l\widehat{\left(b_4\right)}{p}_i\circ {\mu }_{A_1}^l\left(b_2\right)=p_i\circ {\mu }_{A_2}^l\widehat{\left(b_1\right)}$ $p_i\circ {\mu }_{A_1}^u\left(b_1\right)=p_i\circ {\mu }_{A_2}^u\widehat{\left(b_4\right)}{p}_i\circ {\mu }_{A_1}^u\left(b_2\right)=p_i\circ {\mu }_{A_2}^u\widehat{\left(b_1\right)}$ $p_i\circ {\mu }_{A_1}^l\left(b_3\right)=p_i\circ {\mu }_{A_2}^l\widehat{\left(b_2\right)}{p}_i\circ {\mu }_{A_1}^l\left(b_4\right)=p_i\circ {\mu }_{A_2}^l\widehat{\left(b_3\right)}$ $p_i\circ {\mu }_{A_1}^u\left(b_3\right)=p_i\circ {\mu }_{A_2}^u\widehat{\left(b_2\right)}{p}_i\circ {\mu }_{A_1}^u\left(b_4\right)=p_i\circ {\mu }_{A_2}^u\widehat{\left(b_3\right)}$ and $p_i\circ {\mu }_{B_1}^l\left(b_1{b}_2\right)=p_i\circ {\mu }_{B_2}^l\left(\widehat{b_4}\widehat{b_3}\right)p_i\circ {\mu }_{B_1}^l\left(b_2{b}_3\right)=p_i\circ {\mu }_{B_2}^l\left(\widehat{b_1}\widehat{b_4}\right)$ $p_i\circ {\mu }_{B_1}^u\left(b_1{b}_2\right)=p_i\circ {\mu }_{B_2}^u\left(\widehat{b_4}\widehat{b_3}\right)p_i\circ {\mu }_{B_1}^u\left(b_2{b}_3\right)=p_i\circ {\mu }_{B_2}^u\left(\widehat{b_1}\widehat{b_4}\right)$ $p_i\circ {\mu }_{B_1}^l\left(b_2{b}_4\right)=p_i\circ {\mu }_{B_2}^l\left(\widehat{b_1}\widehat{b_2}\right)p_i\circ {\mu }_{B_1}^u\left(b_2{b}_4\right)=p_i\circ {\mu }_{B_2}^u\left(\widehat{b_1}\widehat{b_2}\right)$ Therefore, there exists an isomorphism $\phi :G_1\to G_2$.

Proof

THEOREM 1

Let $G_1=\left(V_1,A_1,B_1\right)$ of $G_1^{\ast }=\left(V_1,E_1\right)$ and $G_2=\left(V_2,A_2,B_2\right)$ of $G_2^{\ast }=\left(V_2,E_2\right)$ be two complete $m$-PIVFGs. Then $G_1$ is isomorphic to $G_2$ iff $\overline{G_1}$ is isomorphic to $\overline{G_2}$.

Proof.

Let $G_1=\left(V_1,A_1,B_1\right)$ is isomorphic to $G_2=\left(V_2,A_2,B_2\right)$, then there exists a bijective mapping $\phi :V_1\to V_2$ satisfying

1. $p_i\circ {\mu }_{A_1}^l\left(x\right)=p_i\circ {\mu }_{A_2}^l\left(\phi \left(x\right)\right)$, $p_i\circ {\mu }_{A_1}^u\left(x\right)=p_i\circ {\mu }_{A_2}^u\left(\phi \left(x\right)\right)$, $\mathrm{\forall }x\in V_1$ and for each $i=1,2,\dots ,m$.

2. $p_i\circ {\mu }_{B_1}^l\left(xy\right)=p_i\circ {\mu }_{B_2}^l\left(\phi \left(x\right)\phi \left(y\right)\right)$, $p_i\circ {\mu }_{B_1}^u\left(x\right)=p_i\circ {\mu }_{B_2}^u\left(\phi \left(x\right)\phi \left(y\right)\right)$, $\mathrm{\forall }xy\in E_1$ and for each $i=1,,2,\dots ,m$.

Again from the definition of complement for the complete graph, $\begin{array}{rl}{p}_i\circ {\mu }_{\overline{B_1}}^l\left(xy\right)& =\text{min}\left\{p_i\circ {\mu }_{A_1}^l\left(x\right),p_i\circ {\mu }_{A_1}^l\left(y\right)\right\}\\ & =\text{min}\left\{p_i\circ {\mu }_{A_2}^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_{A_2}^l\left(\phi \left(y\right)\right)\right\}\\ & =p_i\circ {\mu }_{\overline{B_2}}^l\left(\phi \left(x\right)\phi \left(y\right)\right),\\ and{p}_i\circ {\mu }_{\overline{B_1}}^u\left(xy\right)& =\text{min}\left\{p_i\circ {\mu }_{A_1}^u\left(x\right),p_i\circ {\mu }_{A_1}^u\left(y\right)\right\}\\ & =\text{min}\left\{p_i\circ {\mu }_{A_2}^u\left(\phi \left(x\right)\right),p_i\circ {\mu }_{A_2}^u\left(\phi \left(y\right)\right)\right\}\\ & =p_i\circ {\mu }_{\overline{B_2}}^u\left(\phi \left(x\right)\phi \left(y\right)\right)\mathrm{\forall }xy\in E_{1}andforeachi=1,2,\dots ,m.\end{array}$ This implies that $\overline{G_1}$ is isomorphic to $\overline{G_2}$. The proof of the converse part is the same as above.

Proof

DEFINITION 5.3

An $m$-PIVFG $G=\left(V,A,B\right)$ is said to be self complementary if $G\cong \overline{G}$.

Example 10 Let us consider a $3$-PIVFG $G=\left(V,A,B\right)$ described by Figure 14, where $\begin{array}{rl}A& =\left(\frac{x}{⟨\left[0.2,0.4\right],\left[0.4,0.6\right],\left[0.2,0.8\right]⟩},\frac{y}{⟨\left[0.2,0.4\right],\left[0.4,0.6\right],\left[0.2,0.8\right]⟩},\right.\\ & \left.\frac{z}{⟨\left[0.1,0.8\right],\left[0.2,0.6\right],\left[0.4,0.6\right]⟩}\right),\\ B& =\left(\frac{xy}{⟨\left[0.1,0.2\right],\left[0.2,0.3\right],\left[0.1,0.4\right]⟩},\frac{xz}{⟨\left[0.1,0.4\right],\left[0.2,0.6\right],\left[0.4,0.6\right]⟩}\right)\end{array}$ Complement of $G$, i.e. $\overline{G}=\left(V,\overline{A},\overline{B}\right)$ (See Figure 15) where $\begin{array}{rl}\overline{A}& =\left(\frac{x}{\left[0.2,0.4\right],\left[0.4,0.6\right],\left[0.2,0.8\right]>},\frac{y}{⟨\left[0.2,0.4\right],\left[0.4,0.6\right],\left[0.2,0.8\right]⟩},\right.\\ & \left.\frac{z}{⟨\left[0.1,0.8\right],\left[0.2,0.6\right],\left[0.4,0.6\right]⟩}\right)\\ and\overline{B}& =\left(\frac{xy}{⟨\left[0.1,0.2\right],\left[0.2,0.3\right],\left[0.1,0.4\right]⟩},\frac{yz}{⟨\left[0.1,0.8\right],\left[0.2,0.6\right],\left[0.4,0.6\right]⟩}\right)\end{array}$ Here, we see $G$ is isomorphic to $\overline{G}$. Hence, $G$ is self-complementary.

Figure 14. A $3$-PIVFG $G$

Figure 15. Complement $\overline{G}$_.

Proof

PROPOSITION 2

If $G=\left(V,A,B\right)$ is a complete $m$-PIVFG that is then G is self complementary (Figures 16 and 17).

Figure 16. A $3$-PIVFG $G_1=\left(V_1,A_1,B_1\right)$.

Figure 17. A $3$-PIVFG $G_2=\left(V_2,A_2,B_2\right)$.

Proof.

Let $G=\left(V,A,B\right)$ be a complete $m$-PIVFG such that $p_i\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}$ and $p_i\circ {\mu }_B^u\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$, $\mathrm{\forall }x,y\in V$.

Now $\begin{array}{rl}{p}_i\circ {\mu }_B^l\left(xy\right)& =\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}\\ & =\text{min}\left\{p_i\circ {\mu }_A^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_A^l\left(\phi \left(y\right)\right)\right\}\\ & =p_i\circ {\mu }_{\overline{B}}^l\left(xy\right)\end{array}$ Similarly, we can prove that $p_i\circ {\mu }_B^u\left(xy\right)=p_i\circ {\mu }_{\overline{B}}^u\left(xy\right)$ for any $xy\in E$. Therefore, $G$ is self-complementary.

Note 1 Let $G=\left(V,A,B\right)$ of $G^{\ast }=\left(V,E\right)$ be a strong $m$-PIVFG. Then $\overline{G}$ is a strong $m$-PIVFG if $\begin{array}{rl}{p}_i\circ {\mu }_{\overline{B}}^l\left(xy\right)& =\left\{\begin{array}{ll}0;& if0<p_i\circ {\mu }_B^l\left(xy\right)\le 1\\ \text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\};& if{p}_i\circ {\mu }_B^l\left(xy\right)=0\end{array}\right.\\ p_i\circ {\mu }_{\overline{B}}^u\left(xy\right)& =\left\{\begin{array}{ll}0;& if0<p_i\circ {\mu }_B^u\left(xy\right)\le 1\\ \text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\};& if{p}_i\circ {\mu }_B^u\left(xy\right)=0\end{array}\right.\end{array}$

Proof

THEOREM 2

Let $G=\left(V,A,B\right)$ be a strong $m$-PIVFG of the crisp graph $G^{\ast }=\left(V,E\right)$ and $\overline{G}=\left(V,\overline{A},\overline{B}\right)$ be the complement of $G$ then,

1. $p_i\circ {\mu }_{\overline{B}}^l\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)$

2. $p_i\circ {\mu }_{\overline{B}}^u\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right)$ for $xy\in E$, $i=1,2,\dots ,m$.

Proof.

Let $xy\in E$

1. If $0<p_i\circ {\mu }_B^l\left(xy\right)\le 1$ for each $i=1,2,\dots ,m$; then $xy\in E$. For $i=1,2,\dots ,m$, as G is strong $\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)=0=p_i\circ {\mu }_{\overline{B}}^l\left(xy\right)$. Similarly, if $0<p_i\circ {\mu }_B^u\left(xy\right)\le 1$ for each $i=1,2,\dots ,m$; then $xy\in E$. For $i=1,2,\dots ,m$, as G is strong, $\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right)=0=p_i\circ {\mu }_{\overline{B}}^u\left(xy\right)$.

2. If for $i=1,2,\dots ,m$; $p_i\circ {\mu }_B^l\left(xy\right)=0$, then $\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}=p_i\circ {\mu }_{\overline{B}}^l\left(xy\right)$. Similarly, if for $i=1,2,\dots ,m$; $p_i\circ {\mu }_B^u\left(xy\right)=0$, then $\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}-p_i\circ {\mu }_B^u\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}=p_i\circ {\mu }_{\overline{B}}^u\left(xy\right)$. Hence the proof.

Proof

THEOREM 3

Let $G$ be a self complementary strong $m$-PIVFG, then for $xy\in E$, and for each $i=1,2,\dots ,m$ $\sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(xy\right)=\frac{1}{2}\sum _{x\ne y}min\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}$ and $\sum _{x\ne y}{p}_i\circ {\mu }_B^u\left(xy\right)=\frac{1}{2}\sum _{x\ne y}min\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$.

Proof.

Let $G=\left(V,A,B\right)$ be a self-complementary strong $m$-PIVFG. Then $\mathrm{\forall }xy\in E$, for each $i=1,2,\dots ,m$, $p_i\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}$ and $p_i\circ {\mu }_B^u\left(xy\right)=\text{min}\{p_i\circ {\mu }_A^u(x),p_i\circ {\mu }_A^u(y\left)\right\}$ and there exists an isomorphism $\phi :G\to \overline{G}$ such that

1. $p_i\circ {\mu }_A^l\left(x\right)=p_i\circ {\mu }_{\overline{A}}^l\phi \left(x\right)$, $p_i\circ {\mu }_A^u\left(x\right)=p_i\circ {\mu }_{\overline{A}}^u\phi \left(x\right)$ $\mathrm{\forall }$ $x\in V$.

2. $p_i\circ {\mu }_B^l\left(xy\right)=p_i\circ {\mu }_{\overline{B}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)$, $p_i\circ {\mu }_B^u\left(x\right)=p_i\circ {\mu }_{\overline{B}}^u\left(\phi \left(x\right)\phi \left(y\right)\right)$ $\mathrm{\forall }$ $x,y\in V$ and for $i=1,2,\dots ,m$. Let $xy\in E$ and for $i=1,2,\dots ,m$, then by the Definition 2, $p_i\circ {\mu }_{\overline{B}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_A^l\left(\phi \left(y\right)\right)\right\}-p_i\circ {\mu }_B^l\left(\phi \left(x\right)\phi \left(y\right)\right)$. That is, $p_i\circ {\mu }_B^l\left(xy\right)=\text{min }\{p_i\circ {\mu }_A^l(\phi \left(x\right)),p_i\circ {\mu }_A^l(\phi \left(y\right)\}-p_i\circ {\mu }_B^l(\phi \left(x\right)\phi \left(y\right))\Rightarrow p_i\circ {\mu }_B^l(xy)+p_i\circ {\mu }_B^l(\phi \left(x\right)\phi \left(y\right))=\text{min }\{p_i\circ {\mu }_A^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_A^l\left(\phi \right(y\left)\right\}$ . Therefore, $\sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(xy\right)+\sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(\phi \left(x\right)\phi \left(y\right)\right)=\sum _{x\ne y}\text{min}\left\{p_i\circ {\mu }_A^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_A^l\left(\phi \left(y\right)\right)\right\}=\sum _{x\ne y}min\{p_i\circ {\mu }_A^l(x),p_i\circ {\mu }_A^l(y\left)\right\}\Rightarrow 2\sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(xy\right)=\sum _{x\ne y}\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}\Rightarrow \sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(xy\right)=\frac{1}{2}\sum _{x\ne y}\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}$. Similarly we can prove, $\sum _{x\ne y}{p}_i\circ {\mu }_B^u\left(xy\right)=\frac{1}{2}\sum _{x\ne y}\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$. Hence, the result.

Proof

THEOREM 4

Let $G=\left(V,A,B\right)$ be a strong $m$-PIVFG of $G^{\ast }=\left(V,E\right)$. If $p_i\circ {\mu }_B^l\left(xy\right)=\frac{1}{2}min\{p_i\circ {\mu }_A^l(x),p_i\circ {\mu }_A^l(y\left)\right\}$ and $p_i\circ {\mu }_B^u\left(xy\right)=\frac{1}{2}min\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$ $\mathrm{\forall }xy\in E$, $i=1,2,\dots ,m$, then $G$ is self-complementary.

Proof.

Let $G=\left(V,A,B\right)$ be a strong $m$-PIVFG, satisfying $p_i\circ {\mu }_B^l\left(xy\right)=\frac{1}{2}\text{min }\{p_i\circ {\mu }_A^l(x),p_i\circ {\mu }_A^l(y\left)\right\}$ and $p_i\circ {\mu }_B^u\left(xy\right)=\frac{1}{2}\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$, $\mathrm{\forall }xy\in E$, $i=1,2,\dots ,m$, then the identity mapping $I:V\to V$ is an isomorphism from $G$ to $\overline{G}$ . Clearly $I$ satisfies the condition of vertices for isomorphism, that is, $p_i\circ {\mu }_A^l\left(x\right)=p_i\circ {\mu }_{\overline{A}}^l\left(I\left(x\right)\right)$ and $p_i\circ {\mu }_A^u\left(x\right)=p_i\circ {\mu }_{\overline{A}}^u\left(I\left(x\right)\right)\mathrm{\forall }x\in V$. And by the Theorem 2, $\mathrm{\forall }xy\in E$ and $i=1,2,\dots ,m,p_i\circ {\mu }_B^l\left(I\left(xy\right)\right)=p_i\circ {\mu }_{\overline{B}}^l\left(xy\right)=\text{min }\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-\frac{1}{2}\text{min}\{p_i\circ {\mu }_A^l(x),p_i\circ {\mu }_A^l(y\left)\right\}=\frac{1}{2}\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}=p_i\circ {\mu }_B^l\left(xy\right).$ That is, $p_i\circ {\mu }_{\overline{B}}^l\left(xy\right)=p_i\circ {\mu }_B^l\left(xy\right)$. Similarly, $p_i\circ {\mu }_{\overline{B}}^u\left(xy\right)=p_i\circ {\mu }_B^u\left(xy\right)$, $\mathrm{\forall }xy\in E$, $i=1,2,\dots ,m$. That imply $I$ satisfies also the condition of edges for isomorphism. Therefore, $G\cong \overline{G}$. That is $G$ is self-complementary.

Proof

THEOREM 5

Let $G_1=\left(V_1,A_1,B_1\right)$ and $G_2=\left(V_2,A_2,B_2\right)$ be two strong $m$-PIVFG. Then $G_1\cong G_2$ iff $\overline{G_1}\cong \overline{G_2}$.

Proof.

Assume that $G_1=\left(V_1,A_1,B_1\right)$ and $G_2=\left(V_2,A_2,B_2\right)$ be two strong $m$-PIVFG and let us assume $G_1\cong G_2$. Then by definition, there exists a bijective mapping $\phi :V_1\to V_2$ satisfying

1. $p_i\circ {\mu }_{A_1}^l\left(x\right)=p_i\circ {\mu }_{A_2}^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_{A_1}^u\left(x\right)=p_i\circ {\mu }_{A_2}^u\left(\phi \left(x\right)\right)\mathrm{\forall }x\in V_1$ and

2. $p_i\circ {\mu }_{B_1}^l\left(xy\right)=p_i\circ {\mu }_{B_2}^l\left(\phi \left(x\right)\phi \left(y\right)\right),p_i\circ {\mu }_{B_1}^u\left(xy\right)=p_i\circ {\mu }_{B_2}^u\left(\phi \left(x\right)\phi \left(y\right)\right),\mathrm{\forall }xy\in E_1$ and for each $i=1,2,\dots ,m$.

Case I: For $i=1,2,\dots ,m$ and for every $xy\in E_1$. If $p_i\circ {\mu }_{B_1}^u\left(xy\right)=0then{p}_i\circ {\mu }_{\overline{B_1}}^l\left(xy\right)=\text{min }\left\{p_i\circ {\mu }_{A_1}^l\left(x\right),p_i\circ {\mu }_{A_1}^l\left(y\right)\right\}=\text{min }\left\{p_i\circ {\mu }_{A_2}^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_{A_2}^l\left(\phi \left(y\right)\right)\right\}=p_i\circ {\mu }_{\overline{B_2}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)and{p}_i\circ {\mu }_{\overline{B_1}}^u\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_{A_1}^u\left(x\right),p_i\circ {\mu }_{A_1}^u\left(y\right)\right\}=\text{min}\{p_i\circ {\mu }_{A_2}^u(\phi \left(x\right)),p_i\circ {\mu }_{A_2}^u(\phi \left(y\right)\left)\right\}=p_i\circ {\mu }_{\overline{B_2}}^u\left(\phi \left(x\right)\phi \left(y\right)\right)\mathrm{\forall }xy\in E_{1}andforeach.$ …  …  …  …  …  …  …  …  …  …  … ..

Case II: If for $0<p_i\circ {\mu }_{B_1}^l\left(xy\right)\le 1$ and $0<p_i\circ {\mu }_{B_1}^u\left(xy\right)\le 1$ then, $0<p_i\circ {\mu }_{B_2}^l\left(\phi \left(x\right)\phi \left(y\right)\right)\le 1$ and $0<p_i\circ {\mu }_{B_2}^u\left(\phi \left(x\right)\phi \left(y\right)\right)\le 1$. So, $p_i\circ {\mu }_{\overline{B_1}}^l\left(xy\right)=0=p_i\circ {\mu }_{\overline{B_2}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)$ and $p_i\circ {\mu }_{\overline{B_1}}^u\left(xy\right)=0=p_i\circ {\mu }_{\overline{B_2}}^u\left(\phi \left(x\right)\phi \left(y\right)\right)$ $\mathrm{\forall }xy\in E_1$ and for each $i=1,2,\dots ,m$. Hence, $\overline{G_1}\cong \overline{G_2}$.

Conversely, let $\overline{G_1}\cong \overline{G_2}$, then there exists a bijective mapping $\phi :V_1\to V_2$ satisfying

1. $p_i\circ {\mu }_{\overline{A_1}}^l\left(x\right)=p_i\circ {\mu }_{\overline{A_2}}^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_{\overline{A_1}}^u\left(x\right)=p_i\circ {\mu }_{\overline{A_2}}^u\left(\phi \left(x\right)\right)$,

2. $p_i\circ {\mu }_{\overline{B_1}}^l\left(xy\right)=p_i\circ {\mu }_{\overline{B_2}}^l\left(\phi \left(x\right)\phi \left(y\right)\right),p_i\circ {\mu }_{\overline{B_1}}^u\left(xy\right)=p_i\circ {\mu }_{\overline{B_2}}^u\left(\phi \left(x\right)\phi \left(y\right)\right).$

Case I: If $xy\in E_1$ and for each $i=1,2,\dots ,m$, $p_i\circ {\mu }_{B_1}^l\left(xy\right)=0$, then $p_i\circ {\mu }_{\overline{B_2}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)=p_i\circ {\mu }_{\overline{B_1}}^l\left(xy\right)=\text{min }\left\{p_i\circ {\mu }_{A_1}^l\left(x\right),p_i\circ {\mu }_{A_1}^l\left(y\right)\right\}=\text{min }\left\{p_i\circ {\mu }_{\overline{A_1}}^l\left(x\right),p_i\circ {\mu }_{\overline{A_1}}^l\left(y\right)\right\}=\text{min }\{p_i\circ {\mu }_{\overline{A_2}}^l(\phi \left(x\right),p_i\circ {\mu }_{\overline{A_2}}^l\left(\phi \right(y\left)\right\}=\text{min }\{p_i\circ {\mu }_{A_2}^l(\phi \left(x\right),p_i\circ {\mu }_{A_2}^l\left(\phi \left(y\right)\right)\}.$ Again, $p_i\circ {\mu }_{\overline{B_2}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)=\text{min}\left\{p_i\circ {\mu }_{A_2}^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_{A_2}^l\left(\phi \left(y\right)\right)\right\}-p_i\circ {\mu }_{B_2}^l\left(\phi \left(x\right)\phi \left(y\right)\right)$. So, $p_i\circ {\mu }_{B_2}^l\left(\phi \left(x\right)\phi \left(y\right)\right)=0=p_i\circ {\mu }_{B_1}^l\left(xy\right)$ for $i=1,2,\dots ,m$.

Case II: If for $i=1,2,\dots ,m$, $0<p_i\circ {\mu }_{B_1}^l\left(xy\right)\le 1$ then, $p_i\circ {\mu }_{\overline{B_2}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)=p_i\circ {\mu }_{\overline{B_1}}^l\left(xy\right))=0$. Thus, $p_i\circ {\mu }_{B_2}^l\left(\phi \left(x\right)\phi \left(y\right)\right)=\text{min}\{p_i\circ {\mu }_{A_2}^l(\phi \left(x\right),p_i\circ {\mu }_{A_2}^l\left(\phi \right(y\left)\right\}-0=\text{min}\{p_i\circ {\mu }_{A_2}^l(\phi \left(x\right),p_i\circ {\mu }_{A_2}^l\left(\phi \right(y\left)\right\}=p_i\circ {\mu }_{B_1}^l\left(xy\right)$. Similarly we can prove, $p_i\circ {\mu }_{B_2}^u\left(\phi \left(x\right)\phi \left(y\right)\right)=p_i\circ {\mu }_{B_1}^u\left(xy\right)$. Hence, $G_1\cong G_2$.

Proof

DEFINITION 5.4

Let $G_1=\left(V_1,A_1,B_1\right)$ of $G^{\ast }=\left(V_1,E_1\right)$ and $G_2=\left(V_2,A_2,B_2\right)$ of $G^{\ast }=\left(V_2,E_2\right)$ be two $m$-PIVFG. A weak isomorphism $\phi :G_1\to G_2$ is a bijective mapping $\phi :V_1\to V_2$ satisfying the following conditions,

1. $\phi$ is homomorphism

2. $p_i\circ {\mu }_{A_1}^l\left(x\right)=p_i\circ {\mu }_{A_2}^l\left(\phi \left(x\right)\right)$, $p_i\circ {\mu }_{A_1}^u\left(x\right)=p_i\circ {\mu }_{A_2}^u\left(\phi \left(x\right)\right)$ for each $x\in V_1$ and for each $i=1,2,\dots ,m$, i.e. the weight of the nodes of the intervals are preserved but the weight of the edges are not necessarily preserved.

Example 11 Let us consider any two $3$-PIVFGs $\begin{array}{rl}{G}_1& =\left(V_1,A_1,B_1\right):A_1=\left(\frac{b_1}{⟨\left[0.2,0.5\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\frac{b_2}{⟨\left[0.3,0.4\right],\left[0.4,0.6\right],\left[0.4,0.8\right]⟩},\right.\\ & \left.\frac{b_3}{⟨\left[0.4,0.6\right],\left[0.5,0.6\right],\left[0.6,0.8\right]⟩}\right)\\ B_1& =\left(\frac{b_1{b}_2}{⟨\left[0.2,0.5\right],\left[0.3,0.5\right],\left[0.3,0.7\right]⟩},\frac{b_2{b}_3}{⟨\left[0.3,0.4\right],\left[0.4,0.5\right],\left[0.4,0.7\right]⟩}\right)\\ G_2& =\left(V_2,A_2,B_2\right):A_2=\left(\frac{{\hat{b}}_1}{⟨\left[0.2,0.5\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\frac{{\hat{b}}_2}{⟨\left[0.3,0.4\right],\left[0.4,0.6\right],\left[0.4,0.8\right]⟩},\right.\\ & \left.\frac{{\hat{b}}_3}{⟨\left[0.4,0.6\right],\left[0.5,0.6\right],\left[0.6,0.8\right]⟩}\right)\\ B_2& =\left(\frac{{\hat{b}}_1{\hat{b}}_2}{⟨\left[0.2,0.4\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\frac{{\hat{b}}_2{\hat{b}}_3}{⟨\left[0.3,0.4\right],\left[0.4,0.5\right],\left[0.4,0.7\right]⟩}\right)\end{array}$ We define a mapping $\phi :V_1\to V_2$ such that $\begin{array}{rl}\phi \left(b_1\right)& =\widehat{b_1},\phi \left(b_2\right)=\widehat{b_2},\phi \left(b_3\right)=\widehat{b_3},p_i\circ {\mu }_{A_1}^l\left(b_1\right)=p_i\circ {\mu }_{A_2}^l\widehat{\left(b_1\right)},p_i\circ {\mu }_{A_1}^l\left(b_2\right)\\ & =p_i\circ {\mu }_{A_2}^l\widehat{\left(b_2\right)},p_i\circ {\mu }_{A_1}^u\left(b_1\right)\\ & =p_i\circ {\mu }_{A_2}^u\widehat{\left(b_1\right)},p_i\circ {\mu }_{A_1}^u\left(b_2\right)=p_i\circ {\mu }_{A_2}^u\widehat{\left(b_2\right)},p_i\circ {\mu }_{A_1}^l\left(b_3\right)\\ & =p_i\circ {\mu }_{A_2}^l\widehat{\left(b_3\right)},p_i\circ {\mu }_{A_1}^u\left(b_3\right)\\ & =p_i\circ {\mu }_{A_2}^u\widehat{\left(b_3\right)}for{b}_i\in V_1,but,p_i\circ {\mu }_{B_1}^l\left(b_1{b}_2\right)\\ & \ne p_i\circ {\mu }_{B_2}^l\left(\phi \left(b_1\right)\phi \left(b_2\right)\right),p_i\circ {\mu }_{B_1}^l\left(b_2{b}_3\right)\\ & \ne p_i\circ {\mu }_{B_2}^l\left(\phi \left(b_2\right)\phi \left(b_3\right)\right),p_i\circ {\mu }_{B_1}^u\left(b_1{b}_2\right)\ne p_i\circ {\mu }_{B_2}^u\left(\phi \left(b_1\right)\phi \left(b_2\right)\right)p_i\circ {\mu }_{B_1}^u\left(b_2{b}_3\right)\\ & \ne p_i\circ {\mu }_{B_2}^u\left(\phi \left(b_2\right)\phi \left(b_3\right)\right).\end{array}$ Since all the conditions satisfied, thus, $G_1$ is weak-isomorphic to $G_2$.

Proof

THEOREM 6

Let us consider a weak isomorphism $\phi :G\to \overline{G}$, then for $xy\in E$, and for each $i=1,2,\dots ,m,$ $\sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(xy\right)\le \frac{1}{2}\sum _{x\ne y}min\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}and\sum _{x\ne y}{p}_i\circ {\mu }_B^u\left(xy\right)\le \frac{1}{2}\sum _{x\ne y}min\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$

Proof.

Let us consider a weak isomorphism $\phi$ from $G=\left(V,A,B\right)$ to it's complement $\overline{G}$ i.e. $\phi :G\to \overline{G}$. Then $\phi :G\to \overline{G}$ such that

1. $p_i\circ {\mu }_A^l\left(x\right)=p_i\circ {\mu }_{\overline{A}}^l\phi \left(x\right)$, $p_i\circ {\mu }_A^u\left(x\right)=p_i\circ {\mu }_{\overline{A}}^u\phi \left(x\right)\cdot \mathrm{\forall }\cdot x\in V$

2. $p_i\circ {\mu }_B^l\left(xy\right)\le p_i\circ {\mu }_{\overline{B}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)$, $p_i\circ {\mu }_B^u\left(x\right)\le p_i\circ {\mu }_{\overline{B}}^u\left(\phi \left(x\right)\phi \left(y\right)\right)\cdot \mathrm{\forall }\cdot xy\in E$ and for $i=1,2,\dots ,m$. Now, $p_i\circ {\mu }_B^l\left(xy\right)\le p_i\circ {\mu }_{\overline{B}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)=min\left\{p_i\circ {\mu }_A^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_A^l\left(\phi \left(y\right)\right)\right\}-p_i\circ {\mu }_B^l\left(\phi \left(x\right)\phi \left(y\right)\right)$ or, $p_i\circ {\mu }_B^l\left(xy\right)+p_i\circ {\mu }_B^l\left(\phi \left(x\right)\phi \left(y\right)\right)\le min\{p_i\circ {\mu }_A^l(\phi \left(x\right)),p_i\circ {\mu }_A^l(\phi \left(y\right)\left)\right\}$.

Taking summation both sides, $\begin{array}{rl}& \sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(xy\right)+\sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(\phi \left(x\right)\phi \left(y\right)\right)\le \sum _{x\ne y}min\left\{p_i\circ {\mu }_A^l\left(\phi \left(x\right)\right),p_i\circ {\mu }_A^l\left(\phi \left(y\right)\right)\right\}\\ & =\sum _{x\ne y}min\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}or,2\sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(xy\right)\\ & \le \sum _{x\ne y}min\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}or,\\ & \sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(xy\right)\le \frac{1}{2}\sum _{x\ne y}\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}.\end{array}$ Similarly we can prove, $\sum _{x\ne y}{p}_i\circ {\mu }_B^u\left(xy\right)\le \frac{1}{2}\sum _{x\ne y}\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$. Hence, the result.

Proof

THEOREM 7

Let $G=\left(V,A,B\right)$ be an $m$-PIVFG of $G^{\ast }=\left(V,E\right)$. If $p_i\circ {\mu }_B^l\left(xy\right)\le \frac{1}{2}min\{p_i\circ {\mu }_A^l(x),p_i\circ {\mu }_A^l(y\left)\right\}$ and $p_i\circ {\mu }_B^u\left(xy\right)\le \frac{1}{2}min\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$ $\mathrm{\forall }xy\in E$, $i=1,2,\dots ,m$, then $G$ has a weak isomorphism $\phi$ from $G$ to it's complement $\overline{G}$.

Proof.

Let $G=\left(V,A,B\right)$ be an $m$-PIVFG, satisfying $p_i\circ {\mu }_B^l\left(xy\right)\le \frac{1}{2}\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}$ and $p_i\circ {\mu }_B^u\left(xy\right)\le \frac{1}{2}\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$, $\mathrm{\forall }xy\in E$, $i=1,2,\dots ,m$, then the identity mapping $I:V\to V$ satisfies the condition $p_i\circ {\mu }_A^l\left(x\right)=p_i\circ {\mu }_{\overline{A}}^l\left(I\left(x\right)\right)$ and $p_i\circ {\mu }_A^u\left(x\right)=p_i\circ {\mu }_{\overline{A}}^u\left(I\left(x\right)\right)\mathrm{\forall }x\in V$ and, $\mathrm{\forall }xy\in E$ and $i=1,2,\dots ,m,p_i\circ {\mu }_{\overline{B}}^l\left(I\left(x\right)I\left(y\right)\right)=p_i\circ {\mu }_{\overline{B}}^l\left(xy\right)=\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-p_i\circ {\mu }_B^l\left(xy\right)\ge \text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}-\frac{1}{2}\text{min}\{p_i\circ {\mu }_A^l(x),p_i\circ {\mu }_A^l(y\left)\right\}=\frac{1}{2}\text{min}\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}\ge p_i\circ {\mu }_B^l\left(xy\right)$. That is, $p_i\circ {\mu }_{\overline{B}}^l\left(I\left(x\right)I\left(y\right)\right)\ge p_i\circ {\mu }_B^l\left(xy\right)$. Similarly, $p_i\circ {\mu }_{\overline{B}}^u\left(I\left(x\right)I\left(y\right)\right)\ge p_i\circ {\mu }_B^u\left(xy\right)$, $\mathrm{\forall }xy\in E$, $i=1,2,\dots ,m$. That imply $I$ satisfies also the condition for weak isomorphism from $G$ to it's complement $\overline{G}$. Hence, $G$ has a weak isomorphism $\phi$ from $G$ to it's complement $\overline{G}$.

Proof

DEFINITION 5.5

Let $G_1=\left(V_1,A_1,B_1\right)$ of $G^{\ast }=\left(V_1,E_1\right)$ and $G_2=\left(V_2,A_2,B_2\right)$ of $G^{\ast }=\left(V_2,E_2\right)$ be two $m$-PIVFGs. A co-weak isomorphism $\phi :G_1\to G_2$ is a bijective mapping $\phi :V_1\to V_2$ satisfying the following conditions,

1. $\phi$ is homomorphism.

2. $p_i\circ {\mu }_{B_1}^l\left(xy\right)=p_i\circ {\mu }_{B_2}^l\left(\phi \left(x\right)\phi \left(y\right)\right),p_i\circ {\mu }_{B_1}^u\left(x\right)=p_i\circ {\mu }_{B_2}^u\left(\phi \left(x\right)\phi \left(y\right)\right)$, $\mathrm{\forall }xy\in E_1$ and for each $i=1,2,\dots ,m$.

Example 12 Let us consider any two $3$-PIVFGs $\begin{array}{rl}{G}_1& =\left(V_1,A_1,B_1\right):A_1=\left(\frac{b_1}{⟨\left[0.2,0.5\right],\left[0.3,0.6\right],\left[0.3,0.7\right]⟩},\frac{b_2}{⟨\left[0.3,0.6\right],\left[0.4,0.6\right],\left[0.4,0.8\right]⟩},\right.\\ & \left.\frac{b_3}{\left[0.4,0.6\right],\left[0.5,0.6\right],\left[0.6,0.8\right]}\right)\\ B_1& =\left(\frac{b_1{b}_2}{\left[0.2,0.3\right],\left[0.3,0.5\right],\left[0.5,0.7\right]},\frac{b_2{b}_3}{\left[0.3,0.4\right],\left[0.4,0.5\right],\left[0.4,0.7\right]}\right)\\ G_2& =\left(V_2,A_2,B_2\right):A_2=\left(\frac{{\hat{b}}_1}{⟨\left[0.3,0.5\right],\left[0.4,0.6\right],\left[0.4,0.8\right]⟩},\frac{{\hat{b}}_2}{⟨\left[0.2,0.3\right],\left[0.3,0.7\right],\left[0.4,0.8\right]⟩},\right.\\ & \left.\frac{{\hat{b}}_3}{⟨\left[0.2,0.4\right],\left[0.4,0.6\right],\left[0.3,0.8\right]⟩}\right)\\ B_2& =\left(\frac{{\hat{b}}_1{\hat{b}}_2}{⟨\left[0.3,0.4\right],\left[0.4,0.5\right],\left[0.4,0.7\right]⟩},\frac{{\hat{b}}_2{\hat{b}}_3}{⟨\left[0.2,0.3\right],\left[0.4,0.6\right],\left[0.3,0.8\right]⟩}\right)\end{array}$ Here, we define a mapping $\phi :V_1\to V_2$ like $\phi \left(b_1\right)=\widehat{b_3},\phi \left(b_2\right)=\widehat{b_2},\phi \left(b_3\right)=\widehat{b_1},p_i\circ {\mu }_{A_1}^l\left(b_1\right)\ne p_i\circ {\mu }_{A_2}^l\widehat{\left(b_3\right)},p_i\circ {\mu }_{A_1}^l\left(b_2\right)\ne p_i\circ {\mu }_{A_2}^l\widehat{\left(b_2\right)},p_i\circ {\mu }_{A_1}^u\left(b_1\right)\ne p_i\circ {\mu }_{A_2}^u\widehat{\left(b_3\right)},p_i\circ {\mu }_{A_1}^u\left(b_2\right)\ne p_i\circ {\mu }_{A_2}^u\widehat{\left(b_2\right)},p_i\circ {\mu }_{A_1}^l\left(b_3\right)\ne p_i\circ {\mu }_{A_2}^l\widehat{\left(b_1\right)},p_i\circ {\mu }_{A_1}^u\left(b_3\right)\ne p_i\circ {\mu }_{A_2}^u\widehat{\left(b_1\right)},for{b}_i\in V_1,i=1,2,3.$ Thus, $\phi :G_1\to G_2$ is a co-weak isomorphism (See Figures 18 and 19).

Figure 18. A $3$-PIVFG $G_1=\left(V_1,A_1,B_1\right)$.

Figure 19. A $3$-PIVFG $G_2=\left(V_2,A_2,B_2\right).$

Proof

THEOREM 8

Let us consider a co-weak isomorphism $\phi :G\to \overline{G}$, then for $xy\in E$, and for each $i=1,2,\dots ,m,\sum _{x\ne y}{p}_i\circ {\mu }_B^l\left(xy\right)\ge \frac{1}{2}\sum _{x\ne y}min\left\{p_i\circ {\mu }_A^l\left(x\right),p_i\circ {\mu }_A^l\left(y\right)\right\}and\sum _{x\ne y}{p}_i\circ {\mu }_B^u\left(xy\right)\ge \frac{1}{2}\sum _{x\ne y}min\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$

Proof.

Let us consider a co-weak isomorphism $\phi$ from $G=\left(V,A,B\right)$ to it's complement $\overline{G}$ i.e. $\phi :G\to \overline{G}$ . Then $\phi :G\to \overline{G}$ such that

1. $p_i\circ {\mu }_A^l\left(x\right)\le p_i\circ {\mu }_{\overline{A}}^l\phi \left(x\right)$, $p_i\circ {\mu }_A^u\left(x\right)\le p_i\circ {\mu }_{\overline{A}}^u\phi \left(x\right)$ $\mathrm{\forall }$ $x\in V$

2. $p_i\circ {\mu }_B^l\left(xy\right)=p_i\circ {\mu }_{\overline{B}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)$, $p_i\circ {\mu }_B^u\left(x\right)=p_i\circ {\mu }_{\overline{B}}^u\left(\phi \left(x\right)\phi \left(y\right)\right)$ $\mathrm{\forall }$ $xy\in E$ and for each $i=1,2,\dots ,m$. Now, $p_i\circ {\mu }_B^l\left(xy\right)=p_i\circ {\mu }_{\overline{B}}^l\left(\phi \left(x\right)\phi \left(y\right)\right)=min\{p_i\circ {\mu }_A^l(\phi \left(x\right)),p_i\circ {\mu }_A^l(\phi \left(y\right)\left)\right\}-p_i\circ {\mu }_B^l\left(\phi \left(x\right)\phi \left(y\right)\right)$ or, $p_i\circ {\mu }_B^l\left(xy\right)+p_i\circ {\mu }_B^l\left(\phi \left(x\right)\phi \left(y\right)\right)=min\{p_i\circ {\mu }_A^l(\phi \left(x\right)),p_i\circ {\mu }_A^l(\phi \left(y\right)\left)\right\}$. Taking summation both sides, Similarly we can prove, $\sum _{x\ne y}{p}_i\circ {\mu }_B^u\left(xy\right)\ge \frac{1}{2}\sum _{x\ne y}\text{min}\left\{p_i\circ {\mu }_A^u\left(x\right),p_i\circ {\mu }_A^u\left(y\right)\right\}$. Hence, the result.

6. Application

Fuzzy graphs have many applications for problems concerning group structures, solving fuzzy intersection equations, etc. An $m$-PFG has applications in decision-making problems including co-operative games, medical diagnosis, signal processing, pattern recognition, robotics, database theory, expert systems and so on. Also, $m$-PIVFG is used in many decision-making problems. This happens when a democratic country elects its leader, a group of people decide which movie to watch when a company decides which product design to manufacturing, when a group of judges choose a participate in a reality show, etc. Here we consider an example of a singing competition. Let, $V=\left\{Aman,Survi,Karan,Piu,Bibhu\right\}$ be the set of five candidates and $J=\left\{a,b,c,d\right\}$ be the set of four judges. They have to select a candidate for the winning trophy depending on their qualities that are voice tone, smoothness, confidence, facial expression, presentation. Suppose Judge ‘a’ is an expert of ‘Sufi music’, judge ‘b’ an expert of ‘Ghazal music’, judge ‘c’ an expert of ‘folk music’ and judge ‘d’ an expert of ‘Indian filmy music’. By default, all the Judges have sufficient knowledge in ‘Classical music’. For each candidate a judge from $J$ can give marks in the form of interval value in [0,1] to $x\in V$; such as,

Assuming Table 5 is constructed by the four Judges. The first column represents the performance marks of Aman given by four Judges. Similar to other columns. On the other hand first row represents the marks to all participants given by First Judge. From this table, one can construct a $5$-PIVFG shown in Figure 20. The first row can be denoted by $A\left(a\right)$, i.e. $A\left(a\right)=⟨\left[0.3,0.6\right],\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.7\right],\left[0.1,0.5\right]⟩$. Also, $p_1\circ A\left(a\right)=\left(0.3,0.6\right)$ means a score of the candidate Aman by the judge ‘a’ for the trophy is in between 30 and 60% depending on the qualities Tone, Smoothness, Confidence, Facial expression and Presentation. Similarly for others. Also, an edge represents score by Judges whose fields of music are common. For example Judge ‘a’ who is an expert of ‘Sufi music’ also has ideas on ‘Ghazal music’. Here, the edges $ab=⟨\left[0.2,0.3\right],\left[0.3,0.5\right],\left[0.2,0.4\right],\left[0.1,0.6\right],\left[0.1,0.5\right]⟩$ $bc=⟨\left[0.1,0.3\right],\left[0.2,0.4\right],\left[0.4,0.5\right],\left[0.2,0.6\right],\left[0.3,0.7\right]⟩$ $ad=⟨\left[0.1,0.2\right],\left[0.2,0.6\right],\left[0.2,0.5\right],\left[0.1,0.6\right],\left[0.1,0.5\right]⟩$ $cd=⟨\left[0.1,0.2\right],\left[0.2,0.5\right],\left[0.3,0.4\right],\left[0.2,0.6\right],\left[0.3,0.6\right]⟩$ $bd=⟨\left[0.1,0.2\right],\left[0.2,0.5\right],\left[0.3,0.6\right],\left[0.2,0.6\right],\left[0.4,0.6\right]⟩$

Figure 20. For the graph $G_1.$

Table 5. Marks given to each candidate.

	$Aman\left(v_1\right)$	$Survi\left(v_2\right)$	$Karan\left(v_3\right)$	$Piu\left(v_4\right)$	$Bibhu\left(v_5\right)$
$a$	$\left[0.3,0.6\right]$	$\left[0.4,0.6\right]$	$\left[0.2,0.5\right]$	$\left[0.1,0.7\right]$	$\left[0.1,0.5\right]$
$b$	$\left[0.2,0.3\right]$	$\left[0.3,0.5\right]$	$\left[0.4,0.6\right]$	$\left[0.2,0.6\right]$	$\left[0.4,0.9\right]$
$c$	$\left[0.1,0.4\right]$	$\left[0.2,0.6\right]$	$\left[0.4,0.9\right]$	$\left[0.2,0.8\right]$	$\left[0.3,0.7\right]$
$d$	$\left[0.1,0.2\right]$	$\left[0.2,0.6\right]$	$\left[0.3,0.7\right]$	$\left[0.2,0.6\right]$	$\left[0.4,0.6\right]$

The judges give marks to the singers by the following rule:

Marks ={(upper limit of the interval + lower limit of the interval)÷2}×100. Marks of each candidate (v_i) given by the judges are listed in following table. Then each pair of judges give rank (R_i) to all the candidates (v_i) according to their marks (Tables 6–8).

Table 6. Marks given to each candidate.

	$v_1$	$v_2$	$v_3$	$v_4$	$v_5$
$ab$	$25$	$40$	$30$	$35$	$30$
$bc$	$20$	$30$	$45$	$40$	$50$
$ad$	$15$	$40$	$35$	$35$	$30$
$cd$	$15$	$35$	$40$	$40$	$45$
$bd$	$15$	$35$	$45$	$40$	$50$

Table 7. Rank given to each candidate.

	$R_1$	$R_2$	$R_3$	$R_4$	$R_5$
$ab$	$v_2$	$v_4$	$v_3$ and $v_5$	$v_1$
$bc$		$v_3$	$v_4$	$v_2$	$v_1$
$ad$	$v_2$	$v_3$ and $v_4$	$v_5$	$v_1$
$cd$	$v_5$	$v_3$ and $v_4$	$v_2$	$v_1$	$v_5$
$bd$	$v_5$	$v_3$	$v_4$	$v_1$	$v_1$

Table 8. Score of each candidate.

Candidate	Score
Aman	8
Survi	17
Karan	19
Piu	18
Bibhu	21

Depending on the performance of the competitions, each pair of judges prepared a panel for the candidates. Again, to find the combined rank of each candidate based on the rank of all judges we consider weights for a different rank. Suppose $w_i$ be the weights for the rank i. Obviously $w_i>w_j$ for $i<j$. Thus the combined rank or say a score of a candidate is given by the formula $s_j=\sum i\times w_i$. Using this formula the score (s_j) of all five candidates are calculated below:

Hence according to the final score, Bibhu get the first position, Karan gets the second position, Piu gets the third position, Survi gets the fourth position and Aman gets the fifth position. The determination of which singer to win the trophy is called the decision-making problem. Moreover, $m$-PIVFG has applications in different areas of computer science, neural intelligence, astronomy, autonomous system and industrial field and so on.

7. Conclusion and Future Research Direction

We have been seen that IVFG being viewed as a generalization of fuzzy graph and $m$-PFG also viewed as an extension of bi-polar fuzzy graph. In this study, we have been introduced the $m$-PIVFG, a generalization of IVFG and $m$-PFG, and its complements with examples. The definition of complement has been failed in some cases. Therefore, we have been modified the definition with examples. The definitions of homomorphism, isomorphism, weak isomorphism, co-weak isomorphism of $m$-PIVFG have been defined with proper given examples. Furthermore, we have been stated the complete $m$-PIVFG and strong $m$-PIVFG. In fact, some properties related to complements of complete $m$-PIVFG and strong $m$-PIVFG have been described. Thereafter, we also have been discussed few properties regarding self-complementary of $m$-PIVFG.

We should feature that regarding this investigation, there are distinctive developing regions that we need not demonstrate here as they are outside of our feasible region. In any case, there can be interesting points for future research; for example, one may examine the $m$-PIVFG with various kinds of environments [39], e.g. domination, Pythagorean, fuzzy soft graph [40–44], etc. In the future, we shall investigate other results of $m$-PIVFG and extend them to solve various problems of decision-making problems under different fuzzy environments.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Sanchari Bera

Sanchari Bera is a Research Scholar in the Department of Applied Mathematics with Oceanology and Computer Programming, Vidyasagar University, Midnapore-721102, West Bengal, India. She received her B.Sc (Hons.) and M. Sc. degrees in Mathematics from Raja Narendra Lal Khan Women's College (Autonomous) and Vidyasagar University, West Bengal, India in 2012 and 2014, respectively. Her main research interests include Graph Theory and Fuzzy Graph Theory. She has published two research papers in reputed journals.

Madhumangal Pal

Madhumangal Pal is currently a Professor of Applied Mathematics, Vidyasagar University. He has received Gold and Silver medals from Vidyasagar University for rank first and second in M.Sc. and B.Sc. examinations respectively. Also, he received ‘Computer Division Medal’ from Institute of Engineers (India) in 1996 for best research work. In 2013, he has received Bharat Jyoti Award for the significant contribution in academic. Prof. Pal has successfully guided 34 research scholars for Ph.D. degrees and has published more than 320 articles in international and national journals. His specializations include Algorithmic and Fuzzy Graph Theory, Fuzzy Matrices, Genetic Algorithms and Parallel Algorithms. Prof. Pal is the author of eight text books published from India and United Kingdom and two edited book published by IGI Global, USA. He has published 21 book chapters in several edited books. Prof. Pal completed three research project funded by UGC and DST and one project is going on. Prof. Pal is the Editor-in-Chief of Journal of Physical Sciences', ‘Annals of Pure and Applied Mathematics’, area editor of ‘International Journal of Computational Intelligence Systems (SCI Indexed Journal)’ and member of the editorial Boards of many journals. Also, he has visited China, Greece, London, Taiwan, Malaysia, Thailand, Hong Kong, Dubai and Bangladesh to participated, delivered invited talks and to chair conference event. He is also a member of the American Mathematical Society, USA, Calcutta Mathematical Society, Advanced Discrete Mathematics and Application, Neutrosophic Science International Association, USA, etc. As per Google Scholar, the citation of Prof. Pal is 6233, h-index is 40 and i10-index is 184, as on 25.06.2020. He is the member of several administrative and academic bodies in Vidyasagar University and other institutes/organizations.