On KM-Fuzzy Metric Hypergraphs

ABSTRACT

This paper, applies the concept of KM-fuzzy metric spaces and introduces a novel concept of KM-fuzzy metric hypergraphs based on KM-fuzzy metric spaces. In special cases, we add some conditions to axioms of KM-fuzzy metric hypergraphs(to obtain of elementary hypergraphs, C-accessible hypergraphs, Cor-able hypergraphs, fuzzy hypergraphs) and so obtain locally strong KM-fuzzy metric hypergraphs and strong KM-fuzzy metric hypergraphs. This study, investigates on the finite KM-fuzzy metric spaces with respect to metrics, KM-fuzzy metrics and constructs KM-fuzzy metric spaces on any given non-empty sets. It tries to extend the concept of KM-fuzzy metric spaces to union of KM-fuzzy metric spaces and product of KM-fuzzy metric spaces and in this regard investigates on union and product of KM-fuzzy metric hypergraphs.

Keywords:

• KM-fuzzy metric space
• T-norm
• KM-fuzzy metric hypergraph
• fundamental fuzzy sequence
• core fuzzy hypergraph

1. Introduction

The mathematical concept of theory of hypergraphs has been introduced by Berge as a generalisation of theory of graph with the motivation that hypergraphs are an extension of classical results of graph theory around 1960 [1]. One of the applications of hypergraph structures is a modelling for the complex hypernetworks. Since sometimes graph structures give very limited information about of complex networks, so we say that the main motivation of hypergraph structures is for covering graph defects in the applications. Also the notion of hypergraph has been considered as a basic tool to present the hyperstructure of a system by the clustering and partitating methods. Today, hypergraphs have important applications and are used in complex hypernetworks such as computer science, wireless sensor hypernetwork, machine learning. So there has been a lot of researches about using hypergraphs in relational databases, which might be viewed as a sort of data mining. There are also some researches about networks where matroids and hypergraphs are used together in the demonstrations [2]. In classical set theory, the mathematical concepts introduce purely and without any quality or criteria, that it is not attractive to use in world. So Zadeh introduced the concept of fuzzy set theory as one of a generalisation of set theory to deal with uncertainties [3]. This theory describes an important role in modelling and controlling unsure hypersystems in nature, society and industry. Follow this, fuzzy topological spaces are a generalisation of topological spaces and have a fundamental role in construction of fuzzy metric spaces as a extension of the concept of metric spaces. Theory of fuzzy metric space works on distance between of two points as nonnegative fuzzy numbers and has some applications. The structure of fuzzy metric space, is equipped with mathematical tools such as triangular norms and fuzzy subsets dependent on time parameter and other variables. This theory has been proposed by different researchers with different definitions points view [4–7], that this study applies a notion of KM-fuzzy metric space by Kramosil and Michalek introduced in 1975 [6]. Kaufmann [8], introduced and provided the theory of fuzzy hypergraphs as a generalisation of concept of hypergraphs, in such a way that fuzzy hypergraphs have important applications to decision making, mobile network and similar applications [9,10]. Further materials regarding graphs and hypergraphs are available in the literature too [11–23].

Regarding these points, we introduce the novel concept of KM-fuzzy metric hypergraphs. Also with respect to the concept of KM-fuzzy metric hypergraphs we proved that for every given set one can construct a metric space. KM-fuzzy metric spaces have some important tools as triangular norms and fuzzy subsets, so it is one of main reasons for choosing the KM-fuzzy metric spaces to construct of the KM-fuzzy metric hypergraphs. Although the parameter of time(unlimited time) in KM-fuzzy metric spaces is a problem in our study, but the concept of fuzzy hypergraphs and their applications lead us to introduce this concept. We apply the KM-fuzzy metrics to measurement limitation on vertices and hyperedges of KM-fuzzy metric hypergraphs, so the KM-fuzzy metrics play a key role in our study. The fuzzy metric spaces are not necessarily finite space, so one of our motivation of this work is a construction of finite KM-fuzzy metric space and their extension based on KM-fuzzy metric hypergraphs. The main of our motivation of this work is to present the concept of fuzzy hypergraphs based on t-norm such as Domby t-norm, Godel t-norm and etc. We applied the notation of KM-fuzzy metric space to generate of finite KM-fuzzy metric hypergraph. It is extended some production operations on KM-fuzzy metric spaces and so it is generalised the KM-fuzzy metric hypergraphs to larger class. Also the notation of fundamental sequence in KM-fuzzy metric hypergraphs is introduced and based on fundamental sequence the concept of core hypergraphs is presented.

2. Preliminaries

In this section, we recall some definitions and results, which we need in what follows.

Definition 2.1

[1,15]

Let X be a finite set. A hypergraph on X is a pair $H=(X,\{E_i{\}}_{i=1}^{{}^m})$ such that for all $1\le i\le m,\mathrm{\varnothing }\ne E_i\subseteq X$ and $\bigcup _{i=1}^m{E}_i=X$. The elements $x_1,x_2,\dots ,x_n$ of X are called $($hyper$)$vertices, and the sets $E_1,E_2,\dots ,E_m$ are called the hyperedges of the hypergraph H. In hypergraphs, hyperedges can contain an element $($loop$)$ two elements $($edge$)$ or more than three elements. A hypergraph $H=(X,\{E_i{\}}_{i=1}^{{}^m})$ is called a complete hypergraph, if for any $x,y\in X$ there is $1\le i\le m$ such that $\{x,y\}\subseteq E_i$. A hypergraph $H=(X,\{E_i{\}}_{i=1}^n)$ is called as a joint complete hypergraph, if $|X|=n$ for all $1\le i\le n,|E_i|=i$ and $E_i\subseteq E_{i+1}$ element $($loop$)$. If for all $1\le k\le m$ $|E_k|=2$, the hypergraph becomes an ordinary $($undirected$)$ graph. and n rows representing the vertices $x_1,x_2,\dots ,x_n$, where for all $1\le i\le n$ and for all $1\le j\le m,$ we have $m_{ij}=1$ if $x_i\in E_j$ and $m_{ij}=0$ if $x_i\notin E_j$.

Definition 2.2

[24]

Let X be a finite set and $\mathcal{E}$ be a finite family of non trivial fuzzy subsets of X such that $X=\bigcup _{\mu \in \mathcal{E}}\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left(\mu \right)$, where $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left(\mu \right)=\{x\in X|\mu (x)\ne 0\}$. Then the pair $\mathcal{H}=(X,\mathcal{E})$ is called a fuzzy hypergraph on X and $\mathcal{E}$ is called the fuzzy edge set of $\mathcal{H}$ which is denoted by $\mathcal{E}\left(\mathcal{H}\right)$. The height of $\mathcal{H}=(X,\mathcal{E})$ is defined by $h\left(\mathcal{H}\right)=\underset{\mu \in \mathcal{E}}{\bigvee }h\left(\mu \right)$, where for all $\mu \in \mathcal{E},h\left(\mu \right)=\underset{x\in X}{\bigvee }\mu \left(x\right)$ denotes the height of μ.

Definition 2.3

[25]

A binary operation $T:[0,1]\times [0,1]\to [0,1]$ is a t-norm if it for all $x,y,z,w\in [0,1]$ satisfies the following:

1. $T(1,x)=x$;

2. $T(x,y)=T(y,x)$;

3. $T\left(T\right(x,y),z)=T(x,T(y,z\left)\right)$;

4. If $w\le x$ and $y\le z$ then $T(w,y)\le T(x,z)$.

Definition 2.4

[26]

A triplet $(X,\rho ,T)$ is called a KM-fuzzy metric space, if X is an arbitrary non–empty set, T is a left-continuous t-norm and $\rho :X^2\times {\mathbb{R}}^{\ge 0}\to [0,1]$ is a fuzzy set, such that for each $x,y,z,\in X$ and $t,s\ge 0$, we have:

1. $\rho (x,y,0)=0$,

2. $\rho (x,x,t)=1$ for all t>0,

3. $\rho (x,y,t)=\rho (y,x,t)$ (commutative property),

4. $T\left(\rho \right(x,y,t),\rho (y,z,s\left)\right)\le \rho (x,z,t+s)$ (triangular inequality),

5. $\rho (x,y,-):{\mathbb{R}}^{\ge 0}\to [0,1]$ is a left-continuous map,

6. $\underset{t\to \mathrm{\infty }}{lim}\rho \left(\right(x,y,t\left)\right)=1$,

7. $\rho (x,y,t)=1,\mathrm{\forall }t>0$ implies that x = y.

If $(X,\rho ,T)$ satisfies in conditions (i)–(vii), then it is called KM-fuzzy pseudometric space and ρ is called a KM-fuzzy pseudometric. a fuzzy version of the triangular inequality. The value $\rho (x,y,t)$ is considered as the degree of nearness from

Theorem 2.5

[26]

Let $(X,\rho ,T)$ be a KM-fuzzy metric space. Then $\rho (x,y,-):{\mathbb{R}}^{\ge 0}\to [0,1]$ is a non-decreasing map.

3. Extension Operations on KM-Fuzzy Metric Spaces

In this section, we extend the concept of KM-fuzzy metric spaces to union and product of KM-fuzzy metric spaces. From now on, for all $x,y\in [0,1]$ we consider $T_{min}(x,y)=min\{x,y\}$, $T_{pr}(x,y)=xy$, $\begin{array}{rl}& T_{lu}(x,y)=max(0,x+y-1),T_{do}(x,y)=\left\{\begin{array}{ll}\frac{xy}{x+y-xy}& \text{if}(x,y)\ne (0,0)\\ 0& \text{if}(x,y)=(0,0)\end{array}\right.\mathrm{a}\mathrm{n}\mathrm{d}\\ & {\mathcal{C}}_T=\{T:[0,1]\times [0,1]\to [0,1\left]|T\text{is a continuous t-norm}\right\}.\end{array}$ Let $(X_1,{\rho }_1,T)$ and $(X_2,{\rho }_2,T)$ be KM-fuzzy metric spaces, $(x_1,y_1),(x_2,y_2)\in X_1\times X_2$ and $t\in {\mathbb{R}}^{\ge 0}$. For an arbitrary $T\in {\mathcal{C}}_T$, define ${\rho }^{\mathrm{T}}:(X_1\times X_2{)}^2\times {\mathbb{R}}^{\ge 0}\to [0,1]$ by ${\rho }^{\mathrm{T}}((x_1,y_1),(x_2,y_2),t)=T\left({\rho }_1\right(x_1,x_2,t),{\rho }_2(y_1,y_2,t\left)\right)$. So we have the following theorem.

Theorem 3.1

Let $(X_1,{\rho }_1,T)$ and $(X_2,{\rho }_2,T)$ be KM-fuzzy metric spaces. Then $(X_1\times X_2,{\rho }^{T_{min}},T)$ is a KM-fuzzy metric space.

Proof.

Let $(x_1,y_1),(x_2,y_2),(x_3,y_3)\in X_1\times X_2$ and $t,s\in {\mathbb{R}}^{\ge 0}$.

1. Since for all $x_1,x_2\in X_1,y_1,y_2\in X_2,{\rho }_1(x_1,x_2,0)=0$ and ${\rho }_2(y_1,y_2,0)=0$, we have ${\rho }^{T_{min}}((x_1,y_1),(x_2,y_2),0)=0$.

2. ${\rho }^{T_{min}}((x_1,y_1),(x_2,y_2),t)=1$ if and only if $T_{min}\left({\rho }_1\right(x_1,x_2,t),{\rho }_2(y_1,y_2,t\left)\right)=1$ if and only if ${\rho }_1(x_1,x_2,t)={\rho }_2(y_1,y_2,t)=1$ if and only if $(x_1,y_1)=(x_2,y_2)$.

3. It is clear that ${\rho }^{T_{min}}$ is a commutative map.

4. $T({\rho }^{T_{min}}\left(\right(x_1,y_1),(x_2,y_2),t),{\rho }^{T_{min}}\left(\right(x_2,y_2),(x_3,y_3),s))=T(T_{min}\left({\rho }_1\right(x_1,x_2,t),{\rho }_2(y_1,y_2,t\left)\right),T_{min}\left({\rho }_1\right(x_2,x_3,s),{\rho }_2(y_2,y_3,s\left)\right))\le T_{min}\left(T({\rho }_1\right(x_1,x_2,t),{\rho }_1(x_2,x_3,s)),T({\rho }_2(y_1,y_2,t),{\rho }_2(y_2,y_3,s\left))\right))\le T_{min}({\rho }_1(x_1,x_3,t+s),{\rho }_2(y_1,y_3,t+s))={\rho }^{T_{min}}((x_1,y_1),(x_3,y_3),t+s).$

5. Since ${\rho }_1,{\rho }_2$ are left-continuous maps, we get that ρ is a left continuous map.

6. Let $t\to \mathrm{\infty }$. Then $\mathrm{L}\mathrm{i}\mathrm{m}{T}_{min}\left({\rho }_1\right(x_1,x_2,t),{\rho }_2(y_1,y_2,t\left)\right)=T_{min}\left(\mathrm{L}\mathrm{i}\mathrm{m}{\rho }_1\right(x_1,x_2,t)$, $\mathrm{L}\mathrm{i}\mathrm{m}{\rho }_2(y_1,y_2,t))=T_{min}(1,1)=1$. Thus $(X_1\times X_2,{\rho }^{T_{min}},T)$ is a KM-fuzzy metric space.

Let $X_1\cap X_2=\mathrm{\varnothing },$ $(X_1,{\rho }_1,T)$ and $(X_2,{\rho }_2,T)$ be KM-fuzzy metric spaces, $x,y\in X_1\cup X_2$ and $t\in {\mathbb{R}}^{\ge 0}$. Consider $ϵ(x,y,t)=\underset{\begin{array}{c}x,u\in X_1\\ y,v\in X_2\end{array}}{\bigwedge }\left({\rho }_1\right(x,u,t)\wedge {\rho }_2(y,v,t\left)\right))$, define ${\rho }_1\cup {\rho }_2:(X_1\cup X_2{)}^2\times {\mathbb{R}}^{\ge 0}\to [0,1]$ by $({\rho }_1\cup {\rho }_2)(x,y,t)=\left\{\begin{array}{ll}{\rho }_1(x,y,t)& \text{if}x,y\in X_1,\\ {\rho }_2(x,y,t)& \text{if}x,y\in X_2,\\ ϵ(x,y,t)& \text{if}x\in X_1,y\in X_2,\end{array}\right..$ So we have the following theorem.

Theorem 3.2

Let $(X_1,{\rho }_1,T)$ and $(X_2,{\rho }_2,T)$ be KM-fuzzy metric spaces. Then $(X_1\cup X_2,{\rho }_1\cup {\rho }_2,T)$ is a KM-fuzzy metric space, where $X_1\cap X_2=\mathrm{\varnothing }$.

Proof.

Let $x,y,z\in X_1\cup X_2$ and $t\in {\mathbb{R}}^{\ge 0}$. We only prove the triangular inequality property and other cases are immediate.

Let $x,y\in X_1$(for $x,y\in X_2$ is similar), then $T(({\rho }_1\cup {\rho }_2)(x,y,t),({\rho }_1\cup {\rho }_2)(y,z,s))=T({\rho }_1(x,y,t),({\rho }_1\cup {\rho }_2)(y,z,s)).$ If $z\in X_1$, then $\begin{array}{rl}& T(({\rho }_1\cup {\rho }_2)(x,y,t),({\rho }_1\cup {\rho }_2)(y,z,s))=T({\rho }_1(x,y,t),{\rho }_1(y,z,s))\\ & \le T({\rho }_1(x,y,t),{\rho }_1(y,z,s))\le {\rho }_1(x,z,t+s)=({\rho }_1\cup {\rho }_2)(x,z,t+s).\end{array}$ If $z\in X_2$, then $T(({\rho }_1\cup {\rho }_2)(x,y,t),({\rho }_1\cup {\rho }_2)(y,z,s))=T({\rho }_1(x,y,t),ϵ)\le ϵ=({\rho }_1\cup {\rho }_2)(x,z,t+s).$

Let $x\in X_1,y\in X_2$. Then $T(({\rho }_1\cup {\rho }_2)(x,y,t),({\rho }_1\cup {\rho }_2)(y,z,s))=T(ϵ,({\rho }_1\cup {\rho }_2)(y,z,s)).$ If $z\in X_2$, since $x\in X_1$ and $y\in X_2$, we get that $({\rho }_1\cup {\rho }_2)(x,z,t+s)=ϵ$ and so $T(ϵ,({\rho }_1\cup {\rho }_2)(y,z,s))=T(ϵ,{\rho }_2(y,z,s))\le ϵ=({\rho }_1\cup {\rho }_2)(x,z,t+s).$ If $z\in X_1$, since $x\in X_1$ and $y\in X_2$, we get that $({\rho }_1\cup {\rho }_2)(x,z,t+s)\ne ϵ$ and so $T(ϵ,({\rho }_1\cup {\rho }_2)(y,z,s))=T(ϵ,ϵ)\le ϵ\le {\rho }_1(x,z,t+s))=({\rho }_1\cup {\rho }_2)(x,z,t+s).$ It follows that $(X_1\cup X_2,{\rho }_1\cup {\rho }_2,T)$ is a KM-fuzzy metric space.

Corollary 3.3

Let $(X_1,\rho ,T)$ and $(X_2,\rho ,T)$ be KM-fuzzy metric spaces, where $X_1\cap X_2=\mathrm{\varnothing }$. Then $(X_1\cup X_2,\rho ,T)$ is a KM-fuzzy metric space.

Theorem 3.4

Let $(X,\rho ,T)$ be a KM-fuzzy metric space and φ be a bijection on X. Then there exists a fuzzy set ${\rho }^{\prime }:\phi (X{)}^2\times {\mathbb{R}}^{\ge 0}\to [0,1]$ such that $\left(\phi \right(X),{\rho }^{\prime },T)$ is a KM-fuzzy metric space.

Proof.

Let x, y, X and $t\in {\mathbb{R}}^{\ge 0}$. Define ${\rho }^{\prime }:\phi (X{)}^2\times {\mathbb{R}}^{\ge 0}\to [0,1]$ by ${\rho }^{\prime }\left(\phi \right(x),\phi (y),t)=\rho (x,y,t)$. It is clear that $\left(\phi \right(X),{\rho }^{\prime },T)$ is a KM-fuzzy metric space.

4. KM-Fuzzy Metric Hypergraph

In this section, we introduce a novel concept as ((locally)strong, trivial, elementary) KM-fuzzy metric hypergraphs and analyse some of their properties. Also, we investigate the notation of fundamental sequence and generate some type of core hypergraphs in any given KM-fuzzy metric hypergraph.

A fuzzy version of the triangular inequality. The value $M(x,y,t)$ is considered as the degree of nearness from

Definition 4.1

Let $(X,\rho ,T)$ be a KM-fuzzy metric space and $\mathcal{E}=\{{\mu }_i{\}}_{i=1}^n$ be a family of fuzzy subset of X. If there exists $t\in {\mathbb{R}}^{\ge 0}$ $($for t = 0, we call starting time$)$ such that for all $1\le i\le n$ and for all $x,y\in dom\left({\mu }_i\right)$, $T({\mu }_i\left(x\right),{\mu }_i\left(y\right))\le \rho (x,y,t)$, then $H=(X,\rho ,T,\mathcal{E})$ is called a KM-fuzzy metric hypergraph on X and $\mathcal{E}$ is called the KM-fuzzy metric edge set of H. The incidence matrix of a KM-fuzzy metric hypergraph is a matrix $M_G=(a_{ij}{)}_{n\times m}$, with m columns representing the fuzzy hyperedges ${\mu }_1,{\mu }_2,\dots ,{\mu }_m$ and n rows representing the vertices $x_1,x_2,\dots ,x_n$, where $a_{ij}={\mu }_j\left(x_i\right)$ if $x_i\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_j\right)$, $a_{ij}=\mathrm{\infty }$ if $x_i\notin \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_j\right)$ (∞ is a symbol, means that $x_i\notin \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_j\right)$).

Remark 4.2

By Definition 2.2, in any fuzzy hypergraph $\mathcal{H}=(X,\mathcal{E})$, since $X=\bigcup _{\mu \in \mathcal{E}}\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left(\mu \right)$, for all $\mu \in \mathcal{E}$ and $x\in X$, we get that $\mu \left(x\right)\ne 0$. But in given a KM-fuzzy metric hypergraph $H=(X,\rho ,T,\mathcal{E})$, may there exist $\mu \in \mathcal{E}$ and $x\in X$ in such a way that $\mu \left(x\right)=0$.

Proposition 4.3

Let $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph on X. Then for all $1\le i\le n$ and for all $x,y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right),$ in starting time we have ${\mu }_i\left(x\right)=0$ or ${\mu }_i\left(y\right)=0$.

Proof.

Let $1\le i\le n$ and $x,y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$. Since $H=(X,\rho ,T,\mathcal{E})$ is a KM-fuzzy metric hypergraph on X, we get that $T({\mu }_i\left(x\right),{\mu }_i\left(y\right))\le \rho (x,y,0)$. Hence $T({\mu }_i\left(x\right),{\mu }_i\left(y\right))=0$ and so ${\mu }_i\left(x\right)=0$ or ${\mu }_i\left(y\right)=0$.

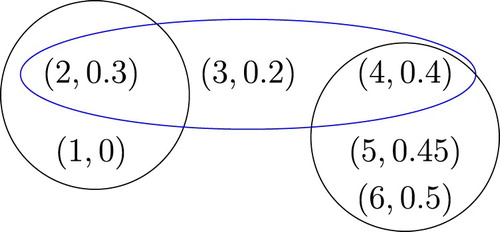
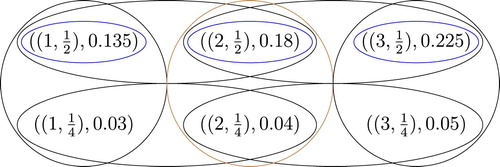
Example 4.4

Let $X=\{1,2,3,4,5,6\}$ and $x,y\in X$. For all $x,y\in X,$ define $\rho (x,y,0)=0$ and $\rho (x,y,t>0)=\frac{min\{x,y\}+t}{max\{x,y\}+t}$. Thus $H=(X,\rho ,T_{min},\mathcal{E})$ is a KM-fuzzy metric hypergraph with t = 1 (it is not a fuzzy hypergraph) in Figure 1. For simplify, we compute ${\eta }_2$ in Table 1. Since $\mathrm{d}\mathrm{o}\mathrm{m}\left({\eta }_2\right)=\{2,3,4\}$ and ${\eta }_2\left(2\right)=0.3,{\eta }_2\left(3\right)=0.2,{\eta }_2\left(4\right)=0.4$, we get ${\eta }_2=\left\{\right(2,0.3),(3,0.2),(4,0.4),(1,\mathrm{\infty }),(5,\mathrm{\infty }),(6,\mathrm{\infty }\left)\right\}$.

Figure 1. KM-fuzzy metric hypergraph $H=(X,\rho ,T_{min},\mathcal{E})$ for t = 1.

Theorem 4.5

Let $(X,\rho ,T)$ be a KM-fuzzy metric space and $\mathcal{E}=\{{\mu }_i{\}}_{i=1}^n$ be a family of fuzzy subset of X and $t\in {\mathbb{R}}^{\ge 0}$.

1. If for all $1\le i\le n,|\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)|=1,$ then $H=(X,\rho ,T,\mathcal{E})$ is a KM-fuzzy metric hypergraph on X.

2. If for all $1\le i\le n$ and for all $x,y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right),$ we have ${\mu }_i\left(x\right)\le \rho (x,y,t),$ then $H=(X,\rho ,T,\mathcal{E})$ is a KM-fuzzy metric hypergraph on X.

Table 1. The corresponding incidence matrix of Figure 1.

$x_i$	${\mu }_1$	${\mu }_2$	${\mu }_3$
1	0	∞	∞
2	0.3	0.3	∞
3	∞	0.2	∞
4	∞	0.4	0.4
5	∞	∞	0.45
6	∞	∞	0.5

Proof.

(i) Let $t\in {\mathbb{R}}^{\ge 0}$. Since for all $1\le i\le n,|\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)|=1$, we get that there exists $x_i\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$ such that ${\mu }_i\left(x_i\right)\ne 0$ and for all $y_i\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)\setminus \left\{x_i\right\}$ we have ${\mu }_i\left(y_i\right)=0$. Let $1\le j\le n$ be an arbitrary and fixed. Then for all $y_j\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_j\right),T\left({\mu }_j\right(x_j),{\mu }_j(y_j\left)\right)=0\le \rho (x_j,y_j,t)$ and $T\left({\mu }_j\right(x_j),{\mu }_j(x_j\left)\right)=1\le \rho (x_j,x_j,t)$. It follows that $H=(X,\rho ,T,\mathcal{E})$ is a KM-fuzzy metric hypergraph on X.

(ii) Let $t\in {\mathbb{R}}^{\ge 0}$ and for all $1\le i\le n$ and for all $x,y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right),$ clearly $T\left({\mu }_i\right(x),{\mu }_i(y\left)\right)\le T_{min}\left({\mu }_i\right(x),{\mu }_i(y\left)\right)$. Because for all $1\le i\le n$ and for all $x,y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right),$ we have ${\mu }_i\left(x\right)\le \rho (x,y,t)$, so ${\mu }_i\left(x\right)\le \rho (x,y,t)$ implies $T\left({\mu }_i\right(x),{\mu }_i(y\left)\right)\le T_{min}\left({\mu }_i\right(x),{\mu }_i(y\left)\right)\le \rho (x,y,t)$. Thus $H=(X,\rho ,T,\mathcal{E})$ is a KM-fuzzy metric hypergraph on X.

A KM-fuzzy metric hypergraph which is satisfied in condition $\left(i\right)$ of Theorem 4.5, will call an elementary KM-fuzzy metric hypergraph.

Definition 4.6

Let $(X,\rho ,T)$ be a KM-fuzzy metric space and $\mathcal{E}=\{{\mu }_i{\}}_{i=1}^n$ be a family of fuzzy subset of X. If there exists $t\in {\mathbb{R}}^{\ge 0}$ (for t = 0, we call starting time) such that for all $1\le i\le n$ and for all $x,y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$, if $T({\mu }_i\left(x\right),{\mu }_i\left(y\right))=\rho (x,y,t)$, then $H=(X,\rho ,T,\mathcal{E})$ is called a strong KM-fuzzy metric hypergraph on X and $\mathcal{E}$ is called the KM-fuzzy metric edge set of H. In strong KM-fuzzy metric hypergraph $H=(X,\rho ,T,\mathcal{E})$, for all $1\le i\le n,$ if $|{\mu }_i|=1$, then x can be equal to y, so ${\mu }_i\left(x\right)={\mu }_i\left(x\right)=1$. If there exists ${\mu }_i\in \mathcal{E}$ and $x,y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$ in such a way that $T({\mu }_i\left(x\right),{\mu }_i\left(y\right))=\rho (x,y,t)$, we say that $H=(X,\rho ,T,\mathcal{E})$ is a locally strong KM-fuzzy metric hypergraph.

Theorem 4.7

Let X be a KM-fuzzy metric space, $\mathcal{E}=\{{\mu }_i{\}}_{i=1}^n$ be a family of fuzzy subsets of X and $T\in {\mathcal{C}}_T$. Then there exists a KM-fuzzy metric ρ on X such that $H=(X,\rho ,T,\mathcal{E})$ is a strong KM-fuzzy metric hypergraph on X.

Proof.

Let $1\le i\le n$ and $x,y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$. Define $\rho (x,y,0)=0$ and $\rho (x,y,t>0)=\left\{\begin{array}{ll}T\left({\mu }_i\right(x),{\mu }_i(y\left)\right)& \text{if}x\ne y,\\ 1& \text{otherwise.}\end{array}\right.$ One can see that in non starting time, $H=(X,\rho ,T,\mathcal{E})$ is a strong KM-fuzzy metric hypergraph on X.

In the following, for given any non-empty set one can construct a KM-fuzzy metric space and so a KM-fuzzy metric hypergraph.

Corollary 4.8

Let X be a non-empty set, $\mathcal{E}=\{{\mu }_i{\}}_{i=1}^n$ be a family of fuzzy subset of X and $T\in {\mathcal{C}}_T$. Then there exists a fuzzy subset $\rho :X^2\times {\mathbb{R}}^{\ge 0}⟶[0,1],$ such that $(X,\rho ,T)$ is a KM-fuzzy metric space and $H=(X,\rho ,T,\mathcal{E})$ is a KM-fuzzy metric hypergraph on X.

Definition 4.9

Let $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph. If for all $1\le i\le n,\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)=\mathrm{\varnothing }$, then $H=(X,\rho ,T,\mathcal{E})$ is called a trivial KM-fuzzy metric hypergraph.

Corollary 4.10

Let $H=(X,\rho ,T,\mathcal{E})$ be a trivial KM-fuzzy metric hypergraph and $M_G=(a_{ij}{)}_{n\times m}$ be the incidence matrix of H. Then for all $1\le i\le n$ and $1\le j\le m,$ we have $a_{ij}=0$ or $a_{ij}=\mathrm{\infty }$.

Let $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph on X and $\alpha \in [0,1]$, where $\mathcal{E}=\{{\mu }_i{\}}_{i=1}^n$. Consider ${\alpha }_{min}=\underset{i=1}{\overset{n}{\bigwedge }}\left(\underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)}{\bigwedge }{\mu }_i\right(x\left)\right)$ and ${\mathcal{E}}^{\alpha }=\{{\mu }_i^{\alpha }{\}}_{i=1}^n$, where ${\mu }_i^{\alpha }=\left\{x|{\mu }_i\right(x)\ge \alpha \}$.

In the following, we extract hypergraphs from KM-fuzzy metric hypergraphs and α-level subsets.

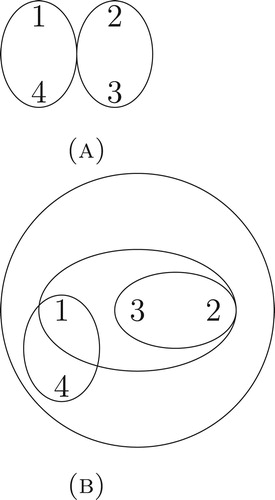
Theorem 4.11

Let in non starting time, $(X,\rho ,T)$ be a KM-fuzzy metric space and $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph on X.

1. For all $0\ne \alpha \le {\alpha }_{min},$ $H^{\prime }=(\bigcup {\mathcal{E}}^{\alpha },{\mathcal{E}}^{\alpha })$ is a hypergraph.

2. If $H=(X,\rho ,T,\mathcal{E})$ is a trivial KM-fuzzy metric hypergraph, then for all $\alpha \in [0,1],$ $H^{\alpha }=(X,{\mathcal{E}}^{\alpha })$ is a hypergraph.

3. If $H=(X,\rho ,T,\mathcal{E})$ is a strong KM-fuzzy metric hypergraph, then for all $\alpha \le {\alpha }_{min},$ $H^{\alpha }=(X,{\mathcal{E}}^{\alpha })$ is a hypergraph.

4. If for all $i\in {\mathbb{N}}_k$, ${\mu }_i\subseteq {\mu }_{i+1}$, and $|\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)|=|\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)|,$ then for all $\alpha \le {\alpha }_{min},H^{\alpha }=(X,{\mathcal{E}}^{\alpha })$ is a hypergraph.

5. If $H^{\alpha }=(X,{\mathcal{E}}^{\alpha })$ is a hypergraph and $\alpha \le \text{β},$ then $H^{\text{β}}\subseteq H^{\alpha }$.

Proof.

(i) We show that $\mathcal{E}\ne \mathrm{\varnothing }$. Since $(X,\rho ,T,\mathcal{E})$ is a non-trivial KM-fuzzy metric hypergraph, there exists $1\le i\le n$ such that $supp\left({\mu }_i\right)\ne \mathrm{\varnothing }$. Then for all $0\ne \alpha \le {\alpha }_{min}$, ${\mu }_i^{\alpha }\ne \mathrm{\varnothing }$ and so ${\mathcal{E}}^{\alpha }\ne \mathrm{\varnothing }$.

(ii) Since for all $1\le i\le n$, $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)=\mathrm{\varnothing }$, it is seen that $\alpha =0$. Thus $\bigcup _{i=1}^n{\mu }_i^{\alpha }=X$ and so $H=(X,{\mathcal{E}}^{\alpha })$ is a hypergraph.

(iii) Since in non starting time, $(X,\rho ,T,\mathcal{E})$ is a strong KM-fuzzy metric hypergraph, for all $1\le i\le n$ and $x,y\in supp\left({\mu }_i\right)$, we obtain that $\rho (x,y,t)\ne 0$. Hence ${\mu }_i\left(x\right)\wedge {\mu }_i\left(y\right)=\rho (x,y,t)$ implies that ${\mu }_i\left(x\right)\ne 0$ and ${\mu }_i\left(y\right)\ne 0$. It follows that for all $\alpha \le {\alpha }_{min}$, $\bigcup {\mathcal{E}}^{\alpha }=X$ and so $H=(X,{\mathcal{E}}^{\alpha })$ is a hypergraph.

(iv) Let $x\in X$. Then for all $1\le i\le n$ we conclude that ${\mu }_i\left(x\right)\ge \alpha$. Since for all $1\le i\le n,{\mu }_i\left(x\right)\le {\mu }_{i+1}\left(x\right)$, we get that $x\in {\mathcal{E}}^{\alpha }$. ${\mu }_1^{\alpha }=\{x_1,x_2\}$. So we get $x_1,x_2,\dots ,x_n$ such that ${\mu }_n^{\alpha }=\{x_1,x_2,\dots ,x_n\}=X$. It follows that for all $\alpha \le {\alpha }_{min},H^{\alpha }=(X,{\mathcal{E}}^{\alpha })$ is a hypergraph.

(v) Let $x\in H^{\text{β}}=(X,\{{\mu }_i^{\text{β}}{\}}_{i=1}^n)$. Then there is $1\le i\le n$ such that $x\in {\mu }_i^{\text{β}}$ and so ${\mu }_i\left(x\right)\ge \text{β}\ge \alpha$. It follows that $x\in {\mu }_i^{\alpha }$ and so $x\in H^{\alpha }=(X,\{{\mu }_i^{\alpha }{\}}_{i=1}^n)$.

Theorem 4.12

Let $(X,\rho ,T_{min},\mathcal{E})$ be a KM-fuzzy metric hypergraph. Then

1. if $\bigcup _{i=1}^n\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)=\bigcup _{i=1}^n\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right),$ then $(X,\mathcal{E})$ is a fuzzy hypergraph,

2. $H^{\mathrm{\prime }}=(\bigcup _{i=1}^n{\mu }_i^{{\alpha }_i},\{{\mu }_i^{{\alpha }_i}{\}}_{i=1}^n)$ is a loop $($joint$)$ hypergraph, where ${\alpha }_i=h\left({\mu }_i\right)$ is height of ${\mu }_i$.

Proof.

(i) It is clear by definition.

(ii) Since ${\alpha }_i=h\left({\mu }_i\right)$, for all $1\le i\le n$ we get that $|{\mu }_i^{{\alpha }_i}|=1$ and so $H^{\mathrm{\prime }}=(\bigcup _{i=1}^n{\mu }_i^{{\alpha }_i},\{{\mu }_i^{{\alpha }_i}{\}}_{i=1}^n)$ is a loop (joint) hypergraph.

Theorem 4.13

Let $H=(X,\rho ,T,\mathcal{E})$ be a strong KM-fuzzy metric hypergraph. Then in non starting time $(X,\mathcal{E})$ is a fuzzy hypergraph.

Proof.

Since $(X,\rho ,T,\mathcal{E})$ is a strong KM-fuzzy metric hypergraph, we get that for all $1\le i\le n$, $T\left({\mu }_i\right(x),{\mu }_i(y\left)\right)=\rho (x,y,t)$. Because t is not in starting time, then $\rho (x,y,t)\ne 0$ and so $T\left({\mu }_i\right(x),{\mu }_i(y\left)\right)\ne 0$. It follows that for all $1\le i\le n$, ${\mu }_i\not\equiv 0$ and so $(X,\mathcal{E})$ is a fuzzy hypergraph.

In what follows, we can generate KM-fuzzy metric hypergraphs from fuzzy hypergraphs.

Theorem 4.14

Let $H=(X,\mathcal{E})$ be a fuzzy hypergraph. Then there exists a fuzzy subset $\rho :X^2\times {\mathbb{R}}^{\ge 0}⟶[0,1]$ such that in each non starting time, $(X,\rho ,T_{min},\mathcal{E})$ is a KM-fuzzy metric hypergraph.

Proof.

Let $x,y\in X$. Since $H=(X,\mathcal{E})$ is a fuzzy hypergraph, there exists ${\mu }_i,{\mu }_j\in \mathcal{E}$ in such a way that $x\in supp\left({\mu }_i\right),y\in supp\left({\mu }_j\right)$. For all $x,y\in X$, define $\rho (x,y,0)=0$ and $\rho (x,y,t)=\left\{\begin{array}{ll}\frac{min\left\{{\mu }_i\right(x),{\mu }_i(y\left)\right\}+t}{max\left\{{\mu }_i\right(x),{\mu }_i(y\left)\right\}+t}& \text{if {}x,y\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\text{},}\\ h\left(H\right)& \text{otherwise.}\end{array}\right.$ where $h\left(H\right)=\underset{\mu \in \mathcal{E}}{\bigvee }h\left(\mu \right)$. One can see that each non starting time, $H=(X,\rho ,T_{min},\mathcal{E})$ is a KM-fuzzy metric hypergraph.

Corollary 4.15

Let X be a non-empty set and $T\in {\mathcal{C}}_T$. Then there exists a fuzzy subset $\rho :X^2\times {\mathbb{R}}^{\ge 0}⟶[0,1],$ such that $(X,\rho ,T)$ is a KM-fuzzy metric space.

Proof.

Firstly we construct a fuzzy hypergraph $H=(X,\mathcal{E})$. Then by Theorem 4.14, there is a fuzzy subset $\rho :X^2\times {\mathbb{R}}^{\ge 0}⟶[0,1]$ such that $(X,\rho ,T)$ is a KM-fuzzy metric space.

Theorem 4.16

Let in non starting time, $H=(X,\rho ,T,\mathcal{E})$ be an elementary KM-fuzzy metric hypergraph. Then $H^{\alpha }=(X,{\mathcal{E}}^{\alpha })$ is an elementary hypergraph.

Proof.

Let $\mu \in \mathcal{E}$. Then $|supp\left(\mu \right)|=1$ and so $|{\mu }^{\alpha }|=1$. By Theorem 4.11, $H^{\alpha }=(X,{\mathcal{E}}^{\alpha })$ is elementary hypergraph.

Definition 4.17

Let $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph and $0<t<{\alpha }_1=h\left(H\right)$. The sequence of real numbers ${\alpha }_1>{\alpha }_2>\cdots >{\alpha }_n>0$ is called a fundamental sequence, if (i), ${\alpha }_{i+1}\le \text{β}\le {\alpha }_i$, implies that ${\mathcal{E}}^{\text{β}}={\mathcal{E}}^{{\alpha }_i}$ and (ii), ${\mathcal{E}}^{{\alpha }_i}\subseteq {\mathcal{E}}^{{\alpha }_{i+1}}$. Also $\mathcal{F}\left(H\right)=\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\}$ and $Cor\left(H\right)=\{H^{{\alpha }_1},H^{{\alpha }_2},\dots ,H^{{\alpha }_n}\}$ is called the set of core hypergraphs H.

Example 4.18

Let $X=\{1,2,3,4\}$ and $x,y\in X$. For all $x,y\in X,$ define $\rho (x,y,0)=0$ and $\rho (x,y,t>0)=\frac{min\{x,y\}+t}{max\{x,y\}+t}$. Thus for t = 1, $H=(X,\rho ,T_{pr},\mathcal{E})$ is a KM-fuzzy metric hypergraph in Table 2.

Table 2. KM-fuzzy metric hypergraph $H=(X,\rho ,T,\mathcal{E})$.

$x_i$	${\mu }_1$	${\mu }_2$	${\mu }_3$	${\mu }_4$
1	0.05	0.08	0	0.03
2	∞	0.05	0.08	0.03
3	∞	0.05	0.08	0.03
4	0.05	0.08	0	∞

Computations show that ${\mathcal{E}}^{0.08}=\left\{\right\{1,4\},\{2,3\left\}\right\}={\mathcal{E}}^{0.05}$, ${\mathcal{E}}^{0.03}=\left\{\right\{1,4\},\{2,3\},\{1,2,3\},\{1,2,3,4\left\}\right\}$ and ${\mathcal{E}}^{0.03}\ne {\mathcal{E}}^{0.08}$. In addition, if $0.03<\text{β}\le 0.08$, then ${\mathcal{E}}^{\text{β}}={\mathcal{E}}^{0.08}$ and $0<\text{β}\le 0.03$ implies that ${\mathcal{E}}^{\text{β}}={\mathcal{E}}^{0.03}$. Thus $\mathcal{F}\left(H\right)=\{{\alpha }_1=0.08,{\alpha }_2=0.03\}$ and $Cor\left(H\right)=\{H^{{\alpha }_1},H^{{\alpha }_2}\}$, where $H^{{\alpha }_1}$ and $H^{{\alpha }_1}$ are in Figure 2.

Definition 4.19

Let $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph and C be a class of hypergraphs on X. Then $\mathrm{C}\mathrm{o}\mathrm{r}\left(H\right)$ is a C-accessible hypergraph or say C is a $\mathrm{C}\mathrm{o}\mathrm{r}\left(H\right)$-derivable or $\mathrm{C}\mathrm{o}\mathrm{r}$-able hypergraph, if $\mathrm{C}\mathrm{o}\mathrm{r}\left(H\right)\cap C\ne \mathrm{\varnothing }$.

Figure 2. $\mathrm{C}\mathrm{o}\mathrm{r}\left(H\right)$. (a) Hypergraph $H^{{\alpha }_1}$. (b) Hypergraph $H^{{\alpha }_2}$.

Theorem 4.20

Let $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph with incidence matrix $M=\left(m_{ij}\right)$ and $\mathcal{E}=\{{\mu }_i{\}}_{i=1}^n$. If for all $1\le i\le |X|$ and $1\le j\le |X|,m_{ij}=c_i\in ]0,1],$ then

1. $\mathcal{F}\left(H\right)=\{c_1,c_2,\dots ,c_{|X|}\};$

2. $\mathrm{C}\mathrm{o}\mathrm{r}\left(H\right)=\left\{\right\{(X,X)\left\}\right\}.$

Proof.

(i, ii) Let $X=\{x_1,x_2,\dots ,x_m\}$. Because for all $1\le i\le |X|$ and $1\le j\le n,m_{ij}=c_i\in ]0,1]$, there exists $1\le k\le |X|$ in such a way that $=h\left(H\right)=c_k$. But $\left(\right]0,1],\le )$ is a chain, so we can rearrange $c_1>c_2>\cdots >c_{|X|}.$ In addition for all $1\le i\le |X|,{\mathcal{E}}^{c_i}=\{x_1,x_2,\dots ,x_i\}$ and for all $c_{i+1}\le \text{β}\le c_i,$ we get that ${\mathcal{E}}^{\text{β}}={\mathcal{E}}^{c_i}$. It is clear that $\mathrm{C}\mathrm{o}\mathrm{r}\left(H\right)=\left\{\right\{(X,X)\left\}\right\}.$

Theorem 4.21

Let $H=(X,\rho ,T,\mathcal{E})$ be a strong elementary KM-fuzzy metric hypergraph. Then

1. $h\left(H\right)=1;$

2. $\mathcal{F}\left(H\right)=\left\{h\right(H\left)\right\};$

3. $\mathrm{C}\mathrm{o}\mathrm{r}\left(H\right)=\left\{\right\{(X,\{x\left\}\right)\}|x\in X\}.$

Proof.

(i, ii, iii) Since $H=(X,\rho ,T,\mathcal{E})$ is a strong elementary KM-fuzzy metric hypergraph, for all ${\mu }_i\in \mathcal{E}$ and $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right),{\mu }_i\left(x\right)=1$ so by Theorem 4.20, the proof is completed.

Corollary 4.22

Let X be a non-empty set. Then any elementary hypergraph on X is a $\mathrm{C}\mathrm{o}\mathrm{r}$-able hypergraph.

Theorem 4.23

Let X be a non-empty set. Then any joint complete hypergraph on X is a $\mathrm{C}\mathrm{o}\mathrm{r}$-able hypergraph.

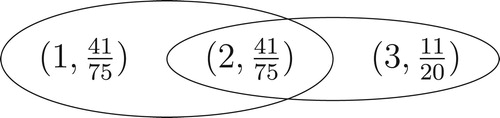
Proof.

Let $X=\{x_1,x_2,\dots ,x_n\}$ and $T\in {\mathcal{C}}_T$. By Corollary 4.8, define a fuzzy hypergraph $H=(X,\rho ,T,\mathcal{E})$ by incidence matrix $M=\left(m_{ij}\right)$, where $m_{ij}=c\in ]0,1]$, if $i\ge j$ and $m_{ij}=\mathrm{\infty }$, if i<j. Thus $\mathcal{F}\left(H\right)=\left\{c\right\}$ and so $H^c=\left\{\right\{x_1\},\{x_1,x_2\},\{x_1,x_2,x_3\},\dots ,\{x_1,x_2,\dots ,x_n\left\}\right\}$. It follows that $\mathrm{C}\mathrm{o}\mathrm{r}\left(H\right)\cap C\ne \mathrm{\varnothing }$, where C is class of joint complete hypergraphs on X.

A hypergraph $H=(G,\{E_i{\}}_{i=1}^n)$ is called a discrete complete hypergraph, if for any $1\le i\ne j\le n,|E_i|=|E_j|$ and $E_i\cap E_j=\mathrm{\varnothing }$. Let $H=(X,\{E_i{\}}_{i=1}^k)$ be a discrete complete hypergraph, $m\in \mathbb{N}$ and $1\le j,j^{\prime }\le k.$ Denote the set of all discrete complete hypergraphs with $|E_j|=|E_{j^{\prime }}|=m$ on H (m–hyperedges), by ${\mathcal{D}}_c^{\left(m\right)}\left(H\right)$ and the set of all discrete complete hypergraphs on H, by ${\mathcal{D}}_c\left(H\right)$.

Theorem 4.24

Let X be a non-empty set. Then any discrete complete hypergraph on X is a $\mathrm{C}\mathrm{o}\mathrm{r}$-able hypergraph.

Proof.

Let $X=\{x_1,x_2,\dots ,x_n\}$ and $T\in {\mathcal{C}}_T$. By Corollary 4.8, define a fuzzy hypergraph $H=(X,\rho ,T,\mathcal{E})$ by incidence matrix $M=\left(m_{ij}\right)$, where $m_{ji}=m_{(j+1)i}=m_{(j+2)i}=\cdots =m_{\left(ik\right)i}=c\in ]0,1]$, $k=\frac{n}{m},(j,i)\in \left\{\right(1,1),(k+1,2),(2k+1,3),\dots ,((m-1)k+1,m\left)\right\}$ and $m_{ij}=\mathrm{\infty }$, for other cases. Thus $\mathcal{F}\left(H\right)=\left\{c\right\}$ and so $H^c=\left\{\right\{x_1,x_2,\dots ,x_m\}$, $\{x_{m+1},x_{m+2},\dots x_{2m}\},\dots ,\{x_{(k-1)m+1},x_{(k-1)m+2},\dots x_n\}\}$. It follows that $Cor\left(H\right)\cap {\mathcal{D}}_c^{\left(m\right)}\left(H\right)\ne \mathrm{\varnothing }$, where ${\mathcal{D}}_c^{\left(m\right)}\left(H\right)$ is class of discrete complete hypergraphs on X.

5. Operation on KM-Fuzzy Metric Hypergraphs

F. Harary [27] and L. Maninska [28], introduced and presented some of type of product on hypergraphs and get new hypergraphs. In this section, we will define some products on KM-fuzzy metric hypergraphs and via these productions, get new KM-fuzzy metric hypergraphs. From now on, we consider $H_1=(X_1,{\rho }_1,T,{\mathcal{E}}_1)$, $H_2=(X_2,{\rho }_2,T,{\mathcal{E}}_2)$ as KM-fuzzy metric hypergraphs on sets $X_1$ and $X_2$, respectively.

Remember that for fuzzy subsets μ and ${\mu }^{\prime }$ on X and $X^{\prime }$, square product of fuzzy subset $\mu \bullet {\mu }^{\prime }:\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right)\times \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)\to [0,1]$ by $(\mu \bullet {\mu }^{\prime })\left(\right(x,y\left)\right)=T_{min}\left(\mu \right(x),{\mu }^{\prime }(y\left)\right)$ [24].

Definition 5.1

Let $H_1$, $H_2$ be KM-fuzzy metric hypergraphs on sets $X_1$ and $X_2$, respectively. Define square product of KM-fuzzy metric hypergraphs by $H_1\bullet H_2=(X_1\times X_2,{\rho }^{T_{min}},T,{\mathcal{E}}_1\bullet {\mathcal{E}}_2)$, where ${\mathcal{E}}_1\bullet {\mathcal{E}}_2=\{\mu \bullet {\mu }^{\prime }|\mu \in {\mathcal{E}}_1,{\mu }^{\prime }\in {\mathcal{E}}_2\}$ and $\mu \bullet {\mu }^{\prime }=\left\{(\right(x,y),T_{min}(\mu \left(x\right),{\mu }^{\prime }\left(y\right)))|x\in \mathrm{d}\mathrm{o}\mathrm{m}(\mu ),y\in \mathrm{d}\mathrm{o}\mathrm{m}({\mu }^{\prime }\left)\right\}$.

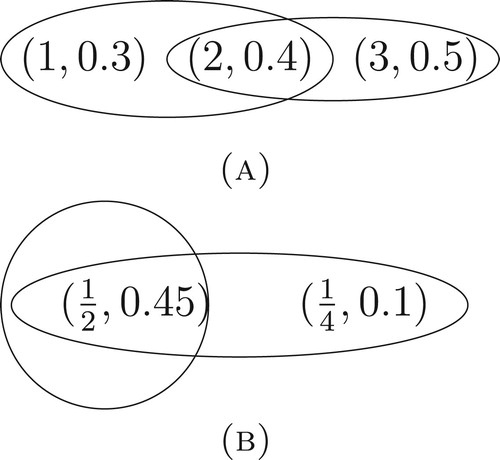
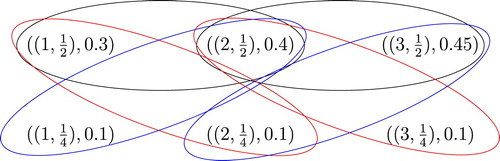
Example 5.2

Let $X_1=\{1,2,3\}$ and $X_2=\{\frac{1}{2},\frac{1}{4}\}$. For all $x,y\in X_1,$ define ${\rho }_1(x,y,0)=0$, ${\rho }_1(x,y,t>0)=\frac{min\{x,y\}+t}{max\{x,y\}+t}$, for all $x,y\in X_2,$ ${\rho }_2(x,y,0)=0$ and ${\rho }_2(x,y,t>0)=\frac{t}{d_1(x,y)+t}$. Thus $H_1=(X_1,{\rho }_1,T_{pr},{\mathcal{E}}_1)$ and $H_2=(X_2,{\rho }_2,T_{pr},{\mathcal{E}}_2)$ are KM-fuzzy metric hypergraphs for $t_1=1$ and $t_2=2$, respectively as Figure 3. Thus we obtain the square product of KM-fuzzy metric hypergraph in Figure 4.

Figure 3. KM-fuzzy metric hypergraph $H_1,H_2$. (a) $H_1=(X_1,\rho ,T_{pr},{\mathcal{E}}_1)$. (b) $H_2=(X_2,\rho ,T_{pr},{\mathcal{E}}_2)$.

For instance, we have $\begin{array}{rl}{\mu }_1\bullet {\mu }_1^{\prime }& =\left\{\right(1,0.3),(2,0.4\left)\right\}\bullet \left\{\right(\frac{1}{2},0.45\left)\right\}=\left\{\right((1,\frac{1}{2}),min(0.45,0.3),\left(\right(2,\frac{1}{2}),min(0.45,0.4\left)\right\}\\ & =\left\{\right((1,\frac{1}{2}),0.3),((2,\frac{1}{2}),,0.4\left)\right\}.\end{array}$

Figure 4. KM-fuzzy metric hypergraph $H_1\bullet H_2=(X_1\times X_2,{\rho }^{T_{min}},T_{pr},{\mathcal{E}}_1\bullet {\mathcal{E}}_2$) for t = 2.

Theorem 5.3

Let $H_1$ and $H_2$ be KM-fuzzy metric hypergraphs on $X_1,$ $X_2,$ respectively. Then

1. For all $1\le i\le n,1\le j\le n^{\prime },$ ${\mu }_i\in {\mathcal{E}}_1$ and ${\mu }_j^{\prime }\in {\mathcal{E}}_2,$ we have $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}({\mu }_i\bullet {\mu }_i^{\mathrm{\prime }})=\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\times \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i^{\mathrm{\prime }}\right)$.

2. $H_1\bullet H_2=(X_1\times X_2,{\rho }^{T_{min}},T_{min},{\mathcal{E}}_1\bullet {\mathcal{E}}_2)$ is a KM-fuzzy metric hypergraph on $X_1\times X_2$.

Proof.

(i) Let $(x,y)\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}({\mu }_i\bullet {\mu }_j^{\prime })$. Then $({\mu }_i\bullet {\mu }_j^{\prime })(x,y)>0$, so ${\mu }_i\left(x\right)>0$ and ${\mu }_j^{\prime }\left(y\right)>0$. Hence $x\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)$ and $y\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_j^{\prime }\right)$ and so $(x,y)\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\times \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_j^{\prime }\right)$. The conversely is similar to.

(ii) For all $1\le i\le n,1\le j\le n^{\prime }$ and for all $(x_1,y_1),(x_2,y_2)\in \mathrm{d}\mathrm{o}\mathrm{m}({\mu }_i\bullet {\mu }_j^{\prime })$, since $H_1$ is a KM-fuzzy metric hypergraphs on $X_1$ and $H_2$ is a KM-fuzzy metric hypergraphs on $X_2$, for some $t_1,t_2\in {\mathbb{R}}^{\ge 0}$, take $t=max\{t_1,t_2\}$ so by Theorem 2.5, we get that $\begin{array}{rl}& T(({\mu }_i\bullet {\mu }_j^{\prime })(x_1,y_1),({\mu }_i\bullet {\mu }_j^{\prime })(x_2,y_2))=T(\left({\mu }_i\right(x_1)\wedge {\mu }_j^{\prime }(y_1\left)\right),\left({\mu }_i\right(x_2)\wedge {\mu }_j^{\prime }(y_2))\\ & \le T({\mu }_i\left(x_1\right),{\mu }_i\left(x_2\right))\le {\rho }_1(x_1,x_2,t)\text{and}\\ & T(({\mu }_i\bullet {\mu }_j^{\prime })(x_1,y_1),({\mu }_i\bullet {\mu }_j^{\prime })(x_2,y_2))=T(\left({\mu }_i\right(x_1)\wedge {\mu }_j^{\prime }(y_1\left)\right),\left({\mu }_i\right(x_2)\wedge {\mu }_j^{\prime }(y_2))\\ & \le T({\mu }_j^{\prime }\left(y_1\right),{\mu }_j^{\prime }\left(y_2\right))\le {\rho }_2(y_1,y_2,t)\text{so}\\ & T(({\mu }_i\bullet {\mu }_j^{\prime })(x_1,y_1),({\mu }_i\bullet {\mu }_j^{\prime })(x_2,y_2))\le {\rho }_1(x_1,x_2,t)\wedge {\rho }_1(y_1,y_2,t)={\rho }^{T_{min}}((x_1,y_1),(x_2,y_2),t).\end{array}$ Thus $H_1\bullet H_2=(X_1\times X_2,{\rho }^{T_{min}},T_{min},{\mathcal{E}}_1\bullet {\mathcal{E}}_2)$ is a KM-fuzzy metric hypergraph on $X_1\times X_2$.

Definition 5.4

Let $H_1$, $H_2$ be KM-fuzzy metric hypergraphs on sets $X_1$ and $X_2$, respectively. Define Cartesian product of KM-fuzzy metric hypergraphs by $H_1\otimes H_2=(X_1\times X_2,{\rho }^{T_{min}},T,{\mathcal{E}}_1\otimes {\mathcal{E}}_2)$, where ${\mathcal{E}}_1\otimes {\mathcal{E}}_2=\{\mu \otimes {\mu }^{\prime }|\mu \in {\mathcal{E}}_1,{\mu }^{\prime }\in {\mathcal{E}}_2\}$ and the Cartesian product of fuzzy subsets $\mu \otimes {\mu }^{\prime }:\left\{x\right\}\times \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right),\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right)\times \left\{y\right\}\to [0,1]$ are defined by $\mu \otimes {\mu }^{\prime }=\left\{(\right(x,y),T_{pr}(\mu \left(x\right),{\mu }^{\prime }\left(y\right)))|y\in \mathrm{d}\mathrm{o}\mathrm{m}({\mu }^{\prime }),((x,y),T_{pr}(\mu \left(x\right),{\mu }^{\prime }\left(y\right)))|x\in \mathrm{d}\mathrm{o}\mathrm{m}(\mu \left)\right\}$. Indeed,

$\left\{(\right(x_1,y_1),\eta (x_1,y_1\left)\right)),\dots ,((x_k,y_k),\eta (x_k,y_k)\left))\right\}\in {\mathcal{E}}_1\otimes {\mathcal{E}}_2\iff \mathrm{\exists }\mu \in {\mathcal{E}}_1,\mathrm{\exists }{\mu }^{\prime }\in {\mathcal{E}}_2$ such that for all $1\le i\le k,\eta (x_i,y_i)=T_{pr}\left(\mu \right(x_i),{\mu }^{\prime }(y_i\left)\right)$ and

(i) for $\mu \in {\mathcal{E}}_1,\{x_1,x_2,\dots ,x_k\}=\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right)$ and $y_1=y_2=\cdots =y_k$ or

(ii) for ${\mu }^{\prime }\in {\mathcal{E}}_2,\{y_1,y_2,\dots ,y_k\}=\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)$ and $x_1=x_2=\cdots =x_k$.

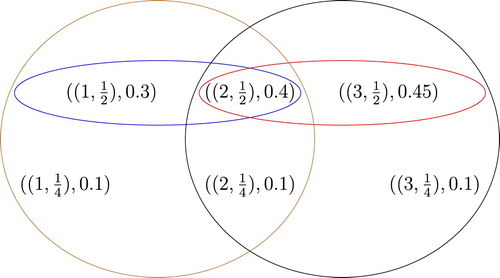
Example 5.5

Consider the fuzzy hypergraphs $H_1,H_2$ in Example 5.2. Thus we obtain the square product of KM-fuzzy metric hypergraph for t = 2, in Table 3 and Figure 5. For instance, we compute ${\eta }_1$ and ${\eta }_{10}$. We have ${\mu }_1=\left\{\right(1,0.3),(2,0.4\left)\right\},{\mu }_2=\left\{\right(3,0.5),(2,0.4\left)\right\},{\mu }_1^{\prime }=\left\{\right(\frac{1}{2},0.45\left)\right\},{\mu }_2^{\prime }=\left\{\right(\frac{1}{2},0.45),(\frac{1}{4},0.1\left)\right\}$. By definition $\begin{array}{rl}{\eta }_1& =\left\{\right((1,\frac{1}{2}),0.45\times 0.3),((1,\frac{1}{4}),0.1\times 0.3\left)\right\}=\left\{\right((1,\frac{1}{2}),0.135),((1,\frac{1}{4}),0.03\left)\right\},\\ {\eta }_{10}& =\left\{\right((3,\frac{1}{2}),0.45\times 0.5\left)\right\}=\left\{\right((1,\frac{1}{2}),0.225\left)\right\}.\end{array}$

Figure 5. KM-fuzzy metric hypergraph $H_1\otimes H_2=(X_1\times X_2,{\rho }^{T_{min}},T_{pr},{\mathcal{E}}_1\otimes {\mathcal{E}}_2$), for t = 2.

Table 3. KM-fuzzy metric hypergraph $H_1\otimes H_2=(X_1\times X_2,{\rho }^{T_{min}},T_{pr},{\mathcal{E}}_1\otimes {\mathcal{E}}_2),$ for t = 2.

$x_i$	${\eta }_1$	${\eta }_2$	${\eta }_3$	${\eta }_4$	${\eta }_5$	${\eta }_6$	${\eta }_7$	${\eta }_8$	${\eta }_9$	${\eta }_{10}$
$(1,\frac{1}{2})$	0.135	∞	∞	0.135	∞	∞	∞	0.135	∞	∞
$(2,\frac{1}{2})$	∞	0.18	∞	0.18	0.18	∞	∞	∞	0.18	∞
$(3,\frac{1}{2})$	∞	∞	0.225	∞	0.225	∞	∞	∞	∞	0.225
$(1,\frac{1}{4})$	0.03	∞	∞	∞	∞	0.03	∞	∞	∞	∞
$(2,\frac{1}{4})$	∞	0.04	∞	∞	∞	0.04	0.04	∞	∞	∞
$(3,\frac{1}{4})$	∞	∞	0.05	∞	∞	0	0.05	∞	∞	∞

Theorem 5.6

Let $H_1$, $H_2$ be KM-fuzzy metric hypergraphs on $X_1,$ $X_2$ respectively. Then

1. For all $1\le i\le n,1\le j\le n^{\prime },$ ${\mu }_i\in {\mathcal{E}}_1$ and ${\mu }_j^{\prime }\in {\mathcal{E}}_2,$ we have $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}({\mu }_i\otimes {\mu }_i^{\mathrm{\prime }})=\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\times \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i^{\mathrm{\prime }}\right)$.

2. $H_1\otimes H_2=(X_1\times X_2,{\rho }^{T_{min}},T_{pr},{\mathcal{E}}_1\otimes {\mathcal{E}}_2)$ is a KM-fuzzy metric hypergraph on $X_1\times X_2$.

Proof.

(i) Let $(x,y)\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}({\mu }_i\otimes {\mu }_j^{\prime })$. Then $({\mu }_i\otimes {\mu }_j^{\prime })(x,y)>0$, so ${\mu }_i\left(x\right)>0$ and ${\mu }_j^{\prime }\left(y\right)>0$. Hence $x\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)$ and $y\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_j^{\prime }\right)$ and so $(x,y)\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\times \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_j^{\prime }\right)$. The conversely is similar to.

(ii) Let $\left\{(\right(x_1,y_1),\eta (x_1,y_1\left)\right)),\dots ,((x_k,y_k),\eta (x_k,y_k)\left))\right\}\in {\mathcal{E}}_1\otimes {\mathcal{E}}_2\iff \mathrm{\exists }\mu \in {\mathcal{E}}_1,\mathrm{\exists }{\mu }^{\prime }\in {\mathcal{E}}_2$ such that for all $1\le i\le k,\eta (x_i,y_i)=T_{pr}\left(\mu \right(x_i),{\mu }^{\prime }(y_i\left)\right)$ and

$\left(1\right)$ for $\mu \in {\mathcal{E}}_1,\{x_1,x_2,\dots ,x_k\}=\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right)$ and $y_1=y_2=\cdots =y_k$ or

$\left(2\right)$ for ${\mu }^{\prime }\in {\mathcal{E}}_2,\{y_1,y_2,\dots ,y_k\}=\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)$ and $x_1=x_2=\cdots =x_k$. Let $1\le i,j\le r$ and $(x_i,y_i),(x_j,y_j)\in \left\{\right(x_1,y_1),\dots ,(x_r,y_r\left)\right\}$. Then $x_i=x_j$ and $y_i,y_j\in X_2$ or $y_i=y_j$ and $x_i,x_j\in X_1$. If $x_i=x_j$ and $y_i,y_j\in X_2$, then ${\rho }^{\mathrm{T}}((x_i,y_i),(x_j,y_j),t)=T\left({\rho }_1\right(x_i,x_i,t),{\rho }_2(x_j,y_j,t\left)\right)=T(1,{\rho }_2(x_j,y_j,t\left)\right)={\rho }_2(x_j,y_j,t)$. If $y_i=y_j$ and $x_i,x_j\in X_1$, then ${\rho }^{\mathrm{T}}((x_i,y_i),(x_j,y_j),t)=T\left({\rho }_1\right(x_i,x_j,t),{\rho }_2(y_i,y_j,t\left)\right)=T\left({\rho }_1\right(x_i,x_j,t\left)\right),1)={\rho }_1(x_i,x_j,t\left)\right).$ For all $1\le i\le n,1\le j\le n^{\prime }$ and for all $(x_1,y_1),(x_2,y_2)\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}({\mu }_i\otimes {\mu }_j^{\prime })$, since $H_1$ is a KM-fuzzy metric hypergraphs on $X_1$ and $H_2$ is a KM-fuzzy metric hypergraphs on $X_2$, for some $t_1,t_2\in {\mathbb{R}}^{\ge 0}$, take $t=max\{t_1,t_2\}$ so by Theorem 2.5, we get that $\begin{array}{rl}& T(({\mu }_i\otimes {\mu }_j^{\prime })(x_1,y_1),({\mu }_i\otimes {\mu }_j^{\prime })(x_2,y_2))=T(T_{pr}\left({\mu }_i\right(x_1),{\mu }_j^{\prime }(y_1\left)\right),T_{pr}\left({\mu }_i\right(x_2),{\mu }_j^{\prime }(y_2))\\ & \le T({\mu }_i\left(x_1\right),{\mu }_i\left(x_2\right))\le T({\mu }_i\left(x_1\right),{\mu }_i\left(x_2\right))\le {\rho }_1(x_1,x_2,t)\text{and}\\ & T(({\mu }_i\otimes {\mu }_j^{\prime })(x_1,y_1),({\mu }_i\otimes {\mu }_j^{\prime })(x_2,y_2))=T(T_{pr}\left({\mu }_i\right(x_1),{\mu }_j^{\prime }(y_1\left)\right),T_{pr}\left({\mu }_i\right(x_2),{\mu }_j^{\prime }(y_2))\\ & \le T({\mu }_j^{\prime }\left(y_1\right),{\mu }_j^{\prime }\left(y_2\right))\le T({\mu }_j^{\prime }\left(y_1\right),{\mu }_j^{\prime }\left(y_2\right))\le {\rho }_2(y_1,y_2,t)\text{so}\\ & T(({\mu }_i\otimes {\mu }_j^{\prime })(x_1,y_1),({\mu }_i\otimes {\mu }_j^{\prime })(x_2,y_2))\le {\rho }_1(x_1,x_2,t)\wedge {\rho }_1(y_1,y_2,t)={\rho }^{T_{min}}((x_1,y_1),(x_2,y_2),t).\end{array}$ Thus $H_1\otimes H_2=(X_1\times X_2,{\rho }^{T_{min}},T_{pr},{\mathcal{E}}_1\otimes {\mathcal{E}}_2)$ is a KM-fuzzy metric hypergraph on $X_1\times X_2$.

Definition 5.7

Let $H_1$, $H_2$ be KM-fuzzy metric hypergraphs on sets $X_1$ and $X_2$, respectively. Define the minimal rank preserving direct product of fuzzy subset $\mu {\times }_{min}{\mu }^{\prime }:\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right){\times }_{min}\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)\to [0,1]$ by

$\left\{(\right(x_1,y_1),\eta (x_1,y_1\left)\right)),\dots ,((x_k,y_k),\eta (x_k,y_k)\left))\right\}\in {\mathcal{E}}_1{\times }_{min}{\mathcal{E}}_2\iff \mathrm{\exists }\mu \in {\mathcal{E}}_1,\mathrm{\exists }{\mu }^{\prime }\in {\mathcal{E}}_2$ such that for all $1\le i\le k,\eta (x_i,y_i)=T_{min}\left(\mu \right(x_i),{\mu }^{\prime }(y_i\left)\right)$ and for $\mu \in {\mathcal{E}}_1,\{x_1,x_2,\dots ,x_k\}=\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right)$ and $\{y_1,\dots ,y_r\}$ is a multiset of elements of $\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)$ such that $\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)\subseteq \{y_1,y_2,\dots ,y_k\}$ and define minimal rank preserving direct product of KM-fuzzy metric hypergraphs by $H_1{\times }_{min}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T,{\mathcal{E}}_1{\times }_{min}{\mathcal{E}}_2)$, where ${\mathcal{E}}_1{\times }_{min}{\mathcal{E}}_2=\{\mu {\times }_{min}{\mu }^{\prime }|\mu \in {\mathcal{E}}_1,{\mu }^{\prime }\in {\mathcal{E}}_2\}$.

Example 5.8

Consider the fuzzy hypergraphs $H_1,H_2$ in Example 5.2. Thus we obtain the minimal rank preserving direct product of KM-fuzzy metric hypergraph for t = 2, in Table 4 and Figure 6.

Figure 6. KM-fuzzy metric hypergraph $H_1{\times }_{min}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T_{pr},{\mathcal{E}}_1{\times }_{min}{\mathcal{E}}_2$), for t = 2.

Table 4. KM-fuzzy metric hypergraph $H_1{\times }_{min}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T_{pr},{\mathcal{E}}_1{\times }_{min}{\mathcal{E}}_2$) for t = 2.

$x_i$	${\eta }_1$	${\eta }_2$	${\eta }_3$	${\eta }_4$	${\eta }_5$	${\eta }_6$
$(1,\frac{1}{2})$	0.3	∞	∞	∞	0.3	∞
$(2,\frac{1}{2})$	0.4	0.4	0.4	∞	∞	0.4
$(3,\frac{1}{2})$	∞	0.45	∞	0.45	∞	∞
$(1,\frac{1}{4})$	∞	∞	0.1	∞	∞	∞
$(2,\frac{1}{4})$	∞	∞	∞	0.1	0.1	∞
$(3,\frac{1}{4})$	∞	∞	∞	∞	0	0.1

For instance, ${\mu }_1{\times }_{min}{\mu }_1^{\prime }=\left\{\right(1,0.3),(2,0.4\left)\right\}{\times }_{min}\left\{\right(\frac{1}{2},0.45),(\frac{1}{4},0.1\left)\right\}$ gives some following hyperedges: $\begin{array}{rl}& \mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}1:\left\{\right((1,\frac{1}{4}),min(0.1,0.3),\left(\right(2,\frac{1}{2}),min(0.45,0.4\left)\right\}=\left\{\right((1,\frac{1}{4}),0.1),((2,\frac{1}{2}),0.4\left)\right\};\\ & \mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}2:\left\{\right((1,\frac{1}{2}),min(0.45,0.3),\left(\right(2,\frac{1}{4}),min(0.1,0.4\left)\right\}=\left\{\right((1,\frac{1}{2}),0.3),((2,\frac{1}{4}),0.1\left)\right\}.\end{array}$

Theorem 5.9

Let $H_1$ and $H_2$ be KM-fuzzy metric hypergraphs on $X_1,$ $X_2,$ respectively. Then

1. For all $1\le i\le n,1\le j\le n^{\prime },$ ${\mu }_i\in {\mathcal{E}}_1$ and ${\mu }_j^{\prime }\in {\mathcal{E}}_2$, we have $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i{\times }_{min}{\mu }_i^{\mathrm{\prime }}\right)=\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\times \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i^{\mathrm{\prime }}\right)$.

2. $H_1{\times }_{min}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T_{min},{\mathcal{E}}_1{\times }_{min}{\mathcal{E}}_2)$ is a KM-fuzzy metric hypergraph on $X_1\times X_2$.

Proof.

(i) Let $(x,y)\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i{\times }_{min}{\mu }_j^{\prime }\right)$. Then $\left({\mu }_i{\times }_{min}{\mu }_j^{\prime }\right)(x,y)>0$, so ${\mu }_i\left(x\right)>0$ and ${\mu }_j^{\prime }\left(y\right)>0$. Hence $x\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)$ and $y\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_j^{\prime }\right)$ and so $(x,y)\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\times \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_j^{\prime }\right)$. The conversely is similar to.

(ii) We have $\left\{(\right(x_1,y_1),\eta (x_1,y_1\left)\right)),\dots ,((x_k,y_k),\eta (x_k,y_k)\left))\right\}\in {\mathcal{E}}_1{\times }_{min}{\mathcal{E}}_2\iff \mathrm{\exists }\mu \in {\mathcal{E}}_1,\mathrm{\exists }{\mu }^{\prime }\in {\mathcal{E}}_2$ such that for all $1\le i\le k,\eta (x_i,y_i)=T_{min}\left(\mu \right(x_i),{\mu }^{\prime }(y_i\left)\right)$ and for $\mu \in {\mathcal{E}}_1,\{x_1,x_2,\dots ,x_k\}=\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right)$ and $\{y_1,\dots ,y_r\}$ is a multiset of elements of $\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)$ such that $\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)\subseteq \{y_1,y_2,\dots ,y_k\}$. For all $1\le i\le n,1\le j\le n^{\prime }$ and for all $(x_1,y_1),(x_2,y_2)\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i{\times }_{min}{\mu }_j^{\prime }\right)$, since $H_1$ is a KM-fuzzy metric hypergraphs on $X_1$ and $H_2$ is a KM-fuzzy metric hypergraphs on $X_2$, for some $t_1,t_2\in {\mathbb{R}}^{\ge 0}$, take $t=min\{t_1,t_2\}$ so by Theorem 2.5, we get that $\begin{array}{rl}& T(\left({\mu }_i{\times }_{min}{\mu }_j^{\prime }\right)(x_1,y_1),\left({\mu }_i{\times }_{min}{\mu }_j^{\prime }\right)(x_2,y_2))=T(\left({\mu }_i\right(x_1)\wedge {\mu }_j^{\prime }(y_1\left)\right),\left({\mu }_i\right(x_2)\wedge {\mu }_j^{\prime }(y_2))\\ & \le T({\mu }_i\left(x_1\right),{\mu }_i\left(x_2\right))\le T({\mu }_i\left(x_1\right),{\mu }_i\left(x_2\right))\le {\rho }_1(x_1,x_2,t)\text{and}\\ & T(\left({\mu }_i{\times }_{min}{\mu }_j^{\prime }\right)(x_1,y_1),\left({\mu }_i{\times }_{min}{\mu }_j^{\prime }\right)(x_2,y_2))=T(\left({\mu }_i\right(x_1)\wedge {\mu }_j^{\prime }(y_1\left)\right),\left({\mu }_i\right(x_2)\wedge {\mu }_j^{\prime }(y_2))\\ & \le T({\mu }_j^{\prime }\left(y_1\right),{\mu }_j^{\prime }\left(y_2\right))\le T({\mu }_j^{\prime }\left(y_1\right),{\mu }_j^{\prime }\left(y_2\right))\le {\rho }_2(y_1,y_2,t)\text{so}\\ & T(\left({\mu }_i{\times }_{min}{\mu }_j^{\prime }\right)(x_1,y_1),\left({\mu }_i{\times }_{min}{\mu }_j^{\prime }\right)(x_2,y_2))\le {\rho }_1(x_1,x_2,t)\wedge {\rho }_1(y_1,y_2,t)\\ & ={\rho }^{T_{min}}((x_1,y_1),(x_2,y_2),t).\end{array}$ Thus $H_1{\times }_{min}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T_{min},{\mathcal{E}}_1{\times }_{min}{\mathcal{E}}_2)$ is a KM-fuzzy metric hypergraph on $X_1\times X_2$.

Definition 5.10

Let $H_1$, $H_2$ be KM-fuzzy metric hypergraphs on sets $X_1$ and $X_2$, respectively. Define the maximal rank preserving direct product of fuzzy subset $\mu {\times }_{max}{\mu }^{\prime }:\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right){\times }_{max}\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)\to [0,1]$ by

$\left\{(\right(x_1,y_1),\eta (x_1,y_1\left)\right)),\dots ,((x_k,y_k),\eta (x_k,y_k)\left))\right\}\in {\mathcal{E}}_1{\times }_{max}{\mathcal{E}}_2\iff \mathrm{\exists }\mu \in {\mathcal{E}}_1,\mathrm{\exists }{\mu }^{\prime }\in {\mathcal{E}}_2$ such that for all $1\le i\le k,\eta (x_i,y_i)=T_{min}\left(\mu \right(x_i),{\mu }^{\prime }(y_i\left)\right)$ and

(i) for $\mu \in {\mathcal{E}}_1,\{x_1,x_2,\dots ,x_k\}=\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right)$ and $\{y_1,\dots ,y_r\}$ is a multiset of elements of $\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)$ such that $\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)\subseteq \{y_1,y_2,\dots ,y_k\}$ or

(ii) for ${\mu }^{\prime }\in {\mathcal{E}}_2,\{y_1,y_2,\dots ,y_k\}=\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }^{\prime }\right)$ and $\{x_1,\dots ,x_r\}$ is a multiset of elements of $\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right)$ such that $\mathrm{d}\mathrm{o}\mathrm{m}\left(\mu \right)\subseteq \{x_1,x_2,\dots ,x_k\}$ and define maximal rank preserving direct product of KM-fuzzy metric hypergraphs by $H_1{\times }_{max}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T,{\mathcal{E}}_1{\times }_{max}{\mathcal{E}}_2)$, where ${\mathcal{E}}_1{\times }_{max}{\mathcal{E}}_2=\{\mu {\times }_{max}{\mu }^{\prime }|\mu \in {\mathcal{E}}_1,{\mu }^{\prime }\in {\mathcal{E}}_2\}$.

Theorem 5.11

Let $H_1$ and $H_2$ be KM-fuzzy metric hypergraphs on $X_1,$ $X_2,$ respectively. Then

1. For all $1\le i\le n,1\le j\le n^{\prime },$ ${\mu }_i\in {\mathcal{E}}_1$ and ${\mu }_j^{\prime }\in {\mathcal{E}}_2,$ we have $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i{\times }_{max}{\mu }_i^{\mathrm{\prime }}\right)=\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\times \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i^{\mathrm{\prime }}\right)$.

2. $H_1{\times }_{max}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T_{min},{\mathcal{E}}_1{\times }_{max}{\mathcal{E}}_2)$ is a KM-fuzzy metric hypergraph on $X_1\times X_2$.

Proof.

It is similar to Theorem 5.9.

Definition 5.12

Let $H_1$, $H_2$ be KM-fuzzy metric hypergraphs on sets $X_1$ and $X_2$, respectively. Define the strong minimal product of fuzzy subset ${\mu }_i{\odot }_{min}{\mu }_j^{\prime }:\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right){\odot }_{min}\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_j^{\prime }\right)\to [0,1]$ by $\left\{(\right(x_1,y_1),\eta (x_1,y_1\left)\right)),\dots ,((x_k,y_k),\eta (x_k,y_k)\left))\right\}\in {\mathcal{E}}_1{\odot }_{min}{\mathcal{E}}_2$ if and only if

$\left\{(\right(x_1,y_1),\eta (x_1,y_1\left)\right)),\dots ,((x_k,y_k),\eta (x_k,y_k)\left))\right\}\in ({\mathcal{E}}_1\otimes {\mathcal{E}}_2)\cup \left({\mathcal{E}}_1{\times }_{min}{\mathcal{E}}_2\right).$ So define strong minimal product of KM-fuzzy metric hypergraphs by $H_1{\odot }_{min}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T,{\mathcal{E}}_1{\odot }_{min}{\mathcal{E}}_2)$, where ${\mathcal{E}}_1{\odot }_{min}{\mathcal{E}}_2=\{{\mu }_i{\odot }_{min}{\mu }_j^{\prime }|1\le i\le n,1\le j\le n^{\prime }\}$.

Example 5.13

Consider the fuzzy hypergraphs $H_1,H_2$ in Example 5.2. Thus we obtain the strong minimal product of KM-fuzzy metric hypergraph, for t = 2 in Table 5. For instance, we compute ${\eta }_6$. We have ${\mu }_1=\left\{\right(1,0.3),(2,0.4\left)\right\},{\mu }_2=\left\{\right(3,0.5),(2,0.4\left)\right\},{\mu }_1^{\prime }=\left\{\right(\frac{1}{2},0.45\left)\right\},{\mu }_2^{\prime }=\left\{\right(\frac{1}{2},0.45),(\frac{1}{4},0.1\left)\right\}$. By definition $\begin{array}{rl}{\eta }_6& =\left\{\right({\mu }_1{\odot }_{min}{\mu }_1^{\prime }\left)\right(2,\frac{1}{2}),({\mu }_2{\odot }_{min}{\mu }_2^{\prime }\left)\right(3,\frac{1}{4}\left)\right\}\\ & =\left\{\right((2,\frac{1}{2}),0.4\wedge 0.45),((3,\frac{1}{4}),0.5\wedge 0.1\left)\right\}=\left\{\right((2,\frac{1}{2}),0.4),((3,\frac{1}{4}),0.1\left)\right\}.\end{array}$

Table 5. KM-fuzzy metric hypergraph $H_1{\odot }_{min}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T,{\mathcal{E}}_1{\odot }_{min}{\mathcal{E}}_2),$ for t = 2.

$x_i$	${\eta }_1$	${\eta }_2$	${\eta }_3$	${\eta }_4$	${\eta }_5$	${\eta }_6$	${\eta }_7$	${\eta }_8$	${\eta }_9$	${\eta }_{10}$	${\eta }_{11}$	${\eta }_{12}$	${\eta }_{13}$	${\eta }_{14}$
$(1,\frac{1}{2})$	0.3	∞	∞	∞	0.3	∞	∞	∞	0.3	∞	∞	0.3	∞	∞
$(2,\frac{1}{2})$	0.4	0.4	0.4	∞	∞	0.4	∞	∞	∞	0.4	∞	∞	0.4	∞
$(3,\frac{1}{2})$	∞	0.45	∞	0.45	∞	∞	∞	∞	∞	∞	0.45	∞	∞	0.45
$(1,\frac{1}{4})$	∞	∞	0.1	∞	∞	∞	0.1	∞	0.1	∞	∞	∞	∞	∞
$(2,\frac{1}{4})$	∞	∞	∞	0.1	0.1	∞	0.1	0.1	∞	0.1	∞	∞	∞	∞
$(3,\frac{1}{4})$	∞	∞	∞	∞	∞	0.1	∞	0.1	∞	∞	0.1	∞	∞	∞

Theorem 5.14

Let $H_1$ and $H_2$ be KM-fuzzy metric hypergraphs on $X_1,$ $X_2,$ respectively. Then

1. For all $1\le i\le n,1\le j\le n^{\prime },$ ${\mu }_i\in {\mathcal{E}}_1$ and ${\mu }_j^{\prime }\in {\mathcal{E}}_2,$ we have $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i{\odot }_{min}{\mu }_i^{\mathrm{\prime }}\right)=\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\times \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i^{\mathrm{\prime }}\right)$.

2. $H_1{\odot }_{min}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T_{min},{\mathcal{E}}_1{\odot }_{min}{\mathcal{E}}_2)$ is a KM-fuzzy metric hypergraph on $X_1\times X_2$.

Proof.

It is obtained by Theorem 5.6 and 5.9.

Definition 5.15

Let $H_1$, $H_2$ be KM-fuzzy metric hypergraphs on sets $X_1$ and $X_2$, respectively. Define the strong maximal product of fuzzy subset ${\mu }_i{\odot }_{max}{\mu }_j^{\prime }:\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right){\odot }_{max}\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_j^{\prime }\right)\to [0,1]$ by $\left\{(\right(x_1,y_1),\eta (x_1,y_1\left)\right)),\dots ,((x_k,y_k),\eta (x_k,y_k)\left))\right\}\in {\mathcal{E}}_1{\odot }_{max}{\mathcal{E}}_2$ if and only if

$\left\{(\right(x_1,y_1),\eta (x_1,y_1\left)\right)),\dots ,((x_k,y_k),\eta (x_k,y_k)\left))\right\}\in ({\mathcal{E}}_1\otimes {\mathcal{E}}_2)\cup \left({\mathcal{E}}_1{\times }_{max}{\mathcal{E}}_2\right).$ So define strong product of KM-fuzzy metric hypergraphs by $H_1{\odot }_{max}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T,{\mathcal{E}}_1{\odot }_{max}{\mathcal{E}}_2)$, where ${\mathcal{E}}_1{\odot }_{max}{\mathcal{E}}_2=\{{\mu }_i{\odot }_{max}{\mu }_j^{\prime }|1\le i\le n,1\le j\le n^{\prime }\}$.

Theorem 5.16

Let $H_1$ and $H_2$ be KM-fuzzy metric hypergraphs on $X_1,$ $X_2,$ respectively. Then

1. For all $1\le i\le n,1\le j\le n^{\prime },$ ${\mu }_i\in {\mathcal{E}}_1$ and ${\mu }_j^{\prime }\in {\mathcal{E}}_2,$ we have $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i{\odot }_{max}{\mu }_i^{\mathrm{\prime }}\right)=\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i\right)\times \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_i^{\mathrm{\prime }}\right)$.

2. $H_1{\odot }_{max}{H}_2=(X_1\times X_2,{\rho }^{T_{min}},T_{min},{\mathcal{E}}_1{\odot }_{max}{\mathcal{E}}_2)$ is a KM-fuzzy metric hypergraph on $X_1\times X_2$.

Proof.

It is similar to Theorem 5.14.

Definition 5.17

Let $(X,\rho ,T)$ be a KM-fuzzy metric space. If $H=(X,\rho ,T,\mathcal{E})$ is a KM-fuzzy metric hypergraph on X, then for any ${\mu }_i\in \mathcal{E}$, and each $x\in X$ that $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$, define the complement of fuzzy subset $\overline{{\mu }_i}\left(x\right)=\underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }{\mu }^{(s,x)}$, where ${\mu }^{(s,x)}=\underset{y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }\left(\rho \right(x,y,t)-T({\mu }_s(x),{\mu }_s(y\left))\right)$ and ${\mu }_s\in \mathcal{E}$.

We will denote the complement of a KM-fuzzy metric hypergraph $H=(X,\rho ,T,\mathcal{E})$, by $\overline{H}=(X,\rho ,T,\overline{\mathcal{E}})$, where $\overline{\mathcal{E}}=\{\overline{{\mu }_i}{\}}_{i=1}^n$.

Example 5.18

Consider the KM-fuzzy metric hypergraph $H_1=(X,\rho ,T,\mathcal{E})$ in Example 5.2. Thus we obtain the complement of KM-fuzzy metric hypergraph, for t = 1 in Figure 7. For instance, $\overline{{\mu }_1}\left(1\right)={\mu }^{(1,1)}=\left(\rho \right(1,1,1)-T_{pr}(0.3,0.3\left)\right)\wedge \left(\rho \right(1,2,1)-T_{pr}(0.3,0.4\left)\right)=\frac{41}{75}$. In similar a way, $\overline{{\mu }_1}\left(2\right)={\mu }^{(1,2)}\wedge {\mu }^{(2,2)}=\overline{{\mu }_2}\left(2\right)=\frac{41}{75}$.

Figure 7. KM-fuzzy metric hypergraph ${\overline{H}}_1=(X,\rho ,T_{pr},\overline{\mathcal{E}}),$ for t = 1.

Theorem 5.19

Let $(X,\rho ,T)$ be a KM-fuzzy metric space and $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph on X. Then

1. for all $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)$ and ${\mu }_s\in \mathcal{E},$ we have ${\mu }^{(s,x)}\le 1-{\mu }_s\left(x\right);$

2. if $x\in \bigcap _{j=1}^k\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_{i_j}\right),$ then for all $i_1\le m,m^{\prime }\le i_k,$ we have $\overline{{\mu }_m}\left(x\right)=\overline{{\mu }_{m^{\prime }}}\left(x\right),$ where $1\le k\le n;$

3. for all $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$ and ${\mu }_i\in \mathcal{E},$ we have $\overline{{\mu }_i}\left(x\right)\le 1-{\mu }_i\left(x\right)$.

Proof.

(i) Let ${\mu }_s\in \mathcal{E}$ and $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)$. Then $\begin{array}{rl}{\mu }^{(s,x)}& =\underset{y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }\left(\rho \right(x,y,t)-T({\mu }_s(x),{\mu }_s(y\left))\right)\le \rho (x,x,t)-T({\mu }_s\left(x\right),{\mu }_s\left(x\right))\\ & =1-T({\mu }_s\left(x\right),{\mu }_s\left(x\right))\le 1-{\mu }_s\left(x\right).\end{array}$

(ii) Let $1\le k\le n$ and $i_1\le m,m^{\prime }\le i_k$. Since $x\in \bigcap _{j=1}^k\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_{i_j}\right)$, we get that $\overline{{\mu }_m}\left(x\right)=\underset{i=1}{\overset{k}{\bigwedge }}{\mu }^{(i,x)}=\overline{{\mu }_{m^{\prime }}}\left(x\right)$.

(iii) Let $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$ and ${\mu }_i\in \mathcal{E}$. Then by item (i), we get that $\overline{{\mu }_i}\left(x\right)=\underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }{\mu }^{(s,x)}\le {\mu }^{(i,x)}\le 1-{\mu }_i\left(x\right)$.

Theorem 5.20

Let $(X,\rho ,T)$ be a KM-fuzzy metric space, $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph on X, ${\mu }_i\in \mathcal{E}$ and $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$. Then

1. if ${\overline{\mu }}_i\left(x\right)={\mu }_i\left(x\right),$ then ${\mu }_i\left(x\right)\le 1-T\left({\mu }_i\right(x),{\mu }_i(x\left)\right);$

2. if $T=T_{pr},$ then ${\overline{\mu }}_i\left(x\right)={\mu }_i\left(x\right),$ implies that ${\mu }_i\left(x\right)\in [0,\frac{-1+\sqrt{5}}{2}];$

3. if $T=T_{do},$ then ${\overline{\mu }}_i\left(x\right)={\mu }_i\left(x\right),$ implies that ${\mu }_i\left(x\right)\in [0,2-\sqrt{2}];$

4. if $T=T_{lu},$ then ${\overline{\mu }}_i\left(x\right)={\mu }_i\left(x\right),$ implies that ${\mu }_i\left(x\right)\in [\frac{1}{2},\frac{2}{3}];$

Proof.

Obviously it is obtained.

Let $(X,\rho ,T)$ be a KM-fuzzy metric space, $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph on X. For simplify, we denote $\overline{\mu }={\mu }^{(}1),\overline{\overline{\mu }}={\mu }^{(}2)$ and for all $n\in \mathbb{N},\overline{{\mu }^{(n-1)}}={\mu }^{\left(n\right)}.$

Corollary 5.21

Let $(X,\rho ,T)$ be a KM-fuzzy metric space, $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph on X, ${\mu }_i\in \mathcal{E}$ and $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$. Then

1. ${\mu }_i^2\left(x\right)\le 1-T(1-T\left({\mu }_i\right(x),{\mu }_i(x\left)\right),1-T\left({\mu }_i\right(x),{\mu }_i(x\left)\right));$

2. if $T=T_{pr},$ then ${\mu }_i^{\left(2\right)}\left(x\right)={\mu }_i\left(x\right),$ implies that ${\mu }_i\left(x\right)\in [0,\frac{-1+\sqrt{5}}{2}];$

3. ${\mu }_i^n\left(x\right)\le 1-T(T\left({\mu }_i^{(n-1)}\right(x),{\mu }_i^{(n-1)}(x));$

4. if $T=T_{pr},$ then ${\mu }_i^n\left(x\right)\le 1-(1-(1-(1-\cdots (1-{\mu }_i^2(x){)}^2{)}^2$.

Theorem 5.22

Let $(X,\rho ,T)$ be a KM-fuzzy metric space and $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph on X. Then

1. for all $x,x^{\prime }\in dom\left({\mu }_s\right),t\in {\mathbb{R}}^{\ge 0}$ and ${\mu }_s\in \mathcal{E},$ we have ${\mu }^{(s,x)}\wedge {\mu }^{(s,x^{\prime })}\le \rho (x,x^{\prime },t);$

2. $\overline{H}=(X,\rho ,T,\overline{\mathcal{E}})$ is a KM-fuzzy metric hypergraph.

Proof.

(i) Let ${\mu }_s\in \mathcal{E}$ and $x,x^{\prime }\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right),t\in {\mathbb{R}}^{\ge 0}$. Since $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)$, by definition we have ${\mu }^{(s,x)}=\underset{y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }\left(\rho \right(x,y,t)-T({\mu }_s(x),{\mu }_s(y\left))\right)\le \rho (x,x^{\prime },t)-T({\mu }_s\left(x\right),{\mu }_s\left(x^{\prime }\right))\le \rho (x,x^{\prime },t)$. In a similar way one can see that ${\mu }^{(s,x)}\le \rho (x,x^{\prime },t)$ and so ${\mu }^{(s,x)}\wedge {\mu }^{(s,x^{\prime })}\le \rho (x,x^{\prime },t)$.

(ii) Let ${\mu }_i,{\mu }_s\in \mathcal{E}$ and $x,x^{\prime }\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right),t,t^{\prime }\in {\mathbb{R}}^{\ge 0}$. Then by Theorem 5.19, $\begin{array}{rl}& T\left({\overline{\mu }}_i\right(x),{\overline{\mu }}_i(x^{\prime }\left)\right)=T(\underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_j\right)}{\bigwedge }{\mu }^{(j,x)},\underset{x^{\prime }\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_{j^{\prime }}\right)}{\bigwedge }{\mu }^{(j^{\prime },x^{\prime })})\le T({\mu }^{(i,x)},{\mu }^{(i,x^{\prime })})\\ & =T\left(\right(\underset{y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }\left(\rho \right(x,y,t)-T({\mu }_s(x),{\mu }_s(y\left))\right),\underset{y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }\left(\rho \right(x,y,t^{\prime })-T({\mu }_s(x),{\mu }_s(y\left))\right)).\end{array}$ Since $x,x^{\prime }\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)$, for some $t\in {\mathbb{R}}^{\ge 0}$ we get that $\begin{array}{rl}& T\left({\overline{\mu }}_i\right(x),{\overline{\mu }}_i(x^{\prime }\left)\right)\le T\left(\right(\underset{y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }\left(\rho \right(x,y,t)-T({\mu }_s(x),{\mu }_s(y\left))\right),\\ & \underset{y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }\left(\rho \right(x,y,t^{\prime })-T({\mu }_s(x),{\mu }_s(y\left))\right))\\ & \le T\left(\right(\rho (x,x^{\prime },t)-T({\mu }_s\left(x\right),{\mu }_s\left(x^{\prime }\right))),(\rho (x,x^{\prime },t^{\prime })-T({\mu }_s\left(x\right),{\mu }_s\left(x^{\prime }\right))\left)\right)\\ & \le T\left(\rho \right(x,x^{\prime },t),\rho (x,x^{\prime },t^{\prime })\le \rho (x,x^{\prime },t).\end{array}$ It follows that $\overline{H}=(X,\rho ,T,\overline{\mathcal{E}})$ is a KM-fuzzy metric hypergraph.

Theorem 5.23

Let $(V,\rho ,T)$ be a KM-fuzzy metric space, $H=(X,\rho ,T,\mathcal{E})$ be a KM-fuzzy metric hypergraph on X and ${\mu }_i\in \mathcal{E}$. Then

1. $\overline{{\mu }_i}\equiv 1$ implies that $h\left(H\right)=0;$

2. $\overline{{\mu }_i}\equiv 1$ implies that $|\mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_i\right)|=1;$

3. if $\overline{{\mu }_i}\left(x\right)=0$, then ${\mu }_i\left(x\right)\ne 0;$

4. $\overline{{\mu }_i}\equiv 0$ implies that H is a locally strong KM-fuzzy metric hypergraph.

Proof.

(i, ii) Since $\overline{{\mu }_i}\equiv 1$, we get that for all $x\in X,{\mu }_i\left(x\right)=1$. It follows that for all ${\mu }_s\in \mathcal{E}$ where $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)$ and $\underset{x\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_s\right)}{\bigwedge }{\mu }^{(s,x)}=1$. Thus for all $y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)$ we have $\left(\rho \right(x,y,t)=T({\mu }_s(x),{\mu }_s(y\left))\right)+1$. It concludes that $T\left({\mu }_s\right(x),{\mu }_s(y\left)\right)=0$ and so $\rho (x,y,t)=1$. Hence x = y and ${\mu }_s\left(x\right)=0$ and so $h\left(H\right)=0$.

(iii, iv) Since $\overline{{\mu }_i}\equiv 0$, we get that for all $x\in X,{\mu }_i\left(x\right)=0$. It follows that there exists ${\mu }_s\in \mathcal{E}$ where $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)$ and $\underset{x\in \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mu }_s\right)}{\bigwedge }{\mu }^{(s,x)}=0$. Thus there exists $y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)$ in such a way that $\left(\rho \right(x,y,t)=T({\mu }_s(x),{\mu }_s(y\left))\right)$. It concludes that $\rho (x,y,t)=T\left({\mu }_s\right(x),{\mu }_s(y\left)\right)=0$ and so ${\mu }_s\left(x\right)\ne 0,{\mu }_s\left(y\right)\ne 0$.

Corollary 5.24

Let $(V,\rho ,T)$ be a KM-fuzzy metric space, $H=(X,\rho ,T,\mathcal{E})$ is a KM-fuzzy metric hypergraph on X and ${\mu }_i\in \mathcal{E}$. Then

1. $\overline{{\mu }_i}\equiv 1$ if and only if $h\left(H\right)=0;$

2. if ${{\mu }_i}^{(n-1)}\equiv 0,$ then for all $x\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right),$ we have ${{\mu }_i}^{\left(n\right)}\left(x\right)=\underset{y\in \mathrm{d}\mathrm{o}\mathrm{m}\left({\mu }_s\right)}{\bigwedge }\rho (x,y,t)$.

6. Discussion of Results and Conclusion

The current paper has introduced a novel concept of fuzzy algebra as KM-fuzzy metric hypergraph. Indeed it has presented a new generalisation of hypergraphs based on KM-fuzzy metric spaces. This work extended and obtained some properties in KM-fuzzy metric spaces. Based on KM-fuzzy metric hypergraphs, every non empty set converted to a KM-fuzzy metric space. It is showed that the product and union of KM-fuzzy metric spaces is a KM-fuzzy metric space, the extended KM-fuzzy metric spaces are constructed using of the some algebraic operations on KM-fuzzy metric spaces. Moreover, the concept of complement of KM-fuzzy metric hypergraphs is defined and investigated some its properties. Incidence matrix of KM-fuzzy metric hypergraphs, is introduced and investigated some their properties. Using the concept of valued-cuts, we connected the concept of KM-fuzzy metric hypergraphs to hypergraphs. In addition, fundamental sequence as a tool in KM-fuzzy metric hypergraphs is introduced and based on fundamental sequence the concept of core hypergraphs is presented. In study of KM-fuzzy metric hypergraphs, despite having key mathematical tools there are some limitations. The union of two KM-fuzzy metric hypergraphs is not necessarily, a KM-fuzzy metric hypergraph so the class of KM-fuzzy metric hypergraphs is not closed under any given algebraic operation. In addition KM-fuzzy metric hypergraphs are different with fuzzy hypergraphs, so could not generalise the capabilities of fuzzy hypergraphs to KM-fuzzy metric hypergraphs.

We hope that these results are helpful for further studies in theory of graphs. In our future studies, we hope to obtain more results regarding instuitic metric graphs, neutrosophic metric graphs, KM-neutrosophic metric hypergraphs, bipolar KM-fuzzy metric graphs, automorphism of KM-fuzzy metric graphs and reducing complexity with respect to KM-fuzzy metric directed hypergraphs.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Mohammad Hamidi

Mohammad Hamidi was born in Vidouja Village, Kashan, Isfahan, Iran in 1979. He received the B.S. degrees in mathematics from the University of Kashan, Kashan, in 2002, the M.S. degrees in mathematics (algebra) from the Isfahan University of Technology, Isfahan in 2005 and the Ph.D. degree in in mathematics (algebras and hyperalgebras and fuzzy logic) from Tehran Payame Noor University, Tehran, in 2014. From 2002 to 2005, he was a Research Assistant with the Mathematics University. Since 2014, he has been an Assistant Professor with the Mathematics Department, Payame Noor University of Tehran. Since 2019, he has been an Associate Professor with the Mathematics Department, Payame Noor University of Tehran. He is the author of two books, more than 70 articles, and more than 3 research projecst. His research interests include applications of fuzzy graph and single valued veutrosophic graphs in hypernetworks and complex hypernetworks such as Wireless sensor networks.

Sirus Jahanpanah

Sirus Jahanpanah was born in bavaryan Village, roozabad, fars, Iran in 1977. He received the B.S. degrees in mathematics from the University of Shiraz, Shiraz, in 2002, the M.S. degrees in mathematics (algebra) from the University of shiraz, shiraz in 2006 and the Ph.D. student in mathematics (algebras and hyperalgebras and fuzzy logic) at the Tehran Payame Noor University, Tehran . Since 2007, he has been an Instructor with the Mathematics Department, Payame Noor University of Fars. He is the author of two books, more than 7 articles, and more than 4 research projecst.

Akefe Radfar

Akefe Radfar was born in Isfahan, Iran in 1977. She received the B.S. degrees in mathematics from the University of Isfahan, Isfahan, in 1999, the M.S. degrees in mathematics (algebra) from the Shahrekord University of Shahrekord, in 2005 and the Ph.D. degree in mathematics (algebras and hyperalgebras and fuzzy logic) from Tehran Payame Noor University, Tehran, in 2011. From 2008 to 2010, she was a Research Assistant with the Mathematics University. Since 2010, she has been an Assistant Professor with the Mathematics Department, Payame Noor University of Tehran. she has more than 30 articles.