Numerical Accuracy of the Predictor-Corrector Method to Solve Fuzzy Differential Equations Based on the Stochastic Arithmetic

Abstract

In this work, a reliable scheme is proposed to solve fuzzy differential equation based on the predictor-corrector methods (PC-methods) under generalized H-differentiability. For this purpose, the stochastic arithmetic(SA) and the CESTAC* method are applied to validate the results. Also, the numerical accuracy of the method is proved and an algorithm is given based on the new arithmetic. In order to implement C++ codes, the CADNA† library is used. In this case, the optimal number of nodes and optimal step size are found. The examples illustrate the efficiency and importance of using the SA in place of the floating-point arithmetic(FPA).

Keywords:

• Fuzzy differential equation(FDE)
• Predictor-Corrector method
• multi-step method
• stochastic arithmetic
• CESTAC method
• CADNA library

1. Introduction

Solving fuzzy differential equations (FDE) in both initial and boundary conditions are important topics in fuzzy mathematics and its applications [1]. In recent years different numerical and analytical approaches were proposed to find the fuzzy solution of a given FDE such as [2–12]. In all of these works, in order to implement the computer programs, a mathematical package like Matlab, Mathematica,…is considered and the results are found based on the common computer arithmetic which is the FPA. In this case, a fixed step size is chosen, then in the fixed nodes, the approximate solution is obtained. Also, in all examples, the exact solution is given and compared with the approximate solution to check the accuracy of the results and the convergence of the method. Since the FPA is not able to rely and validate the results and detect the instabilities during the run of the program, the packages which are worked on this arithmetic are not able to determine a satisfactory result from the computational point of view. In other words, because of the accumulation of errors due to the round-off error propagation, the final results obtained from a numerical algorithm may be inaccurate and the FPA is not able to detect the accuracy of results. Also, in this arithmetic, it is not possible to find the optimal step size in difference schemes like PC-methods and it is necessary to consider a tolerance of accuracy like eps in the termination criterion, which is not proper to stop the computations. Hence, an arbitrary step size is chosen and the results are found without validating them. It is important computationally to validate the results and control the variations of the step size in iterative and approximate methods and find the optimal results to ensure that based on the machine accuracy, the final solution, the number of iterations and the step size are optimized. Hence, a reliable and efficient method for evaluating the round-off error is necessary if one wants to correct step size control. For these reasons, the FPA must be substituted by other arithmetic which is able to optimize and validate the results. This new arithmetic is called the SA proposed by La Porte and Vignes[13]. They introduced the CESTAC method which is a method to implement the SA in a code written by Fortran or C++ on the Linux operating system [14–16]. This method enables one to estimate the number of the exact significant digits of any computed result. The CESTAC method is based on a probabilistic approach of the round-off error propagation which replaces the FPA by a random arithmetic [15,17–25].

In [26–29], the authors applied the CADNA library to solve a FDE by using the fuzzy Runge-Kutta method as a single-step scheme and the finite differences method to solve fuzzy boundary value problem. By using this library, the optimal step size is computed, and the optimal approximate solution of the FDE in the nodal points is found. In this work, a procedure is presented for solving fuzzy differential equations under generalized H-differentiability based on the PC-methods. Also, based on the idea proposed by Bede [6] and Bede and Gal [30], which describes that a FDE under the H-differentiability and gH-differentiability is equivalent to a system of crisp ordinary differential equations (ODEs) under certain conditions, the solution of FDE is found. Furthermore, by using the CESTAC method and the CADNA library, the optimal step size of the fuzzy multi-step methods is computed and the accuracy of results is dynamically controlled and estimated.

This paper is organized as follows. In Section 2, the basic definitions of fuzzy sets theory is presented. In Section 3, the main idea is explained. In this section, a theorem is proved to show the accuracy of the fuzzy multi-step methods. The CESTAC method and its fuzzy case in companion with an algorithm which is implemented by the CADNA library are given in Section 4. In Section 5, two sample FDEs with initial fuzzy conditions are solved by means of the CADNA library based on the proposed algorithm to illustrate the importance of using the SA in validating the results of the algorithm and finding the optimal step size.

2. Preliminaries

The basic definitions of fuzzy mathematics are given in [1,3–5,31–33]. In this section, we review some of them.

Definition 2.1

[34]

Given the definition domain U, the mapping $X:U⟶[0,1],$ is called a fuzzy set. $X\left(u\right)$ is denoted as the membership function, whose values are located in a closed interval $[0,1]$. If only the point values 0 and 1 are suitable, the fuzzy set X degenerates into a classical one, which means that the classical set is a special form of the fuzzy sets.

Definition 2.2

[34]

Given a fuzzy set X, for any $r\in [0,1]$, the classical set $[X{]}^r=\{u:u\in U,X\left(u\right)\ge r\}$ is defined as the r-cut set, where r is the cut level. Usually, the r-cut sets are considered as intervals of confidence, since in the case of convex fuzzy sets, they are closed fuzzy intervals associated with a gradation of confidence between $[0,1]$. For a fuzzy interval X, its $r-$cuts are closed intervals in $\mathbb{R}$ and we denote them by $[X{]}^r=[x^{-}\left(r\right),x^{+}\left(r\right)].$ Two widely used of fuzzy intervals are triangular and trapezoidal fuzzy numbers. Let us denote by $\mathcal{F}\left(\mathbb{R}\right)$ the set of all fuzzy numbers, however, fuzzy numbers are generalized closed intervals.

Also, support of X is $supp\left(X\right)=\{u\in U:X(u)>0\}.$ For two fuzzy sets X and Y, the addition $X\oplus Y$ and the scalar multiplication $\alpha \odot X,\alpha \in \mathbb{R}$ are defined as having the level cuts $\begin{array}{rl}[X\oplus Y{]}^r& =[X{]}^r+[Y{]}^r=\{x+y:x\in [X{]}^r,y\in \left[Y{]}^r\right\},\\ [\alpha \odot X{]}^r& =\alpha [X{]}^r,r\in [0,1].\end{array}$ Also, the product and division of two fuzzy numbers $X,Z\in \mathcal{F}\left(\mathbb{R}\right)$ are defined as: $\begin{array}{rl}{\left[X\otimes Z\right]}^r& =\left[\underset{s,t\in \{+,-\}}{min}{x}^s\left(r\right).z^t\left(r\right),\underset{s,t\in \{+,-\}}{max}{x}^s\left(r\right).z^t\left(r\right)\right],\\ {\left[X\oslash Z\right]}^r& =\left[\underset{s,t\in \{+,-\}}{min}\frac{x^s\left(r\right)}{z^t\left(r\right)},\underset{s,t\in \{+,-\}}{max}\frac{x^s\left(r\right)}{z^t\left(r\right)}\right],0\notin supp\left(Z\right).\end{array}$

Definition 2.3

The generalized Hukuhara difference of two intervals, $X,Y\in \mathcal{F}\left(\mathbb{R}\right)$, (gH-difference) is defined as follows [1]: $\begin{array}{r}X{\ominus }_{gH}Y=Z\iff X=Y+ZorY=X+(-Z).\end{array}$ Consider $[Z{]}^r=[z^{-}\left(r\right),z^{+}\left(r\right)]$ then $z^{-}\left(r\right)=min\left\{x^{-}\right(r)-y^{-}(r),x^{+}(r)-y^{+}(r\left)\right\}$ and $z^{+}\left(r\right)=max\left\{x^{-}\right(r)-y^{-}(r),x^{+}(r)-y^{+}(r\left)\right\}.$

Definition 2.4

[1]

Define $D:\mathcal{F}\left(\mathbb{R}\right)\times \mathcal{F}\left(\mathbb{R}\right)⟶{\mathbb{R}}^{+}$ by (1) $\begin{array}{rl}D(u_1,u_2)& :=\underset{r\in [0,1]}{sup}max\{\left|{u_1}^{-}\left(r\right)-{u_2}^{-}\left(r\right)\right|,\left|{u_1}^{+}\left(r\right)-{u_2}^{+}\left(r\right)\right|\}\\ & =\underset{r\in [0,1]}{sup}{D}_H\left([u_1{]}^r,[u_2{]}^r\right),\end{array}$(1) which is called the Hausdorff distance between two fuzzy numbers $u_1,u_2\in \mathcal{F}\left(\mathbb{R}\right)$ with the following properties: $\begin{array}{rl}& D(u_1\oplus v,u_2\oplus v)=D(u_1,u_2),\mathrm{\forall }{u}_1,u_2,v\in \mathcal{F}\left(\mathbb{R}\right),\\ & D(\lambda \odot u_1,\lambda \odot u_2)=\left|\lambda \right|D(u_1,u_2),\mathrm{\forall }\lambda \in \mathbb{R},u_1,u_2\in \mathcal{F}\left(\mathbb{R}\right),\\ & D({\lambda }_1\odot u_1,{\lambda }_2\odot u_1)=\left|{\lambda }_1-{\lambda }_2\right|D(u_1,\tilde{0}),\mathrm{\forall }{\lambda }_1,{\lambda }_2\ge 0,u_1\in \mathcal{F}\left(\mathbb{R}\right),\\ & D(u_1\oplus u_2,v_1\oplus v_2)\le D(u_1,v_1)+D(u_2,v_2),\mathrm{\forall }{u}_1,u_2,v_1,v_2\in \mathcal{F}\left(\mathbb{R}\right).\end{array}$

Definition 2.5

[1,3]

A function $X:\mathbb{R}⟶\mathcal{F}\left(\mathbb{R}\right)$ is called a fuzzy function. If for arbitrary fixed $t_0\in \mathbb{R}$ and $ϵ>0,$ a $\delta >0$ such that (2) $|t-t_0|<\delta \Rightarrow D\left(X\right(t),X(t_0\left)\right)<ϵ,$(2) exists, X is said to be continuous.

Definition 2.6

Generalized derivative

Gomes et al. [1] Let $X^{\left(j\right)}:\mathbb{R}⟶\mathcal{F}\left(\mathbb{R}\right)$ (jth-order differential of X) for all $j=0,1,\dots ,n-1$ and $t_0\in \mathbb{R}$. $X^{\left(j\right)}$ is called gH-differentiable (gH-differentiable for short) at $t_0$, if there exists $X^{\left(j\right)}\left(t_0\right)\in \mathcal{F}\left(\mathbb{R}\right)$ for all $j=0,1,\dots ,n-1$, such that $\underset{h\to 0}{lim}\frac{1}{h}\odot \left(X^{\left(j\right)}(t_0+h){\ominus }_{gH}{X}^{\left(j\right)}\left(t_0\right)\right)=X_{gH}^{(j+1)}\left(t_0\right),$ also we say that $X^{\left(j\right)},j=0,1,\dots ,n-1$ is $g{H}_i$-differentiable at $t_0$ if $\left[X_{g{H}_i}^{\left(j\right)}\right(t){]}^r=[x^{{-}^{\left(j\right)}}(t;r),x^{{+}^{\left(j\right)}}(t;r)],$ and we say that $X^{\left(j\right)},j=0,1,\dots ,n-1$ is $g{H}_{ii}$-differentiable at $t_0$ if $\left[X_{g{H}_{ii}}^{\left(j\right)}\right(t){]}^r=[x^{{+}^{\left(j\right)}}(t;r),x^{{-}^{\left(j\right)}}(t;r)].$

Definition 2.7

[1,35–37]

The fuzzy initial value problem (FIVP)is defined using a fuzzy differential equation and a fuzzy initial value as follows: (3) ${\tilde{x}}^{\mathrm{\prime }}\left(t\right)=\tilde{g}(t,\tilde{x}(t\left)\right),\tilde{x}\left(t_0\right)=\tilde{A},t\in I=[t_0,T],$(3) where $\tilde{g}$ is a fuzzy continuous mapping from $\tilde{g}:[t_0,T]\times \mathcal{F}\left(\mathbb{R}\right)$ into $\mathcal{F}\left(\mathbb{R}\right)$.

Theorem 2.8

[1]

Let us consider ${\tilde{x}}^{\mathrm{\prime }}\left(t\right)=\tilde{g}(t,\tilde{x}(t\left)\right)$ where $\tilde{g}:[t_0,T]\times \mathcal{F}\left(\mathbb{R}\right)⟶\mathcal{F}\left(\mathbb{R}\right)$ is such that

1. $\left[\tilde{g}\right(t,\tilde{x}\left(t\right)){]}^r=[g^{-}(t,x)\left(r\right),g^{+}(t,x)\left(r\right)]$ for each $r\in [0,1]$.

2. The functions $g^{-}(t,x)\left(r\right)$, and $g^{+}(t,x)\left(r\right)$ are equi-continuous, i.e. for any $ϵ>0$ there exists $\delta >0$ such that for any $(t,x),(t_1,x_1)\in [t_0,T]\times \mathbb{R},$ we have $\left|g^{-}(t,x)\left(r\right)-g^{-}(t_1,x_1)\left(r\right)\right|<ϵ$ and $\left|g^{+}(t,x)\left(r\right)-g^{+}(t_1,x_1)\left(r\right)\right|<ϵ$ whenever $∥(t,x)-(t_1,x_1)∥<\delta$.

3. $\left[g\right(t,x\left(t\right)){]}^r$ is named uniformly bounded on any bounded set, if exist $l>0$ such that $\begin{array}{r}\left|g^{-}(t_1,x_1)\left(r\right)-g^{-}(t_2,x_2)\left(r\right)\right|<lmax\{\left|t_1-t_2\right|,\left|x_1-x_2\right|\},\end{array}$ and also $\begin{array}{r}\left|g^{+}(t_1,x_1)\left(r\right)-g^{+}(t_2,x_2)\left(r\right)\right|<lmax\{\left|t_1-t_2\right|,\left|x_1-x_2\right|\}.\end{array}$ Then, the fuzzy initial value problem (FIVP) and the corresponding crisp system of initial value problems(IVPs) are equivalent.

3. Main Idea

Let the FIVP (3(3) ${\tilde{x}}^{\mathrm{\prime }}\left(t\right)=\tilde{g}(t,\tilde{x}(t\left)\right),\tilde{x}\left(t_0\right)=\tilde{A},t\in I=[t_0,T],$(3) ). A l-step method for solving Equation (3(3) ${\tilde{x}}^{\mathrm{\prime }}\left(t\right)=\tilde{g}(t,\tilde{x}(t\left)\right),\tilde{x}\left(t_0\right)=\tilde{A},t\in I=[t_0,T],$(3) ) has a fuzzy difference equation with the following general form: (4) ${\tilde{v}}_{i+1}=\sum _{j=0}^{l-1}{}^{\ast }{a}_{l-1-j}\odot {\tilde{v}}_{i-j}\oplus h\odot \sum _{j=0}^l{}^{\ast }{b}_{l-j}\odot \tilde{g}(t_{i+1-j},{\tilde{v}}_{i+1-j}),$(4) where $\sum ^{\ast }$ denotes the fuzzy summation, and $v_{i+1}$ is the approximation of the solution at the mesh point $t_{i+1}$, l is an integer greater than 1 and $i=l-1,l,\dots ,N-1$, $h=T/N$, $t_j=jh,j=0,1,\dots ,l$, the values $a_0,a_1,\dots ,a_{l-1}$ and $b_0,b_1,\dots ,b_l$ are constants, and the starting values $v_0=\alpha ,v_1={\alpha }_1,v_2={\alpha }_2,\dots ,v_{l-1}={\alpha }_{l-1},$ are specified.

When $b_l=0,$ the method (4(4) ${\tilde{v}}_{i+1}=\sum _{j=0}^{l-1}{}^{\ast }{a}_{l-1-j}\odot {\tilde{v}}_{i-j}\oplus h\odot \sum _{j=0}^l{}^{\ast }{b}_{l-j}\odot \tilde{g}(t_{i+1-j},{\tilde{v}}_{i+1-j}),$(4) ) is called an explicit method, otherwise, it is called an implicit method. The starting values in method (4(4) ${\tilde{v}}_{i+1}=\sum _{j=0}^{l-1}{}^{\ast }{a}_{l-1-j}\odot {\tilde{v}}_{i-j}\oplus h\odot \sum _{j=0}^l{}^{\ast }{b}_{l-j}\odot \tilde{g}(t_{i+1-j},{\tilde{v}}_{i+1-j}),$(4) ) must be specified, generally by assuming $v_0=\alpha$ and generating the remaining values by a single-step method such as fourth order Runge-Kutta method.

By using of the interpolating polynomial bases on Newton backward-difference formula, we have get $v_{i+1}=v_{i-1}+h\odot \sum _{l=0}^p{}^{\ast }{c}_l\odot {\mathrm{\nabla }}^l\tilde{g}(t_i,{\tilde{v}}_i),p=0,1,2,\dots ,$ where the constants $c_l=(-1{)}^l{\int }_0^1\left(\genfrac{}{}{0em}{}{-s}{k}\right)\mathrm{d}s,$ with variable substitution $t=t_i+sh$, and $\mathrm{d}t=h\mathrm{d}s$ [8,38].

In the following, we have got some of the fuzzy predictor-corrector(FPC) methods with their initial values [3–5,8,39].

The FPC 3-step method is obtained as follows: (5) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right)\oplus \frac{h}{12}\odot \\ \left[5\odot \tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right){\ominus }_{gH}16\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 23\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right){\ominus }_{gH}\frac{h}{12}\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \frac{2h}{3}\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\oplus \frac{5h}{12}\odot \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}(t_{i+2}\left)\right),\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(5) The improved fuzzy predictor-corrector 3-step method(FIPC) is considered as follows: (6) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{2}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)+\tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 4\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_i\right)+\frac{h}{2}\odot \left[\tilde{g}\right(t_i,\tilde{v}\left(t_i\right))\oplus 2\odot \tilde{g}(t_{i+1},\tilde{v}\left(t_{i+1}\right))\oplus \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)\left)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(6) The fuzzy Milne-Simpson's predictor-corrector 4-step method(FMPC) is obtained as follows: (7) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-3}\right)\oplus \frac{4h}{3}\odot \left[2\odot \tilde{g}(t_{i-2},\tilde{v}(t_{i-2}\left)\right){\ominus }_{gH}\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 2\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{3}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 4\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-3}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_{i-2}\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_2,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_3.\end{array}\end{array}\right.$(7) The local truncation errors of the explicit k-step (or implicit $(k-1)$-step) method, based on the crisp case mentioned in [40–42], can be written as: (8) $\begin{array}{r}{\tilde{v}}_i\left(h\right){\ominus }_{gH}\tilde{x}\left(t_i\right)={\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k+\mathcal{O}\left(h^{k+1}\right),\end{array}$(8) where $\tilde{x}\left(t_i\right)$ is the exact solution of the Equation (3(3) ${\tilde{x}}^{\mathrm{\prime }}\left(t\right)=\tilde{g}(t,\tilde{x}(t\left)\right),\tilde{x}\left(t_0\right)=\tilde{A},t\in I=[t_0,T],$(3) ) at the point $t_i$ and ${\tilde{v}}_i\left(h\right)$ is the approximate solution with step size h at this point. So, ${\tilde{\gamma }}_k$ are known constants dependent on k and independent of h.

From Equation (8(8) $\begin{array}{r}{\tilde{v}}_i\left(h\right){\ominus }_{gH}\tilde{x}\left(t_i\right)={\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k+\mathcal{O}\left(h^{k+1}\right),\end{array}$(8) ), if $\theta h,0<\theta \ll 1$ is considered as step size, then (9) $\begin{array}{r}{\tilde{v}}_i\left(\theta h\right){\ominus }_{gH}\tilde{x}\left(t_i\right)={\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot (\theta h{)}^k+\mathcal{O}(h^{k+1}).\end{array}$(9) From Equations (8(8) $\begin{array}{r}{\tilde{v}}_i\left(h\right){\ominus }_{gH}\tilde{x}\left(t_i\right)={\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k+\mathcal{O}\left(h^{k+1}\right),\end{array}$(8) ) and (9(9) $\begin{array}{r}{\tilde{v}}_i\left(\theta h\right){\ominus }_{gH}\tilde{x}\left(t_i\right)={\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot (\theta h{)}^k+\mathcal{O}(h^{k+1}).\end{array}$(9) ), for two successive iterations, (10) $\begin{array}{r}{\tilde{v}}_i\left(h\right){\ominus }_{gH}{\tilde{v}}_i\left(\theta h\right)={\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot \left(1-{\theta }^k\right)h^k+\mathcal{O}\left(h^{k+1}\right).\end{array}$(10)

Theorem 3.1

The fuzzy multi-step method approximates Equations (5(5) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right)\oplus \frac{h}{12}\odot \\ \left[5\odot \tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right){\ominus }_{gH}16\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 23\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right){\ominus }_{gH}\frac{h}{12}\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \frac{2h}{3}\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\oplus \frac{5h}{12}\odot \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}(t_{i+2}\left)\right),\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(5) ), (6(6) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{2}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)+\tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 4\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_i\right)+\frac{h}{2}\odot \left[\tilde{g}\right(t_i,\tilde{v}\left(t_i\right))\oplus 2\odot \tilde{g}(t_{i+1},\tilde{v}\left(t_{i+1}\right))\oplus \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)\left)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(6) ), (7(7) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-3}\right)\oplus \frac{4h}{3}\odot \left[2\odot \tilde{g}(t_{i-2},\tilde{v}(t_{i-2}\left)\right){\ominus }_{gH}\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 2\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{3}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 4\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-3}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_{i-2}\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_2,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_3.\end{array}\end{array}\right.$(7) ) converge to the exact solution.

Proof.

See [3–7,43].

Theorem 3.2

The fuzzy multi-step method as Equations (5(5) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right)\oplus \frac{h}{12}\odot \\ \left[5\odot \tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right){\ominus }_{gH}16\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 23\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right){\ominus }_{gH}\frac{h}{12}\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \frac{2h}{3}\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\oplus \frac{5h}{12}\odot \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}(t_{i+2}\left)\right),\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(5) ), (6(6) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{2}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)+\tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 4\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_i\right)+\frac{h}{2}\odot \left[\tilde{g}\right(t_i,\tilde{v}\left(t_i\right))\oplus 2\odot \tilde{g}(t_{i+1},\tilde{v}\left(t_{i+1}\right))\oplus \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)\left)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(6) ), (7(7) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-3}\right)\oplus \frac{4h}{3}\odot \left[2\odot \tilde{g}(t_{i-2},\tilde{v}(t_{i-2}\left)\right){\ominus }_{gH}\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 2\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{3}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 4\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-3}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_{i-2}\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_2,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_3.\end{array}\end{array}\right.$(7) ) is stable.

Proof.

See [3–5,44].

Bede [6] defined the Characterization Theorem that provides certain conditions under which a FDE is equivalent to a system of ODEs with respect to H-differentiability. Thereafter, Bede and Gal [30] proposed another version of this theorem for solving FDEs under gH-differentiability. Both of these characterization theorems are employed to transfer the FDEs under fuzzy differentiability to systems of ODEs. Based on Definition 2.6, $g{H}_{\left(i\right)}$-differentiable, $g{H}_{\left(ii\right)}$-differentiable and Theorem 2.8 [6,7], each of Equations (5(5) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right)\oplus \frac{h}{12}\odot \\ \left[5\odot \tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right){\ominus }_{gH}16\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 23\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right){\ominus }_{gH}\frac{h}{12}\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \frac{2h}{3}\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\oplus \frac{5h}{12}\odot \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}(t_{i+2}\left)\right),\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(5) ), (6(6) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{2}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)+\tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 4\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_i\right)+\frac{h}{2}\odot \left[\tilde{g}\right(t_i,\tilde{v}\left(t_i\right))\oplus 2\odot \tilde{g}(t_{i+1},\tilde{v}\left(t_{i+1}\right))\oplus \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)\left)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(6) ) and (7(7) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-3}\right)\oplus \frac{4h}{3}\odot \left[2\odot \tilde{g}(t_{i-2},\tilde{v}(t_{i-2}\left)\right){\ominus }_{gH}\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 2\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{3}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 4\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-3}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_{i-2}\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_2,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_3.\end{array}\end{array}\right.$(7) ), under certain conditions, can be replaced by two equivalent systems of IVPs.

Definition 3.3

[26]

For two distinct fuzzy numbers $\tilde{y}$ and $\tilde{z}$ in $\mathcal{F}\left(\mathbb{R}\right),$ the notation $C_{\tilde{y},\tilde{z}}$ means the common proximity between $\tilde{y}$ and $\tilde{z}$, which is defined as, (11) $\begin{array}{r}{C}_{\tilde{y},\tilde{z}}=\log D\left(\tilde{y}\oslash \left(\tilde{y}{\ominus }_{{}_{gH}}\tilde{z}\right)-\frac{1}{2},\tilde{0}\right).\end{array}$(11)

Remark 3.1

By defuzzification, Equation (11(11) $\begin{array}{r}{C}_{\tilde{y},\tilde{z}}=\log D\left(\tilde{y}\oslash \left(\tilde{y}{\ominus }_{{}_{gH}}\tilde{z}\right)-\frac{1}{2},\tilde{0}\right).\end{array}$(11) ) can be written as follows $\begin{array}{r}{C}_{y,z}=\log \left|\frac{y}{y-z}-\frac{1}{2}\right|,\end{array}$ where the notation $C_{y,z}$ is the estimate number of common significant digits between two distinct real numbers $y$ and $z$ [15,17,22].

The following theorem is proved to show the accuracy of the fuzzy explicit k-step method (or implicit $(k-1)$-step method) by considering the common proximity of each corresponding components of the computed solution and the exact solution for a given FIVP.

Theorem 3.4

Let ${\tilde{v}}_i\left(h\right)$, ${\tilde{v}}_i\left(\theta h\right),0<\theta \ll 1$ be the approximate values of $\tilde{x}\left(t_i\right)$ in two successive iterations obtained from FIVP (3(3) ${\tilde{x}}^{\mathrm{\prime }}\left(t\right)=\tilde{g}(t,\tilde{x}(t\left)\right),\tilde{x}\left(t_0\right)=\tilde{A},t\in I=[t_0,T],$(3) ) based on fuzzy multi-step method respectively. Then (12) $C_{{\tilde{v}}_i\left(h\right),{\tilde{v}}_i\left(\theta h\right)}=C_{{\tilde{v}}_i\left(h\right),\tilde{x}\left(t_i\right)}+\log \left(\frac{1}{1-{\theta }^k}\right)+\mathcal{O}\left(h\right).$(12)

Proof.

From Equation (8(8) $\begin{array}{r}{\tilde{v}}_i\left(h\right){\ominus }_{gH}\tilde{x}\left(t_i\right)={\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k+\mathcal{O}\left(h^{k+1}\right),\end{array}$(8) ), since for h enough small, $\frac{1}{(1+\mathcal{O}(h\left)\right)}=(1+\mathcal{O}(h\left)\right)$ we deduce $\begin{array}{rl}{\tilde{v}}_i\left(h\right)\oslash \left({\tilde{v}}_i\left(h\right){\ominus }_{gH}\tilde{x}\left(t_i\right)\right)& ={\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k+\mathcal{O}\left(h^{k+1}\right)\right)\\ & ={\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\odot \left(1+\mathcal{O}\left(h\right)\right)\right)\\ & =\left(1+\mathcal{O}\left(h\right)\right)\odot {\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right),\end{array}$ then by considering $-\frac{1}{2}$ as abounded function which can be denoted by $\mathcal{O}\left(1\right)$, we obtain (13) $\begin{array}{r}{\tilde{v}}_i\left(h\right)\oslash \left({\tilde{v}}_i\left(h\right){\ominus }_{gH}\tilde{x}\left(t_i\right)\right)-\frac{1}{2}=\left(1+\mathcal{O}\left(h\right)\right)\odot {\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right).\end{array}$(13) Based on Definition (3.3) and properties of distance D, from Equation (13(13) $\begin{array}{r}{\tilde{v}}_i\left(h\right)\oslash \left({\tilde{v}}_i\left(h\right){\ominus }_{gH}\tilde{x}\left(t_i\right)\right)-\frac{1}{2}=\left(1+\mathcal{O}\left(h\right)\right)\odot {\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right).\end{array}$(13) ), we get $\begin{array}{rl}{C}_{{\tilde{v}}_i\left(h\right),\tilde{x}\left(t_i\right)}& =\log D\left(\left(1+\mathcal{O}\left(h\right)\right)\odot {\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right),\tilde{0}\right)\\ & =\log \left(\left(1+\mathcal{O}\left(h\right)\right)D\left({\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right),\tilde{0}\right)\right)\\ & =\log D\left({\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right),\tilde{0}\right)+\log \left(1+\mathcal{O}\left(h\right)\right),\end{array}$ therefore (14) $C_{{\tilde{v}}_i\left(h\right),\tilde{x}\left(t_i\right)}=\log D\left({\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right),\tilde{0}\right)+\mathcal{O}\left(h\right).$(14) Similarly from Equation (10(10) $\begin{array}{r}{\tilde{v}}_i\left(h\right){\ominus }_{gH}{\tilde{v}}_i\left(\theta h\right)={\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot \left(1-{\theta }^k\right)h^k+\mathcal{O}\left(h^{k+1}\right).\end{array}$(10) ), (15) $\begin{array}{rl}{\tilde{v}}_i\left(h\right)\oslash \left({\tilde{v}}_i\left(h\right){\ominus }_{gH}{\tilde{v}}_i\left(\theta h\right)\right)-\frac{1}{2}& =\left(1+\mathcal{O}\left(h\right)\right)\odot \frac{1}{1-{\theta }^k}\odot {\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)\\ & +\mathcal{O}\left(1\right).\end{array}$(15) By Definition (3.3) and properties of distance D, from Equation (15(15) $\begin{array}{rl}{\tilde{v}}_i\left(h\right)\oslash \left({\tilde{v}}_i\left(h\right){\ominus }_{gH}{\tilde{v}}_i\left(\theta h\right)\right)-\frac{1}{2}& =\left(1+\mathcal{O}\left(h\right)\right)\odot \frac{1}{1-{\theta }^k}\odot {\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)\\ & +\mathcal{O}\left(1\right).\end{array}$(15) ), we obtain (16) $\begin{array}{r}{C}_{{\tilde{v}}_i\left(h\right),{\tilde{v}}_i\left(\theta h\right)}=\log D\left({\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right),\tilde{0}\right)+\log \left(\frac{1}{1-{\theta }^k}\right)+\mathcal{O}\left(h\right).\end{array}$(16) According to Equations (14(14) $C_{{\tilde{v}}_i\left(h\right),\tilde{x}\left(t_i\right)}=\log D\left({\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right),\tilde{0}\right)+\mathcal{O}\left(h\right).$(14) ) and (16(16) $\begin{array}{r}{C}_{{\tilde{v}}_i\left(h\right),{\tilde{v}}_i\left(\theta h\right)}=\log D\left({\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right),\tilde{0}\right)+\log \left(\frac{1}{1-{\theta }^k}\right)+\mathcal{O}\left(h\right).\end{array}$(16) ) $C_{{\tilde{v}}_i\left(h\right),{\tilde{v}}_i\left(\theta h\right)}=C_{{\tilde{v}}_i\left(h\right),\tilde{x}\left(t_i\right)}+\log \left(\frac{1}{1-{\theta }^k}\right)+\mathcal{O}\left(h\right).$

In Equation (12(12) $C_{{\tilde{v}}_i\left(h\right),{\tilde{v}}_i\left(\theta h\right)}=C_{{\tilde{v}}_i\left(h\right),\tilde{x}\left(t_i\right)}+\log \left(\frac{1}{1-{\theta }^k}\right)+\mathcal{O}\left(h\right).$(12) ) since $0\le \theta <<1$ hence $0<\log \left(\frac{1}{1-{\theta }^k}\right)<1.$ Therefore, it means that, when the fuzzy multi-step methods are used in order to estimate $\tilde{x}\left(t_i\right)$ then, for h small enough, the common proximity between two successive fuzzy values ${\tilde{v}}_i\left(h\right)$ and ${\tilde{v}}_i\left(\theta h\right)$ are almost equal to the common proximity between $\tilde{x}\left(t_i\right)$ and ${\tilde{v}}_i\left(h\right)$. Therefore, if the fuzzy CESTAC method is used then, the computations of the sequence ${\tilde{v}}_i\left(h\right)$'s are stopped when for an index like $h_{opt},C_{{\tilde{v}}_i\left(h_{opt}\right),{\tilde{v}}_i\left(\theta h_{opt}\right)}\simeq C_{{\tilde{v}}_i\left(h_{opt}\right),\tilde{x}\left(t_i\right)}$. In this case, ${\tilde{v}}_i\left(h_{opt}\right)$ is a suitable approximation of $\tilde{x}\left(t_i\right)$.

In Equation (14(14) $C_{{\tilde{v}}_i\left(h\right),\tilde{x}\left(t_i\right)}=\log D\left({\tilde{v}}_i\left(h\right)\oslash \left({\tilde{\gamma }}_k\otimes {\tilde{x}}^{(k+1)}\left(t_i\right)\odot h^k\right)+\mathcal{O}\left(1\right),\tilde{0}\right)+\mathcal{O}\left(h\right).$(14) ), if k = 4 and $\theta =\frac{1}{2}$ then, $C_{{\tilde{v}}_i\left(h\right),{\tilde{v}}_i\left(\theta h\right)}=C_{{\tilde{v}}_i\left(h\right),\tilde{x}\left(t_i\right)}+\log \left(\frac{16}{15}\right)+O\left(h\right).$ Also, if k = 3 and $\theta =\frac{1}{3}$ then, $C_{{\tilde{v}}_i\left(h\right),{\tilde{v}}_i\left(\theta h\right)}=C_{{\tilde{v}}_i\left(h\right),\tilde{x}\left(t_i\right)}+\log \left(\frac{27}{26}\right)+O\left(h\right).$

4. CESTAC Method

In many numerical iterative and approximate recursive schemes, the absolute error is applied to show the accuracy of the method. In order to apply the absolute error, the existence of the exact solution is necessary. In the iterative algorithms which are constructed based on the common FPA, the termination criterion depends on a tolerance parameter like epsilon (eps) as follows: (17) $\left|Z_m-\psi \right|<eps,$(17) where ψ is the exact solution and $Z_m$ is the m-th computed result obtained from the iterative algorithm. This criterion may not be acceptable. If eps is chosen very large, the iterations are stopped before getting access to a suitable approximation. If eps is chosen very small then, unnecessary iterations are done without improving the accuracy of the results. So, it can not be determined the optimal iteration m by applying a tolerance in the stopping criterion. Also, if one applies the criterion $\left|Z_m-Z_{m+1}\right|<eps$, in place of the condition (17(17) $\left|Z_m-\psi \right|<eps,$(17) ), it is not any guarantee to confirm $Z_m$ is an approximation of ψ without knowing the exact solution. This is because of the nature of the FPA. Therefore, it needs to be suggested another way which is independent of this tolerance. For this purpose, we must replace the FPA by a new arithmetic so that it is able to omit the tolerance epsilon in the termination criterion. This new environment is the stochastic arithmetic. The details of this arithmetic can be found in [13,15–21,25,45]. In order to use this arithmetic in a discrete case, the CESTAC method should be applied [15,36,45]. This method is able to validate the results and detect any instability step by step during the run of a code. The algorithm of this method is based on the concept of common significant digits. In this case, the following termination criterion is substituted which is independent of the value epsilon. (18) $\left|Z_m-Z_{m+1}\right|=@.0,$(18) where the symbol $@.0$ is denoted as the informatical zero which means the corresponding value (difference between two sequential results) has not any significant digits and hence in the point of computational view we can say $Z_m\cong Z_{m+1}.$ Equation (18(18) $\left|Z_m-Z_{m+1}\right|=@.0,$(18) ) means when the difference between two sequential results is an informatical zero, the computations must be stopped and any calculations after m-th iteration is redundant. In order to implement the CESTAC method, the CADNA library was designated by Chesnueax [22,46]. This library is able to perform the discrete stochastic arithmetic and the CESTAC method automatically on any C++ or Fortran code. So, in order to apply it, the main code must be written in one of these programming languages.

The CESTAC method was developed by La Porte and Vignes [13]. This method is able to detect numerical instabilities which occur during the run and estimate accuracy of the computed results. During the run, as soon as the number of the significant digits of any result becomes zero, an informatical zero is detected and the result is printed by the notation $@.0$.

The basic idea of the CESTAC method is to replace the usual FPA with a random arithmetic. Consequently, each result appears as a random variable. This approach leads toward two concepts: stochastic numbers and stochastic arithmetic.

The applying of the CESTAC method in a scientific program has the following advantages:

1. The accuracy of any numerical result is estimated, during the running of a program.

2. The numerical instabilities are detected and the branching are checked.

3. Unnecessary iterations are eliminated, which the FPA is not able to distinguish them. In some cases, the termination criterion of iterative methods is not suitable so that the implementation of the algorithm is continued without improvement in the accuracy of the result. In the SA, instead of the termination criterion, a criterion that directly reflects the mathematical condition, is replaced, that must be satisfied by the solution.

4. It is able to find the optimal step of the iterative methods, which after this step, the accuracy of the result does not increase or maybe decrease, because of the rounding error accumulation.

5. It is an effective and powerful tool that helps to achieve the validation of scientific programs and gives them a reliability.

Let F be a set of real values which are reproduced by computer and the arbitrary value ψ is demonstrated as $\mathrm{\Psi }\in F$. In the personal computer, Ψ with the binary FPA, ρ mantissa bits and the rounding error term is shown by (19) $\mathrm{\Psi }=\psi -ϵ2^{E-\theta }\rho ,$(19) where $2^{-\theta }\rho$ is the missing segment of mantissa which is obtained from round-off error, ε is the sign of ψ, E is the binary power of the outcome. If ρ is a random parameter on $[-1,1]$ which is distributed uniformly and is applied to perturb on the last mantissa bit of Ψ then, the random result of Ψ can be calculated where mean $\left(\mu \right)$ and standard deviation $\left(\sigma \right)$ are applied to guarantee the precision of results [13,45,47–49].

In PC, for $\theta =24,53$ the results can be obtained by single or double precision respectively. By M times performing the process for ${\mathrm{\Psi }}_i,i=1,\dots ,M$ the distribution of them is in the quasi Gaussian form. Therefore, the mean of them is equal with the exact value of ψ and the values of μ and σ can be estimated by these M samples. The following algorithm of the CESTAC method is presented where ${\tau }_{\delta }$ is the value of T distribution with M−1 degree of freedom and confidence interval $1-\delta$.

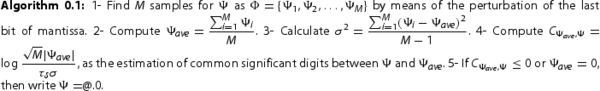
In the sequel, Algorithm 4.1 is developed in fuzzy case.

4.1. Fuzzy CESTAC Method

Let $\tilde{y}$ be a fuzzy number in $\mathcal{F}\left(\mathbb{R}\right)$. Then, $\tilde{y}$ is represented as $\tilde{w}$ in the computer. It can be shown that: (20) $\begin{array}{r}\tilde{w}=\tilde{y}{\ominus }_{gH}ϵ2^{E-P}\odot \tilde{z},\end{array}$(20) where, ε is the sign of $y^{\pm }\left(r\right)$, and $2^{-P}{z}^{\pm }\left(r\right)$ is the lost part of the mantissa due to round-off error for $r\in [0,1]$ and E is the binary exponent of the results. In single precision case, $P=24$ and in double precision case P = 53. In the fuzzy CESTAC method, $z^{\pm }\left(r\right),0\le r\le 1$ is considered as a fuzzy random variable uniformly distributed on $[-1,1]$. In order to find samples for the obtained random variables, we perturb the last mantissa bit of the values $w^{\pm }\left(r\right)$, $0\le r\le 1$. The algorithm of the fuzzy CESTAC method is as follows where ${\tau }_{\text{β}}$ is the value of T distribution with $N-1$ degree of freedom and confidence interval $1-\text{β}$. If $M=3$ and $\text{β}=0.05$ then ${\tau }_{\text{β}}=\mathrm{4.303.}$

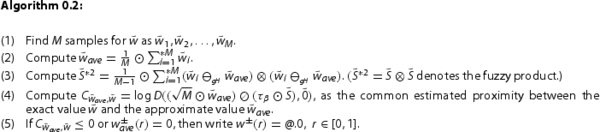
Now, the following algorithm is introduced which is performed in the CADNA library based on the fuzzy CESTAC method to solve a given FIVP by applying one of the mentioned multi-step methods. In this case, $D\left({\tilde{v}}_i\right(h),{\tilde{v}}_i(\theta h\left)\right)=@.0$ is chosen as the termination criterion which means the Hausdorff distance between two sequential results is an informatical zero. In this algorithm, ${\tilde{v}}_i\left(h\right)$ and ${\tilde{v}}_i\left(\theta h\right)$ are the approximate values of $\tilde{x}\left(t_i\right)$ in two successive iterations obtained from the fuzzy multi-step methods, respectively. By implementing Algorithm 4.2, the optimal step size and optimal values of the computed results are obtained with their accuracy and therefore the results are validated.

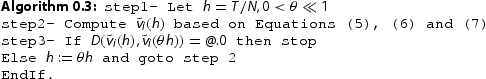
In [1,9,10,50], a fuzzy initial value problem (FIVP) was converted to a system of ordinary differential equations, then by applying the Characterization Theorem the solution of this system presents a fuzzy solution for the FIVP. In the next section, it is considered this scheme to solve the examples based on Algorithm 4.3 using the CADNA library to validate the results.

5. Numerical Examples

In this section, two examples are solved based on the proposed algorithm by means of the CADNA library in the stochastic arithmetic. The first example is based on $g{H}_i$ and the second example is based on $g{H}_{ii}$. The programs have been written in $C++$ and executed on a Linux machine using CADNA library based on Algorithm 4.3. In the tables, FPC, FIPC and FMPC methods are the multi-step schemes mentioned in Equations (5(5) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right)\oplus \frac{h}{12}\odot \\ \left[5\odot \tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right){\ominus }_{gH}16\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 23\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_{i+1}\right){\ominus }_{gH}\frac{h}{12}\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \frac{2h}{3}\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\oplus \frac{5h}{12}\odot \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}(t_{i+2}\left)\right),\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(5) ), (6(6) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{2}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)+\tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus 4\odot \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+2}\right)=\tilde{v}\left(t_i\right)+\frac{h}{2}\odot \left[\tilde{g}\right(t_i,\tilde{v}\left(t_i\right))\oplus 2\odot \tilde{g}(t_{i+1},\tilde{v}\left(t_{i+1}\right))\oplus \tilde{g}(t_{i+2},{\tilde{v}}^{\left(0\right)}\left(t_{i+2}\right)\left)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i+1}\right)={\tilde{\alpha }}_2.\end{array}\end{array}\right.$(6) ) and (7(7) $\left\{\begin{array}{l}\begin{array}{l}{\tilde{v}}^{\left(0\right)}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-3}\right)\oplus \frac{4h}{3}\odot \left[2\odot \tilde{g}(t_{i-2},\tilde{v}(t_{i-2}\left)\right){\ominus }_{gH}\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 2\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\right],\\ \left(predictor\right)\\ \tilde{v}\left(t_{i+1}\right)=\tilde{v}\left(t_{i-1}\right)\oplus \frac{h}{3}\odot \left[\tilde{g}(t_{i-1},\tilde{v}(t_{i-1}\left)\right)\oplus 4\odot \tilde{g}(t_i,\tilde{v}(t_i\left)\right)\oplus \tilde{g}(t_{i+1},\tilde{v}(t_{i+1}\left)\right)\right],\\ \left(corrector\right)\\ \tilde{v}\left(t_{i-3}\right)={\tilde{\alpha }}_0,\tilde{v}\left(t_{i-2}\right)={\tilde{\alpha }}_1,\tilde{v}\left(t_{i-1}\right)={\tilde{\alpha }}_2,\tilde{v}\left(t_i\right)={\tilde{\alpha }}_3.\end{array}\end{array}\right.$(7) ) respectively.

Example 5.1

Consider the fuzzy initial value problem [4]. (21) ${\tilde{x}}_{g{H}_i}^{\mathrm{\prime }}\left(t\right)\oplus \tilde{x}\left(t\right)=1+t,$(21) with initial conditions $\left[x\right(0){]}^r=[0.96+0.04r,1.01-0.01r],r\in (0,1].$ The exact solution at $t=0.1$ $\left[x\right(0.1){]}^r=[0.1+(0.96+0.04r)e^{(-0.1)},0.1+(1.01-0.01r)e^{(-0.1)}],r\in (0,1].$

Based on Algorithm 4.3, the optimal step sizes of these methods are shown in Table 1. Also, for $\theta =1/3,t=0.1$, the results of Algorithm 4.3 are shown in Tables 2, 3 and 4, respectively. The Hausdorff distance between the approximate solutions ${\tilde{v}}_i\left(h\right)$ and ${\tilde{v}}_i\left(\theta h\right)$ in two successive iterations with the Hausdorff distance between the exact solution $\tilde{x}\left(t_i\right)$ and the approximate solution ${\tilde{v}}_i\left(h\right)$ of Equation (21(21) ${\tilde{x}}_{g{H}_i}^{\mathrm{\prime }}\left(t\right)\oplus \tilde{x}\left(t\right)=1+t,$(21) ) at $t=0.1$ are compared. In the tables, $D_1=D\left({\tilde{v}}_i\right(h),\tilde{x}(t_i\left)\right)$ and $D_2=D\left({\tilde{v}}_i\right(h),{\tilde{v}}_i(\theta h\left)\right)$ and the optimal step size for each method is shown. Moreover, Table 5 shows the results of this algorithm for $t=0.5$ in the FIPC-3step method. Also, Table 6 shows the estimate number of common significant digits for end-points of r-cuts, $r=0\left(0.1\right)1$, between two sequential results are compared with the computed significant digits common to the approximate and the exact values for the FIPC-4step method.

Table 1. The optimal step size of Example 5.1.

θ	1/2			1/3
Method	FPC-3step	FIPC-3step	FMPC-4step	FPC-3step	FIPC-3step	FMPC-4step
$h_{opt}$	${\displaystyle \frac{1}{640}}$	${\displaystyle \frac{1}{160}}$	${\displaystyle \frac{1}{80}}$	${\displaystyle \frac{1}{2430}}$	${\displaystyle \frac{1}{810}}$	${\displaystyle \frac{1}{270}}$

Table 2. Numerical results of Example 5.1.

FPC-3step method, $\theta =1/3,t=0.1$
i	h	r	$v_i^{-}(h;r)$	$v_i^{+}(h;r)$	$D_1$	$D_2$
1	${\displaystyle \frac{0.1}{3}}$	0.0	0.9687483E+000	0.101378E+001
		0.1	0.9723573E+000	0.101288E+001
		0.2	0.9759662E+000	0.1011992E+001	–	–
		⋮	⋮	⋮
		1	0.1004837E+001	0.1004837E+001
2	${\displaystyle \frac{0.1}{9}}$	0.0	0.9689204E+000	0.1013609E+001
		0.1	0.972512E+000	0.1012732E+001
		0.2	0.9761037E+000	0.1011854E+001	0.276E−003	0.171E−003
		⋮	⋮	⋮
		1	0.100483E+001	0.100483E+001
⋮	⋮	⋮	⋮	⋮	⋮	⋮
4	${\displaystyle \frac{0.1}{81}}$	0.0	0.9686382E+000	0.101387E+001
		0.1	0.9722576E+000	0.1012069E+001
		0.2	0.976172E+000	0.101178E+001	0.36E−003	0.22E−004
		⋮	⋮	⋮
		1	0.100483E+001	0.100483E+001
5	${\displaystyle \frac{0.1}{243}}$	0.0	0.969014E+000	0.10135E+001
		0.1	0.972596E+000	0.101264E+001
		0.2	0.976178E+000	0.101177E+001	0.37E−003	@.0
		⋮	⋮	⋮
		1	0.100483E+001	0.100483E+001

Table 3. Numerical results of Example 5.1.

FIPC-3step method, $\theta =1/3,t=0.1$
i	h	r	$v_i^{-}(h;r)$	$v_i^{+}(h;r)$	$D_1$	$D_2$
1	${\displaystyle \frac{0.1}{3}}$	0.0	0.9686382E+000	0.101387E+001
		0.1	0.9722576E+000	0.1012974E+001
		0.2	0.9758761E+000	0.101116E+001	–	–
		⋮	⋮	⋮
		1	0.1004831E+001	0.100483E+001
2	${\displaystyle \frac{0.1}{9}}$	0.0	0.9686431E+000	0.101388E+001
		0.1	0.9722625E+000	0.101298E+001
		0.2	0.9758818E+000	0.101207E+001	@.0	0.5E−005
		⋮	⋮	⋮
		1	0.1004836E+001	0.1004836E+001
3	${\displaystyle \frac{0.1}{27}}$	0.0	0.9686438E+000	0.101388E+001
		0.1	0.972263E+000	0.101298E+001
		0.2	0.9758823E+000	0.101207E+001	@.0	0.7E−006
		⋮	⋮	⋮
		1	0.100483E+001	0.100483E+001
4	${\displaystyle \frac{0.1}{81}}$	0.0	0.968643E+000	0.10138E+001
		0.1	0.972263E+000	0.101298E+001
		0.2	0.975882E+000	0.101207E+001	@.0	@.0
		⋮	⋮	⋮
		1	0.100483E+001	0.100483E+001

Table 4. Numerical results of Example 5.1.

FMPC-4step method, $\theta =1/3,t=0.1$
i	h	r	$v_i^{-}(h;r)$	$v_i^{+}(h;r)$	$D_1$	$D_2$
1	${\displaystyle \frac{0.1}{3}}$	0.0	0.9686439E+000	0.1013885E+001
		0.1	0.9722631E+000	0.1012980E+001
		0.2	0.9758825E+000	0.1012075E+001	–	–
		⋮	⋮	⋮
		1	0.1004837E+001	0.100483E+001
2	${\displaystyle \frac{0.1}{9}}$	0.0	0.9686364E+000	0.1013893E+001
		0.1	0.9722564E+000	0.101298E+001
		0.2	0.9758765E+000	0.1012082E+001	0.75E−005	0.3E−005
		⋮	⋮	⋮
		1	0.1004837E+001	0.1004837E+001
3	${\displaystyle \frac{0.1}{27}}$	0.0	0.9686405E+000	0.101388E+001
		0.1	0.9722604E+000	0.101298E+001
		0.2	0.975879E+000	0.1012078E+001	@.0	@.0
		⋮	⋮	⋮
		1	0.100483E+001	0.100483E+001

Table 5. Numerical results of Example 5.1.

FIPC-3step method, $\theta =1/2,t=0.5$
i	h	r	$v_i^{-}(h;r)$	$v_i^{+}(h;r)$	$D_1$	$D_2$
1	${\displaystyle \frac{0.5}{2}}$	0.0	0.1082269E+001	0.1112596E+001
		0.1	0.1084695E+001	0.1111989E+001
		0.2	0.1087121E+001	0.1111382E+001	–	–
		⋮	⋮	⋮
		1	0.1106530E+001	0.1106530E+001
2	${\displaystyle \frac{0.5}{4}}$	0.0	0.1082064E+001	0.1112380E+001
		0.1	0.108448E+001	0.1111773E+001
		0.2	0.108691E+001	0.111116E+001	0.213E-003	0.213E−003
		⋮	⋮	⋮
		1	0.1106317E+001	0.1106317E+001
3	${\displaystyle \frac{0.5}{8}}$	0.0	0.1082195E+001	0.111251E+001
		0.1	0.1084621E+001	0.1111912E+001
		0.2	0.108704E+001	0.1111305E+001	0.13E−003	0.76E−004
		⋮	⋮	⋮
		1	0.110645E+001	0.1106454E+001
⋮	⋮	⋮	⋮	⋮	⋮	⋮
6	${\displaystyle \frac{0.5}{64}}$	0.0	0.108226E+001	0.111259E+001
		0.1	0.108469E+001	0.111198E+001
		0.2	0.108711E+001	0.111138E+001	0.4E−005	@.0
		⋮	⋮	⋮
		1	0.110652E+001	0.110652E+001
7	${\displaystyle \frac{0.1}{128}}$	0.0	0.108226E+001	0.111259E+001
		0.1	0.108469E+001	0.111198E+001
		0.2	0.108712E+001	0.111138E+001	@.0	@.0
		⋮	⋮	⋮
		1	0.11065E+001	0.110653E+001

Table 6. Comparison of the common significant digits $\left(C\right)$ in the FMPC-4step method, $h_{opt}=\frac{0.1}{27}$ for Example 5.1.

r	$C_{v_i^{-}(h;r),v_i^{-}(\theta h;r)}$	$C_{v_i^{-}(h;r),x_i^{-}\left(0.1\right)}$	$C_{v_i^{+}(h;r),v_i^{+}(\theta h;r)}$	$C_{v_i^{+}(h;r),x_i^{+}\left(0.1\right)}$
0.0	0.12E+002	0.12E+002	0.12E+002	0.12E+002
0.1	0.12E+002	0.12E+002	0.12E+002	0.123E+002
0.2	0.12E+002	0.12E+002	0.12E+002	0.12E+002
0.3	0.12E+002	0.12E+002	0.121E+002	0.13E+002
0.4	0.128E+002	0.13E+002	0.122E+002	0.13E+002
0.5	0.13E+002	0.122E+002	0.1E+002	0.1E+002
0.6	0.13E+002	0.123E+002	0.1E+002	0.1E+002
0.7	0.13E+002	0.13E+002	0.1E+002	0.1E+002
0.8	0.14E+002	0.134E+002	0.133E+002	0.14E+002
0.9	0.1E+002	0.1E+002	0.1E+002	0.1E+002
1.0	@.0	@.0	@.0	@.0

Example 5.2

Let the following fuzzy stiff equation: (22) ${\tilde{x}}_{g{H}_{i}i}^{\mathrm{\prime }}\left(t\right)=\tilde{c}\otimes \tilde{x}\left(t\right),$(22) with initial condition $\left[x\right(0){]}^r=[0.96+0.04r,1.03-0.03r],r\in (0,1],$ where $\tilde{c}=(-25.05/-25/-24.97).$ The analytical solution is $\begin{array}{r}{x}^{-}(t;r)=x^{-}(0;r)e^{c^{-}t}=(0.96+0.04r)e^{(-25.05+0.05r)t},\\ x^{+}(t;r)=x^{+}(0;r)e^{c^{+}t}=(1.03-0.03r)e^{(-24.97-0.03r)t}.\end{array}$

The $h_{opt}$ for each multi-step method is determined in Table 7 based on Algorithm 4.3.

Table 7. The optimal step size of Example 5.2.

θ	1/2			1/3
Method	FPC-3step	FIPC-3step	FMPC-4step	FPC-3step	FIPC-3step	FMPC-4step
$h_{opt}$	${\displaystyle \frac{0.1}{2048}}$	${\displaystyle \frac{0.1}{512}}$	${\displaystyle \frac{0.1}{512}}$	${\displaystyle \frac{0.1}{6561}}$	${\displaystyle \frac{0.1}{729}}$	${\displaystyle \frac{0.1}{729}}$

The fuzzy stiff differential equations are characterized as those whose exact solution has a term of the form $e^{\tilde{c}t}$ where $\tilde{c}$ is a small negative fuzzy number. This is usually only a part of the solution which is called transient solution. The transient portion of a stiff equation will rapidly decrease to zero as t increases. In Equation (22(22) ${\tilde{x}}_{g{H}_{i}i}^{\mathrm{\prime }}\left(t\right)=\tilde{c}\otimes \tilde{x}\left(t\right),$(22) ) $\tilde{c}$ is nearly $-25$. The results of multi-step methods in the case $\theta =1/2$ at $t=0.1$ are shown in Tables 8, 9 and 10. Also, Table 11 illustrates the result of the proposed algorithm with t = 0.5 and Table 12 determines the common significant digits of the end-points for different r-cuts in the FIPC-3step method.

Table 8. Numerical results of Example 5.2.

FPC-3step method, $\theta =1/2$, $t=0.1$
i	h	r	$v_i^{-}(h;r)$	$v_i^{+}(h;r)$	$D_1$	$D_2$
2	${\displaystyle \frac{0.1}{4}}$	0.0	0.803239E−001	0.1016841E+000
		0.1	0.814453E−001	0.100669E+000
		0.2	0.825666E−001	0.996547E−001	0.16882E−001	0.1016841E+000
		⋮	⋮	⋮
		1	0.915343E−001	0.915342E−001
3	${\displaystyle \frac{0.1}{8}}$	0.0	0.768867E−001	0.8756085E−001
		0.1	0.774680E−001	0.870753E−001
		0.2	0.780496E−001	0.865899E−001	0.27592E−002	0.141232E−001
		⋮	⋮	⋮
		1	0.8271046E−001	0.827104E−001
4	${\displaystyle \frac{0.1}{16}}$	0.0	0.783973E−001	0.849148E−001
		0.1	0.787701E−001	0.846366E−001
		0.2	0.791432E−001	0.843586E−001	0.1132E−003	0.26460E−002
		⋮	⋮	⋮
		1	0.8213854E−001	0.821385E−001
⋮	⋮	⋮	⋮	⋮	⋮	⋮
10	${\displaystyle \frac{0.1}{1024}}$	0.0	0.793893E−001	0.83816E−001
		0.1	0.796574E−001	0.83642E−001
		0.2	0.799261E−001	0.834693E−001	0.984E−003	0.1E−004
		⋮	⋮	⋮
		1	0.82084E−001	0.82084E−001
11	${\displaystyle \frac{0.1}{2048}}$	0.0	0.79394E−001	0.83811E−001
		0.1	0.79662E−001	0.83638E−001
		0.2	0.79930E−001	0.83465E−001	0.69E−003	@.0
		⋮	⋮	⋮
		1	0.82085E−001	0.820851E−001

Table 9. Numerical results of Example 5.2.

FIPC-3step method, $\theta =1/2$, $t=0.1$
i	h	r	$v_i^{-}(h;r)$	$v_i^{+}(h;r)$	$D_1$	$D_2$
2	${\displaystyle \frac{0.1}{4}}$	0.0	0.741218E−001	0.801331E−001
		0.1	0.744630E−001	0.798738E−001
		0.2	0.748044E−001	0.7961454E−001	0.46683E−002	0.801331E−001
		⋮	⋮	⋮
		1	0.775463E−001	0.775463E−001
3	${\displaystyle \frac{0.1}{8}}$	0.0	0.780348E−001	0.843083E−001
		0.1	0.783911E−001	0.840377E−001
		0.2	0.787476E−001	0.837674E−001	0.4932E−003	0.41751E−002
		⋮	⋮	⋮
		1	0.816095E−001	0.816095E−001
4	${\displaystyle \frac{0.1}{16}}$	0.0	0.783540E−001	0.84656E−001
		0.1	0.787119E−001	0.84384E−001
		0.2	0.790702E−001	0.841130E−001	0.143E−003	0.345E−003
		⋮	⋮	⋮
		1	0.819451E−001	0.81945E−001
⋮	⋮	⋮	⋮	⋮	⋮	⋮
8	${\displaystyle \frac{0.1}{256}}$	0.0	0.78485E−001	0.84799E−001
		0.1	0.78843E−001	0.84527E−001
		0.2	0.79203E−001	0.842550E−001	@.0	0.4E−005
		⋮	⋮	⋮
		1	0.82083E−001	0.82083E−001
9	${\displaystyle \frac{0.1}{512}}$	0.0	0.784861E−001	0.84801E−001
		0.1	0.78845E−001	0.84529E−001
		0.2	0.79203E−001	0.84255E−001	@.0	@.0
		⋮	⋮	⋮
		1	0.82084E−001	0.82084E−001

Table 10. Numerical results of Example 5.2.

FMPC-4step method, $\theta =1/2$, t = 0.1
i	h	r	$v_i^{-}(h;r)$	$v_i^{+}(h;r)$	$D_1$	$D_2$
2	${\displaystyle \frac{0.1}{4}}$	0.0	0.729963E−001	0.8622912E−001
		0.1	0.737009E−001	0.856108E−001
		0.2	0.744055E−001	0.849927E−001	0.54906E−002	0.8622913E−001
		⋮	⋮	⋮
		1	0.8004966E−001	0.800496E−001
3	${\displaystyle \frac{0.1}{8}}$	0.0	0.762335E−001	0.869008E−001
		0.1	0.7681009E−001	0.864111E−001
		0.2	0.773869E−001	0.859216E−001	0.2253E−002	0.32372E−002
		⋮	⋮	⋮
		1	0.820095E−001	0.820095E−001
4	${\displaystyle \frac{0.1}{16}}$	0.0	0.762335E−001	0.869008E−001
		0.1	0.7681009E−001	0.864111E−001
		0.2	0.773869E−001	0.859216E−001	0.2253E−002	0.32372E−002
		⋮	⋮	⋮
		1	0.820095E−001	0.820095E−001
⋮	⋮	⋮	⋮	⋮	⋮	⋮
8	${\displaystyle \frac{0.1}{256}}$	0.0	0.784538E−001	0.84834E−001
		0.1	0.78815E−001	0.84559E−001
		0.2	0.79177E−001	0.84283E−001	0.30E−004	0.37E−004
		⋮	⋮	⋮
		1	0.820848E−001	0.82084E−001
9	${\displaystyle \frac{0.1}{512}}$	0.0	0.78471E−001	0.84817E−001
		0.1	0.78831E−001	0.84543E−001
		0.2	0.79191E−001	0.84270E−001	@.0	@.0
		⋮	⋮	⋮
		1	0.82085E−001	0.82085E−001

Table 11. Numerical results of Example 5.2.

FPC-3step method, $\theta =1/2$, t = 0.5
i	h	r	$v_i^{-}(h;r)$	$v_i^{+}(h;r)$	$D_1$	$D_2$
6	${\displaystyle \frac{0.1}{64}}$	0.0	0.330108E−005	0.414505E−005
		0.1	0.33461E−005	0.41060E−005
		0.2	0.339136E−005	0.406714E−005	0.25995E−004	0.24859E−006
		⋮	⋮	⋮
		1	0.37569E−005	0.37569E−005
7	${\displaystyle \frac{0.1}{128}}$	0.0	0.358700E−005	0.380149E−005
		0.1	0.360097E−005	0.379414E−005
		0.2	0.361500E−005	0.378683E−005	0.3435E−006	0.97753E−007
		⋮	⋮	⋮
		1	0.372933E−005	0.37293E−005
⋮	⋮	⋮	⋮	⋮	⋮	⋮
12	${\displaystyle \frac{0.1}{4096}}$	0.0	0.36379E−005	0.37442E−005
		0.1	0.36466E−005	0.37423E−005
		0.2	0.36553E−005	0.374051E−005	0.4E−009	0.1522E−008
		⋮	⋮	⋮
		1	0.37266E−005	0.37266E−005
13	${\displaystyle \frac{0.1}{8192}}$	0.0	0.363839E−005	0.37438E−005
		0.1	0.36470E−005	0.37419E−005
		0.2	0.365568E−005	0.37401E−005	@.0	0.13E−009
		⋮	⋮	⋮
		1	0.37266E−005	0.37266E−005

Table 12. Comparison of the common significant digits $\left(C\right)$ in the FIPC-3step method, $h_{opt}=\frac{0.1}{512}$ for Example 5.2.

r	$C_{v_i^{-}(h;r),v_i^{-}(\theta h;r)}$	$C_{v_i^{-}(h;r),x_i^{-}\left(0.1\right)}$	$C_{v_i^{+}(h;r),v_i^{+}(\theta h;r)}$	$C_{v_i^{+}(h;r),x_i^{+}\left(0.1\right)}$
0.0	0.99E+001	0.1E+002	0.1E+002	0.1E+002
0.1	0.93E+001	0.1E+002	0.98E+001	0.1E+002
0.2	0.93E+001	0.1E+002	0.99E+001	0.1E+002
0.3	0.98E+001	0.1E+002	0.99E+001	0.1E+002
0.4	0.94E+001	0.1E+002	0.97E+001	0.1E+002
0.5	0.93E+001	0.1E+002	0.98E+001	0.1E+002
0.6	0.96E+001	0.1E+002	0.99E+001	0.1E+002
0.7	0.99E+001	0.1E+002	0.98E+001	0.1E+002
0.8	0.98E+001	0.1E+002	0.99E+001	0.1E+002
0.9	0.99E+001	0.1E+002	0.98E+001	0.1E+002
1.0	@.0	@.0	@.0	@.0

6. Conclusion

In this paper, the use of the fuzzy CESTAC method and the CADNA library were discussed which allows us to find the optimal step ($h_{opt}$) of the fuzzy multi-step methods as the PC methods under gH-differentiability and validate the results in solving a fuzzy differential equation with initial conditions. As we observed in the tables, by using the optimal termination criterion in Algorithm 1 which uses the computational zero, to stop correctly the iterative process, to save computer time, because many useless iterations are not performed, and on the other hand, furnished by the fuzzy multi-step methods, to estimate the accuracy of the optimal iteration. Consequently, it is suggested due to the numerical problems of the FPA, the SA is replaced to implement the algorithms of solving the FDEs with a reliable scheme.

Acknowledgments

The authors would like to thank the anonymous referees for their constructive comments to improve the quality of this work.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Mohammad Ali Fariborzi Araghi

Mohammad Ali Fariborzi Araghi was born in Tehran, Iran. He received B.SC. degree in mathematics from Kharazmi university, M.SC. degree in applied mathematics from Islamic Azad university, Karaj branch and Ph.D. degree in applied mathematics, numerical analysis field, from Islamic Azad university, Science and Research branch. He is the associate professor of Islamic Azad university, Central Tehran branch. His research interests are numerical solutions of integral or differential equations and applications of fuzzy mathematics.

Hasan Barzegar Kelishami

Hasan Barzegar Kelishami was born in Gilan, Iran. He received B.SC. degree in mathematics from Islamic Azad university, Karaj branch, M.SC. degree in applied mathematics from Islamic Azad university, Science and Research branch and Ph.D. degree in applied mathematics, numerical analysis field, from Islamic Azad university, Central Tehran branch. He is a lecturer of Islamic Azad university, North Tehran branch, now. His research interests are numerical solutions of integral or differential equations and applications of fuzzy mathematics.