Fuzzy Regression in Predicting Math Achievement, Based on Philosophic-Mindedness, Creativity, Mathematics Self-efficacy, and Mathematics Self-concept

ABSTRACT

The present study proposes a flexible/soft model for investigating the role of philosophic-mindedness, creativity, mathematics self-efficacy, and mathematics self-concept in predicting math achievement. To do this end, a fuzzy regression model is developed. Two common criteria are used to evaluate the obtained model. Moreover, the predictability of the model is explained. The case study involves 28 male students from Marand, Iran (year 2015–2016) who took part in a test of mathematics achievement. The participants were junior high-school students in science field of study who were asked to answer four questionnaires pertaining to philosophic-mindedness, creativity, mathematics self-efficacy, and mathematics self-concept. The analysis of the results through fuzzy regression revealed that philosophical-mindedness is not linked to participants' math achievement, while the variables of creativity, mathematics self-efficacy, and mathematics self-concept are positively correlated. The results of this study provide suggestions to any educational system in planning for students' math achievement growth. The proposed methodology is general, so that it can be employed in other educational levels and fields of study.

Keywords:

• Soft model
• fuzzy number
• membership function
• possibilistic regression

1. Introduction

Most of the research done to date in educational mathematics stems from psychological variables such as attitude, school climate atmosphere, self-concept, self-efficacy, and intelligence. However, there is less attention to the philosophical variables such as logical thinking, philosophical-mindedness, and philosophical methods which play pivotal roles in teaching-learning procedure. Besides, studies related to math achievement has been mostly conducted in the form of classical statistical models, whereas the relationship between psychological and philosophical variables is an inexact one.

Considering the above-mentioned points, the present study investigates a new approach to study the math achievement according to the most important psychological and philosophical variables, through applying a soft model for modeling and data analysis. In line with this, the present study aims at investigating the role of philosophic-mindedness, creativity, mathematics self-efficacy, and mathematics self-concept in predicting math achievement.

Mathematics self-efficacy is defined as the evaluation of self-efficacy beliefs in academic settings in successfully performing a task or completing a math problem [1,2]. Anjum [3] and Wilkins [4] provide evidence that mathematics self-efficacy directly or indirectly affects the students' math achievement. Mathematics self-concept is an another important factor in mathematical development of students. Self-concept refers to beliefs and understandings a person holds about him or herself [5]. Anjum [3] and Wilkins [4] have emphasized the effect of mathematics self-concept on math proficiency level. Moreover, creativity and philosophic-mindedness are two other features which play a significant role in math achievement. Sterenberg [6] declares that creativity is the ability to create novel ideas in higher level which contain innovative potentiality, flexibility, and sensitivity to the existing beliefs and this gives a person the ability to think about other findings via logical and rational thoughts so that it provides the beneficial outcome to him and others. Fleith and Renzulli [7] provide evidence that creativity has positive effect on the students' self-concept.

In most of the studies in the field of education – including the studies mentioned above – observational data are assumed to be measured/reported precisely and the relationships among variables are analyzed accurately in the form of classical exact formulas. On the other hand, many applied issues deal with

1. imprecise data and/or

2. approximate relationship among factors.

For instance, for the first item, if we ask students about their interest in mathematics, the answers are usually presented as fuzzy/imprecise words such as very high, high, not so much, a little, more-or-less, and so on. Generally, the response to the questions/measuring about qualitative variables, such as satisfaction, motive, ability, consistency, self-efficacy, and creativity is often presented as fuzzy/imprecise words. As an example for the second item, consider the relationship among math achievement and intelligence, self-concept, and motive. It is obvious that such a relation is fuzzy/imprecise rather than crisp/exact. We can assume that, for example, self-concept has ‘more-or-less’ positive effect on math achievement, while intelligence has ‘high’ positive effect on math achievement.

Regards to the above discussion, the present study seeks to investigate a new soft pattern in which an approximate relationships among philosophic-mindedness, creativity, mathematics self-efficacy, and mathematics self-concept in math achievement are formed, for a few works regarding fuzzy sets in education, see Kim et al. [8] and Marmur and Zazkis [9].

The paper is organized as follows. In Section 2, the methodology of the study as well as the population and sampling method are explained. In Section 3, the methods of measuring variables and the used questionnaires are expressed. Section 4 involves the results in detail. A short discussion is provided in Section 5. Two topics of fuzzy sets and fuzzy regression are briefly reviewed in Appendices 1 and 2, respectively.

2. Methods

The participants of the research are 36 male students from Marand, a small city on the North West of Iran, during the educational year (2015–2016). The participants were selected by a random sampling method. After data collection procedure, 8 out of 36 participants were excluded from the study. The data are analyzed based on answers of 28 students. Since the data in this study were imprecise, a fuzzy regression model was deployed in order to investigate the research questions. This model is used to determine the predictive factors influencing the performance of the variables in this study. The analysis of the model stems from the associations among variables.

Furthermore, sensitivity analysis of the model is studied based on (1) validity level and (2) the amount of total ambiguity of the model. Fuzzy regression has the advantage of having no restrictive assumptions of the classical regression. Particularly, in small scale samples, due to the lack of reliability of the assumptions of classical regression, the use of fuzzy regression is more reasonable.

3. Instrumentation

Five philosophical/psychological characteristics and the math achievement are considered in this study as follows.

3.1. Philosophic-mindedness Questionnaire

According to Smith's philosophic-mindedness model [10,11], five-level Likert-scale questionnaire (completely disagree, disagree, agree, and strongly agree) with 30 items was developed. Exploratory factor analysis and confirmatory factor analysis was deployed for analyzing the questionnaire. Moreover, the validity and reliability of the questionnaire were checked. The Cronbach's coefficient alpha proved a high reliability and consistency of measurement ($\alpha =0.72$).

3.2. Creativity Questionnaire

The creativity questionnaire was adopted from Raudsepp's [12]. It consisted of four-level Likert-scale questionnaire (completely disagree, disagree, agree, and strongly agree). In creativity questionnaire also used exploratory factor analysis and confirmatory factor analysis. Besides, the validity and reliability of the questionnaire were checked. The Cronbach's coefficient alpha represents a high reliability and consistency of measurement ($\alpha =0.73$).

3.3. Mathematics Self-efficacy Questionnaire

The pattern of mathematics self-efficacy questionnaire is based on Bandura's instructions [13] self-efficacy questionnaire. With regard to the content and other testing parameters, it is similar to performance measurement area. It was adopted from Pajares [1], and questions were developed in terms of ‘I can do’ instead of ‘I will do’. Also, the participants' level of ability in each item was signified with a 13-level scale from zero (I cannot do it at all) to 10 (I can do it completely). The content validity and construct validity were confirmed via exploratory factor analysis and confirmatory factor analysis. Moreover, the reliability test (Cronbach's Alpha) showed that the self-efficacy questionnaire is highly reliable ($\alpha =0.91$).

3.4. Mathematics Self-concept Scale

Self-concept scale is based on mathematically related factors, adopted from the model of Marsh et al. [14]. The questionnaire consists of 12 questions and has five Likert scale alternatives of strongly agree, agree, sometimes agree, sometimes disagree, disagree, and strongly disagree. These options were scored from 5 strongly agree, 4 agree, 3 sometimes agree and sometimes disagree, 2 disagree, and 1 strongly disagree. The construct validity of the questionnaire was verified by exploratory factor analysis and confirmatory factor analysis. The result of the psychometric test showed that question 11 was inflated (although factor loadings are almost identical in both factors in one question). Thus item 11 was eliminated and the mathematics self-concept variable with 11 relatively strong indicators was determined as one of the research variables. Furthermore, the reliability test (Cronbach's Alpha) for the total 12 questions was $\alpha =0.854$.

3.5. Mathematics Achievement Test

In order to assess students' math achievement, it was decided to use the mathematics written exam administered at the end of the school year with a score range of 0–20.

4. Results

According to the designed questionnaires, data collected are presented in Table 1. It should be noted that the collected data were normalized based on the idea used in Adriaenssens et al. [15].

Table 1. Collected data.

Self-effi.	Self-concept	Creativity	Philo. mind.	Math achi.
0.79	0.62	0.56	0.84	0.94
0.69	0.30	0.42	0.50	0.51
0.58	0.17	0.65	0.69	0.45
0.89	0.55	0.81	0.72	0.75
0.52	0.12	0.51	0.71	0.38
0.82	0.65	0.90	0.81	0.16
0.65	0.12	0.42	0.72	0.18
0.61	0.37	0.60	0.67	0.43
0.85	0.50	0.75	0.71	0.50
0.74	0.57	0.49	0.65	0.41
0.62	0.12	0.65	0.57	0.21
0.74	0.57	0.37	0.64	0.40
0.91	0.60	0.65	0.69	0.68
0.20	0.35	0.49	0.71	0.29
0.10	0.30	0.51	0.53	0.44
0.45	0.10	0.47	0.72	0.50
0.77	0.42	0.56	0.72	0.63
0.61	0.60	0.58	0.62	0.30
0.00	0.22	0.28	0.59	0.20
0.98	0.70	0.51	0.65	0.84
0.58	0.17	0.46	0.76	0.35
0.62	0.42	0.56	0.71	0.44
0.60	0.42	0.56	0.65	0.44
0.77	0.52	0.47	0.67	0.44
0.40	0.22	0.37	0.57	0.58
0.63	0.32	0.51	0.72	0.53
0.75	0.37	0.57	0.71	0.43
0.65	0.25	0.37	0.55	0.50

The main question of this research is, which one of the variables of philosophic-mindedness, creativity, mathematics self-efficacy, and mathematics self-concept is the best predictor of math achievement; and how such variables are related?

To achieve the answer for the main question, first we examine some statistical investigations. The results are given in Table 2. This table demonstrates that there is a positive correlation among students' math achievement, mathematics self-efficacy, and mathematics self-concept. However, there is no such correlation among variables of philosophic-mindedness and creativity ($p-\mathrm{value}<0.05$). Also, the results reveal that the highest mean score belongs to philosophic-mindedness and the lowest one for mathematics self-concept.

Following the preliminary statistical analysis stage, fuzzy regression was employed to provide a soft relationship among the variables. To investigate the research question, multiple fuzzy regression of academic performance on variables like philosophical-mindedness, creativity, self-efficacy, as well as mathematics self-concept was evaluated using the objective function: $minZ=2(206s_0+73.82s_1+47.32s_2+59.43s_3+69.60s_4)$ which totally consisted of 206 conditions. For instance, two conditions related to the first observation are: $\begin{array}{rl}& a_0+0.79a_1+0.62a_2+0.56a_3+0.84a_4\\ & +(1-h)(s_0+0.79s_1+0.62s_2+0.56s_3+0.84s_4)\ge 0.94\\ & a_0+0.79a_1+0.62a_2+0.56a_3+0.84a_4\\ & -(1-h)(s_0+0.79s_1+0.62s_2+0.56s_3+0.84s_4)\le 0.94\end{array}$ and fuzzy regression coefficients are estimated according to various hs in the symmetric model.

Finally, using a suitable software (we used the LINGO software), the above linear programming problem was solved and the fuzzy coefficients of different models, based on different values of h, were estimated.

Table 3 summarizes the results of multiple fuzzy linear regression model of students' achievement on philosophic-mindedness, creativity, mathematics self-efficacy, and mathematics self-concept variables. The results indicate that as the amount of h gets higher, the amount of credit level of the model keeps rising. This, also, increases the total uncertainty (TU) of the model (i.e. the sum of spreads of the coefficients). By the same token, the total uncertainty of the model should be considered due to the accurate selection of h. It is also likely to consider h = 0.50 as a common and sensible value. In the present data, because of the high IC and a slight increase in the model uncertainty, the credit level h = 0.50 sounds reasonable. Considering such a value for credited level of h, the fuzzy coefficients of the model are estimated as follows: $\begin{array}{rl}& \widetilde{A_0}=(0.25,0.00{)}_T,\widetilde{A_1}=(0.00,0.87{)}_T\\ & \widetilde{A_2}=(0.45,0.25{)}_T,\widetilde{A_3}=(0.11,0.00{)}_T\end{array}$ Therefore, the optimal fuzzy model regression is obtained as follows: $\begin{array}{rl}\tilde{Y}& =(0.25,0.00{)}_T+(0.00,0.87{)}_T\mathrm{Creativity}\\ & +(0.45,0.25{)}_T\mathrm{Mathself}-\mathrm{concept}+(0.11,0.00{)}_T\mathrm{Mathself}-\mathrm{efficacy}\end{array}$ The above equation shows that philosophic-mindedness has no significant role in students' math performance, while the mathematics self-efficacy, mathematics self-concept, and creativity play significant roles. For example, if the observed value for mathematics self-efficacy, mathematics self-concept, and creativity are 0.79, 0.62, and 0.56, respectively, the predictive score for participant's math performance is ‘about 0.615’. The term ‘about 0.615’ means the symmetric triangular fuzzy numbers $(0.615,1.25{)}_T$. This means that it is not possible to have a score higher than 1.25 (the most optimistic) or less than −0.029 (the most pessimistic), and the most likely score is 0.61.

Table 2. Mean, standard deviation (s.d.), and coefficient of correlation between variables.

	Variable	mean	s.d.	1	2	3	4	5
1	Mathematics self-efficacy	0.62	0.22	1
2	Mathematics self-concept	0.38	0.18	0.59${}^{\ast \ast }$	1
3	Creativity	0.53	0.13	0.49${}^{\ast \ast }$	0.45${}^{\ast }$	1
4	Philosophic mindedness	0.67	0.07	0.38${}^{\ast }$	0.26	0.47${}^{\ast }$	1
5	Math achievement	0.45	018	0.46${}^{\ast }$	0.42${}^{\ast }$	0.09	0.17	1

${}^{\ast }$Correlation is significant at the 0.05 level (two-tailed). ${}^{\ast \ast }$Correlation is significant at the 0.01 level (two-tailed).

Table 3. Results of regression model and sensitivity analysis for math performance criterion variable.

h	$a_0$	$a_1$	$a_2$	$a_3,a_4$	$s_0,s_1$	$s_2$	$s_3$	$s_4$	TU	IC	MDM
0.2	0.25	0.11	0.44	0.00	0.00	0.16	0.53	0.00	19.70	0.35	0.61
0.4	0.25	0.10	0.45	0.00	0.00	0.21	0.72	0.00	26.27	0.29	0.71
0.5	0.25	0.11	0.44	0.00	0.00	0.25	0.87	0.00	31.68	0.48	0.75
0.6	0.25	0.10	0.45	0.00	0.00	0.41	1.01	0.00	39.26	0.98	0.80
0.8	0.25	0.09	047	0.00	0.00	0.50	2.31	0.00	39.80	0.97	0.99

In addition, the above equation shows that keeping other variables constant, math performance would increase exactly 0.11 adding one unit to math self-efficacy variable. Similarly, adding one unit to math self-concept, educational performance will increase about 0.44. Besides, adding one unit to creativity variable, the students' educational math performance will almost show no increase.

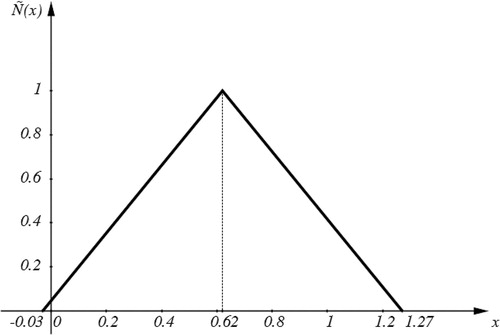
4.1. Prediction for a New Case

The obtained model can be used to predict mathematics performance for a new case. Assume that, for example, in a new case, the observed value for mathematics self-efficacy, mathematics self-concept, and creativity are $0.79,0.62,$ and $0.56,$ respectively. Then, using the optimum fuzzy regression model, the predictive score for participant's math performance is ‘about 0.62’. The fuzzy value ‘about 0.62’ is characterized by the symmetrical triangular fuzzy number $(0.62,0.65{)}_T$. This means that it is very less likely to have a score over 1.27 (the most optimistic) or less than $-0.03$ (the most pessimistic), and the most likely score (in fact, most possibility for score) is 0.62 (Figure 1).

Figure 1. The membership function of the fuzzy number $(0.62,0.65)$ representing the concept of math achievement ‘about 0.62’.

5. Discussion and Conclusion

The results of the first hypothesis of the research in the form of possible fuzzy regression model revealed that among four variables, with the exclusion of philosophic mindedness, other variables of mathematics self-efficacy, mathematics self-concept, and creativity are predictive factors in students' math performance. This finding indicates that students with a higher philosophic mindedness do not necessarily achieve better math score even though other research variables are also involved in making this prediction. Studies in the literature also found that self-efficacy and self-concept contribute more to a higher mathematics achievement [1,3,16–18].

The soft approach provided in this study is a general approach to modeling fuzzy/imprecise concepts, and can be used for modeling and prediction in every educational study. While the data related to the variable under investigation are fuzzy/imprecise, generalizing the proposed model can be considered as a subject for future investigations.

Acknowledgments

The authors wish to express their thanks to the referees for valuable comments. The first author would like to acknowledge the financial support of University of Tehran for this research under grant number 30005/01/03.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

S. M. Taheri

S. Mahmoud Taheri received the B.Sc. degree in statistics and the M.Sc. degree in mathematical statistics from the Ferdowsi University of Mashhad, Mashhad, Iran, in 1988 and 1991, respectively, and the Ph.D. degree in statistical inference from Shiraz University, Shiraz, Iran, in 2000. He is a professor with the College of Engineering, University of Tehran, Tehran, Iran. His research interests include statistical inference, Bayesian statistics, probability, statistics, and modeling in fuzzy environments.

M. Asadi

Masoud Asadi received the B.S. degree in Guidance and Counseling in 2007, and the M.A. degree in Counseling, in 2009, from University of Shahid Beheshti and Kharazmi University, respectively. He completed the Ph.D. in Counseling in Kharazmi University in 2015. He is an Associate Professor with the Department of Counseling and Psychology, Arak University, Arak, Iran. He has published 40 research papers in scientific journals. His research interests are in the areas of fuzzy mathematical methods in counseling and psychology.

A. Shiralipour

Asghar Shiralipour received the B.Sc. in Mathematics from University of Tabriz in 2007. He obtained the M.A. degree in Educational Research from Kharazmi University in 2009. Currently, he is a math teacher at high schools. He has published 20 research papers in scientific journals. His research interests are in the areas of fuzzy mathematical methods in psychology and education.

Appendices

Appendix 1.

Fuzzy sets

The notion of set occurs frequently as we tend to organize, summarize, and formulize knowledge about concepts or objects. Based on classical concept of set, we limit to talk about the precise (completely exact) sets, for instance,

1. A: the set of 12-year-old students,

2. B: the set of couples with age differences exactly two years,

3. C: the set of staff with more than 0.80 job satisfaction,

4. D: the set of students with IQ (intelligence quotients) more than 113.

Being intuitively appealing, sets introduce a fundamental notion of dichotomy. In its essence, any process of dichotomization imposes a binary classification: either accept or reject an object as belonging to a given set. For example, every 12-year-old student is a member of set A and an 11-year-old student is not a member of A. Besides, an employee with 0.81 job satisfaction is a member of set C while an employee with 0.79 job satisfaction is not a member of that set.

Formally speaking, a set A of X (the reference set, or the set of all possible objectives in each subject) contains certain elements of X and does not contain other elements of X. We may express such crisp classification through a function (called: indicator function) $A(x),x\in X$, of the form $A(x)=\{\begin{array}{ll}1& x\in A\\ 0& x\notin A\end{array}$ Actually, the function $A:X\to \{0,1\}$ induces a constraint, with a rigid boundary on the objects of X that may be assigned to a set A.

The concept of fuzzy sets is to relax this requirement and admit intermediate values of class membership. This allows for an enriched and more realistic framework for modeling the real-world concepts. In fact, most categories used in psychology do not possess rigid boundaries. Consider, for instance, notions like young, IQ, management skills, life satisfaction, emotional intelligence (EQ), and creativity. All of these concepts do not have rigid boundaries, so that we cannot define such categories as classical binary sets. In fact, whether on object belongs to such categories is a matter of degree expressed by a number between 0 and 1, i.e. a number in the unit interval $[0,1]$. The closer that number is to 1, the higher the grade of the objects membership in particular category. The function representing such membership is called membership function, which is a function from X to $[0,1]$ (rather than $\{0,1\}$). The membership values express the degree to which each object is compatible with the properties or features distinctive to the fuzzy set. Fuzzy sets are formally defined as follows:

Definition A.1

A fuzzy set is characterized by a members function mapping elements of a domain (universe of discourse) X the unit interval $[0,1]$, i.e. $\tilde{A}:X\to [0,1]$.

The value of $\tilde{A}(x)$ (the membership value of $x\in X$) represents the degree of x belonging to the fuzzy set $\tilde{A}$. Clearly, a fuzzy set is a generalization of the concept of a set whose membership function takes on only two values $\{0,1\}$.

Example A.1

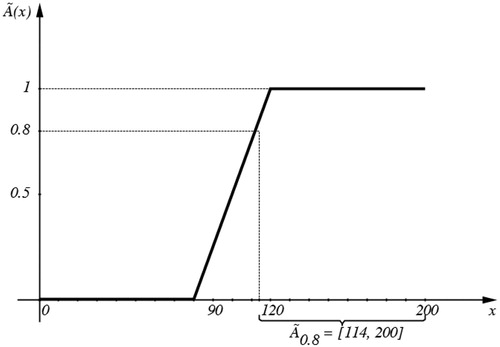
Consider the concept of high IQ. Regarding $X=[0,200]$ as the reference set, we can define the fuzzy concept high IQ by a fuzzy set with the following membership function (see Figure A1).

Figure A1. The membership function of the fuzzy set $\tilde{A}$ in Example A.1, representing the concept of ‘high IQ’.

Let us explain how we can construct such a membership function. Clearly 50, 58, and 65 are not understood as high IQ values. As a minimum threshold, we may assign a null value to express its degree of compatibility with the concept of high IQ, for any value less than 90. Likewise, 120 and over are certainly high IQ, and so we assign a value 1 to express a full degree of compatibility with the concept. However, for the remaining values, i.e. the values between 90 and 120, we may consider partial quantification of belongingness. For instance we may consider an increasing linear function to represent such memberships. Therefore, we reach to a membership function showing in Figure A1.

Definition A.2

The α-cut of a fuzzy set $\tilde{A}$, denuded by ${\tilde{A}}_{\alpha }$, is a (non-fuzzy) set consisting of elements whose membership values exceed the threshold level α, ${\tilde{A}}_{\alpha }=\{x|\tilde{A}(x)\ge \alpha \}$.

Example A.2

In Example A.1, for instance we have (see Figure A2). ${\tilde{A}}_{0.8}=\{x|\tilde{A}(x)\ge 0.8\}=[114,200].$

Figure A2. The 0.8 cut of the fuzzy set ‘high IQ’ in Example A.1.

Fuzzy numbers. Fuzzy numbers are fuzzy sets with special consideration for easy calculations.

Definition A.3

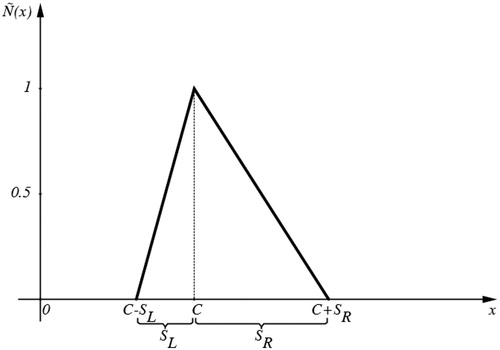
A fuzzy set $\tilde{N}$ of the real line R is called a fuzzy number, if ${\tilde{A}}_{\alpha }$ for any $0<\alpha \le 1$ is a non-empty closed interval. A specific class of fuzzy numbers, which is rich enough to cover most of the applications, is the so-called triangular fuzzy numbers (TFN) $\tilde{N}=(C,S_L,S_R{)}_T$ with central value C, left and right spreads $S_L,S_R\ge 0$, and the following membership function, see Figure A2. In special case, when $S_L=S_R$, then $\tilde{N}$ is called symmetric and is denoted by $(C,S{)}_T$. $\tilde{N}(x)=\{\begin{array}{ll}0& x<C-S_L\\ {\displaystyle \frac{x-(C+S_L)}{S_L}}& C-S_L\le x<C\\ {\displaystyle \frac{(C+S_R)-x}{S_R}}& C\le x<C+S_R\\ 0& x\ge C+S_R\end{array}$

Example A.3

Consider the concept of ‘IQ about 110’. We can formulize such a concept by a triangular fuzzy number $\tilde{M}$ with the following membership function. Also we can characterize the concept ‘IQ very near to 110’ by another triangular fuzzy number, say $\tilde{N}$, with the following triangular membership function. $\begin{array}{rl}\tilde{M}(x)& =\{\begin{array}{ll}0& x<100\\ {\displaystyle \frac{x-100}{10}}& 100\le x<110\\ {\displaystyle \frac{120-x}{10}}& 110\le x<120\\ 0& x\ge 120\end{array}\\ \tilde{N}(x)& =\{\begin{array}{ll}0& x<105\\ {\displaystyle \frac{x-105}{5}}& 105\le x<110\\ {\displaystyle \frac{115-x}{5}}& 110\le x<115\\ 0& x\ge 115\end{array}\end{array}$

Appendix 2.

Fuzzy regression

Regression modeling is a fundamental tool in many applied fields. The classical statistical regression gives a crisp relationship between a dependent variable and some independent (explanatory) variables based on a given data. However, the statistical regression has two limitations in two cases:

1. when the phenomenon under consideration has not stochastic variability but is also uncertain in some sense,

2. the available data are imprecise rather than crisp.

In these situations, it is natural to seek a fuzzy functional relationship for modeling/analyzing the given data.

Over the last decades, two main approaches to fuzzy regression were developed. The first approach, which is called the possibilistic regression, was proposed by Tanaka et al. [19] and was developed by many authors (see, e.g. [20,21]). The second approach is based on the distances between the observed values and estimated values of the dependent variable (as in statistical regression), see, e.g. Pourahmad et al. [22], D'Urso and Massari [23], Yoon et al. [24], Salmani et al. [25], Taheri and Chachi [26] and Arefi [27]. For a review on this topic, see Taheri [28].

The possibilistic regression, in which the coefficients of the model are fuzzy rather than crisp, seems to be a proper model in behavioral and psychological studies. In such studies, we often come across imprecise (fuzzy) relationship between variables. For instance, higher logical intelligence leads to a moderate increase in math performance of the students. Similarly, there is more-or-less strong relation between a teacher's higher satisfaction and his/her better performance in the classroom.

Suppose that we have a collected data set denoted by $(y_i,x_{0i},x_{1i},\dots ,x_{pi}),i=1,2,\dots ,n,n>p,$ where $x_{0i}=1$, $i=1,2,\dots ,n$, $j=1,\dots ,p$. Here, $x_{ij}$ is the crisp observation on the jth independent variable (such as intelligence, self-efficacy, academic attitude, and student's motivation) For the ith case, $y_i$ is the crisp observation on the dependent variable.

On the basis of such dataset, we wish to find, in an optimal way, the coefficient of the fuzzy regression model $\tilde{Y}={\tilde{A}}_0+{\tilde{A}}_1{x}_1+\cdots +\widetilde{A_p}{x}_p$ where $\tilde{Y}$, the output of the model, is a fuzzy number, $x=(x_0,x_1,\dots ,x_p)$ is the crisp input vector, and ${\tilde{A}}_0,{\tilde{A}}_1,\dots ,\widetilde{A_p}$ are triangular fuzzy numbers, where ${\tilde{A}}_j=(a_j,S_{Lj},S_{Rj}{)}_T,j=0,1,\dots ,p$. In any practical problem, ${\tilde{A}}_0,{\tilde{A}}_1,\dots ,\widetilde{A_p}$ for which the above equation expresses the best fit to the given the collected data points, can be obtained according to certain criteria. We consider a criterion related to the accuracy validity of the model and another criterion related to the precision. To do this and, therefore, in order to estimate the coefficients ${\tilde{A}}_j$, $j=0,\dots ,p$ we assume that:

1. For the observation $y_i,i=1,\dots ,n,$ the value of $y_i$ has degree of membership as large as h in the fuzzy estimation $\widetilde{Y_i}$ from the fuzzy model, i.e. $\widetilde{Y_i}(y_i)\ge h,i=1,2,\dots ,n.$ The value of h may be determined by the user and is called the credit level of the model. Usually, h is considered at least 0.5.

2. The fuzzy coefficients should be such that the total uncertainty (TU) of the model is minimum. Since the uncertainty of a fuzzy number increases with its spreads, minimizing the sum of the spreads of fuzzy outputs, leads to a minimum value of the total uncertainty of the model.

Therefore, the estimation of the fuzzy coefficients leads to a linear programming problem in which the objective function is the sum of the spreads of the fuzzy outputs, i.e. $Z=n(S_{0L}+S_{0R})+\sum _{i=1}^p[(S_{iL}+S_{iR})\sum _{j=1}^n{x}_{ji}]$ On the other hand, using the fuzzy arithmetic [29], the constraints in item 1 above, can be written as follows: $\begin{array}{rl}& (1-h)S_{0L}+(1-h)\sum _{i=1}^p(S_{iL}{x}_{ji})-a_0-\sum _{i=1}^p(a_i{x}_{ji})\ge -y_j,j=1,2,\dots ,n\\ & (1-h)S_{0R}+(1-h)\sum _{i=1}^p(S_{iR}{x}_{ji})+a_0+\sum _{i=1}^p(a_i{x}_{ji})\ge +y_j,j=1,2,\dots ,n\end{array}$ Finally, the fuzzy coefficients of the model can be estimated by solving the above linear programming problem.

Note. It is clear that the minimum of the objective function increases as h increases. There is, therefore, a trade-off between the degree of $y_i$ in $Y_i$ and the minimum sum of spreads of the outputs. Such a scenario is similar to the trade-off between the length and the confidence coefficient in the statistical confidence interval.

Evaluation methods. To evaluate the fuzzy regression models, we employ two indices. The first one, is the Mean Degree of Memberships (MDM), which is defined as follows: $\mathrm{MDM}=\frac{1}{n}\sum _{i=1}^n\widetilde{Y_i}(y_i)$ The second one, which is based on the common concept of squared errors, is called indicator of confidence (IC). Assume that SSE and SST represent $SSE=2\sum _{i=1}^n(y_i-{\widetilde{Y_i}}_C{)}^2$ and $SST=\sum _{i=1}^n(y_i-{\widetilde{Y_i}}_L{)}^2+\sum (y_i-{\widetilde{Y_i}}_R{)}^2$, respectively. Then, IC is defined as follows: $IC=1-\frac{SSE}{SST}$ In practice, large membership degrees of the observed values as well as large values of IC confirm that the model constructed from the data supports the data well. Both values of MDM and IC are between 0 and 1, so that, a value near 1 indicator good model fitting.

Figure A3. A typical triangular fuzzy number.