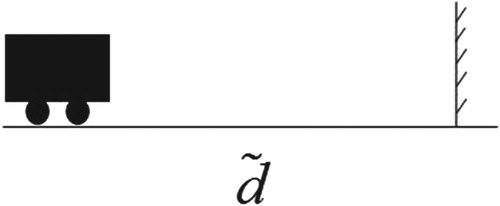The Numerical Solution of Full Fuzzy Algebraic Equations

Abstract

In this article, we try to solve a full fuzzy algebraic equation with a fuzzy variable and fuzzy coefficients. This can be done by a numerical iterative process. We offer an algorithm to produce a sequence that may converge to a root of such an equation.

Keywords:

• Approximation
• algebraic fuzzy equation
• nonlinear system

1. Introduction

In many purposes of a system, we may need to solve a fuzzy equation. Zadeh introduced some properties of fuzzy equations in [1] and some other types of such equations were discussed by some researchers [2, 3] and they tried to solve them analytically. Solving an algebraic equation of degree at most 3 has no analytical method even in crisp form. So it is necessary to find the numerical solution of an equation. In [4], fuzzy nonlinear equations with fuzzy unknown were considered. A research effort has been done on algebraic fuzzy equations by using neural network [5]. Two numerical iterative methods have been presented in [6, 7] to find the roots of an algebraic fuzzy equation of degree n, one with fuzzy coefficients and crisp unknown and the other one with crisp coefficients and fuzzy unknown. In the present essay, we introduce a numerical method to solve a full fuzzy algebraic equation, such that all numbers are fuzzy, both the unknown variable and coefficients. The organisation of the present paper is as follows. In Section 2, we represent a full fuzzy algebraic equation and we discuss solving a nonlinear system of equations. In Section 3, an algorithm is introduced to numerically solving a full fuzzy algebraic fuzzy equation. Some examples are given in Section 4, and Section 5 contains the conclusion of this work.

2. Preliminaries

The presentation of a fuzzy number $\tilde{f}$ by a pair of functions as $(\underset{\_}{f},\overline{f})$ is called the parametric form of $\tilde{f}$, such that over $[0,1]$, we have: $\underset{\_}{f}$ is a left continuous and monotonically increasing function, $\overline{f}$ is a left continuous and monotonically decreasing function, and $\underset{\_}{f}\le \overline{f}$ [8–12]. We consider the set of all fuzzy numbers by $\mathbb{F}$.

Suppose $\tilde{f}=(\underset{\_}{f},\overline{f})$ and $\tilde{g}=(\underset{\_}{g},\overline{g})$ are both belonging to $\mathbb{F}$. Then some operations are defined as follows:

• $k\tilde{f}=\{\begin{array}{lll}(k\underset{\_}{f},x\overline{f}),& k>0,(k\overline{f},x\underset{\_}{f}),& k<0;\end{array}$

• $\tilde{f}+\tilde{g}=(\underset{\_}{f}+\underset{\_}{g},\overline{f}+\overline{g})$;

• $\tilde{f}-\tilde{g}=(\underset{\_}{f}-\overline{g},\overline{f}-\underset{\_}{g})$.

• If $\tilde{w}=\tilde{f}.\tilde{g}$, then $\begin{array}{r}\underset{\_}{w}=min\{\underset{\_}{f}.\underset{\_}{g},\underset{\_}{f}.\overline{g},\overline{f}.\underset{\_}{g},\overline{f}.\overline{g}\}\\ \overline{w}=max\{\underset{\_}{f}.\underset{\_}{g},\underset{\_}{f}.\overline{g},\overline{f}.\underset{\_}{g},\overline{f}.\overline{g}\}\end{array}$

A fuzzy number $\tilde{f}$ is called non-negative (non-positive) if $\underset{\_}{f}\ge 0(\overline{f}\le 0)$ on $[0,1]$. Also $\tilde{f}\in \mathbb{F}$ is called positive (negative), if $\underset{\_}{f}>0(\overline{f}<0)$ on $[0,1]$. It is obvious that for non-negative fuzzy numbers $\tilde{f}$ and $\tilde{g}$ we have $\tilde{f}\tilde{g}=(\underset{\_}{f}.\underset{\_}{g},\overline{f}.\overline{g})$, and for non-positive fuzzy numbers $\tilde{f}$ and $\tilde{g}$ we have $\tilde{f}\tilde{g}=(\overline{f}.\overline{g},\underset{\_}{f}.\underset{\_}{g})$.

Definition 2.1

$r-$cut of a fuzzy number $\tilde{v}$ is the interval $[\underset{\_}{v}(r),\overline{v}(r)]$, and we use the notation $[\tilde{v}{]}^r$ for it.

Definition 2.2

${\tilde{P}}_n(\tilde{x})$ is a fuzzy polynomial of degree at most n with fuzzy coefficients, if there are some fuzzy numbers ${\tilde{a}}_0,\dots ,{\tilde{a}}_n$, such that (1) ${\tilde{P}}_n(\tilde{x})=\sum _{j=0}^n{\tilde{a}}_j{\tilde{x}}^j.$(1)

For a positive integer n, an algebraic equation with full fuzzy feature of degree n, can be defined as (2) ${\tilde{P}}_n(\tilde{x})=\tilde{b},$(2) where ${\tilde{a}}_0,\dots {\tilde{a}}_n,\tilde{x}\in \mathbb{F}$, ${\tilde{a}}_n\ne 0$ and $\tilde{b}\in \mathbb{F}$.

Definition 2.3

A ‘m-degree polynomial form’ fuzzy number $\tilde{v}$ is defined by a pair $\tilde{v}=(p_m,q_m)$, such that $p_m$ and $q_m$ are two polynomials of degree at most m  [13–15].

We use ${\mathbb{P}\mathbb{F}}_m$ for the set of all m-degree polynomial form fuzzy numbers  [13, 14, 16]. Let $F:{\mathbb{R}}^s⟶{\mathbb{R}}^d$ be a function such that maps $Z^T=(y_1,\dots ,y_s)$ to $F^T(Z)=(f_1(Z),\dots ,f_d(Z))$, where $d\ge s$. To solve the system of equations (3) $F(Z)=0,$(3) by Gauss–Newton method [17], we consider $A(Z)$ as the Jacobian of F: $A(Z)=[\frac{\mathrm{\partial }{F}_i(Z)}{\mathrm{\partial }{y}_j}]$, $j=1,\dots ,s$ and $i=1,\dots ,d$. Considering $Z^{(0)}$ as an initial vector, we try to improve this guess, so the system $A(Z^{(k)})H^{(k)}=-F(Z^{(k)})$ should be solved in each iteration and then the approximated solution will be improved by considering $Z^{(k+1)}=Z^{(k)}+H^{(k)}$. This system of equation can be solved by a least square method as the following: (4) $A(Z^{(k)}{)}^{T}A(Z^{(k)})H^{(k)}=-A(Z^{(k)}{)}^{T}F(Z^{(k)}).$(4) Some conditions on convergence and uniqueness of the solution of (3(3) $F(Z)=0,$(3) ) are proposed [18–20]. Let $\tilde{b}=(\underset{\_}{b},\overline{b})$ and ${\tilde{a}}_j=({\underset{\_}{a}}_j,{\overline{a}}_j)$ for $j=0,\dots ,n$ are known fuzzy numbers. We try to solve the following full fuzzy algebraic equation from degree n: (5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) in which we have ${\tilde{a}}_n\ne 0$. We consider $\tilde{x}=(\underset{\_}{x},\overline{x})$ as the unknown fuzzy root of Equation (5(5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) ).

3. Solving the Algebraic Fuzzy Equation

Let the unknown $\tilde{x}$ be a fuzzy number belonging to ${\mathbb{P}\mathbb{F}}_k$. Also let we have ${\tilde{a}}_j\in {\mathbb{P}\mathbb{F}}_m$ and $\tilde{b}\in {\mathbb{P}\mathbb{F}}_l$, in which $l\le nk+m$. We discuss about Equation (5(5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) ), by four cases:

• First we consider the case that the unknown fuzzy number $\tilde{x}$ be non-negative and for all $j=0,\dots ,n$, we have ${\tilde{a}}_j\ge 0$. By these assumptions, Equation (5(5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) ) changes to the two following equations: (6) $\begin{array}{r}\sum _{j=0}^n{\underset{\_}{a}}_j{\underset{\_}{x}}^j=\underset{\_}{b},\end{array}$(6) (7) $\begin{array}{r}\sum _{j=0}^n{\overline{a}}_j{\overline{x}}^j=\overline{b}.\end{array}$(7) Now by the assumptions on fuzzy numbers, we consider that $\begin{array}{rl}{\underset{\_}{a}}_j& =\sum _{i=0}^m{\underset{\_}{a}}_{ij}{r}^i,{\overline{a}}_j=\sum _{i=0}^m{\overline{a}}_{ij}{r}^i,\\ \underset{\_}{b}& =\sum _{i=0}^l{\underset{\_}{b}}_i{r}^i,\overline{b}=\sum _{i=0}^l{\overline{b}}_i{r}^i,\\ \underset{\_}{x}& =\sum _{i=0}^k{\alpha }_i{r}^i,\overline{x}=\sum _{i=0}^k{\beta }_i{r}^i.\end{array}$ By these assumptions, Equation (6(6) $\begin{array}{r}\sum _{j=0}^n{\underset{\_}{a}}_j{\underset{\_}{x}}^j=\underset{\_}{b},\end{array}$(6) ) changes to (8) $\sum _{j=0}^n\left\{\left(\sum _{i=0}^m{\underset{\_}{a}}_{ij}{r}^i\right)\left(\sum _{i=0}^k{\alpha }_i{r}^i{)}^j\right)\right\}=\sum _{i=0}^l{\underset{\_}{b}}_i{r}^i.$(8) Since ${\tilde{a}}_j\in {\mathbb{P}\mathbb{F}}_k$, $\tilde{x}\in {\mathbb{P}\mathbb{F}}_m$, we have (9) ${\tilde{P}}_n(\tilde{x})=\sum _{j=0}^n{\tilde{a}}_j{\tilde{x}}^j\in {\mathbb{P}\mathbb{F}}_{nk+m}.$(9) By rewriting (8(8) $\sum _{j=0}^n\left\{\left(\sum _{i=0}^m{\underset{\_}{a}}_{ij}{r}^i\right)\left(\sum _{i=0}^k{\alpha }_i{r}^i{)}^j\right)\right\}=\sum _{i=0}^l{\underset{\_}{b}}_i{r}^i.$(8) ) by an ordering on the power of r and by considering (9(9) ${\tilde{P}}_n(\tilde{x})=\sum _{j=0}^n{\tilde{a}}_j{\tilde{x}}^j\in {\mathbb{P}\mathbb{F}}_{nk+m}.$(9) ), for $i=0,\dots ,nk+m$, the coefficient of $r^i$ is a function ${\hat{L}}_i$ and we have (10) $\sum _{i=0}^{nk+m}{\hat{L}}_i({\alpha }_0,\dots ,{\alpha }_k)r^i=\sum _{i=0}^l{\underset{\_}{b}}_i{r}^i.$(10) After taking the corresponding coefficients in both sides equal, for $i=0,\dots ,nk+m$, we have an equation: (11) ${\hat{L}}_i({\alpha }_0,\dots ,{\alpha }_k)=\{\begin{array}{ll}{\underset{\_}{b}}_i,& i=0,\dots ,l,\\ 0,& i=l+1,\dots ,nk+m.\end{array}$(11) Similarly, by rewriting (7(7) $\begin{array}{r}\sum _{j=0}^n{\overline{a}}_j{\overline{x}}^j=\overline{b}.\end{array}$(7) ) by an ordering on the power of r and by considering (9(9) ${\tilde{P}}_n(\tilde{x})=\sum _{j=0}^n{\tilde{a}}_j{\tilde{x}}^j\in {\mathbb{P}\mathbb{F}}_{nk+m}.$(9) ), for $i=0,\dots ,nk+m$, the coefficient of $r^i$ is a function ${\hat{U}}_i$ and we have (12) $\sum _{i=0}^{nk+m}{\hat{U}}_i({\beta }_0,\dots ,{\beta }_k)r^i=\sum _{i=0}^l{\overline{b}}_i{r}^i,$(12) and by taking the corresponding coefficients in both sides equal, for $i=0,\dots ,nk+m$, we have an equation: (13) ${\hat{U}}_i({\beta }_0,\dots ,{\beta }_k)=\{\begin{array}{ll}{\overline{b}}_i,& i=0,\dots ,l,\\ 0,& i=l+1,\dots ,nk+m.\end{array}$(13)

• Let $\tilde{x}$ be non-negative and for some j, ${\tilde{a}}_j$ be negative. Thus Equation (5(5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) ) changes to the two following equations: (14) $\begin{array}{rl}& \sum _{a_j\ge 0}{\underset{\_}{a}}_j{\underset{\_}{x}}^j+\sum _{a_j<0}{\underset{\_}{a}}_j{\overline{x}}^j=\underset{\_}{b},\end{array}$(14) (15) $\begin{array}{rl}& \sum _{a_j\ge 0}{\overline{a}}_j{\overline{x}}^j+\sum _{a_j<0}{\overline{a}}_j{\underset{\_}{x}}^j=\overline{b}.\end{array}$(15)

• In the case that ${\tilde{a}}_j$'s are all non-negative and $\tilde{x}$ is negative, Equation (5(5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) ) changes to the following equations: (16) $\begin{array}{r}\sum _{j\mathrm{even}}{\underset{\_}{a}}_j{\underset{\_}{x}}^j+\sum _{j\mathrm{odd}}{\overline{a}}_j{\underset{\_}{x}}^j=\underset{\_}{b},\end{array}$(16) (17) $\begin{array}{r}\sum _{j\mathrm{even}}{\overline{a}}_j{\overline{x}}^j+\sum _{j\mathrm{odd}}{\underset{\_}{a}}_j{\overline{x}}^j=\overline{b}.\end{array}$(17)

• If $\tilde{x}$ be negative and for some j, ${\tilde{a}}_j$ be negative, then Equation (5(5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) ) changes to the following equations: (18) $\sum _{\begin{array}{c}{a}_j\ge 0\\ j\mathrm{even}\end{array}}{\underset{\_}{a}}_j{\underset{\_}{x}}^j+\sum _{\begin{array}{c}{a}_j\ge 0\\ j\mathrm{odd}\end{array}}{\underset{\_}{a}}_j{\overline{x}}^j+\sum _{\begin{array}{c}{a}_j<0\\ j\mathrm{even}\end{array}}{\overline{a}}_j{\underset{\_}{x}}^j+\sum _{\begin{array}{c}{a}_j<0\\ j\mathrm{odd}\end{array}}{\overline{a}}_j{\overline{x}}^j=\underset{\_}{b}$(18) and (19) $\sum _{\begin{array}{c}{a}_j\ge 0\\ j\mathrm{even}\end{array}}{\overline{a}}_j{\overline{x}}^j+\sum _{\begin{array}{c}{a}_j\ge 0\\ j\mathrm{odd}\end{array}}{\overline{a}}_j{\underset{\_}{x}}^j+\sum _{\begin{array}{c}{a}_j<0\\ j\mathrm{even}\end{array}}{\underset{\_}{a}}_j{\overline{x}}^j+\sum _{\begin{array}{c}{a}_j<0\\ j\mathrm{odd}\end{array}}{\underset{\_}{a}}_j{\underset{\_}{x}}^j=\overline{b}.$(19)

In the last three cases, rewriting the equations by an ordering on the power of r leads us to introduce two functions ${\hat{L}}_i$ and ${\hat{U}}_i$ for $i=0,\dots ,nk+m$, which are the coefficients of $r^i$ (${\hat{L}}_i$ respect to (14(14) $\begin{array}{rl}& \sum _{a_j\ge 0}{\underset{\_}{a}}_j{\underset{\_}{x}}^j+\sum _{a_j<0}{\underset{\_}{a}}_j{\overline{x}}^j=\underset{\_}{b},\end{array}$(14) ), (16(16) $\begin{array}{r}\sum _{j\mathrm{even}}{\underset{\_}{a}}_j{\underset{\_}{x}}^j+\sum _{j\mathrm{odd}}{\overline{a}}_j{\underset{\_}{x}}^j=\underset{\_}{b},\end{array}$(16) ) or (18(18) $\sum _{\begin{array}{c}{a}_j\ge 0\\ j\mathrm{even}\end{array}}{\underset{\_}{a}}_j{\underset{\_}{x}}^j+\sum _{\begin{array}{c}{a}_j\ge 0\\ j\mathrm{odd}\end{array}}{\underset{\_}{a}}_j{\overline{x}}^j+\sum _{\begin{array}{c}{a}_j<0\\ j\mathrm{even}\end{array}}{\overline{a}}_j{\underset{\_}{x}}^j+\sum _{\begin{array}{c}{a}_j<0\\ j\mathrm{odd}\end{array}}{\overline{a}}_j{\overline{x}}^j=\underset{\_}{b}$(18) ) and ${\hat{U}}_i$ respect to (15(15) $\begin{array}{rl}& \sum _{a_j\ge 0}{\overline{a}}_j{\overline{x}}^j+\sum _{a_j<0}{\overline{a}}_j{\underset{\_}{x}}^j=\overline{b}.\end{array}$(15) ), (17(17) $\begin{array}{r}\sum _{j\mathrm{even}}{\overline{a}}_j{\overline{x}}^j+\sum _{j\mathrm{odd}}{\underset{\_}{a}}_j{\overline{x}}^j=\overline{b}.\end{array}$(17) ) or (19(19) $\sum _{\begin{array}{c}{a}_j\ge 0\\ j\mathrm{even}\end{array}}{\overline{a}}_j{\overline{x}}^j+\sum _{\begin{array}{c}{a}_j\ge 0\\ j\mathrm{odd}\end{array}}{\overline{a}}_j{\underset{\_}{x}}^j+\sum _{\begin{array}{c}{a}_j<0\\ j\mathrm{even}\end{array}}{\underset{\_}{a}}_j{\overline{x}}^j+\sum _{\begin{array}{c}{a}_j<0\\ j\mathrm{odd}\end{array}}{\underset{\_}{a}}_j{\underset{\_}{x}}^j=\overline{b}.$(19) )). For $i=0,\dots ,nk+m$ both functions ${\hat{L}}_i$ and ${\hat{U}}_i$ are functions of ${\alpha }_j$'s and ${\beta }_j$'s. Thus we have (20) ${\hat{L}}_i({\alpha }_0,\dots ,{\alpha }_k,{\beta }_0,\dots ,{\beta }_k)=\{\begin{array}{ll}{\underset{\_}{b}}_i,& i=0,\dots ,l,\\ 0,& i=l+1,\dots ,nk+m,\end{array}$(20) and (21) ${\hat{U}}_i({\alpha }_0,\dots ,{\alpha }_k,{\beta }_0,\dots ,{\beta }_k)=\{\begin{array}{ll}{\overline{b}}_i,& i=0,\dots ,l,\\ 0,& i=l+1,\dots ,nk+m.\end{array}$(21) Let us introduce two functions $L_i$ and $U_i$ as follows: (22) $L_i=\{\begin{array}{ll}{\hat{L}}_i-{\underset{\_}{b}}_i,& i=0,\dots ,l,\\ {\hat{L}}_i,& i=l+1,\dots ,nk+m,\end{array}$(22) and (23) $U_i=\{\begin{array}{ll}{\hat{U}}_i-{\underset{\_}{b}}_i,& i=0,\dots ,l,\\ {\hat{U}}_i,& i=l+1,\dots ,nk+m.\end{array}$(23) Therefore we have (24) $\{\begin{array}{l}{L}_i=0,i=0,1,\dots ,nk+m,\\ U_i=0,i=0,1,\dots ,nk+m.\end{array}$(24) Equation (24(24) $\{\begin{array}{l}{L}_i=0,i=0,1,\dots ,nk+m,\\ U_i=0,i=0,1,\dots ,nk+m.\end{array}$(24) ) is a nonlinear system of equations with $d=2(nk+m+1)$ equations and s = 2k + 2 unknowns, so it can be solved by an iterative Gauss–Newton method. Suppose that t = nk + m Defining (25) $A=\left(\begin{array}{cccccc}{\displaystyle \frac{\mathrm{\partial }{L}_0}{\mathrm{\partial }{\alpha }_0}}& \dots & {\displaystyle \frac{\mathrm{\partial }{L}_0}{\mathrm{\partial }{\alpha }_k}}& {\displaystyle \frac{\mathrm{\partial }{L}_0}{\mathrm{\partial }{\beta }_0}}& \dots & {\displaystyle \frac{\mathrm{\partial }{L}_0}{\mathrm{\partial }{\beta }_k}}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{\mathrm{\partial }{L}_t}{\mathrm{\partial }{\alpha }_0}}& \dots & {\displaystyle \frac{\mathrm{\partial }{L}_t}{\mathrm{\partial }{\alpha }_k}}& {\displaystyle \frac{\mathrm{\partial }{L}_t}{\mathrm{\partial }{\beta }_0}}& \dots & {\displaystyle \frac{\mathrm{\partial }{L}_t}{\mathrm{\partial }{\beta }_k}}\\ {\displaystyle \frac{\mathrm{\partial }{U}_0}{\mathrm{\partial }{\alpha }_0}}& \dots & {\displaystyle \frac{\mathrm{\partial }{U}_0}{\mathrm{\partial }{\alpha }_k}}& {\displaystyle \frac{\mathrm{\partial }{U}_0}{\mathrm{\partial }{\beta }_0}}& \dots & {\displaystyle \frac{\mathrm{\partial }{U}_0}{\mathrm{\partial }{\beta }_k}}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{\mathrm{\partial }{U}_t}{\mathrm{\partial }{\alpha }_0}}& \dots & {\displaystyle \frac{\mathrm{\partial }{U}_t}{\mathrm{\partial }{\alpha }_k}}& {\displaystyle \frac{\mathrm{\partial }{U}_t}{\mathrm{\partial }{\beta }_0}}& \dots & {\displaystyle \frac{\mathrm{\partial }{U}_t}{\mathrm{\partial }{\beta }_k}}\end{array}\right)$(25) and (26) $B=-\left(\begin{array}{c}{L}_0\\ ⋮\\ L_t\\ U_0\\ ⋮\\ U_t\end{array}\right),Z=\left(\begin{array}{c}{\alpha }_0\\ ⋮\\ {\alpha }_k\\ {\beta }_0\\ ⋮\\ {\beta }_k\end{array}\right),H=\left(\begin{array}{c}{h}_1\\ h_2\\ ⋮\\ h_{2k+2}\end{array}\right),$(26) we have (27) $AH=B.$(27) A and B are used instead of $A(Z)$ and $B(Z)$, respectively. By solving this system with an initial vector $Z^{(0)}$, a sequence $\{Z^{(k)}\}$ will be obtained as follows: we consider an initial vector $Z^{(0)}$. For $k=1,2,\dots$, we compute $A^{(k)}$ and $B^{(k)}$ and then we solve $A^{(k)}{H}^{(k)}=B^{(k)}$ by a least square method: (28) ${A^{(k)}}^T{A}^{(k)}{H}^{(k)}={A^{(k)}}^T{B}^{(k)},$(28) and the obtaining vector will be improved by (29) $Z^{(k+1)}=Z^{(k)}+H^{(k)}.$(29) Again $A^{(k)}$ and $B^{(k)}$ are used instead of $A(Z^{(k)})$ and $B(Z^{(k)})$, respectively. If $\{Z^{(k)}\}$ converges to a vector $Z^{\ast }$; then ${\tilde{x}}^{\ast }$ is a solution of (5(5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) ) where (30) ${\underset{\_}{x}}^{\ast }=\sum _{i=0}^n{\alpha }_i^{\ast }{r}^i,{\overline{x}}^{\ast }=\sum _{i=0}^n{\beta }_i^{\ast }{r}^i.$(30) Therefore the algorithm will be as follows:

Lemma 3.1

If the fuzzy Equation (5(5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) ) has a root ${\tilde{x}}^{\ast }$ then $[{\tilde{x}}^{\ast }{]}^1$ is a root of the equation $\sum _{j=1}^n[{\tilde{a}}_j{]}^1[{\tilde{x}}^j{]}^1=[\tilde{b}{]}^1.$

Corollary 3.2

The algebraic fuzzy equation of degree n (5(5) ${\tilde{a}}_n{\tilde{x}}^n+\cdots +{\tilde{a}}_1\tilde{x}+{\tilde{a}}_0=\tilde{b},$(5) ) has at most n fuzzy roots with distinct cores.

Theorem 3.3

If the equation is crisp then the sequence is given by the following recurrence equation: (31) $x_{\nu +1}=x_{\nu }-\frac{a_n{x}_{\nu }^n+\dots +a_1{x}_{\nu }+a_0-b}{n{a}_{n-1}{x}_{\nu }^{n-1}+\dots +2a_2{x}_{\nu }+a_1}.$(31)

Proof.

For a crisp function algebraic equation $P_n(x)=a_n{x}^n+\cdots +a_{1}x+a_0=b$, we have $\underset{\_}{x}={\alpha }_0$ and $\overline{x}={\beta }_0$, where ${\alpha }_0={\beta }_0$. For this equation, we have (32) $\{\begin{array}{l}{L}_0=a_n{\alpha }_0^n+\cdots +a_1{\alpha }_0+a_0-b,\\ U_0=a_n{\beta }_0^n+\cdots +a_1{\beta }_0+a_0-b.\end{array}$(32) The system (27(27) $AH=B.$(27) ) for this equation is as follows: $\left(\begin{array}{cc}{\displaystyle \frac{d{L}_0}{d{\alpha }_0}}& 0\\ 0& {\displaystyle \frac{d{U}_0}{d{\beta }_0}}\end{array}\right)\left(\begin{array}{c}{h}_1\\ h_2\end{array}\right)=-\left(\begin{array}{c}{L}_0\\ U_0\end{array}\right)$ Using ${\alpha }_0={\beta }_0=x$, we have $L_0=U_0$, and $h_1^{(\nu )}=h_2^{(\nu )}=-\frac{P_n(x_{\nu })}{P_n^{\prime }(x_{\nu })}$, therefore in the iteration $\nu +1$, we have $x_{\nu +1}=x_{\nu }-\frac{P_n(x_{\nu })}{P_n^{\prime }(x_{\nu })}$.

By using the following lemma, we find that Algorithm 3.1 always generate a sequence.

Lemma 3.4

[21]

The system (28(28) ${A^{(k)}}^T{A}^{(k)}{H}^{(k)}={A^{(k)}}^T{B}^{(k)},$(28) ) always has a solution, for any k.

4. Numerical Examples

In this section, we present some examples of full fuzzy algebraic equations. All examples are solved by commercial software Mathematica 10.

Example 4.1

Consider the following equation: $(r,2-r){\tilde{x}}^2+(2r,3-r)\tilde{x}+(r,2-r)=\tilde{b},$ such that $\tilde{b}=(r^3+4r^2+4r,-r^3+9r^2-28r+29).$ For this equation, we have n = 2, l = 3 and m = 1. The least acceptable value of k is 1. By considering k = 1 and the initial fuzzy number $\tilde{x}=(0,0)$, after 6 iterations and 12 digits accuracy, we obtain ${\tilde{x}}^{\ast }=(r+1,3-r)$. In this case, $[{\tilde{x}}^{\ast }{]}^1$ is the solution of $x^2+2x+1=9$.

Example 4.2

For equation: $(r,2-r){\tilde{x}}^2+(2r,3-r)\tilde{x}+(r,2-r)=\tilde{b},$ with $\tilde{b}=(r^5+2r^3+r,-4r^3+22r^2-43r+29),$ we have n = 2, l = 5 and m = 1. The least acceptable value of k is 2. By considering k = 2 and the initial fuzzy number $\tilde{x}=(1,1)$, after 6 iterations and 11 digits accuracy, we obtain ${\tilde{x}}^{\ast }=(r^2,3-2r)$. In this case, $[{\tilde{x}}^{\ast }{]}^1$ is the solution of $x^2+2x+1=4$.

Example 4.3

Consider the following equation: $(r,2-r){\tilde{x}}^2+(r-3,-2r)\tilde{x}+(r,2-r)=\tilde{b},$ such that $\tilde{b}=(r^3+3r^2+12r-12,-r^3+8r^2-37r+34).$ For this equation, we have n = 2, l = 3 and m = 1 and one of the coefficients is non-positive. The least acceptable value of k is 1. By considering k = 1 and the initial fuzzy number $\tilde{x}=(1,1)$, after 7 iterations and 8 digits accuracy, we obtain ${\tilde{x}}^{\ast }=(r+2,4-r)$. In this case, $[{\tilde{x}}^{\ast }{]}^1$ is the solution of $x^2-2x+1=4$.

Example 4.4

Consider the following equation: $(r+1,4-2r){\tilde{x}}^2+(r,2-r)\tilde{x}+(1,1)=\tilde{b},$ such that $\tilde{b}=(9r^3+8r^2+6r-7,-2r^3+17r^2-64r+65).$ For this equation, we have n = 2, l = 3 and m = 1. The least acceptable value of k is 1. By considering k = 1 and the initial fuzzy number $\tilde{x}=(-1,-1)$, after 7 iterations and 8 digits accuracy, we obtain ${\tilde{x}}^{\ast }=(r-4,-3r)$. In this case, $[{\tilde{x}}^{\ast }{]}^1$ is the solution of $2x^2+x+1=16$. Here the root of equation is non-positive.

Example 4.5

For the following equation: $(r+2,5-2r){\tilde{x}}^2+(2r-6,-2r-2)\tilde{x}+(2,2)=\tilde{b},$ with $\tilde{b}=(r^3+4r^2+2r+2,-2r^3+15r^2-38r+34),$ we have n = 2, l = 3 and m = 1 and one of the coefficients is negative. The least acceptable value of k is 1. By considering k = 1 and the initial fuzzy number $\tilde{x}=(-1,-1)$, after 8 iterations and 8 digits accuracy, we obtain ${\tilde{x}}^{\ast }=(r-2,-r)$. In this case, $[{\tilde{x}}^{\ast }{]}^1$ is the solution of $3x^2-4x+2=9$. Here the root of equation is non-positive.

Example 4.6

Suppose that we want to solve the following equation: $\begin{array}{rl}& (r,2-r){\tilde{x}}^4+(r,3-2r){\tilde{x}}^3+(r,2-r)\\ & =(r^5+r^4+r,-r^5+12r^4-55r^3+122r^2-133r+58).\end{array}$ For this equation, we have n = 4, l = 5 and m = 1. The least acceptable value of k is 1. By considering k = 1 and the initial fuzzy number $\tilde{x}=(1,1)$, after 10 iterations we obtain ${\tilde{x}}^{\ast }=(r,2-r)$. In this case, $[{\tilde{x}}^{\ast }{]}^1$ is the solution of $x^4+x^3+1=3$.

Example 4.7

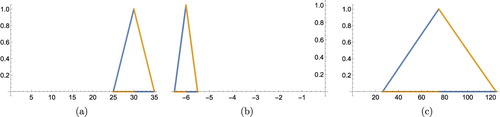
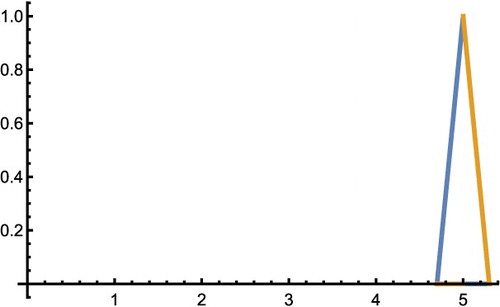
Suppose that a car is moving in a straight line with the velocity $\tilde{v}$. If this car breaks, after a time $\tilde{t}$ it will stop. The distance satisfies in the following relation: (33) $\frac{1}{2}\tilde{a}{\tilde{t}}^2+\tilde{v}\tilde{t}=\tilde{d},$(33) in which $\tilde{a}$ is the constant negative acceleration and $\tilde{t}$ is the stopping time, and all variables are linguistic (Figure 1). 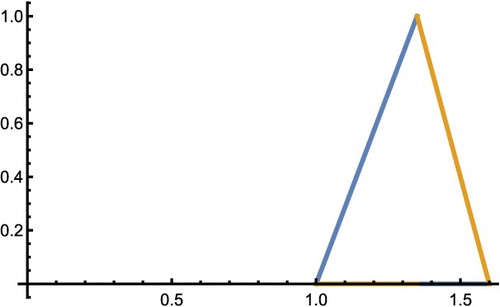If acceleration is about $-6\frac{m}{s^2}$ and the velocity is about $30\frac{m}{s}$, then by solving the equation, it will be clear that the car will stop after about 5 s (Figures 2 and 3).

Figure 1. The time of breaking.

Figure 2. The coefficients of quadratic equation: (a) Velocity, (b) Acceleration and (c) Distance.

Figure 3. Stopping time.

Example 4.8

Consider the following fuzzy linear differential equation of order n: ${\tilde{a}}_n\frac{{\mathrm{d}}^n\tilde{x}}{\mathrm{d}{t}^n}+\cdots +{\tilde{a}}_1\frac{\mathrm{d}\tilde{x}}{\mathrm{d}t}+{\tilde{a}}_0\tilde{x}=\tilde{0},$ where $t$ is the independent crisp variable. 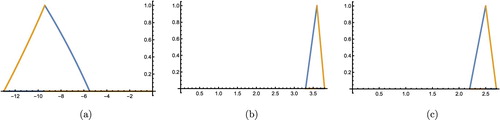In order to find the solution of this ODE one must solve the following fuzzy algebraic equation of degree n: ${\tilde{a}}_n{\tilde{w}}^2+\cdots +{\tilde{a}}_1\tilde{w}+{\tilde{a}}_0=\tilde{0}.$ For example by considering ${\tilde{a}}_2,{\tilde{a}}_1$ and ${\tilde{a}}_0$ as shown in Figure 4, the solution of quadratic equation is the fuzzy number which is shown in Figure 5 and the solution of related differential equation is $\tilde{x}(t)=\exp ((1+0.35r,1.6-0.25r)t)$ (Figures 4 and 5).

Figure 4. The coefficients of quadratic equation: (a) ${\tilde{a}}_2$, (b) ${\tilde{a}}_1$ and (c) ${\tilde{a}}_0$.

Figure 5. Root of equation.

5. Conclusion

In this work, we presented a method to find a numerical solution of a full fuzzy algebraic equation. The method can be used for any kind of fuzzy equations, with non-positive or non-negative roots and with non-positive or non-negative coefficients. Some possible future research directions may consist of the more general case than the four cases which considered in this paper, and using the proposed for multiple roots of an equation.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Notes on contributors

Majid Amirfakhrian

Majid Amirfakhrian was born and raised in Tehran, Iran. He went to the University of Guilan, Rasht, Iran for his post–secondary education. He received his Master of Science in Applied Mathematics from the Sharif University of Technology and completed his Ph.D. through the Azad University, Science and Research branch. He joined the Azad University, Central Tehran Branch (IAUCTB) in 2002. He was promoted to a full professorship of Applied Mathematics at IAUCTB in 2015. His main research interests lie in Numerical Analysis and Approximation, Fuzzy Approximation, Data Sciences, Multivariate Approximation, Image Processing, and Numerical Partial Differential Equations. He has side interests in Optimization and Statistics.

S. R. Fayyaz Behrooz

S. R. Fayyaz Behrooz was born on November 22, 1978, and grown up in Tabriz, Iran. She received an M.S. degree from Tabriz University in 2004 and a B.S. degree from Islamic Azad University, Tabriz Branch in 2002. She is currently a Ph.D. student at the Islamic Azad University, Central Tehran Branch, Iran. She is a faculty member at Islamic Azad University, Osku Branch since 2008. Her main research interest includes Numerical and Computational Methods in Science and Fuzzy problems.