Advanced search
Publication Cover
Journal of Taibah University for Science Volume 12, 2018 - Issue 3
Submit an article Journal homepage
1,558
Views
6
CrossRef citations to date
0
Altmetric
Original articles

Exact solitary wave solution for the fractional and classical GEW-Burgers equations: an application of Kudryashov method

R. I. NuruddeenDepartment of Mathematics, Federal University Dutse, Dutse, NigeriaORCID Iconhttp://orcid.org/0000-0002-5321-1958
ORCID Icon &
Aminu M. NassDepartment of Mathematics, University of Hafar Al Batin, Hafar Al-Batin, Saudi ArabiaCorrespondence[email protected]
[email protected]
ORCID Iconhttp://orcid.org/0000-0002-6672-5835
ORCID Icon
Pages 309-314 | Received 19 Nov 2017, Accepted 20 Mar 2018, Published online: 09 May 2018

ABSTRACT

The fractional partial differential equations have wide applications in science and engineering. In this paper, the Kudryashov techniques were utilized to obtain an exact solution of both fractional generalized equal width (GEW)-Burgers and classical GEW-Burgers equations. The general analytical solutions of the two partial differential equations are constructed for n>1. The graphical representation of the solutions is given in comparison with some previous results in the literature. The advantages and disadvantages of the method were listed.

2010 MATHEMATICS SUBJECT CLASSIFICATION:

1. Introduction

The non-linear partial differential equations of fractional order are important class of differential equations used in modelling many science and engineering applications. This is strongly connected to their various applications and abilities in describing lots of complicated physical situations.

In this paper, we discuss the analytical solutions of fractional generalized equal width (GEW)-Burgers equation, i.e.(1) and generalized non-linear equal width (EW) classical GEW-Burgers equation by Morrison et al. [Citation1], i.e.(2) that is used in one-dimensional wave propagation attached with dispersive waves together with dissipative effects in non-linear media where p,q and r are real constants. Several methods have been used in the literature to construct the solutions of fractional order partial differential equations, ranging from semi-analytical methods to numerical techniques [Citation1–38]. However, little work is available in the literature in respect to the analytical methods especially for the GEW-Burgers equation. Hamdi et al. [Citation6] coupled some techniques to construct hyperbolic tangent exact solution of the GEW-Burgers equation [Citation6].

In this study, we employ the Kudryashov method [Citation7] to analytically treat and examine the fractional GEW-Burgers equation (Equation1) and classical GEW-Burgers equation (Equation2). The fractional GEW-Burgers equation considered features fractional order derivatives in both the spatial and temporal variables, defined in the sense of the new conformable fractional derivative. We have successfully constructed the general solutions for the two equations for any n>1 and later establish a comparison between the result found and that of the classical GEW-Burgers equation obtained by Hamdi et al. [Citation6]. Three-dimensional graphical representations for some solutions and two-dimensional plots for the sake of comparisons were also presented. The compared solutions are found to be in good agreement.

The main advantages of the Kudryashov method in comparison to others are: the method is simple in application and it can be used to find all solitary wave solutions and all single periodic solutions, when we get the expansion of the general solutions of non-linear differential equations in the Laurent series. Second, exact solution can be obtained by considering different functions. Finally, the method can use a unique formulae for all non-linear differential equations in the polynomial form [Citation7].

This paper is organized as follows: in Section 2, we give some basic definitions and properties of the conformable fractional derivatives. While in Section 3, we introduce the Kudryashov method [Citation7] and the application of the method to the space–time fractional GEW-Burgers equation and classical GEW-Burgers equation, respectively, followed by conclusion in Section 4.

2. Conformable fractional derivative and some properties

In this section, we provide the reader basic properties and definition of conformable fractional derivatives.

If , the s order conformable derivative of u is defined by(3)

Some important properties of the conformable fractional derivative are summarized in Theorems 2.1 and 2.2.

Theorem 2.1:

Suppose and are α-differentiable at t>0 and , then

  1. for all .

  2. for all constant function .

  3. for all a constant.

  4. for all .

  5. .

  6. , .

  7. If in addition to is differentiable, then .

Theorem 2.2:

Let be a differentiable function and suppose is also differentiable defined in the range of , with , then where stands for the conformable fractional derivative with respect to temporal variable [Citation8,Citation9].

3. The Kudryashov method of solution

In this section, steps needed to apply the method are presented. We start by considering the conformable fractional differential equation,(4) Kudryashov method follows by reducing (Equation4) to ordinary differential equation using the wave transformation, i.e.(5) where α is a fractional order and c is a non-zero constant. Substituting the transformation (Equation4) into (Equation5), we get a reduced ordinary differential equation of the polynomial form, i.e.(6)

Kudryashov method offers a truncated finite series of the form:(7) where is given by the function(8) which satisfies the ordinary differential equation,(9) where are constants; N is a positive integer determined by the homogeneous balancing method.

Substituting (Equation7) into (Equation6) yields a polynomial in . The resultant algebraic system of equations is then solved for , , () and c.

3.1. Application

Finally, we apply the method presented in the previous section to construct the analytical solutions of conformable space–time fractional GEW-Burgers and generalized classical GEW-Burgers partial differential equations.

Examples 3.1:

Consider the conformable space–time fractional GEW-Burgers equation of the form:(10) using the wave transformation,Equation (Equation10) is reduced to an ordinary differential equation,(11) Integrating Equation (Equation11) once, and assuming the constant of integration zero, we get(12) Balancing the highest order derivative with the highest non-linear order () in (Equation11), we get .

Applying the transformation , Equation (Equation12) becomes(13) by balancing the highest derivative order of (Equation13) with the highest non-linear order () in (Equation13), we get which implies using (Equation7) that(14) Substituting (Equation14) into (Equation13) and by equating the coefficients of various degrees of to zero, we obtain the following algebraic system equations:(15) Solving the system (Equation15), we obtain the following cases: Case I: For n=2, (16) From which, using (Equation14) and (Equation16), we have(17) which subsequently led to(18)

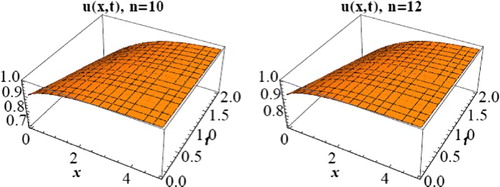
Case II: In general for any value of n, solving the systems (Equation15), we obtain the following arbitrary constants: which implies from (Equation14),(19) therefore, the general solution has the form:(20) Thus for values of , we get from (Equation20) the following solutions:(21) (22) (23) (24) The graphical representations of some solutions are presented in .

Figure 1. 3D solitary wave profile of (Equation20) when , d = 1.5, c = 1, and n = 2,4.

Figure 1. 3D solitary wave profile of (Equation20(20) ) when , d = 1.5, c = 1, and n = 2,4.

Figure 2. 3D solitary wave profile of (Equation20) when , d = 1.5, c = 1, and n = 6,8.

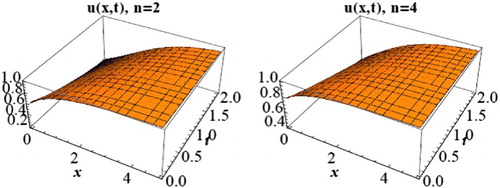
Figure 2. 3D solitary wave profile of (Equation20(20) ) when , d = 1.5, c = 1, and n = 6,8.

Figure 3. 3D solitary wave profile of (Equation20) when , d = 1.5, c = 1, and n = 10,12.

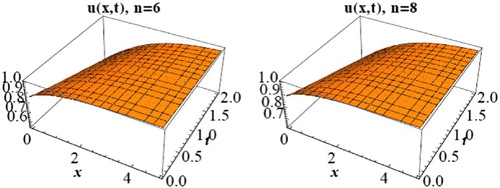
Figure 3. 3D solitary wave profile of (Equation20(20) ) when , d = 1.5, c = 1, and n = 10,12.

Examples 3.2:

Consider the GEW-Burgers equation, i.e.(25) where p,q and r are real constants. Applying the Kudryashov method, we obtain the solution of the GEW-Burgers equation (Equation25) as(26) The solution of (Equation2) obtained here, i.e. (Equation26), is exactly the same with the fractional version of GEW-Burgers equation in (Equation10) for with little discrepancy in p that is found to be . Nevertheless, this do not change the solution in (Equation25), since p,q and r are not reflecting in the solution. Also, see for the graphical representations of some solutions.

Figure 4. 3D solitary wave profile of Equation (Equation25) when , d = 1.5, c = 1 and n = 2,4.

Figure 4. 3D solitary wave profile of Equation (Equation25(25) ) when , d = 1.5, c = 1 and n = 2,4.

Figure 5. 3D solitary wave profile of Equation (Equation24) when , d = 1.5, c = 1 and n = 6,8.

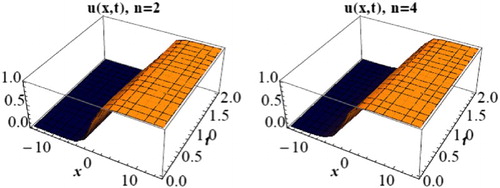
Figure 5. 3D solitary wave profile of Equation (Equation24(24) ) when , d = 1.5, c = 1 and n = 6,8.

Figure 6. 3D solitary wave profile of Equation (Equation24) when , d = 1.5, c = 1 and n = 10,12.

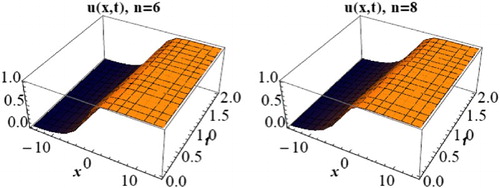
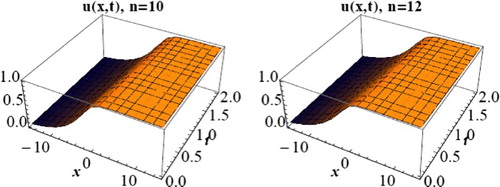
Figure 6. 3D solitary wave profile of Equation (Equation24(24) ) when , d = 1.5, c = 1 and n = 10,12.

Remark 3.3:

It is clear from the graphical representations of the solutions presented above, the behaviours of the solutions depend on the values of the constants and the fractional order.

3.2. Comparison of results

In Hamdi et al. [Citation6], the classical GEW-Burgers equation (Equation2) was studied coupling some techniques and found the following exact solution was obtained [Citation6]:(27) Thus we feel it is imperative to establish a comparison between our solution (Equation25) and that of Hamdi et al. (Equation27) [Citation6].

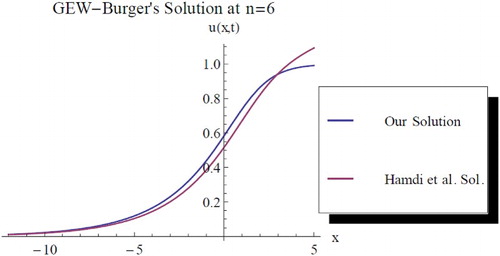
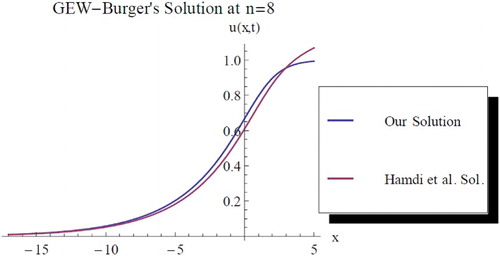
In so doing , we make choice of the following parameters: , k = 0.5 and in Equation (Equation25) and and in (Equation27), while c = 1 in both solutions. However, following results are obtained upon this assumption and we thus represent them graphically as follows at different values of n. Finally, the two results are found to be in good agreement; also one can obtain distinct results by maintaining the above parameters with d = 1. See for the graphical representations of some cases.

Figure 7. Comparison between our solution and Hamdi et al. solution at , c = 1, d = 1.5, , t = 1.8, k = 0.45.

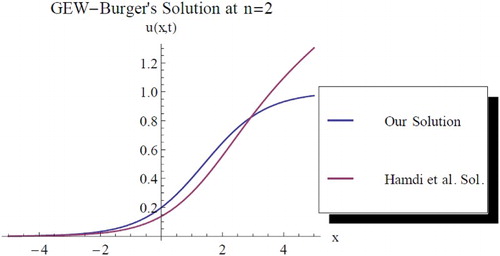
Figure 7. Comparison between our solution and Hamdi et al. solution at , c = 1, d = 1.5, , t = 1.8, k = 0.45.

Figure 8. Comparison between our solution and Hamdi et al. solution at , c = 1, d = 1.5, , t = 1.8, k = 0.45.

Figure 8. Comparison between our solution and Hamdi et al. solution at , c = 1, d = 1.5, , t = 1.8, k = 0.45.

Figure 9. Comparison between our solution and Hamdi et al. solution at , c = 1, d = 1.5, , t = 1.8, k = 0.45.

Figure 9. Comparison between our solution and Hamdi et al. solution at , c = 1, d = 1.5, , t = 1.8, k = 0.45.

Figure 10. Comparison between our solution and Hamdi et al. solution at , c = 1, d = 1.5, , t = 1.8, k = 0.45.

Figure 10. Comparison between our solution and Hamdi et al. solution at , c = 1, d = 1.5, , t = 1.8, k = 0.45.

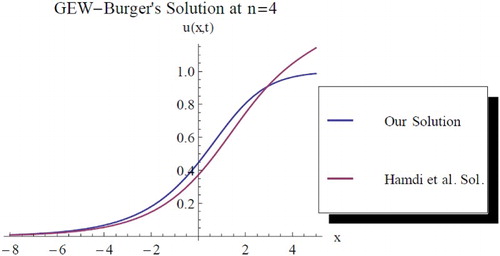
4. Conclusion

In conclusion, the conformable space–time fractional and classical GEW-Burgers equations are extensively examined by employing the powerful Kudryashov method. The generalized solutions for the two equations are established for any given n > 1. A kind of comparison analysis between the classical GEW-Burgers equation solution obtained and that of Hamdi et al. [Citation6] is also presented and the two results are found to be in agreement. The comparison was established through graphical representations for the solutions. Thus the Kudryashov method is highly recommended for generalized and non-generalized problems and in this direction, respectively.

Disclosure statement

No potential conflict of interest was reported by the authors.

References

  • Morrison PJ, Meiss JD, Carey JR. Scattering of regularized-long-wave solitary waves. Phys D. 1984;11:324–336. doi: 10.1016/0167-2789(84)90014-9
  • Zeybek H, Karakoc SBG. Application of the collation method with B-splines to the GEW equation. Electron Trans Numer Anal. 2017;46:71–88.
  • Hamdi S, Gottlieb JJ, Hansen JS. Numerical solutions of the equal width wave equation using an adaptive method of lines. Boca Raton (FL): Chapman & Hall/CRC Press; 2001. p. 65–116.
  • Zhang L. A finite difference scheme for generalized regularized long-wave equation. Appl Math Comput. 2005;168(2):962–972.
  • Evans DJ, Raslan KR. Solitary waves for the generalized equal width (GEW) equation. Int J Comput Math. 2005;82(4):445–455. doi: 10.1080/0020716042000272539
  • Hamdi S, Enright WH, Schiesser WE, et al. Exact solutions of the generalized equal width equation. Comp Sci Appl. 2003;2668:725–734.
  • Kudryashov NA. One method for finding exact solutions of nonlinear differential equations. Commun Nonlinear Sci Numer Simul. 2012;17(6):2248–2253. doi: 10.1016/j.cnsns.2011.10.016
  • Khalil R, Al Horani M, Yousef A, et al. A new definition of fractional derivative. J Comput Appl Math. 2014;264:65–70. doi: 10.1016/j.cam.2014.01.002
  • Abu Hammad M, Khalil R. Conformable fractional heat differential equation. Int J Pure Appl Math. 2014;94(2):215–221. doi: 10.12732/ijpam.v94i2.8
  • Khan K, Akbar MA. Study of analytical method to seek for exact solutions of variant Boussinesq equations. Springerplus. 2014;3:324. DOI:10.1186/2193-1801-3-324.
  • Pego RL, Quintero JR. Two dimensional solitary waves for Benney–Luke equation. Phys D. 1999;132:476–496. doi: 10.1016/S0167-2789(99)00058-5
  • Islam SMR, Khan K, Al Woadud KMA. Analytical studies on the Benney–Luke equation in mathematical physics. Waves Random Media Complex Media. 2017;28:300–309. doi:10.1080/17455030.2017.1342880 doi: 10.1080/17455030.2017.1342880
  • Raslan KR, Ali KK, Shallal MA. The modified extended tanh method with the Riccati equation for solving the space–time fractional EW and MEW equations. Chaos Solitons Fractals. 2017;103:404–409. doi: 10.1016/j.chaos.2017.06.029
  • Raslan KR, EL-Danaf TS, Ali KK. Exact solution of the space–time fractional coupled EW and coupled MEW equations. Eur Phys J Plus. 2017;132:319. doi: 10.1140/epjp/i2017-11590-9
  • Hosseini K, Bekir A, Ansari R. Exact solutions of nonlinear conformable time-fractional Boussinesq equations using the exp(−φ(ξ))-expansion method. Opt Quantum Electron. 2017;49:131. doi: 10.1007/s11082-017-0968-9
  • Nuruddeen RI, Nass AM. Exact solutions of wave-type equations by the Aboodh decomposition method. Stochastic Model Appl. 2017;21(1):23–30.
  • Bekir AE, Guner OA. Analytical approach for the space–time nonlinear partial differential fractional equation. Int J Nonlinear Sci Numer Simul. 2014;15:463–470. doi: 10.1515/ijnsns-2013-0145
  • Matinfar M, Eslami M, Kordy M. The functional variable method for solving the fractional Korteweg–de Vries equations and the coupled Korteweg–de Vries equations. Pramana. 2015;85:583–592. doi: 10.1007/s12043-014-0912-5
  • Yaslan HC. New analytic solutions of the conformable space–time fractional Kawahara equation. Int J Light Electron Optics. 2017;140:123–126. doi: 10.1016/j.ijleo.2017.04.015
  • Fan E. Extended tanh-function method and its applications to nonlinear equations. Phys Lett A. 2000;277:212–218. doi: 10.1016/S0375-9601(00)00725-8
  • Fu Z, Liu S, Liu S, et al. New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations. Phys Lett A. 2001;290:72–76. doi: 10.1016/S0375-9601(01)00644-2
  • Nuruddeen RI, Muhammad L, Nass AM, et al. A review of the integral transforms-based decomposition methods and their applications in solving nonlinear PDEs. Palestine J. Math. 2017;7(1):262–280.
  • Wazwaz A. A variety of soliton solutions for the Boussinesq–Burgers equation and the higher-order Boussinesq–Burgers equation. Filomat. 2017;31(3):831–840. DOI:10.2298/FIL1703831W doi: 10.2298/FIL1703831W
  • Sivaporn A, Surattana S, Sanoe K. New exact solutions for the time fractional clannish random Walker's parabolic equation by the improved tan(φ(ξ)/2)-expansion method. AMM, Chiang Mai University, Chiang Mai, Thailand; 2017.
  • Islam MT, Akbar MA, Azad AK. Multiple closed form solutions to the KdV and modified KdV equations through the rational (G/G)-expansion method. J Assoc Arab Univ Basic Appl Sci. 2017;24:160–168.
  • Islam MT, Akbar MA, Azad MAK. A rational (G/G)-expansion method and its application to modified KdV–Burgers equation and the (2+1)-dimensional Boussinesq equation. Nonlinear Stud. 2015;6(4):1–11.
  • Seadawy AR, Lu D, Khater MMA. Solitary wave solutions for the generalized Zakharov–Kuznetsov–Banjamin–Bona-Mohany nonlinear evolution equation. J Ocean Eng Sci. 2017;2:137–142. doi: 10.1016/j.joes.2017.05.002
  • Arshad M, Lu D, Wang J. (N+1)-dimensional fractional reduced differential transform method for fractional order partial differential equations. Commun Nonlinear Sci Numer Simul. 2017;48:509–519. doi: 10.1016/j.cnsns.2017.01.018
  • Seadawy AR, Lu D, Khater MMA. Solitary wave solutions for the generalized Zakharov–Kuznetsov–Benjamin–Bona-Mahony nonlinear evolution equation. J Ocean Eng Sci. 2017;2:137–142. doi: 10.1016/j.joes.2017.05.002
  • Arshad M, Seadawy AR, Lu D. Bright–dark solitary wave solutions of generalized higher-order nonlinear Schrodinger equation and its application in optics. J Electromagn Waves Appl. 2017;31(16):1711–1721. doi: 10.1080/09205071.2017.1362361
  • Khater MMA, Kumar D. New exact solutions for the time fractional coupled Boussinesq–Burger equation and approximate long water wave equation in shallow water. J Ocean Eng Sci. 2017;2(3):223–228. doi: 10.1016/j.joes.2017.07.001
  • Mostafa MAK, Aly Seadawy R, Lu D. Elliptic and solitary wave solutions for Bogoyavlenskii equations system, couple Boiti–Leon–Pempinelli equations system and time-fractional Cahn–Allen equation. J Ocean Eng Sci. 2017;7:2325–2333.
  • Mohyud-Din ST, Irshad A, Ahmed N, et al. Exact solutions of (3+1)-dimensional generalized KP equation arising in physics. Results Phys. 2017;7:3901–3909. doi: 10.1016/j.rinp.2017.10.007
  • Khan U, Ellahi R, Khan R, et al. Extracting new solitary wave solutions of Benny–Luke equation and Phi-4 equation of fractional order by using (G′/G)-expansion method. Opt Quantum Electron. 2017;49:362. doi: 10.1007/s11082-017-1191-4
  • Irshad A, Mohyud-Din ST, Ahmed N, et al. A new modification in simple equation method and its applications on nonlinear equations of physical nature. Results Phys. 2017;7:4232–4240. doi: 10.1016/j.rinp.2017.10.048
  • Bibi S, Mohyud-Din ST, Khan U, et al. Khater method for nonlinear Sharma Tasso–Olever (STO) equation of fractional order. Results Phys. 2017;7:4440–4450. doi: 10.1016/j.rinp.2017.11.008
  • Bibi S, Mohyud-Din ST, Ullah R, et al. Exact solutions for STO and (3+1)-dimensional KdV–ZK equations using (G′/G2)-expansion method. Results Phys. 2017;7:4434–4439. doi: 10.1016/j.rinp.2017.11.009
  • Rahmatullah , Ellahi R, Mohyud-Din ST, et al. Exact traveling wave solutions of fractional order Boussinesq-like equations by applying exp-function method. Results Phys. 2018;8:114–120. doi: 10.1016/j.rinp.2017.11.023
Download PDF

Related research

People also read lists articles that other readers of this article have read.

Recommended articles lists articles that we recommend and is powered by our AI driven recommendation engine.

Cited by lists all citing articles based on Crossref citations.
Articles with the Crossref icon will open in a new tab.