The combined effects of anisotropic porous medium and stably stratified fluid on free convective flow through an annulus

ABSTRACT

This paper documents the semi-analytical results for transient natural convection fluid flow between two concentric vertical cylinders of infinite lengths in the presence of anisotropic porous medium and stratified fluid. The solutions for the time-dependent coupled second order partial differential equations modelling the flow formation are obtained by using trio-methods: Laplace transform techniques, a numerical procedure based on the Riemann Sum Approximation method and D’Alembert method. Line graphs and contour maps for the fluid velocity and temperature profiles are presented for different physical parameters of interest featuring in the solutions. The inclusion of the stratification and anisotropic parameters in the model has been found to aid the regulation of the fluid flow. Furthermore, from the numerical simulation conducted, it is found that for some saturated stratified fluids, the steady and transient state velocities (as well as the temperatures of the fluid) coincide at large time.

KEYWORDS:

• Anisotropic porous materials
• stably stratified fluid
• Riemann sum approximation
• D’Alembert method and vertical annulus

1. Introduction

The growing importance of the application of porous materials either naturally existing or artificially developed has led to several investigations (experimentally or theoretically) involving fluid flow through various forms of porous materials. Application of porous media in modelling biological tissues and peristaltic flow have been documented by several researchers. A mathematical simulation modelling the flow in a gallbladder filled with stones has been formulated and studied in detail. This study as conducted by Soliman et al. [1] considered the peristaltic motion induced by a sinusoidal travelling wave of incompressible, electrically conducting Maxwell fluid in the porous walls of a two-dimensional channel through a porous medium. The research established that the Hall parameter has an increasing effect on the mean velocity distribution, the reversal flow as well as the perturbation function. Abdelsalam and Vafai [2] examined the particulate suspension effect on peristaltically induced unsteady pulsatile flow in a narrow artery. The general model on peristaltic motion where the effect of magnetic field with viscoelastic parameters on the flow was taken into account has also been examined by Abdelsalam and Vafai [3]. Khaled et al. [4] investigated the peristaltic flow of a compressible Maxwell fluid resulting from the surface acoustic wave in a parallel-plane micro-channel through a porous medium in the presence of a constant magnetic field. Detailed accounts on the application of porous media in biological tissues can be found in Khaled and Vafai [5], Eldabe et al. [6] and Abdelsalam and Vafai [7]. In addition, other applications of fluid flow through porous systems can also be found in areas such as oil exploration and recover, drying process and in underground fluid flow. For instance, a detailed literature review on heat transfer through porous passages has been documented by Nield and Bejah [8]. Chen et al. [9] investigated the various non-Darcian effects such as the no-slip boundary conditions, flow inertia force and variable porosity on the mixed convection fluid flow about an isothermal vertical cylinder embedded in a saturated porous matrix. In this excellent research masterpiece, the authors demonstrated that the non-Darcian effects have strong bearing on the fluid flow and heat transfer as against those effects predicted by the Darcy flow model. Using numerical approaches, Sparrow et al. [10] studied the dual effects of variable Reynolds number and angle of divergence in the fluid flow formation in a conical duct. Using Homotopy perturbation procedure, Abdelsalam and Bhatti [11] discussed a theoretical model that estimates the effect of some physical parameters on the characteristics of blood-like fluid flow.

Most of the early works related to fluid flow via porous media generally take into account the isotropic nature of the porous system. However, porous passages where transport properties such as permeability and diffusivity are directionally inclined exist. Such porous media termed as anisotropy porous media are generally characterized by non-uniform distribution, fractural structure and orientation of the grain beads or fibres of the porous materials. Accordingly, anisotropic porous media abound in nature and in scientific applications such as underground rock formation and geological sedimentation processes where fluids generally exhibit upward convective thrust resulting from buoyancy induced by high temperature. Other anisotropic porous structures encountered include light coming through a polarizer, filter beds, river beds and soil sands. Several papers have been published in this field. Rees and Storesletten [12] studied the instability of flow resulting from heated inclined surfaces by taking into account the effects of anisotropy and lateral mass flux. Degan et al. [13] carried out a theoretical analysis on convective transfer and the penetrative length of convection fluid flow in a vertical cylindrical well filled with anisotropic porous matrix. These authors examined the influence of the anisotropic permeability ratio $k^{\ast }$ and the convective heat transfer inside a well. They showed that for a large value of anisotropic permeability ratio $\left(k^{\ast }>1\right)$, a weak convective heat transfer and a relatively high penetrative fluid flow are observed. For small value of anisotropic permeability ratio $\left(k^{\ast }<1\right)$, a converse trend is however noticed. In addition, Bera and Khalili [14] observed that if the anisotropic permeability ratio; $k^{\ast }>1,$ an increase of the anisotropic angle of orientation $\left(\theta \right)$, within the closed interval [$0^o,{90}^o]$ tends to suppress the total permeability along the main flow direction which consequently results in decrease in the fluid convection current. The authors further showed that a slight rotation of the permeability tensor largely alter the strength of the fluid flow formation as well as the pattern of the energy and concentration profiles. The effects of anisotropic parameters and temperature dependent variable properties on the mixed convection flow and heat transfer have also been investigated by Vajravelu and Prasad [15]. While investigating the influence of hydrodynamic anisotropy on fluid flow and skin friction between two porous layers, Karmakar and Sekhar [16] observed that for a given permeability ratio less than unity, the velocity distribution in a given porous layer is maximum when the anisotropic angle of inclination equals $0^0$ and minimum when the angle of inclination is ${90}^0.$ Filip et al. [17] investigated the fully developed assisting mixed convection flow through a porous channel with an anisotropic permeability when the walls of the transport channels are kept at constant heat fluxes.

On the other hand, the nature of the fluid flowing through a porous medium is worth being investigated since it also generally influenced the flow pattern. For instance, while investigating the problem involving the transient natural convection mode of heat transfer driven by internal heat generating/absorbing fluids such as liquid-metals and other conventional coolants, Jha and Musa [18] showed that increase in the generating/absorbing parameter generally leads to the cooling of the flowing fluid and thereby causing the thermal boundary layer to become much thinner, decrease the thermal buoyancy effects and therefore suppresses the fluid temperature and momentum. Thus in this work, fluids commonly associated with the dynamics of fluid parcels (stratified fluids) are also taken into account alongside anisotropy. Such fluids consist of fluid layers of different densities such that under gravitational influence, they are arranged in such a way that fluids of higher densities are found beneath those of lower densities. According to Deka and Paul [20], the thermal stratification is the combination of the vertical temperature advection and the rate of reversible work done on the fluid particles by compression. The authors also observed that the inclusion of thermal stratification term in the energy equation in vertical equations of motion is quite a recent concept, as a result of which the flow situation comes out as steady at large times, whereas without thermal stratification it grows continuously against time. In addition, Shapiro and Fedorovich [19] presented an analytical solution for laminar natural convection flows of stably stratified fluid along vertical plates and cylinders subject to periodic surface-temperature variations. In another article, Deka and Paul [21] investigated the transient free convection flow past an infinite moving vertical cylinder in a stably stratified fluid. Other well-documented results on effect of stratified fluid in convection fluid flow include the works of Shapiro and Fedorovich [22], Deka and Bhattacharya [23] and Magyari et al. [24].

Like anisotropic porous structures, stratified fluids are also found in nature and with diverse applications especially in oceanography and metrology. Hence the problem of fluid flow via anisotropic porous passages becomes more interesting when simultaneously studied along with stratified fluids. Thus the objective of this research paper is to determine the combined effects of these physical parameters on transient convection fluid flow in a vertical annulus. In solving the complex coupled partial differential equation governing the flow model, three methods have been employed namely; Laplace transform techniques, D’Alembert method and Riemann Sum Approximation method.

2. Mathematical analysis

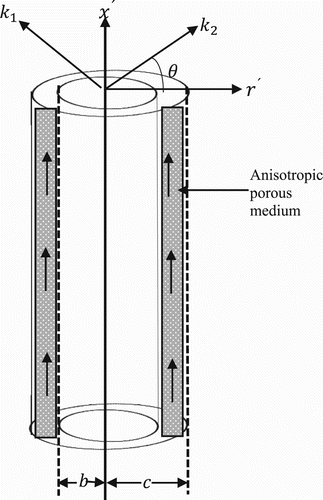
The flow considered in this article is a time-dependent natural convection flow of viscous, incompressible, stratified fluid in an annulus filled with anisotropic porous material. The fluid flow is upwardly driven in the direction of $x^{\mathrm{\prime }}$-axis while the $r^{\mathrm{\prime }}$-axis is taken along the radial direction. The radii of the inner and outer cylinders are $b$ and $c$, respectively, as presented in Figure 1. The quantities $k_1$ and $k_2$ represent the permeabilities along the principal axes of the anisotropic porous passage while the anisotropic angle of inclination $\theta$ is the angle between the horizontal direction and the principal axis with the permeability $k_2$. At ${\mathit{t}}^{\mathbf{\prime }}\le 0$, the stratified fluid, the outer cylinder and the inner cylinder are all maintained at the same constant temperature. At $t^{\mathrm{\prime }}>0,$ the outer surface of the inner cylinder is heated to a temperature $\left(T_w\right)$ while the inner surface of the outer cylinder is maintained at a temperature $\left(T_0\right)$ which is less than that of the outer surface of the inner cylinder. Accordingly, following Degan and Vasseur [25] and Deka and Paul [20], natural convection in the concentric cylinder described by Equations (1) and (2) and consistence with the initial and boundary conditions in Equation (4) occurs. (1) $\frac{\mathrm{\partial }{U}^{\mathrm{\prime }}}{\mathrm{\partial }{t}^{\mathrm{\prime }}}={\upsilon }_{eff}\left(\frac{{\mathrm{\partial }}^2{U}^{\mathrm{\prime }}}{\mathrm{\partial }{r}^{{}^{\mathrm{\prime }}2}}+\frac{1}{r^{\mathrm{\prime }}}\frac{\mathrm{\partial }{U}^{\mathrm{\prime }}}{\mathrm{\partial }{r}^{\mathrm{\prime }}}\right)+g\beta \left(T^{\mathrm{\prime }}-T_0\right)-\frac{U^{\mathrm{\prime }}\nu }{\overline{\overline{K}}}$(1) (2) $\frac{\mathrm{\partial }{T}^{\mathrm{\prime }}}{\mathrm{\partial }{t}^{\mathrm{\prime }}}=\alpha \left(\frac{{\mathrm{\partial }}^2{T}^{\mathrm{\prime }}}{\mathrm{\partial }{r}^{{}^{\mathrm{\prime }}2}}+\frac{1}{r^{\mathrm{\prime }}}\frac{\mathrm{\partial }{T}^{\mathrm{\prime }}}{\mathrm{\partial }{r}^{\mathrm{\prime }}}\right)-S^{\mathrm{\prime }}{U}^{\mathrm{\prime }}$(2) where according to Degan and Vasseur [25], $\overline{\overline{K}}$ is the symmetrical second-order permeability tensor defined by: (3) $\overline{\overline{K}}=\left[\begin{array}{cc}{k}_{1}si{n}^2\left(\theta \right)+k_{2}co{s}^2\left(\theta \right)& \left(k_1-k_2\right)sin\left(\theta \right)cos\left(\theta \right)\\ \left(k_2-k_1\right)sin\left(\theta \right)cos\left(\theta \right)& k_{2}si{n}^2\left(\theta \right)+k_{1}co{s}^2\left(\theta \right)\end{array}\right]$(3)

Figure 1 The physical geometry of the problem.

The initial and boundary conditions for the problem in dimensional forms are: (4) $\begin{array}{ll}t\le 0;U^{\mathrm{\prime }}=0,T^{\mathrm{\prime }}=T_0& \text{at}b\le r^{\mathrm{\prime }}\le c\\ t>0;& \text{at}{r}^{\mathrm{\prime }}=b\\ & \text{at}{r}^{\mathrm{\prime }}=c\\ \phantom{t>0;}\{\begin{array}{l}{U}^{\mathrm{\prime }}=0,T^{\mathrm{\prime }}=T_w^{\mathrm{\prime }}\\ U^{\mathrm{\prime }}=0,T^{\mathrm{\prime }}=T_0\end{array}\end{array}\}$(4)

To simplify the governing mathematical equations, the following non-dimensional quantities are defined and applied in equations (1), (2) and (4): (5) $\begin{array}{rl}U& =\frac{U^{\mathrm{\prime }}\upsilon }{g\beta \left(T_w^{\mathrm{\prime }}-T_0\right)b^2},T=\frac{T^{\mathrm{\prime }}-T_0}{T_w^{\mathrm{\prime }}-T_0},R=\frac{r^{\mathrm{\prime }}}{b},\lambda =\frac{c}{b},\\ & \gamma =\frac{{\upsilon }_{eff}}{\upsilon },t=\frac{t^{\mathrm{\prime }}\upsilon }{{\text{b}}^2}S=\frac{S^{\mathrm{\prime }}g\beta b^4}{{\nu }^2},Pr=\frac{\upsilon }{\alpha },\text{and}Da=\frac{k_1}{b^2}\end{array}$(5)

So that the governing equations now assumed the following dimensionless forms: (6) $\frac{\mathrm{\partial }U}{\mathrm{\partial }t}=\gamma \left(\frac{{\mathrm{\partial }}^{2}U}{\mathrm{\partial }{R}^2}+\frac{1}{R}\frac{\mathrm{\partial }U}{\mathrm{\partial }R}\right)+T-a\frac{U}{Da}$(6) (7) $\frac{\mathrm{\partial }T}{\mathrm{\partial }t}=\frac{1}{Pr}\left(\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{R}^2}+\frac{1}{R}\frac{\mathrm{\partial }T}{\mathrm{\partial }R}\right)-SU$(7)

Subject to the following dimensionless initial and boundary conditions: (8) $\begin{array}{r}\begin{array}{ll}\mathit{t}\le 0;U=0,T=0& \text{at}1\le R\le \lambda \\ t>0;& \text{at}R=1\\ & \text{at}R=\lambda \\ \phantom{t>0;}\{\begin{array}{l}U=0,T=1\\ U=0,T=0\end{array}\end{array}\}\end{array}$(8)

The quantity “$a$” in Equation (6) is obtained from Equation (3) and it is the anisotropic parameter defined as: $a=si{n}^2\left(\theta \right)+k^{\ast }co{s}^2\left(\theta \right)$ where $k^{\ast }=\frac{k_1}{k_2}$ and $\theta$ are the anisotropic parameters.

Taking the Laplace with respect to $t$, of Equations (6) and (7) defined as: $\begin{array}{rl}\overline{U}\left(R,p\right)& ={\int }_0^{\mathrm{\infty }}U\left(R,t\right)e^{-pt}dt\text{and}\\ \overline{T}\left(R,p\right)& ={\int }_0^{\mathrm{\infty }}T\left(R,t\right)e^{-pt}dt,\text{yield:}\end{array}$ (9) $\frac{d^2\overline{U}}{d{R}^2}+\frac{1}{R}\frac{d\overline{U}}{dR}-\frac{\overline{U}}{\gamma }\left(p+\frac{a}{Da}\right)=-\frac{\overline{T}}{\gamma }$(9) (10) $\frac{d^2\overline{T}}{d{R}^2}+\frac{1}{R}\frac{d\overline{T}}{dR}-sPr\overline{U}=pPr\overline{T}$(10)

Here, $p>0$ is the Laplace parameter.

As a result of the coupling nature of Equations (9) and (10), D’Alembert method used by Ziyaddin and Huseyin [26], which allows for the systematic decoupling of the couple differential equations while still retaining their initial orders is employed. Multiplying through Equation (9) by $Z$ and adding the result to equation (10) yields: (11) $\frac{d^2}{d{R}^2}\left(Z\overline{U}+\overline{T}\right)+\frac{1}{R}\frac{d}{dR}\left(Z\overline{U}+\overline{T}\right)-{\omega }^2\left(Z\overline{U}+\overline{T}\right)=0$(11) where the expressions for $Z$ and ${\omega }^2$ are, respectively, defined in Appendix B.

The general solution of Equation (11) in terms of modified Bessel functions is given by: (12) $Z\overline{U}+\overline{T}=A_1{I}_0\left(\omega R\right)+A_2{K}_0\left(\omega R\right)$(12)

From the boundary conditions stated in Equation (8), $A_1$ and $A_2$ (see Appendix B) are obtained.

So that Equation (12) now can be expressed as: (13) $Z\overline{U}+\overline{T}=\frac{I_0\left(\omega \lambda \right)K_0\left(\omega R\right)-I_0\left(\omega R\right)K_0\left(\omega \lambda \right)}{p\left(I_0\right(\omega \lambda \left)K_0\right(\omega )-I_0(\omega \left)K_0\right(\omega \lambda \left)\right)}$(13)

To solve for $\overline{U}$ and $\overline{T}$, $Z$ and $\omega$ in Equation (13) are replaced with $Z_1$, $Z_2$ $,{\omega }_1$ and ${\omega }_2$ one after the other to give: (14) $Z_1\overline{U}+\overline{T}=\frac{I_0\left({\omega }_1\lambda \right)K_0\left({\omega }_{1}R\right)-I_0\left({\omega }_{1}R\right)K_0\left({\omega }_1\lambda \right)}{p\left(I_0\right({\omega }_1\lambda \left)K_0\right({\omega }_1)-I_0({\omega }_1\left)K_0\right({\omega }_1\lambda \left)\right)}$(14) (15) $Z_2\overline{U}+\overline{T}=\frac{I_0\left({\omega }_2\lambda \right)K_0\left({\omega }_{2}R\right)-I_0\left({\omega }_{2}R\right)K_0\left({\omega }_2\lambda \right)}{p\left(I_0\right({\omega }_2\lambda \left)K_0\right({\omega }_2)-I_0({\omega }_2\left)K_0\right({\omega }_2\lambda \left)\right)}$(15) where $Z_1$, $Z_2$ and ${\omega }_1,{\omega }_2$ (see Appendix B) are the roots of $Z$ and $\omega$, respectively.

Hence solving Equations (14) and (15) simultaneously, the expressions for the velocity and temperature fields, respectively, are obtained: (16) $\begin{array}{rl}\overline{U}& =\frac{1}{p\left(Z_1-Z_2\right)}(\frac{I_0\left({\omega }_1\lambda \right)K_0\left({\omega }_{1}R\right)-I_0\left({\omega }_{1}R\right)K_0\left({\omega }_1\lambda \right)}{\left(I_0\left({\omega }_1\lambda \right)K_0\left({\omega }_1\right)\right)-I_0\left({\omega }_1\right)K_0\left({\omega }_1\lambda \right)}\\ & -\frac{I_0\left({\omega }_2\lambda \right)K_0\left({\omega }_{2}R\right)-I_0\left({\omega }_{2}R\right)K_0\left({\omega }_2\lambda \right)}{\left(I_0\left({\omega }_2\lambda \right)K_0\left({\omega }_2\right)\right)-I_0\left({\omega }_2\right)K_0\left({\omega }_2\lambda \right)})\end{array}$(16) (17) $\begin{array}{rl}\overline{T}& =\frac{1}{p\left(Z_1-Z_2\right)}\\ & \times (Z_1\left(\frac{I_0\left({\omega }_2\lambda \right)K_0\left({\omega }_{2}R\right)-I_0\left({\omega }_{2}R\right)K_0\left({\omega }_2\lambda \right)}{\left(I_0\left({\omega }_2\lambda \right)K_0\left({\omega }_2\right)\right)-I_0\left({\omega }_2\right)K_0\left({\omega }_2\lambda \right)}\right)\\ & -Z_2\left(\frac{I_0\left({\omega }_1\lambda \right)K_0\left({\omega }_{1}R\right)-I_0\left({\omega }_{1}R\right)K_0\left({\omega }_1\lambda \right)}{\left(I_0\left({\omega }_1\lambda \right)K_0\left({\omega }_1\right)\right)-I_0\left({\omega }_1\right)K_0\left({\omega }_1\lambda \right)}\right))\end{array}$(17)

In order to invert the expressions (16) and (17) from Laplace domain to their corresponding time domain, a numerical inversion procedure (Riemann sum approximation method) employed by Jha and Isa [27] is used. Accordingly, the inverse $U\left(R,t\right)$ of any Laplace transform $\overline{U}\left(R,p\right)$ can be approximated from the expression: (18) $\begin{array}{rl}& U\left(R,t\right)\\ & =\frac{e^{\epsilon t}}{t}\left[\frac{1}{2}\overline{U}\left(R,\epsilon \right)+Re\sum _{k=1}^n\overline{U}\left(R,\epsilon +\frac{ik\pi }{t}\right){\left(-1\right)}^k\right]\end{array}$(18) where $Re$ and $i=\sqrt{-1}$ are real and imaginary numbers, respectively. Also, $n$ is the number of iteration used in the method and $\epsilon$ is the real part of Bromwich contour used for inverting a function from the Laplace domain to its corresponding time domain. If the number of iteration must be minimized and faster convergence is to be achieved, Tzou [28] suggested that the product of the real part of Bromwich contour $\left(\epsilon \right)$ and time $\left(t\right)$ most be equal to 4.7.

3. Validation of method

To establish the accuracy of the Riemann sum approximation method, the exact solutions for the steady-state velocity and temperature equations for the problem are derived. The numerical values of the steady and transient state solutions are then compared at large time.

The expression for steady-state velocity and temperature distributions are obtained by setting $\frac{\mathrm{\partial }U}{\mathrm{\partial }t}=\frac{\mathrm{\partial }T}{\mathrm{\partial }t}=0$ in Equations (6) and (7). The resulting coupled differential equations are: (19) $\frac{d^{2}U}{d{R}^2}+\frac{1}{R}\frac{dU}{dR}-\frac{a}{\gamma Da}U=-\frac{T}{\gamma }$(19) (20) $\frac{d^{2}T}{d{R}^2}+\frac{1}{R}\frac{dT}{dR}-SPrU=0$(20)

Solving Equations (19) and (20) by D’Alembert method under the boundary conditions defined in Equations (8), the steady-state expressions for velocity and temperature equations are obtained: (21) $\begin{array}{rl}U& =\frac{1}{\left(Z_1^{\ast }-Z_2^{\ast }\right)}\left[\right(\frac{K_0\left({\omega }_1^{\ast }\lambda \right)I_0\left({\omega }_1^{\ast }R\right)}{\left(I_0\left({\omega }_1^{\ast }\lambda \right)K_0\left({\omega }_1^{\ast }\right)\right)-I_0\left({\omega }_1^{\ast }\right)K_0\left({\omega }_1^{\ast }\lambda \right)}\\ & +\frac{I_0\left({\omega }_1^{\ast }\lambda \right)K_0\left({\omega }_1^{\ast }R\right)}{\left(K_0\left({\omega }_1^{\ast }\lambda \right)I_0\left({\omega }_1^{\ast }\right)\right)-K_0\left({\omega }_1^{\ast }\right)I_0\left({\omega }_1^{\ast }\lambda \right)})\\ & -(\frac{K_0\left({\omega }_2^{\ast }\lambda \right)I_0\left({\omega }_2^{\ast }R\right)}{\left(I_0\left({\omega }_2^{\ast }\lambda \right)K_0\left({\omega }_2^{\ast }\right)\right)-I_0\left({\omega }_2^{\ast }\right)K_0\left({\omega }_2^{\ast }\lambda \right)}\\ & +\frac{I_0\left({\omega }_1^{\ast }\lambda \right)K_0\left({\omega }_1^{\ast }R\right)}{\left(K_0\left({\omega }_2^{\ast }\lambda \right)I_0\left({\omega }_2^{\ast }\right)\right)-K_0\left({\omega }_2^{\ast }\right)I_0\left({\omega }_2^{\ast }\lambda \right)}\left)\right]\end{array}$(21) (22) $\begin{array}{rl}T& =\frac{Z_2^{\ast }}{\left(Z_1^{\ast }-Z_2^{\ast }\right)}(\frac{K_0\left({\omega }_1^{\ast }\lambda \right)I_0\left({\omega }_1^{\ast }R\right)}{\left(I_0\left({\omega }_1^{\ast }\lambda \right)K_0\left({\omega }_1^{\ast }\right)\right)-I_0\left({\omega }_1^{\ast }\right)K_0\left({\omega }_1^{\ast }\lambda \right)}\\ & +\frac{I_0\left({\omega }_1^{\ast }\lambda \right)K_0\left({\omega }_1^{\ast }R\right)}{\left(K_0\left({\omega }_1^{\ast }\lambda \right)I_0\left({\omega }_1^{\ast }\right)\right)-K_0\left({\omega }_1^{\ast }\right)I_0\left({\omega }_1^{\ast }\lambda \right)})\\ & -\frac{Z_1^{\ast }}{\left(Z_1^{\ast }-Z_2^{\ast }\right)}(\frac{K_0\left({\omega }_2^{\ast }\lambda \right)I_0\left({\omega }_2^{\ast }R\right)}{\left(I_0\left({\omega }_2^{\ast }\lambda \right)K_0\left({\omega }_2^{\ast }\right)\right)-I_0\left({\omega }_2^{\ast }\right)K_0\left({\omega }_2^{\ast }\lambda \right)}\\ & +\frac{I_0\left({\omega }_1^{\ast }\lambda \right)K_0\left({\omega }_1^{\ast }R\right)}{\left(K_0\left({\omega }_2^{\ast }\lambda \right)I_0\left({\omega }_2^{\ast }\right)\right)-K_0\left({\omega }_2^{\ast }\right)I_0\left({\omega }_2^{\ast }\lambda \right)})\end{array}$(22)

Here also, the expressions for $Z_1^{\ast },Z_2^{\ast }$, ${\omega }_1^{\ast }$ and ${\omega }_2^{\ast }$ are given in Appendix B.

The numerical values for the transient state velocity and temperature profiles obtained using Riemann sum approximation method as depicted in Table 1 has been observed to be in excellent agreement with the numerical results for the corresponding steady-state solutions of the velocity and temperature equations obtained analytically at large time. This can clearly be seen from the percentage differences in the computed numerical values for the different cases presented on the table. This numerical agreement between the two data separately obtained confirms the accuracy of the Riemann sum approximation method employed.

Table 1. Comparing the numerical values for Riemann sum approximation method with the exact solutions obtained for steady states velocity and temperature profiles when $Da=0.01,\theta ={30}^0,K^{\ast }=0.2,$ $\gamma =1.5,$ $S=0.04$ and $Pr=7.1$.

		Velocity			Temperature
$t$	$R$	Riemann Sum Approximation Method for transient state	Exact solution for steady state	Difference (%)	Riemann Sum Approximation Method for transient state	Exact solution for steady state	Difference (%)
7	1.2	0.0066	0.0066	0	0.7368	0.7368	0
	1.4	0.0059	0.0059	0	0.5144	0.5144	0
	1.6	0.0039	0.0039	0	0.3218	0.3218	0
	1.8	0.0019	0.0019	0	0.1519	0.1519	0
8	1.2	0.0066	0.0066	0	0.7368	0.7368	0
	1.4	0.0059	0.0059	0	0.5144	0.5144	0
	1.6	0.0039	0.0039	0	0.3218	0.3218	0
	1.8	0.0019	0.0019	0	0.1519	0.1519	0
9	1.2	0.0066	0.0066	0	0.7368	0.7368	0
	1.4	0.0059	0.0059	0	0.5144	0.5144	0
	1.6	0.0039	0.0039	0	0.3218	0.3218	0
	1.8	0.0019	0.0019	0	0.1519	0.1519	0

4. Results and discussion

This study focusses on the combined effects of anisotropic porous material and stratified fluid on the natural convection fluid flow through a vertical annulus. In other to have an insight into the problem, numerical simulation conducted for some representative values of some physical parameters of interest emerging in the solutions are discussed with the aid of line graphs.

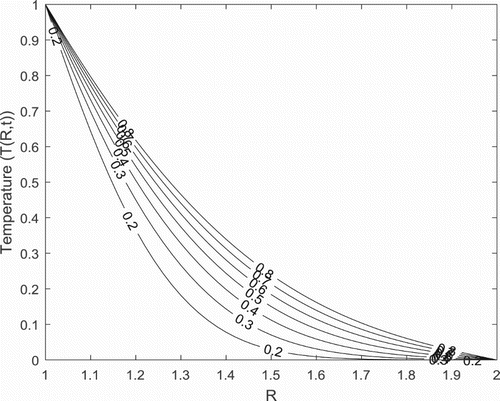
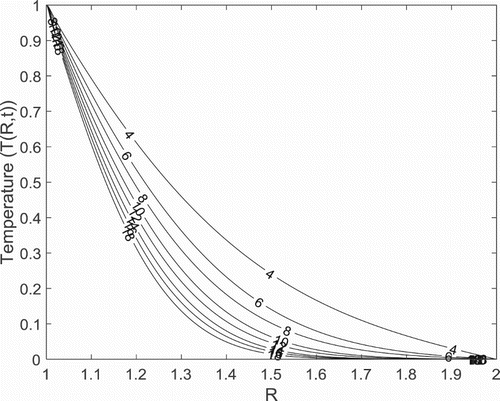
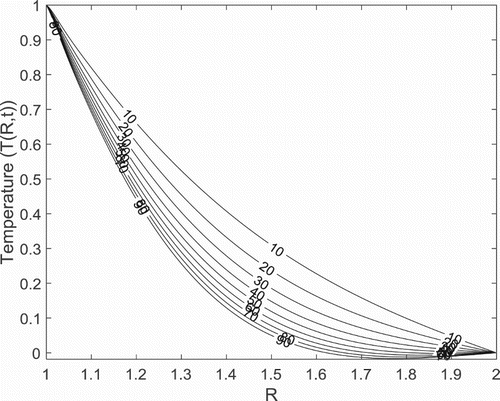
In Figures 2–4, the temperature of the fluid appears to decrease from the outer surface of the inner cylinder and steeply approaches zero as the fluid flow progresses towards the inner surface of the outer cylinder. In addition, while the temperature is seen to increase with the increase in time $\left(t\right)$, as illustrated in Figure 2, it decreases with increase in Prandtl number $\left(Pr\right)$ and stratification parameter $\left(S\right)$ as presented in Figures 3 and 4, respectively. 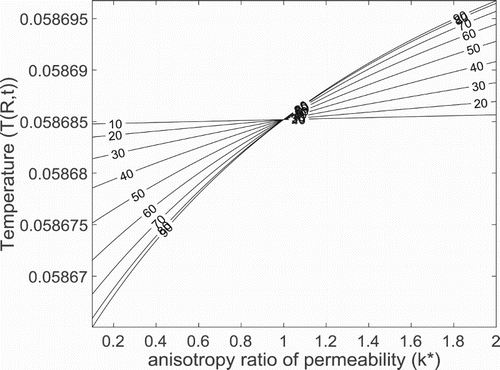These patterns displayed by these parameters are attributed, for $Pr,$ to the decrease in the thermal diffusivity as the Prandtl number is increased while in the case of stratification parameter $\left(S\right)$, to the layering effect of the thermal stratification which inhibits temperature penetration. In addition, numerical simulation conducted as presented in Figure 5 with respect to the effects of the simultaneous variation of the anisotropic parameters $({\mathit{k}}^{\ast }$ and $\mathit{\theta })$ on the temperature in the concentric annulus revel that if ${\mathit{k}}_1<{\mathit{k}}_2$ so that the anisotropic ratio of permeability, ${\mathit{k}}^{\ast }<1,$ the penetration of temperature into the system is enhanced as the anisotropic angle of orientation, $\mathit{\theta }$ is decreased. The simulation further indicates that if ${\mathit{k}}^{\ast }>1,$ the temperature increases as the anisotropic angle of inclination is increased from $0^0$ to ${90}^0.$

Figure 2. Temperature profile with different values of $t$ for $Pr=7.1,$ $\theta ={30}^0,$ $S=0.04,Da=0.1,$ $\gamma =2.0$, $\lambda =2.0$ and $k^{\ast }=0.2$.

Figure 3. Temperature profile with different values of $Pr$ for $t=0.4,$ $\theta ={30}^0,$ $S=0.04,Da=0.1,$ $\gamma =2.0$, $\lambda =2.0$ and $k^{\ast }=0.2$.

Figure 4. Temperature profile with different values of $S$ for $Pr=7.1,$ $\theta ={30}^0,$ $t=4.0,Da=0.1,$ $\gamma =2.0$, $\lambda =2.0$ and $k^{\ast }=0.2$.

Figure 5. Temperature profile with different values of $\theta$ and $k^{\ast }$ for $Pr=7.1,$ $S=0.04,Da=0.1,$ $\gamma =0.5$, $\lambda =2.0,R=1.5$ and $t=0.4$.

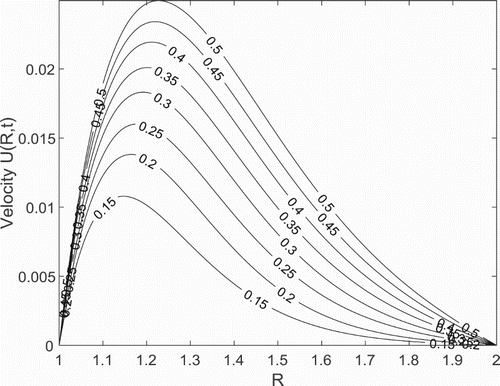
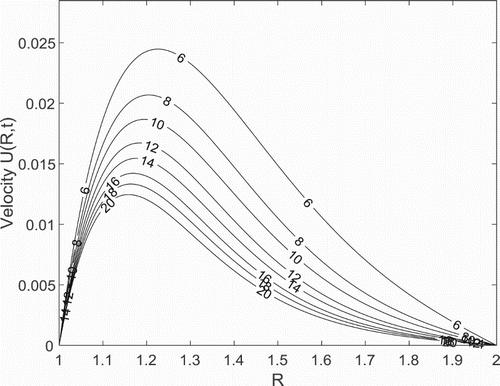
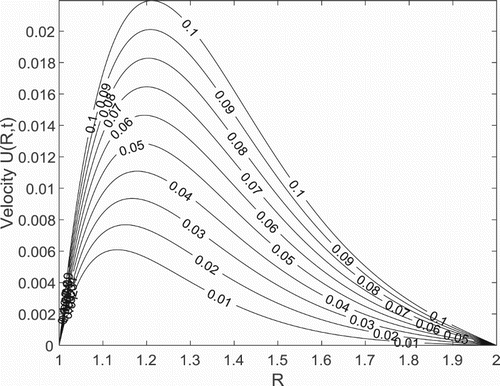
Figures 6–10 show the fluid velocity distributions in the concentric cylinder for the variations of time $\left(t\right)$, Prandtl number $\left(Pr\right)$, Stratification parameter $\left(S\right)$, anisotropic parameters $(k^{\ast }$and $\theta )$ and the Darcy number $\left(Da\right)$, respectively. The graphs show that the maximum velocity distribution of the fluid for all the different parameters considered are closed to the outer surface of the inner cylinder and is least at the inner surface of the outer cylinder. In particular, from Figure 6, the fluid velocity is observed to increase as time $\left(t\right)$ increases as expected. On the other hand, Figures 7 and 8 show that as a result of decrease in the fluid thermal diffusivity and resistive force within the fluid layers, respectively, a weak convection current in created within the fluid resulting to the suppression in the fluid motion as Prandtl number $\left(Pr\right)$ and stratification parameter $\left(S\right)$ are, respectively, increased. This drop in fluid temperature as well as in the fluid velocity resulting from the layering effect occasioned from the increase in stratification parameter $\left(\mathit{S}\right)$ was also stressed by Deka and Paul [20]

Figure 6. Velocity profile with different values of $t$ for $Pr=7.1,$ $\theta ={30}^0,$ $S=0.04,Da=0.1,$ $\gamma =0.5$, $\lambda =2.0$ and $k^{\ast }=0.2$.

Figure 7. Velocity profile with different values of $Pr$ for $Da=0.1,$ $\theta ={30}^0,$ $S=0.04,t=0.4,$ $\gamma =0.5$, $\lambda =2.0$ and $k^{\ast }=0.2$.

Figure 8. Velocity profile with different values of $S$ for $Pr=7.1,$ $k^{\ast }=0.2,$ $\theta ={30}^0,Da=0.1,$ $\gamma =0.5$, $\lambda =2.0$ and t$=4.0$.

Figure 9. Velocity profile with different values of $\theta$ for $k^{\ast }$ for $Pr=7.1,$ $S=0.04,Da=0.1,$ $\gamma =0.5$, $\lambda =2.0,R=1.5$ and t$=0.4$.

Figure 10. Velocity profile with different values of $Da$ for $Pr=7.1,$ $\theta ={30}^0,$ $S=0.04,t=0.4,$ $\gamma =0.5$, $\lambda =2.0$ and $k^{\ast }=0.2$.

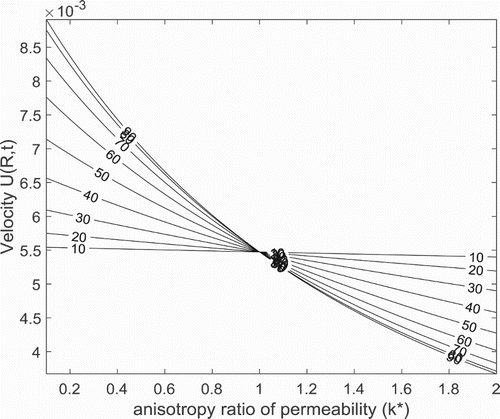
In Figure 9, a contour map is presented to examine the combined influence of the anisotropic parameters on the fluid velocity. According to Bera and Khalili [14] the permeability of the porous media acts as a conductivity of the fluid flow, therefore, it measures the flow strength of the medium. It is clear from the relation: $\mathit{a}=\mathit{s}\mathit{i}{\mathit{n}}^2\left(\mathit{\theta }\right)+{\mathit{k}}^{\ast }\mathit{c}\mathit{o}{\mathit{s}}^2\left(\mathit{\theta }\right)$ obtained from Equation (3) that if $\mathit{\theta }=0^0$ and ${\mathit{k}}^{\ast }=1$ (i.e. ${\mathit{k}}_1={\mathit{k}}_2$) the preferential orientation of the grain beads of the porous materials is neglected. This, in line with the existing literature, corresponds to fluid flow through isotropic porous medium. According to Degan et al. [29], if ${\mathit{k}}^{\ast }<1$ an increase in permeability ${\mathit{k}}_2$ along the horizontal direction is observed. Similarly, if ${\mathit{k}}^{\ast }>1$, a suppression of the permeability of the anisotropic porous matrix along the main flow direction of the fluid flow is observed. Thus the ratio of permeability can be seen, physically, as a regulator of the preferential direction of the fluid flow through the beads of the porous structures as the anisotropic angle of inclination is varied. Accordingly, a close study of Figure 9 shows that if $k^{\ast }>1,$ increasing the anisotropic angle of inclination $\left(\theta \right)$ decreases the permeability of the anisotropic porous system along the vertical direction. As a result, a weak convection current within the flowing fluid is created and thereby suppressing the velocity of the fluid. While for $k^{\ast }<1$, a converse trend is observed. Furthermore, if $k^{\ast }=1$, (and $\theta =0^0$) the contour map shows that an isotropic porous system is obtained as already explained. These findings are in excellent agreement with the observations made by Bera and Khalili [14].

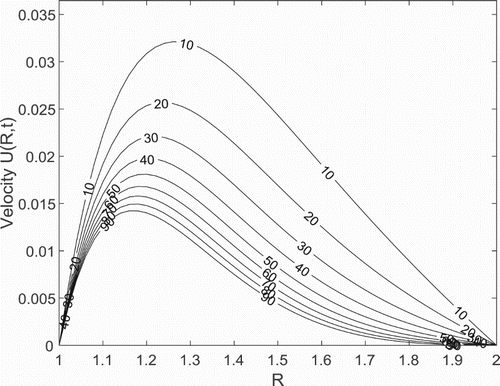
Figure 10 displayed the role of measure of permeability of the anisotropic porous medium $\left(Da\right)$ on the fluid velocity. From the figure, it is observed that increasing the permeability along the principal axis, $k_1$ results in the increase of the measure of the permeability of the anisotropic porous medium $\left(Da=\frac{k_1}{b^2}\right)$. Accordingly, an increase in the velocity is noticed.

5. Conclusion

The main aim of this work is to investigate, primarily, the effect of anisotropic porous medium and stably stratified fluid on a transient free convection fluid flow contained in an annulus. A method that readily enables the decoupling of the coupled governing equations in a very systematic form thereby avoiding the possible complications that might arise if directly solved is employed. The accuracy of the procedures employed in this article has been established. It is found that the steady and transient states velocities independently obtained (as well as the temperatures of the fluid) coincide as $t\to \text{Pr}$. In addition, the numerical simulation conducted also established that the stratification parameter acts as resistive forces on the fluid layers. Therefore increasing the stratification parameter hinders the temperature distribution in the annulus and consequently, the fluid velocity is found to be decreased. It is further observed that the response by the temperature and fluid velocity distribution in the annulus with respect to the variation of the anisotropic parameters $({\mathit{k}}^{\ast }$ and $\mathit{\theta })$ are exactly the same as those predicted by Bera and Khalili [14].

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Muhammad K. Musa http://orcid.org/0000-0002-0420-4014

Appendix A

Nomenclature

β	=	coefficient of thermal expansion [$K^{-1}$]
${\upsilon }_{eff}$	=	effective viscosity of the saturated porous media $m^2{s}^{-1}$
$\upsilon$	=	kinematic viscosity of the fluid $m^2{s}^{-1}$
$\alpha$	=	thermal diffusivity $m^2{s}^{-1}$
$g$	=	acceleration due to gravity $m{s}^{-2}$
$\gamma$	=	ratio of viscosities [−]
$k_1$ and $k_2$	=	permeabilities along the principal axes of the anisotropic porous medium [m]
$k^{\ast }$	=	ratio of anisotropy Permeability [−]
$\theta$	=	anisotropic angle of inclination [Decree or Rad]
$S$	=	dimensionless stratification parameter [−]
$S^{\mathrm{\prime }}$	=	dimensional stratification parameter [$m{K}^{-1}$]
$Da$	=	Darcy number [−]
$Pr$	=	Prandtl number [−]
$\overline{T}$	=	temperature of the fluid in Laplace domain $K$
$T$	=	dimensionless temperature of the fluid [−]
$T^{\mathrm{\prime }}$	=	dimensional temperature of the fluid $K$
$T_0$	=	reference temperature $K$
$T_w$	=	temperature of the outer surface of the inner cylinder$K$
$t^{\mathrm{\prime }}$	=	dimensional time$s$
t	=	dimensionless time [−]
$U^{\mathrm{\prime }}$	=	dimensional velocity of the fluid $m{s}^{-1}$
$\overline{U}$	=	dimensionless fluid velocity in Laplace domain [−]
$U$	=	dimensionless fluid velocity [−]
$R$	=	dimensionless radial coordinate [−]
$b$ and $c$	=	inner and outer surface radii [m]

Appendix B

Expressions for constant used

$\begin{array}{rl}{A}_1& =-\frac{K_0\left(\omega \lambda \right)}{p\left(I_0\right(\omega \lambda \left)K_0\right(\omega )-I_0(\omega \left)K_0\right(\omega \lambda \left)\right)}\\ A_2& =\frac{I_0\left(\omega \lambda \right)}{p\left(I_0\right(\omega \lambda \left)K_0\right(\omega )-I_0(\omega \left)K_0\right(\omega \lambda \left)\right)}\\ Z& =\frac{Z\left(p+\frac{a}{Da}\right)+\gamma SPr}{\left(\gamma pPr-Z\right)}\\ {\omega }^2& =\frac{\gamma pPr-Z}{\gamma }\end{array}$ $\begin{array}{rl}{\omega }_1& =\sqrt{\left(\frac{\gamma pPr-Z_1}{\gamma }\right)}\\ {\omega }_2& =-\sqrt{\left(\frac{\gamma pPr-Z_2}{\gamma }\right)}\\ {\omega }_1^{\ast }& =\sqrt{\frac{Z_1^{\ast }}{\gamma }}\\ {\omega }_1^{\ast }& =-\sqrt{\frac{Z_2^{\ast }}{\gamma }}\\ Z_1^{\ast }& =\frac{1}{2}\left(\frac{a}{Da}+\sqrt{{\left(\frac{a}{Da}\right)}^2+4SPr}\right)\\ Z_2^{\ast }& =\frac{1}{2}\left(\frac{a}{Da}-\sqrt{{\left(\frac{a}{Da}\right)}^2+4SPr}\right)\end{array}$ $\begin{array}{rl}{Z}_1& =-\frac{1}{2}\left(p+\frac{a}{Da}-\gamma pPr\right)\\ & +\frac{1}{2}\left(\sqrt{{\left(p+\frac{a}{Da}-\gamma pPr\right)}^2-4\gamma SPr}\right)\end{array}$ $\begin{array}{rl}{Z}_2& =-\frac{1}{2}\left(p+\frac{a}{Da}-\gamma pPr\right)\\ & -\frac{1}{2}\left(\sqrt{{\left(p+\frac{a}{Da}-\gamma pPr\right)}^2-4\gamma SPr}\right)\end{array}$