Relaxed I-SHOT trust-region algorithm for solving multi-objective economic emission load dispatch problem

ABSTRACT

In this paper, a new algorithm for tackling nonlinear constrained multi-objective optimization problems is introduced. This algorithm, which we call relaxed the interactive sequential hybrid optimization technique (relaxed I-SHOT), is based on a hybrid method between the I-SHOT method and step method (STEM) to transform a multi-objective problem into a single-objective one. An active set strategy is used together with a suggested penalty method to transform a single-objective constrained optimization problem into unconstrained one. A trust-region globalization strategy is added to the algorithm to solve the obtained unconstrained problem to ensure global convergence. The suggested approach is utilized to solve the multi-objective economic emission load dispatch (EELD) problems to assert the effectiveness of the proposed algorithm. The proposed algorithm is tested on the standard IEEE 30-bus 6-generator test system. The results of the proposed approach are compared against those reported in the literature. The comparison asserts the potential of the proposed algorithm to solve the EELD problem.

KEYWORDS:

• Multi-objective optimization
• economic emission load dispatch
• relaxed I-SHOT
• trust-region
• penalty method
• active set

1. Introduction

A majority of the engineering decision-making problems have multiple design objectives and these problems are called multi-objective problems. There are many methods for solving such problems, which are usually classified into four classes: interactive methods, a posteriori methods, a priori methods and no-preference methods. Over the years, variant optimization methods from the previous classes were used to solve multi-objective optimization problems [1–5]. To improve the resultant solution from these methods, researchers tend to make hybrid methods from methods in one class or different classes so as to combine the advantages of these methods.

We are concerned with a new hybrid method which is used to convert a multi-objective optimization problem to a single one. This method (which we call relaxed I-SHOT) is a hybrid method of interactive sequential hybrid optimization technique (I-SHOT) and step method (STEM). In the interactive methods, the designer's preferences take part in the formation of a sample of the Pareto solutions, then an interaction between the designer and the analyst takes place to generate more points on the Pareto set until a designed solution is selected by the designer. In the relaxed I-SHOT method, the relaxation technique in the STEM is added to the main steps of the I-SHOT method, which provides an interaction between the decision-maker (DM) and the analyst to reach a sufficient Pareto-optimal solution. The I-SHOT method deals with all objectives with the same strategy, but with the relaxation technique, the DM is able to classify the objectives in every iteration and improve some unacceptable objective values by relaxation or increment of the other acceptable objectives’ values. The relaxed I-SHOT method inherits the ability of the classical I-SHOT to detect non-convex regions of the Pareto set.

The multi-objective optimization problem is solved using a trust-region globalization strategy. The globalized strategy converges from any starting point and this is a modification to the local strategy. By using this approach, there is no limitation to the number of objective functions. The proposed globalization trust-region method is efficient for solving non-convex multi-objective optimization problems and ill-defined systems.

In this work, we convert the single-objective constrained problem to an unconstrained problem using an active set strategy in [6] combined with the penalty method. The main advantage of the suggested active set is that it is identified and updated naturally by the step. Two penalty parameters are used in this work: one for the active set transformed inequality constraints and the other for equality constraints. Some penalty functions have been suggested and many contributions addressing the convergence of these methods have been made [7].

The trust-region strategy used for solving the single-objective constrained and unconstrained optimization problems and multi-objective problems has proved to be very successful both theoretically and practically [6,8,9].

To ensure the effectiveness of our proposed algorithm, the algorithm is applied to solve the EELD problem. The EELD problem is the process of satisfying the required power load demand using the available generating units while minimizing the cost of operation and all unit operational constraints are also satisfied. In addition, the increasing public awareness of the environmental protection has forced the utilities to modify their design to reduce atmospheric emissions of the thermal power plants [1,10]. Hence, the EELD problem is formulated as a constrained multi-objective problem with conflicting objectives, minimize the fuel cost and emission level simultaneously.

We are concerned with the emission as an objective function, and the multi-objective EELD problem is converted to a corresponded single-objective problem using our new hybrid approach.

The following notations are used in this paper. The sequence of points generated by the algorithm is denoted . A subscripted function means function values at a particular point. For example, $f_k=f\left(x_k\right)$, $\mathrm{\nabla }{f}_k={\mathrm{\nabla }}_{x}f\left(x_k\right)$, ${\mathrm{\nabla }}^2{f}_k={{\mathrm{\nabla }}^2}_{x}f\left(x_k\right)$ and so on. Finally, all norms are $l_2$-norms.

This paper is organized as follows. In Section 2, we introduce in detail the new hybrid method for solving multi-objective problems. Section 3 is devoted to the solution of the single-objective problem obtained from the proposed multi-objective algorithm. The mathematical formulation of the EELD problem is presented in Section 4. In Section 5, implementation of the proposed algorithm for treatment of the EELD problem is presented. In Section 6, numerical results and discussions are presented. Finally, the conclusion is given in Section 7.

2. Relaxed I-SHOT for solving multi-objective problems

2.1. Formulation and terminology

A general mathematical form for multi-objective optimization problem with $nj$ objective functions can be formulated as follows: (1) $\begin{array}{ccc}\text{minimize}& f_j\left(x\right),& j=1,\dots ,nj,\\ \text{subject}\text{to}& h_e\left(x\right)=0,& e=1,\dots ,ne,\\ & g_i\left(x\right)\le 0,& i=1,\dots ,ni,\end{array}$(1) where $x\in {\mathbb{R}}^n$ is a design vector, $f_j\left(x\right)$ is the jth objective function to be minimized, $h_e\left(x\right)$ is the eth equality constraints and $g_i\left(x\right)$ is the ith inequality constraints.

One of the important methods for solving such problems is the interactive method. The main idea in interactive algorithms is that the DM interacts with the analyst or with the utilized computer programme. The analyst solves to find an initial solution and then, with the help of the DM, obtains the new solution. If the DM is satisfied with the new solution (or one of them), then the process is stopped. Otherwise the analyst makes a new interaction with the DM.

We present two of the important algorithms for solving multi-objective optimization problems, which are based on the interactive approach, the I-SHOT method and STEM. Then, we introduce a new algorithm based on the interactive approach, which is a hybrid method from these two methods.

2.2. I-SHOT method

The I-SHOT method is a hybrid method combines the advantage upon the weighting method and ϵ-constrained method, see ([11,12]). In the weighting method, the multi-objective problem is transformed into a single-objective problem by making a linear combination of the objective functions with weights, and in the $\epsilon$-constrained method by constraining all objective functions except one and then solve the problem by minimizing that remaining objective. The weighting method and the $\epsilon$-constrained cannot detect points in a non-convex Pareto set. In this method, by using the interactive approach, problem (1) is transformed into the following form: (2) $\begin{array}{cc}\text{minimize}& F\left(x\right)=\sum _{j=1}^{nj}{w}_j\left(\frac{f_j\left(x\right)-{\epsilon }_{j_{\mathrm{good}}}}{{\epsilon }_{j_{\mathrm{bad}}}-{\epsilon }_{j_{\mathrm{good}}}}\right)\\ \text{subject}\text{to}& f_j\left(x\right)\le {\tilde{\epsilon }}_{j}j=1,\dots ,nj\\ & h\left(x\right)=0,\\ & g\left(x\right)\le 0,\\ & {\tilde{\epsilon }}_j\in [{\epsilon }_{j_{\mathrm{good}}},{\epsilon }_{j_{\mathrm{bad}}}],\end{array}$(2) where ${\epsilon }_{j_{\mathrm{good}}},{\epsilon }_{j_{\mathrm{bad}}}$ are calculated using payoff table [12] and (3) $w_j=\left(\begin{array}{cc}{W}_j+\frac{1-\hat{W}}{\hat{W}}{W}_j& \text{if }\hat{W}>1,\\ W_j& \text{if }\hat{W}=1,\\ W_j+\frac{1-\hat{W}}{nj-\hat{W}}(1-W_j)& \text{if }\hat{W}<1,\end{array}\right.$(3) such that $W_j=\text{random(}0,1)$ and $\hat{W}={\sum }_{j=1}^{n}j{W}_j$.

If the solution of (2) is acceptable for the DM, then the process is stopped, else an interaction between the analyst and the DM is established to make a reduction to the range $\left[{\epsilon }_{j_{good}},{\epsilon }_{j_{bad}}\right]$ by using the following formula: (4) $\begin{array}{rl}{\epsilon }_{\mathrm{good}}^{\mathrm{new}}& ={\epsilon }_{j_{\mathrm{good}}}+\frac{\mathrm{\Delta }{\epsilon }_j}{\hat{r}},\\ {\epsilon }_{\mathrm{bad}}^{\mathrm{new}}& ={\epsilon }_{j_{\mathrm{bad}}}-\frac{\mathrm{\Delta }{\epsilon }_j}{\hat{r}},\end{array}$(4) where $\mathrm{\Delta }{\epsilon }_j={\epsilon }_{j_{bad}}-{\epsilon }_{j_{good}}$ and $\hat{r}$ is the reduction factor. Then Equation (2) is solved again until the DM is satisfied by the Pareto-optimal solution.

The main advantage of the I-SHOT method is that it can obtain Pareto solutions for a non-convex problem. The method gives the DM the opportunity to control the trade-off analysis to a designed solution (final solution). Also, by using this method, proper Pareto points are detected. But in real-world multi-objective problems, this method has a major defect. The defect is that, in the solution algorithm of the method as described in [11], the algorithm interacts with all objectives at the same way in reduction of the range of the Pareto set by using the same value of the reduction factor $\hat{r}$ and in updating ${\hat{\epsilon }}_j$. In real problems, the range of the objectives $[{\epsilon }_{j_{\mathrm{good}}},{\epsilon }_{j_{\mathrm{bad}}}]$ is different in width from one objective function to another and the solutions occur in every iteration of the I-SHOT algorithm; DM can be satisfied with some objective values and need to modify only the other objectives in the next iteration. The I-SHOT method in this form does not allow the DM to classify the objective functions to make a relaxation to some objective functions, which have satisfactory values in the previous iteration to reduce the values of the other objective functions in the next iteration.

2.3. STEM method

STEM is one of the first interactive methods developed for multi-objective optimization problems. In this method, after obtaining the initial solution by using the weighted Tchebycheff method [12], the DM classifies the objective functions into two categories, objective functions with acceptable values which are satisfactory to the DM $f_j(j\in J^{>})$ and other objective functions with unacceptable values, $f_j(j\in J^{<}),$ where $J^{>}\text{and}{J}^{<}$ is the set that contains the numbers of the objective functions with acceptable and unacceptable values, respectively such that $J^{>}\cup J^{<}=\{1,\dots ,nj\}$. So the problem can be solved by making an increment in values of $f_j(j\in J^{>})$ to achieve a decrement in the unacceptable objective functions values $f_j(j\in J^{<})$. This process is called the relaxation technique, which is formulated in [12] as follows: (5) $\begin{array}{cc}\text{minimize}& \text{max}\text{[}{w}_j|f_j\left(x\right)-z_j^{\ast }|\text{]}j=1,\dots ,nj,\\ \text{subject}\text{to}& f_j\left(x\right)\le {\epsilon }_j\text{for all}j\in J^{>},\\ & f_j\left(x\right)\le f_j\left(x_k\right)\text{for all}j\in J^{<},\\ & x\in D,\end{array}$(5) where $w_j$ is the weight coefficient (which is set equal to zero for the relaxed functions $f_j(j\in J^{>})$), $z_j^{\ast }$ is the ideal objective vector (which should be known to apply this method) and $x_k$ is the solution of the previous iteration.

By solving Equation (5), we calculate a new solution; if the DM is satisfied, then the process is stopped. Otherwise the DM makes a new classification to the objective functions and the problem is solved for the next iteration. The procedure is repeated until the DM is satisfied by the current objective vector and all of its components. The procedure must also be stopped if the DM is not satisfied with any of the components of the current objective vector. In this case, the STEM cannot find a satisfactory solution. The main defects of the STEM are that it is classified as an ad hoc method and the solutions calculated using it are not necessarily Pareto optimal, but it can obtain weakly Pareto-optimal solutions.

2.4. Relaxed I-SHOT algorithm

Relaxed I-SHOT method is a new hybrid method from the I-SHOT and STEM, which has the main structure of I-SHOT method but it adopts the relaxation technique in the STEM. Generally, Pareto-optimal solutions set generated is not predicted. So in some cases, the DM may not be satisfied with all solutions introduced because the solutions generated are all satisfied for some objectives’ value and the other is not. By adding the relaxation technique to the I-SHOT method, the DM has the ability to improve the unsatisfied objectives’ value by an acceptable increment in the satisfied objectives’ value, as described in step 7 in the following algorithm.

The following algorithm presented a main description of the proposed relaxed I-SHOT method.

Algorithm 1

Relaxed I-SHOT Algorithm

Step 1 (Compute ${\epsilon }_j$ and ${\hat{\epsilon }}_j$)

Solve problem (1) for all j = 1, … , nj to construct the payoff table.

${\epsilon }_j$ and ${\hat{\epsilon }}_j$ are calculated using the payoff table such that ${\epsilon }_j=z_j^{\ast }$ and ${\hat{\epsilon }}_j=$ upper bound of the objective $j$ values which is the maximal value of the column $j$ in the payoff table.

Step 2(Ask the DM)

The DM is required to choose number of weight vectors (the number of Pareto optimal solutions to be generated in every iteration), to select ${\epsilon }_{j_{\mathrm{good}}}\in [{\epsilon }_j,{\hat{\epsilon }}_j]$, ${\epsilon }_{j_{\mathrm{bad}}}\in [{\epsilon }_j,{\hat{\epsilon }}_j]$ and to select ${\tilde{\epsilon }}_j\in [{\epsilon }_{j_{\mathrm{good}}},{\epsilon }_{j_{\mathrm{bad}}}]$.

Step 3 (Generate weighting vectors)

Solve problem (3) to generate the weighting vectors.

Step 4 (Solve the I-SHOT hybrid problem)

Solve the hybrid I-SHOT problem (2).

Step 5 (Test for stopping)

If the DM is satisfied with the generated Pareto set then the process is stopped.

If the DM is not satisfied with all objective functions value in the Pareto set, go to Step 6.

If the DM is satisfied with only some objective functions value in the Pareto set, go to Step 7.

Step 6 (Compute a new value for ${\epsilon }_{j_{\mathrm{good}}}\text{and}{\epsilon }_{j_{\mathrm{bad}}}$)

Update ${\epsilon }_{j_{\mathrm{good}}}\text{and}{\epsilon }_{j_{\mathrm{bad}}}$ using (4).

Set ${\epsilon }_{j_{\mathrm{good}}}={\epsilon }_{j_{\mathrm{good}}}^{\mathrm{new}}$ and ${\epsilon }_{j_{\mathrm{bad}}}={\epsilon }_{j_{\mathrm{bad}}}^{\mathrm{new}}$.

Go to step 4.

Step 7 (Ask the DM)

The DM is asked to classify the objective functions into two categories: $f_j(j\in J^{>})$ which have acceptable values in solving problem (2) in the previous iteration, $f_j(j\in J^{<})$ which have unacceptable values in solving problem (2) in the previous iteration and the relaxation value $p$ for the acceptable objective values.

If $j\in J^{>}$

then ${\tilde{\epsilon }}_{j_{\mathrm{new}}}={\tilde{\epsilon }}_j+p$, ${\epsilon }_{j_{\mathrm{good}}}^{\mathrm{new}}={\epsilon }_{j_{\mathrm{good}}}$ and ${\epsilon }_{j_{\mathrm{bad}}}^{\mathrm{new}}={\epsilon }_{j_{\mathrm{bad}}}$,

where $p$ is a relaxation parameter and ${\tilde{\epsilon }}_j^h={\tilde{\epsilon }}_{j_{new}}$.

else

Update ${\epsilon }_{j_{\mathrm{good}}}$ and ${\epsilon }_{j_{\mathrm{bad}}}$ using Equation (4).

end

Set ${\epsilon }_{j_{\mathrm{good}}}={\epsilon }_{j_{\mathrm{good}}}^{\mathrm{new}}$ and ${\epsilon }_{j_{\mathrm{bad}}}={\epsilon }_{j_{\mathrm{bad}}}^{\mathrm{new}}$ .

Step 8 (Solve the relaxed I-SHOT problem)

Solve the Relaxed I-SHOT single objective constrained problem which has the following form (6) $\begin{array}{cc}\text{minimize}& F\left(x\right)=\sum _{j=1}^{nj}{w}_j\left(\frac{f_j\left(x\right)-{\epsilon }_{j_{\mathrm{good}}}}{{\epsilon }_{j_{\mathrm{bad}}}-{\epsilon }_{j_{\mathrm{good}}}}\right),\\ \text{subject}\text{to}& f_j\left(x\right)\le {\tilde{\epsilon }}_j^h\text{for}\text{all }j\in J^{>},\\ & f_j\left(x\right)\le {\tilde{\epsilon }}_{j_m}\text{for}\text{all }j\in J^{<},\\ & h\left(x\right)=0,\\ & g\left(x\right)\le 0,\end{array}$(6) where ${\tilde{\epsilon }}_{j_m}=\text{min}\left(f_j\right(x_k\left)\right)$ for all $j\in J^{<}$ and ${\tilde{\epsilon }}_j=[{\tilde{\epsilon }}_j^h,{\tilde{\epsilon }}_{j_m}]$.

Go to step 5.

Repeat until the DM is satisfied with the proper Pareto set generated.

Using the above algorithm, the constrained multi-objective optimization problem is converted to a constrained single-objective problem.

3. Solving single-objective problem

The equality and inequality single-objective constrained problem (6) is converted into an unconstrained problem using an active set strategy together with the penalty method.

3.1. Active set strategy

The main idea of the active set strategy is to create the active inequality constraints and convert them to equalities at every iteration. Then, by using well-developed methods, the equality constrained problem is solved (see, for example, [6]). The main idea in the penalty method used for solving the equality constrained optimization problem is to replace the problem with a sequence of unconstrained optimization problems while the penalty parameter does not tend to infinity [13,14].

The single-objective constrained optimization problem (6) can be formulated as follows: (7) $\begin{array}{cc}\text{minimize}& F\left(x\right),\\ \text{subject}\text{to}& h\left(x\right)=0,\\ & \tilde{g}\left(x\right)\le 0,\\ & \end{array}$(7) where $F\left(x\right)={\sum }_{j=1}^{nj}{w}_j\left(\frac{f_j\left(x\right)-{\epsilon }_{j_{\mathrm{good}}}}{{\epsilon }_{j_{\mathrm{bad}}}-{\epsilon }_{j_{\mathrm{good}}}}\right),$ and $\tilde{g}\left(x\right)=\left[f_j\right(x)-{\tilde{\epsilon }}_j,g(x\left)\right]$. The functions $F\left(x\right):{\mathbb{R}}^n\to \mathbb{R}$, $h\left(x\right):{\mathbb{R}}^n\to {\mathbb{R}}^{ne}$, and $\tilde{g}\left(x\right):{\mathbb{R}}^n\to {\mathbb{R}}^{nj+ni}$ are twice continuously differentiable. Following the active set strategy in [6], we define a $0-1$ diagonal indicator matrix $D\left(x\right)\in {\mathbb{R}}^{nj+ni\times nj+ni}$, whose diagonal entries are (8) $d_e\left(x\right)=\left(\begin{array}{cc}1& \text{if }{\tilde{g}}_e\left(x\right)\ge 0,\\ 0& \text{if }{\tilde{g}}_e\left(x\right)<0.\end{array}\right.$(8) Using the above matrix, problem (7) is transformed into the following equality constrained optimization problem: (9) $\begin{array}{ll}\text{minimize}& F\left(x\right),\\ \text{subject}\text{to}& h\left(x\right)=0,\\ & \frac{1}{2}\tilde{g}{\left(x\right)}^{T}D\left(x\right)\tilde{g}\left(x\right)=0.\\ & \end{array}$(9) Using the proposed penalty method, the equality constrained optimization problem (9) is transformed into the following unconstrained optimization problem with two penalty active inequality constrains and equality constrains parameters, $\rho >0$, $r>0$, respectively. Two penalty parameters used in this algorithm to reduce the number of computations by ensuring that the predicted reduction is positive before testing the step. Using the proposed penalty method approach, the equality constrained optimization problem (9) is transformed into the following unconstrained optimization problem: (10) $\begin{array}{ll}\text{minimize}& \phi (x;\rho ;r)=F\left(x\right)+\frac{\rho }{2}\parallel D\left(x\right)\tilde{g}\left(x\right){\parallel }_2^2\\ & +\frac{r}{2}\parallel h\left(x\right){\parallel }_2^2,\\ \text{subject}\text{to}& x\in {\mathbb{R}}^{2n},\end{array}$(10) In the following section, we present a detailed description of the main steps of our trust-region algorithm for solving multi-objective problem formulated as unconstrained optimization problem (10).

3.2 Trust-region algorithm outline

In this section, we present the description of the active set trust-region algorithm which is used to solve the single-objective problem (10). Then we present the main algorithm that is used to solve the multi-objective optimization problem.

3.2.1. Computing a trail step

By solving the following trust-region subproblem, we compute the trail step $s_k$. (11) $\begin{array}{ll}\text{minimize}& F_k+\mathrm{\nabla }{F}_k^{T}s+\frac{1}{2}{s}^T{H}_{k}s\\ & +\frac{{\rho }_k}{2}\parallel D_k({\tilde{g}}_k+\mathrm{\nabla }{\tilde{g}}_k^{T}s){\parallel }^2\\ & +\frac{r_k}{2}\parallel h_k+\mathrm{\nabla }{h}_k^{T}s{\parallel }^2\\ \text{subject}\text{to}& \parallel s\parallel \le {\delta }_k,\end{array}$(11) where $H_k$ is the Hessian matrix of the function $F\left(x\right)$ or an approximation to it. Since our convergence theory is based on the fraction of cauchy decrease condition, a generalized dogleg algorithm introduced by Toint [15] and Steihaug [16] can be used to compute the step.

3.2.2. Testing the trail step and updating ${\mathit{\delta }}_{\mathit{k}}$

Once $s_k$ is computed, it needs to be tested to determine whether it is accepted. We use $\phi (x;\rho ;r)$ as a merit function.

The actual reduction in the merit function according to change form $x_k$ to $x_{k+1}$ is defined as (12) $\begin{array}{rl}Are{d}_k& =F\left(x_k\right)-F\left(x_{k+1}\right)\\ & +\frac{{\rho }_k}{2}\left[{\tilde{g}}_k^T{D}_k{\tilde{g}}_k-{\tilde{g}}_{k+1}^T{D}_{k+1}{\tilde{g}}_{k+1}\right]\\ & +\frac{r_k}{2}\left[\parallel h_k{\parallel }^2-\parallel h_{k+1}{\parallel }^2\right].\end{array}$(12) The predicted reduction in the merit function is defined as (13) $\begin{array}{rl}Pre{d}_k& =-\mathrm{\nabla }{F}_k^T{s}_k-\frac{1}{2}{s}_k^T{H}_k{S}_k\\ & +\frac{{\rho }_k}{2}\left[\parallel D_k{\tilde{g}}_k{\parallel }^2-\parallel D_k({\tilde{g}}_k+\mathrm{\nabla }{\tilde{g}}_k^T{s}_k){\parallel }^2\right]\\ & +\frac{r_k}{2}\left[\parallel h_k{\parallel }^2-\parallel h_k+\mathrm{\nabla }{h}_k^T{s}_k{\parallel }^2\right].\end{array}$(13) After computing a trail step, to ensure that $Pre{d}_k\ge 0$, the penalty parameter $r_k$ is updated using the scheme presented in [17] and it is described in step 4 of algorithm 2. After that, we use the following algorithm to test the calculated step to know whether it is accepted.

Algorithm 2

Test the computing step

$0<{\alpha }_1<1<{\alpha }_2$ and $0<{\eta }_1<{\eta }_2<1$.

If ${\displaystyle \frac{Are{d}_k}{Pre{d}_k}}<{\eta }_1$, then:

Reduce the trust-region radius by setting ${\delta }_k={\alpha }_1\parallel s_k\parallel$ and then calculate a new trail step using the new trust region radius.

Else if ${\eta }_1\le {\displaystyle \frac{Are{d}_k}{Pre{d}_k}}<{\eta }_2$, then:

Accept the step: $x_{k+1}=x_k+s_k$.

Set the trust-region radius: ${\delta }_{k+1}=max({\delta }_k,{\delta }_{min})$.

Else

Accept the step: $x_{k+1}=x_k+s_k$.

Set the trust-region radius: ${\delta }_{k+1}=min\{{\delta }_{max},max({\delta }_{min},{\alpha }_2{\delta }_k\left)\right\}$.

End if.

After accepting the step, we update the Hessian matrix and the penalty parameter ${\rho }_k$. To update ${\rho }_k$, we use the scheme presented in [18], which is described in step 6 of algorithm 2. The penalty parameter $r_k\to r^{\ast }$ and the positive number ${\rho }_k\to {\rho }^{\ast }$ as $k\to \mathrm{\infty }$ [19].

Finally, the algorithm is terminated when either $\parallel \mathrm{\nabla }{F}_k\parallel +\parallel \mathrm{\nabla }{\tilde{g}}_k{D}_k{\tilde{g}}_k\parallel +\parallel h_k\parallel \le {\epsilon }_2$ or $\parallel s_k\parallel \le {\epsilon }_1$, for some ${\epsilon }_1,{\epsilon }_2>0$.

3.2.3. Active set trust-region algorithm

The following algorithm formally describes the proposed trust-region algorithm for solving problem (7).

Algorithm 3

Active set trust-region algorithm

Step 0 (Initialization)

Given $x_0\in {\mathbb{R}}^n$. Compute $D_0$. Set ${\rho }_0=1,r_0=1,{\sigma }_0=1and\beta =0.1$. Choose ${\epsilon }_1,{\epsilon }_2,{\alpha }_1,{\alpha }_2,{\eta }_{1}and{\eta }_2$ such that ${\epsilon }_1>0,{\epsilon }_2>0,$ $0<{\alpha }_1<1<{\alpha }_2$, and $0<{\eta }_1<{\eta }_2<1$. Choose ${\delta }_{min}$, ${\delta }_{max}$ and ${\delta }_0$ such that ${\delta }_{min}\le {\delta }_0\le {\delta }_{max}$. Set $k=0$.

Step 1 (Test for convergence)

If $\parallel \mathrm{\nabla }{F}_k\parallel +\parallel \mathrm{\nabla }{\tilde{g}}_k{D}_k{\tilde{g}}_k\parallel +\parallel h_k\parallel \le {\epsilon }_2,$

then stop.

End if.

Step 2 (Compute a trail step)

Compute the step by solving Equation (11).

If $\parallel s_k\parallel \le {\epsilon }_1$, then stop.

Else set $x_{k+1}=x_k+s_k$.

End if.

Step 3 (Update the active set)

Compute $D_{k+1}$.

Step 4 (Update $r_k$)

If $Pre{d}_k\le {\displaystyle \frac{r_k}{4}}[\parallel h_k{\parallel }^2-\parallel h_k+\mathrm{\nabla }{h}_k^T{s}_k{\parallel }^2]$, then

Set $r_k={\displaystyle \frac{\begin{array}{c}4\left[\mathrm{\nabla }{F}_k^T{s}_k+frac12s_k^T{H}_k{S}_k\right.\\ \left.-{\displaystyle \frac{{\rho }_k}{2}}\left[\parallel D_k{\tilde{g}}_k{\parallel }^2-\parallel D_k({\tilde{g}}_k+\mathrm{\nabla }{\tilde{g}}_k^T{s}_k){\parallel }^2\right]\right]\end{array}}{\parallel h_k{\parallel }^2-\parallel h_k+\mathrm{\nabla }{h}_k^T{s}_k{\parallel }^2}}+\beta$.

Else Set $r_k=max(r_{k-1},{\rho }_k^2)$.

End if.

Step 5 (Test the step and update the trust-region radius)

Test and update using algorithm 2.

Step 6 (Update ${\rho }_k$)

If

$-\mathrm{\nabla }{F}_k^T{s}_k-{\displaystyle \frac{1}{2}}{s}_k^T{H}_k{S}_k+{\displaystyle \frac{{\rho }_k}{2}}[\parallel D_k{\tilde{g}}_k{\parallel }^2-\parallel D_k({\tilde{g}}_k+\mathrm{\nabla }{\tilde{g}}_k^T{s}_k\left){\parallel }^2\right]\le {\sigma }_k\parallel \mathrm{\nabla }{\tilde{g}}_k{D}_k{\tilde{g}}_k\parallel min(\parallel \mathrm{\nabla }{\tilde{g}}_k{D}_k{\tilde{g}}_k\parallel ,{\delta }_k)$, then

set ${\rho }_{k+1}=2{\rho }_k$ and ${\sigma }_{k+1}={\displaystyle \frac{1}{2}}{\sigma }_k$.

Else

Set ${\rho }_{k+1}={\rho }_k$ and ${\sigma }_{k+1}={\sigma }_k$.

End if.

Step 7 Set $k=k+1$ and go to step 1.

A global convergence theorem of the trust-region algorithm (3) is presented in [17].

3.3. The main algorithm

The main steps of our approach for solving problem (1) are described in detail in algorithm 4.

Algorithm 4

Main algorithm

Step 1 (Transform the multi-objective problem into a single-objective problem)

Run algorithm 1.

Step 2 (Construct the payoff table)

Run algorithm 3 to solve problem (2) for $j=1,2$.

Step 3 (Solve the hybrid relaxed I-SHOT problem)

Run algorithm 3 to solve problem (6).

Continuously until the DM is satisfied from the Pareto-optimal set generated.

To ensure the effectiveness of the proposed algorithm, we apply it in solving the EELD problem.

4. EELD problem formulation

The EELD problem is to minimize two simultaneous non-commensurable and conflicting objective functions, fuel cost and emission, while satisfying several equality and inequality constraints [1]. This means that the minimization of emission is contrary to the maintenance of cost economy. Generally the deterministic EELD problem is formulated as follows.

4.1. Problem objectives

In the EELD problem, there are two objective functions to be minimized, as described in detail as follows.

4.1.1. Fuel cost objective function

The generator cost curves are usually represented by quadratic functions. The total fuel cost $f_1$ in ($/h) stated in [20] as follows: (14) $f_1=\sum _{i=1}^n\left(a_i+b_i{P}_{Gi}+c_i{P}_{Gi}^2\right),$(14) where $n$ is the number of generators; $P_{Gi}$ is the real output power of the ith generator $a_i$; $b_i$ and $c_i$ are the cost coefficients of the ith generator.

4.1.2. Emission dispatch objective function

The total emission $f_2$ in (ton/h) of environmental pollutants such as nitrogen oxides $\text{N}{\text{O}}_x$ and sulphur oxides $\text{S}{\text{O}}_x$ due to burning fuels in fossil-fueled thermal units for production of power to meet the load demand can be expressed as [20] (15) $f_2=\sum _{i=1}^n\left({10}^{-2}\right({\alpha }_i+{\beta }_i{P}_{Gi}+{\gamma }_i{P}_{Gi}^2)+{\zeta }_i{e}^{{\lambda }_i{P}_{Gi}}),$(15) where ${\alpha }_i$, ${\beta }_i$, ${\gamma }_i$, ${\zeta }_i$ and ${\lambda }_i$ are coefficients of the ith generator emission characteristics.

4.2. Problem constraints

The optimization problem is bounded by the following equality and inequality constraints.

4.2.1. Power balance constraint

The total power generated should cover the total load demand and the real power losses in the transmission lines. Hence, (16) $\sum _{i=1}^n{P}_{Gi}-P_D-P_{\mathrm{loss}}=0,$(16) where $P_D$ is the total load demand and $P_{\mathrm{loss}}$ represents the transmission losses. The real power loss in transmission lines in Equation (16) is given in [21] as follows: (17) $P_{\mathrm{loss}}=\sum _{i=1}^n\sum _{j=1}^n\left(A_{ij}\right(P_i{P}_j+Q_i{Q}_j)+B_{ij}(Q_i{P}_j-P_i{Q}_j\left)\right),$(17) where $A_{ij}=\left(R_{ij}/V_i{V}_j\right)\text{cos(}{\delta }_i-{\delta }_j)$, $P_i=P_{Gi}-P_{Di}$, $Q_i=Q_{Gi}-Q_{Di}$, and $B_{ij}=\left(R_{ij}/V_i{V}_j\right)\text{sin(}{\delta }_i-{\delta }_j)$ such that $n$ is the number of buses, $P_i$ is the real power injection at bus $i$, $Q_i$ is the reactive power injection at bus $i$, $R_{ij}$ is the series resistance connecting buses $i$ and $j$, $V_i$ is a voltage magnitude at bus $i$ and ${\delta }_i$ is the voltage angle at bus $i$.

4.2.2. Maximum and minimum limits of power generation

For stable operation, real power generated by each generator is restricted by minimum and maximum limits, i.e.

$P_{G{i}_{min}}$ $\le$ $P_{Gi}$ $\le$ $P_{G{i}_{max}}$, $Q_{G{i}_{min}}$ $\le$ $Q_{Gi}$ $\le$ $Q_{G{i}_{max}}$, $V_{G{i}_{min}}$ $\le$ $V_{Gi}$ $\le$ $V_{G{i}_{max}}$.

4.2.3. Security constraints

A very large number of constraints are to be considered in the security-constrained EELD problem. But for typical systems, there is a small possibility of becoming overloaded for the large proportion of lines. So the EELD problem should consider only the critical lines which are in violation, or near violation of their respective security limits. We consider only the critical lines which are binding in the optimal solution. The detection of the critical lines is assumed to be done by the experiences of the DM. Minimizing the following objective function, we can obtain an improvement in the security $S=\sum _{q=1}^m\left(\frac{{\left(T_q\right(P_G\left)\right)}^2}{T_q^{\max }}\right),$ where $m$ is the number of monitored lines, $T_q\left(P_G\right)$ and $T_q^{\max }$ is the real power flow and the maximum limit of the real power flow of the qth line, respectively. By utilizing the generalized generation distribution factors (GGDF), the line flow of the qth line is formulated in terms of the control variables $P_{Gs}$ in [22] as follows: $T_q\left(P_G\right)=\sum _{i=1}^n\left(D_{qi}{P}_{Gi}\right),$ where $D_{qi}$ is the GGDF for the line $q$ due to generator $i$.

For secure operation, the transmission line loading $S_l$ is constrained by its upper limit $s_{l\text{max}}$ as $S_l\le S_{l\text{max}},l=1,\dots ,n_l,$ where $n_l$ is the number of transmission lines.

Aggregating the objectives and constraints, the EELD problem can be mathematically formulated as a nonlinear equality and inequality constrained multi-objective optimization problem as follows: (18) $\begin{array}{cc}\text{minimize}& f_1=\sum _{i=1}^n(a_i+b_i{P}_{Gi}+c_i{P}_{Gi}^2),\\ \text{minimize}& f_2=\sum _{i=1}^n\text{(1}{0}^{-2}({\alpha }_i+{\beta }_i{P}_{Gi}+{\gamma }_i{P}_{Gi}^2)\\ & +{\zeta }_i{e}^{{\lambda }_i{P}_{Gi}}),\\ \text{subject}\text{to}& \sum _{i=1}^n{P}_{Gi}-P_D-P_{\mathrm{loss}}=0,\\ & P_{G{i}_{\min }}\le P_{Gi}\le P_{G{i}_{\max }},\\ & Q_{G{i}_{\min }}\le Q_{Gi}\le Q_{G{i}_{\max }},\\ & V_{G{i}_{\min }}\le V_{Gi}\le V_{G{i}_{\max }},\\ & S_l\le S_{l\text{max}},\end{array}$(18) where $i=1,\dots ,n$ and $l=1,\dots ,n_1$.

The above problem can be formulated as follows: (19) $\begin{array}{cc}\text{minimize}& f_j\left(x\right),\\ \text{subject}\text{to}& h\left(x\right)=0,\\ & g\left(x\right)\le 0,\\ & \end{array}$(19) where $j=1,2$, $h\left(x\right)={\sum }_{i=1}^n{P}_{Gi}-P_D-P_{\mathrm{loss}}$ and $g\left(x\right)=[P_{G{i}_{\min }}-P_{Gi},P_{Gi}-P_{G{i}_{\max }},Q_{G{i}_{\min }}-Q_{Gi},Q_{Gi}-Q_{G{i}_{\max }},V_{G{i}_{\min }}-V_{Gi},V_{Gi}-V_{G{i}_{\max }},S_l-S_{l\text{max}}{]}^T.$

The functions $f_j\left(x\right):{\mathbb{R}}^n\to \mathbb{R},h\left(x\right):{\mathbb{R}}^n\to \mathbb{R},\text{and}g\left(x\right):{\mathbb{R}}^{3n+n_l}\to {\mathbb{R}}^{6n+n_l}$ are twice continuously differentiable where $j=1,2.$

Algorithm (4) is applied in the next section for solving the EELD problem formulated as Equation (19).

5. Implementation of the proposed algorithm

We apply Algorithm 4 to the EELD problem and it is tested on the standard IEEE 30-bus system having 6 generating units. The values of fuel cost and emission coefficient are described in Table 1. The parameters of the proposed algorithm implementation are selected as follows: ${\alpha }_1=0.05,{\alpha }_2=2,{\eta }_1=1\times {10}^{-4},{\eta }_2=0.5,{\epsilon }_1=1\times {10}^{-8}$ and ${\epsilon }_2=1\times {10}^{-8}$.

Table 1. Generator cost and emission coefficients of the considered EELD problem.

Parameters		$G_1$	$G_2$	$G_3$	$G_4$	$G_5$	$G_6$
Cost	$a$	$10$	$10$	$20$	$10$	$20$	$10$
	$b$	$200$	$150$	$180$	$100$	$180$	$150$
	$c$	$100$	$120$	$40$	$60$	$40$	$100$
Emission	$\alpha$	$4.091$	$2.543$	$4.258$	$5.426$	$4.258$	$6.131$
	$\beta$	$-5.554$	$-6.047$	$-5.094$	$-3.55$	$-5.094$	$-5.555$
	$\gamma$	$6.49$	$4.638$	$4.586$	$3.38$	$4.586$	$5.151$
	$\zeta$	$2.0E-4$	$5.0E-4$	$1.0E-6$	$2.0E-3$	$1.0E-6$	$1.0E-5$
	$\lambda$	$2.857$	$3.333$	$8.000$	$2.000$	$8.000$	$6.667$

In the proposed algorithm, we begin from any starting point $x_0$. The initial trust-region radius selected to be ${\delta }_0=max(\parallel s_0^{cp}\parallel ,{\delta }_{\min })$, where ${\delta }_{min}=1\times {10}^{-3}$. The maximum trust-region radius is selected to be ${\delta }_{\text{max}}={10}^5{\delta }_0$.

Successful termination with respect to the proposed active set trust-region algorithm indicates that the termination condition of the algorithm is met with ${\epsilon }_2$. In contrast, unsuccessful termination means that the number of iterations is greater than 300, the number of function evaluations is greater than 500 or the length of the trail step is less than ${\epsilon }_1$.

6. Results and discussions

To investigate the effectiveness of the proposed algorithm, relaxed I-SHOT active set Trust-region algorithm (RIAT), we compare the obtained results with different previous algorithms that handled the same problem. These algorithms include the strength Pareto evolutionary algorithm (SPEA) [1], the non-dominating sorting genetic algorithm (NSGA) [1], the Niched Pareto genetic algorithm (NPGA) [1], the multi-objective particle swarm optimization (MOPSO) [2], the fuzzy clustering-based particle swarm optimization (FCPSO) [3], the trust-region-based augmented Lagrangian method (TRALM) [23] and the $\epsilon$-constraint algorithm (EC) [24].

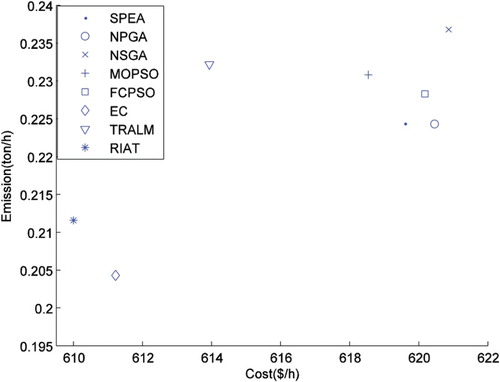
Table 2 is presented as a comparison of the best fuel costs of the previously mentioned algorithms. This table shows that the fuel cost obtained by the RIAT algorithm is less than the ones of the other algorithms and the corresponding emission value of the best cost of our approach is less than the other algorithms except in EC. These results are visualized in Figure 1.

Figure 1. Best cost solutions of some algorithms to the considered EELD problem.

Table 2. Comparison of best fuel costs of some algorithms to the considered EELD problem.

	SPEA [1]	NPGA [1]	NSGA [1]	MOPSO [2]	FCPSO [27]	EC [23]	TRALM [28]	RIAT [proposed]
${\mathit{P}}_{\mathit{G}1}$	$0.1319$	$0.1127$	$0.1358$	$0.1524$	$0.1596$	$0.2183$	$0.1648$	$0.1799$
${\mathit{P}}_{\mathit{G}2}$	$0.3654$	$0.3747$	$0.3151$	$0.3472$	$0.3535$	$0.3554$	$0.3456$	$0.3552$
${\mathit{P}}_{\mathit{G}3}$	$0.7791$	$0.8057$	$0.8418$	$0.7857$	$0.7974$	$0.5776$	$0.6619$	$0.5148$
${\mathit{P}}_{\mathit{G}4}$	$0.9282$	$0.9031$	$1.0431$	$1.0180$	$0.9719$	$0.7590$	$1.1079$	$0.9073$
${\mathit{P}}_{\mathit{G}5}$	$0.1308$	$0.1347$	$0.0631$	$0.0995$	$0.0862$	$0.5393$	$0.1691$	$0.5148$
${\mathit{P}}_{\mathit{G}6}$	$0.5292$	$0.5331$	$0.4664$	$0.4669$	$0.4961$	$0.4080$	$0.4147$	$0.3987$
Cost ($/h)	$619.60$	$620.46$	$620.87$	$618.54$	$620.18$	$611.22$	$613.93$	$610.0006$
Emission (ton/h)	$0.2244$	$0.2243$	$0.2368$	$0.2308$	$0.2283$	$0.2043$	$0.2322$	$0.21157$

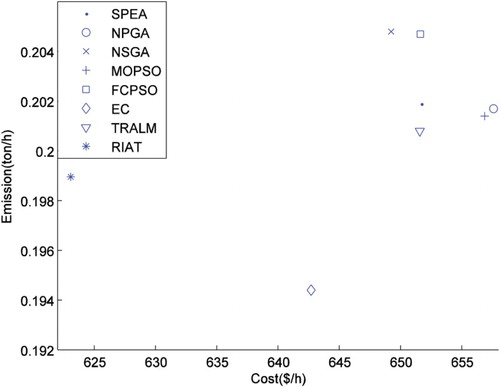
Table 3 is presented to compare the best emissions of the previous mentioned algorithms. This table shows that the emission amount obtained by the RIAT algorithm is less than the ones of the other algorithms except in EC approach. The best emission corresponding cost in our approach is less than all corresponding costs in other algorithms. The enhancement in the best emission of EC algorithm upon our approach is small when compared to the enhancement of the corresponding cost in our approach, as illustrated in Figure 2.

Figure 2. Best emission solutions of some algorithms to the considered EELD problem.

Table 3. Comparison of best emissions of some algorithms to the considered EELD problem.

	SPEA [1]	NPGA [1]	NSGA [1]	MOPSO [2]	FCPSO [27]	EC [23]	TRALM [28]	RIAT [proposed]
${\mathit{P}}_{\mathit{G}1}$	$0.4419$	$0.4753$	$0.4403$	$0.4589$	$0.4796$	$0.4122$	$0.4649$	$0.2805$
${\mathit{P}}_{\mathit{G}2}$	$0.4598$	$0.5162$	$0.4940$	$0.5121$	$0.5287$	$0.4667$	$0.5164$	$0.4278$
${\mathit{P}}_{\mathit{G}3}$	$0.6944$	$0.6513$	$0.7509$	$0.6524$	$0.6711$	$0.5514$	$0.6201$	$0.5238$
${\mathit{P}}_{\mathit{G}4}$	$0.4616$	$0.4363$	$0.5060$	$0.4331$	$0.5318$	$0.4059$	$0.4764$	$0.6902$
${\mathit{P}}_{\mathit{G}5}$	$0.1952$	$0.1896$	$0.1375$	$0.1981$	$0.1257$	$0.5731$	$0.2091$	$0.5238$
${\mathit{P}}_{\mathit{G}6}$	$0.6131$	$0.5988$	$0.5364$	$0.6129$	$0.5299$	$0.4550$	$0.5771$	$0.4378$
Cost ($/h)	$651.71$	$657.59$	$649.24$	$656.87$	$651.62$	$642.70$	$651.57$	$623.0762$
Emission (ton/h)	$0.2019$	$0.2017$	$0.2048$	$0.2014$	$0.2047$	$0.1944$	$0.2008$	$0.19896$

The best compromise solution is calculated using the membership function given in [25] and [3]. This membership function is used to calculate each member of the Pareto-optimal set for each method. After this calculation, the best compromise solution is the one that has the maximum value of membership function.

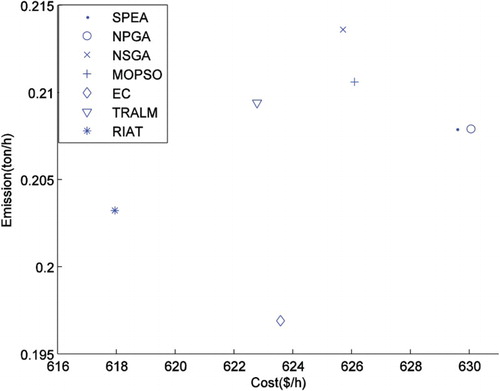
Table 4 is presented to compare the existing best compromise solutions of the previously considered algorithms. This table shows a reasonable compromise solution for the proposed RIAT algorithm. These results are visualized in Figure 3.

Figure 3. Best compromise solutions of some algorithms to the considered EELD problem.

Table 4. Comparison of best compromise solutions of some algorithms to the considered EELD problem.

	SPEA [1]	NPGA [1]	NSGA [1]	MOPSO [2]	FCPSO [27]	EC [23]	TRALM [28]	RIAT [proposed]
${\mathit{P}}_{\mathit{G}1}$	$0.3052$	$0.2998$	$0.2712$	$0.2882$	Compromise solution was not	$0.3149$	$0.3126$	$0.2467$
					considered in the paper
${\mathit{P}}_{\mathit{G}2}$	$0.4389$	$0.4325$	$0.3670$	$0.3956$		$0.4076$	$0.4262$	$0.4044$
${\mathit{P}}_{\mathit{G}3}$	$0.7163$	$0.7342$	$0.8099$	$0.7320$		$0.5613$	$0.6508$	$0.5198$
${\mathit{P}}_{\mathit{G}4}$	$0.6978$	$0.6853$	$0.7550$	$0.7520$		$0.5795$	$0.7994$	$0.7822$
${\mathit{P}}_{\mathit{G}5}$	$0.1552$	$0.1560$	$0.1357$	$0.1489$		$0.5544$	$0.1809$	$0.5198$
${\mathit{P}}_{\mathit{G}6}$	$0.5507$	$0.5561$	$0.5239$	$0.5463$		$0.4419$	$0.4941$	$0.4111$
Cost ($/h)	$629.59$	$630.06$	$625.71$	$626.10$		$623.58$	$622.78$	$617.9484$
Emission (ton/h)	$0.2079$	$0.2079$	$0.2136$	$0.2106$		$0.1969$	$0.2094$	$0.2032$

To investigate the effectiveness of using relaxed I-SHOT approach, we compare our obtained results with the results obtained using the I-SHOT method and we use the same algorithm for solving the obtained single-objective problem described in Section 3.2.3 and we call this algorithm as IAT.

Table 5 is presented to compare the best fuel cost, the best emission and the best compromise solution of RIAT and IAT algorithms. As can be seen from this table, the best emission of IAT algorithm is better than the one obtained using RIAT. By using the relaxation technique, we make an increment in emission value to make a sufficient decrement in fuel cost value. So the best fuel cost and best compromise solution of RIAT algorithm are better than those of the IAT algorithm.

Table 5. Comparison of results of RIAT and IAT algorithms to the considered EELD problem.

	Best Cost		Best emission		Best Compromise solution
	IAT	RIAT	IAT	RIAT	IAT	RIAT
${\mathit{P}}_{\mathit{G}1}$	$0.2060$	$0.1799$	$0.3321$	$0.2805$	$0.2559$	$0.2467$
${\mathit{P}}_{\mathit{G}2}$	$0.4036$	$0.3552$	$0.4731$	$0.4278$	$0.4344$	$0.4044$
${\mathit{P}}_{\mathit{G}3}$	$0.5070$	$0.5148$	$0.5217$	$0.5238$	$0.5188$	$0.5198$
${\mathit{P}}_{\mathit{G}4}$	$0.8501$	$0.9073$	$0.5833$	$0.6902$	$0.7249$	$0.7822$
${\mathit{P}}_{\mathit{G}5}$	$0.5070$	$0.5148$	$0.5217$	$0.5238$	$0.5188$	$0.5198$
${\mathit{P}}_{\mathit{G}6}$	$0.1401$	$0.3987$	$0.4581$	$0.4378$	$0.43106$	$0.4111$
Cost ($/h)	$615.3636$	$610.0006$	$631.8569$	$623.0762$	$621.1265$	$617.9484$
Emission (ton/h)	$0.207083$	$0.21157$	$0.195267$	$0.19896$	$0.20044$	$0.20322$

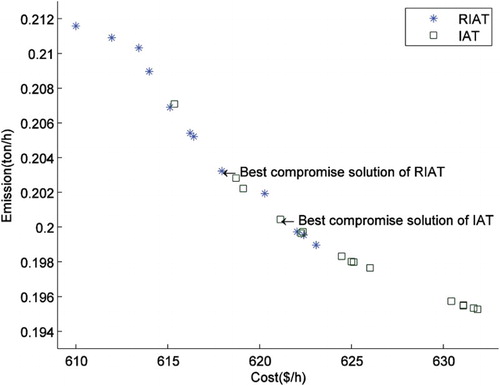
The Pareto front of RIAT and IAT algorithms is presented in Figure 4. The graph asserts the fact that the algorithm makes an increment in emission value to make a decrement in fuel cost value.

Figure 4. Pareto-optimal fronts of RIAT and IAT to the considered EELD problem.

The results obtained when implementing the proposed trust-region algorithm on the constrained multi-objective EELD optimization problem indicate that it is an efficient tool for this type of problems. The results also illustrate the global convergence of this modified method, which makes it more suitable for practical computations with lower computational complexity and easier implementation.

Also, the proposed multi-objective approach RIAT algorithm allows more control over the optimization process and reduces the feasible region at every iteration with the interaction of the DM preferences so that the most preferred solution (decision vector) can be found.

7. Conclusions

In this work, we introduce a hybrid method between two interactive multi-objective methods, I-SHOT method and STEM (which we called relaxed I-SHOT method). By using the Relaxed I-SHOT method, the multi-objective constrained optimization problem is transformed into a single objective constrained optimization problem. The active set strategy is used together with the penalty method to converted the single objective constrained optimization problem into an unconstrained optimization problem. Then we are concerned with the proposed trust-region algorithm to solve the unconstrained optimization problem. The previous process is collected in RIAT algorithm.

This algorithm is considered as a globally search method to form a Pareto-optimal set where multiple Pareto-optimal solutions can be found in one run. We need to select one operating point, which will satisfy the different goals to some extent. The Relaxed I-SHOT method makes the interaction between the DM and the obtained Pareto-optimal set introduce more preferred solutions to the DM, from which he(she) can select the best compromise solution.

The proposed approach gives the DM great control over the optimization process. The Relaxed I-SHOT method gives the DM the ability to classify the objectives, make an improvement to some objectives values by small relaxation (increment) in the other objective values. Generally, the Pareto-optimal solutions obtained cannot be predicted. Though the DM can be sufficient for some objectives values and not sufficient with other objectives values, so the relaxation technique improves the unacceptable objective values. The proposed approach with two penalty parameters method reduces the number of computations needed when solving the obtained single-objective optimization problem by ensuring that the predicted reduction is positive before testing the step.

In this work, the proposed algorithm was applied to the EELD problem, which is formulated as a multi-objective optimization problem with two conflicting objectives, fuel cost and emission level. The results obtained by our algorithm is less than most of the other algorithms in the literature for the values of best fuel cost or the best emission level. The obtained results of the best compromise solution and best fuel cost described how relaxation method gives more control when the DM wants to reduce the fuel cost by some increment in the emission level. The obtained results present the efficiency of the proposed RIAT algorithm in solving real problems. The approach is applied to the EELD problem with no limitation to the number of objectives. The proposed algorithm is efficient for solving ill-defined systems and non-convex multi-objective optimization problems.

Disclosure statement

No potential conflict of interest was reported by the authors.