A time dependent slip flow of a couple stress fluid between two parallel plates through state space

ABSTRACT

In this work, the time dependent flow of an incompressible couple stress fluid passing two infinite parallel plates is investigated. The fluid motion is generated by applying a constant pressure gradient together with a sudden motion of one of the two plates. The linear slip velocity and the vanishing couple stresses on the boundary are applied on both plates. A generalized solution is obtained analytically by utilizing the integral Laplace transform together with the state space technique in the Laplace domain. The inversion of Laplace transform is obtained numerically by using a standard numerical method adopted by Honig and Hirdes. The effects of couple stress viscosity coefficient and slip parameters on both plates are studied numerically. The results show that the increase in the couple stress and slip coefficients results in a decrease in the fluid velocity in the case of stationary plates. However the velocity of the fluid is amplified by the increase of these parameters when the upper plate is set in motion.

KEYWORDS:

• Couple stress fluid
• slip condition
• state space technique

Introduction

Throughout the last four centuries, the study of non- Newtonian fluids has gained great attention by mathematicians and physicists such as Newton, Navier, and Euler, due to its importance in industrial, scientific and technological fields. Moreover, they proposed many models and different equations to explain the behaviour of such fluids. Couple stress fluids model is one of the most significant non-Newtonian fluid models which has been introduced by Stokes in 1964 [1]. It gives a simple generalization for the classical Navier-Stokes theory. In this model, the polar effects such as the presence of body couples and couple stresses are assumed to contribute to the fluid flow. Its equation of motion is similar to that of classical Navier-Stokes theory in addition to an extra term of higher order. The stress tensor is non-symmetric and an additional tensor namely couple stress tensor exist. This theory models many types of fluids microstructure e.g. liquid crystals, muddy water and animal blood [2].

Numerous studies have been recorded in the theory of couple stress fluids. Devakar and Iyengar considered Stokes’ problems for couple stress fluid using the classical no-slip condition [3]. They also discussed the run up flow between parallel plates with the same boundary conditions [4]. In addition, they investigated the generalized Stokes’ problem [5]. In recent years, Saad and Ashmawy studied the unsteady plane Couette flow of couple stress fluid between two parallel plates with slip condition [6]. The latter solved the problem of couple stress fluid through an infinite circular cylinder [7].

In this paper, we investigate the motion of an incompressible couple stress fluid flow limited between two parallel plates keeping one of the two plates stationary while the other is set in motion in addition to the presence of a time dependent pressure gradient. The Laplace transform together with the state space technique are applied to obtain the solution of the problem in the Laplace domain. The Laplace transform is inverted to the physical domain numerically using a standard algorithm adopted by Honig and Hirdes [8]. The solution of the problem is discussed through graphs.

Formulation of the problem

Assuming that there is no body forces and body couples, the unsteady flow of an incompressible couple stress fluid is governed by the following differential equations [1,2]:

Conservation of mass (1) $q_{i,i}=0.$(1) Conservation of momentum (2) $\mu q_{i,jj}-\eta q_{i,jjkk}-p_{,i}=\rho \left[\frac{\mathrm{\partial }{q}_i}{\mathrm{\partial }t}+q_k{q}_{i,k}\right],$(2) where $q_i,p$ and $\rho$ are respectively the velocity vector, pressure at any point, and the fluid density. The viscosity coefficient is denoted by µ, and $\eta$ is the couple stress viscosity coefficient.

The non-symmetric stress and couple stress tensors are defined respectively by [1,2] (3) $t_{i,j}=-p{\delta }_{i,j}+2\mu d_{ij}-\frac{1}{2}{\epsilon }_{ijk}{m}_{sk,s},$(3) (4) $m_{ij}=m{\delta }_{ij}+4(\eta w_{j,i}+{\eta }^{\mathrm{\prime }}{w}_{i,j}),$(4) where ${\delta }_{i,j}$ and ${\epsilon }_{ijk}$ are the Kronecker delta and alternating tensor respectively. ${\eta }^{\mathrm{\prime }}$is the couple stress coefficient, and m is the trace of the couple stress tensor.

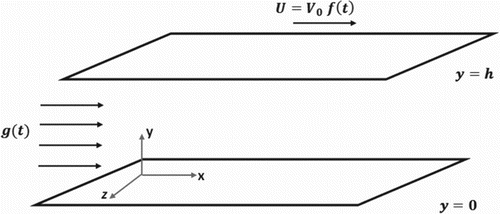
The rate of deformation vector and the vorticity vector, respectively, are evaluated by (5) $d_{ij}=\frac{1}{2}(q_{i,j}+q_{j,i}),$(5) (6) $w_i=\frac{1}{2}\left({\epsilon }_{ijk}{q}_{k,j}\right).$(6) Let us consider now the unsteady flow of an incompressible couple stress fluid flanked by two infinite horizontal parallel plates separated by distance “h”. Initially, both plates and the fluid are at rest. Suddenly, the upper plate is moved with velocity U=$V_{0}f\left(t\right)$, where $V_0$ is a constant with velocity dimensions and $f\left(t\right)$ is an arbitrary function of time. Instantaneously, a time dependent pressure gradient is applied in the direction of the positive x-axis. The velocity of the fluid has only one non-vanishing component. Hence, the velocity vector can be written as $\mathit{q}=\left(u\right(y,t),0,0)$ (Figure 1).

Figure 1. Geometry of the problem.

The velocity field “$\mathit{q}$” automatically satisfied the equation of conservation of mass, and using this quantity, the equation of conservation of momentum reduces to (7) $\rho \frac{\mathrm{\partial }u}{\mathrm{\partial }t}=-\frac{\mathrm{\partial }P}{\mathrm{\partial }x}+\mu \frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}-\eta \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}.$(7) Initially, the fluid is at rest.

Hence, (8) $u(y,0)=0.$(8) The slip boundary conditions applied on the two plates are given by [9–11] (9) ${\beta }_{1}u(y,t)=\mu \frac{\mathrm{\partial }u}{\mathrm{\partial }y}-\eta \frac{{\mathrm{\partial }}^{3}u}{\mathrm{\partial }{y}^3}\text{at }y=0,$(9) (10) ${\beta }_2\left\{u\right(y,t)-V_{0}f(t\left)\right\}=-\mu \frac{\mathrm{\partial }u}{\mathrm{\partial }y}+\eta \frac{{\mathrm{\partial }}^{3}u}{\mathrm{\partial }{y}^3}\text{at }y=h.$(10) The parameters ${\beta }_1$and ${\beta }_2$ represent, respectively, the slip coefficients of the lower and upper plates. These parameters depend only on the fluid nature and the material of the solid boundaries, and they vary between zero and infinity.

The vanishing couple stress conditions at the boundaries are the following (11) $\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}=0\text{at }y=0,$(11) (12) $\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}=0\text{at }y=h.$(12) Now, consider the non-dimensional variables (13) $\hat{u}=\frac{u}{V_0},\hat{y}=\frac{y}{h},\hat{t}=\frac{V_0}{h}t,\hat{x}=\frac{x}{h},\hat{P}=\frac{hP}{\mu V_0}.$(13) Using these variables, we can write the differential equation (7) in the form (14) $\frac{{\mathrm{\partial }}^4\hat{u}}{\mathrm{\partial }{\hat{y}}^4}-a^2\frac{{\mathrm{\partial }}^2\hat{u}}{\mathrm{\partial }{\hat{y}}^2}+\xi \frac{\mathrm{\partial }\hat{u}}{\mathrm{\partial }\hat{t}}=a^{2}g\left(t\right),$(14) Such that, (15) $a^2=\frac{h^2\mu }{\eta },\xi =a^2\frac{h\rho V_0}{\mu },g\left(t\right)=-\frac{\mathrm{\partial }\hat{P}}{\mathrm{\partial }\hat{x}}.$(15) In addition, we can write the initial and boundary conditions (8)–(12) in terms of the non-dimensional variables (13), after dropping the hats, as (16) $u(y,0)=0,$(16) (17) $u(y,t)=\frac{1}{{\alpha }_1}\left\{\frac{\mathrm{\partial }u}{\mathrm{\partial }y}-\frac{1}{a^2}\frac{{\mathrm{\partial }}^{3}u}{\mathrm{\partial }{y}^3}\right\}\text{at }y=0,$(17) (18) $u(y,t)=f\left(t\right)+\frac{1}{{\alpha }_2}\left\{-\frac{\mathrm{\partial }u}{\mathrm{\partial }y}+\frac{1}{a^2}\frac{{\mathrm{\partial }}^{3}u}{\mathrm{\partial }{y}^3}\right\}\text{at }y=1,$(18) (19) $\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}=0\text{at }y=0,$(19) (20) $\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}=0\text{at }y=1,$(20) where, ${\alpha }_1=\frac{h{\beta }_1}{\mu }$ and ${\alpha }_2=\frac{h{\beta }_2}{\mu }$.

Taking the Laplace transform of equation (14) and applying the initial condition (16), we get (21) $\frac{{\mathrm{\partial }}^4\overline{u}(y,s)}{\mathrm{\partial }{y}^4}-a^2\frac{{\mathrm{\partial }}^2\overline{u}(y,s)}{\mathrm{\partial }{y}^2}+\xi s\overline{u}(y,s)=a^2\overline{g}\left(s\right).$(21) Also, the boundary conditions (17)-(20), after applying Laplace transform, are reduced to (22) $\overline{u}(y,s)=\frac{1}{{\alpha }_1}\left\{\frac{\mathrm{\partial }\overline{u}(y,s)}{\mathrm{\partial }y}-\frac{1}{a^2}\frac{{\mathrm{\partial }}^3\overline{u}(y,s)}{\mathrm{\partial }{y}^3}\right\}\text{at }y=0,$(22) (23) $\begin{array}{rl}\overline{u}(y,s)& =\overline{f}\left(s\right)+\frac{1}{{\alpha }_2}\left\{-\frac{\mathrm{\partial }\overline{u}(y,s)}{\mathrm{\partial }y}+\frac{1}{a^2}\frac{{\mathrm{\partial }}^3\overline{u}(y,s)}{\mathrm{\partial }{y}^3}\right\}\\ & \text{at }y=1,\end{array}$(23) (24) $\frac{{\mathrm{\partial }}^2\overline{u}(y,s)}{\mathrm{\partial }{y}^2}=0\text{at }y=0,$(24) (25) $\frac{{\mathrm{\partial }}^2\overline{u}(y,s)}{\mathrm{\partial }{y}^2}=0\text{at }y=1.$(25)

The formula of Laplace transform is given as (26) $\overline{f}\left(y,s\right)={\int }_0^{\mathrm{\infty }}{e}^{-st}F(y,t\text{)d}t.$(26)

State space approach

A state space is a mathematical model of a physical system represented as a set of input, output and state variables connected by a differential equation in matrix form. The concept of the state of a dynamic system refers to a minimum set of variables, namely state variables, which accurately describe the system. This technique is suitable for illustrating the high-order dimensional systems since it reduces its order and makes it easy to solve. The state space method has been used extensively by many authors to solve complicated problems in the theory of thermo-elasticity [12–14]. Other researchers utilized the same technique to investigated micropolar fluid flow problems [15–17]. To our knowledge, no one has used the aforementioned technique in the theory of couple stress fluids yet.

Solution using state space approach

To apply the state space technique, we first write the differential equation (21) in the matrix form (27) $\frac{\mathrm{\partial }\overline{\mathit{V}}(y,s)}{\mathrm{\partial }y}=\mathit{A}\left(s\right)\overline{\mathit{V}}(y,s)+\mathit{B}(y,s),$(27) where, $\begin{array}{rl}\mathit{A}\left(s\right)& =\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ -\xi s& 0& a^2& 0\end{array}\right),\overline{\mathit{V}}(y,s)=\left(\begin{array}{c}u\\ {\overline{u}}^{\mathrm{\prime }}\\ {\overline{u}}^{{}^{\mathrm{\prime \prime }}}\\ {\overline{u}}^{\mathrm{\prime \prime \prime }}\end{array}\right),\\ \mathit{B}(y,s)& =\left(\begin{array}{c}0\\ 0\\ 0\\ a^2\overline{g}\left(s\right)\end{array}\right),\end{array}$ ${\overline{u}}^{\mathrm{\prime }}=\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }y},{\overline{u}}^{{}^{\mathrm{\prime \prime }}}=\frac{\mathrm{\partial }{\overline{u}}^{\mathrm{\prime }}}{\mathrm{\partial }y},{\overline{u}}^{\mathrm{\prime \prime \prime }}=\frac{\mathrm{\partial }{\overline{u}}^{{}^{\mathrm{\prime \prime }}}}{\mathrm{\partial }y},{\overline{u}}^{\mathrm{\prime \prime \prime \prime }}=\frac{\mathrm{\partial }{\overline{u}}^{\mathrm{\prime \prime \prime }}}{\mathrm{\partial }y}.$ Then (21) becomes (28) $\frac{\mathrm{\partial }}{\mathrm{\partial }y}\left(\begin{array}{c}u\\ {\overline{u}}^{\mathrm{\prime }}\\ {\overline{u}}^{{}^{\mathrm{\prime \prime }}}\\ {\overline{u}}^{\mathrm{\prime \prime \prime }}\end{array}\right)=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ -\xi s& 0& a^2& 0\end{array}\right)\left(\begin{array}{c}u\\ {\overline{u}}^{\mathrm{\prime }}\\ {\overline{u}}^{{}^{\mathrm{\prime \prime }}}\\ {\overline{u}}^{\mathrm{\prime \prime \prime }}\end{array}\right)+\left(\begin{array}{c}0\\ 0\\ 0\\ a^2\overline{g}\left(s\right)\end{array}\right).$(28) The formal solution of the differential equation (27) is found to be (29) $\begin{array}{rl}\overline{\mathit{V}}(y,s)& =\exp \left[\mathit{A}\right(s\left)y\right]\left\{\overline{\mathit{V}}\right(0,s)\\ & +{\int }_{\tau =0}^y\exp [-\mathit{A}(s\left)\tau \right]\mathit{B}\left(s\right)\text{d}\tau \}.\end{array}$(29) The characteristic equation of the square matrix $\mathit{A}\left(s\right)$ is given by (30) $k^4-a^2{k}^2+\xi s=0.$(30) The roots of the above characteristic equation are ±$k_1$ and ±$k_2$

where $k_1=\sqrt{\frac{a^2+\sqrt{a^4-4\xi s}}{2}},k_2=\sqrt{\frac{a^2-\sqrt{a^4-4\xi s}}{2}}.$ The expansion of Maclaurin series of $\exp \left[\mathit{A}\right(s\left)y\right]$ is defined by (31) $\exp \left[\mathit{A}\right(s\left)y\right]=\sum _{j=0}^{\mathrm{\infty }}\frac{{\left(\mathit{A}\right(s\left)y\right)}^j}{j!}.$(31) Since every square matrix satisfies its own characteristic equation “Cayley-Hamilton theorem”, we can write (32) ${\mathit{A}}^4-a^2{\mathit{A}}^2+\xi s\mathit{I}=0.$(32) So, we can express ${\mathit{A}}^4$ and the higher powers of A in terms of I, A, ${\mathit{A}}^2$,${\mathit{A}}^3$, where I is the unit matrix of order 4. Therefore, we can write $\exp \left[\mathit{A}\right(s\left)y\right]$ as a finite series in the form (33) $\exp \left[\mathit{A}\right(s\left)y\right]=\mathit{L}(y,s)=a_0\mathit{I}+a_1\mathit{A}+a_2{\mathit{A}}^2+a_3{\mathit{A}}^3.$(33) Moreover, using the fact that ±$k_1$ and ±$k_2$ are the characteristic roots of $\mathit{A}\left(s\right)$, we can write (34) $\exp \left[k_{i}y\right]=a_0+a_1{k}_i+a_2{k_i}^2+a_3{k_i}^3,i=1,2.$(34) (35) $\exp [-k_{i}y]=a_0-a_1{k}_i+a_2{k_i}^2-a_3{k_i}^3,i=1,2.$(35) Solving this system allow us to determine $a_0,a_1,a_2,$ and $a_3,$which depend on y and s, $\begin{array}{rl}{a}_0& =\frac{1}{H}\{k_1^2\cosh (k_{2}y)-k_2^2\text{cosh}(k_{1}y\left)\right\},\\ a_1& =\frac{1}{H}\left\{\frac{k_1^2}{k_2}\sinh \left(k_{2}y\right)-\frac{k_2^2}{k_1}\text{sinh}\left(k_{1}y\right)\right\},\end{array}$ $\begin{array}{rl}{a}_2& =\frac{1}{H}\left\{\cosh \left(k_{1}y\right)-\text{cosh}\left(k_{2}y\right)\right\},\\ a_3& =\frac{1}{H}\left\{\frac{1}{k_1}\sinh \left(k_{1}y\right)-\frac{1}{k_2}\text{sinh}\left(k_{2}y\right)\right\},\end{array}$ where, $H=k_1^2-k_2^2$.

As a result, and after substituting the matrices $\mathit{I},\mathit{A},{\mathit{A}}^2,{\mathit{A}}^3$ in the expression (33) the matrix L(y, s), is completely obtained. The elements of $L_{ij}$(i, j = 1 2,3,4) are given below $\begin{array}{rl}{L}_{11}& =\frac{1}{H}\{k_1^2\cosh (k_{2}y)-k_2^2\text{cosh}(k_{1}y\left)\right\},\\ L_{12}& =\frac{1}{H}\left\{\frac{k_1^2}{k_2}\sinh \left(k_{2}y\right)-\frac{k_2^2}{k_1}\text{sinh}\left(k_{1}y\right)\right\},\end{array}$ $\begin{array}{rl}{L}_{13}& =\frac{1}{H}\{\cosh (k_{1}y)-\text{cosh}(k_{2}y\left)\right\},\\ L_{14}& =\frac{1}{H}\left\{\frac{1}{k_1}\sinh \left(k_{1}y\right)-\frac{1}{k_2}\text{sinh}\left(k_{2}y\right)\right\},\end{array}$ $\begin{array}{rl}{L}_{21}& =-\xi s{L}_{14}=L_{32},L_{22}=L_{11},L_{23}=L_{12}+a^2{L}_{14}\\ & =L_{34},L_{24}=L_{13},L_{31}=-\xi s{L}_{13}=L_{42},\end{array}$ $\begin{array}{rl}{L}_{32}& =-\xi s{L}_{14}=L_{44},L_{33}=L_{11}+a^2{L}_{13},\\ L_{41}& =-\xi s{L}_{23},L_{43}=a^2{L}_{12}+\{a^4-\xi s\}{L}_{14}.\end{array}$

We can now rewrite the solution (29) in terms of $\mathit{L}(y,s)$ as (36) $\overline{\mathit{V}}(y,s)=\mathit{L}(y,s)\left\{\overline{\mathit{V}}(0,s)+\left(\begin{array}{c}D(y,s)\\ E(y,s)\\ F(y,s)\\ G(y,s)\end{array}\right)\right\},$(36) (37) $\left(\begin{array}{c}D(y,s)\\ E(y,s)\\ F(y,s)\\ G(y,s)\end{array}\right)={\int }_{\tau =0}^y\exp [-\mathit{A}(s\left)\tau \right]\mathit{B}\left(s\right)\text{d}\tau .$(37) By definition, (38) $\exp [-\mathit{A}(s\left)y\right]=\sum _{j=0}^{\mathrm{\infty }}\frac{{(-1)}^j{\left(\mathit{A}\right(s\left)y\right)}^j}{j!},$(38) which can be reduced to a finite series using “Cayley Hamilton Theorem”, such as (39) ${\mathit{L}}^{\ast }(y,s)=\exp \left[\mathit{A}\right(s\left)y\right]=a_0\mathit{I}-a_1\mathit{A}+a_2{\mathit{A}}^2-a_3{\mathit{A}}^3.$(39) Then, (40) ${\mathit{L}}^{\ast }(y,s)=\left(\begin{array}{cccc}{L}_{11}& -L_{12}& L_{13}& -L_{14}\\ -L_{21}& L_{22}& -L_{23}& L_{24}\\ L_{31}& -L_{32}& L_{33}& -L_{34}\\ -L_{41}& L_{42}& -L_{43}& L_{44}\end{array}\right),$(40) (41) $\left(\begin{array}{c}D(y,s)\\ E(y,s)\\ F(y,s)\\ G(y,s)\end{array}\right)=a^2\overline{g}\left(s\right){\int }_{\tau =0}^y\left(\begin{array}{c}-L_{14}\\ L_{24}\\ -L_{34}\\ L_{44}\end{array}\right)\mathrm{\partial }\tau .$(41) Therefore, the solution can be written in the form (42) $\begin{array}{rl}\overline{u}(y,s)& =L_{11}\overline{u}(0,s)+L_{12}{\overline{u}}^{{}^{\mathrm{\prime }}}(0,s)+L_{13}{\overline{u}}^{{}^{\mathrm{\prime \prime }}}(0,s)\\ & +L_{14}{\overline{u}}^{\mathrm{\prime \prime \prime }}(0,s)+N_1(y,s),\end{array}$(42) (43) $\begin{array}{rl}{\overline{u}}^{\mathrm{\prime }}(y,s)& =L_{21}\overline{u}(0,s)+L_{22}{\overline{u}}^{{}^{\mathrm{\prime }}}(0,s)+L_{23}{\overline{u}}^{{}^{\mathrm{\prime \prime }}}(0,s)\\ & +L_{24}{\overline{u}}^{\mathrm{\prime \prime \prime }}(0,s)+N_2(y,s),\end{array}$(43) (44) $\begin{array}{rl}{\overline{u}}^{\mathrm{\prime \prime }}(y,s)& =L_{31}\overline{u}(0,s)+L_{32}{\overline{u}}^{{}^{\mathrm{\prime }}}(0,s)+L_{33}{\overline{u}}^{{}^{\mathrm{\prime \prime }}}(0,s)\\ & +L_{34}{\overline{u}}^{\mathrm{\prime \prime \prime }}(0,s)+N_3(y,s),\end{array}$(44) (45) $\begin{array}{rl}{\overline{u}}^{\mathrm{\prime \prime \prime }}\left(y,s\right)& =L_{41}\overline{u}\left(0,s\right)+L_{42}{\overline{u}}^{{}^{\mathrm{\prime }}}\left(0,s\right)+L_{43}{\overline{u}}^{{}^{\mathrm{\prime \prime }}}\left(0,s\right)\\ & +L_{44}{\overline{u}}^{\mathrm{\prime \prime \prime }}\left(0,s\right)+N_4\left(y,s\right).\end{array}$(45) Such that, $\begin{array}{rl}{N}_i(y,s)& =L_{i1}D(y,s)+L_{i2}E(y,s)+L_{i3}F(y,s)+L_{i4}G(y,s),\\ & i=1,2,3,4.\end{array}$ After applying the boundary conditions (23),(25),we can get the two unknowns ${\overline{u}}^{{}^{\mathrm{\prime }}}(0,s)$ and ${\overline{u}}^{\mathrm{\prime \prime \prime }}(0,s)$ assuming that $L_{ij}^1$ (i, j = 1,2,3,4) are the values of $L_{ij}$ at $y=1,$ such as $\begin{array}{rl}{\overline{u}}^{{}^{\mathrm{\prime }}}(0,s)& =-l\left\{-N_1(1,s)-\frac{1}{{\alpha }_2}{N}_2(1,s)\right.\\ & +\left.\frac{1}{{\alpha }_2{a}^3}{N}_4(1,s)+\overline{f}\left(s\right)\right\}\\ & -\frac{{\alpha }_1}{L_{31}^1+{\alpha }_1{L}_{32}^1}\{1+qm\}{N}_3(y,s),\end{array}$ $\begin{array}{rl}{\overline{u}}^{\mathrm{\prime \prime \prime }}(0,s)& =\frac{1}{\mathrm{\Delta }}\left\{-N_1(1,s)-\frac{1}{{\alpha }_2}{N}_2(1,s)\right.\\ & +\frac{{\alpha }_{1}m}{L_{31}^1+{\alpha }_1{L}_{32}^1}{N}_3(y,s)\\ & +\left.\frac{1}{{\alpha }_2{a}^3}{N}_4(1,s)+\overline{f}\left(s\right)\right\},\end{array}$ where, $m=\frac{L_{11}^1}{{\alpha }_1}+L_{12}^1+\frac{L_{21}^1}{{\alpha }_2{\alpha }_1}+\frac{L_{22}^1}{{\alpha }_2}-\frac{L_{41}^1}{{\alpha }_1{\alpha }_2{a}^2}-\frac{L_{42}^1}{{\alpha }_2{a}^2},$ $n=L_{14}^1-\frac{L_{11}^1}{{\alpha }_1{a}^2}+\frac{L_{24}^1}{{\alpha }_2}-\frac{L_{21}^1}{{\alpha }_1{\alpha }_2{a}^2}-\frac{L_{44}^1}{{\alpha }_2{a}^2}+\frac{L_{41}^1}{{\alpha }_1{\alpha }_2{a}^4},$ $\begin{array}{rl}\mathrm{\Delta }& =\frac{-{\alpha }_{1}m}{L_{31}^1+{\alpha }_1{L}_{32}^1}\left(L_{34}^1-\frac{L_{31}^1}{{\alpha }_1{a}^2}\right)+n,\\ l& =\frac{{\alpha }_1}{\mathrm{\Delta }\left(L_{31}^1+{\alpha }_1{L}_{32}^1\right)}\left(L_{34}^1-\frac{L_{31}^1}{{\alpha }_1{a}^2}\right).\end{array}$

Inversion of laplace transform numerically

In order to invert the Laplace transforms obtained we employ the standard numerical inversion algorithm adopted by Honig and Hirdes [8]. In this algorithm, the inverse Laplace transform of the function $\overline{R}\left(s\right)$ is approximated by (46) $\begin{array}{rl}R\left(t\right)& =\frac{e^{bt}}{T}\left\{\frac{1}{2}\overline{R}\left(b\right)+Re\left(\sum _{k=1}^N\overline{R}\left(b+\frac{ik\pi }{T}\right)e^{ik\pi t/T}\right)\right\},\\ & 0<t<2T.\end{array}$(46)

The number N is a sufficiently large integer chosen such that $e^{bt}Re\left\{\overline{R}\left(b+\frac{ik\pi }{T}\right)e^{iN\pi t/T}\right\}<\epsilon ,$ where $\epsilon$ a small positive number that corresponds to the degree of accuracy required and b is a positive free parameter that must be greater than the real part of all singularities of $\overline{R}\left(s\right)$. In this regards, we consider three cases listed below.

Numerical results

In this section, we present the obtained results graphically for the variation of the velocity through the mean of the inversion numerical technique outlined above. Two different cases are considered.

Case1: flow due to oscillatory motion of the upper plate with no pressure gradient

In this case, we assume that the upper plate is set in motion with a an oscillating velocity given by $U=V_0\text{sin}\left(\omega t\right)$, where $\omega$ is the angular velocity, with no pressure gradient.

Case2: flow due to oscillatory pressure gradient with stationary plates

In this case, the two plates are assumed to be stationary and the motion is generated by applying a time dependent pressure gradient of the form $\frac{\mathrm{\partial }p}{\mathrm{\partial }x}=-\text{sin}\left(\omega t\right).$

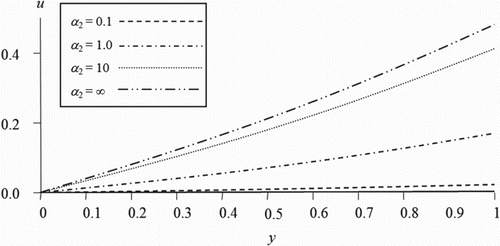
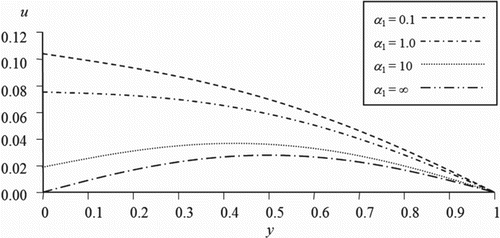
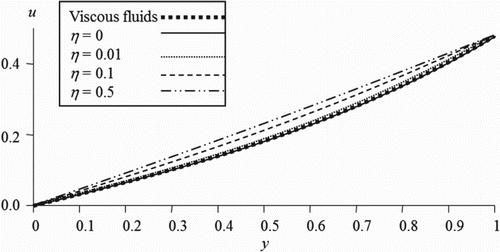
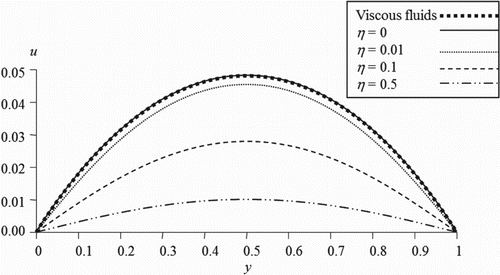
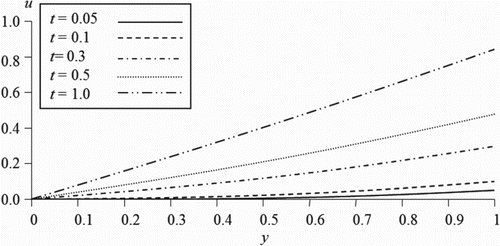
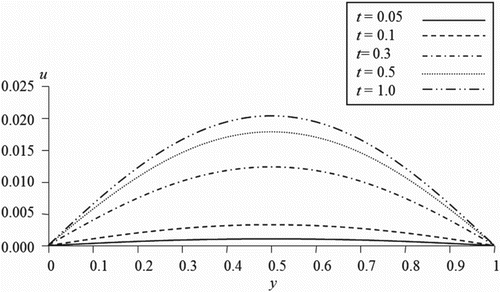
In the figures illustrated in this section, we plot the velocity of the couple stress fluid flow versus the distance between the two plates for different values of the time, slip and couple stress viscosity parameters. Figure 2 shows the variation of the velocity for different values of the slip parameter of the upper plate while the other parameters are kept fixed. It is observed that, as the slip parameter increases the fluid velocity increases near the moving plate. However, Figure 3 reveals that as the slip parameter on the stationary plate increases, the fluid velocity decreases. This indicates that the more the fluid slips at the boundary the less its velocity is affected by the motion of the boundary. Figures 4 and 5 illustrate the velocity profile for various values of the couple stress viscosity parameter in the first and second case respectively. It is noticed that the fluid velocity is proportional to the couple stress parameter in the first case while the trend is reversed when the motion is generated by a pressure gradient. As expected, it is observed from Figures 4 and 5 that our results when the couple stress viscosity parameter is taken zero is coincident with the previous results available in the literature for the case of classical viscous fluids [18]. On the other hand, Figures 6 and 7 represent the behaviour of the velocity for different values of time parameter. It can be seen that the increase of the time parameter enhances the magnitude of the fluid velocity in both cases.

Figure 2. Velocity profile when α₁ approaches infinity and t = 0.5 for case 1.

Figure 3. Velocity profile when α₂ approaches infinity and t = 0.5 for case 2.

Figure 4. Velocity profile when α₁ and α₂ approaches infinity and t = 0.5 for case 1.

Figure 5. Velocity profile when α₁ and α₂ approaches infinity and t = 0.5 for case 2.

Figure 6. Velocity profile when α₁ and α₂ approaches infinity and η =0.1 for case 1.

Figure 7. Velocity profile when α₁ and α₂ approaches infinity and η =0.1 for case 2.

Conclusion

This work focuses on the study of the unsteady motion of an incompressible couple stress fluid between two infinite parallel plates. The motion is generated by letting one of the two plates starts to move with a time dependent velocity while the other is set stationary in addition to the presence of pressure gradient. The results showed that when the two plates are kept stationary, the slip parameters have an opposing effect on the velocity of the fluid. However, the fluid velocity is amplified by the slip parameter in case of a moving plate with no pressure gradient. Similarly, the velocity field is affected by the presence of the couple stress coefficient considerably. Moreover, the velocity of the fluid is remarkably increased with the time parameter.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

S. S. Ilani http://orcid.org/0000-0002-4050-3652

E. A. Ashmawy http://orcid.org/0000-0002-1223-2760