Folding on manifolds and their fundamental group

ABSTRACT

In this paper, the induced sequence of folding and unfolding on the fundamental group will be obtained from a sequence of folding and unfolding on a manifold. The limit of folding and unfolding on the fundamental group is deduced. The sequences of the commutative diagram of fundamental groups will be achieved from the sequences of the commutative diagram of manifolds. The connection between a manifold and a fundamental group is assigned.

KEYWORDS:

• Folding
• unfolding
• fundamental group

SUBJECT CLASSIFICATION CODES:

• 51H20
• 57N10
• 57M05
• 14F35
• 20F34

1. Introduction and definitions

Classical results in algebraic topology give that groups are naturally realized as fundamental groups of spaces. For instance, free groups arise as fundamental groups of wedges of circles, any group can be realized as the fundamental group of some CW-complex, and pushouts of groups arise via the van Kampen theorem. This ability to construct geometric interpretations of discrete groups has important applications in both topology and algebra. The fundamental group was introduced by Poincare on a topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other. Intuitively, it records information about the basic shape, or holes, of the topological space [1]. Let $X$ be a topological space and $x_0\in X$, the set ${\pi }_1\left(X,x_0\right)=\left\{\text{homotopy classes of loops in }\left(X,x_0\right)\right\}$, together with the product operation $\left[f\right]\left[g\right]=\left[f.g\right]$ is called the fundamental group where ${\pi }_1$ is a functor map between categories [1]. The fundamental groups of some types of a manifold were studied in [2–7]. An n-dimensional manifold is a Hausdorff space $M$ such that each point in $M$ has a neighbourhood homeomorphic to $R^n$ [8]. A submanifold of a manifold $M$ is a subset $N$ which itself has the structure of a manifold [1,8]. Let $X$ be a topological space and let $A\subseteq X$ be a subspace. We say $A$ is a retract of $X$ if there exists a continuous map $r:X\to A$ such that $r\left(a\right)=a,\mathrm{\forall }a\in A$ [8,9]. Given spaces $X$ and $Y$ where $x_0\in X$ and $y_0\in Y$, and $X\cap Y=\mathrm{\varnothing }$, then we define the wedge sum $X\vee Y$ as the quotient of $X\cap Y$ by identification $x_0\sim y_0$ [1]. Let $M_1$ and $M_2$ be two smooth manifolds of dimension $m_1$ and $m_2$ respectively. A map $\mathcal{F}:M_1\to M_2$ is said to be an isometric folding of $M_1$ into $M_2$ if for every piecewise geodesic path $\mathrm{{\rm Y}}:I\to M_1$ the induced path $\mathcal{F}\circ \mathrm{{\rm Y}}:I\to M_2$ is piecewise geodesic and of the same length as $\mathrm{{\rm Y}}$ [10]. If $\mathcal{F}$ does not preserve length it is called topological folding [11]. A map $\phi :M_1\to M_2$ is said to be unfolding of $M_1$ into $M_2$ if, for every piecewise geodesic path $\mathrm{{\rm Y}}:I\to M_1$, the induced path $\phi \circ \mathrm{{\rm Y}}:I\to M_2$ is piecewise geodesic with a length greater than $\mathrm{{\rm Y}}$ [12]. For more information about the folding on manifolds and topological spaces, see [13–17].

2. The main result

Theorem 2.1:

Given a compact connected closed $n$-dimensional topological manifold $M$. Then, each folding $\mathcal{F}:M\to M$ induces $\overline{\mathcal{F}}:{\pi }_1\left(M\right)\to {\pi }_1\left(M\right)$ such that $\overline{\mathcal{F}}\left({\pi }_1\left(M\right)\right)={\pi }_1\left(\mathcal{F}\right(M)$.

Proof:

Let $M$ be compact connected closed $n$-dimensional topological manifold, then, $\begin{array}{rl}\overline{\mathcal{F}}\left({\pi }_1\left(M\right)\right)& =\overline{\mathcal{F}}\left\{\left[\alpha \right]:\text{where}\alpha \text{is}\text{a}\text{loop}\text{based }\text{at}{x}_0ϵM\right\}\\ & =\{\left[\mathcal{F}\left(\alpha \right)\right]:\text{where}\mathcal{F}\left(\alpha \right)\text{is}\text{a}\text{loop}\text{based}\text{at}\\ & \mathcal{F}\left(x_0\right)ϵ\mathcal{F}\left(M\right)\}={\pi }_1(\mathcal{F}\left(M)\right).\end{array}$  ▪

Theorem 2.2:

Let $M$ be a compact connected closed 1-dimension topological manifold. Then there are only two different foldings $\mathcal{F}:M\to M$, which induces $\overline{\mathcal{F}}:{\pi }_1\left(M\right)\to {\pi }_1\left(M\right)$such that rank $\overline{\mathcal{F}}\left({\pi }_1\left(M\right)\right)\le 1.$

Proof:

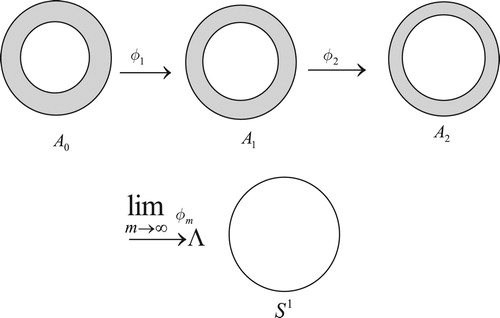
Let $M$ be a compact closed manifold of dimension 1, then $M$ is homeomorphic to $S^1$. Now consider the folding $\mathcal{F}:M\to M$, such that $\mathcal{F}\left(M\right)\approx S^1$ which induces $\overline{\mathcal{F}}:{\pi }_1\left(M\right)\to {\pi }_1\left(M\right)$ such that $\overline{\mathcal{F}}\left({\pi }_1\left(M\right)\right)={\pi }_1\left(\mathcal{F}\right(M))$ and so rank $\overline{\mathcal{F}}\left({\pi }_1\left(M\right)\right)=1$. Also, if $\mathcal{F}:M\to M$ is a folding such that $\mathcal{F}\left(M\right)\ne S^1$, then $\mathcal{F}\left(M\right)$ is a bounded one-dimensional submanifold of $M$ that is homeomorphic to $\left[a,b\right]$, thus we obtain the induced $\overline{\mathcal{F}}:{\pi }_1\left(M\right)\to {\pi }_1\left(M\right)$, for which $\overline{\mathcal{F}}\left({\pi }_1\left(M\right)\right)={\pi }_1\left(\mathcal{F}\right(M))$ and rank $\overline{\mathcal{F}}\left({\pi }_1\left(M\right)\right)=0$.

Theorem 2.3:

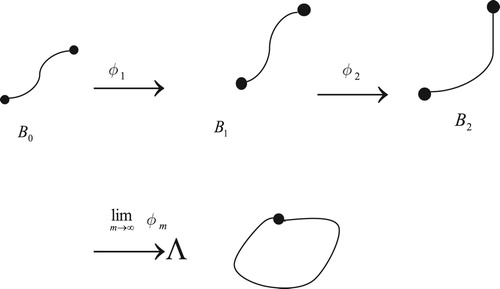
(i) Let $B_0$ be a bounded one-dimensional submanifold of $R^n$, that is homeomorphic to (0,1), then there is a sequence of unfolding $\{{\phi }_i:B_{i-1}\to B_i:i=1,2,\dots ,m\}$ with variation curvature which induces a sequence of unfoldings $\{{\overline{\phi }}_i:{\pi }_1(B_{i-1})\to {\pi }_1(B_i):i=1,2,\dots ,m\}$ such that $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(B_{m-1}\right)\left)\right)$ is an infinite cyclic group.

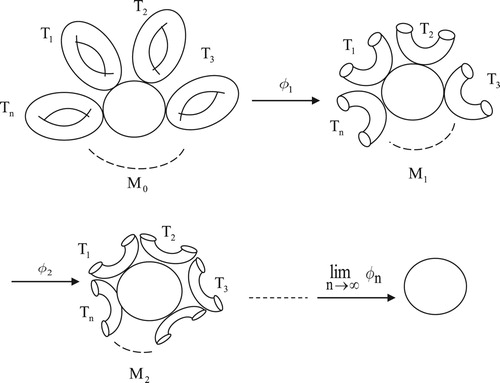
(ii) Let $M_0={\bigcup }_{j=1}^n(S^1\vee T_i)$, n-tori touch the circle then, there is a sequence of folding by a cut $\{{\mathcal{F}}_i:M_{i-1}\to M_i:i=1,2,\dots ,m\}$ which induces a sequence of foldings $\{{\overline{\mathcal{F}}}_i:{\pi }_1(M_{i-1})\to {\pi }_1(M_i):i=1,2,\dots ,m\}$ such that $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\mathcal{F}}}_m\right({\pi }_1\left(M_{m-1}\right)\left)\right)$ is an infinite cyclic group.

Proof:

(i) Let $B_0$ be a bounded one-dimensional submanifold of $R^n$ that is homeomorphic to $\left(0,1\right)$. Then, consider the following sequence of unfoldings with variation curvature: ${\phi }_1:B_0\to B_1,{\phi }_2:B_1\to B_2,\dots ,{\phi }_m:B_{m-1}\to B_m$ for which $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\phi }_m\right(B_{m-1}\left)\right)\approx S^1$ as in Figure 1, which induces ${\overline{\phi }}_1:{\pi }_1\left(B_0\right)\to {\pi }_1\left(B_1\right),{\overline{\phi }}_2:{\pi }_1\left(B_1\right)\to {\pi }_1\left(B_2\right),\dots ,{\overline{\phi }}_m:{\pi }_1\left(B_{m-1}\right)\to {\pi }_1\left(B_m\right)$, for which $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(B_{m-1}\right)\left)\right)={\pi }_1\left(\underset{m\to \mathrm{\infty }}{\text{lim}}{\phi }_m(B_{m-1}\right))={\pi }_1(S^1)$. Hence, $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(B_{m-1}\right))$) is an infinite cyclic group.

Figure 1. Limit folding on a bounded one-dimensional submanifold of $R^n$.

(ii) Let $\begin{array}{rl}& {\mathcal{F}}_1:M_0\to M_1,M_0\subseteq M_1,{\mathcal{F}}_2:M_1\to M_2,M_1\\ & \subseteq M_2,\dots ,{\mathcal{F}}_m:M_{m-1}\to M_m,M_{m-1}\subseteq M_m\end{array}$ for which $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\mathcal{F}}_m\right(B_{m-1}\left)\right)\approx S^1$ as in Figure 2, which induces $\begin{array}{rl}& {\overline{\mathcal{F}}}_1:{\pi }_1\left(M_0\right)\to {\pi }_1\left(M_1\right),{\overline{\mathcal{F}}}_2:{\pi }_1\left(M_1\right)\\ & \to {\pi }_1\left(M_2\right),\dots ,{\overline{\mathcal{F}}}_m:{\pi }_1\left(M_{m-1}\right)\to {\pi }_1\left(M_m\right)\end{array}$ for which $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\mathcal{F}}}_m\right({\pi }_1\left(M_{m-1}\right)\left)\right)={\pi }_1\left(\underset{m\to \mathrm{\infty }}{\text{lim}}{\mathcal{F}}_m(M_{m-1}\right))={\pi }_1(S^1)$ Hence, $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\mathcal{F}}}_m\right({\pi }_1\left(M_{m-1}\right)\left)\right)$ is an infinite cyclic group.

Figure 2. Limit folding on n-tori touch the circle.

Theorem 2.4:

Let $M_0=T^1\vee I$. Then there is a sequence of unfolding for which $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(M_m\right)\left)\right)=Z\ast F^2$, where F₂ is a free abelian group of rank 2.

Proof:

Consider the following sequence of unfolding: ${\phi }_1:M_0\to M_1,{\phi }_2:M_1\to M_2,\dots ,{\phi }_m:M_{m-1}\to M_m$ for which $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\phi }_m\right(M_{m-1}\left)\right)=T^1\vee S^1$ as in Figure 3, thus $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(M_m\right)\left)\right)={\pi }_1\left(\underset{m\to \mathrm{\infty }}{\text{lim}}{\phi }_m(M_m\right))=Z\ast F_2$ where F₂ is a free abelian group of rank 2.

Figure 3. Limit unfolding of $T^1\vee I$.

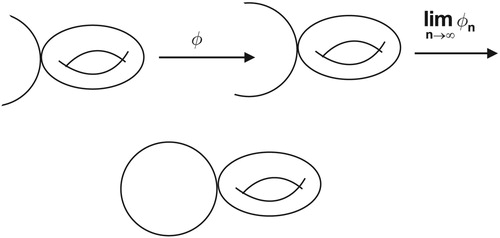
Theorem 2.5:

Let $A_0=\left\{\left(r,\theta \right),1\le r\le 2\right\}$, then there is a sequence of unfoldings $\{{\mathcal{F}}_i:A_{i-1}\to A_i:i=1,2,\dots ,m\}$ which induces a sequence of unfoldings $\{{\overline{\mathcal{F}}}_i:{\pi }_1(A_{i-1})\to {\pi }_1(A_i):i=1,2,\dots ,m\}$ such that $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\mathcal{F}}}_m\right({\pi }_1\left(A_{m-1}\right)\left)\right)$ is an infinite cyclic group.

Proof:

Let $A=\left\{\left(r,\theta \right),1\le r\le 2\right\},S^1=\left\{\left(r,\theta \right),r=1\right\}$. Also consider the following sequence of unfoldings: ${\phi }_1:A_0\to A_1,{\phi }_2:A_1\to A_2,\dots ,{\phi }_m:A_{m-1}\to A_m,$ for which $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\phi }_m\right(A_{m-1}\left)\right)\approx S^1$ as in Figure 4, which induces ${\overline{\phi }}_1:{\pi }_1\left(A_0\right)\to {\pi }_1\left(A_1\right),{\overline{\phi }}_2:{\pi }_1\left(A_1\right)\to {\pi }_1\left(A_2\right),\dots ,{\overline{\phi }}_m:{\pi }_1\left(A_{m-1}\right)\to {\pi }_1\left(A_m\right)$ such that $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(A_{m-1}\right)\left)\right)={\pi }_1\left(\underset{m\to \mathrm{\infty }}{\text{lim}}{\phi }_m(A_{m-1}\right))={\pi }_1(S^1)$. Hence, $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(A_{m-1}\right)\left)\right)$ is an infinite cyclic group.

Figure 4. Limit unfolding of $A_0$.

Theorem 2.6:

Let $X_0$ denote the field of real numbers. Then there is a sequence of unfoldings ${\phi }_i:X_{i-1}\to X_i$ with variation curvature which induce foldings ${\overline{\phi }}_i:{\pi }_1\left(X_{i-1}\right)\to {\pi }_1\left(X_i\right):i=1,2,\dots ,m$, such that $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(X_{m-1}\right)\left)\right)$ is a free group on a countable set of generators.

Proof:

Consider the following sequence of unfoldings with variation curvature: ${\phi }_1:X_0\to X_1,{\phi }_2:X_1\to X_2,\dots ,{\phi }_m:X_{m-1}\to X_m$ such that $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\phi }_m\right(X_{m-1}\left)\right)={\vee }_{\mathrm{\infty }}^1{C}_i^1$ as in Figure 5, which induce a folding ${\overline{\phi }}_i:{\pi }_1\left(X_{i-1}\right)\to {\pi }_1\left(X_i\right):i=1,2,\dots ,m$, thus $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(X_{m-1}\right)\left)\right)={\pi }_1\left(\underset{m\to \mathrm{\infty }}{\text{lim}}{\phi }_m(X_{m-1}\right))={}_{i=1}^{\mathrm{\infty }}\ast Z.$ Therefore, $\underset{m\to \mathrm{\infty }}{\text{lim}}\left({\overline{\phi }}_m\right({\pi }_1\left(X_{m-1}\right)\left)\right)$ is a free group on a countable set of generators.

Figure 5. Limit unfolding of $R$.

Theorem 2.7:

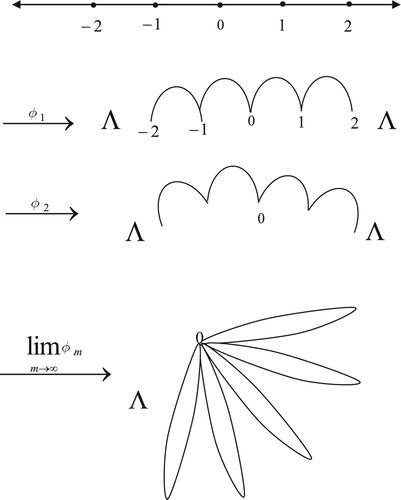
Let $M=\left(R{\cup }^{S^1}\times Z\right)/\backsim$ where given $i\in R$ with $\left(\left(0,-1\right),i\right)\in S^1\times Z$ and $M_k=\left(\left[k,k\right]{\cup }^{S^1}\times \left\{-k,\right.\right.\left.\phantom{{\cup }^{S^1}}\left.\dots ,k\right\}\right)/\backsim$, $kϵN$, that is $M_k$ the interval $\left[-k,k\right]$ with $2k+1$ circles attached. Then $\mathrm{\forall }kϵN$, the folding ${\mathcal{F}}_k:M\to M$ induces ${\overline{\mathcal{F}}}_k:{\pi }_1\left(M\right)\to {\pi }_1\left(M\right)$ for which rank ${\overline{\mathcal{F}}}_k\left({\pi }_1\left(M\right)\right)=k$.

Proof:

Let ${\mathcal{F}}_k:M\to M$ be a folding map such that ${\mathcal{F}}_k\left(M\right)=M_k$,, $\mathrm{\forall }kϵN$ where $M_k=\left(\left[k,k\right]{\cup }^{S^1}\times \left\{-k,\right.\right.\left.\phantom{{\cup }^{S^1}}\left.\dots ,k\right\}\right)/\backsim$ as in Figure 6, which induces ${\overline{\mathcal{F}}}_k:{\pi }_1\left(M\right)\to {\pi }_1\left(M\right)$ for which rank ${\overline{\mathcal{F}}}_k\left({\pi }_1\left(M\right)\right)=k$.

Figure 6. Folding on $M$.

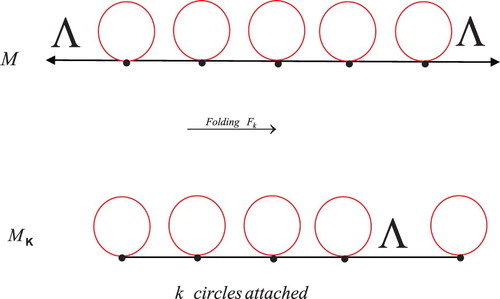
Theorem 2.8:

Suppose that $M$ is a manifold of dimension one, $N$ is a submanifold of $M$ and let ${\mathcal{F}}_i$, ${\phi }_i$ and $r_i,i=1,2,\dots ,n$ are sequences of folding, unfolding and retraction map respectively. Then there is a sequence of the commutative diagram of manifolds which induces a sequence of the commutative diagram of the fundamental groups.

Proof:

Consider the following sequences of the commutative diagram: $\begin{array}{rl}& M\stackrel{{\mathcal{F}}_1}{\to }{M}_1\stackrel{{\mathcal{F}}_2}{\to }{M}_2---\stackrel{\underset{m\to \mathrm{\infty }}{\text{lim}}{\mathcal{F}}_m}{\to }\text{point }\left(0\text{- dimensional manifold}\right)\\ & \downarrow r_1\downarrow r_2\downarrow r_3\downarrow \underset{m\to \mathrm{\infty }}{\text{lim}}{r}_m\\ & N\stackrel{{\phi }_1}{\to }{N}_1\stackrel{{\phi }_2}{\to }{N}_2---\stackrel{\underset{m\to \mathrm{\infty }}{\text{lim}}{\phi }_m}{\to }\text{point }\left(0\text{- dimensional manifold}\right)\end{array}$  ▪

Since ${\pi }_1$is a functor between manifolds and fundamental groups, we get the following sequence of the commutative diagram of fundamental groups: $\begin{array}{rl}& {\pi }_1\left(M\right)\stackrel{{\overline{\mathcal{F}}}_1}{\to }{\pi }_1\left(M_1\right)\stackrel{{\overline{\mathcal{F}}}_2}{\to }{\pi }_1\left(M_2\right)---\stackrel{\underset{m\to \mathrm{\infty }}{\text{lim}}{\overline{\mathcal{F}}}_m}{\to }{\pi }_1\left(\text{point}\right)\\ & \downarrow {\overline{r}}_1\downarrow {\overline{r}}_2\downarrow {\overline{r}}_3\downarrow \underset{m\to \mathrm{\infty }}{\text{lim}}{\overline{r}}_m\\ & {\pi }_1\left(N\right)\stackrel{{\overline{\phi }}_1}{\to }{\pi }_1\left(N_1\right)\stackrel{{\overline{\phi }}_2}{\to }{\pi }_1\left(N_2\right)---\stackrel{\underset{m\to \mathrm{\infty }}{\text{lim}}{\overline{\phi }}_m}{\to }{\pi }_1\left(\text{point}\right).\end{array}$

3. Conclusion

In the present paper, we achieved the limit of folding and unfolding on the fundamental group. The relation between limits of foldings and retractions on the induced fundamental groups from viewpoint of a commutative diagram is obtained. New types of folding on the fundamental groups are deduced.

Acknowledgements

The author expresses his sincere thanks to the reviewers for valuable comments and suggestions, which helped to improve the quality of the paper.

Disclosure statement

No potential conflict of interest was reported by the author.

ORCID

M. Abu-Saleem http://orcid.org/0000-0002-6399-2452