The (G′/G)-expansion method for solving a nonlinear PDE describing the nonlinear low-pass electrical lines

ABSTRACT

In this paper, we apply the (G′/G)-expansion method based on three auxiliary equations, namely, the generalized Riccati equation $G^{\mathrm{\prime }}\left(\xi \right)=r+pG\left(\xi \right)+q{G}^2\left(\xi \right)$, the Jacobi elliptic equation $(G^{\mathrm{\prime }}\left(\xi \right){)}^2=R+Q{G}^2\left(\xi \right)+P{G}^4\left(\xi \right)$ and the second order linear ordinary differential equation (ODE) $G^{\mathrm{\prime \prime }}\left(\xi \right)+\lambda G^{\mathrm{\prime }}\left(\xi \right)+\mu G\left(\xi \right)=0$ to find many new exact solutions of a nonlinear partial differential equation (PDE) describing the nonlinear low-pass electrical lines. The given nonlinear PDE has been derived and can be reduced to a nonlinear ODE using a simple transformation. Soliton wave solutions, periodic function solutions, rational function solutions and Jacobi elliptic function solutions are obtained. Comparing our new solutions obtained in this paper with the well-known solutions is given. Furthermore, plotting 2D and 3D graphics of the exact solutions is shown.

• The (G′/G)-expansion method
• exact solutions
• soliton wave solutions
• periodic solution
• the generalized Riccati equation
• Jacobi elliptic function solutions

1. Introduction

In the recent years, investigations of exact solutions to nonlinear PDEs play an important role in the study of nonlinear physical phenomena in such as fluid mechanics, hydrodynamics, optics, plasma physics, solid state physics, biology and so on. Several methods for finding the exact solutions to nonlinear equations in mathematical physics have been presented, such as the inverse scattering method [1], the Hirota bilinear transform method [2], the truncated Painlevé expansion method [3,4], the Bäcklund transform method [5,6], the exp-function method [7–9], the tanh-function method [10–12], the Jacobi elliptic function expansion method [13–15], the (G′/G)-expansion method [16–20], the (G′/G,1/G)-expansion method [21–23], the generalized projective Riccati equations method [24–26] and so on.

The objective of this paper is to use the (G′/G)-expansion method with the aid of Computer algebraic system Maple to construct many exact solutions of the following nonlinear PDE governing wave propagation in nonlinear low-pass electrical transmission lines [15,27]: (1.1) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{2}V(x,t)}{\mathrm{\partial }{t}^2}-\alpha \frac{{\mathrm{\partial }}^2{V}^2(x,t)}{\mathrm{\partial }{t}^2}+\beta \frac{{\mathrm{\partial }}^2{V}^3(x,t)}{\mathrm{\partial }{t}^2}\\ & -{\delta }^2\frac{{\mathrm{\partial }}^{2}V(x,t)}{\mathrm{\partial }{x}^2}-\frac{{\delta }^4}{12}\frac{{\mathrm{\partial }}^{4}V(x,t)}{\mathrm{\partial }{x}^4}=0,\end{array}$(1.1) where $\alpha$, $\beta$ and $\delta$ are positive real constants, while $V(x,t)$ is the voltage in the transmission lines. The variable $x$ is interpreted as the propagation distance and $t$ is the slow time. The physical details of the derivation of Equation (1.1) using the Kirchhoff's laws given in [27]. Equation (1.1) has been discussed in [15,27] using a new Jacobi elliptic function expansion method and an auxiliary equation method respectively, and its exact solutions have been found.

This paper is organized as follows: In Section 2, the description of the (G'/G)-expansion method is given. In Section 3, we use the given method described in Section 2, to find exact solutions of Equation (1.1). In Section 4, physical explanations of some results are presented. In Section 5, some conclusions are obtained.

2. Description of the (G'/G)-expansion method

Consider a nonlinear PDE in the form: $P(V,V_x,V_t,V_{xx},V_{tt},\dots )=0,$ where $V=V(x,t)$ is a unknown function, $P$ is a polynomial in $V$ and its partial derivatives in which the highest-order derivatives and nonlinear terms are involved. Let us now give the main steps of the (G'/G)-expansion method [16–20]:

Step 1. We look for the voltage $V$ in the travelling form: $V(x,t)=V\left(\xi \right),\xi =\sqrt{k}(x-\omega t),$ where $k$ is a positive parameter, and $\omega$ is the velocity of propagation. To reduce Equation (2.1) to the following nonlinear ODE: $H(V,V^{\mathrm{\prime }},V^{\mathrm{\prime \prime }},\dots )=0,$ where $H$ is a polynomial of $V\left(\xi \right)$ and its total derivatives $V^{\mathrm{\prime }}\left(\xi \right),V^{\mathrm{\prime \prime }}\left(\xi \right),\dots$ and ${}^{\mathrm{\prime }}=\frac{\text{d}}{\text{d}\xi }$.

Step 2. We assume that the solution of Equation (2.3) has the form: $V\left(\xi \right)=\sum _{i=0}^N{a_i\left(\frac{G^{\mathrm{\prime }}}{G}\right)}^i$ where $a_i$ $(i=1,2,\dots ,N)$ are constants to be determined later, provided $a_N\ne 0$ and $G=G\left(\xi \right)$ satisfies the following three auxiliary equations:

• (1) The generalized Riccati equation $G^{\mathrm{\prime }}\left(\xi \right)=r+pG\left(\xi \right)+q{G}^2\left(\xi \right),$

• (2) The Jacobi elliptic equation $(G^{\mathrm{\prime }}\left(\xi \right){)}^2=R+Q{G}^2\left(\xi \right)+P{G}^4\left(\xi \right),$

• (3) The second order linear ODE $G^{\mathrm{\prime \prime }}\left(\xi \right)+\lambda G^{\mathrm{\prime }}\left(\xi \right)+\mu G\left(\xi \right)=0,$

where $r,p,q,R,Q,P,\lambda$ and $\mu$ are real constants to be determined later.

Step 3. We determine the positive integer $N$ in (2.4) by balancing the highest-order derivatives and the highest nonlinear terms in Equation (2.3).

Step 4. Substituting (2.4) along with Equations (2.5)–(2.7) into Equation (2.3) and collecting all the coefficients of $G^i\left(\xi \right),(i=0,\pm 1,\pm 2,\dots )$ for Equation (2.5), ${\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)}^i,(i=0,1,2,\dots )$ for Equations (2.6) and (2.7), then setting these coefficients to zero, yield a set of algebraic equations, which can be solved by using the Maple or Mathematica to find the values of $a_i$ $(i=0,1,2,\dots ,N)$, $r,p,q,R,Q,P,\lambda$ and $\mu$.

Step 5. It is well-known that Equations (2.5)–(2.7) have many families of solutions obtained in [16–20].

Step 6. Substituting the values of $a_i$, $r,p,q,R,Q,P,\lambda$ and $\mu$ as well as the solutions of Step 5, into (2.4) we have the exact solutions of Equation (2.1).

3. On solving Equation (1.1) using the proposed method of Section 2

In this section, we apply the $\left(\frac{G^{\mathrm{\prime }}}{G}\right)$ -expansion method of Section 2 to find new exact solutions of Equation (1.1). To this aim, we use the transformation (2.2) to reduce Equation (1.1) to the following nonlinear ODE: $\begin{array}{rl}& \frac{{\text{d}}^2}{\text{d}{\xi }^2}\left\{\frac{k^2{\delta }^4}{12}\frac{{\text{d}}^{2}V}{\text{d}{\xi }^2}+\left(k{\delta }^2-k{\omega }^2\right)V+\alpha k{\omega }^2{V}^2-\beta k{\omega }^2{V}^3\right\}\\ & =0.\end{array}$ Integrating Equation (3.1) with respect to $\xi$ twice, and vanishing the constants of integration, we find the following ODE: $\frac{K^2}{12}\frac{{\text{d}}^{2}V}{\text{d}{\xi }^2}+\left(K-U\right)V+\alpha U{V}^2-\beta U{V}^3=0.$ where $K=k{\delta }^2$ and $U=k{\omega }^2$.

Balancing $\frac{{\text{d}}^{2}V}{\text{d}{\xi }^2}$ with $V^3$ gives $N=1$. Therefore, (2.4) reduces to $V\left(\xi \right)=a_0+a_1\left(\frac{G^{\mathrm{\prime }}}{G}\right),$ where $a_0$ and $a_1$ are constants to be determined such that $a_1\ne 0$.

3.1. Exact solutions of eq. (1.1) depending on the Riccati equation

In this subsection, substituting (3.3) along with the generalized Riccati equation (2.5) into Equation (3.2) and collecting all the coefficients of $G^i\left(\xi \right),(i=0,\pm 1,\pm 2,\pm 3,\pm 4)$ and setting them to zero, we get a system of algebraic equations for $a_i$ $(i=0,1)$, $r,p,q,U$ and $K$. Using the Maple or Mathematica, we get the following results:

Result 1. $\begin{array}{rl}& K=\frac{-24{\alpha }^2}{p^2\left(2{\alpha }^2-9\beta \right)},U=\frac{216{\alpha }^2\beta }{p^2{\left(2{\alpha }^2-9\beta \right)}^2},\\ & a_0=0,a_1=\frac{2\alpha }{3p\beta },r=0.\end{array}$

Substituting (3.1.1) into (3.3) yields $V\left(\xi \right)=\frac{2\alpha }{3p\beta }\left(\frac{G^{\mathrm{\prime }}}{G}\right),$ where $\xi =\sqrt{\frac{-24{\alpha }^2}{p^2{\delta }^2\left(2{\alpha }^2-9\beta \right)}}x-\sqrt{\frac{216{\alpha }^2\beta }{p^2{\left(2{\alpha }^2-9\beta \right)}^2}}t$, $2{\alpha }^2<9\beta$, $\beta >0$ and $p\ne 0.$

With reference to solving Equation (2.7) [19], we deduce that the exact solutions of Equation (1.1) as follows: $V_1\left(\xi \right)=\frac{2\alpha }{3\beta }\left(\frac{\cosh \left(p\xi \right)-\sinh \left(p\xi \right)}{d+\cosh \left(p\xi \right)-\sinh \left(p\xi \right)}\right),$ $V_2\left(\xi \right)=\frac{2\alpha }{3\beta }\left(\frac{d}{d+\cosh \left(p\xi \right)+\sinh \left(p\xi \right)}\right),$ Result 2. $\begin{array}{rl}& K=\frac{-24{\alpha }^2}{2{\alpha }^2\left(p^2-4qr\right)-9\beta p^2},\\ & U=\frac{216{\alpha }^2\beta }{{\left(2{\alpha }^2\left(p^2-4qr\right)-9\beta p^2\right)}^2},a_0=0,a_1=\frac{2\alpha }{3p\beta }.\end{array}$ Substituting (3.1.5) into (3.3) yields $V\left(\xi \right)=\frac{2\alpha }{3p\beta }\left(\frac{G^{\mathrm{\prime }}}{G}\right),$ where $\xi =\sqrt{\frac{-24{\alpha }^2}{2{\alpha }^2{\delta }^2\left(p^2-4qr\right)-9\beta p^2}}x-\sqrt{\frac{216{\alpha }^2\beta }{{\left(2{\alpha }^2\left(p^2-4qr\right)-9\beta p^2\right)}^2}}t,2{\alpha }^2{\delta }^2\left(p^2-4qr\right)<9\beta p^2$ and $\beta >0$.

In this result, we deduce that the exact solutions of Equation (1.1) as follows: $V_3\left(\xi \right)=\frac{\alpha }{3\beta p}\left(\frac{\left(p^2-4qr\right){\mathrm{sech}}^2\left(\frac{\sqrt{p^2-4qr}}{2}\xi \right)}{p+\sqrt{p^2-4qr}\tanh \left(\frac{\sqrt{p^2-4qr}}{2}\xi \right)}\right),$ $V_4\left(\xi \right)=-\frac{\alpha }{3\beta p}\left(\frac{\left(p^2-4qr\right){\mathrm{csch}}^2\left(\frac{\sqrt{p^2-4qr}}{2}\xi \right)}{p+\sqrt{p^2-4qr}\coth \left(\frac{\sqrt{p^2-4qr}}{2}\xi \right)}\right),$ $\begin{array}{rl}& V_5\left(\xi \right)=-\frac{2\alpha \left(p^2-4qr\right)}{3\beta p}\\ & \times \left(\frac{\begin{array}{c}{\mathrm{csch}}^2\left(\sqrt{p^2-4qr}\xi \right)+\mathrm{csch}\left(\sqrt{p^2-4qr}\xi \right)\\ \coth \left(\sqrt{p^2-4qr}\xi \right)\end{array}}{\begin{array}{c}p+\sqrt{p^2-4qr}\\ \left(\coth \left(\sqrt{p^2-4qr}\xi \right)+\mathrm{csch}\left(\sqrt{p^2-4qr}\xi \right)\right)\end{array}}\right),\end{array}$ $\begin{array}{rl}& V_6\left(\xi \right)=-\frac{\alpha \left(p^2-4qr\right)}{3p\beta \cosh \left(\frac{1}{2}\sqrt{-p^2+4qr}\zeta \right)}\\ & \times \left(\frac{1}{\begin{array}{c}\left(\sqrt{p^2-4qr}\sinh \left(\frac{1}{2}\sqrt{p^2-4qr}\zeta \right)\right.\\ \left.-p\cosh \left(\frac{1}{2}\sqrt{p^2-4qr}\zeta \right)\right)\end{array}}\right),\end{array}$ $\begin{array}{rl}& V_7\left(\xi \right)=\frac{\alpha \left(p^2-4qr\right)}{3p\beta sinh\left(\frac{1}{2}\sqrt{-p^2+4qr}\zeta \right)}\\ & \times \left(\frac{1}{\begin{array}{c}\sqrt{p^2-4qr}cosh\left(\frac{1}{2}\sqrt{p^2-4qr}\zeta \right)\\ -p\sinh \left(\frac{1}{2}\sqrt{p^2-4qr}\zeta \right)\end{array}}\right),\end{array}$ where $p^2-4qr>0$. $\begin{array}{rl}& V_8\left(\xi \right)\\ & =\frac{1}{3}\frac{\alpha \left(p^2-4qr\right)\left(1+{\tan }^2\left(\frac{1}{2}\sqrt{-p^2+4qr}\zeta \right)\right)}{p\beta \left(-\sqrt{-p^2+4qr}\tan \left(\frac{1}{2}\sqrt{-p^2+4qr}\zeta \right)-p\right)},\end{array}$ $\begin{array}{rl}& V_9\left(\xi \right)\\ & =\frac{1}{3}\frac{\alpha \left(p^2-4qr\right)\left({\cot }^2\left(\frac{1}{2}\sqrt{-p^2+4qr}\zeta \right)+1\right)}{p\beta \left(p+\sqrt{-p^2+4qr}\cot \left(\frac{1}{2}\sqrt{-p^2+4qr}\zeta \right)\right)},\end{array}$ $\begin{array}{rl}& V_{10}\left(\xi \right)=\frac{\alpha \left(p^2-4qr\right)}{3p\beta \cos \left(\frac{1}{2}\sqrt{-p^2+4qr}\zeta \right)}\\ & \times \left(\frac{1}{\begin{array}{c}\sqrt{-p^2+4qr}\sin \left(\frac{1}{2}\sqrt{-p^2+4qr}\zeta \right)\\ +p\cos \left(\frac{1}{2}\sqrt{-p^2+4qr}\zeta \right)\end{array}}\right),\end{array}$ where $p^2-4qr>0$. $V_{11}\left(\xi \right)=\frac{2}{3}\frac{\alpha \left(-\sinh \left(p\zeta \right)+\cosh \left(p\zeta \right)\right)}{\beta \left(d+\cosh \left(p\zeta \right)-\sinh \left(p\zeta \right)\right)},$ $V_{12}\left(\xi \right)=\frac{2}{3}\frac{\alpha d}{\left(\sinh \left(p\zeta \right)+\cosh \left(p\zeta \right)\right)}.$ Also, there are many other exact solutions of Equation (1.1), which are omitted here for simplicity.

3.2. Exact solutions of Equation (1.1) depending on the Jacobi elliptic equation

In this subsection, substituting (3.3) along with the Jacobi elliptic equation (2.6) into Equation (3.2) and collecting all the coefficients of ${\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)}^i,(i=0,1,2,\dots )$ and setting them to be zero, we have the following algebraic equations: ${\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)}^3:\frac{1}{6}{K}^2{a}_1-\beta U{a}_1^3=0,$ ${\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)}^2:-3\beta U{a}_0{a}_1^2+\alpha U{a}_1^2=0,$ $\begin{array}{rl}& \left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right):\frac{-1}{6}{K}^2{a}_{1}Q+(K-U)a_1+2\alpha U{a}_0{a}_1\\ & -3\beta U{a}_0^2{a}_1=0,\end{array}$ ${\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)}^0:(K-U)a_0+\alpha U{a}_0^2-\beta U{a}_0^3=0.$ On solving the above algebraic equations (3.2.1) using the Maple or Mathematica, we have the following result: $\begin{array}{rl}& K=-\frac{6{\alpha }^2}{Q(2{\alpha }^2-9\beta )},U=\frac{54{\alpha }^2\beta }{Q{(2{\alpha }^2-9\beta )}^2},\\ & a_0=-\frac{\alpha }{3\beta },a_1=\pm \frac{\alpha }{3\beta \sqrt{Q}},P=P,R=R,\end{array}$ where $Q>0.$

Substituting (3.2.2) into (3.3) yields $V\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{1}{\sqrt{Q}}\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{Q(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{Q{(2{\alpha }^2-9\beta )}^2}}t,2{\alpha }^2<9\beta ,\beta >0.$

With reference to solving Equation (2.6) [20], we deduce that the Jacobi elliptic functions solutions and other exact solutions of Equation (1.1) as follows:

Case 1. Choosing $P=-m^2,Q=2m^2-1,R=1-m^2,$ and $G\left(\xi \right)=\mathrm{cn}\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{13}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{\mathrm{sc}\left(\xi \right)dn\left(\xi \right)}{\sqrt{2m^2-1}}\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{(2m^2-1)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{(2m^2-1){(2{\alpha }^2-9\beta )}^2}}t.$

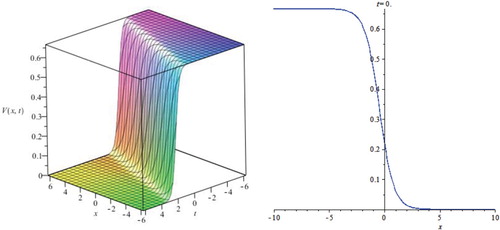
If $m\to 1$, then Equation (1.1) has the kink soliton wave solutions $V_{14}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \tanh \left(\xi \right)\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{{(2{\alpha }^2-9\beta )}^2}}t.$

Case 2. Choosing $P=-1,Q=2-m^2,R=m^2-1,$ and $G\left(\xi \right)=\mathrm{dn}\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{15}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{m^{2}cd\left(\xi \right)sn\left(\xi \right)}{\sqrt{2-m^2}}\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{(2-m^2)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{(2-m^2){(2{\alpha }^2-9\beta )}^2}}t$.

If $m\to 1$, then we have the same exact solutions (Equation (3.2.5)).

Case 3. Choosing $P=1-m^2,Q=2-m^2,R=1,$ and $G\left(\xi \right)=\mathrm{sc}\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{16}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{ds\left(\xi \right)}{\mathrm{cn}\left(\xi \right)\sqrt{2-m^2}}\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{(2-m^2)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{(2-m^2){(2{\alpha }^2-9\beta )}^2}}t.$

If $m\to 0$, then Equation (1.1) has the trigonometric solutions $V_{17}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{sec\left(\xi \right)csc\left(\xi \right)}{\sqrt{2}}\right],$ where $\xi =\sqrt{-\frac{3{\alpha }^2}{(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{27{\alpha }^2\beta }{{(2{\alpha }^2-9\beta )}^2}}t.$

If $m\to 1$, then Equation (1.1) has the anti-kink soliton wave solutions $V_{18}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \coth \left(\xi \right)\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{{(2{\alpha }^2-9\beta )}^2}}t.$

Case 4. Choosing $P=\frac{1}{4},Q=\frac{1-2m^2}{2},R=\frac{1}{4},$ and $G\left(\xi \right)=ns\left(\xi \right)\pm cs\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{19}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{\sqrt{2}ds\left(\xi \right)}{\sqrt{1-2m^2}}\right],$ where $\xi =\sqrt{-\frac{12{\alpha }^2}{(1-2m^2)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{108{\alpha }^2\beta }{(1-2m^2){(2{\alpha }^2-9\beta )}^2}}t$.

If $m\to 0$, then Equation (1.1) has the trigonometric solutions $V_{20}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \sqrt{2}\csc \left(\xi \right)\right],$ where $\xi =\sqrt{-\frac{12{\alpha }^2}{(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{108{\alpha }^2\beta }{{(2{\alpha }^2-9\beta )}^2}}t.$

Case 5. Choosing $P=-1,Q=2-m^2,R=m^2-1,$ and $G\left(\xi \right)=\mathrm{nd}\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{21}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{m^{2}cn\left(\xi \right)sd\left(\xi \right)}{\sqrt{2-m^2}}\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{(2-m^2)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{(2-m^2){(2{\alpha }^2-9\beta )}^2}}t.$

If $m\to 1$, then we have the same exact solutions (Equation (3.2.5)).

Case 6. Choosing $P=1-m^2,Q=2-m^2,R=1,$ and $G\left(\xi \right)=\mathrm{cs}\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{22}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{nc\left(\xi \right)ds\left(\xi \right)}{\sqrt{2-m^2}}\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{(2-m^2)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{(2-m^2){(2{\alpha }^2-9\beta )}^2}}t.$

If $m\to 0$, then we have the same exact solutions (Equation (3.2.8)).

If $m\to 1$, then we have the same exact solutions (Equation (3.2.9)).

Case 7. Choosing $P=m^2(m^2-1),Q=2m^2-1,R=1,$ and $G\left(\xi \right)=\mathrm{ds}\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{23}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{cd\left(\xi \right)ns\left(\xi \right)}{\sqrt{2m^2-1}}\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{(2m^2-1)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{(2m^2-1){(2{\alpha }^2-9\beta )}^2}}t.$

If $m\to 1$, then we have the same exact solutions (Equation (3.2.9)).

Case 8. Choosing $P=(m^2-1),Q=2-m^2,R=-1,$ and $G\left(\xi \right)=nd\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{24}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{m^{2}cd\left(\xi \right)sd\left(\xi \right)dn\left(\xi \right)}{\sqrt{2-m^2}}\right],$ where $\xi =\sqrt{-\frac{6{\alpha }^2}{(2-m^2)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{54{\alpha }^2\beta }{(2-m^2){(2{\alpha }^2-9\beta )}^2}}t.$

If $m\to 1$, then we have the same exact solutions (Equation (3.2.5)).

Case 9. Choosing $P=\frac{m^2-1}{4},Q=\frac{m^2+1}{2},R=\frac{m^2-1}{4},$ and $G\left(\xi \right)=msd\left(\xi \right)\pm nd\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{25}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{m\sqrt{2}cd\left(\xi \right)}{\sqrt{1+m^2}}\right],$ where $\xi =\sqrt{-\frac{12{\alpha }^2}{(m^2+1)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{108{\alpha }^2\beta }{(m^2+1){(2{\alpha }^2-9\beta )}^2}}t.$

If $m\to 1$, then we have the trivial solution.

Case 10. Choosing $P=\frac{1}{4},Q=\frac{1-2m^2}{2},R=\frac{1}{4},$ and $G\left(\xi \right)=ns\left(\xi \right)\pm cs\left(\xi \right)$, we obtain the Jacobi elliptic function solutions $V_{26}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{\sqrt{2}ds\left(\xi \right)}{\sqrt{1-2m^2}}\right],$ where $\xi =\sqrt{-\frac{12{\alpha }^2}{(1-2m^2)(2{\alpha }^2-9\beta ){\delta }^2}}x-\sqrt{\frac{108{\alpha }^2\beta }{(1-2m^2){(2{\alpha }^2-9\beta )}^2}}t.$

If $m\to 0$, then we have the same exact solutions (Equation (3.2.11)).

3.3. Exact solutions of Equation (1.1) depending on the second order linear ODE

Here, substituting (3.3) along with the second order linear ODE (2.7) into Equation (3.2) and collecting all the coefficients of ${\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)}^i,(i=0,1,2,3)$ and setting them to be zero, we have the following algebraic equations: ${\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)}^3:\frac{1}{6}{K}^2{a}_1-U\beta a_1^3=0,$ ${\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)}^2:\frac{1}{4}{K}^2\lambda a_1+U\alpha a_1^2-3U\beta a_0{a}_1^2=0,$ $\begin{array}{rl}& \left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right):\frac{1}{12}{K}^2{a}_1({\lambda }^2+2\mu )+(K-U)a_1\\ & +2U\alpha a_0{a}_1-3U\beta a_0^2{a}_1=0,\end{array}$ $\begin{array}{rl}& {\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right)}^0:\frac{1}{12}{K}^2\lambda \mu a_1+(K-U)a_0\\ & +U\alpha a_0^2-U\beta a_0^3=0.\end{array}$

On solving the above algebraic equations (3.3.1) using the Maple or Mathematica, we have the following result: $\begin{array}{rl}& K=-\frac{24{\alpha }^2}{({\lambda }^2-4\mu )(2{\alpha }^2-9\beta )},\\ & U=\frac{216{\alpha }^2\beta }{({\lambda }^2-4\mu ){(2{\alpha }^2-9\beta )}^2},\\ & a_0=\frac{\alpha }{3\beta }\left(1\pm \frac{\lambda }{\sqrt{{\lambda }^2-4\mu }}\right),\\ & a_1=\pm \frac{2\alpha }{3\beta \sqrt{{\lambda }^2-4\mu }}.\end{array}$

Substituting (3.3.2) into (3.3) yields $\begin{array}{rl}V\left(\xi \right)& =\frac{\alpha }{3\beta }\left(1\pm \frac{\lambda }{\sqrt{{\lambda }^2-4\mu }}\right)\\ & \pm \frac{2\alpha }{3\beta \sqrt{{\lambda }^2-4\mu }}\left(\frac{G^{\mathrm{\prime }}\left(\xi \right)}{G\left(\xi \right)}\right),\end{array}$ $\begin{array}{rl}& \xi =\sqrt{-\frac{24{\alpha }^2}{{\delta }^2({\lambda }^2-4\mu )(2{\alpha }^2-9\beta )}}x\\ & -\sqrt{\frac{216{\alpha }^2\beta }{({\lambda }^2-4\mu ){(2{\alpha }^2-9\beta )}^2}}t,2{\alpha }^2<9\beta ,\beta >0,\\ & \text{and }{\lambda }^2-4\mu \ne 0.\end{array}$

With reference to solving Equation (2.7) [16–18], we deduce that the hyperbolic functions solutions and the trigonometric functions solutions as follows:

Case 1. If ${\lambda }^2-4\mu >0$, then we have the hyperbolic functions solutions $V_{27}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \frac{\begin{array}{c}{A}_1\sinh \left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }\xi \right)\\ +A_{2}cosh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }\xi \right)\end{array}}{\begin{array}{c}{A}_{1}cosh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }\xi \right)\\ +A_2\sinh \left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }\xi \right)\end{array}}\right],$ In particular, if we set $A_1\ne 0,A_2=0,\lambda >0$ and $\mu =0$, in (3.3.4), then we get the kink soliton wave solutions $V_{28}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \tanh \left(\frac{\lambda }{2}\xi \right)\right],$

while, if we set $A_1=0,A_2\ne 0,\lambda >0$ and $\mu =0$, then we get the anti-kink soliton wave solutions $V_{29}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm \coth \left(\frac{\lambda }{2}\xi \right)\right],$ where $\xi =\sqrt{-\frac{24{\alpha }^2}{{\delta }^2{\lambda }^2(2{\alpha }^2-9\beta )}}x-\sqrt{\frac{216{\alpha }^2\beta }{{\lambda }^2{(2{\alpha }^2-9\beta )}^2}}t.$

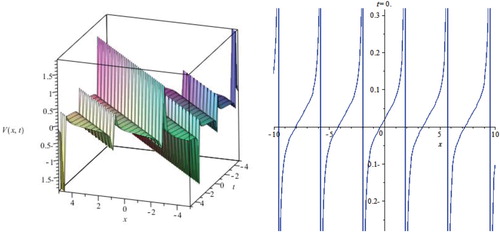
Case 2. If ${\lambda }^2-4\mu <0$, then we have the trigonometric functions solutions $\begin{array}{rl}& V_{30}\left(\xi \right)=\frac{\alpha }{3\beta }\left[1\pm i\frac{\begin{array}{c}{A}_1\cos \left(\frac{1}{2}\sqrt{4\mu -{\lambda }^2}\xi \right)\\ -A_2\sin \left(\frac{1}{2}\sqrt{4\mu -{\lambda }^2}\xi \right)\end{array}}{\begin{array}{c}{A}_1\sin \left(\frac{1}{2}\sqrt{4\mu -{\lambda }^2}\xi \right)\\ +A_2\cos \left(\frac{1}{2}\sqrt{4\mu -{\lambda }^2}\xi \right)\end{array}}\right],\\ & i=\sqrt{-1}\end{array}$ In particular, if we set $A_1=0,A_2\ne 0,\lambda >0$ and $\mu =0$, in (3.3.7), then we get the same kink soliton wave solutions (3.3.5), while, if we set $A_1\ne 0,A_2=0,\lambda >0$ and $\mu =0$, then we get the same anti-kink soliton wave solutions.

4. Physical explanations of some results

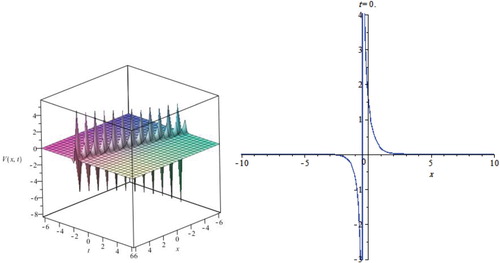
 In this section, we have presented some graphs of the exact solutions. These solutions are soliton solutions, periodic solutions and Jacobi elliptic functions solutions. Exact solutions of the results describe different nonlinear waves. For the established exact solutions with hyperbolic solutions are special kinds of solitary waves solutions. Now, let us examine Figures 1–3 as it illustrates some of our solutions obtained in this paper. To this aim, we select some special values of the parameters obtained, for example, in some of the solutions (3.1.3), (3.1.7) and (3.2.4) of the nonlinear PDE (1.1). For more convenience, the graphical representations of these solutions are shown in the figures.

Figure 1. The plot of solution (3.1.3) when $\alpha =2,\beta =2,\delta =2,p=1,d=2.$

Figure 2. The plot of solution (3.1.7) when $\alpha =2,\beta =2,\delta =3,p=d=q=1,r=-1.$

Figure 3. The plot of solution (3.2.4) when $\alpha =3,\beta =26+4\sqrt{42},\delta =\frac{2\sqrt{18+3\sqrt{42}}}{6+\sqrt{42}},m=\frac{3}{4}.$

5. Conclusions

In this paper, we have solved the nonlinear PDE describing the nonlinear low-pass electrical transmission lines (1.1) using the (G′/G)-expansion method with the aid of three auxiliary equations (2.5)–(2.6) described in Section 2. By the aid of Maple or Mathematica, we have found many solutions of Equation (1.1) which are new. On comparing our results with the results obtain in [15,27] using the new Jacobi elliptic function expansion method and the auxiliary equation method respectively, we deduce that our results are different and new. Also, we have noted that our results (3.3.5) and (3.3.6) are in agreement with the results (3.2.5) and (3.2.9) of Section 3.2 obtained in this paper respectively, when $\lambda =2$. Furthermore, all solutions obtained in this paper have been checked with the Maple by putting them back into the original equations. Finally, the proposed method in this paper can be applied to many other nonlinear PDEs in mathematical physics.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Ayad M. Shahoot http://orcid.org/0000-0003-3483-4110

Khaled A. E. Alurrfi http://orcid.org/0000-0002-0281-0301

Mohamed O. M. Elmrid http://orcid.org/0000-0002-5511-8925

Ali M. Almsiri http://orcid.org/0000-0002-0718-1620

Abdullah M. H. Arwiniya http://orcid.org/0000-0002-5563-6773