Transient Dean flow in an annulus: a semi-analytical approach

Abstract

The mathematical model of a fully developed laminar transient flow formation between the gaps of two horizontally stationary concentric tubes forming concentric annulus due to the impact of sudden application of azimuthal pressure gradient is analysed. Analytical and numerical solutions of the momentum equations are obtained by the aid of two-step process. The first step is by solving the governing partial differential equation analytically by using Laplace transform technique in the Laplace domain. Using Riemann–sum approximation of Laplace inversion, the velocity and skin friction are then inverted to time domain. Expressions for steady-state velocity and skin friction are obtained for the validations of the method employed. In the course of numerical computations, it is observed that increase in dimensionless time $\left(T\right)$ leads to increase in velocity as well as skin friction at the surfaces of tubes. It is also found that at large values of dimensionless time $\left(T\right)$, the velocity and skin friction reach steady state.

KEYWORDS:

• Transient
• Dean flow
• annulus
• Riemann–sum approximation

Nomenclature

$R$:	=	Dimensionless radial distance
$r_1$:	=	Radius of the inner tube $\left(m\right)$
$r_2$:	=	Radius of the outer tube $\left(m\right)$
$t$:	=	Time $\left(s\right)$
$\mathcal{L}$:	=	Laplace transform operator
${\mathcal{L}}^{-1}$:	=	Inverse Laplace transform operator
$T$:	=	Dimensionless time
$v_r$:	=	Radial velocity $\left(m/s\right)$
$v_{\varphi }$:	=	Circumferential velocity $\left(m/s\right)$
$U_0$:	=	Reference velocity $\left(m/s\right)$
$p$:	=	Static pressure $\left(N/m^{2}orKg/m{s}^2\right)$
$V$:	=	Dimensionless velocity
$\overline{V}$:	=	Dimensionless velocity in Laplace domain
$s$:	=	Laplace parameter
$I_1:$	=	First-order modified Bessel function of the first kind
$K_1:$	=	First-order modified Bessel function of the second kind
$I_2:$	=	Second-order modified Bessel function of the first kind
$K_2:$	=	Second-order modified Bessel function of the second kind

Greek

$ϵ$:	=	Real part of Bronwich contour.
$\lambda$:	=	Ratio of the radii of the tubes
$\rho$:	=	Fluid density $\left(Kg/m^3\right)$
$\mu$:	=	Dynamic viscosity of the fluid $\left(Kg/ms\right)$
${\tau }_R$:	=	Skin friction between fluid layers
${\overline{\tau }}_1$:	=	Skin friction in Laplace domain at $R=1$
${\overline{\tau }}_{\lambda }$:	=	Skin friction in Laplace domain at $R=\lambda$
${\tau }_1$:	=	Skin friction at the outer surface of the inner tube
${\tau }_{\lambda }$:	=	Skin friction at the inner surface of the outer tube
${\tau }_{1s}$:	=	Steady-state skin friction at the outer surface of the inner tube
${\tau }_{\lambda s}$:	=	Steady-state skin friction at the inner surface of the outer tube

1. Introduction

Dean Flow is very important because of its many application in electrical, mechanical and nuclear engineering including biomedical engineering, where the fluid flows appear in most of the apparatuses (peristaltic pumps, extracorporeal circulation or heart-lung machine) conveying fluids.

Fluid flow patterns in laboratory scale, pilot plant scale and commercial scale equipment where a fluid is contained between concentric (stationary and rotating) cylinders has received a notable attention in fluid mechanics, applied mathematics, chemical engineering and biotechnology. Understanding the flow behaviour in a horizontal/vertically oriented annular gap whose both walls are stationary or one of the walls rotates is an important problem within the broader scope of fluid flows within annular regions. This fluid–solid hydrodynamic contacting pattern, which is often refer to as an annular flow, occurs in many practical technology-driven applications as mentioned above.

Dean [1] is believed to be the first to study the motion of fluid in a curved channel due to a pressure gradient acting round the channel and the problem is termed Dean flow which is defined as the motion of fluid been due to a pressure gradient acting round the channel.

In recent years, a series of investigations have been conducted in the field of Dean Flow. To cite a few works in this path, Tsangaris [2] analytically studied the viscous flow of an incompressible fluid due to an oscillating pressure gradient along a straight circular annular pipe with rigid walls in which the maximum velocity reduces rapidly by increasing the ratio of the smaller radius to the greater radius of the annulus.

Again, Tsangaris and Vlachakis [3] also considered the effect of oscillating pressure gradients of viscous, incompressible fluid flow between porous channels and found out that the effect of Womersley number, the ratio of the radii of the annulus are important. Deka and Takhar [4] have done research on the hydrodynamic stability of Dean flow with the radial flow. They used unit disturbance method (classical Runge–Kutta scheme combined with a shooting method). According to their study, they observed that radially outward flow and strong inward flow have a stabilizing effect, while weak inward flow has a destabilizing effect on the stability. On their part, Barman et al. [5] numerically investigated the fluid motion between rotating concentric cylinders and found out that the fluid velocity profiles approach a fully developed state only after travelling a distance that is much greater than the annular gap between the cylinders and also shows that the pressure exerted on the inner cylinder increases monotonically with rotational speed.

Other related works to the present investigation are found in the literature [6–9]. In [8], Manos et al. analytically and numerically investigated the oscillatory viscoelastic flow in a circular wall. Dean and Hurst [6] studied the fluid motion in a channel. They stated that in the streamline motion of fluid in a curved pipe the primary motion along the line of the pipe is accompanied by a secondary motion in the plane of the cross-section and it reduces the total rate of flow through the pipe due to a given pressure gradient. Erdogan et al. [7] give an exact solution of the steady flow of a Second-Grade fluid between two coaxial porous cylinders where they found out that for large values of cross-Reynolds number, the velocity profile near the boundaries shows a different behaviour than that of the Newtonian fluid. Also, Wang [9] considered the effect of curvature and torsion on the low Reynolds number flow in a helical pipe. [10] explored experimentally the transition from laminar to turbulent in Taylor–Dean Flow. In their experimental setup, three different flows are produced; Dean flow, closed Taylor–Dean Flow and open Taylor–Dean flow, respectively. It is reported that increasing Taylor number for a fixed Dean number, laminar to turbulent transitions occurs in the flow. The characteristics of laminar to turbulent flow are turbulent bursts, travelling waves with two trains in the same or opposite direction, cells split merging, diagonally travelling rolls and vortex paths in the same or opposite direction. Again, in another article [11], investigated how turbulence is rising in Dean type flow. Similarities of transition to turbulence of the Dean and Taylor–Couette flow is carried out experimentally. Although it is limited to flow produced by pumping the fluid around the annulus of coaxial cylinders where the outer cylinder is open azimuthally (Open Taylor–Couette flow) and the spatial-temporal characterization of the instabilities is taken into consideration. In the work of [12], the stability of a two-layer Dean flow in an annulus is investigated numerically with respect to three-dimensional perturbations by using a global Galerkin method. Results were observed for the large inner radius that instability becomes three-dimensional if one of the fluid layers is thin. [13] investigated semi-analytically fully developed the flow of a temperature distribution in Dean Flow. Their results indicated that at the centre of the Dean roll cells, the measured temperatures are more uniform and higher than the analytical ones which is caused by intrusive mixing of the thermocouple probe which intensifies the mixing and then the convective heat transfer because the fluid temperature with the presence of the probe appears higher than the fluid temperature without the probe.

In furtherance of the forgoing, [14] considered the critical condition and the structure of the vortex flow at the onset of instability of a purely elastic instability in Dean and Taylor – Dean flow of an Oldroyd – B fluid between rotating cylinders with an applied azimuthal pressure gradient. It is observed that the instability is a stationary mode when the pressure gradient becomes dominant flow driving the force, while it is an oscillatory instability when the shearing by the cylinder rotation is dominant and also the direction of the pressure gradient controls the characteristics of the instability. Pressure gradient applied along the cylinder rotation destabilizes the flow, while if applied against the rotation, the flow is substantially stabilized.

Azaditalab et al. [15] carried out a numerical investigation on the effect of nanoparticle addition in a vertical Taylor–Couette system. They also considered the skin friction reduction on Nanofluid flows on the system. Jha and Apere [16] considered the solution of the time-dependent MHD Couette flow problem in a porous annulus formed by two concentric porous cylinders of infinite length where the fluid is induced either by impulsive or the accelerated movements of the outer cylinders. They found out that suction accelerates the flow whereas injection retards the flow. The analytical solutions of the equations of motion of a Newtonian fluid for the fully developed laminar flow between two concentric cylinders when an oscillating circumferential pressure gradient is imposed (finite-gap oscillating Dean flow) was presented by Tsangaris et al. [17]. Tsangaris and Vlachakis [18] extended the problem to the case when the walls of the cylinders are porous.

Heat and mass transfer as well as energy analysis of Couette–Poiseuille flow of MHD and nanofluid has been studied thoroughly by [19–21]. To begin with, Zeeshan et al. [21] explored energy activation analysis using analytical HAM technique on nanofluid Couette–Poiseuille fluid flow in the presence of chemical reaction taking into consideration convective boundary conditions. It is observed that the nanoparticle concentration is directly proportional to the chemical reaction with activation energy and Brownian motion performance on nanoparticle concentration gives a contrary pattern to that of a thermophoresis parameter.

Similarly, [20] used the analytical HAM technique on a viscous, incompressible, MHD power law nanofluid in a horizontal Couette–Poiseuille channel taking into account the elctro-osmotic effect. It is recorded in their results that, increase in electro-osmotic parameter decreases the skin friction at the moving isolated walls. On the other hand, skin friction increases as suction and injection, thermal radiation and magnetic parameter increase as reported by [19] considering nanoliquid on MHD Poiseuille flow with variable thermal conductivity.

On the effect of electro-osmosis and mixed convection on nano-bio-fluid with non-spherical particles in a curved channel was studied numerically by [20]. It is shown experimentally that a rise in heat transfer due to the presence of blade shape particles occur. Further researches on heat transfer where rotational parameters are considered by [22,23]. For the case of positive and negative rotation of the channel, [23] comprehensively analysed transient fully developed two-dimensional thermal flow of viscous incompressible fluid through a rotating a curved duct. It is found that increasing $Tr$ (Taylor number) in the negative direction, unsteady flow undergoes through various flow instabilities. Increasing $Tr$ in the positive direction, unsteady flow scenario “chaotic $\to$ multi – periodic $\to$ periodic $\to$ steady state” occurs.

Similarly, [22] on their part investigated positive and negative rotation of the channel taking into account Dean–Taylor flow with convective heat transfer through a coiled duct.

In all the studies mentioned above, to the best of authors’ findings, there was none that considered the fully developed transient Dean flow in concentric tubes forming concentric annulus. Hence the motivation of this present study.

The aim of this study is, therefore, to present analytical and numerical solution of transient Dean Flow of an incompressible fluid in concentric tubes forming concentric annulus. The fluid motion is due to the imposition of an azimuthal pressure gradient. The governing equations are solved using Laplace transform technique in conjunction with the Riemann–sum approximation method of Laplace inversion. The analytical solution of the steady state is solved separately to validate the method employed in this study. The main features of these solutions are discussed.

2. Mathematical analysis

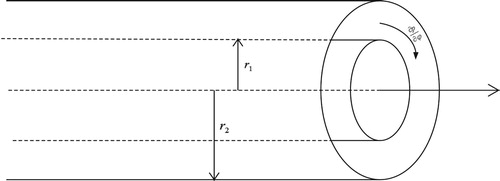
Consider the unsteady incompressible fluid of constant viscosity $\mu$, the fluid flows in an annulus between concentric horizontally stationary tubes. The inner and outer tubes have radii $r_1$ and $r_2$, respectively. At time $t\le 0$, the fluid is assumed to be at rest, when $t>0$, fluid moves in the azimuthal direction in the region $r_2-r_1$ $(r_2>r_1)$. The time-dependent flow formation in the region is due to sudden application of an azimuthal pressure gradient $\left(\frac{\mathrm{\partial }p}{\mathrm{\partial }\varphi }\right)$. The geometry of the problem is depicted in Figure 1.

Figure 1. Geometry of the annular system with a finite circumferential angle.

The incompressible Navier–Stokes equations along with the continuity equation for a fluid of constant viscosity $\mu$, which in a polar coordinate reference frame can be written as (1) $\begin{array}{rl}& \frac{\mathrm{\partial }\left(r{v}_r\right)}{\mathrm{\partial }r}+\frac{\mathrm{\partial }{v}_{\varphi }}{\mathrm{\partial }\varphi }=0\end{array}$(1) (2) $\begin{array}{rl}\rho & \left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }t}+v_r\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}+\frac{v_{\varphi }}{r}\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }\varphi }-\frac{v_{\varphi }^2}{r}\right)=-\frac{\mathrm{\partial }p}{\mathrm{\partial }r}\\ & +\mu \left(\frac{{\mathrm{\partial }}^2{v}_r}{\mathrm{\partial }{r}^2}+\frac{1}{r}\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}+\frac{1}{r}\frac{{\mathrm{\partial }}^2{v}_{\varphi }}{\mathrm{\partial }{\varphi }^2}-\frac{v_r}{r^2}-\frac{2}{r^2}\frac{\mathrm{\partial }{v}_{\varphi }}{\mathrm{\partial }\varphi }\right)\end{array}$(2) (3) $\begin{array}{rl}\rho & \left(\frac{\mathrm{\partial }{v}_{\varphi }}{\mathrm{\partial }t}+v_r\frac{\mathrm{\partial }{v}_{\varphi }}{\mathrm{\partial }r}+\frac{v_{\varphi }}{r}\frac{\mathrm{\partial }{v}_{\varphi }}{\mathrm{\partial }\varphi }-\frac{v_r{v}_{\varphi }}{r}\right)=-\frac{1}{r}\frac{\mathrm{\partial }p}{\mathrm{\partial }\varphi }\\ & +\mu \left(\frac{{\mathrm{\partial }}^2{v}_{\varphi }}{\mathrm{\partial }{r}^2}+\frac{1}{r}\frac{\mathrm{\partial }{v}_{\varphi }}{\mathrm{\partial }r}+\frac{1}{r^2}\frac{{\mathrm{\partial }}^2{v}_{\varphi }}{\mathrm{\partial }{\varphi }^2}-\frac{v_{\varphi }}{r^2}+\frac{2}{r^2}\frac{\mathrm{\partial }{v}_{\varphi }}{\mathrm{\partial }\varphi }\right)\end{array}$(3)

Since the cylinders are of infinite length and the flow is assumed to be fully developed $\left(v_r=0\right)$ and continuity equation, $v_{\varphi }$ is proved to be a function of the radial coordinate $r$ and time $t$ only, $v_{\varphi }=v\left(r,t\right)$, and the momentum and continuity equations reduce to the following forms as [18] (4) $\rho \frac{v^2}{r}=\frac{\mathrm{\partial }p}{\mathrm{\partial }r}$(4) (5) $\rho \frac{\mathrm{\partial }v}{\mathrm{\partial }t}=-\frac{1}{r}\frac{\mathrm{\partial }p}{\mathrm{\partial }\varphi }+\mu \left(\frac{{\mathrm{\partial }}^{2}v}{\mathrm{\partial }{r}^2}+\frac{1}{r}\frac{\mathrm{\partial }v}{\mathrm{\partial }r}-\frac{v}{r^2}\right)$(5)

The initial and boundary conditions for the problem are (6) $\begin{array}{c}t\le 0:v=0\text{ for }{r}_1\le r\le r_2\\ t>0\left\{\begin{array}{l}v=0\text{ at }r=r_1\\ v=0\text{ at }r=r_2\end{array}\right.\end{array}$(6) where $v$ is the circumferential velocity component, $\rho$ is the fluid density, $p$ and $\mu$ are the static pressure and dynamic viscosity of the fluid, respectively.

3. Dimensionless analysis

By introducing the dimensionless variables as follows, we have (7) $R=\frac{r}{r_1},\lambda =\frac{r_2}{r_1},T=\frac{\upsilon t}{{r_1}^2},V=\frac{v}{U_0},U_0=\frac{-r_1\frac{\mathrm{\partial }p}{\mathrm{\partial }\varphi }}{\rho \upsilon }$(7) Equations (2) and (3) reduces to (8) $\frac{\mathrm{\partial }V}{\mathrm{\partial }T}=\frac{1}{R}+\left(\frac{{\mathrm{\partial }}^{2}V}{\mathrm{\partial }{R}^2}+\frac{1}{R}\frac{\mathrm{\partial }V}{\mathrm{\partial }R}-\frac{V}{R^2}\right)$(8)

The initial and boundary conditions are (9) $\begin{array}{r}T\le 0:V=0for1\le R\le \lambda \\ T>0\left\{\begin{array}{l}V=0atR=1\\ V=0atR=\lambda \end{array}\right.\end{array}$(9)

4. Solution to the problem

4.1. Velocity

The solution of Equation (5) can be obtained using the Laplace transforms technique. Defining the transform variables as [24] $\mathcal{L}\left(V\left(R,T\right)\right)=\overline{V}\left(R,s\right)=\underset{0}{\overset{\mathrm{\infty }}{\int }}V\left(R,T\right)e^{-sT}dT,\left(s>0\right)$ where $s$ is the Laplace parameter and taking the Laplace transformation of Equation (8), the following equation is obtained (10) $\frac{d^2\overline{V}}{d{R}^2}+\frac{1}{R}\frac{d\overline{V}}{dR}-\left(1+s{R}^2\right)\frac{\overline{V}}{R^2}=-\frac{1}{Rs}$(10) with the boundary condition (11) $\left.\begin{array}{c}\overline{V}=0atR=1\\ \overline{V}=0atR=\lambda \end{array}\right\}$(11) Using the approach of Tsangaris and Vlachakis [18], Equation (10) which is a linear non-homogeneous differential equation can be reduced by using the transformation shown below: (12) $\overline{V}\left(R,s\right)=V_h\left(R,s\right)+\frac{1}{R{s}^2}$(12) where $V_h\left(R,s\right)$ is the homogeneous solution of Equation (10) and substituting Equation (12) on Equation (10) with boundary condition (11), the velocity profile in the Laplace domain is given as (13) $\begin{array}{r}\overline{V}\left(R,s\right)=\frac{1}{s^2}\frac{\begin{array}{c}\left[K_1\left(\lambda \sqrt{s}\right)-\frac{K_1\left(\sqrt{s}\right)}{\lambda }\right]I_1\left(R\sqrt{s}\right)\\ +\left[\frac{I_1\left(\sqrt{s}\right)}{\lambda }-I_1\left(\lambda \sqrt{s}\right)\right]K_1\left(R\sqrt{s}\right)\end{array}}{\begin{array}{c}\left[I_1\left(\lambda \sqrt{s}\right)K_1\left(\sqrt{s}\right)\right.\\ -\left.I_1\left(\sqrt{s}\right)K_1\left(\lambda \sqrt{s}\right)\right]\end{array}}+\frac{1}{R{s}^2}\end{array}$(13) where $I_1$ and $K_1$ are the modified Bessel functions of the first and second kind and first order, respectively.

4.2. Skin frictions

The skin friction ${\overline{\tau }}_R$ is defined as ${\overline{\tau }}_R=R\frac{d}{dR}\left(\frac{\overline{V}}{R}\right),$ it is obtained by differentiating Equation (13) with respect to $R.$ (14) $\begin{array}{rl}& \mathcal{L}\left({\tau }_1\left(R,T\right)\right)={\overline{\tau }}_1={\left.R\frac{d}{dR}\left(\frac{\overline{V}}{R}\right)\right|}_{R=1}\\ & =\sqrt{s}\left[C_1{I}_2\left(\sqrt{s}\right)-C_2{K}_2\left(\sqrt{s}\right)\right]-\frac{2}{s^2}\end{array}$(14) (15) $\begin{array}{rl}& \mathcal{L}\left({\tau }_{\lambda }\left(R,T\right)\right)={\overline{\tau }}_{\lambda }={\left.R\frac{d}{dR}\left(\frac{\overline{V}}{R}\right)\right|}_{R=\lambda }\\ & =\sqrt{s}\left[C_1{I}_2\left(\lambda \sqrt{s}\right)-C_2{K}_2\left(\lambda \sqrt{s}\right)\right]-\frac{2}{{\lambda }^2{s}^2}\end{array}$(15) where $I_2$ is the 2^nd-order modified Bessel function of the first kind and $K_2$ is the 2^nd-order modified Bessel function of the second kind and $C_1$ and $C_2$ are constants given as $C_1=\frac{1}{s^2}\frac{\left[K_1\left(\lambda \sqrt{s}\right)-\frac{K_1\left(\sqrt{s}\right)}{\lambda }\right]}{\left[I_1\left(\lambda \sqrt{s}\right)K_1\left(\sqrt{s}\right)-I_1\left(\sqrt{s}\right)K_1\left(\lambda \sqrt{s}\right)\right]}$ $C_2=\frac{1}{s^2}\frac{\left[\frac{I_1\left(\sqrt{s}\right)}{\lambda }-I_1\left(\lambda \sqrt{s}\right)\right]}{\left[I_1\left(\lambda \sqrt{s}\right)K_1\left(\sqrt{s}\right)-I_1\left(\sqrt{s}\right)K_1\left(\lambda \sqrt{s}\right)\right]}$

In other to determine the velocity and skin friction in time domain due to the complexity of Equation (13), (14) and (15), we use a numerical approach based on Riemann–sum approximation used by [25–27] which has been found to be very efficient and promising tool in transforming from Laplace domain to time domain. In this method, any function in the $s$ domain can be inverted to the time $T$ domain as follows [24] (16) $\begin{array}{rl}& {\mathcal{L}}^{-1}\left(\overline{V}\left(R,s\right)\right)=V\left(R,T\right)\\ & =\frac{e^{ϵT}}{T}\left[\frac{1}{2}\overline{V}\left(R,ϵ\right)+\text{ Re }\sum _{k=1}^n\overline{V}\left(R,ϵ+\frac{ik\pi }{T}\right){\left(-1\right)}^k\right]\end{array}$(16) (17) $\begin{array}{rl}& {\mathcal{L}}^{-1}\left({\overline{\tau }}_1\left(R,s\right)\right)={\tau }_1\left(R,T\right)\\ & =\frac{e^{ϵT}}{T}\left[\frac{1}{2}{\overline{\tau }}_1\left(R,ϵ\right)+\text{ Re }\sum _{k=1}^n{\overline{\tau }}_1\left(R,ϵ+\frac{ik\pi }{T}\right){\left(-1\right)}^k\right]\end{array}$(17) (18) $\begin{array}{rl}& {\mathcal{L}}^{-1}\left({\overline{\tau }}_{\lambda }\left(R,s\right)\right)={\tau }_1\left(R,T\right)\\ & =\frac{e^{ϵT}}{T}\left[\frac{1}{2}{\overline{\tau }}_{\lambda }\left(R,ϵ\right)+\text{ Re }\sum _{k=1}^n{\overline{\tau }}_{\lambda }\left(R,ϵ+\frac{ik\pi }{T}\right){\left(-1\right)}^k\right]\end{array}$(18) where Re refers to the “real part of” $i=\sqrt{-1}$ is the imaginary number, $n$ is the number of terms used in the Riemann–sum approximation and $ϵ$ is the real part of the Bronwich contour that is used in inverting Laplace transforms. The Riemann–sum approximation for the Laplace inversion involves a single summation for the numerical process. Its accuracy depends on the value of $ϵ$ and the truncation error dictated by $n.$ According to Tzou [28], the value of $ϵ$ must be selected so that the Bronwich contour encloses all the branch points. For faster convergence, the quantity $ϵT=4.7$ gives the most satisfactory results.

5. Validation of the method

In other to validate the accuracy of the method employed (Riemann–sum approximation), the solutions of the partial differential equation at steady state for both the velocity and skin frictions are obtained and which should coincide with the transient solutions at large value of time $\left(T\right)$.

5.1. Steady-state solutions

The expression for the steady-state velocity distribution $V_s$ is obtained by setting $\frac{\mathrm{\partial }V}{\mathrm{\partial }T}$ in Equation (8) to zero. We then obtain the following ordinary differential equation (19) $\frac{d^2{V}_s}{d{R}^2}+\frac{1}{R}\frac{d{V}_s}{dR}-\frac{V_s}{R^2}=-\frac{1}{R}$(19)

Applying the transformation below (20) $R=e^{\psi }$(20)

The above equation is transformed into the following ordinary differential equation (21) $\frac{d^2{V}_s}{d{\psi }^2}-V_s=-e^{\psi }$(21)

Using equations (20) and (21), the solution of Equation (19) which is the steady-state velocity distribution is given as (22) $V_s\left(R\right)=\frac{{\lambda }^2\ln \lambda }{2\left(1-{\lambda }^2\right)}\left(\frac{1}{R}-R\right)-\frac{R}{2}\ln R$(22)

The steady-state skin friction ${\tau }_{1s}$ and ${\tau }_{\lambda s}$ is obtained similarly as follows (23) ${\tau }_{1s}={\left.R\frac{d}{dR}\left(\frac{V_s}{R}\right)\right|}_{R=1}=\frac{{\lambda }^2\ln \lambda }{\left({\lambda }^2-1\right)}-\frac{1}{2}$(23) (24) ${\tau }_{\lambda s}={\left.R\frac{d}{dR}\left(\frac{V_s}{R}\right)\right|}_{R=\lambda }=\frac{\ln \lambda }{\left({\lambda }^2-1\right)}-\frac{1}{2}$(24)

6. Results and discussion

In order to get physical insight into the problem, a MATLAB programme is written to compute and generate a graph for velocity profile and the skin friction in Figures 2–4 for various values of time $T,$ and radial distance $R.$ Unless otherwise stated we have employed the following values of time $T=0.2,0.4\text{ and }4.0$ and of ratio of the radii of the tubes $\lambda =1.4,1.6,1.8,\text{ and }2.0$.

Figure 2. Velocity profile for different values of time T and radius R.

Figure 3. Skin friction on the outer surface of the inner tube (R = 1).

Figure 4. Skin friction on the inner surface of the outer tube (R = λ).

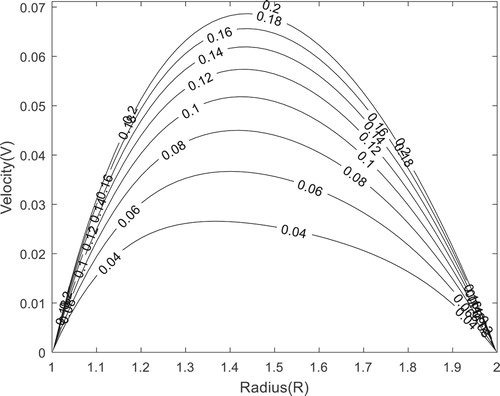
The results of this analysis; transient Dean flow driven by the constant azimuthal pressure gradient between horizontally stationary concentric tubes indicates that the velocity distribution exhibits a Stokes layer character, with high-velocity gradient moving closer to the solid boundaries. Similarly, a phenomenon known as annular effect were stated by Richardson and Tyler [29] where they have shown by experiments that in Helmholtz resonators the velocity close to the walls is greater than at the centre itself.

Figure 2 shows the velocity profile of the fluid motion. It is observed that the velocity of the fluid at the outer surface of the inner tube is higher than the velocity of the fluid at the inner surface of the outer tube.

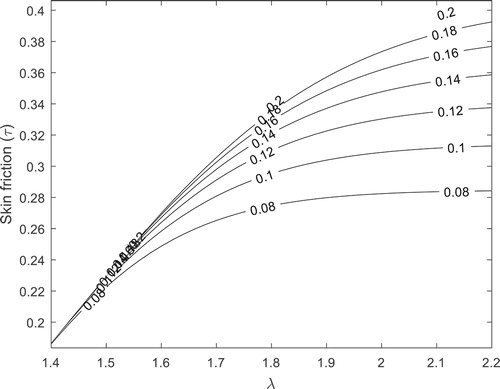
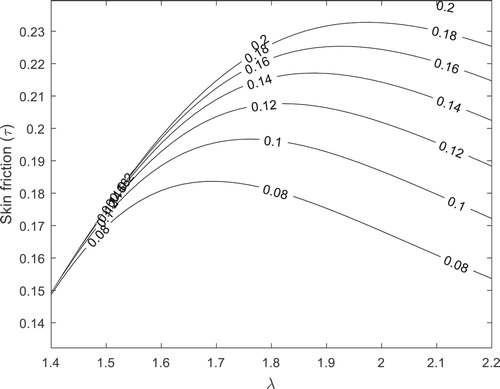
The non-dimensional skin friction as given in Equations (17) and (18) are presented graphically in Figures 3 and 4. The responses of the skin friction in these figures are studied. On the outer surface of the inner tube $R=1$, it is shown that the skin friction increases with increases in the ratio of the radii ($\lambda$). Also, it is found that the skin friction on the outer surface of the inner tube behaves similarly.

A comparison is made in Table 2 between the results obtained using the Riemann–sum approximation method and those obtained analytically at steady state. It is observed that at large time, the velocity profile and the skin friction approach steady state which confirms the accuracy of the method employed in the present problem.

Table 1. Numerical values of the velocity obtained using Riemann–sum approximation method and those obtained analytically at steady state.

Velocity profile
$T$	$R$	Riemann–Sum	Exact solution
$0.2$	1.2	0.0530	0.0600
	1.4	0.0707	0.0813
	1.6	0.0645	0.0745
	1.8	0.0402	0.0460
$0.4$	1.2	0.0591	0.0600
	1.4	0.0800	0.0813
	1.6	0.0733	0.0745
	1.8	0.0453	0.0460
Steady state	1.2	0.0600	0.0600
	1.4	0.0813	0.0813
	1.6	0.0745	0.0745
	1.8	0.0460	0.0460

Table 2. Numerical values of the skin friction obtained using Riemann–sum approximation method and those obtained analytically at steady state.

		Skin friction $\left(R=1\right)$		Skin friction $\left(R=\lambda \right)$
T	$\lambda$	Riemann–Sum	Exact solution	Riemann–Sum	Exact solution
$0.2$	1.2	0.0968	0.0967	0.0857	0.0856
	1.4	0.1871	0.1870	0.1496	0.1495
	1.6	0.2706	0.2713	0.1982	0.1987
	1.8	0.3390	0.3502	0.2292	0.2376
$0.4$	1.2	0.0968	0.0967	0.0858	0.0856
	1.4	0.1871	0.1870	0.1496	0.1495
	1.6	0.2714	0.2713	0.1988	0.1987
	1.8	0.3499	0.3502	0.2373	0.2376
Steady state	1.2	0.0967	0.0967	0.0856	0.0856
	1.4	0.1870	0.1870	0.1495	0.1495
	1.6	0.2713	0.2713	0.1987	0.1987
	1.8	0.3502	0.3502	0.2376	0.2376

7. Conclusion

Transient Dean Flow of a viscous incompressible fluid in the annular gap of horizontally stationary concentric tubes due to an azimuthal pressure gradient has been studied. The governing momentum equation coupled with the continuity equation is obtained and solved exactly in the Laplace domain. The Riemann–sum approximation method is used to invert the velocity and skin friction obtained through the Laplace transform technique into the time domain. The effects of the ratio of the radii of the tubes and dimensionless time have been depicted graphically.

The main findings are as follows:

1. The velocity and skin friction at the outer surface of the inner tube and at the inner surface of the outer tube approach steady state at large values of time $T.$

2. The velocity of the fluid decreases both at the outer surface of the inner tube and at the inner surface of the outer tube and increases at the middle of the concentric tubes. This phenomenon is reported experimentally by Richardson and Tyler [29] for the case of pulsating flow in a straight circular pipe.

3. Skin friction is found to be a decreasing function of the ratio of the radii of the tubes.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Jibrin Danjuma Yahaya http://orcid.org/0000-0002-3701-1585