Advanced search
Publication Cover
Journal of Taibah University for Science Volume 13, 2019 - Issue 1
Submit an article Journal homepage
878
Views
2
CrossRef citations to date
0
Altmetric
Research Articles

Sum-edge characteristic polynomials of graphs

Mert Sinan OzDepartment of Mathematics, Faculty of Engineering and Natural Sciences, Bursa Technical University, Bursa, TurkeyORCID Iconhttps://orcid.org/0000-0002-6206-0362
ORCID Icon,
Cilem YamacDepartment of Mathematics, Faculty of Arts and Science, Uludag University, Bursa, TurkeyORCID Iconhttps://orcid.org/0000-0001-6044-1578
ORCID Icon &
Ismail Naci CangulDepartment of Mathematics, Faculty of Arts and Science, Uludag University, Bursa, TurkeyCorrespondence[email protected]
ORCID Iconhttps://orcid.org/0000-0002-0700-5774
ORCID Icon
Pages 193-200 | Received 12 Apr 2018, Accepted 21 Nov 2018, Published online: 10 Dec 2018

Abstract

Modelling a chemical compound by a (molecular) graph helps us to obtain some required information about the chemical and physical properties of the corresponding molecular structure. Linear algebraic notions and methods are used to obtain several properties of graphs usually by the help of some graph matrices and these studies form an important sub area of Graph Theory called spectral graph theory. In this paper, we deal with the sum-edge matrices defined by means of vertex degrees. We calculate the sum-edge characteristic polynomials of several important graph classes by means of the corresponding sum-edge matrices.

AMS 2010 Subject Classifications Number:

1. Introduction

Let G=(V,E) be a graph with ∣V(G)∣=n vertices and ∣E(G)∣=m edges. For a vertex v∈V(G), we denote the degree of v by dv or dG(v). In particular, a vertex with degree one is called a pendant vertex. With slight abuse of language, one can use the term “pendant edge” for an edge having a pendant vertex. If u and v are two vertices of G connected by an edge e, then this situation is denoted by e=uv. In such a case, the vertices u and v are called adjacent vertices and the edge e is said to be incident with u and v. The study of adjacency and incidency with the help of corresponding matrices is a well known application of Graph Theory to Molecular Chemistry and the sub area of Graph Theory dealing with the energy of a graph is called Spectral Graph Theory which uses linear algebraic methods to calculate eigenvalues of a graph resulting in the molecular energy of that graph. In that sense, matrices are very helpful in the spectral study of graphs modelling some chemical structures. Apart from three most important kinds of matrices, that are Laplacian, adjacency and incidency matrices, there are nearly one hundred types of graph matrices, some giving important information about the molecules that are modelled by the corresponding graph, see e.g. [Citation1, Citation2] for general notions on the graph matrices. In [Citation3–5], some formulae and recurrence relations on spectral polynomials of some graphs were calculated.

As mentioned above, one of the ways of studying graphs is to make use of the matrices corresponding the graph and for this aim, a large number of matrices have been defined and used. The most popular ones are the adjacency, incidency and Laplacian matrices. In the recent years, some mew matrices by means of the values of several topological indices have been defined. In this paper, we shall consider the sum-edge characteristic polynomials obtained as the characteristic polynomial of the sum-edge matrix.

2. Sum-Edge matrices and characteristic polynomials

One of these matrices called the sum-edge matrix of G is a square n×n matrix SMe(G)=[aij]n×n determined by the adjacency of vertices as follows: aij=dG(vi)+dG(vj),if the vertices vi and vjare adjacent0,otherwise. For a graph G, we shall denote the sum-edge characteristic polynomial obtained by taking the sum-edge matrix of G instead of the classical adjacency matrix by PGse(λ). In this paper, we shall determine this sum-edge characteristic polynomial of some well-known graph classes and also give some general results for r-regular graphs.

There is a special matrix which appears in many calculations in this paper. This matrix is

The characteristic polynomial corresponding to this matrix is denoted by PΔn(λ) and is equal to PΔn(λ)=∑k=0⌊n/2⌋(−1)k24kn−kn−2kλn−2k. We now recall a well-known property of determinants:

Lemma 2.1

If we divide a matrix into four block matrices A0CB, or

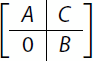
where A and B are square matrices, the determinant of this matrix is equal to |A||B|.

We shall now determine sum-edge characteristic polynomial of an r-regular graph. For r>2, because of the variety of r-regular graphs, it seems that there is no unique method to calculate PΔn(λ). Only when r=2, we can calculate this sum-edge characteristic polynomial easily. As all 2-regular graphs are either cyclic graphs when the graph is connected, or each component is a cycle when the graph is not connected. In the latter case, we can easily obtain this sum-edge characteristic polynomial using determinant properties if we know this polynomial for a connected 2-regular graph:

Theorem 2.1

The formula for the sum-edge characteristic polynomial of the cycle graph Cn obtained by means of the sum-edge matrix is PCnse(λ)=−22n+1−∑k=0⌊(n−2)/2⌋(−1)k24k+5×n−2−kn−2−2kλn−2−2k+∑k=0⌊(n−1)/2⌋(−1)k24k×n−1−kn−1−2kλn−2k.

Proof.

The sum-edge matrix of Cn is SMe(Cn)=04000⋯00440400⋯00004040⋯00000404⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯40440000⋯040. Hence ∣λI−SMe(Cn)∣=λ−4000⋯00−4−4λ−400⋯0000−4λ−40⋯00000−4λ−4⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−4−40000⋯0−4λ.

If we calculate this determinant according to the last row, we get =(−1)n+2⋅4−40000⋯00−4λ−4000⋯000−4λ−400⋯0000−4λ−40⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯λ−4000000⋯−4λ−4+(−1)2n⋅4λ−4000⋯00−4−4λ−400⋯0000−4λ−40⋯00000−4λ−4⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ000000⋯0−4−4+(−1)2n⋅λλ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ

If we calculate the determinant of the first matrix with respect to the first row and calculate the determinant of the second matrix according to the last column, then we get =(−1)n+5⋅16−40000⋯000λ−4000⋯000−4λ−400⋯0000−4λ−40⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯λ−4000000⋯−4λ−4+(−1)2n+3⋅16λ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ+(−1)3n+1⋅16−4λ−400⋯0000−4λ−40⋯00000−4λ−4⋯000000−4λ⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−400000⋯0−4λ00000⋯00−4+(−1)4n−1⋅16λ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ+λλ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ One can find the dimensions of the matrices are (n−2)×(n−2), (n−2)×(n−2), (n−2)×(n−2), (n−2)×(n−2), and (n−1)×(n−1), respectively.

Thanks to the determinant property of lower triangular matrices, we get PCnse(λ)=(−1)n+516(−4)n−2+(−1)2n+316PΔn−2(λ)+(−1)3n+116(−4)n−2+(−1)4n−116PΔn−2(λ)+λPΔn−1(λ)⋅=−32⋅4n−2−32PΔn−2(λ)+λPΔn−1(λ). Hence we get PCnse(λ)=−22n+1−∑k=0⌊(n−2)/2⌋(−1)k24k+5×n−2−kn−2−2kλn−2−2k+∑k=0⌊(n−1)/2⌋(−1)k24k×n−1−kn−1−2kλn−2k.

Now we calculate the sum-edge characteristic polynomial of some other graph classes. We have already considered the cycle graphs during our general study of regular graphs. Now we start with the path graph Pn.

Theorem 2.2

The formula for the sum-edge characteristic polynomial of the path graph Pn is PPnse(λ)=∑k=0⌊(n−2)/2⌋(−1)k24kn−2−kn−2−2kλn−2k−18∑k=0⌊(n−3)/2⌋(−1)k24kn−3−kn−3−2kλn−2−2k+81∑k=0⌊(n−4)/2⌋(−1)k24kn−4−kn−4−2kλn−4−2k if n≥ 4 and PP1se(λ)=λ, PP2se(λ)=λ2−4, PP3se(λ)=λ3−18λ.

Proof.

The sum-edge characteristic polynomial PPnse(λ) of a path graph Pn is obtained by taking the determinant PPnse(λ)=λ−3000⋯000−3λ−400⋯0000−4λ−40⋯00000−4λ−4⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯λ−4000000⋯−4λ−300000⋯0−3λ. For n=1, the one dimensional matrix whose single entry is 0. Therefore PP1se(λ)=λ. For n=2,3, the proof is obvious.

If we calculate PPnse(λ) for n≥ 4 with respect to the first row, we get PPnse(λ)=λλ−4000⋯000−4λ−400⋯0000−4λ−40⋯00000−4λ−4⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−300000⋯0−3λ+3−3−4000⋯0000λ−400⋯0000−4λ−40⋯00000−4λ−4⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−300000⋯0−3λ. If we calculate the determinant of the second matrix according to the first column, we get PPnse(λ)=λλ−4000⋯000−4λ−400⋯0000−4λ−40⋯00000−4λ−4⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−300000⋯0−3λ−9λ−4000⋯000−4λ−400⋯0000−4λ−40⋯00000−4λ−4⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−300000⋯0−3λ. The dimension of the first matrix is (n−1)×(n−1) and the dimension of the second matrix is (n−2)×(n−2). Let's calculate the determinant of the first and second matrices with respect to the last row, then we get =−3λ(−1)2n−3λ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ0000⋯0−4−3+(−1)2n−2λ2λ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ+27(−1)2n−5λ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ0000⋯0−4−3+−9λ(−1)2n−4λ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ. If we calculate the determinants of first and third matrices according to the last column, we get =−9λλ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ+λ2λ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ+81λ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ−9λλ−40⋯000−4λ−4⋯0000−4λ⋯000⋅⋅⋅⋅⋅⋅000⋯λ−40000⋯−4λ−4000⋯0−4λ. The dimension of the first and last matrices are (n−3)×(n−3); the dimension of the second matrix is (n−2)×(n−2), and finally the dimension of the third matrix is (n−4)×(n−4). PPnse(λ)=λ2PΔn−2(λ)−18λPΔn−3(λ)+81PΔn−4(λ). Consequently, we can write the formula for sum-edge characteristic polynomial of the path graph Pn as follows: PPnse(λ)=∑k=0⌊(n−2)/2⌋(−1)k24kn−2−kn−2−2kλn−2k−18∑k=0⌊(n−3)/2⌋(−1)k24kn−3−kn−3−2kλn−2−2k+81∑k=0⌊(n−4)/2⌋(−1)k24kn−4−kn−4−2kλn−4−2k.

Now we can obtain the sum-edge characteristic polynomial of the tadpole graphs:

Theorem 2.3

The formula for the sum-edge characteristic polynomial of the tadpole graph Tr,s obtained by means of the sum-edge matrix is PTr,sse(λ)=PΔr−1(λ)λ2−16−50λPΔr−2(λ)−25⋅22r−3λ,s=1PΔr−1(λ)(λ3−34λ)−50(λ2−9)(PΔr−2(λ)+22r−4),s=2λPΔs−1(λ)λPΔr−1(λ)−50PΔr−2(λ)+22r−4+PΔs−2(λ)−34λPΔr−1(λ)+450PΔr−2(λ)+22r−4+225PΔs−3(λ)PΔr−1(λ),s>2.

Proof.

Let s=1. First note that PTr,1se(λ)=λ−4000⋯000−4λ−500⋯00−50−5λ−40⋯00000−4λ−4⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−40−5000⋯0−4λ. If we calculate this determinant with respect to second row, we get =4−40000⋯000−5λ−400⋯0000−4λ−40⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−4−50000⋯0−4λ+λλ0000⋯0000λ−400⋯0000−4λ−40⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−400000⋯0−4λ+5λ−4000⋯0000−5−400⋯00000λ−40⋯00000−4λ−4⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−40−5000⋯0−4λ+(−1)r+3(−5)λ−4000⋯0000−5λ−40⋯00000−4λ0⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−40−5000⋯0−4λ. If we calculate the third determinant with respect to the second row and calculate the last determinant according to the last row, we get PTr,1se(λ)=−16PΔr−1(λ)+λ2PΔr−1(λ)+5−5λ0000⋯00−60λ−400⋯0000−4λ−40⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−400000⋯0−4λ+4λ−400⋯00000−40⋯00000λ−4⋯000000−4⋯000⋅⋅⋅⋅⋯⋅⋅⋅0000⋯0−4λ0−500⋯00−4+5⋅(−1)r+45⋅(−1)r+3λ0000⋯0000λ−400⋯0000−4λ−40⋯000⋅⋅⋅⋅⋅⋯⋅⋅⋅00000⋯−4λ−400000⋯0−4λ+−4λ−400⋯0000−5λ−4⋯00000−4λ⋯000000−4⋯000⋅⋅⋅⋅⋯⋅⋅⋅0000⋯0−4λ0000⋯00−4. Then we get PTr,1se(λ)=PΔr−1(λ)λ2−16−50λPΔr−2(λ)−25⋅22r−3λ. Let s=2. The form of PTr,2se(λ) is PTr,2se(λ)=λ−300000⋯000−3λ−50000⋯0000−5λ−5000⋯00−500−5λ−400⋯000000−4λ−40⋯000⋅⋅⋅⋅⋯⋅⋅⋅⋅⋅⋅0000⋯00−4λ−400000⋯000−4λ−400−50⋯0000−4λ. If we calculate this determinant with respect to the third row, then we get =5λ000000⋯000−3−500000⋯0000−5λ−4000⋯00000−4λ−400⋯000000−4λ−40⋯000⋅⋅⋅⋯⋅⋅⋅⋅⋅⋅⋅000⋯000−4λ−40000⋯0000−4λ−40−50⋯00000−4λ+λλ−300000⋯000−3λ00000⋯00000λ−4000⋯00000−4λ−400⋯000000−4λ−40⋯000⋅⋅⋅⋯⋅⋅⋅⋅⋅⋅⋅000⋯000−4λ−40000⋯0000−4λ−4000⋯00000−4λ+5λ−300000⋯000−3λ−50000⋯00000−5−4000⋯000000λ−400⋯000000−4λ−40⋯000⋅⋅⋅⋅⋯⋅⋅⋅⋅⋅⋅0000⋯00−4λ−400000⋯000−4λ−400−50⋯0000−4λ+(−1)r+5(−5)λ−300000⋯00−3λ−50000⋯0000−5λ−400⋯00000−4λ−40⋯000000−4λ−4⋯00⋅⋅⋅⋅⋯⋅⋅⋅⋅⋅0000⋯00−4λ−40000⋯000−4λ00−50⋯0000−4 If we calculate the determinant of the third matrix according to the third row, this third determinant becomes λ−300000⋯00−3λ−50000⋯00000−4000⋯00000λ−400⋯00000−4λ−40⋯00⋅⋅⋅⋅⋯⋅⋅⋅⋅⋅0000⋯00−4λ−400−50⋯000−4λ. If we continue to reduce this determinant according to the third row until the lower right block matrix is in the form 0−4−5λ, then the third determinant is calculated. Similarly continuing, we get PTr,2se(λ)=PΔr−1(λ)(λ3−34λ)−50(λ2−9)(PΔr−2(λ)+22r−4). Finally, let s>2. The form of PTr,sse(λ) is PTr,sse(λ)=λ−300⋯000000000−3λ−40⋯00000000⋅0−4λ0⋯00000000⋅⋅⋯⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅0⋯00−4λ−40000⋯000⋯000−4λ−5000⋯000⋯0000−5λ−500⋯0−50⋯00000−5λ−40⋯000⋯000000−4λ−4⋯00⋅⋯⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅0⋯000000000−4λ−40⋯00000−50000−4λ.

If we calculate the determinant of this matrix according to the (s+1)th row, and continuing as above, we get PTr,sse(λ)=λPΔs−1(λ)[λPΔr−1(λ)−50PΔr−2(λ)+22r−4]+PΔs−2(λ)−34λPΔr−1(λ)+450PΔr−2(λ)+22r−4+225PΔs−3(λ)PΔr−1(λ). Hence the result follows.

Recall that the determinant of any matrix A is equal to the product of its eigenvalues λk. So we have

Theorem 2.4

The formula for the sum-edge characteristic polynomial of the star graph Sn obtained by means of the sum-edge matrix is PSnse(λ)=λn−2λ2−n2(n−1).

Proof.

Let n=2. Then ∣SMe(S2)∣=−4≠0. So, none of the eigenvalues can be zero, then the form of PSnse(λ) is PSnse(λ)=λ−n000⋯00−nλ−n−n−n⋯−n−n0−nλ00⋯000−n000⋯00⋅⋅⋅⋯⋅⋅0⋅0−n0⋯00λ00−n0⋯000λ. If we divide the matrix into block matrices so that the upper left one is 2×2 and the lower right one is (n−2)×(n−2) and if we use the following elementary row operations nλR3+R2⟶R2nλR4+R2⟶R2⋯nλRn+R2⟶R2. If the process continue, then we get PSnse(λ)=λ−n0000⋯00−nλ−(n−2)n2λ0000⋯000−nλ000⋯00⋅⋅⋅⋅⋅⋅⋅⋅⋅0−n000⋯0λ00−n000⋯00λ. By Lemma 2.1, we obtain =λ2−(n−2)n2−n2λn−2=λn−2λ2−n2(n−1). Let now n≥3. ∣SMe(Sn)∣=0n000⋯00n0nnn⋯nn0n000⋯00⋅⋅⋅⋅⋅⋅⋅⋅0n0⋯00000n0⋯0000. Thanks to elementary row operations, we see that ∣SMe(Sn)∣=0. By the above argument, at least one of the eigenvalues must be equal to zero. If λ=0, then we get ∣λI−SMe(Sn)∣=∣0I−SMe(Sn)∣=∣−SMe(Sn)∣=(−1)n∣SMe(Sn)∣=0. Also PSnse(λ)=λn−2λ2−n2(n−1). In this equation PSnse(0)=0 so the result is verified.

If λ≠0, then we have the form of PSnse(λ) as PSnse(λ)=λ−n000⋯00−nλ−n−n−n⋯−n−n0−nλ00⋯000−n000000⋅⋅⋅⋯⋅⋅⋅⋅0−n0⋯00λ00−n0⋯000λ. Proceeding as above, the result is obtained.

Now we calculate the sum-edge characteristic polynomial of the complete graph Kn:

Theorem 2.5

The formula for the sum-edge characteristic polynomial of the complete graph Kn obtained by means of the sum-edge matrix is PKnse(λ)=λ−2(n−1)2λ+2(n−1)n−1.

Proof.

PKnse(λ)=λ−2(n−1)−2(n−1)−2(n−1)λ−2(n−1)⋅⋅⋅−2(n−1)⋯−2(n−1)−2(n−1)⋯−2(n−1)⋯−2(n−1)⋯−2(n−1)⋅⋅λ−2(n−1)−2(n−1)λ. If we use the elementary row operation R1+R2+⋯+Rn⟶R1, we get =λ−2(n−1)2λ−2(n−1)2λ−2(n−1)2−2(n−1)λ−2(n−1)⋅⋅⋅−2(n−1)⋯−2(n−1)−2(n−1)⋯−2(n−1)⋯λ−2(n−1)2⋯−2(n−1)⋅⋅λ−2(n−1)−2(n−1)λ=λ−2(n−1)2111−2(n−1)λ−2(n−1)⋅⋅⋅−2(n−1)⋯−2(n−1)−2(n−1)⋯−2(n−1)⋯1⋯−2(n−1)⋅⋅λ−2(n−1)−2(n−1)λ. If we use the elementary row operations 2(n−1)R1+R2⟶R22(n−1)R1+R3⟶R3⋯2(n−1)R1+Rn⟶Rn, we get =λ−2(n−1)21110λ+2(n−1)0⋅⋅⋅0⋯00⋯0⋯1⋯0⋅⋅λ+2(n−1)00λ+2(n−1)=λ−2(n−1)2λ+2(n−1)n−1.

Finally, we shall calculate the sum-edge characteristic polynomial of the complete bipartite graph Kr,s. We shall omit the proof as it is similar to the above cases.

Theorem 2.6

The formula for the sum-edge characteristic polynomial of the complete bipartite graph Kr,s obtained by means of the sum-edge matrix is PKr,sse(λ)=λr+s−2λ2−(r+s)2rs.

Disclosure statement

No potential conflict of interest was reported by the authors.

References

  • Bapat RB. Graphs and matrices. London: Springer; 2014.
  • Janežič D, Miličević A, Nikolić S, et al. Graph theoretical matrices in chemistry. Kragujevac: CRC Press/Taylor and Francis Group; 2015.
  • Celik F, Cangul IN. Formulae and recurrence relations on spectral polynomials of some graphs. Adv Stud Contemp Math. 2017;27(3):325–332.
  • Celik F, Cangul IN. Some recurrence relations for the energy of cycle and path graphs. Proc Jangjeon Math Soc. 2018;21(3):347–355.
  • Celik F, Cangul IN. On the spectra of cycles and paths. Turkic World Math Soc J Appl Eng Math. 2019 (in press).
Download PDF

Related research

People also read lists articles that other readers of this article have read.

Recommended articles lists articles that we recommend and is powered by our AI driven recommendation engine.

Cited by lists all citing articles based on Crossref citations.
Articles with the Crossref icon will open in a new tab.