The motion of infinitesimal body in CR4BP with variable masses and Albedo effect

ABSTRACT

This paper presents the effect of Albedo on the behaviour of the fourth body in the CR4BP with the variation of masses of all bodies. By using Meshcherskii transformation, we have determined the equations of motion and found how Jacobi-integral constant varies with time due to variable masses. We have plotted the Lagrangian points, the periodic orbits, Poincaré surface of sections and basins of attraction for four cases (a. Classical Case, b. Variation of mass, c. Solar radiation pressure effect, d. Albedo effect). And then, we checked the stability of Lagrangian points at the Albedo effect only and got all the points are unstable.

Keywords:

• Lagrangian points
• stability
• radiation pressure
• periodic orbits
• Poincaré surface of sections
• basins of attraction
• variable masses
• Albedo

Mathematics Subject Classifications:

• 08A72
• 70F15
• 37N05

1. Introduction

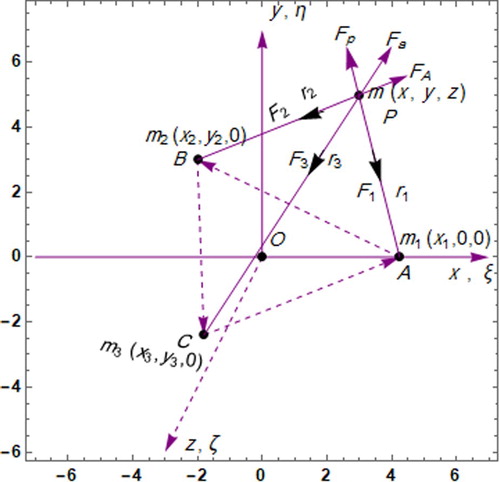
In the restricted four-body problem (R4BP), three bodies are placed at vertices of a triangle, they are moving under their mutual gravitational attractions around their common centre of mass and fourth body is moving in the space under the influence of the primaries but not influencing them.

Many mathematicians and physicists have studied this model. Moulton [1] evaluated the particular solution of the four-body problem. Simo [2] studied linear stability of relative Lagrangian solutions in the four-body problem. Majorana [3] checked the stability of the Lagrangian points which depends on the values of primary masses. Michalodmitrakis [4] generalized R3BP to R4BP in which he studied about the equilibrium points, regions of possible motion and periodic orbits. Baltagiannis and Papadakis [5] investigated R4BP and got the equilibrium points depending the primaries masses. Abdullah [6] determined the periodic orbits around Lagrangian points in three cases (i) the spherical shape of all the primaries, (ii) one of the primaries as oblate body, (iii) two of the primaries as oblate bodies. Papadakis [7] studied the 3D symmetric periodic orbits of R4BP, through simple vertical bifurcation from plane orbits.

And also many scientists have studied about the solar radiation pressure in R4BP. Kalvouridis et al. [8] studied R4BP with the effect of solar radiation pressure but not considered the albedo effect. Papadouris et al. [9,10] studied the existence, the location, stability and periodic orbits of the equilibrium points on and out of the orbital plane in the photo-gravitational R4BP. Singh and Vincent [11,12] studied equilibrium points in CR4BP with the effect of solar radiation pressure and also not considered the albedo effect.

Many mathematicians studied CR3BP and CR4BP when the masses vary with time as Jeans [13], Meshcherskii [14], Shrivastava et al. [15], Lichtenegger [16], Singh et al. [17–21], Lukyanov [22], Zhang et al. [23], Abouelmagd et al. [24], Ansari et al. [25–30], Alhussain [31,32].

The sun is the greatest source of radiations in our solar system. The radiations emitted by the sun, some radiations absorbed by the planets and some radiations reflected back into the space. This reflected radiations are known as Albedo.

The circular as well as elliptic case of restricted three-body problem taking into account albedo effect is studied by Anselmo et al. [33], Bhanderi et al. [34], Harris et al. [35], Idrisi et al. [36–40], MacDonald et al. [41], Pontus et al. [42], Rocco [43].On the other hand, many scientists illustrated the basins of attraction in both CR3BP and CR4BP cases as Douskos [44], Kumari et al.[45], Zotos [46,47], Ansari [28–30].

Taking on account of the above literature, we have performed the motion of the fourth body in CR4BP in which the masses of the all four body vary and also albedo effect is considered. This study contains various sections. First, we have formulated the equations of motion and also determined the expression for the variation of Jacobi Integral constant. Second, plotted numerically the Lagrangian points, periodic orbits, Poincaré surface of sections and basins of attraction in four cases. Third, checked the stability of the all points under the effect of perturbations. And finally, concluded the problem.

2. Equations of motion

Let $m_1\left(t\right)$, $m_2\left(t\right)$, $m_3\left(t\right)$ and $m\left(t\right)$ be four variable masses in which three primaries $m_1\left(t\right)$, $m_2\left(t\right)$ and $m_3\left(t\right)$ are placed at an equilateral triangle ABC with side ℓ. They are moving under their mutual gravitational force around their common centre which is considered as origin O. Here $m_1\left(t\right)$ is taken as the solar radiation pressure $\left(F_p\right)$ due to which $m_2\left(t\right)$ and $m_3\left(t\right)$ are producing Albedo $F_A$ and $F_a$, respectively (i.e. Albedo = (radiation reflected back into space)/(incident radiation)). The fourth body $m\left(t\right)$ is moving in space under gravitational forces $(F_1,F_2$ and $F_3)$ of the primaries but not influencing them. The total force on infinitesimal body will be $F=(F_1-F_p)+(F_2-F_A)+(F_3-F_a)=F_1(1-{\epsilon }_1)+F_2(1-{\epsilon }_2)+F_3(1-{\epsilon }_3)$, where $0\le {\epsilon }_1=F_p/F_1<1,0\le {\epsilon }_2=F_A/F_2<{\epsilon }_1,0\le {\epsilon }_3=F_a/F_3<{\epsilon }_1.$ Let the coordinates of $m_1\left(t\right)$, $m_2\left(t\right)$, $m_3\left(t\right)$ and $m\left(t\right)$ in the rotating frame be $(x_1,0,0),(x_2,y_2,0),(x_3,y_3,0)$ and $(x,y,z)$, respectively (Figure 1). Let the inertial frame be coincident with the rotating frame which has angular velocity $\omega \left(t\right).$ Following the procedure given in Abouelmagd et al. [24] and Alhussain [32], we can write the equations of motion of the fourth body in the rotating coordinate system when the variation is non-isotropic with zero momentum as (1) $\begin{array}{rl}& \frac{\dot{m}\left(t\right)}{m\left(t\right)}(\dot{x}-\omega (t\left)y\right)+(\ddot{x}-\dot{\omega }(t)y-2\omega (t)\dot{y}-{\omega }^2(t\left)x\right)\\ & =-\frac{{\mu }_1\left(t\right)(x-x_1)(1-{\epsilon }_1)}{r_1^3}-\frac{{\mu }_2\left(t\right)(x-x_2)(1-{\epsilon }_2)}{r_2^3}\\ & -\frac{{\mu }_3\left(t\right)(x-x_3)(1-{\epsilon }_3)}{r_3^3},\\ & \frac{\dot{m}\left(t\right)}{m\left(t\right)}(\dot{y}+\omega (t\left)x\right)+(\ddot{y}+\dot{\omega }(t)x+2\omega (t)\dot{x}-{\omega }^2(t\left)y\right)\\ & =-\frac{{\mu }_1\left(t\right)y(1-{\epsilon }_1)}{r_1^3}-\frac{{\mu }_2\left(t\right)y(1-{\epsilon }_2)}{r_2^3}\\ & -\frac{{\mu }_3\left(t\right)y(1-{\epsilon }_3)}{r_3^3},\\ & \frac{\dot{m}\left(t\right)}{m\left(t\right)}\dot{z}+\ddot{z}=-\frac{{\mu }_1\left(t\right)z(1-{\epsilon }_1)}{r_1^3}-\frac{{\mu }_2\left(t\right)z(1-{\epsilon }_2)}{r_2^3}\\ & -\frac{{\mu }_3\left(t\right)z(1-{\epsilon }_3)}{r_3^3}.\end{array}$(1) where $r_i^2=(x-x_i{)}^2+(y-y_i{)}^2+z^2$ are the distances from the primaries to the fourth body, respectively, ${\mu }_i\left(t\right)=G{m}_i\left(t\right)$. Using Meshcherskii transformation $\begin{array}{rl}x& =\xi R\left(t\right),y=\eta R\left(t\right),z=\zeta R\left(t\right),\frac{\mathrm{d}t}{\mathrm{d}\tau }=R^2\left(t\right),\\ r_i& ={\rho }_{i}R\left(t\right),\omega \left(t\right)=\frac{{\omega }_0}{R^2\left(t\right)},\\ x_i& ={\xi }_{i}R\left(t\right),y_i={\eta }_{i}R\left(t\right),\mu \left(t\right)={\mu }_1\left(t\right)+{\mu }_2\left(t\right)\\ & +{\mu }_3\left(t\right)=\frac{{\mu }_0}{R\left(t\right)},{\mu }_i\left(t\right)=\frac{{\mu }_{i0}}{R\left(t\right)},\\ m\left(t\right)& =\frac{m_0}{R\left(t\right)},R\left(t\right)=\sqrt{\alpha t^2+2\beta t+\gamma },\end{array}$ where $\alpha ,\beta ,\gamma ,{\mu }_0,{\mu }_{i0},m_0$ are constants for $i=1,2,3$ and $R\left(t\right)$ shows the relation between both times t and τ.

The system (1(1) $\begin{array}{rl}& \frac{\dot{m}\left(t\right)}{m\left(t\right)}(\dot{x}-\omega (t\left)y\right)+(\ddot{x}-\dot{\omega }(t)y-2\omega (t)\dot{y}-{\omega }^2(t\left)x\right)\\ & =-\frac{{\mu }_1\left(t\right)(x-x_1)(1-{\epsilon }_1)}{r_1^3}-\frac{{\mu }_2\left(t\right)(x-x_2)(1-{\epsilon }_2)}{r_2^3}\\ & -\frac{{\mu }_3\left(t\right)(x-x_3)(1-{\epsilon }_3)}{r_3^3},\\ & \frac{\dot{m}\left(t\right)}{m\left(t\right)}(\dot{y}+\omega (t\left)x\right)+(\ddot{y}+\dot{\omega }(t)x+2\omega (t)\dot{x}-{\omega }^2(t\left)y\right)\\ & =-\frac{{\mu }_1\left(t\right)y(1-{\epsilon }_1)}{r_1^3}-\frac{{\mu }_2\left(t\right)y(1-{\epsilon }_2)}{r_2^3}\\ & -\frac{{\mu }_3\left(t\right)y(1-{\epsilon }_3)}{r_3^3},\\ & \frac{\dot{m}\left(t\right)}{m\left(t\right)}\dot{z}+\ddot{z}=-\frac{{\mu }_1\left(t\right)z(1-{\epsilon }_1)}{r_1^3}-\frac{{\mu }_2\left(t\right)z(1-{\epsilon }_2)}{r_2^3}\\ & -\frac{{\mu }_3\left(t\right)z(1-{\epsilon }_3)}{r_3^3}.\end{array}$(1) ) becomes (2) $\begin{array}{rl}& {\xi }^{″}-2{\omega }_0{\eta }^{\prime }-(\alpha t+\beta ){\xi }^{\prime }=\frac{\mathrm{\partial }V}{\mathrm{\partial }\xi },\\ & {\eta }^{″}+2{\omega }_0{\xi }^{\prime }-(\alpha t+\beta ){\eta }^{\prime }=\frac{\mathrm{\partial }V}{\mathrm{\partial }\eta },\\ & {\zeta }^{″}-(\alpha t+\beta ){\zeta }^{\prime }=\frac{\mathrm{\partial }V}{\mathrm{\partial }\zeta },\end{array}$(2) where $\begin{array}{rl}V& =\frac{1}{2}\left(\right(\alpha t+\beta {)}^2+{\omega }_0^2-(\alpha \gamma -{\beta }^2)\left)\right({\xi }^2+{\eta }^2)\\ & +\frac{1}{2}\left(\right(\alpha t+\beta {)}^2-(\alpha \gamma -{\beta }^2)){\zeta }^2\\ & -(\alpha t+\beta )\xi \eta +\frac{{\mu }_{10}(1-{\epsilon }_1)}{{\rho }_1}+\frac{{\mu }_{20}(1-{\epsilon }_2)}{{\rho }_2}\\ & +\frac{{\mu }_{30}(1-{\epsilon }_3)}{{\rho }_3},\\ {\rho }_i^2& =(\xi -{\xi }_i{)}^2+(\eta -{\eta }_i{)}^2+{\zeta }^2.\end{array}$ Prime (${}^{\prime }$) is w.r.to τ. Putting unit of mass, distance and time $t_0$ such that $\begin{array}{rl}& {\mu }_0=1,G=1,\ell =1,{\omega }_0=1,\\ & \alpha t_0+\beta ={\alpha }_1\left(constant\right).\end{array}$ New parameter as ${\mu }_{10}={\mu }_{20}={\mu }_{30}=\upsilon =1/3$ (all the masses of the primaries are taken as equal), where υ is the ratio of the mass.

Figure 1. The geometric configuration of the problem in CR4BP with Albedo.

Finally, (2(2) $\begin{array}{rl}& {\xi }^{″}-2{\omega }_0{\eta }^{\prime }-(\alpha t+\beta ){\xi }^{\prime }=\frac{\mathrm{\partial }V}{\mathrm{\partial }\xi },\\ & {\eta }^{″}+2{\omega }_0{\xi }^{\prime }-(\alpha t+\beta ){\eta }^{\prime }=\frac{\mathrm{\partial }V}{\mathrm{\partial }\eta },\\ & {\zeta }^{″}-(\alpha t+\beta ){\zeta }^{\prime }=\frac{\mathrm{\partial }V}{\mathrm{\partial }\zeta },\end{array}$(2) ) becomes (3) $\begin{array}{rl}& {\xi }^{″}-2{\eta }^{\prime }-{\alpha }_1{\xi }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\xi },\\ & {\eta }^{″}+2{\xi }^{\prime }-{\alpha }_1{\eta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\eta },\\ & {\zeta }^{″}-{\alpha }_1{\zeta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\zeta }.\end{array}$(3) where $\mathrm{\Lambda }=\frac{1}{2}({\alpha }_1^2+k)({\xi }^2+{\eta }^2+{\zeta }^2)-\frac{1}{2}{\zeta }^2-{\alpha }_1\xi \eta +\left(\upsilon (1-{\epsilon }_1)/{\rho }_1\right)+\left(\upsilon (1-{\epsilon }_2)/{\rho }_2\right)+\left(\upsilon (1-{\epsilon }_3)/{\rho }_3\right),$ ${\rho }_i^2=(\xi -{\xi }_i{)}^2+(\eta -{\eta }_i{)}^2+{\zeta }^2,\alpha \gamma -{\beta }^2=1-k$ and $({\xi }_1,{\eta }_1)=(1/\sqrt{3},0)$,$({\xi }_2,{\eta }_2)=(-1/2\sqrt{3},\frac{1}{2})$, $({\xi }_3,{\eta }_3)=(-1/2\sqrt{3},\frac{-1}{2}).$

If there are constant masses, then there is a constant motion (i.e. Moulton [48]), the Jacobi Integral constant defined as (4) $J_c=2\mathrm{\Lambda }-2\left(\right({\xi }^{\prime }{)}^2+({\eta }^{\prime }{)}^2+({\zeta }^{\prime }{)}^2).$(4) Multiplying in the first part of (3(3) $\begin{array}{rl}& {\xi }^{″}-2{\eta }^{\prime }-{\alpha }_1{\xi }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\xi },\\ & {\eta }^{″}+2{\xi }^{\prime }-{\alpha }_1{\eta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\eta },\\ & {\zeta }^{″}-{\alpha }_1{\zeta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\zeta }.\end{array}$(3) ) by ${\xi }^{\prime }$, in the second part of (3(3) $\begin{array}{rl}& {\xi }^{″}-2{\eta }^{\prime }-{\alpha }_1{\xi }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\xi },\\ & {\eta }^{″}+2{\xi }^{\prime }-{\alpha }_1{\eta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\eta },\\ & {\zeta }^{″}-{\alpha }_1{\zeta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\zeta }.\end{array}$(3) ) by ${\eta }^{\prime }$ and in the third equation of (3(3) $\begin{array}{rl}& {\xi }^{″}-2{\eta }^{\prime }-{\alpha }_1{\xi }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\xi },\\ & {\eta }^{″}+2{\xi }^{\prime }-{\alpha }_1{\eta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\eta },\\ & {\zeta }^{″}-{\alpha }_1{\zeta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\zeta }.\end{array}$(3) ) by ${\zeta }^{\prime }$ and add and using Equation (4(4) $J_c=2\mathrm{\Lambda }-2\left(\right({\xi }^{\prime }{)}^2+({\eta }^{\prime }{)}^2+({\zeta }^{\prime }{)}^2).$(4) ), we get the variation of the Jacobi Integral constant as (5) $\frac{\mathrm{d}{J}_c}{\mathrm{d}\tau }=-2{\alpha }_1\left(\right({\xi }^{\prime }{)}^2+({\eta }^{\prime }{)}^2+({\zeta }^{\prime }{)}^2),$(5) where $J_c$ is the Jacobi Integral Constant.

3. Computational work

Here, plotted numerically the Lagrangian points, the periodic orbits, the Poincaré surfaces of section and the basins of attraction for four different cases by using Mathematica software:

1. Classical case (i.e. $k=1,{\alpha }_1=0,{\epsilon }_1=0,{\epsilon }_2=0,{\epsilon }_3=0$),

2. Variation of masses (i.e. $k=0.4,{\alpha }_1=0.2,{\epsilon }_1=0,{\epsilon }_2=0,{\epsilon }_3=0$),

3. Solar radiation pressure (i.e. $k=0.4,{\alpha }_1=0.2,{\epsilon }_1=0.5,{\epsilon }_2=0,{\epsilon }_3=0$),

4. Albedo effect (i.e. $k=0.4,{\alpha }_1=0.2,{\epsilon }_1=0.5,{\epsilon }_2=0.3,{\epsilon }_3=0.2$).

3.1. Lagrangian points during motions

The Lagrangian points are the solutions of ${\mathrm{\Lambda }}_{\xi }=0,{\mathrm{\Lambda }}_{\eta }=0$, and ${\mathrm{\Lambda }}_{\zeta }=0,$ but the solutions of these equations represent the locations during in-plane motions when $(\xi \ne 0,\eta \ne 0,\zeta =0)$, (Figure 2) and represent the locations of the out of planes when $(\xi \ne 0,\eta =0,\zeta \ne 0)$, (Figure 3) and $(\xi =0,\eta \ne 0,\zeta \ne 0)$,(Figure 4), where (6) $\begin{array}{rl}{\mathrm{\Lambda }}_{\xi }& =({\alpha }_1^2+k)\xi -{\alpha }_1\eta -\frac{\upsilon (\xi -{\xi }_1)(1-{\epsilon }_1)}{{\rho }_1^3}\\ & -\frac{\upsilon (\xi -{\xi }_2)(1-{\epsilon }_2)}{{\rho }_2^3}-\frac{\upsilon (\xi -{\xi }_3)(1-{\epsilon }_3)}{{\rho }_3^3},\end{array}$(6) (7) $\begin{array}{rl}{\mathrm{\Lambda }}_{\eta }& =({\alpha }_1^2+k)\eta -{\alpha }_1\xi -\frac{\upsilon \eta (1-{\epsilon }_1)}{{\rho }_1^3}\\ & -\frac{(1-{\epsilon }_2)\upsilon (\eta -{\eta }_2)}{{\rho }_2^3}-\frac{\upsilon (\eta -{\eta }_3)(1-{\epsilon }_3)}{{\rho }_3^3},\end{array}$(7) (8) $\begin{array}{rl}{\mathrm{\Lambda }}_{\zeta }& =({\alpha }_1^2+k-1)\zeta -\frac{(1-{\epsilon }_1)\upsilon \zeta }{{\rho }_1^3}-\frac{(1-{\epsilon }_2)\upsilon \zeta }{{\rho }_2^3}\\ & -\frac{\upsilon \zeta (1-{\epsilon }_3)}{{\rho }_3^3}.\end{array}$(8)

Figure 2. The positions of Lagrangian points during in-plane motion (i.e. $\xi \ne 0,\eta \ne 0,\zeta =0$) in four cases.

Figure 3. The positions of Lagrangian points during out of plane motion (i.e. $\xi \ne 0,\eta =0,\zeta \ne 0$ ) in four cases.

Figure 4. The positions of Lagrangian points during out of plane motion (i.e. $\xi =0,$ $\eta \ne 0,$ $\zeta \ne 0$) in four cases.

3.1.1. During in-plane motion (i.e. $\xi \ne 0,\eta \ne 0,\zeta =0$) positions of Lagrangian points

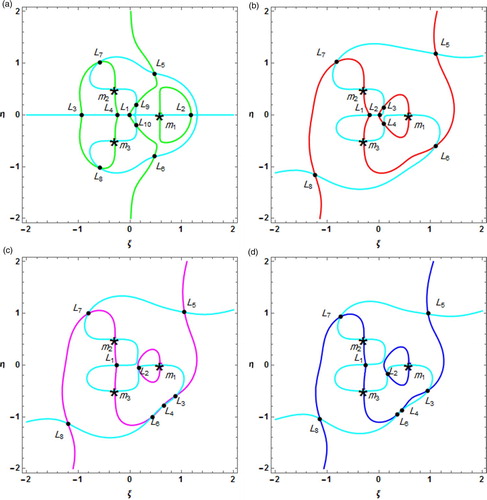
During in-plane motion, we have plotted graphs for the locations of the Lagrangian points in four cases. We found ten Lagrangian points in which four points ($L_1,L_2,L_3,L_4$) are collinear and six points ($L_5,L_6,L_7,L_8,L_9,L_{10}$) are non-collinear and also ($L_5,L_6$), ($L_7,L_8$), ($L_9,L_{10}$) are symmetrical with respect to the ξ-axis in the classical case (Figure 2(a)). It is observed that the Lagrangian points ($L_1,L_4,L_9,L_{10}$) and ($L_2,L_3,L_5,L_6,L_7,L_8$) exist inside and outside of the Lagrangian configuration, respectively. In the variable mass case, we found eight Lagrangian points (Figure 2(b)) in which two points $L_1,L_2$ are collinear but rest six points $L_3,L_4,L_5,L_6,L_7,L_8$ are non-collinear. Here only ($L_3,L_4$) are symmetrical and rests points are non-symmetrical. It is observed that the Lagrangian points ($L_1,L_2,L_3,L_4$) and ($L_5,L_6,L_7,L_8$) exist inside and outside of the Lagrangian configuration, respectively. In the solar radiation case, we found eight Lagrangian points (Figure 2(c)) in which two points $L_1,L_2$ are collinear and six points $L_3,L_4,L_5,L_6,L_7,L_8$ are non-collinear. It is observed that the Lagrangian points ($L_1,L_2$) and ($L_3,L_4,L_5,L_6,L_7,L_8$) exist inside and outside of the Lagrangian configuration, respectively. On the other hand with the Albedo effects, we found eight Lagrangian points (Figure 2(d)) in which only one point ($L_1$) is on the ξ-axis and rest seven points are non-collinear. Here also the Lagrangian points ($L_1,L_2$) and ($L_3,L_4,L_5,L_6,L_7,L_8$) exist inside and outside of the Lagrangian configuration, respectively. In all the figures, black dot and black stars denote the locations of Lagrangian points and the primaries, respectively.

3.1.2. During out of plane (i.e. $\xi \ne 0,\eta =0,\zeta \ne 0$ and $\xi =0,\eta \ne 0,\zeta \ne 0$) the locations of Lagrangian points

During out of plane (i.e. $\xi \ne 0,\eta =0,\zeta \ne 0$), we found three Lagrangian points on the ξ-axis in the first case (Figure 3(a)). The points ($L_1,L_3$) and $L_2$ lie left and right side of the origin, respectively. In the variable mass case, we found four Lagrangian points on the ξ-axis (Figure 3(b)). The points ($L_3,L_4$) and $L_2$ lie left and right side of the origin, respectively, but point $L_1$ lie at the origin. In the solar radiation case, we found four Lagrangian points on the ξ-axis (Figure 3(c)). The points ($L_3,L_4$) and $L_1,L_2$ lie left and right side of the origin, respectively. On the other hand with the albedo effect, we found four Lagrangian points on the ξ-axis (Figure 3(d)). The points ($L_3,L_4$) and $L_1,L_2$ lie left and right side of the origin, respectively. It is observed from the Figure 3(e) that Lagrangian points are moving away from the origin from the classical case to the variable mass case and then towards the origin in the other cases. The black star denotes the location of the primary $m_1$.

On the other hand, during the out of plane (i.e. $\xi =0,\eta \ne 0,\zeta \ne 0$ ), we found five Lagrangian points (Figure 4) in all four cases. The points ($L_4,L_5$) and $L_2,L_3$ lie left and right side of the origin, respectively, but the point $L_1$ lie at the origin. It is also observed from the Figure 4(e) that Lagrangian points are moving away from the origin from the classical case to the variable mass case and then towards the origin in the other cases.

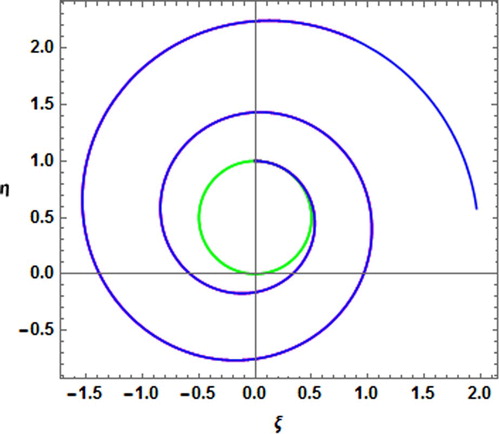
3.2. Periodic orbits

Here, periodic orbits studied in four cases. In the classical case, we found that the orbit is periodic (in green colour) but in the other three cases orbits are not periodic (Figure 5). In these three cases, orbits are overlapped but they have time difference in orbits, i.e. very small effect on the periodic orbits due to these perturbations.

Figure 5. Periodic orbits in four cases: (a). Green, (b). Red, (c). Magenta, (d). Blue. But Red, Magenta and Blue are overlapped.

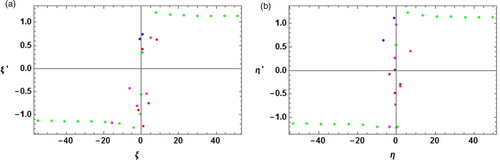
3.3. Poincaré surface of section

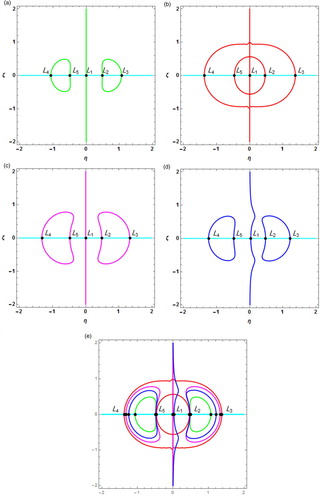
This section is devoted to illustrate the Poincaré surfaces for four cases in both the $(\xi -{\xi }^{\prime })$-plane (Figure 6(i)) and the $(\eta -{\eta }^{\prime })$-plane (Figure 6(ii)). We found that in both planes, the surfaces have the same discrete type pattern.

Figure 6. Poincaré surface of sections: (a). Classical case (Green),(b). variable mass case (Red), (c). radiation pressure (Magenta), (d). Albedo effect (Blue).

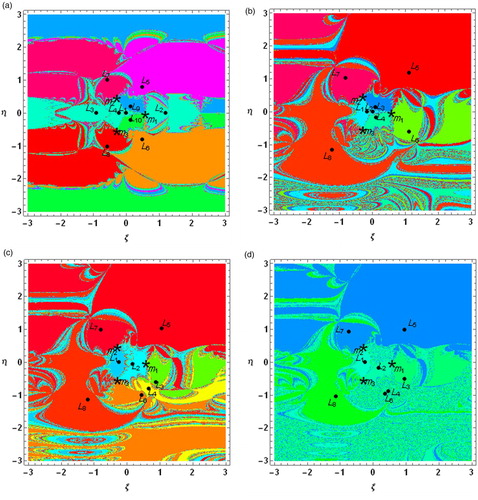
3.4. Basins of attraction

The N-R method is used very frequently for solving non-linear system of equations because it shows much better rate of convergence. And hence our aim is to draw the basins of attraction for CR4BP by using the N-R iterative method for the different cases (a. Classical Case, b. Variation of mass case, c. Solar radiation pressure effect, d. Albedo effect). The iterative algorithm of our problem is given by (9) $\begin{array}{rl}{\xi }_{n+1}& ={\xi }_n-{\left(\frac{{\mathrm{\Lambda }}_{\xi }{\mathrm{\Lambda }}_{\eta \eta }-{\mathrm{\Lambda }}_{\eta }{\mathrm{\Lambda }}_{\xi \eta }}{{\mathrm{\Lambda }}_{\xi \xi }{\mathrm{\Lambda }}_{\eta \eta }-{\mathrm{\Lambda }}_{\xi \eta }{\mathrm{\Lambda }}_{\eta \xi }}\right)}_{({\xi }_n,{\eta }_n)},\\ {\eta }_{n+1}& ={\eta }_n-{\left(\frac{{\mathrm{\Lambda }}_{\eta }{\mathrm{\Lambda }}_{\xi \xi }-{\mathrm{\Lambda }}_{\xi }{\mathrm{\Lambda }}_{\eta \xi }}{{\mathrm{\Lambda }}_{\xi \xi }{\mathrm{\Lambda }}_{\eta \eta }-{\mathrm{\Lambda }}_{\xi \eta }{\mathrm{\Lambda }}_{\eta \xi }}\right)}_{({\xi }_n,{\eta }_n)},\end{array}$(9) where ${\xi }_n,{\eta }_n$ are the coordinates of the $n^{th}$ step of the N-R process. 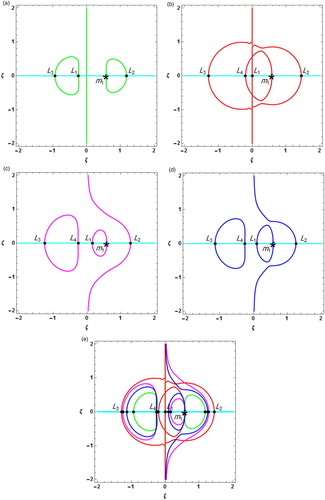If the initial point converges to one of the Lagrangian points then the point $(\xi ,\eta )$ is a member of the basin of attraction of the root. This stops when the successive process converges to a point. In the classical case (Figure 7(a)), $L_1,L_2,L_3$ and $L_4$ represent mint green colour regions, $L_5$ represents light purple colour region, $L_6$ represents orange colour region, $L_7,L_8$ represent red colour regions, $L_9$ represents light blue colour region and $L_{10}$ represents light green colour region. The basins of attraction corresponding to the Lagrangian points $L_1,L_3,L_4,L_5,L_6,L_7,L_8$ extend to infinity but the basins of attraction corresponding to the Lagrangian points $L_2,L_9,L_{10}$ cover finite area. In the variable mass case (Figure 7(b)), $L_1$ and $L_2$ represent cyan colour regions, $L_3$ represents light blue colour region, $L_4$ represents mint green colour region, $L_6$ represents light green colour region and $L_5,L_7,L_8$ represent red colour regions. The basins of attraction corresponding to the Lagrangian points $L_1,L_2,L_3,L_4,L_6$ cover finite areas but corresponding to the Lagrangian points $L_5,L_7,L_8$ extend to infinity. In the solar radiation pressure case (Figure 7(c)), $L_1$, $L_2$, $L_3$, $L_4$, $L_6$ and $(L_5,L_7,L_8)$ represent light blue, cyan, light green, yellow, orange and red colour regions, respectively. The basins of attraction corresponding to the all Lagrangian points $L_1,L_2,L_3,L_4,L_5,L_6,L_7$ and $L_8$ extend to infinity. On the other-hand, in the case of albedo (Figure 7(d)), $L_1$, $L_2$, $(L_3,L_8)$ and $(L_5,L_7)$ represent cyan colour, mint green colour, light green colours and light blue colour regions, respectively but $L_4$ and $L_6$ have mixed colour regions.

Figure 7. The basin of attraction for the (a): classical case, (b): variable mass case, (c): solar radiation pressure case, (d): Albedo case.

4. Linear stability

We check the stability of Lagrangian points under the effect of Albedo by taking $\xi ={\xi }_0+{\xi }_d,\eta ={\eta }_0+{\eta }_d,\zeta ={\zeta }_0+{\zeta }_d$ in system (3(3) $\begin{array}{rl}& {\xi }^{″}-2{\eta }^{\prime }-{\alpha }_1{\xi }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\xi },\\ & {\eta }^{″}+2{\xi }^{\prime }-{\alpha }_1{\eta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\eta },\\ & {\zeta }^{″}-{\alpha }_1{\zeta }^{\prime }=\frac{\mathrm{\partial \Lambda }}{\mathrm{\partial }\zeta }.\end{array}$(3) ), we get (10) $\begin{array}{rl}{\xi }_d^{″}-2{\eta }_d^{\prime }-{\alpha }_1{\xi }_d^{\prime }& ={\xi }_d{\mathrm{\Lambda }}_{\xi \xi }^0+{\eta }_d{\mathrm{\Lambda }}_{\xi \eta }^0+{\zeta }_d{\mathrm{\Lambda }}_{\xi \zeta }^0,\\ {\eta }_d^{″}+2{\xi }_d^{\prime }-{\alpha }_1{\eta }_d^{\prime }& ={\xi }_d{\mathrm{\Lambda }}_{\eta \xi }^0+{\eta }_d{\mathrm{\Lambda }}_{\eta \eta }^0+{\zeta }_d{\mathrm{\Lambda }}_{\eta \zeta }^0,\\ {\zeta }_d^{″}-{\alpha }_1{\zeta }_d^{\prime }& ={\xi }_d{\mathrm{\Lambda }}_{\zeta \xi }^0+{\eta }_d{\mathrm{\Lambda }}_{\zeta \eta }^0+{\zeta }_d{\mathrm{\Lambda }}_{\zeta \zeta }^0,\end{array}$(10) where ${\xi }_d,{\eta }_d$ and ${\zeta }_d$ are displacements of fourth body from the Lagrangian point.

To solve system (10(10) $\begin{array}{rl}{\xi }_d^{″}-2{\eta }_d^{\prime }-{\alpha }_1{\xi }_d^{\prime }& ={\xi }_d{\mathrm{\Lambda }}_{\xi \xi }^0+{\eta }_d{\mathrm{\Lambda }}_{\xi \eta }^0+{\zeta }_d{\mathrm{\Lambda }}_{\xi \zeta }^0,\\ {\eta }_d^{″}+2{\xi }_d^{\prime }-{\alpha }_1{\eta }_d^{\prime }& ={\xi }_d{\mathrm{\Lambda }}_{\eta \xi }^0+{\eta }_d{\mathrm{\Lambda }}_{\eta \eta }^0+{\zeta }_d{\mathrm{\Lambda }}_{\eta \zeta }^0,\\ {\zeta }_d^{″}-{\alpha }_1{\zeta }_d^{\prime }& ={\xi }_d{\mathrm{\Lambda }}_{\zeta \xi }^0+{\eta }_d{\mathrm{\Lambda }}_{\zeta \eta }^0+{\zeta }_d{\mathrm{\Lambda }}_{\zeta \zeta }^0,\end{array}$(10) ), let ${\xi }_d=C_1{e}^{\lambda \tau },{\eta }_d=C_2{e}^{\lambda \tau },{\zeta }_d=C_3{e}^{\lambda \tau },$ where $C_1,C_2$ and $C_3$ are constants. Then system (10(10) $\begin{array}{rl}{\xi }_d^{″}-2{\eta }_d^{\prime }-{\alpha }_1{\xi }_d^{\prime }& ={\xi }_d{\mathrm{\Lambda }}_{\xi \xi }^0+{\eta }_d{\mathrm{\Lambda }}_{\xi \eta }^0+{\zeta }_d{\mathrm{\Lambda }}_{\xi \zeta }^0,\\ {\eta }_d^{″}+2{\xi }_d^{\prime }-{\alpha }_1{\eta }_d^{\prime }& ={\xi }_d{\mathrm{\Lambda }}_{\eta \xi }^0+{\eta }_d{\mathrm{\Lambda }}_{\eta \eta }^0+{\zeta }_d{\mathrm{\Lambda }}_{\eta \zeta }^0,\\ {\zeta }_d^{″}-{\alpha }_1{\zeta }_d^{\prime }& ={\xi }_d{\mathrm{\Lambda }}_{\zeta \xi }^0+{\eta }_d{\mathrm{\Lambda }}_{\zeta \eta }^0+{\zeta }_d{\mathrm{\Lambda }}_{\zeta \zeta }^0,\end{array}$(10) ) become (11) $\begin{array}{rl}& C_1({\lambda }^2-{\alpha }_1\lambda -{\mathrm{\Lambda }}_{\xi \xi }^0)-C_2(2\lambda +{\mathrm{\Lambda }}_{\xi \eta }^0)-C_3{\mathrm{\Lambda }}_{\xi \zeta }^0=0,\\ & C_1(2\lambda -{\mathrm{\Lambda }}_{\eta \xi }^0)+C_2({\lambda }^2-{\alpha }_1\lambda -{\mathrm{\Lambda }}_{\eta \eta }^0)-C_3{\mathrm{\Lambda }}_{\eta \zeta }^0=0,\\ & -C_1{\mathrm{\Lambda }}_{\zeta \xi }^0-C_2{\mathrm{\Lambda }}_{\zeta \eta }^0+C_3({\lambda }^2-{\alpha }_1\lambda -{\mathrm{\Lambda }}_{\zeta \zeta }^0)=0.\end{array}$(11) The system (11(11) $\begin{array}{rl}& C_1({\lambda }^2-{\alpha }_1\lambda -{\mathrm{\Lambda }}_{\xi \xi }^0)-C_2(2\lambda +{\mathrm{\Lambda }}_{\xi \eta }^0)-C_3{\mathrm{\Lambda }}_{\xi \zeta }^0=0,\\ & C_1(2\lambda -{\mathrm{\Lambda }}_{\eta \xi }^0)+C_2({\lambda }^2-{\alpha }_1\lambda -{\mathrm{\Lambda }}_{\eta \eta }^0)-C_3{\mathrm{\Lambda }}_{\eta \zeta }^0=0,\\ & -C_1{\mathrm{\Lambda }}_{\zeta \xi }^0-C_2{\mathrm{\Lambda }}_{\zeta \eta }^0+C_3({\lambda }^2-{\alpha }_1\lambda -{\mathrm{\Lambda }}_{\zeta \zeta }^0)=0.\end{array}$(11) ), will be solution for $C_1,C_2$ and $C_3$ if $\begin{array}{rl}& \left|\begin{array}{ccc}{\lambda }^2-{\alpha }_1\lambda -{\mathrm{\Lambda }}_{\xi \xi }^0& -(2\lambda +{\mathrm{\Lambda }}_{\xi \eta }^0)& -{\mathrm{\Lambda }}_{\xi \zeta }^0\\ 2\lambda -{\mathrm{\Lambda }}_{\eta \xi }^0& {\lambda }^2-{\alpha }_1\lambda -{\mathrm{\Lambda }}_{\eta \eta }^0& -{\mathrm{\Lambda }}_{\eta \zeta }^0\\ -{\mathrm{\Lambda }}_{\zeta \xi }^0& -{\mathrm{\Lambda }}_{\zeta \eta }^0& {\lambda }^2-{\alpha }_1\lambda -{\mathrm{\Lambda }}_{\zeta \zeta }^0\end{array}\right|\\ & =0,\end{array}$ which is equivalent to (12) $\begin{array}{rl}& {\lambda }^6-3{\alpha }_1{\lambda }^5+{\lambda }^4(4+3{\alpha }_1^2-{\mathrm{\Lambda }}_{\xi \xi }^0-{\mathrm{\Lambda }}_{\eta \eta }^0-{\mathrm{\Lambda }}_{\zeta \zeta }^0)\\ & +{\alpha }_1{\lambda }^3(-4-{\alpha }_1^2+2{\mathrm{\Lambda }}_{\xi \xi }^0+2{\mathrm{\Lambda }}_{\eta \eta }^0+2{\mathrm{\Lambda }}_{\zeta \zeta }^0)\\ & +{\lambda }^2(-({\mathrm{\Lambda }}_{\xi \eta }^0{)}^2-({\mathrm{\Lambda }}_{\xi \zeta }^0{)}^2+{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\eta \eta }^0-({\mathrm{\Lambda }}_{\eta \zeta }^0{)}^2\\ & -4{\mathrm{\Lambda }}_{\zeta \zeta }^0+{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\zeta \zeta }^0+{\mathrm{\Lambda }}_{\zeta \zeta }^0{\mathrm{\Lambda }}_{\eta \eta }^0\\ & -{\alpha }_1^2{\mathrm{\Lambda }}_{\xi \xi }^0-{\alpha }_1^2{\mathrm{\Lambda }}_{\eta \eta }^0-{\alpha }_1^2{\mathrm{\Lambda }}_{\zeta \zeta }^0)\\ & +{\alpha }_1\lambda \left(\right({\mathrm{\Lambda }}_{\xi \eta }^0{)}^2+({\mathrm{\Lambda }}_{\xi \zeta }^0{)}^2-{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\eta \eta }^0+({\mathrm{\Lambda }}_{\eta \zeta }^0{)}^2\\ & -{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\zeta \zeta }^0-{\mathrm{\Lambda }}_{\eta \eta }^0{\mathrm{\Lambda }}_{\zeta \zeta }^0)\\ & +\left(\right({\mathrm{\Lambda }}_{\xi \zeta }^0{)}^2{\mathrm{\Lambda }}_{\eta \eta }^0-2{\mathrm{\Lambda }}_{\xi \eta }^0{\mathrm{\Lambda }}_{\xi \zeta }^0{\mathrm{\Lambda }}_{\eta \zeta }^0+{\mathrm{\Lambda }}_{\xi \xi }^0({\mathrm{\Lambda }}_{\eta \zeta }^0{)}^2\\ & +({\mathrm{\Lambda }}_{\xi \eta }^0{)}^2{\mathrm{\Lambda }}_{\zeta \zeta }^0-{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\eta \eta }^0{\mathrm{\Lambda }}_{\zeta \zeta }^0)=0.\end{array}$(12) From the solution of Equation (12(12) $\begin{array}{rl}& {\lambda }^6-3{\alpha }_1{\lambda }^5+{\lambda }^4(4+3{\alpha }_1^2-{\mathrm{\Lambda }}_{\xi \xi }^0-{\mathrm{\Lambda }}_{\eta \eta }^0-{\mathrm{\Lambda }}_{\zeta \zeta }^0)\\ & +{\alpha }_1{\lambda }^3(-4-{\alpha }_1^2+2{\mathrm{\Lambda }}_{\xi \xi }^0+2{\mathrm{\Lambda }}_{\eta \eta }^0+2{\mathrm{\Lambda }}_{\zeta \zeta }^0)\\ & +{\lambda }^2(-({\mathrm{\Lambda }}_{\xi \eta }^0{)}^2-({\mathrm{\Lambda }}_{\xi \zeta }^0{)}^2+{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\eta \eta }^0-({\mathrm{\Lambda }}_{\eta \zeta }^0{)}^2\\ & -4{\mathrm{\Lambda }}_{\zeta \zeta }^0+{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\zeta \zeta }^0+{\mathrm{\Lambda }}_{\zeta \zeta }^0{\mathrm{\Lambda }}_{\eta \eta }^0\\ & -{\alpha }_1^2{\mathrm{\Lambda }}_{\xi \xi }^0-{\alpha }_1^2{\mathrm{\Lambda }}_{\eta \eta }^0-{\alpha }_1^2{\mathrm{\Lambda }}_{\zeta \zeta }^0)\\ & +{\alpha }_1\lambda \left(\right({\mathrm{\Lambda }}_{\xi \eta }^0{)}^2+({\mathrm{\Lambda }}_{\xi \zeta }^0{)}^2-{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\eta \eta }^0+({\mathrm{\Lambda }}_{\eta \zeta }^0{)}^2\\ & -{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\zeta \zeta }^0-{\mathrm{\Lambda }}_{\eta \eta }^0{\mathrm{\Lambda }}_{\zeta \zeta }^0)\\ & +\left(\right({\mathrm{\Lambda }}_{\xi \zeta }^0{)}^2{\mathrm{\Lambda }}_{\eta \eta }^0-2{\mathrm{\Lambda }}_{\xi \eta }^0{\mathrm{\Lambda }}_{\xi \zeta }^0{\mathrm{\Lambda }}_{\eta \zeta }^0+{\mathrm{\Lambda }}_{\xi \xi }^0({\mathrm{\Lambda }}_{\eta \zeta }^0{)}^2\\ & +({\mathrm{\Lambda }}_{\xi \eta }^0{)}^2{\mathrm{\Lambda }}_{\zeta \zeta }^0-{\mathrm{\Lambda }}_{\xi \xi }^0{\mathrm{\Lambda }}_{\eta \eta }^0{\mathrm{\Lambda }}_{\zeta \zeta }^0)=0.\end{array}$(12) ), we found that λ has complex values and at least one of them has a positive real value. Hence, all the Lagrangian points are unstable (Table 1).

Table 1. Characteristic roots corresponding to each Lagrangian points in in-plane motion

$S.No.$	Lagrangian points	Corresponding characteristic roots
	In-plane $(\xi ,\eta ,\zeta )$
1	$(-0.26,0,0)$	$-2.280860$, $2.399147$,
		0.099999−2.194133i, 0.099999+2.194133i,
		0.140856−2.077194i, 0.140856+2.077194i
2	$(0.167,-0.17,0)$	$-1.906450$, $1.989821$,
		−2.094738i, 0.100000+2.094738i,
		0.158314 − 1.750458i, 0.158314 + 1.750458i
3	(0.945, −0.5, 0)	−0.612768,
		0.100000 − 1.203127i, 0.100000 + 1.203127i,
		0.237857 − 1.603438i, 0.237857 + 1.603438i
4	(0.45, − 0.87, 0)	$-0.075712$ $-0.229488$i, $-0.075712$ $+0.229488$i,
		− 1.153241i, 0.100000 + 1.153241i,
		0.275712 − 1.526144i, 0.275712 + 1.526144i
5	(0.95, 1, 0)	− 0.050762 − 0.332430i, − 0.050762 + 0.332430i,
		− 0.906229i, 0.099999 + 0.906229i,
		0.250762 − 1.662436i, 0.250762 + 1.662436 i
6	(0.35, −0.96, 0),	−0.325144, $0.206933$,
		0.099999 − 1.152442i, 0.099999 + 1.152442i,
		0.259105 − 1.563100i, 0.259105 + 1.563100i
7	(−1.14, −1.04, 0),	−0.052473 − 0.315767i, -0.052473 + 0.315767i,
		− 0.934706i, 0.100000 + 0.934706i,
		0.252473 − 1.650185i, 0.252473 + 1.650185i
8	(−0.74, 0.94, 0),	−0.859531, $0.831415$,
		0.099999 − 1.264392i, 0.099999 + 1.264392i,
		0.214058 − 1.670974i, 0.214058 + 1.670974i

5. Conclusion

This paper studied the effect of Albedo in CR4BP with variable masses. We determined the equations of motions which are different from the classical case by the variation parameters ${\alpha }_1$ and k and the radiations effect ${\epsilon }_1$, ${\epsilon }_2$ and ${\epsilon }_3$ and also the expression for the variation of Jacobi integral constant have been evaluated which is also depending on the variation parameter ${\alpha }_1$. We have plotted all the figures in four different cases by using the Mathematica software. The Lagrangian points during in-plane motion (Figure 2), we found ten Lagrangian points in the classical case which meet the result of Baltagiannis [9], while in the cases variable mass, solar radiation pressure and albedo we found eight Lagrangian points. During out-of-plane motions (i.e. $\xi \ne 0,\eta =0,\zeta \ne 0$)(Figure 3), we found three Lagrangian points in the classical case and four Lagrangian points in rest three cases. It is observed from Figure 3(e) that Lagrangian points are moving away from the origin from the classical case to the variable mass case and then towards the origin in the other cases.

On the other hand, during the out of plane (i.e. $\xi =0,\eta \ne 0,\zeta \ne 0$), we found five Lagrangian points (Figure 4) in all four cases. It is also observed from Figure 4(e) that Lagrangian points are moving away from the origin from the classical case to the variable mass case and then towards the origin in the other cases. In these four cases, the periodic orbits have been drawn ( Figure 5). In the classical case, orbit is periodic but in the other three cases, orbits are not periodic. It is observed that in three cases orbits are overlapped but they have time difference. The poincaré surface of sections have been determined in two phase spaces ($\xi -{\xi }^{\prime }$, Figure 6(i) and $\eta -{\eta }^{\prime }$, Figure 6(ii)). In both the cases, surfaces are discrete type with a similar pattern.

The N-R basins of attraction have studied in four different cases (Figure 7(a)–(d)). We used the colour code for the Lagrangian points on the $(\xi -\eta )$-plane. Finally, we have examined the stability of Lagrangian points in CR4BP under the effect of Albedo only and got all the Lagrangian points unstable.

Acknowledgments

We are thankful to the Deanship of Scientific Research, Majmaah University, Kingdom of Saudi Arabia, for providing all the research facilities in completion of this research work with grant number 37/29.

Disclosure statement

No potential conflict of interest was reported by the author.

ORCID

Ziyad A. Alhussain  http://orcid.org/0000-0001-8593-0239