Sensitivity measurement for asymmetric two two-level atoms interacting with field obeys SU(1,1) Lie group via atomic inversion

ABSTRACT

A quantum optics model of the asymmetric case of the interaction between two two-level atoms and quantum field, which obeys SU(1,1) Lie group, is proposed. The atom-atom interaction and the rotating wave approximation are suggested in the Hamiltonian operator. Our aim is to obtain the time-dependent wave function of asymmetric case analytically. The analytical method is based on the eigenvalues and corresponding eigenvectors of the coefficient matrix of the interaction Hamiltonian operator. The SU(1,1) quantum system is initially in the Perelomov coherent state. Therefore, the atomic inversion is obtained and discussed for different values of model parameters such as initial atomic angles, Perelomov coherent, the Bargmann index and the detuning parameters. Observe that the quantum optics model is sensitive to the variation in both the Perelomov coherent parameter and the Bargmann index. In addition, there are nonclassical properties of the proposed quantum model in the presence the detuning parameter changes.

KEYWORDS:

• SU(1; 1) quantum system
• two two-level atoms
• atom–atom interaction
• Perelomov coherent state
• atomic population inversion

1. Introduction

The quantum optics model of the interaction between the atoms and field explicates new features of the quantum nature of the atoms as well as radiation field. This quantum nature affects on the properties of the emission spectrum from it. The properties of these emission spectra can be studied via quantum models which represent the fundamental issues. So, the essential issues in quantum mechanics have studied with the aid of many quantum models describing quantum effects in the atom–field interaction. One of the important model of the quantum optics models is the interaction between two two-level atoms and field especially that obeys SU(1,1) Lie group. This field is called SU(1,1) quantum system which generalizes to the generalized Jaynes–Cummings model (JCM) [1–4]. The JCM considers a sample standard model of the interaction between the two-level atom and the single-mode quantized field considering the rotating wave approximation (RWA). Many generalized versions have been presented to modify the JCM in the literature. Most interesting physical and statistical properties have been studied with this model such as entanglement, atomic inversion, collapse and revival, quadrature squeezing, entropy squeezing and sub-Poissonian statistics. On the other hand, some of these quantum models have been realized experimentally [5–7]. So, a study of the atom–field interaction considers one of the most prominent topics in quantum computation and communication, quantum information [8–14], and quantum cryptography [15,16]. As is well known in recent years, the atomic inversion plays a main role in the modern quantum fields. For that reason, it is important to calculate the atomic inversion as on of the statistical and dynamics properties of the atom–field interaction. As known, there are three essential interesting models in the quantum optics field. These models are the atom–atom interaction [17–24], the field–field interaction [25–33] and atom–field interaction [34–46]. In this paper, our aim is to study the effects of two of these types of the interaction between atoms and field which are atom–atom and atom–field interactions. We consider that the field follows the SU(1,1) Lie group. The Hamiltonian operator considering the effects of the atom–atom interaction and the RWA is given as (1) $\begin{array}{rl}\hat{H}& ={\omega }_a{\hat{K}}_z+\sum _{j=1}^2\left[{\omega }_j{\hat{\sigma }}_z^{\left(j\right)}+g_j\left({\hat{K}}_{-}{\hat{\sigma }}_{+}^{\left(j\right)}+{\hat{K}}_{+}{\hat{\sigma }}_{-}^{\left(j\right)}\right)\right]\\ & +i\lambda \left({\hat{\sigma }}_{+}^{\left(1\right)}{\hat{\sigma }}_{-}^{\left(2\right)}-{\hat{\sigma }}_{-}^{\left(1\right)}{\hat{\sigma }}_{+}^{\left(2\right)}\right).\end{array}$(1) Here $\hslash =1$, ${\omega }_j,j=1,2$ are the atomic transition frequencies, j=1 for first atom and j=2 for second atom. ${\omega }_a$ is the field frequency which obeys SU(1,1) Lie group. $g_j,j=1,2$ are the coupling constants between the atoms and the SU(1,1) quantum system. λ is the coupling constant between the two atoms. ${\hat{\sigma }}_{\pm ,z}^{\left(j\right)},j=1,2$ are the raising, lowering and inversion operators for the two-level atomic system which are satisfying the commutation relations (2) $\left[{\hat{\sigma }}_z^{\left(j\right)},{\hat{\sigma }}_{\pm }^{\left(j\right)}\right]=\pm 2{\hat{\sigma }}_{\pm }^{\left(j\right)},\left[{\hat{\sigma }}_{+}^{\left(i\right)},{\hat{\sigma }}_{-}^{\left(j\right)}\right]={\hat{\sigma }}_z^{\left(j\right)}{\delta }_{ij}.$(2) Notice that the SU(1,1) quantum system operators ${\hat{K}}_{\pm }$ and ${\hat{K}}_z$ follow the Lie algebra and satisfy the commutation relations [47–50] (3) $\left[{\hat{K}}_z,{\hat{K}}_{\pm }\right]=\pm {\hat{K}}_{\pm },\left[{\hat{K}}_{-},{\hat{K}}_{+}\right]=2{\hat{K}}_z,$(3) while the corresponding Casimir operator $\hat{K}$ defines as (4) ${\hat{K}}^2={\hat{K}}_z^2-\frac{1}{2}\left({\hat{K}}_{+}{\hat{K}}_{-}+{\hat{K}}_{-}{\hat{K}}_{+}\right).$(4) The effects of the SU(1,1) operators on the eigenstate $|m,k⟩$ are as: (5) $\begin{array}{rl}{\hat{K}}_z|m,k⟩& =(m+k)|m,k⟩,\\ {\hat{K}}^2|m,k⟩& =k(k-1)|m,k⟩,\\ {\hat{K}}_{+}|m,k⟩& =\sqrt{(m+1)(m+2k)}|m+1,k⟩,\\ {\hat{K}}_{-}|m,k⟩& =\sqrt{m(m+2k-1)}|m-1,k⟩,\end{array}$(5) where m is any non-negative integer number, and k is the Bargmann index. Whereas ${\hat{K}}_{-}|0,k⟩=0$.

Moreover for examples, the Casimir operators can be redefined by the boson annihilation $\hat{a}$ and creation ${\hat{a}}^{†}$ operators, which satisfy $[\hat{a},{\hat{a}}^{†}]=1$, such as (6) ${\hat{K}}_z=\frac{1}{2}\left({\hat{a}}^{†}\hat{a}+\frac{1}{2}\right),{\hat{K}}_{+}=\frac{1}{2}{\hat{a}}^{†2},{\hat{K}}_{-}=\frac{1}{2}{\hat{a}}^2,$(6) where the Bargmann index k takes either $k=\frac{1}{4}$, for the even parity states, or $k=\frac{3}{4}$, for odd parity states.

Also, the SU(1,1) Lie group represents the case of the intensity dependent forms as (7) ${\hat{K}}_z=\frac{1}{2}\left({\hat{a}}^{†}\hat{a}+\frac{1}{2}\right),{\hat{K}}_{+}=\sqrt{\hat{n}}{\hat{a}}^{†},{\hat{K}}_{-}=\hat{a}\sqrt{\hat{n}},$(7) where $\hat{n}={\hat{a}}^{†}\hat{a}$ is the number photon operator.

Notice that if there is a single atom and there is not atom–atom interaction ($\lambda =0$), the Hamiltonian (1(1) $\begin{array}{rl}\hat{H}& ={\omega }_a{\hat{K}}_z+\sum _{j=1}^2\left[{\omega }_j{\hat{\sigma }}_z^{\left(j\right)}+g_j\left({\hat{K}}_{-}{\hat{\sigma }}_{+}^{\left(j\right)}+{\hat{K}}_{+}{\hat{\sigma }}_{-}^{\left(j\right)}\right)\right]\\ & +i\lambda \left({\hat{\sigma }}_{+}^{\left(1\right)}{\hat{\sigma }}_{-}^{\left(2\right)}-{\hat{\sigma }}_{-}^{\left(1\right)}{\hat{\sigma }}_{+}^{\left(2\right)}\right).\end{array}$(1) ) was presented in [48,51]. While, if there are symmetric two two-level atoms ($g_1=g_2$) and there isn't atom–atom interaction ($\lambda =0$), the Hamiltonian (1(1) $\begin{array}{rl}\hat{H}& ={\omega }_a{\hat{K}}_z+\sum _{j=1}^2\left[{\omega }_j{\hat{\sigma }}_z^{\left(j\right)}+g_j\left({\hat{K}}_{-}{\hat{\sigma }}_{+}^{\left(j\right)}+{\hat{K}}_{+}{\hat{\sigma }}_{-}^{\left(j\right)}\right)\right]\\ & +i\lambda \left({\hat{\sigma }}_{+}^{\left(1\right)}{\hat{\sigma }}_{-}^{\left(2\right)}-{\hat{\sigma }}_{-}^{\left(1\right)}{\hat{\sigma }}_{+}^{\left(2\right)}\right).\end{array}$(1) ) was presented in [52]. In this work, we present asymmetric two two-level atoms ($g_1\ne g_2$) and the system includes the atom–atom interaction ($\lambda \ne 0$). So, the proposed quantum system (1(1) $\begin{array}{rl}\hat{H}& ={\omega }_a{\hat{K}}_z+\sum _{j=1}^2\left[{\omega }_j{\hat{\sigma }}_z^{\left(j\right)}+g_j\left({\hat{K}}_{-}{\hat{\sigma }}_{+}^{\left(j\right)}+{\hat{K}}_{+}{\hat{\sigma }}_{-}^{\left(j\right)}\right)\right]\\ & +i\lambda \left({\hat{\sigma }}_{+}^{\left(1\right)}{\hat{\sigma }}_{-}^{\left(2\right)}-{\hat{\sigma }}_{-}^{\left(1\right)}{\hat{\sigma }}_{+}^{\left(2\right)}\right).\end{array}$(1) ) represents a generalization quantum model of asymmetric two two-level atoms interaction with quantum field where the atom–atom interaction is considered.

Our aim in this paper is to discuss sensitivity measurement for the asymmetric two two-level atoms interacting with the SU(1,1) quantum system to the detuning parameters and the initial atomic angles. This means that the non-classical properties of the proposed quantum model are studied via the atomic population inversion. So, the time-dependent wave function is obtained analytically using Heisenberg equations of motions in Section 2. While, the atomic population inversion is investigated and discussed in Section 3. Finally, the conclusions are epitomized in Section 4.

2. Analytical solution

To determine the atomic population inversion of the model (1(1) $\begin{array}{rl}\hat{H}& ={\omega }_a{\hat{K}}_z+\sum _{j=1}^2\left[{\omega }_j{\hat{\sigma }}_z^{\left(j\right)}+g_j\left({\hat{K}}_{-}{\hat{\sigma }}_{+}^{\left(j\right)}+{\hat{K}}_{+}{\hat{\sigma }}_{-}^{\left(j\right)}\right)\right]\\ & +i\lambda \left({\hat{\sigma }}_{+}^{\left(1\right)}{\hat{\sigma }}_{-}^{\left(2\right)}-{\hat{\sigma }}_{-}^{\left(1\right)}{\hat{\sigma }}_{+}^{\left(2\right)}\right).\end{array}$(1) ), we should be calculated the time-dependent wave function via the Heisenberg equations of motion as: (8) $\begin{array}{rl}i\frac{\mathrm{d}{\hat{K}}_z}{\mathrm{d}t}& =\left[{\hat{K}}_z,\hat{H}\right]=\sum _{j=1}^2{g}_j\left({\hat{K}}_{+}{\hat{\sigma }}_{-}^{\left(j\right)}-{\hat{K}}_{-}{\hat{\sigma }}_{+}^{\left(j\right)}\right),\\ i\frac{\mathrm{d}{\hat{\sigma }}_z^{\left(1\right)}}{\mathrm{d}t}& =\left[{\hat{\sigma }}_z^{\left(1\right)},\hat{H}\right]=-2g_1\left({\hat{K}}_{+}{\hat{\sigma }}_{-}^{\left(1\right)}-{\hat{K}}_{-}{\hat{\sigma }}_{+}^{\left(1\right)}\right)\\ & +2i\lambda \left({\hat{\sigma }}_{+}^{\left(1\right)}{\hat{\sigma }}_{-}^{\left(2\right)}+{\hat{\sigma }}_{-}^{\left(1\right)}{\hat{\sigma }}_{+}^{\left(2\right)}\right),\\ i\frac{\mathrm{d}{\hat{\sigma }}_z^{\left(2\right)}}{\mathrm{d}t}& =\left[{\hat{\sigma }}_z^{\left(2\right)},\hat{H}\right]=-2g_2\left({\hat{K}}_{+}{\hat{\sigma }}_{-}^{\left(2\right)}-{\hat{K}}_{-}{\hat{\sigma }}_{+}^{\left(2\right)}\right)\\ & -2i\lambda \left({\hat{\sigma }}_{+}^{\left(1\right)}{\hat{\sigma }}_{-}^{\left(2\right)}+{\hat{\sigma }}_{-}^{\left(1\right)}{\hat{\sigma }}_{+}^{\left(2\right)}\right),\end{array}$(8) and consequently, we obtain (9) $i\frac{\mathrm{d}}{\mathrm{d}t}\left({\hat{K}}_z+\frac{1}{2}\sum _{j=1}^2{\hat{\sigma }}_z^{\left(j\right)}\right)=0.$(9) Let us define an operator (10) ${\hat{H}}_0={\hat{K}}_z+\frac{1}{2}\sum _{j=1}^2{\hat{\sigma }}_z^{\left(j\right)},$(10) which is a constant operator of motion. Then the Hamiltonian operator should be rewritten as (11) $\hat{H}={\omega }_a{\hat{H}}_0+{\hat{H}}_{\mathrm{int}},$(11) where the operator ${\hat{H}}_{\mathrm{int}}$ is given by (12) $\begin{array}{rl}{\hat{H}}_{\mathrm{int}}=& \sum _{j=1}^2\left(\frac{{\delta }_j}{2}{\hat{\sigma }}_z^{\left(j\right)}+g_j\left({\hat{K}}_{-}{\hat{\sigma }}_{+}^{\left(j\right)}+{\hat{K}}_{+}{\hat{\sigma }}_{-}^{\left(j\right)}\right)\right)\\ & +i\lambda \left({\hat{\sigma }}_{+}^{\left(1\right)}{\hat{\sigma }}_{-}^{\left(2\right)}-{\hat{\sigma }}_{-}^{\left(1\right)}{\hat{\sigma }}_{+}^{\left(2\right)}\right),\end{array}$(12) and the detuning parameters ${\delta }_j$ are defined as ${\delta }_j=2{\omega }_j-{\omega }_a,j=1,2.$

It is easy to prove that the Hamiltonian operators $\widehat{H_0}$, $\widehat{H_{\mathrm{int}}}$ and H are constants of motion. So, we consider that the initial wave function of the proposed system can be written as (13) $\begin{array}{rl}|\mathrm{\Psi }\left(0\right)⟩& =\left(c_1|+,+⟩+c_2|+,-⟩+c_3|-,+⟩\right.\\ & +\left.c_4|-,-⟩\right)\otimes |\alpha ,k⟩,\end{array}$(13) where, $|+⟩$ and $|-⟩$ are the upper and lower states of the two-level atom, $|+,-⟩=|+⟩|-⟩$ represents the product of the upper state, $|+⟩$, for first atom by the lower state the second atom. $c_i,i=1,2,3,4$ are constants which are arbitrary complex numbers satisfying the superposition condition $\sum _{i=1}^4|c_i{|}^2=1$. So, let us assume that (14) $\begin{array}{rl}{c}_1& =\cos \theta \cos \phi ,c_2=\cos \theta \sin \phi ,\\ c_3& =\sin \theta \cos \phi ,c_4=\sin \theta \sin \phi \end{array}$(14) where, θ and φ are the atomic angles at t=0 which provide the possibilities that the two atoms are either in their ground state, excited state, or in the superposition state. In addition, the state vector $|\alpha ,k⟩$ is considered to be the initial state associated with Perelomov coherent state, which is defined as (15) $\begin{array}{rl}|\alpha ,k⟩& =\sum _{m=0}^{\mathrm{\infty }}{Q}_m|m,k⟩,\\ Q_m& =(1-|\alpha {|}^2{)}^k{\alpha }^m\sqrt{\frac{\mathrm{\Gamma }(2k+m)}{m!\mathrm{\Gamma }\left(2k\right)}},\end{array}$(15) where α is the Perelomov parameter, and $|m,k⟩$ is the eigenvector of the operator $K_z$ with eigenvalue $(m+k)$.

Let us assume that the two atoms are fulfilled in exact resonance case, i.e. ${\delta }_1+{\delta }_2=0$. The aim of this assumption is to overcome the difficulty of the proposed system. The time-dependent wave function at t>0, which is the most complete description for the proposed physical system, should be written as (16) $\begin{array}{rl}|\mathrm{\Psi }\left(t\right)⟩& =\sum _{m=0}^{\mathrm{\infty }}\left(A\right(m,t)|+,+⟩|m,k⟩\\ & +B(m,t)|+,-⟩|m+1,k⟩\\ & +C(m,t)|-,+⟩|m+1,k⟩\\ & +D(m,t)|-,-⟩|m+2,k⟩),\end{array}$(16) In what follows, our aim is to determine the coefficients $A(m,t),B(m,t),C(m,t)$, and $D(m,t)$ by solving the Schrödinger equation $i\left(\mathrm{\partial }|\mathrm{\Psi }\left(t\right)⟩/\mathrm{\partial }t\right)={\hat{H}}_{\mathrm{int}}|\mathrm{\Psi }\left(t\right)⟩$. Here the Hamiltonian operator is concentrated on the interaction picture because the first part of equation (11(11) $\hat{H}={\omega }_a{\hat{H}}_0+{\hat{H}}_{\mathrm{int}},$(11) ), ${\omega }_a{\hat{H}}_0$, represents the component of the phase. From the Schrödinger equation, we obtain the following system of the differential equations (17) $\begin{array}{rl}i\frac{\mathrm{d}A(m,t)}{\mathrm{d}t}& ={\nu }_{2}B(m,t)+{\nu }_{1}C(m,t),\\ i\frac{\mathrm{d}B(m,t)}{\mathrm{d}t}& ={\nu }_{2}A(m,t)+\delta B(m,t)+i\lambda C(m,t)+{\mu }_{1}D(m,t),\\ i\frac{\mathrm{d}C(m,t)}{\mathrm{d}t}& ={\nu }_{1}A(m,t)-i\lambda B(m,t)-\delta C(m,t)+{\mu }_{2}D(m,t),\\ i\frac{\mathrm{d}D(m,t)}{\mathrm{d}t}& ={\mu }_{1}B(m,t)+{\mu }_{2}C(m,t),\end{array}$(17) where ${\nu }_j=g_j\sqrt{(m+1)(m+2k)}$, ${\mu }_j=g_j\sqrt{(m+2)(m+2k+1)}$, and j=1,2.

For solving this system analytically, we can rewrite this system in the matrix formula as (18) $\frac{d}{\mathrm{d}t}\left(\begin{array}{c}A(m,t)\\ B(m,t)\\ C(m,t)\\ D(m,t)\end{array}\right)=-i\left(\begin{array}{cccc}0& {\nu }_2& {\nu }_1& 0\\ {\nu }_2& \delta & i\lambda & {\mu }_1\\ {\nu }_1& -i\lambda & -\delta & {\mu }_2\\ 0& {\mu }_1& {\mu }_2& 0\end{array}\right)\left(\begin{array}{c}A(m,t)\\ B(m,t)\\ C(m,t)\\ D(m,t)\end{array}\right).$(18) Let us assume that $\mathbf{\Omega }\left(m\right)=\left(\begin{array}{cccc}0& {\nu }_2& {\nu }_1& 0\\ {\nu }_2& \delta & i\lambda & {\mu }_1\\ {\nu }_1& -i\lambda & -\delta & {\mu }_2\\ 0& {\mu }_1& {\mu }_2& 0\end{array}\right)$ is the coefficient matrix.

Notice that, we mainly deal with the ratio $g=g_2/g_1$ during the investigation, when $g=1(g\ne 1)$ it is called the symmetric (asymmetric) case. The explicit analytical expressions for the coefficients $A(m,t),B(m,t),C(m,t)$, and $D(m,t)$ for symmetric case g=1 was obtained in [52,53]. While in asymmetric case $(g\ne 1)$, the analytical solution of Equation (18(18) $\frac{d}{\mathrm{d}t}\left(\begin{array}{c}A(m,t)\\ B(m,t)\\ C(m,t)\\ D(m,t)\end{array}\right)=-i\left(\begin{array}{cccc}0& {\nu }_2& {\nu }_1& 0\\ {\nu }_2& \delta & i\lambda & {\mu }_1\\ {\nu }_1& -i\lambda & -\delta & {\mu }_2\\ 0& {\mu }_1& {\mu }_2& 0\end{array}\right)\left(\begin{array}{c}A(m,t)\\ B(m,t)\\ C(m,t)\\ D(m,t)\end{array}\right).$(18) ) is determined exactly as follows [54] (19) $\left(\begin{array}{c}A(m,t)\\ B(m,t)\\ C(m,t)\\ D(m,t)\end{array}\right)=\sum _{j=1}^4\exp (-i{\mathrm{\Omega }}_{j}t)|{\mathbf{\Omega }}_j⟩⟨{\mathbf{\Omega }}_j|\left(\begin{array}{c}{c}_1{Q}_m\\ c_2{Q}_{m+1}\\ c_3{Q}_{m+1}\\ c_4{Q}_{m+2}\end{array}\right),$(19) where, ${\mathrm{\Omega }}_j$ are the eigenvalues and $|{\mathbf{\Omega }}_j⟩$ are the eigenvectors corresponding to the eigenvalues ${\mathrm{\Omega }}_j$ of the coefficient matrix $\mathbf{\Omega }\left(m\right)$.

Now, the eigenvalues and its eigenvectors are obtained analytically as follows (20) $\begin{array}{rl}{\mathrm{\Omega }}_1& =\frac{1}{2}\left(\mathrm{\Lambda }-\sqrt{2{\beta }_1^2+\frac{2{\beta }_3}{\mathrm{\Lambda }}-{\mathrm{\Lambda }}^2}\right),\\ {\mathrm{\Omega }}_2& =\frac{1}{2}\left(\mathrm{\Lambda }+\sqrt{2{\beta }_1^2+\frac{2{\beta }_3}{\mathrm{\Lambda }}-{\mathrm{\Lambda }}^2}\right),\\ {\mathrm{\Omega }}_3& =-\frac{1}{2}\left(\mathrm{\Lambda }+\sqrt{2{\beta }_1^2-\frac{2{\beta }_3}{\mathrm{\Lambda }}-{\mathrm{\Lambda }}^2}\right),\\ {\mathrm{\Omega }}_4& =-\frac{1}{2}\left(\mathrm{\Lambda }-\sqrt{2{\beta }_1^2-\frac{2{\beta }_3}{\mathrm{\Lambda }}-{\mathrm{\Lambda }}^2}\right),\end{array}$(20) and (21) $|{\mathbf{\Omega }}_j⟩={\chi }_j\left(\begin{array}{c}1\\ \frac{{\mathrm{\Omega }}_j({\mu }_2^2+{\nu }_1^2-{\mathrm{\Omega }}_j({\mathrm{\Omega }}_j+\delta \left)\right)}{{\nu }_2({\mu }_2^2-{\mathrm{\Omega }}_j({\mathrm{\Omega }}_j+\delta \left)\right)-{\nu }_1({\mu }_1{\mu }_2-i\lambda {\mathrm{\Omega }}_j)}\\ \frac{-{\mathrm{\Omega }}_j({\mu }_1{\mu }_2+{\nu }_1{\nu }_2-i\lambda {\mathrm{\Omega }}_j)}{{\nu }_2({\mu }_2^2-{\mathrm{\Omega }}_j({\mathrm{\Omega }}_j+\delta \left)\right)-{\nu }_1({\mu }_1{\mu }_2-i\lambda {\mathrm{\Omega }}_j)}\\ \frac{{\mu }_1({\nu }_1^2-{\mathrm{\Omega }}_j({\mathrm{\Omega }}_j+\delta \left)\right)-{\mu }_2({\nu }_1{\nu }_2-i\lambda {\mathrm{\Omega }}_j)}{{\nu }_2({\mu }_2^2-{\mathrm{\Omega }}_j({\mathrm{\Omega }}_j+\delta \left)\right)-{\nu }_1({\mu }_1{\mu }_2-i\lambda {\mathrm{\Omega }}_j)}\end{array}\right).$(21) Here, $\begin{array}{rl}{\beta }_1& =\sqrt{{\delta }^2+{\lambda }^2+{\mu }_1^2+{\mu }_2^2+{\nu }_1^2+{\nu }_2^2},\\ {\beta }_2& =\sqrt{{\mu }_1^2{\nu }_1^2-2{\mu }_1{\mu }_2{\nu }_1{\nu }_2+{\mu }_2^2{\nu }_2^2},\\ {\beta }_3& =\delta ({\mu }_1^2-{\mu }_2^2-{\nu }_1^2+{\nu }_2^2),\\ \mathrm{\Lambda }& =\sqrt{\frac{2}{3}{\beta }_1^2+\frac{12{\beta }_2^2+{\beta }_1^4}{3\xi }+\frac{1}{3}\xi },\\ \xi & =\sqrt[3]{\begin{array}{c}36{\beta }_1^2{\beta }_2^2-{\beta }_2^6+\frac{27}{2}{\beta }_3^2\\ +\sqrt{{\left(36{\beta }_1^2{\beta }_2^2-{\beta }_2^6+\frac{27}{2}{\beta }_3^2\right)}^2-{\left(12{\beta }_2^2+{\beta }_1^4\right)}^3}\end{array}},\\ \gamma & =2{\mu }_1{\mu }_2{\nu }_2{\nu }_1\left({\mathrm{\Omega }}_j(\delta +{\mathrm{\Omega }}_j)-{\mu }_2^2\right)\\ & +{\nu }_2^2{\left({\mu }_2^2-{\mathrm{\Omega }}_j(\delta +{\mathrm{\Omega }}_j)\right)}^2+{\nu }_1^2\left({\lambda }^2{\mathrm{\Omega }}_j^2+{\mu }_1^2{\mu }_2^2\right)\\ {\epsilon }_1& ={\mathrm{\Omega }}_j^2\left({\mathrm{\Omega }}_j^2\left({\delta }^2+2\delta {\mathrm{\Omega }}_j+{\lambda }^2+{\mathrm{\Omega }}_j^2\right)+{\nu }_1^2\left({\lambda }^2\right.\right.\\ & +\left.\left.{\nu }_2^2-2{\mathrm{\Omega }}_j(\delta +{\mathrm{\Omega }}_j)\right)+{\nu }_2^2(\delta +{\mathrm{\Omega }}_j{)}^2+{\nu }_1^4\right)\\ {\epsilon }_2& ={\mu }_2^2\left({\nu }_1^2\left({\nu }_2^2+2{\mathrm{\Omega }}_j^2\right)-{\mathrm{\Omega }}_j\left({\mathrm{\Omega }}_j\left(2{\mathrm{\Omega }}_j(\delta +{\mathrm{\Omega }}_j)-{\lambda }^2\right)\right.\right.\\ & +\left.\left.2{\nu }_2^2(\delta +{\mathrm{\Omega }}_j)\right)\right)+{\mu }_2^4\left({\nu }_2^2+{\mathrm{\Omega }}_j^2\right)\\ {\epsilon }_3& ={\mu }_1^2\left({\left({\nu }_1^2-{\mathrm{\Omega }}_j(\delta +{\mathrm{\Omega }}_j)\right)}^2+{\mu }_2^2\left({\nu }_1^2+{\mathrm{\Omega }}_j^2\right)\right)\\ & -2{\mu }_1{\mu }_2{\nu }_1{\nu }_2\left({\mu }_2^2+{\nu }_1^2-{\mathrm{\Omega }}_j(2\delta +3{\mathrm{\Omega }}_j)\right)\\ {\chi }_j& =\sqrt{\frac{\gamma }{{\epsilon }_1+{\epsilon }_2+{\epsilon }_3}},j=1,2,3,4.\end{array}$ Hereafter, to calculate the atomic population inversion as one of the statistical properties of the proposed quantum model, it is easily to evolute the density matrix $\hat{\rho }\left(t\right)=|\mathrm{\Psi }\left(t\right)⟩⟨\mathrm{\Psi }\left(t\right)|$. Therefore, we can use this density matrix to measure the sensitivity of the proposed quantum model to the detuning parameters and the initial atomic angles via the atomic population inversion in the next section.

3. Atomic population inversion

The atomic population inversion is one of important quantities related with atoms, which represents the difference between the probabilities of finding the atom in the upper atom state and in the lower atom state. This means that the atomic inversion gives us information on the predicted behaviour of the atom during the procession of the atom–field and atom–atom interactions. Our aim is to study the effects of the detuning parameters on the quantum model and the sensitivity measurement of the proposed quantum system to initial atomic angles. Note that we focus on studying the collapse and revival phenomenon which are usually appeared during the interaction between atom and quantum system or between atom and atom. To reach our aim, it requires to calculate the density matrix ${\hat{\rho }}^{\left(j\right)}\left(t\right)$, where j indicates to the number of the interested atom. This density matrix can be obtained by taking the trace over quantum system and one of atoms as follows (22) $\begin{array}{rl}{\hat{\rho }}^{\left(j\right)}\left(t\right)& =T{r}_{{\mathrm{atom}}_i}\left(T{r}_{\mathrm{qs}}|\mathrm{\Psi }\right(t)⟩⟨\mathrm{\Psi }(t\left)|\right),i,j=1,2,\\ & ={\rho }_{11}^{\left(j\right)}\left(t\right)|+{⟩}_{jj}⟨+|+{\rho }_{12}^{\left(j\right)}\left(t\right)|+{⟩}_{jj}⟨-|+{\rho }_{21}^{\left(j\right)}\left(t\right)|-{⟩}_{jj}\\ & ⟨+|+{\rho }_{22}^{\left(j\right)}\left(t\right)|-{⟩}_{jj}⟨-|\end{array}$(22) where, (23) $\begin{array}{rl}{\rho }_{11}^{\left(1\right)}\left(t\right)& =\sum _{m=0}^{\mathrm{\infty }}\left(|A(m,t){|}^2+|B(m,t){|}^2\right),\end{array}$(23) (24) $\begin{array}{rl}{\rho }_{22}^{\left(1\right)}\left(t\right)& =\sum _{m=0}^{\mathrm{\infty }}\left(|C(m,t){|}^2+|D(m,t){|}^2\right),\end{array}$(24) (25) $\begin{array}{rl}{\rho }_{12}^{\left(1\right)}\left(t\right)& =\sum _{m=0}^{\mathrm{\infty }}\left(A\right(m+1,t\left)C^{\ast }\right(m,t)+B(m+1,t)\\ & D^{\ast }(m,t))={\rho }_{21}^{\ast \left(1\right)}(t),\end{array}$(25) (26) $\begin{array}{rl}{\rho }_{11}^{\left(2\right)}\left(t\right)& =\sum _{m=0}^{\mathrm{\infty }}\left(|A(m,t){|}^2+|C(m,t){|}^2\right),\end{array}$(26) (27) $\begin{array}{rl}{\rho }_{22}^{\left(2\right)}\left(t\right)& =\sum _{m=0}^{\mathrm{\infty }}\left(|B(m,t){|}^2+|D(m,t){|}^2\right),\end{array}$(27) (28) $\begin{array}{rl}{\rho }_{12}^{\left(2\right)}\left(t\right)& =\sum _{m=0}^{\mathrm{\infty }}\left(A\right(m+1,t\left)B^{\ast }\right(m,t)+C(m+1,t)\\ & D^{\ast }(m,t))={\rho }_{21}^{\ast \left(2\right)}(t).\end{array}$(28) The atomic inversion, $W^{\left(j\right)}\left(t\right)$, for the jth atom is defined as (29) $W^{\left(j\right)}\left(t\right)={\rho }_{11}^{\left(j\right)}\left(t\right)-{\rho }_{22}^{\left(j\right)}\left(t\right).$(29) To research of the conducts of the atoms during the atom–atom and atom–quantum system interactions, we plot the atomic inversion, $W^{\left(1\right)}\left(t\right)$ for the first atom and $W^{\left(2\right)}\left(t\right)+2$ for the second atom, against the scaled time $T=g_{1}t$. 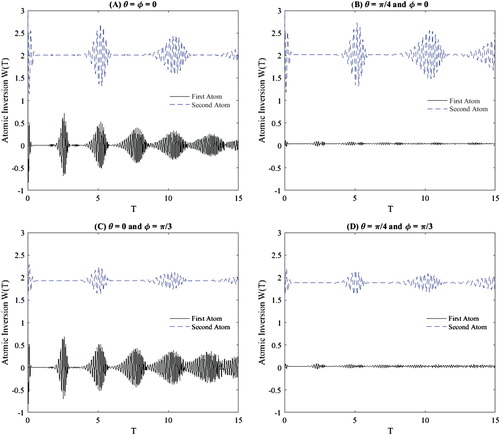Notice in Figure 1 that, the system is sensitive to the parameters of the initial state such that the atomic angles. So, to measure the sensitivity of the atomic inversion to the initial atomic angles, we fixed the values of $\alpha =0.5,g=0.5,\delta =2,\lambda =2,k=20$ and focused on the variation of the initial atomic angles. In Figure 1(A), we put $\theta =\phi =0$ which means that the states of both atoms are excited. As shown in this figure, the atomic population inversion discloses several periods of revivals and collapses. The amplitude of revivals decreases with time. In Figure 1(B), we consider that the initial state of the first atom is the superposition while the the state of the second atom is the excited state i.e $\theta =\pi /4$ and $\phi =0$. Note in this case, the amplitude of revivals for the first atom is very small compared with the amplitude of revivals for the second atom. Explanation that the effect of the quantum field, which obeys SU(1,1) Lie group, on the first atom is weak. In Figure 1(C), the atomic angles take values $\theta =0$ and $\phi =\pi /3$. This means that the initial state of the first atom is the excited state while the state of the second atom is the superposition state. The amplitude of revivals for the first atom is small compared with the second atom. Also, amplitude of revivals deceases with time. In Figure 1(D), we consider that the initial state of both two atom are the superposition state ($\theta =\pi /4$ and $\phi =\pi /3$). We can see that the amplitude of revivals for the second atom is very small. Also the amplitude of revivals for the first atom is small compared with other cases. We note that in Figure 1: the number of revivals for the first atom is double the number of revivals for the second atom at the same time interval which is as a result to take g=0.5. In addition, the amplitude of revivals decreases with increasing the atomic angles during the interval $[0,\pi /4]$. Whilst, the amplitude of revivals increases with increasing the atomic angles through out $[\pi /4,\pi /2]$.

Figure 1. The atomic inversion function $W\left(T\right)$ against the scaled time $(T=g_{1}t)$ at $\alpha =0.5$, g=0.5, k=20, and $\delta =\lambda =2$.

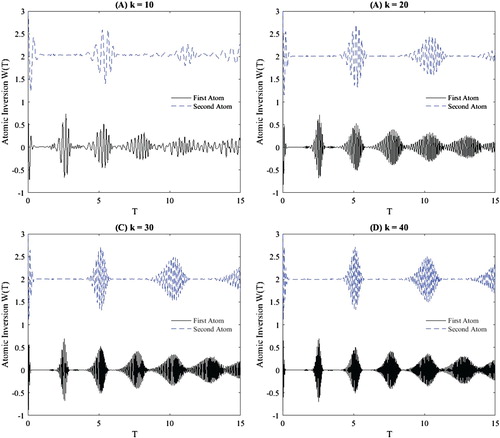
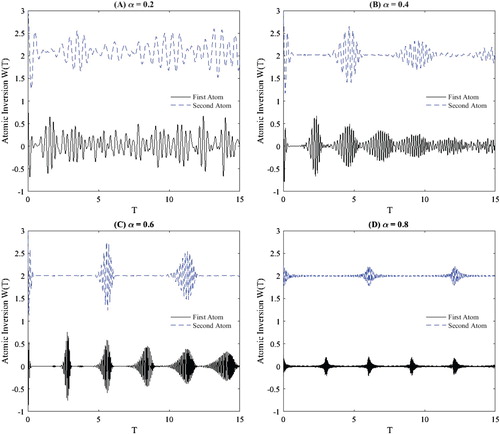
To measure the sensitivity of the atoms in the proposed quantum model to the Bargmann index k and Perelomov coherent parameter α, we choose other parameters as $\alpha =0.5,g=0.5,\delta =2,\lambda =2,\theta =\phi =0$. Firstly, we study the sensitivity of the atoms to the Bargmann index k, where the Perelomov coherent parameter $\alpha =0.5$ is fixed in Figure 2. Observe that the fluctuation of the revivals increases with increasing the Bargmann index k=10,20,30,40. Also, the number of revivals increases slowly. Secondly, the Bargmann index k=20 is fixed in Figure 3. While the Perelomov coherent parameter takes the values $\alpha =0.2,0.4,06,$ and 0.8. For small value of $\alpha =0.2$ in Figure 3(A), the collapses are very small for first atom and disappear for second atom. In other figure, with increasing the Perelomov coherent parameter, the collapse regions increase and the revival regions compress. In addition, the amplitude of revivals for $\alpha =0.8$ is smaller than the amplitude of revivals $\alpha =0.4$ and $\alpha =0.6$ as shown in Figure 3(B–D).

Figure 2. The atomic inversion function $W\left(T\right)$ against the scaled time $(T=g_{1}t)$ at $\alpha =0.5$, g=0.5, $\theta =\phi =0$, and $\delta =\lambda =2$.

Figure 3. The atomic inversion function $W\left(T\right)$ against the scaled time $(T=g_{1}t)$ at g=0.5, k=20, $\theta =\phi =0$, and $\delta =\lambda =2$.

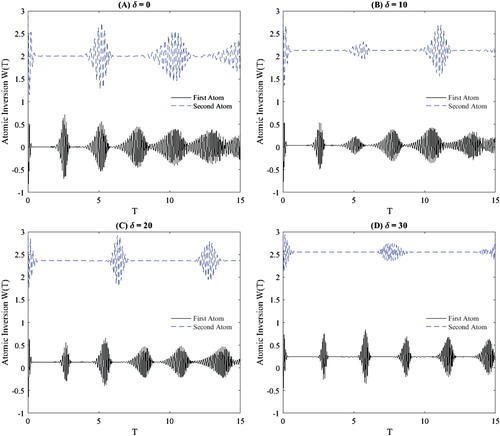
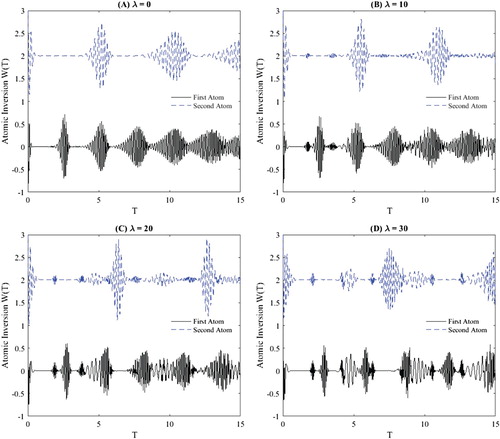
Finally, let us study the effects of the detuning parameters δ and λ on the quantum model. We plot the atomic inversion with increasing the parameters δ and λ as shown in Figures 4 and 5, respectively. Note in Figure 4(A–D) that the collapse regions increase and the revival regions compress with increasing the parameter δ. Also the maximum values of revival amplitudes perturbed. While in Figure 5(A–D), we note that the collapse regions increase with increasing the detuning parameter λ. Notice also, one or more a small revival becomes pronounced into the collapse regions. Furthermore, the density of fluctuations in the revival regions is irregular.

Figure 4. The atomic inversion function $W\left(T\right)$ against the scaled time $(T=g_{1}t)$ at g=0.5, $\alpha =0.5$, k=20, $\theta =\phi =0$, and $\lambda =0$.

Figure 5. The atomic inversion function $W\left(T\right)$ against the scaled time $(T=g_{1}t)$ at g=0.5, $\alpha =0.5$, k=20, $\theta =\phi =0$, and $\delta =0$.

4. Conclusion

The time-dependent wave function for asymmetric two two-level atoms interacting with SU(1,1) quantum system was obtained analytically. Initially, the SU(1,1) quantum system prepared in the Perelomov coherent state and two atoms are in different states dependent on two atomic angles. The atomic population inversion was obtained and discussed with increasing the model parameters such as initial atomic angles, Perelomov coherent parameter, the Bargmann index and the detuning parameters. These effects can be summarized as: For asymmetric case, the number of revivals for the second atom is g times of the number of revivals for the first atom at the same time interval. The amplitude of revivals decreases with increasing the atomic angles during the interval $[0,\pi /4]$. While, the amplitude of revivals increases with increasing the atomic angles through out $[\pi /4,\pi /2]$. The fluctuation of the revivals increases with increasing the Bargmann index. For increasing the Perelomov coherent parameter, the collapse regions increase, the revival regions compress, and the amplitude of revivals decreases. For increasing the detuning parameters δ and λ, the collapse regions increase and the revival regions compress. While for increasing the detuning parameter λ only, one or more a small revival becomes pronounced into the collapse regions. Moreover, the density of fluctuations in the revival regions is irregular. Then, the proposed quantum model is sensitive to the variation in all proposed model parameters. In addition, there is non-classical behaviour in the presence the detuning parameters effects and the atom–atom interaction.

Acknowledgments

The authors would like to express their sincere thanks and gratitude to Prof. A.-S.F. Obada (Professor of Quantum Optics in Department of Mathematics, Faculty of Science, Al-Azhar University, Egypt) for their recommendations which improved the work.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Abdallah A. Nahla  http://orcid.org/0000-0003-3572-4167