A new branch of bialgebraic structures: UP-bialgebras

Abstract

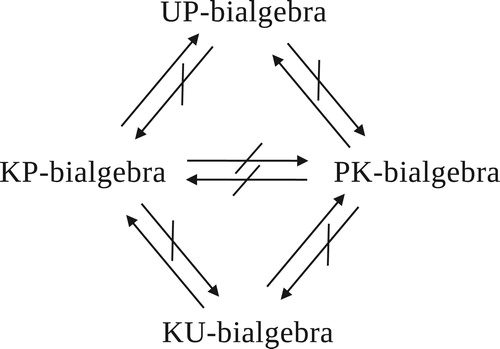
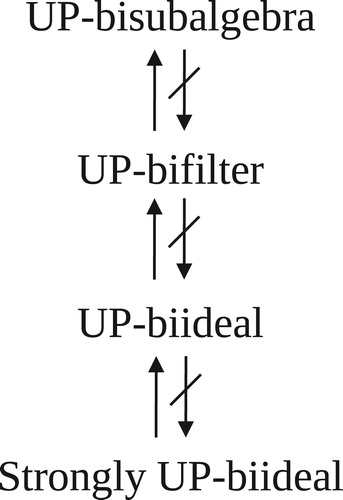
The notion of bialgebraic structures was discussed by Vasantha Kandasamy [Bialgebraic structures and Smarandache bialgebraic structures. India: American Research Press; 2003]. The main target of this paper is to introduce the notions of a KU-bialgebra, a KP-bialgebra, a PK-bialgebra, and a UP-bialgebra and the notions of a UP-bisubalgebra, a UP-bifilter, a UP-biideal, and a strongly UP-biideal of UP-bialgebras, and prove the generalization of the notions and some results related to a UP-subalgebra, a UP-filter, a UP-ideal, and a strongly UP-ideal of UP-algebras. Furthermore, we introduce the notion of a UP-bihomomorphism and study the image and inverse image of a UP-bisubalgebra, a UP-bifilter, a UP-biideal, and a strongly UP-biideal of UP-bialgebras under a UP-bihomomorphism. Finally, we have the generalization diagram of KU/KP/PK/UP-bialgebras (see Figure 1) and the diagram of special subsets of UP-bialgebras (see Figure 2).

Keywords:

• UP-algebra
• UP-bialgebra
• UP-bihomomorphism

Mathematics Subject Classification:

• 03G25

1. Introduction

Among many algebraic structures, algebras of logic form important class of algebras. Examples of these are BCK-algebras [1], BCI-algebras [2], KU-algebras [3], UP-algebra [4] and others (see [5, 6]). BCK and BCI-algebras are two classes of logical algebras. They were introduced by Imai and Iséki [1, 2] in 1966 and have been extensively investigated by many researchers. It is known that the class of BCK-algebras is a proper subclass of the class of BCI-algebras. The branch of the logical algebra, UP-algebras was introduced by Iampan [4], and it is known that the class of KU-algebras [3] is a proper subclass of the class of UP-algebras. It have been examined by several researchers, for example, the notion of derivations of UP-algebras was introduced by Sawika et al. [7], Somjanta et al. [8] introduced the notion of fuzzy sets in UP-algebras, the concept of hesitant fuzzy sets on UP-algebras was introduced by Mosrijai et al. [9], Senapati et al. [10, 11] applied cubic set and interval-valued intuitionistic fuzzy structure in UP-algebras, Romano [12] introduced the notion of proper UP-filters in UP-algebras, Iampan et al. [13] introduced the concept of a partial transformation UP-algebra induced by a UP-algebra, etc.

In 2003, the notion of bialgebraic structures was discussed by Vasantha Kandasamy [14], for instance, bisemigroups, bigroups, bigroupoids, biloops, birings, bisemirings, binear-rings, and so on. Jun et al. [15] introduced the notion of BCK/BCI-bialgebras in 2006. The concept of biideal in BCK/BCI-bialgebras was introduced by Jun [16] later.

In this paper, we introduce the notions of KU/KP/PK/UP-bialgebras and the notions of UP-bisubalgebras, UP-bifilters, UP-biideals, strongly UP-biideals of UP-bialgebras, and prove some results related to UP-subalgebras, UP-filters, UP-ideals, strongly UP-ideals of UP-algebras. Furthermore, we introduce the notion of UP-bihomomorphism and study the image and inverse image of such a subset under a UP-bihomomorphism.

2. Basic results on KU/UP-algebras

Before we begin our study, we will introduce the definition of KU/UP-algebras.

Definition 2.1

[3, 4]

An algebra $A=(A,\cdot ,0)$ of type $(2,0)$ is called a UP-algebra where A is a nonempty set, · is a binary operation on A, and 0 is a fixed element of A (i.e. a nullary operation) if it satisfies the following axioms:

(UP-1)	$(\mathrm{\forall }x,y,z\in A)\left(\right(y\cdot z)\cdot ((x\cdot y)\cdot (x\cdot z))=0)$,
(UP-2)	$(\mathrm{\forall }x\in A)(0\cdot x=x)$,
(UP-3)	$(\mathrm{\forall }x\in A)(x\cdot 0=0)$, and
(UP-4)	$(\mathrm{\forall }x,y\in A)(x\cdot y=0,y\cdot x=0\Rightarrow x=y)$, and is called a KU-algebra if it satisfies (UP-2), (UP-3), (UP-4), and
(KU-1)	$(\mathrm{\forall }x,y,z\in A)\left(\right(y\cdot x)\cdot ((x\cdot z)\cdot (y\cdot z))=0)$.

Example 2.2

[17]

Let $A=\{0,1,2,3,4\}$ be a set with a binary operation · defined by the following Cayley table: $\begin{array}{cccccc}\cdot & 0& 1& 2& 3& 4\\ 0& 0& 1& 2& 3& 4\\ 1& 0& 0& 2& 3& 4\\ 2& 0& 1& 0& 3& 3\\ 3& 0& 0& 2& 0& 2\\ 4& 0& 0& 0& 0& 0\end{array}$ Then $(A,\cdot ,0)$ is a KU-algebra.

Example 2.3

[18]

Let X be a universal set and let $\mathrm{\Omega }\in \mathcal{P}\left(X\right)$. Let ${\mathcal{P}}_{\mathrm{\Omega }}\left(X\right)=\{A\in \mathcal{P}(X)\mid \mathrm{\Omega }\subseteq A\}$. Define a binary operation · on ${\mathcal{P}}_{\mathrm{\Omega }}\left(X\right)$ by putting $A\cdot B=B\cap (A^{\mathrm{\prime }}\cup \mathrm{\Omega })$ for all $A,B\in {\mathcal{P}}_{\mathrm{\Omega }}\left(X\right)$. Then $\left({\mathcal{P}}_{\mathrm{\Omega }}\right(X),\cdot ,\mathrm{\Omega })$ is a UP-algebra and we shall call it the generalized power UP-algebra of type 1 with respect to Ω.

Example 2.4

[18]

Let X be a universal set and let $\mathrm{\Omega }\in \mathcal{P}\left(X\right)$. Let ${\mathcal{P}}^{\mathrm{\Omega }}\left(X\right)=\{A\in \mathcal{P}(X)\mid A\subseteq \mathrm{\Omega }\}$. Define a binary operation * on ${\mathcal{P}}^{\mathrm{\Omega }}\left(X\right)$ by putting $A\ast B=B\cup (A^{\mathrm{\prime }}\cap \mathrm{\Omega })$ for all $A,B\in {\mathcal{P}}^{\mathrm{\Omega }}\left(X\right)$. Then $\left({\mathcal{P}}^{\mathrm{\Omega }}\right(X),\ast ,\mathrm{\Omega })$ is a UP-algebra and we shall call it the generalized power UP-algebra of type 2 with respect to Ω.

In particular, $\left({\mathcal{P}}_{\mathrm{\Omega }}\right(X),\cdot ,\mathrm{\varnothing })$ is the power UP-algebra of type 1, and $\left({\mathcal{P}}^{\mathrm{\Omega }}\right(X),\ast ,X)$ is the power UP-algebra of type 2.

Example 2.5

[19]

Let $\mathbb{N}$ be the set of all natural numbers with two binary operations ° and • defined by $(\mathrm{\forall }x,y\in \mathbb{N})\left(x\circ y=\left\{\begin{array}{ll}y& \mathrm{i}\mathrm{f}x<y,\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.\right)$ and $(\mathrm{\forall }x,y\in \mathbb{N})\left(x\bullet y=\left\{\begin{array}{ll}y& \mathrm{i}\mathrm{f}x>y\mathrm{o}\mathrm{r}x=0,\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.\right)$ Then $(\mathbb{N},\circ ,0)$ and $(\mathbb{N},\bullet ,0)$ are UP-algebras.

Example 2.6

Let $A=\{0,1,2,3,4\}$ be a set with a binary operation · defined by the following Cayley table: $\begin{array}{cccccc}\cdot & 0& 1& 2& 3& 4\\ 0& 0& 1& 2& 3& 4\\ 1& 0& 0& 1& 3& 3\\ 2& 0& 0& 0& 3& 3\\ 3& 0& 0& 0& 0& 3\\ 4& 0& 0& 0& 0& 0\end{array}$ Then $(A,\cdot ,0)$ is a UP-algebra which is not a KU-algebra because $(0\cdot 2)\left(\right(2\cdot 4)\cdot (0\cdot 4\left)\right)=2\cdot (3\cdot 4)=2\cdot 3=3\ne 0$.

In a UP-algebra $A=(A,\cdot ,0)$, the following assertions are valid (see [4, 20]). (1) $\begin{array}{rl}& (\mathrm{\forall }x\in A)(x\cdot x=0),\end{array}$(1) (2) $\begin{array}{rl}& (\mathrm{\forall }x,y,z\in A)(x\cdot y=0,y\cdot z=0\Rightarrow x\cdot z=0),\end{array}$(2) (3) $\begin{array}{rl}& (\mathrm{\forall }x,y,z\in A)(x\cdot y=0\Rightarrow (z\cdot x)\cdot (z\cdot y)=0),\end{array}$(3) (4) $\begin{array}{rl}& (\mathrm{\forall }x,y,z\in A)(x\cdot y=0\Rightarrow (y\cdot z)\cdot (x\cdot z)=0),\end{array}$(4) (5) $\begin{array}{rl}& (\mathrm{\forall }x,y\in A)(x\cdot (y\cdot x)=0),\end{array}$(5) (6) $\begin{array}{rl}& (\mathrm{\forall }x,y\in A)\left(\right(y\cdot x)\cdot x=0\iff x=y\cdot x),\end{array}$(6) (7) $\begin{array}{rl}& (\mathrm{\forall }x,y\in A)(x\cdot (y\cdot y)=0),\end{array}$(7) (8) $\begin{array}{rl}& (\mathrm{\forall }a,x,y,z\in A)\left(\right(x\cdot \left(y\cdot z\right)\left)\cdot \right(x\cdot \left(\right(a\cdot y)\cdot (a\cdot z\left)\right)\left)=0\right),\end{array}$(8) (9) $\begin{array}{rl}& (\mathrm{\forall }a,x,y,z\in A)\left(\right(\left(\right(a\cdot x)\cdot (a\cdot y\left)\right)\cdot z\left)\cdot \right(\left(x\cdot y\right)\cdot z\left)=0\right),\end{array}$(9) (10) $\begin{array}{rl}& (\mathrm{\forall }x,y,z\in A)\left(\right((x\cdot y)\cdot z)\cdot (y\cdot z)=0),\end{array}$(10) (11) $\begin{array}{rl}& (\mathrm{\forall }x,y,z\in A)(x\cdot y=0\Rightarrow x\cdot (z\cdot y)=0),\end{array}$(11) (12) $\begin{array}{rl}& (\mathrm{\forall }x,y,z\in A)\left(\right((x\cdot y)\cdot z)\cdot (x\cdot (y\cdot z))=0),\mathrm{a}\mathrm{n}\mathrm{d}\end{array}$(12) (13) $\begin{array}{rl}& (\mathrm{\forall }a,x,y,z\in A)\left(\right((x\cdot y)\cdot z)\cdot (y\cdot (a\cdot z))=0).\end{array}$(13) On a UP-algebra $A=(A,\cdot ,0)$, we define the UP-ordering ≤ on A [4] as follows: $(\mathrm{\forall }x,y\in A)(x\le y\iff x\cdot y=0).$

Definition 2.7

[4, 8, 21]

A nonempty subset S of a UP-algebra $(A,\cdot ,0)$ is called

1. a UP-subalgebra of A if $(\mathrm{\forall }x,y\in S)(x\cdot y\in S)$.

2. a UP-filter of A if

   1. the constant 0 of A is in S, and

   2. $(\mathrm{\forall }x,y\in A)(x\cdot y\in S,x\in S\Rightarrow y\in S)$.

3. a UP-ideal of A if

   1. the constant 0 of A is in S, and

   2. $(\mathrm{\forall }x,y,z\in A)(x\cdot (y\cdot z)\in S,y\in S\Rightarrow x\cdot z\in S)$.

4. a strongly UP-ideal of A if

   1. the constant 0 of A is in S, and

   2. $(\mathrm{\forall }x,y,z\in A)\left(\right(z\cdot y)\cdot (z\cdot x)\in S,y\in S\Rightarrow x\in S)$.

Guntasow et al. [21] proved the generalization that the notion of UP-subalgebras is a generalization of UP-filters, the notion of UP-filters is a generalization of UP-ideals, and the notion of UP-ideals is a generalization of strongly UP-ideals. Moreover, they also proved that a UP-algebra A is the only one strongly UP-ideal of itself.

Definition 2.8

[4]

Let $(A,\cdot ,0_A)$ and $(B,{\cdot }^{\prime },0_B)$ be UP-algebras. A mapping f form A to B is called a UP-homomorphism if $(\mathrm{\forall }x,y\in A)\left(f\right(x\cdot y)=f(x\left){\cdot }^{\prime }f\right(y\left)\right).$

A UP-homomorphism $f:A\to B$ is called

1. a UP-epimorphism if f is surjective,

2. a UP-monomorphism if f is injective, and

3. a UP-isomorphism if f is bijective.

Moreover, we say A is UP-isomorphic to B, symbolically, $A\cong B$ if there is a UP-isomorphism form A to B.

Let f be a mapping form A to B, and let C and D be nonempty subsets of A and of B, respectively. The set $\left\{f\right(x)\mid x\in C\}$ which denoted by $f\left(C\right)$ is called the image of C under f. In particular, $f\left(A\right)$ which denoted by $\mathrm{I}\mathrm{m}\left(f\right)$ is called the image of f. The dually set $\{x\in A\mid f(x)\in D\}$ which denoted by $f^{-1}\left(D\right)$ is called the inverse image of D under f. Especially, the set $f^{-1}\left(\right\{0_B\left\}\right)$ which written by $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ is called the kernel of f. That is, $\begin{array}{rl}\mathrm{I}\mathrm{m}\left(f\right)& =\left\{f\right(x)\in B\mid x\in A\}\mathrm{a}\mathrm{n}\mathrm{d}\\ \mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)& =\{x\in A\mid f(x)=0_B\}.\end{array}$

Theorem 2.9

[4]

Let A,B and C be UP-algebras. Then the following statements hold:

1. the identity mapping form A to A is a UP-isomorphism,

2. if $f:A\to B$ is a UP-isomorphism, then $f^{-1}:B\to A$ is a UP-isomorphism, and

3. if $f:A\to B$ and $g:B\to C$ are UP-isomorphisms, then $g\circ f:A\to C$ is a UP-isomorphism.

Theorem 2.10

[4]

Let $(A,\cdot ,0_A)$ and $(B,{\cdot }^{\prime },0_B)$ be UP-algebras and let $f:A\to B$ be a UP-homomorphism. Then the following statements hold:

1. $f\left(0_A\right)=0_B,$

2. if $x\le y,$ then $f\left(x\right)\le f\left(y\right)$ for all $x,y\in A,$

3. if C is a UP-subalgebra of A, then the image $f\left(C\right)$ is a UP-subalgebra of B. In particular, $\mathrm{I}\mathrm{m}\left(f\right)$ is a UP-subalgebra of B,

4. if D is a UP-subalgebra of B, then the inverse image $f^{-1}\left(D\right)$ is a UP-subalgebra of A. In particular, $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ is a UP-subalgebra of A,

5. if C is a UP-filter of A such that $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq C,$ then the image $f\left(C\right)$ is a UP-filter of $\mathrm{I}\mathrm{m}\left(f\right),$

6. if D is a UP-filter of B, then the inverse image $f^{-1}\left(D\right)$ is a UP-filter of A. In particular, $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ is a UP-ideal of A,

7. if C is a UP-ideal of A such that $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq C,$ then the image $f\left(C\right)$ is a UP-ideal of $\mathrm{I}\mathrm{m}\left(f\right),$

8. if D is a UP-ideal of B, then the inverse image $f^{-1}\left(D\right)$ is a UP-ideal of A. In particular, $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ is a UP-ideal of A, and

9. $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)=\left\{0_A\right\}$ if and only if f is injective.

Theorem 2.11

Let $(A,\cdot ,0_A)$ and $(B,{\cdot }^{\prime },0_B)$ be UP-algebras and let $f:A\to B$ be a UP-homomorphism. Then the following statements hold:

1. if C is a strongly UP-ideal of A, then the image $f\left(C\right)$ is a strongly UP-ideal of $\mathrm{I}\mathrm{m}\left(f\right),$ and

2. if D is a strongly UP-ideal of B, then the inverse image $f^{-1}\left(D\right)$ is a strongly UP-ideal of A.

Proof.

(1) Assume that C is a strongly UP-ideal of A. Then C=A and so $f\left(C\right)=f\left(A\right)=\mathrm{I}\mathrm{m}\left(f\right)$. By Theorem 2.10 (3), $\mathrm{I}\mathrm{m}\left(f\right)$ is a UP-algebra. Hence, $f\left(C\right)$ is a strongly UP-ideal of $\mathrm{I}\mathrm{m}\left(f\right)$.

(2) Assume that D is a strongly UP-ideal of B. Then D=B and so $f^{-1}\left(D\right)=f^{-1}\left(B\right)=A$. Hence, $f^{-1}\left(D\right)$ is a strongly UP-ideal of A.

3. UP-bialgebras

In this section, we introduce the notions of KU/KP/PK/UP-bialgebras and the notions of UP-bisubalgebras, UP-bifilters, UP-biideals, strongly UP-biideals of UP-bialgebras, and prove some results related to UP-subalgebras, UP-filters, UP-ideals, strongly UP-ideals of UP-algebras.

Definition 3.1

An algebra $A=(A,\cdot ,\ast ,0)$ of type $(2,2,0)$ is called a UP-bialgebra (resp., KU-bialgebra) where A is a nonempty set, · and * are binary operations on A, and 0 is a fixed element of A if there exist two distinct proper subsets $A_1$ and $A_2$ of A with respect to · and *, respectively, such that

1. $A=A_1\cup A_2$,

2. $(A_1,\cdot ,0)$ is a UP-algebra (resp., KU-algebra), and

3. $(A_2,\ast ,0)$ is a UP-algebra (resp., KU-algebra).

We will denote the UP-bialgebra by $A=P\left(A_1\right)\uplus P\left(A_2\right)$ and denote the KU-bialgebra by $A=K\left(A_1\right)\uplus K\left(A_2\right)$. If $(A_1,\cdot ,0)$ is a UP-algebra and $(A_2,\ast ,0)$ is a KU-algebra, then we say that $A=(A,\cdot ,\ast ,0)$ is a PK-bialgebra, which denoted by $A=P\left(A_1\right)\uplus K\left(A_2\right)$. If $(A_1,\cdot ,0)$ is a KU-algebra and $(A_2,\ast ,0)$ is a UP-algebra, then we say that $A=(A,\cdot ,\ast ,0)$ is a KP-bialgebra, which denoted by $A=K\left(A_1\right)\uplus P\left(A_2\right)$. In case of $A_1\cap A_2=\left\{0\right\}$, we call A zero disjoint.

On a UP-bialgebra $A=P\left(A_1\right)\uplus P\left(A_2\right)$ with two binary operations · and *, we define a binary relation ≤ on A as follows: $(\mathrm{\forall }x,y\in A)(x\le y\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r}\cdot \iff x\cdot y=0)$ and $(\mathrm{\forall }x,y\in A)(x\le y\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r}\ast \iff x\ast y=0).$

Example 3.2

Let $A=\{0,1,2,3,4,5\}$ be a set with two binary operations · and * defined by the following Cayley tables: $\begin{array}{ccccccc}\cdot & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 0& 0& 0\\ 2& 0& 2& 0& 0& 0& 0\\ 3& 0& 2& 2& 0& 0& 0\\ 4& 0& 2& 2& 4& 0& 0\\ 5& 0& 2& 2& 2& 2& 2\end{array}$ $\begin{array}{ccccccc}\ast & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 4& 3& 5\\ 1& 0& 0& 1& 5& 5& 5\\ 2& 0& 0& 0& 5& 5& 5\\ 3& 0& 5& 5& 0& 5& 5\\ 4& 0& 5& 5& 5& 0& 5\\ 5& 0& 0& 0& 5& 5& 0\end{array}$ Consider two proper subsets $A_1=\{0,1,2,3,4\}$ and $A_2=\{0,1,2,5\}$ of A. Then $(A_1,\cdot ,0)$ and $(A_2,\ast ,0)$ are UP-algebras. Therefore, $(A,\cdot ,\ast ,0)$ is a UP-bialgebra. Since $(A_1,\cdot ,0)$ and $(A_2,\ast ,0)$ are not KU-algebras, we obtain $(A,\cdot ,\ast ,0)$ is not a KU/KP/PK-bialgebra and we only say that $A=P\left(A_1\right)\uplus P\left(A_2\right)$.

Example 3.3

Let $A=\{0,1,2,3,4,5\}$ be a set with two binary operations · and * defined by the following Cayley tables: $\begin{array}{ccccccc}\cdot & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 0& 0& 0\\ 2& 0& 0& 0& 3& 4& 5\\ 3& 0& 0& 2& 0& 3& 5\\ 4& 0& 0& 2& 0& 0& 5\\ 5& 0& 1& 0& 0& 0& 0\end{array}$ $\begin{array}{ccccccc}\ast & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 3& 4& 5\\ 2& 0& 0& 0& 0& 0& 5\\ 3& 0& 1& 0& 0& 4& 5\\ 4& 0& 1& 0& 3& 0& 0\\ 5& 0& 1& 2& 3& 0& 0\end{array}$ Consider two proper subsets $A_1=\{0,2,3,4,5\}$ and $A_2=\{0,1\}$ of A. Then $(A_1,\cdot ,0)$ and $(A_2,\ast ,0)$ are KU-algebras and also are UP-algebras. Therefore, $(A,\cdot ,\ast ,0)$ is a KU/KP/PK/UP-bialgebra and we can say that $A=K\left(A_1\right)\uplus U\left(A_2\right)=K\left(A_1\right)\uplus P\left(A_2\right)=P\left(A_1\right)\uplus K\left(A_2\right)=P\left(A_1\right)\uplus P\left(A_2\right)$. Because $A_1\cap A_2=\left\{0\right\}$, so we can say that A is zero disjoint.

Example 3.4

Let $A=\{0,1,2,3,4,5\}$ be a set with two binary operations · and * defined by the following Cayley tables: $\begin{array}{ccccccc}\cdot & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 0& 0& 0\\ 2& 0& 0& 0& 0& 0& 0\\ 3& 0& 3& 0& 0& 0& 0\\ 4& 0& 3& 0& 3& 0& 0\\ 5& 0& 3& 0& 3& 4& 0\end{array}$ $\begin{array}{ccccccc}\ast & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 0& 0& 0\\ 2& 0& 0& 0& 4& 0& 0\\ 3& 0& 0& 2& 0& 0& 0\\ 4& 0& 0& 2& 4& 0& 0\\ 5& 0& 0& 0& 0& 0& 0\end{array}$ Consider two proper subsets $A_1=\{0,1,3,4,5\}$ and $A_2=\{0,2,3,4\}$ of A. Then $(A_1,\cdot ,0)$ is a UP-algebra, and $(A_2,\ast ,0)$ is a KU-algebra and also is a UP-algebra. Therefore, $(A,\cdot ,\ast ,0)$ is a PK/UP-bialgebra. Since $(A_1,\cdot ,0)$ is not a KU-algebra, we obtain $(A,\cdot ,\ast ,0)$ is not a KU/KP-bialgebra and we say that $A=P\left(A_1\right)\uplus K\left(A_2\right)=P\left(A_1\right)\uplus P\left(A_2\right)$.

Example 3.5

Let $A=\{0,1,2,3,4,5\}$ be a set with two binary operations · and * defined by the following Cayley tables: $\begin{array}{ccccccc}\cdot & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 0& 0& 0\\ 2& 0& 2& 0& 0& 0& 0\\ 3& 0& 2& 5& 0& 0& 0\\ 4& 0& 0& 0& 0& 0& 0\\ 5& 0& 2& 2& 5& 0& 0\end{array}$ $\begin{array}{ccccccc}\ast & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 0& 0& 0\\ 2& 0& 0& 0& 0& 0& 0\\ 3& 0& 0& 0& 0& 4& 4\\ 4& 0& 0& 0& 3& 0& 3\\ 5& 0& 0& 0& 0& 0& 0\end{array}$ Consider two proper subsets $A_1=\{0,1,2,3,5\}$ and $A_2=\{0,3,4,5\}$ of A. Then $(A_1,\cdot ,0)$ is a KU-algebra and also is a UP-algebra, and $(A_2,\ast ,0)$ is a UP-algebra. Therefore, $(A,\cdot ,\ast ,0)$ is a KP/UP-bialgebra. Since $(A_2,\cdot ,0)$ is not a KU-algebra, we obtain $(A,\cdot ,\ast ,0)$ is not a KU/PK-bialgebra and we say that $A=K\left(A_1\right)\uplus P\left(A_2\right)=P\left(A_1\right)\uplus P\left(A_2\right)$.

Example 3.6

Let $\mathbb{Z}$ be the set of all integer numbers with two binary operations $◃$ and $▹$ defined by $(\mathrm{\forall }x,y\in \mathbb{Z})\left(x◃y=\left\{\begin{array}{ll}y& \mathrm{i}\mathrm{f}x>y\mathrm{o}\mathrm{r}x=0,\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.\right)$ and $(\mathrm{\forall }x,y\in \mathbb{Z})\left(x▹y=\left\{\begin{array}{ll}y& \mathrm{i}\mathrm{f}x<y\mathrm{o}\mathrm{r}x=0,\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.\right)$ Then $({\mathbb{Z}}^{+}\cup \{0\},◃,0)$ and $({\mathbb{Z}}^{-}\cup \{0\},▹,0)$ are UP-algebras. Hence, $(\mathbb{Z},◃,▹,0)$ is a UP-bialgebra.

From [4], we know that the notion of UP-algebras is a generalization of KU-algebras. Hence, we obtain that the notions of KP/PK-bialgebras are a generalization of KU-bialgebras, and the notion of UP-bialgebras is a generalization of KP/PK-bialgebras.

Definition 3.7

A nonempty subset S of a UP-bialgebra $A=P\left(A_1\right)\uplus P\left(A_2\right)$ is called a UP-bisubalgebra (resp., UP-bifilter, UP-biideal, strongly UP-biideal) of A if there exist subsets $S_1$ of $A_1$ and $S_2$ of $A_2$ with respect to · and *, respectively, such that

1. $S_1\ne S_2$ and $S=S_1\cup S_2$,

2. $(S_1,\cdot ,0)$ is a UP-subalgebra (resp., UP-filter, UP-ideal, strongly UP-ideal) of $(A_1,\cdot ,0)$, and

3. $(S_2,\ast ,0)$ is a UP-subalgebra (resp., UP-filter, UP-ideal, strongly UP-ideal) of $(A_2,\ast ,0)$.

In case of $S_1\cap A_2=\left\{0\right\}=A_1\cap S_2$, we call S zero disjoint.

Theorem 3.8

A nonempty subset C of $A=P\left(A_1\right)\uplus P\left(A_2\right)$ is a strongly UP-biideal of A if and only if C=A.

Proof.

Assume that C is a strongly UP-biideal of $A=P\left(A_1\right)\uplus P\left(A_2\right)$. Then there exist distinct subsets $C_1$ of $A_1$ and $C_2$ of $A_2$ with respect to · and *, respectively, such that $C=C_1\cup C_2$, and $(C_1,\cdot ,0)$ and $(C_2,\ast ,0)$ are strongly UP-ideals of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Thus $C_1=A_1$ and $C_2=A_2$. Therefore, $C=C_1\cup C_2=A_1\cup A_2=A$.

Conversely, let $C=A=P\left(A_1\right)\uplus P\left(A_2\right)$. Then there exist distinct subsets $A_1$ of C and $A_2$ of C with respect to · and *, respectively, such that $C=A_1\cup A_2$, and $(A_1,\cdot ,0)$ and $(A_2,\ast ,0)$ are UP-algebras. Thus $A_1$ and $A_2$ are strongly UP-ideal of C. Therefore, C is a strongly UP-biideal of A.

Theorem 3.9

Every UP-bifilter of $A=P\left(A_1\right)\uplus P\left(A_2\right)$ is a UP-bisubalgebra of A.

Proof.

Assume that F is a UP-bifilter of $A=P\left(A_1\right)\uplus P\left(A_2\right)$. Then there exist distinct subsets $F_1$ of $A_1$ and $F_2$ of $A_2$ with respect to · and *, respectively, such that $F=F_1\cup F_2$, and $(F_1,\cdot ,0)$ and $(F_2,\ast ,0)$ are UP-filters of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Since every UP-filter of UP-algebras is a UP-subalgebra, we obtain $(F_1,\cdot ,0)$ and $(F_2,\ast ,0)$ are UP-subalgebras of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Therefore, F is a UP-bisubalgebra of A.

Example 3.10

Let $A=\{0,1,2,3,4,5\}$ be a set with two binary operations · and * defined by the following Cayley tables: $\begin{array}{ccccccc}\cdot & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 2& 2& 0& 0\\ 2& 0& 1& 0& 1& 0& 0\\ 3& 0& 0& 0& 0& 0& 0\\ 4& 0& 0& 0& 0& 0& 0\\ 5& 0& 0& 0& 0& 0& 0\end{array}$ $\begin{array}{ccccccc}\ast & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 0& 4& 5\\ 2& 0& 0& 0& 0& 0& 0\\ 3& 0& 0& 0& 0& 0& 0\\ 4& 0& 0& 0& 0& 0& 5\\ 5& 0& 0& 0& 0& 0& 0\end{array}$ Consider two proper subsets $A_1=\{0,1,2,3\}$ and $A_2=\{0,1,4,5\}$ of A. Then $(A_1,\cdot ,0)$ and $(A_2,\ast ,0)$ are UP-algebras. Therefore, $(A,\cdot ,\ast ,0)$ is a UP-bialgebra. Choose a subset $S=\{0,1,2,5\}$ of A. Consider two proper subsets $S_1=\{0,1,2\}$ and $S_2=\{0,1,5\}$ of B. Then $(S_1,\cdot ,0)$ and $(S_2,\ast ,0)$ are UP-subalgebras of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Therefore, $(S_1,\cdot ,0)$ and $(S_2,\ast ,0)$ are not UP-filters of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively, because $2\cdot 3=1\in S_1$ and $2\in S_1$ but $1\notin S_1$ and, $5\ast 4=0\in S_2$ and $5\in S_2$ but $4\notin S_2$. Hence, F is a UP-bisubalgebra of $(A,\cdot ,\ast ,0)$ but is not a UP-bifilter of $(A,\cdot ,\ast ,0)$.

Theorem 3.11

Every UP-biideal of $A=P\left(A_1\right)\uplus P\left(A_2\right)$ is a UP-bifilter of A.

Proof.

Assume that I is a UP-biideal of $A=P\left(A_1\right)\uplus P\left(A_2\right)$. Then there exist distinct subsets $I_1$ of $A_1$ and $I_2$ of $A_2$ with respect to · and *, respectively, such that $I=I_1\cup I_2$, and $(I_1,\cdot ,0)$ and $(I_2,\ast ,0)$ are UP-ideals of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Since every UP-ideal of UP-algebras is a UP-filter, we obtain $(I_1,\cdot ,0)$ and $(I_2,\ast ,0)$ are UP-filters of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Therefore, I is a UP-bifilter of A.

Example 3.12

Let $A=\{0,1,2,3,4,5\}$ be a set with two binary operations · and * defined by the following Cayley tables: $\begin{array}{ccccccc}\cdot & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 2& 2& 0& 0\\ 2& 0& 1& 0& 2& 0& 0\\ 3& 0& 1& 0& 0& 0& 0\\ 4& 0& 0& 0& 0& 0& 0\\ 5& 0& 0& 0& 0& 0& 0\end{array}$ $\begin{array}{ccccccc}\ast & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 0& 0& 0\\ 2& 0& 0& 0& 0& 0& 0\\ 3& 0& 0& 0& 0& 4& 5\\ 4& 0& 0& 0& 3& 0& 3\\ 5& 0& 0& 0& 0& 0& 0\end{array}$ Consider two proper subsets $A_1=\{0,1,2,3\}$ and $A_2=\{0,3,4,5\}$ of A. Then $(A_1,\cdot ,0)$ and $(A_2,\ast ,0)$ are UP-algebras. Therefore, $(A,\cdot ,\ast ,0)$ is a UP-bialgebra. Choose a subset $F=\{0,1,4\}$ of A. Consider two proper subsets $F_1=\{0,1\}$ and $F_2=\{0,4\}$ of B. Then $(F_1,\cdot ,0)$ and $(F_2,\ast ,0)$ are UP-filters of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Therefore, $(F_1,\cdot ,0)$ and $(F_2,\ast ,0)$ are not UP-ideals of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively, because $2\cdot (1\cdot 3)=0\in F_1$ and $1\in F_1$ but $2\cdot 3=2\notin F_1$ and, $3\ast (4\ast 5)=0\in F_2$ and $4\in F_2$ but $3\ast 5=5\notin F_2$. Hence, F is a UP-bifilter of $(A,\cdot ,\ast ,0)$ but is not a UP-biideal of $(A,\cdot ,\ast ,0)$.

Theorem 3.13

Every strongly UP-biideal of $A=P\left(A_1\right)\uplus P\left(A_2\right)$ is a UP-biideal of A.

Proof.

Assume that C is a strongly UP-biideal of $A=P\left(A_1\right)\uplus P\left(A_2\right)$. Then there exist distinct subsets $C_1$ of $A_1$ and $C_2$ of $A_2$ with respect to · and *, respectively, such that $C=C_1\cup C_2$, and $(C_1,\cdot ,0)$ and $(C_2,\ast ,0)$ are strongly UP-ideals of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Since every strongly UP-ideal of UP-algebras is a UP-ideal, we obtain $(C_1,\cdot ,0)$ and $(C_2,\ast ,0)$ are UP-ideals of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Therefore, C is a UP-biideal of A.

Example 3.14

Let $A=\{0,1,2,3,4,5\}$ be a set with two binary operations · and * defined by the following Cayley tables: $\begin{array}{ccccccc}\cdot & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 2& 3& 4& 0\\ 2& 0& 1& 0& 3& 4& 0\\ 3& 0& 1& 2& 0& 4& 0\\ 4& 0& 0& 0& 0& 0& 0\\ 5& 0& 0& 0& 0& 0& 0\end{array}$ $\begin{array}{ccccccc}\ast & 0& 1& 2& 3& 4& 5\\ 0& 0& 1& 2& 3& 4& 5\\ 1& 0& 0& 0& 0& 0& 0\\ 2& 0& 1& 0& 0& 0& 0\\ 3& 0& 1& 2& 0& 0& 0\\ 4& 0& 0& 0& 0& 0& 0\\ 5& 0& 1& 2& 3& 0& 0\end{array}$ Consider two proper subsets $A_1=\{0,1,2,3,4\}$ and $A_2=\{0,1,2,3,5\}$ of A. Then $(A_1,\cdot ,0)$ and $(A_2,\ast ,0)$ are UP-algebras. Therefore, $(A,\cdot ,\ast ,0)$ is a UP-bialgebra. Choose a subset $I=\{0,1,2,3,5\}$ of A. Consider two proper subsets $I_1=\{0,1,2,3\}$ and $I_2=\{0,2,3,5\}$ of B. Then $(I_1,\cdot ,0)$ and $(I_2,\ast ,0)$ are UP-ideals of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Therefore, I is a UP-biideal of $(A,\cdot ,\ast ,0)$. By Theorem 3.8, we can conclude that I is not a strongly UP-biideal of $(A,\cdot ,\ast ,0)$.

By Theorems 3.9, 3.11, and 3.13 and Examples 3.10, 3.12, and 3.14, we have that the notion of UP-bisubalgebras of UP-bialgebras is the generalization of the notion of UP-bifilters, the notion of UP-bifilters of UP-bialgebras is the generalization of the notion of UP-biideals, and the notion of UP-biideals of UP-bialgebras is the generalization of the notion of strongly UP-biideals.

Theorem 3.15

Let S be a nonempty subset of a UP-bialgebra $A=P\left(A_1\right)\uplus P\left(A_2\right)$ which satisfies the following conditions:

1. $(S\cap A_1,\cdot ,0)$ is a UP-subalgebra $($resp., UP-filter, UP-ideal, strongly UP-ideal$)$ of $(A_1,\cdot ,0),$ and

2. $(S\cap A_2,\ast ,0)$ is a UP-subalgebra $($resp., UP-filter, UP-ideal, strongly UP-ideal$)$ of $(A_2,\ast ,0)$.

Then S is a UP-bisubalgebra $($resp., UP-bifilter, UP-biideal, strongly UP-biideal$)$ of A.

Proof.

Let S be a nonempty subset of a UP-bialgebra $A=P\left(A_1\right)\uplus P\left(A_2\right)$ which satisfies the conditions (1) and (2). In fact, $S\cap A_1\ne S\cap A_2$ and $\begin{array}{rl}(S\cap A_1)\cup (S\cap A_2)& =\left(\right(S\cap A_1)\cup S)\cap \left(\right(S\cap A_1)\cup A_2)\\ & =\left(\right(S\cup S)\cap (A_1\cup S\left)\right)\cap \left(\right(S\cup A_2)\\ & \cap (A_1\cup A_2))\\ & =(S\cap (A_1\cup S\left)\right)\cap \left(\right(S\cup A_2)\cap A)\\ & =S\cap (S\cup A_2)\\ & =S.\end{array}$ Hence, S is a UP-bisubalgebra of A.

Theorem 3.16

Let S be a nonempty subset of a UP-bialgebra $A=P\left(A_1\right)\uplus P\left(A_2\right)$. If S is a zero disjoint UP-bisubalgebra $($resp., zero disjoint UP-bifilter, zero disjoint UP-biideal$)$ of A if and only if it satisfies the following conditions:

1. $(S\cap A_1,\cdot ,0)$ is a UP-subalgebra $($resp., UP-filter, UP-ideal$)$ of $(A_1,\cdot ,0),$ and

2. $(S\cap A_2,\ast ,0)$ is a UP-subalgebra $($resp., UP-filter, UP-ideal$)$ of $(A_2,\ast ,0)$.

Proof.

Assume that S is a zero disjoint UP-bisubalgebra (resp., zero disjoint UP-bifilter, zero disjoint UP-biideal) of a UP-bialgebra $A=P\left(A_1\right)\uplus P\left(A_2\right)$. Then there exist distinct subsets $S_1$ of $A_1$ and $S_2$ of $A_2$ with respect to · and *, respectively, such that $S=S_1\cup S_2$, and $(S_1,\cdot ,0)$ and $(S_2,\ast ,0)$ are UP-subalgebras (resp., UP-filters, UP-ideals) of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. We will show that $S_1=S\cap A_1$ and $S_2=S\cap A_2$. Now, $S_1\subseteq S,S_1\subseteq A_1$ and $S_2\subseteq S,S_2\subseteq A_2$ imply that $S_1\subseteq S\cap A_1$ and $S_2\subseteq S\cap A_2$.

Next, let $x\in S\cap A_1$. Then $x\in S$ and $x\in A_1$.

Case 1.1: $x\in S_1$. It is clear that $S_1\supseteq S\cap A_1$.

Case 1.2: $x\in S_2$. Then $x\in A_1\cap S_2$. Since S is a zero disjoint UP-bisubalgebra (resp., zero disjoint UP-bifilter, zero disjoint UP-biideal) of A, we have $x\in A_1\cap S_2=\left\{0\right\}\subseteq S_1$ and so $x\in S_1$. Thus $S_1\supseteq S\cap A_1$. Therefore, $S_1=S\cap A_1$.

Next, let $y\in S\cap A_2$. Then $y\in S$ and $y\in A_2$.

Case 2.1: $y\in S_2$. It is clear that $S_2\supseteq S\cap A_2$.

Case 2.2: $y\in S_1$. Then $x\in A_2\cap S_1$. Since S is a zero disjoint UP-bisubalgebra (resp., zero disjoint UP-bifilter, zero disjoint UP-biideal) of A, $x\in A_2\cap S_1=\left\{0\right\}\subseteq S_2$ and so $x\in S_2$. Thus $S_2\supseteq S\cap A_2$. Therefore, $S_2=S\cap A_2$.

Hence, $(S\cap A_1,\cdot ,0)$ is a UP-subalgebra (resp., UP-filter, UP-ideal) of $(A_1,\cdot ,0)$, and $(S\cap A_2,\ast ,0)$ is a UP-subalgebra (resp., UP-filter, UP-ideal) of $(A_2,\ast ,0)$.

Conversely, it is straightforward by Theorem 3.15.

Corollary 3.17

Let S be a nonempty subset of a zero disjoint UP-bialgebra $A=P\left(A_1\right)\uplus P\left(A_2\right)$. If S is a UP-bisubalgebra $($resp., UP-bifilter, UP-biideal$)$ of A if and only if it satisfies the following conditions:

1. $(S\cap A_1,\cdot ,0)$ is a UP-subalgebra $($resp., UP-filter, UP-ideal$)$ of $(A_1,\cdot ,0),$ and

2. $(S\cap A_2,\ast ,0)$ is a UP-subalgebra $($resp., UP-filter, UP-ideal$)$ of $(A_2,\ast ,0)$.

Proof.

It is straightforward by Theorem 3.16.

Theorem 3.18

Let C be a nonempty subset of a UP-bialgebra $A=P\left(A_1\right)\uplus P\left(A_2\right)$. Then C is a strongly UP-biideal of A if and only if it satisfies the following conditions:

1. $(C\cap A_1,\cdot ,0)$ is a strongly UP-ideal of $(A_1,\cdot ,0),$ and

2. $(C\cap A_2,\ast ,0)$ is a strongly UP-ideal of $(A_2,\ast ,0)$.

Proof.

Assume that C is a strongly UP-biideal of a UP-bialgebra $A=P\left(A_1\right)\uplus P\left(A_2\right)$. Then there exist distinct subsets $C_1$ of $A_1$ and $C_2$ of $A_2$ with respect to · and *, respectively, such that $C=C_1\cup C_2$, and $(C_1,\cdot ,0)$ and $(C_2,\ast ,0)$ are strongly UP-ideals of $(A_1,\cdot ,0)$ and of $(A_2,\ast ,0)$, respectively. Thus $C_1=A_1$ and $C_2=A_2$. Therefore, $C\cap A_1=C\cap C_1=C_1$ and $C\cap A_2=C\cap C_2=C_2$. Hence, $(C\cap A_1,\cdot ,0)$ is a strongly UP-ideal of $(A_1,\cdot ,0)$, and $(C\cap A_2,\ast ,0)$ is a strongly UP-ideal of $(A_2,\ast ,0)$.

Conversely, it is straightforward by Theorem 3.15.

4. UP-bihomomorphisms

First, we will reconsider the definition of the restriction function. Let $f:A\to B$ be a function from a set A to a set B. If C is a subset of A, then the restriction of f to C is the function $f_{\left[C\right]}:C\to B$. Informally, the restriction of f to C is the same function as f, but is only defined on C.

Because the notion of UP-bialgebras is a generalization of KU/KP/PK-bialgebras, we will only define the following definition on UP-bialgebras.

Definition 4.1

Let $A=P\left(A_1\right)\uplus P\left(A_2\right)$ with two binary operations · and *, and $B=P\left(B_1\right)\uplus P\left(B_2\right)$ with two binary operations ${\cdot }^{\prime }$ and ${\ast }^{\prime }$. A mapping f form A to B is called a UP-bihomomorphism if it satisfies the following properties:

1. $f_{\left[A_1\right]}:A_1\to B_1$ is a UP-homomorphism, and

2. $f_{\left[A_2\right]}:A_2\to B_2$ is a UP-homomorphism.

A UP-bihomomorphism $f:A\to B$ is called

1. a UP-biepimorphism if $f_{\left[A_1\right]}$ and $f_{\left[A_2\right]}$ are UP-epimorphisms,

2. a UP-bimonomorphism if $f_{\left[A_1\right]}$ and $f_{\left[A_2\right]}$ are UP-monomorphisms, and

3. a UP-biisomorphism if $f_{\left[A_1\right]}$ and $f_{\left[A_2\right]}$ are UP-isomorphisms.

Moreover, we say A is UP-biisomorphic to B, symbolically, $A\cong B$ if there is a UP-biisomorphism form A to B.

Theorem 4.2

Let A,B and C be UP-bialgebras. Then the following statements hold:

1. the identity mapping form A to A is a UP-biisomorphism,

2. if $f:A\to B$ is a UP-biisomorphism, then $f^{-1}:B\to A$ is a UP-biisomorphism, and

3. if $f:A\to B$ and $g:B\to C$ are UP-biisomorphisms, then $g\circ f:A\to C$ is a UP-biisomorphism.

Proof.

It is straightforward by Theorem 2.9.

Theorem 4.3

Let $A=P\left(A_1\right)\uplus P\left(A_2\right)$ with two binary operations · and *, and $B=P\left(B_1\right)\uplus P\left(B_2\right)$ with two binary operations ${\cdot }^{\prime }$ and ${\ast }^{\prime }$ and let $f:A\to B$ be a UP-bihomomorphism. Then the following statements hold:

1. $f\left(0_A\right)=0_B,$

2. if $x\le y$ under ·$($resp., $x\le y$ under $\ast ),$ then $f_{\left[A_1\right]}\left(x\right)\le f_{\left[A_1\right]}\left(y\right)$ $($resp., $f_{\left[A_2\right]}\left(x\right)\le f_{\left[A_2\right]}\left(y\right))$ for all $x,y\in A,$ and

3. $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)=\left\{0_A\right\}$ if and only if f is injective.

Proof.

It is straightforward by Theorem 2.10 (1), 2.10 (2), and 2.10 (9).

Theorem 4.4

Let $A=P\left(A_1\right)\uplus P\left(A_2\right)$ with two binary operations · and *, and $B=P\left(B_1\right)\uplus P\left(B_2\right)$ with two binary operations ${\cdot }^{\prime }$ and ${\ast }^{\prime }$ and let $f:A\to B$ be a UP-bihomomorphism. Then the following statements hold:

1. if S is a UP-bisubalgebra of A, then the image $f\left(S\right)$ is a UP-subalgebra of $B_1$ and of $B_2$ or $f\left(S\right)$ is a UP-bisubalgebra of B,

2. if $S=S_1\cup S_2$ is a UP-bifilter of A, and $S_1$ and $S_2$ are subsets of $A_1$ and of $A_2,$ respectivel,y with $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_1\cap S_2,$ then the image $f\left(S\right)$ is a UP-filter of $B_1$ and of $B_2$ or $f\left(S\right)$ is a UP-bifilter of B,

3. if $S=S_1\cup S_2$ is a UP-biideal of A, and $S_1$ and $S_2$ are subsets of $A_1$ and of $A_2,$ respectively, with $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_1\cap S_2,$ then the image $f\left(S\right)$ is a UP-ideal of $B_1$ and of $B_2$ or $f\left(S\right)$ is a UP-biideal of B, and

4. if $f_{\left[A_1\right]}$ and $f_{\left[A_2\right]}$ are surjective and S is a strongly UP-biideal of A, then the image $f\left(S\right)$ is a strongly UP-biideal of B.

Proof.

(1) Assume that S is a UP-bisubalgebra of A. Then there exist distinct subsets $S_1$ of $A_1$ and $S_2$ of $A_2$ with respect to · and *, respectively, such that $S=S_1\cup S_2$, and $(S_1,\cdot ,0_A)$ and $(S_2,\ast ,0_A)$ are UP-subalgebras of $(A_1,\cdot ,0_A)$ and of $(A_2,\ast ,0_A)$, respectively. Since $f\left(S_1\right)=f_{\left[A_1\right]}\left(S_1\right)\subseteq f_{\left[A_1\right]}\left(A_1\right)\subseteq B_1$ and by Theorem 2.10 (3), we have $f\left(S_1\right)$ is a UP-subalgebra of $B_1$. Since $f\left(S_2\right)=f_{\left[A_2\right]}\left(S_2\right)\subseteq f_{\left[A_2\right]}\left(A_2\right)\subseteq B_2$ and by Theorem 2.10 (3), we have $f\left(S_2\right)$ is a UP-subalgebra of $B_2$. Because $S=S_1\cup S_2$, so $f\left(S\right)=f(S_1\cup S_2)=f\left(S_1\right)\cup f\left(S_2\right)$. If $f\left(S_1\right)=f\left(S_2\right)$, then $f\left(S\right)=f\left(S_1\right)$ is a UP-subalgebra of $B_1$ and $f\left(S\right)=f\left(S_2\right)$ is a UP-subalgebra of $B_2$. If $f\left(S_1\right)\ne f\left(S_2\right)$, then $f\left(S\right)$ is a UP-bisubalgebra of A.

(2) Assume that $S=S_1\cup S_2$ is a UP-bifilter of A, and $S_1$ and $S_2$ are distinct subsets of $A_1$ and $A_2$, respectively, with $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_1\cap S_2$. Then distinct subsets $S_1$ of $A_1$ and $S_2$ of $A_2$ with respect to · and *, respectively, such that $S=S_1\cup S_2$, and $(S_1,\cdot ,0_A)$ and $(S_2,\ast ,0_A)$ are UP-filters of $(A_1,\cdot ,0_A)$ and of $(A_2,\ast ,0_A)$, respectively. We obtain $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_1$ and $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_2$ because $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_1\cap S_2$. Since $f\left(S_1\right)=f_{\left[A_1\right]}\left(S_1\right)\subseteq f_{\left[A_1\right]}\left(A_1\right)\subseteq B_1$ and by Theorem 2.10 (5), we have $f\left(S_1\right)$ is a UP-filter of $B_1$. Since $f\left(S_2\right)=f_{\left[A_2\right]}\left(S_2\right)\subseteq f_{\left[A_2\right]}\left(A_2\right)\subseteq B_2$ and by Theorem 2.10 (5), we have $f\left(S_2\right)$ is a UP-filter of $B_2$. Because $S=S_1\cup S_2$, so $f\left(S\right)=f(S_1\cup S_2)=f\left(S_1\right)\cup f\left(S_2\right)$. If $f\left(S_1\right)=f\left(S_2\right)$, then $f\left(S\right)=f\left(S_1\right)$ is a UP-filter of $B_1$ and $f\left(S\right)=f\left(S_2\right)$ is a UP-filter of $B_2$. If $f\left(S_1\right)\ne f\left(S_2\right)$, then $f\left(S\right)$ is a UP-bifilter of A.

(3) Assume that $S=S_1\cup S_2$ is a UP-biideal of A, and $S_1$ and $S_2$ are distinct subsets of $A_1$ and $A_2$, respectively, with $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_1\cap S_2$. Then distinct subsets $S_1$ of $A_1$ and $S_2$ of $A_2$ with respect to · and *, respectively, such that $S=S_1\cup S_2$, and $(S_1,\cdot ,0_A)$ and $(S_2,\ast ,0_A)$ are UP-ideals of $(A_1,\cdot ,0_A)$ and of $(A_2,\ast ,0_A)$, respectively. We obtain $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_1$ and $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_2$ because $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\subseteq S_1\cap S_2$. Since $f\left(S_1\right)=f_{\left[A_1\right]}\left(S_1\right)\subseteq f_{\left[A_1\right]}\left(A_1\right)\subseteq B_1$ and by Theorem 2.10 (7), we have $f\left(S_1\right)$ is a UP-ideal of $B_1$. Since $f\left(S_2\right)=f_{\left[A_2\right]}\left(S_2\right)\subseteq f_{\left[A_2\right]}\left(A_2\right)\subseteq B_2$ and by Theorem 2.10 (7), we have $f\left(S_2\right)$ is a UP-ideal of $B_2$. Because $S=S_1\cup S_2$, so $f\left(S\right)=f(S_1\cup S_2)=f\left(S_1\right)\cup f\left(S_2\right)$. If $f\left(S_1\right)=f\left(S_2\right)$, then $f\left(S\right)=f\left(S_1\right)$ is a UP-ideal of $B_1$ and $f\left(S\right)=f\left(S_2\right)$ is a UP-ideal of $B_2$. If $f\left(S_1\right)\ne f\left(S_2\right)$, then $f\left(S\right)$ is a UP-biideal of A.

(4) Assume that $f_{\left[A_1\right]}$ and $f_{\left[A_2\right]}$ are surjective and S is a strongly UP-biideal of A. Then there exist distinct subsets $S_1$ of $A_1$ and $S_2$ of $A_2$ with respect to · and *, respectively, such that $S=S_1\cup S_2$, and $(S_1,\cdot ,0_A)$ and $(S_2,\ast ,0_A)$ are strongly UP-ideals of $(A_1,\cdot ,0_A)$ and of $(A_2,\ast ,0_A)$, respectively. Thus $S_1=A_1$ and $S_2=A_2$. Since $f\left(S_1\right)=f_{\left[A_1\right]}\left(S_1\right)=f_{\left[A_1\right]}\left(A_1\right)\subseteq B_1$ and by Theorem 2.11 (1), we have $f\left(S_1\right)=f\left(A_1\right)=B_1$ and thus $f\left(S_1\right)$ is a strongly UP-ideal of $B_1$. Since $f\left(S_2\right)=f_{\left[A_2\right]}\left(S_2\right)=f_{\left[A_2\right]}\left(A_2\right)\subseteq B_2$ and by Theorem 2.11 (1), we have $f\left(S_2\right)=f\left(A_2\right)=B_2$ and thus $f\left(S_2\right)$ is a strongly UP-ideal of $B_2$. Because $S=S_1\cup S_2$, so $f\left(S\right)=f(S_1\cup S_2)=f\left(S_1\right)\cup f\left(S_2\right)$. Assume that $f\left(S_1\right)=f\left(S_2\right)$. Then $f\left(S\right)=f\left(S_1\right)$ is a strongly UP-ideal of $B_1$ and $f\left(S\right)=f\left(S_2\right)$ is a strongly UP-ideal of $B_2$. Thus $B_1=f\left(S\right)=B_2$, a contradiction. Therefore, $f\left(S_1\right)\ne f\left(S_2\right)$. Hence, $f\left(S\right)$ is a strongly UP-biideal of A.

The following example show that f is a UP-epimorphism and S is a strongly UP-biideal of A but the image $f\left(S\right)$ is not a strongly UP-biideal of B.

Example 4.5

Let $A=P\left(A_1\right)\uplus P\left(A_2\right)$ with two binary operations · and *, respectively, defined by the following Cayley tables: $\begin{array}{cccccc}\cdot & 0& 1& 2& 3& 4\\ 0& 0& 1& 2& 3& 4\\ 1& 0& 0& 2& 3& 4\\ 2& 0& 1& 0& 3& 4\\ 3& 0& 1& 0& 0& 4\\ 4& 0& 1& 2& 3& 0\end{array}\begin{array}{ccccc}\ast & 0& 1& 5& 6\\ 0& 0& 1& 5& 6\\ 1& 0& 0& 5& 6\\ 5& 0& 0& 0& 6\\ 6& 0& 0& 0& 0\end{array}$ and let $B=P\left(B_1\right)\uplus P\left(B_2\right)$ with two binary operations ${\cdot }^{\prime }$ and ${\ast }^{\prime }$, respectively, defined by the following Cayley tables: $\begin{array}{cccc}{\cdot }^{\prime }& 0^{\prime }& a& b\\ 0^{\prime }& 0^{\prime }& a& b\\ a& 0^{\prime }& 0^{\prime }& b\\ a& 0^{\prime }& 0^{\prime }& 0^{\prime }\end{array}\begin{array}{cccc}{\ast }^{\prime }& 0^{\prime }& a& c\\ 0^{\prime }& 0^{\prime }& a& c\\ a& 0^{\prime }& 0^{\prime }& c\\ c& 0^{\prime }& a& 0^{\prime }\end{array}$ Let $S=S_1\cup S_2$ be such that $S_1=A_1$ and $S_2=A_2$. Then $S_1$ and $S_2$ are strongly UP-ideals of $A_1$ and of $A_2$, respectively. Therefore, S is a strongly UP-biideal of A. We define a mapping f form A to B as follows: $f\left(x\right)=\left\{\begin{array}{ll}{0}^{\prime }& \mathrm{i}\mathrm{f}x\in \{0,1,4,5\},\\ a& \mathrm{i}\mathrm{f}x=2,\\ b& \mathrm{i}\mathrm{f}x=3,\\ c& \mathrm{i}\mathrm{f}x=6.\end{array}\right.$ Then f is a UP-epimorphism. We see that $f\left(S\right)$ is not a strongly UP-biideal of B because $f\left(S_1\right)=\{0^{\prime },a,b\}$ is a strongly UP-ideal of $B_1$ but $f\left(S_2\right)=\{0^{\prime },c\}$ is not a strongly UP-ideal of $B_2$.

Theorem 4.6

Let $A=P\left(A_1\right)\uplus P\left(A_2\right)$ with two binary operations · and *, and $B=P\left(B_1\right)\uplus P\left(B_2\right)$ with two binary operations ${\cdot }^{\prime }$ and ${\ast }^{\prime }$ and let $f:A\to B$ be a UP-bihomomorphism. Then the following statements hold:

1. if D is a UP-bisubalgebra of B, then the inverse image $f^{-1}\left(D\right)$ is a UP-subalgebra of $A_1$ and of $A_2$ or $f^{-1}\left(D\right)$ is a UP-bisubalgebra of A,

2. if D is a UP-bifilter of B, then the inverse image $f^{-1}\left(D\right)$ is a UP-filter of $A_1$ and of $A_2$ or $f^{-1}\left(D\right)$ is a UP-bifilter of A,

3. if D is a UP-biideal of B, then the inverse image $f^{-1}\left(D\right)$ is a UP-ideal of $A_1$ and of $A_2$ or $f^{-1}\left(D\right)$ is a UP-biideal of A, and

4. if D is a strongly UP-biideal of B, then the inverse image $f^{-1}\left(D\right)$ is a strongly UP-biideal of A.

Proof.

(1) Assume that D is a UP-bisubalgebra of B. Then there exist distinct subsets $D_1$ of $B_1$ and $D_2$ of $B_2$ with respect to ${\cdot }^{\prime }$ and ${\ast }^{\prime }$, respectively, such that $D=D_1\cup D_2$, and $(D_1,{\cdot }^{\prime },0_B)$ and $(D_2,{\ast }^{\prime },0_B)$ are UP-subalgebras of $(B_1,{\cdot }^{\prime },0_B)$ and of $(B_2,{\ast }^{\prime },0_B)$, respectively. Since $f^{-1}\left(D_1\right)=f_{\left[A_1\right]}^{-1}\left(D_1\right)\subseteq f_{\left[A_1\right]}^{-1}\left(B_1\right)=A_1$ and by Theorem 2.10 (4), we have $f^{-1}\left(D_1\right)$ is a UP-subalgebra of $A_1$. Since $f^{-1}\left(D_2\right)=f_{\left[A_2\right]}^{-1}\left(D_1\right)\subseteq f_{\left[A_2\right]}^{-1}\left(B_2\right)=A_2$ and by Theorem 2.10 (4), we have $f^{-1}\left(D_2\right)$ is a UP-subalgebra of $A_2$. Because $D=D_1\cup D_2$, so $f^{-1}\left(D\right)=f^{-1}(D_1\cup D_2)=f^{-1}\left(D_1\right)\cup f^{-1}\left(D_2\right)$. If $f^{-1}\left(D_1\right)=f^{-1}\left(D_2\right)$, then $f^{-1}\left(D\right)=f^{-1}\left(D_1\right)$ is a UP-subalgebra of $A_1$ and $f^{-1}\left(D\right)=f^{-1}\left(D_2\right)$ is a UP-subalgebra of $A_2$. If $f^{-1}\left(D_1\right)\ne f^{-1}\left(D_2\right)$, then $f^{-1}\left(D\right)$ is a UP-bisubalgebra of A.

(2) Assume that D is a UP-bifilter of B. Then there exist distinct subsets $D_1$ of $B_1$ and $D_2$ of $B_2$ with respect to ${\cdot }^{\prime }$ and ${\ast }^{\prime }$, respectively, such that $D=D_1\cup D_2$, and $(D_1,{\cdot }^{\prime },0_B)$ and $(D_2,{\ast }^{\prime },0_B)$ are UP-filters of $(B_1,{\cdot }^{\prime },0_B)$ and of $(B_2,{\ast }^{\prime },0_B)$, respectively. Since $f^{-1}\left(D_1\right)=f_{\left[A_1\right]}^{-1}\left(D_1\right)\subseteq f_{\left[A_1\right]}^{-1}\left(B_1\right)=A_1$ and by Theorem 2.10 (6), we have $f^{-1}\left(D_1\right)$ is a UP-filter of $A_1$. Since $f^{-1}\left(D_2\right)=f_{\left[A_2\right]}^{-1}\left(D_2\right)\subseteq f_{\left[A_2\right]}^{-1}\left(B_2\right)=A_2$ and by Theorem 2.10 (6), we have $f^{-1}\left(D_2\right)$ is a UP-filter of $A_2$. Because $D=D_1\cup D_2$, so $f^{-1}\left(D\right)=f^{-1}(D_1\cup D_2)=f^{-1}\left(D_1\right)\cup f^{-1}\left(D_2\right)$. If $f^{-1}\left(D_1\right)=f^{-1}\left(D_2\right)$, then $f^{-1}\left(D\right)=f^{-1}\left(D_1\right)$ is a UP-filter of $A_1$ and $f^{-1}\left(D\right)=f^{-1}\left(D_2\right)$ is a UP-filter of $A_2$. If $f^{-1}\left(D_1\right)\ne f^{-1}\left(D_2\right)$, then $f^{-1}\left(D\right)$ is a UP-bifilter of A.

(3) Assume that D is a UP-biideal of B. Then there exist distinct subsets $D_1$ of $B_1$ and $D_2$ of $B_2$ with respect to ${\cdot }^{\prime }$ and ${\ast }^{\prime }$, respectively, such that $D=D_1\cup D_2$, and $(D_1,{\cdot }^{\prime },0_B)$ and $(D_2,{\ast }^{\prime },0_B)$ are UP-ideals of $(B_1,{\cdot }^{\prime },0_B)$ and of $(B_2,{\ast }^{\prime },0_B)$, respectively. Since $f^{-1}\left(D_1\right)=f_{\left[A_1\right]}^{-1}\left(D_1\right)\subseteq f_{\left[A_1\right]}^{-1}\left(B_1\right)=A_1$ and by Theorem 2.10 (8), we have $f^{-1}\left(D_1\right)$ is a UP-ideal of $A_1$. Since $f^{-1}\left(D_2\right)=f_{\left[A_2\right]}^{-1}\left(D_2\right)\subseteq f_{\left[A_2\right]}^{-1}\left(B_2\right)=A_2$ and by Theorem 2.10 (8), we have $f^{-1}\left(D_2\right)$ is a UP-ideal of $A_2$. Because $D=D_1\cup D_2$, so $f^{-1}\left(D\right)=f^{-1}(D_1\cup D_2)=f^{-1}\left(D_1\right)\cup f^{-1}\left(D_2\right)$. If $f^{-1}\left(D_1\right)=f^{-1}\left(D_2\right)$, then $f^{-1}\left(D\right)=f^{-1}\left(D_1\right)$ is a UP-ideal of $A_1$ and $f^{-1}\left(D\right)=f^{-1}\left(D_2\right)$ is a UP-ideal of $A_2$. If $f^{-1}\left(D_1\right)\ne f^{-1}\left(D_2\right)$, then $f^{-1}\left(D\right)$ is a UP-biideal of A.

(4) Assume that D is a strongly UP-biideal of B. Then there exist distinct subsets $D_1$ of $B_1$ and $D_2$ of $B_2$ with respect to ${\cdot }^{\prime }$ and ${\ast }^{\prime }$, respectively, such that $D=D_1\cup D_2$, and $(D_1,{\cdot }^{\prime },0_B)$ and $(D_2,{\ast }^{\prime },0_B)$ are strongly UP-ideals of $(B_1,{\cdot }^{\prime },0_B)$ and of $(B_2,{\ast }^{\prime },0_B)$, respectively. Thus $D_1=B_1$ and $D_2=B_2$. Since $f^{-1}\left(D_1\right)=f_{\left[A_1\right]}^{-1}\left(D_1\right)=f_{\left[A_1\right]}^{-1}\left(B_1\right)=A_1$, we have $f^{-1}\left(D_1\right)$ is a strongly UP-ideal of $A_1$. Since $f^{-1}\left(D_2\right)=f_{\left[A_2\right]}^{-1}\left(D_1\right)=f_{\left[A_2\right]}^{-1}\left(B_2\right)=A_2$, we have $f^{-1}\left(D_2\right)$ is a strongly UP-ideal of $A_2$. Because $D=D_1\cup D_2$, so $f^{-1}\left(D\right)=f^{-1}(D_1\cup D_2)=f^{-1}\left(D_1\right)\cup f^{-1}\left(D_2\right)$. Assume that $f^{-1}\left(D_1\right)=f^{-1}\left(D_2\right)$. Then $f^{-1}\left(D\right)=f^{-1}\left(D_1\right)$ is a strongly UP-ideal of $A_1$ and $f^{-1}\left(D\right)=f^{-1}\left(D_2\right)$ is a strongly UP-ideal of $A_2$. Thus $A_1=f^{-1}\left(D\right)=A_2$, a contradiction. Therefore, $f^{-1}\left(D_1\right)\ne f^{-1}\left(D_2\right)$. Hence, $f^{-1}\left(D\right)$ is a strongly UP-biideal of A.

5. Conclusions and future work

In this paper, we have introduced the notions of KU/KP/PK/UP-bialgebras and proved some results related to UP-subalgebras, UP-filters, UP-ideals, strongly UP-ideals of UP-algebras. We also proved its generalizations and investigated some of its important properties. Then we have the generalization diagram of KU/KP/PK/UP-bialgebras below (see Figure 1). Also, we have introduced the notion of UP-bisubalgebras (resp., UP-bifilters, UP-biideals, strongly UP-biideals) of UP-bialgebras and investigated some of its important properties. Then we have the diagram of special subsets of UP-bialgebras below (see Figure 2).

Figure 1. diagram of KU/KP/PK/UP-bialgebras.

Figure 2. diagram of special subsets of UP-bialgebras.

In our future study of UP-bialgebras, may be the following topics should be considered:

• To study fuzzy sets in UP-bialgebras.

• To study intuitionistic fuzzy sets in UP-bialgebras.

• To study bipolar fuzzy sets in UP-bialgebras.

Acknowledgments

The authors would also like to thank the anonymous referee for giving many helpful suggestion on the revision of present paper.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Phakawat Mosrijai  http://orcid.org/0000-0002-1637-3819

Aiyared Iampan  http://orcid.org/0000-0002-0475-3320

Additional information

Funding

This work was financially supported by the University of Phayao.