Qualitative analysis for a variable delay system of differential equations of second order

Abstract

This paper analyzes the stability, uniformly stability, asymptotically stability, boundedness, uniformly boundedness and square integrability of solutions of a system of differential equations of second order with variable delay by applying the direct method of Lyapunov- Krasovskii. By means of a new Lyapunov-Krasovskii functional, we simplify and extend some previous work that is found in the recent literature. Finally, the validity and applicability of the proceeded results are indicated by some numerical examples applying MATLAB-Simulink. By the results of this paper, we can obtain the results of Omeike et al. [Stability and boundedness of solutions of certain vector delay differential equations. J Nigerian Math Soc. 2018;37(2):77–87], Theorem 1.1 and Theorem 1.2, under weaker conditions. In addition, we establish two new results on the uniformly stability and integrabilty of solutions the considered equation. Finally, in particular cases, the applicability of the results of this paper can be shown by two new examples. These are the contribution of this paper to the subject and the relevant literature.

KEYWORDS:

• System of differential equations
• second order
• stability
• uniformly stability
• asymptotically stability
• boundedness
• uniformly boundedness
• square integrability
• variable delay

2010 (MOS) SUBJECT CLASSIFICATIONS:

• 34K12
• 34K20

1. Introduction

In the past few decades, qualitative analysis of solutions of ordinary or delay differential equations of second order have attracted increasing attention due to its wide application in physics, engineering, signal processing, medicine, population dynamics and so on. Due to these facts, stability and some related concepts as important index of control systems receive considerable attention. A large number of papers are devoted to various kinds of stability, boundedness, convergence and some other properties of ordinary and delay differential equations and systems of differential equations [1–61]. To the best of our information, the results of these papers are derived by means of the Lyapunov or the Lyapunov- Krasovskii direct method applying various Lyapunov functions or Lyapunov- Krasovskii functionals. In this paper, we are not interested in the details of obtained results and used methods. However, during qualitative analysis of that differential equations, we should point out that suitable candidate function(s) or functional(s) are very effective for construction of stronger and weaker conditions.

In Omeike et al. [27], Omeike et al. considered the following Lienard delay differential equation (DDE) with the variable delay $r\left(t\right)\ge 0$: (1) $X^{\mathrm{\prime }\mathrm{\prime }}+A{X}^{\mathrm{\prime }}+H\left(X\right(t-r\left(t\right)\left)\right)=P(t,X,X^{\mathrm{\prime }}),$(1) in which $t\in {\mathrm{\Re }}^{+}$, ${\mathrm{\Re }}^{+}=[0,\mathrm{\infty })X\in {\mathrm{\Re }}^n,r\left(t\right)0\le r\left(t\right)\le \gamma ,\gamma r^{\mathrm{\prime }}\left(t\right)\le \xi ,0<\xi <1,An\times n-H:{\mathrm{\Re }}^n\to {\mathrm{\Re }}^{n}P:{\mathrm{\Re }}^{+}\times {\mathrm{\Re }}^n\times {\mathrm{\Re }}^n\to {\mathrm{\Re }}^{n}HH\left(0\right)=0$.

Omeike et al. [27] proved the following two theorems on the asymptotically stability and uniformly boundedness, uniformly ultimately boundedness of solutions, respectively, when $P(t,X,X^{\mathrm{\prime }})\equiv 0$ and $P(t,X,X^{\mathrm{\prime }})\ne 0.$ The results of Omeike et al. [27] are given by the following theorems.

Let $P(t,X,X^{\mathrm{\prime }})\equiv 0.$

Theorem 1.1

[27]

Consider DDE (1), let $H\left(0\right)=0$ and suppose that:

$\left(A1\right)0\le r\left(t\right)\le \gamma ,\gamma$ is a positive constant, $r^{\mathrm{\prime }}\left(t\right)\le \xi ,$ $0<\xi <1;$

$\left(A2\right)$ the matrices $A$ and $J_h\left(X\right)$ (Jacobian matrix of $H\left(X\right))$ are symmetric and positive definite, and furthermore that the eigenvalues ${\lambda }_i\left(A\right)$ and ${\lambda }_i\left(J_h\right(X\left)\right),(i=1,2,\dots ,n),$ of $A$ and $J_h\left(X\right),$ respectively, satisfy $0<{\delta }_a\le {\lambda }_i\left(A\right)\le {\mathrm{\Delta }}_a,{\delta }_h\le {\lambda }_i\left(J_h\right(X\left)\right)\le {\mathrm{\Delta }}_h\text{ for }X\in {\mathrm{\Re }}^n,$where ${\delta }_a,$ ${\delta }_h,$ ${\mathrm{\Delta }}_a$ and ${\mathrm{\Delta }}_h$ are finite constants;

$\left(A3\right)$ the matrices $A$ and $J_h\left(X\right)$ commute.

Then the zero solution of DDE (1) is asymptotically stable provided that $\gamma <min\left(\frac{2{\delta }_a{\delta }_h}{{\mathrm{\Delta }}_a{\mathrm{\Delta }}_h},\frac{{\delta }_a}{\mu +{\mathrm{\Delta }}_h}\right).$

Now, let $P(t,X,X^{\mathrm{\prime }})\ne 0.$

Theorem 1.2

[27]

If, in addition to the conditions $\left(A1\right),\left(A2\right)$ and $\left(A3\right)$ of Theorem 1.1, the inequality $\begin{array}{rl}& ||P(t,X,Y)||\le m+\delta (||X||+||Y||),\\ & \left(\text{are positive constants}\right),\end{array}$holds, then the solutions of DDE (1) are uniformly bounded and uniformly ultimately bounded provided the constant $\gamma$ satisfies $\gamma <min\left(\frac{2{\delta }_a{\delta }_h}{{\mathrm{\Delta }}_a{\mathrm{\Delta }}_h},\frac{2{\delta }_a(1-\xi )}{{\mathrm{\Delta }}_h[{\mathrm{\Delta }}_a+2(2-\xi \left)\right]}\right).$

Motivated by the results of Omeike et al. [27], that is, the above Theorem 1.1 and Theorem 1.2, and the mentioned sources, we consider the following system of differential equations of second order with the variable delay $\tau \left(t\right):$ (2) $X^{\mathrm{\prime }\mathrm{\prime }}+F(X,X^{\mathrm{\prime }})X^{\mathrm{\prime }}+H\left(X\right(t-\tau \left(t\right)\left)\right)=P(t,X,X^{\mathrm{\prime }}),$(2) in which $t\in {\mathrm{\Re }}^{+},$ ${\mathrm{\Re }}^{+}=[0,\mathrm{\infty }),X\in {\mathrm{\Re }}^n,\tau \left(t\right)0\le \tau \left(t\right)\le \gamma ,\gamma {\tau }^{\mathrm{\prime }}\left(t\right)\le \xi ,0<\xi <1;Fn\times n-H:{\mathrm{\Re }}^n\to {\mathrm{\Re }}^{n}P:{\mathrm{\Re }}^{+}\times {\mathrm{\Re }}^n\times {\mathrm{\Re }}^n\to {\mathrm{\Re }}^{n}HH\left(0\right)=0.$

DDE (2) is the vector version of the below nonlinear differential equations of second order: $\begin{array}{rl}& {x^{\mathrm{\prime }\mathrm{\prime }}}_i+\sum _{k=1}^n{f}_{ik}(x_1,\dots ,x_n;{x^{\mathrm{\prime }}}_1,\dots ,{x^{\mathrm{\prime }}}_n){x^{\mathrm{\prime }}}_k\\ & +h_i\left(x_1\right(t-\tau \left(t\right)),\dots ,x_n(t-\tau \left(t\right))\\ & =p_i(t,x_1,\dots ,x_n,{x^{\mathrm{\prime }}}_1,\dots ,{x^{\mathrm{\prime }}}_n),(i=1,2,\dots ,n).\end{array}$We can write DDE (2) as the below differential system: (3) $\begin{array}{rl}{X}^{\mathrm{\prime }}& =Y,\\ Y^{\mathrm{\prime }}& =-F(X,Y)Y-H\left(X\right)\\ & +{\int }_{t-\tau \left(t\right)}^t{J}_h\left(X\right(s\left)\right)Y\left(s\right)ds+P(t,X,Y),\end{array}$(3) where $J_h\left(X\right)$ is the Jacobian matrix of $H\left(X\right)$ defined by $J_h\left(X\right)=\left(\frac{\mathrm{\partial }{h}_i}{\mathrm{\partial }{x}_j}\right),(i,j=1,2,\dots ,n),$$(x_1,x_2,\dots ,x_n)$ and $(h_1,h_2,\dots ,h_n)$ are the components of $X$ and $H,$ respectively,

It is assumed that the Jacobian matrix $J_h\left(X\right)$ exists and is continuous. Let $X,$ $Y\in {\mathrm{\Re }}^n.$ Then, we define $⟨X,Y⟩={\sum }_{i=1}^n{x}_i{y}_i,$ $⟨X,X⟩=||X|{|}^2$ and $||A||={\sum }_{i,j=1}^n|a_{ij}|.$

For brevity in notation, if a function is written without its argument, we mean that the argument is always $t.$ For example, $X$ represents $X\left(t\right).$

The aim of this paper is to obtain the results of [27] under weaker conditions and give some additional new results. Besides, the validity and applicability of the results to be proceed are indicated by some numerical examples applying MATLAB-Simulink. These are contributions of the results of this paper to be given below.

2. Basic definitions and fundamental results

For a given number $r\ge 0,$ let $C^n$ denote the space of continuous functions mapping the interval $[-r,0]$ into ${\mathrm{\Re }}^n$ and for $\varphi \in C^n,$ $||\varphi ||=\underset{-r\le \varphi \le 0}{sup}||\varphi \left(\theta \right)||.$ $C_H^n$ denotes the set of $\varphi$ in $C^n$ for which $||\varphi ||<H.$ For any continuous function $x\left(u\right)$ defined on $-r\le u\le B,B>0,$ any fixed $t,$ $0\le t\le B,$ the symbol $x_t$ denotes the function $x(t+\theta ),-r\le \theta \le 0.$

We consider the autonomous delay differential equation (DDE): (4) $x^{\mathrm{\prime }}\left(t\right)=g\left(x_t\right),t\ge 0.$(4) It is assumed that $g\left(\varphi \right)$ is a functional defined for every $\varphi$ in $C_H^n$ and $x^{\mathrm{\prime }}\left(t\right)$ is the right side derivative of $x\left(t\right).$ We say $x\left(\varphi \right)$ is a solution of DDE (4) with the initial condition $\varphi$ in $C_H^n$ at $t=0$ if there is a $B>0$ such that $x\left(\varphi \right)$ is a function from $[-r,B){\mathrm{\Re }}^n{x}_t\left(\varphi \right)C_H^{n}0\le t<B,x_0\left(\varphi \right)=\varphi x\left(\varphi \right)\left(t\right)0\le t<B.$

Lemma 2.1

[8]

Suppose $g\left(0\right)=0.$ Let $V$ be a continuous functional defined on $C_H^n$ with $V\left(0\right)=0$ and let $u\left(s\right)$ be a function, non-negative and continuous for $0\le s<\mathrm{\infty },$ $u\left(s\right)\to \mathrm{\infty }$ as $s\to \mathrm{\infty }$ with $u\left(0\right)=0.$ If for all $\varphi$ in $C_H^n,u\left(||\varphi \left(0\right)||\right)\le V\left(\varphi \right),$ $V^{\mathrm{\prime }}\left(\varphi \right)\le 0,$ then the zero solution of DDE (4) is stable.

Let $R\subset C_H^n$ be a set of all functions $\varphi \in C_H^n$ where $V^{\mathrm{\prime }}\left(\varphi \right)=0.$ If $\left\{0\right\}$ is the largest invariant set in $R,$ then the solution $x=0$ of DDE (4) is asymptotically stable.

Let us consider the following non-autonomous delay differential equation (DDE): (5) $x^{\mathrm{\prime }}=f(t,x_t),x_t=x(t+\theta ),-r\le \theta \le 0,t\ge 0,$(5) where $f:{\mathrm{\Re }}^{+}\times C_H\to {\mathrm{\Re }}^n$ is a continuous mapping, $f(t,0)=0,$ and we suppose that $F$ takes closed bounded sets into bounded sets of ${\mathrm{\Re }}^n.$ Here $(C,||.||)$ is the Banach space of continuous function $\varphi :[-r,0]\to {\mathrm{\Re }}^n$ with supremum norm, $r>0;$ $C_H$ is the open $H$-ball in $C;$ $C_H:=\{\varphi \in (C[-r,0],{\mathrm{\Re }}^n):||\varphi ||<H\}.$ Let $S$ be the set of $\phi \in C$ such that $||\phi ||\ge H.$ We denote by $S^{\bullet }$ the set of all functions $\phi \in C$ such that $|\phi \left(0\right)|\ge H,$ where $H$ is large enough.

Definition 2.1

[4]

A continuous function $W:{\mathrm{\Re }}^n\to {\mathrm{\Re }}^{+}$ with $W\left(0\right)=0,$ $W\left(s\right)>0$ if $s>0,$ and $W$ strictly increasing is a wedge. (We denote wedges by $W$ or $W_i$, where $i$ is an integer.)

Definition 2.2

[4]

Let $D$ be an open set in ${\mathrm{\Re }}^n$ with $0\in D.$ A function $V:[0,\mathrm{\infty })\times D\to [0,\mathrm{\infty })V(t,0)=0W_{1}V(t,x)\ge W_1\left(|x|\right),W_{2}V(t,x)\le W_2\left(|x|\right).$

Theorem 2.1

[4]

Suppose that there is a continuous Lyapunov-Krasovskii for DDE (5) and wedges satisfying the following:

$1^{\circ })$ $W_1\left(|\phi \left(0\right)|\right)\le V(t,\phi )\le W_2\left(||\phi ||\right),$ (where $W_1\left(r\right)$ and $W_2\left(r\right)$ are wedges);

$2^{\circ })$ $V^{\mathrm{\prime }}(t,\phi )\le 0.$

Then the zero solution of DDE (5) is uniformly stable.

Theorem 2.2

[50]

Suppose that there exists a continuous Lyapunov-Krasovskii functional $V(t,\phi )$ defined for all $t\in {\mathrm{\Re }}^{+},$ ${\mathrm{\Re }}^{+}=[0,\mathrm{\infty }),\phi \in S^{\bullet }$

$3^{\circ }\left)a\right(|\phi \left(0\right)|\left)\le V\right(t,\phi \left)\le b_1\right(|\phi \left(0\right)|\left)+b_2\right(||\phi ||),$where $a\left(r\right),$ $b_1\left(r\right),$ $b_2\left(r\right)\in CI,$ $(CI$ denotes the families of continuous increasing functions), and are positive for $r>H$ and $a\left(r\right)-b_2\left(r\right)\to \mathrm{\infty }$ as $r\to \mathrm{\infty };$

$4^{\circ }\left)V^{\mathrm{\prime }}\right(t,\phi )\le 0.$

Then, the solutions of DDE (5) are uniformly bounded.

3. Qualitative results for solutions

In this section, we ensure the main problem of this paper.

3.1. Hypotheses

Suppose the following hypotheses hold:

$\left(A1\right)$ There are positive constants ${\delta }_f$ and ${\mathrm{\Delta }}_f$ such that the symmetric matrix $F$ satisfies ${\delta }_f\le {\lambda }_i\left(F\right(X,Y\left)\right)\le {\mathrm{\Delta }}_f\mathit{\text{for all }}X,Y\in {\mathrm{\Re }}^n.$

$\left(A2\right)$ There are some positive constants ${\delta }_h$ and ${\mathrm{\Delta }}_h$ such that

$H\left(0\right)=0,$ $H\left(X\right)\ne 0,$ $(X\ne 0),J_h\left(X\right)$ is symmetric and ${\delta }_h\le {\lambda }_i\left(J_h\right(X\left)\right)\le {\mathrm{\Delta }}_h$for all $X\in {\mathrm{\Re }}^n;$ $0\le \tau \left(t\right)\le \gamma ,\gamma$ is a positive constant, ${\tau }^{\mathrm{\prime }}\left(t\right)\le \xi ,$ $0<\xi <1.$

$\left(A3\right)$ There is a continuous and non-negative function $\alpha \left(t\right)$ such that $||P(t,X,Y)||\le \alpha \left(t\right)||Y||\mathit{\text{ for all }}t\ge t_0\mathit{\text{ and }}X,Y\in {\mathrm{\Re }}^n,$where $\alpha \left(t\right)\in L^1(0,\mathrm{\infty }),$ $L^1(0,\mathrm{\infty })$ is space of integrable Lebesgue functions.

Lemma 3.1

[27]

If $\mathrm{\Lambda }$ is a real symmetric $n\times n$-matrix and ${\sigma }_2\ge {\lambda }_i\left(\mathrm{\Lambda }\right)\ge {\sigma }_1>0,(i=1,2,\dots ,n),$then for any $X\in {\mathrm{\Re }}^n,$ we have ${\sigma }_1||X|{|}^2\le ⟨\mathrm{\Lambda }X,X⟩\le {\sigma }_2||X|{|}^2,$where ${\sigma }_1$ and ${\sigma }_2$ are the least and the greatest eigenvalues of the matrix $\mathrm{\Lambda }.$

Lemma 3.2

[27]

Let $H\left(X\right)$ be a continuously differentiable vector function with $H\left(0\right)=0.$ Then $\frac{\text{d}}{\text{d}t}{\int }_0^1⟨H\left(\sigma X\right),X⟩\text{d}\sigma =⟨H\left(X\right),Y⟩.$

Lemma 3.3

[27]

Let $H\left(X\right)$ be a continuously differentiable vector function with $H\left(0\right)=0.$ Then ${\delta }_h||X|{|}^2\le 2{\int }_0^1⟨H\left(\sigma X\right),X⟩\text{d}\sigma \le {\mathrm{\Delta }}_h{||X||}^2.$

Proof:

It is clear that $H\left(0\right)=0,$ $\frac{\mathrm{\partial }}{\mathrm{\partial }\sigma }H\left(\sigma X\right)$ = $J_H\left(\sigma X\right)X.$ Then we have $H\left(X\right)={\int }_0^1{J}_h\left(\sigma X\right)X\text{d}\sigma .$

Hence $\begin{array}{rl}{\int }_0^1⟨H\left(\sigma X\right),X⟩\text{d}\sigma & ={\int }_0^1{\int }_0^1⟨{\sigma }_1{J}_h\left({\sigma }_1{\sigma }_{2}X\right)X,X⟩\text{d}{\sigma }_2\text{d}{\sigma }_1\\ & \ge \frac{1}{2}{\delta }_h{||X||}^2.\end{array}$Similarly, it is obvious that $\begin{array}{rl}{\int }_0^1⟨H\left(\sigma X\right),X⟩\text{d}\sigma & ={\int }_0^1{\int }_0^1⟨{\sigma }_1{J}_h\left({\sigma }_1{\sigma }_{2}X\right)X,X⟩\text{d}{\sigma }_2\text{d}{\sigma }_1\\ & \le \frac{1}{2}{\mathrm{\Delta }}_h{||X||}^2.\end{array}$These equalities make enable that $\frac{1}{2}{\delta }_h||X|{|}^2\le {\int }_0^1⟨H\left(\sigma X\right),X⟩\text{d}\sigma \le \frac{1}{2}{\mathrm{\Delta }}_h{||X||}^2.$This result completes the proof.

3.2. Main results

Let $P(t,X,X^{\mathrm{\prime }})\equiv 0.$Our first result is the following theorem.

Theorem 3.1:

Let hypotheses $\left(A1\right)$ and $\left(A2\right)$hold. If $\gamma <\left(\right((1-\xi ){\delta }_f\left)/{\mathrm{\Delta }}_h\right)$ holds, then the zero solution of DDE (2) is uniformly stable and asymptotically stable.

Proof:

We define a continuously differentiable Lyapunov-Krasovskii functional $V(.)=V(X_t,Y_t)$ by $\begin{array}{rl}V(.)& ={\int }_0^1⟨H\left(\sigma X\right),X⟩\text{d}\sigma \frac{1}{2}⟨Y,Y⟩\\ & +\lambda {\int }_{-\tau \left(t\right)}^0{\int }_{t+s}^t⟨Y\left(\theta \right),Y\left(\theta \right)⟩\text{d}\theta \text{d}s,\end{array}$where $\lambda$is a positive constant, and it is chosen later.

It is clear that $V(0,0)=0.$ By Lemmas 3.1–3.3, it follows that $\begin{array}{rl}V(.)& \ge \frac{1}{2}{\delta }_h||X|{|}^2+||Y|{|}^2+\lambda {\int }_{-\tau \left(t\right)}^0{\int }_{t+s}^t{||Y\left(\theta \right)||}^2\text{d}\theta \text{d}s\\ & \ge K_1(||X|{|}^2+||Y|{|}^2),\end{array}$where $K_1=min\{2^{-1}{\delta }_h,1\}.$

By the similar procedure, we can derive that $V(.)\le \frac{1}{2}{\mathrm{\Delta }}_h||X|{|}^2+||Y|{|}^2+\lambda {\int }_{-\tau \left(t\right)}^0{\int }_{t+s}^t{||Y\left(\theta \right)||}^2\text{d}\theta \text{d}s.$Then, we can find a continuous function $u\left(s\right)$ such that $u\left(||\varphi \left(0\right)||\right)\le V\left(\varphi \right),u\left(||\varphi \left(0\right)||\right)\ge 0.$The time derivative of the Lyapunov-Krasovskii functional $V(.)$ along any solution of DDS (2) is given by $\begin{array}{rl}\frac{\text{d}}{\text{d}t}V(X_t,Y_t)& =-⟨H\left(X\right),Y⟩-⟨F(X,Y)Y,Y⟩\\ & +{\int }_{t-\tau \left(t\right)}^t⟨Y\left(t\right),J_h\left(X\right(s\left)\right)Y\left(s\right)⟩\text{d}s\\ & +\frac{\text{d}}{\text{d}t}{\int }_0^1⟨H\left(\sigma X\right),X⟩\text{d}\sigma \\ & +\lambda \frac{\text{d}}{\text{d}t}{\int }_{-\tau \left(t\right)}^0{\int }_{t+s}^t⟨Y\left(\theta \right),Y\left(\theta \right)⟩\text{d}\theta \text{d}s.\end{array}$It is clear that $\frac{\text{d}}{\text{d}t}{\int }_0^1⟨H\left(\sigma X\right),X⟩d\sigma =⟨H\left(X\right),Y⟩$and $\begin{array}{rl}& \frac{\text{d}}{\text{d}t}{\int }_{-\tau \left(t\right)}^0{\int }_{t+s}^t⟨Y\left(\theta \right),Y\left(\theta \right)⟩\text{d}\theta \text{d}s=\tau \left(t\right)⟨Y\left(t\right),Y\left(t\right)⟩\\ & -(1-{\tau }^{\mathrm{\prime }}(t\left)\right){\int }_{t-\tau \left(t\right)}^t⟨Y\left(\theta \right),Y\left(\theta \right)⟩\text{d}\theta .\end{array}$Hence, we have $\begin{array}{rl}\frac{\text{d}}{\text{d}t}V(X_t,Y_t)& =-⟨F(X,Y)Y,Y⟩\\ & +{\int }_{t-\tau \left(t\right)}^t⟨Y\left(t\right),J_h\left(X\right(s\left)\right)Y\left(s\right)⟩\text{d}s\\ & +\lambda \tau \left(t\right)⟨Y,Y⟩-\lambda (1-{\tau }^{\mathrm{\prime }}(t\left)\right)\\ & \times {\int }_{t-\tau \left(t\right)}^t⟨Y\left(\theta \right),Y\left(\theta \right)⟩\text{d}\theta .\end{array}$The assumptions ${\delta }_f\le {\lambda }_i\left(F\right(X,Y\left)\right),$ ${\lambda }_i\left(J_h\right(X\left)\right)\le {\mathrm{\Delta }}_h$ and the inequality $2|f||g|\le f^2+g^2$ (with $f$ and $g$ are real numbers) combined with the classical Cauchy-Schwartz inequality leads $\begin{array}{rl}& \frac{\text{d}}{\text{d}t}V(X_t,Y_t)\\ & \le -{\delta }_f||Y|{|}^2+{\mathrm{\Delta }}_h{\int }_{t-\tau \left(t\right)}^t⟨Y\left(s\right),Y\left(s\right)⟩\text{d}s\\ & +\lambda \gamma {||Y||}^2-\lambda (1-\xi ){\int }_{t-\tau \left(t\right)}^t⟨Y\left(\theta \right),Y\left(\theta \right)⟩\text{d}\theta .\end{array}$Then $\begin{array}{rl}\frac{\text{d}}{\text{d}t}V(X_t,Y_t)& \le -({\delta }_f-\lambda \gamma )||Y|{|}^2-\left(\lambda \right(1-\xi )-{\mathrm{\Delta }}_h)\\ & \times {\int }_{t-\tau \left(t\right)}^t⟨Y\left(\theta \right),Y\left(\theta \right)⟩\text{d}s.\end{array}$Let $\lambda =\frac{{\mathrm{\Delta }}_h}{1-\xi }.$Hence, this equality implies $\frac{\text{d}}{\text{d}t}V(X_t,Y_t)\le -\left({\delta }_f-\frac{{\mathrm{\Delta }}_h}{1-\xi }\gamma \right)||Y|{|}^2.$If $\gamma <\left(\right((1-\xi ){\delta }_f\left)/{\mathrm{\Delta }}_h\right),$ then there exists a positive constant $\rho$ such that $\frac{\text{d}}{\text{d}t}V(X_t,Y_t)\le -\rho ||Y|{|}^2\le 0.$This inequality shows that the time derivative of the Lyapunov-Krasovskii functional $V(X_t,Y_t)$ is negative semidefinite. Hence, we can conclude that the zero solution of DDE (2) is uniformly stable. On the same time, the zero solution of DDE (2) is also stable.

We now consider the set defined by $I_S\equiv \left\{\right(X,Y):\frac{d}{dt}V(X_t,Y_t)=0\}.$If we apply the LaSalle’s invariance principle, then we observe that $(X,Y)\in I_S$ implies that $Y=0.$ Hence, DDS (3) and together $Y=0,$ necessarily, implies $H\left(X\right)=0.$

Since $Y=0\Rightarrow \dot{X}=0,$ then $X=\xi ,$ $\xi (\ne 0),$ is a vector. This equality can be hold if and only if $H\left(\xi \right)=0.$Hence, $H\left(\xi \right)=0\iff \xi =0$so that $H\left(X\right)=0\iff X=0.$ Therefore, we have $X=Y=0.$ In fact, this result shows that the largest invariant set contained in the set $I_S$ is $(0,0)\in I_S.$ Therefore, we can conclude that the zero solution of DDE (2) is asymptotically stable. This result completes the proof of Theorem 3.1.

Corollary 3.1:

In the light of the assumptions of Theorem 3.1, it can be proceeded that all solutions of DDE (2) is uniformly bounded. We omit the details of the proof.

Theorem 3.2:

If assumptions $\left(A1\right)$ and $\left(A2\right)$hold, then the first derivatives of the solutions of DDE (2) are square integrable when $P(.)\equiv 0.$

Proof:

We now give our attention to the Lyapunov-Krasovskii $V(X_t,Y_t)$ which is used in the proof of Theorem 3.1.

It is known from Theorem 3.1 that $\frac{\text{d}}{\text{d}t}V(X_t,Y_t)\le -\rho ||Y|{|}^2\le 0.$Integrating this inequality from $0$ to $t,$ we have $V(X_t,Y_t)-V(X_0,Y_0)\le -\rho {\int }_0^t{||Y\left(s\right)||}^2\text{d}s\le 0.$Hence, it is clear that $V(X_t,Y_t)+\rho {\int }_0^t{||Y\left(s\right)||}^2\text{d}s\le V(X_0,Y_0).$Since $V(X_t,Y_t)$ is positive definite, then we can assume $V(X_0,Y_0)=K_2,K_2\in \mathrm{\Re },K_2>0.$Hence, we can derive $\begin{array}{rl}\rho {\int }_0^t{||Y\left(s\right)||}^2\text{d}s& \le V(X_t,Y_t)+\rho {\int }_0^t{||Y\left(s\right)||}^2\text{d}s\\ & \le V(X_0,Y_0)=K_2.\end{array}$Then ${\int }_0^{\mathrm{\infty }}{||Y\left(s\right)||}^2\text{d}s={\int }_0^{\mathrm{\infty }}{||\dot{X}\left(s\right)||}^2\text{d}s\le {\rho }^{-1}{K}_2<\mathrm{\infty }.$This result completes the proof of Theorem 3.2.

Theorem 3.3:

If the assumptions of Theorem 3.1 hold, then all solutions of DDE (2) and their first order derivatives are bounded as $t\to \mathrm{\infty }$ when $P(.)\equiv 0$.

Proof:

We again consider the estimates $V(X_t,Y_t)\le V(X_t,Y_t)+\rho {\int }_0^{\mathrm{\infty }}{||Y\left(s\right)||}^2\text{d}s\le K_2$and $||X|{|}^2+||Y|{|}^2\le K_1^{-1}V(X_t,Y_t),$which can be found in the former proofs.

Then, in view of these inequalities, we can conclude that $||X|{|}^2+||Y|{|}^2\le K_1^{-1}{K}_2.$This inequality competes the proof of Theorem 3.3.

Let $P(t,X,X^{\mathrm{\prime }})\ne 0.$Our fourth and the last result is the following theorem.

Theorem 3.4:

If assumptions $\left(A1\right)\text{--}\left(A3\right)$hold, then there exists a positive constant $K_2$ such that all solutions DDE (2) satisfy the inequalities $||X\left(t\right)||\le K_3,||X^{\mathrm{\prime }}\left(t\right)||\le K_3$as $t\to +\mathrm{\infty }$ when $P(t,X,X^{\mathrm{\prime }})\ne 0.$

Proof: We re-consider the Lyapunov-Krasovskii functional, which is defined in Theorem 3.1. It is clear that $V(.)\ge K_1(||X|{|}^2+||Y|{|}^2).$Since $P(t,X,X^{\mathrm{\prime }})\ne 0$, then the time derivative of the function $V(.)$ can be revised as follows $\begin{array}{rl}\frac{\text{d}}{\text{d}t}V(X_t,Y_t)& \le ⟨Y,P(t,X,Y)⟩\\ & \le ||Y||||P(t,X,Y)||\\ & \le \alpha \left(t\right)||Y|{|}^2.\end{array}$

Hence, it is clear that $\frac{\text{d}}{\text{d}t}V(X_t,Y_t)\le 2K_1^{-1}\alpha \left(t\right)V(X_t,Y_t).$Integrating the last estimate from $0$ to $t,$ $(t\ge 0),$ we have $V(X_t,Y_t)\le K_2\exp \left(2K_1^{-1}{\int }_0^t\alpha \left(s\right)\text{d}s\right).$

Then, it can be derived that $V(X_t,Y_t)\le K_2\exp \left(2K_1^{-1}{\int }_0^{\mathrm{\infty }}\alpha \left(s\right)\text{d}s\right).$Let $K_3=K_2\exp \left(2K_1^{-1}{\int }_0^{\mathrm{\infty }}\alpha \left(s\right)\text{d}s\right).$Thus, we can conclude that $||X|{|}^2+||Y|{|}^2\le K_1^{-1}{K}_3\text{as}t\to +\mathrm{\infty }.$This completes the proof of Theorem 3.3.

Remark 1:

In the proof of Theorem 3.3, without using the Gronwall-Bellman [1] inequality, we proved the bounded result. In fact, in Theorem 3.3, we have weaker conditions than that can found in literature and delete some reasonless of the conditions therein. This the positive effect of assumption $\left(A3\right)$ in the proof.

Corollary 3.2:

In the light of the assumptions of Theorem 3.3, all solutions of DDE (2) is uniformly bounded (see, Theorem 2.2, also Yoshizawa [50]).

4. Illustrative examples

In this section, in the particular cases, two numerical examples are presented to demonstrate the accuracy and applicability of the obtained results. The graphs of the solutions of the given examples are displayed by MATLAB-Simulink.

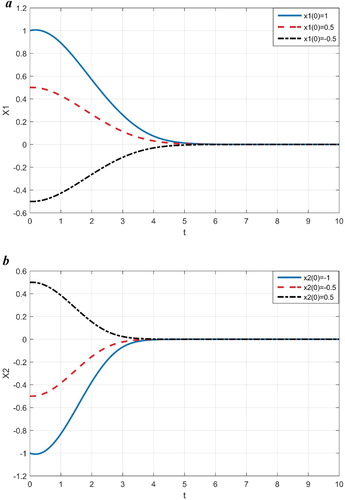
Example 4.1:

In the particular case of DDE (2), we consider the following non-linear DDE with the variable delay, $\tau \left(t\right)=\left(1/4\right){\sin }^{2}t\ge 0:$ (6) $\begin{array}{rl}& \left[\begin{array}{c}{x^{\mathrm{\prime }}}_1\\ {x^{\mathrm{\prime }}}_2\end{array}\right]+\left[\begin{array}{cc}\begin{array}{l}10+\sin t(1+x_1^2\\ +x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}{)}^{-1}\end{array}& 0\\ 0& \begin{array}{l}5+\cos t(1+x_1^2\\ +x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}{)}^{-1}\end{array}\end{array}\right]\\ & \times \left[\begin{array}{c}{x^{\mathrm{\prime }}}_1\\ {x^{\mathrm{\prime }}}_2\end{array}\right]+\left[\begin{array}{l}3x_1(t-4^{-1}{\sin }^{2}t)\\ +arctg{x}_1(t-4^{-1}{\sin }^{2}t)\\ 3x_2(t-4^{-1}{\sin }^{2}t)\\ +arctg{x}_2(t-4^{-1}{\sin }^{2}t)\end{array}\right]\\ & =\left[\begin{array}{c}0\\ 0\end{array}\right].\end{array}$(6) It is clear that $\begin{array}{rl}& P(t,X,X^{\mathrm{\prime }})=0,\end{array}$ $\begin{array}{rl}& F(X,X^{\mathrm{\prime }})=\left[\begin{array}{cc}\begin{array}{l}10+\sin t(1+x_1^2\\ +x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}{)}^{-1}\end{array}& 0\\ 0& \begin{array}{l}5+\cos t(1+x_1^2\\ +x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}{)}^{-1}\end{array}\end{array}\right],\end{array}$where $X=(x_1,x_2),$ $H\left(X\right)=\left[\begin{array}{l}3x_1+arctg{x}_1\\ 3x_2+arctg{x}_2\end{array}\right]$ and the variable delay $\tau \left(t\right)=\left(1/4\right){\sin }^{2}t$ satisfies $0\le \tau \left(t\right)=\left(1/4\right){\sin }^{2}t\le \left(1/4\right)=\gamma ,$ ${\tau }^{\mathrm{\prime }}\left(t\right)=\frac{1}{2}\sin t\cos t\le \frac{1}{2}=\xi ,\text{that}\text{is,}0<\xi =\frac{1}{2}<1.$

Next, as eigenvalues of the matrix $F(.),$ we have ${\lambda }_1\left(F\right(.\left)\right)=10+\frac{\sin t}{1+x_1^2+x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}}$and ${\lambda }_2\left(F\right(.\left)\right)=5+\frac{\cos t}{1+x_1^2+x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}}.$We can derive ${\delta }_f=4\le {\lambda }_i\left(F\right)\le {\mathrm{\Delta }}_f=11,(i=1,2).$Next, the Jacobian matrix of $H\left(X\right)$ is $J_h\left(X\right)=\left[\begin{array}{cc}3+\frac{1}{1+x_1^2}& 0\\ 0& 3+\frac{1}{1+x_2^2}\end{array}\right].$ Hence ${\delta }_h=3\le {\lambda }_i\left(J_h\right(X\left)\right)\le 4={\mathrm{\Delta }}_h,(i=1,2).$Thus, all hypotheses $\left(A1\right)$ and $\left(A2\right)$of Theorem 2.1 hold. In addition, since $\gamma =\frac{1}{4},\xi =\frac{1}{2},{\delta }_f=4,{\mathrm{\Delta }}_h=4,$then $\left(\right((1-\xi ){\delta }_f\left)/\right({\mathrm{\Delta }}_h\left)\right)=\left(1/2\right),$ that is, $\gamma =\left(1/4\right)<\left(\right((1-\xi ){\delta }_f\left)/\right({\mathrm{\Delta }}_h\left)\right)=\left(1/2\right)$ holds. For the particular case of DDE (2) when $P(.)\equiv 0.$, we give DDE (6) in Example 4.1. Then, it can be seen that the zero solution of DDE (6) is uniformly stable, asymptotically stable, and all solutions of DDE (6) are uniformly bounded, their first derivatives are square integrable. Besides, all solutions of DDE (6) and their first order derivatives are bounded as $t\to \mathrm{\infty }$ (see Figure 1a and 1b).

Figure 1. (a) Orbits of x₁ (t) for Example 4.1. (b) Orbits of x₂ (t) for Example 4.1.

Now, let $P(t,X,X^{\mathrm{\prime }})\ne 0.$

Example 4.2:

In the particular case of DDE (2), we now consider the following DDE with the variable delay, $\tau \left(t\right)=\left(1/4\right){\sin }^{2}t\ge 0:$ (7) $\begin{array}{rl}& \left[\begin{array}{l}{x^{\mathrm{\prime }}}_1\\ {x^{\mathrm{\prime }}}_2\end{array}\right]+\left[\begin{array}{cc}\begin{array}{l}10+\sin t(1+x_1^2\\ +x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}{)}^{-1}\end{array}& 0\\ 0& \begin{array}{l}5+\cos t(1+x_1^2\\ +x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}{)}^{-1}\end{array}\end{array}\right]\\ & \left[\begin{array}{l}{x^{\mathrm{\prime }}}_1\\ {x^{\mathrm{\prime }}}_2\end{array}\right]\\ & +\left[\begin{array}{l}3x_1(t-4^{-1}{\sin }^{2}t)\\ +arctg{x}_1(t-4^{-1}{\sin }^{2}t)\\ 3x_2(t-4^{-1}{\sin }^{2}t)\\ +arctg{x}_2(t-4^{-1}{\sin }^{2}t)\end{array}\right]\\ & =\left[\begin{array}{l}\frac{\sin t}{1+t^2+x_1^2+x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}}\\ \frac{\cos t}{1+t^2+x_1^2+x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}}\end{array}\right].\end{array}$(7) It is clear that $\begin{array}{r}P(t,X,X^{\mathrm{\prime }})=\left[\begin{array}{c}\frac{\sin t}{1+t^2+x_1^2+x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}}\\ \frac{\cos t}{1+t^2+x_1^2+x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}}\end{array}\right].\end{array}$Further, we proceed $\begin{array}{rl}||P(t,X,X^{\mathrm{\prime }})||& =∥\left[\begin{array}{l}\frac{\sin t}{1+t^2+x_1^2+x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}}\\ \frac{\cos t}{1+t^2+x_1^2+x_1^{\mathrm{\prime }2}+x_2^2+x_2^{\mathrm{\prime }2}}\end{array}\right]∥\\ & \le \frac{2}{1+t^2}=\alpha \left(t\right).\\ {\int }_0^{\mathrm{\infty }}\alpha \left(s\right)\text{d}s& =2{\int }_0^{\mathrm{\infty }}\frac{1}{1+s^2}\text{d}s=\pi ,\end{array}$that is, $\alpha \in L^1(0,\mathrm{\infty }).$

Thus, all the conditions of Theorem 3.2 are hold. For the particular case of DDE (2), we give DDE (7) in Exampe 4.2. Then, all solutions of DDE (7) are bounded as $t\to +\mathrm{\infty }$ and also uniformly bounded (see Figure 2a and 2b).

Figure 2. (a) Orbits of x₁ (t) for Example 4.2. (b) Orbits of x₂ (t) for Example 4.2.

5. Conclusion

In this paper, we define a Lyapunov-Krasovskii functional to derive new sufficient conditions for the qualitative analysis of solutions; stability, uniformly stability, asymptotically stability, boundedness, uniformly boundedness and square integrability of solutions of a kind of a system of non-linear differential equations of second order with variable delay. We prove four new theorems on the mentioned properties of solutions. Here, the derived sufficient conditions are expressed in terms of that system non-linear of differential equations. By this work, we not only weaken and delete some reasonless conditions of the related theorems in [27], but also improve the results of [27]. That is, we obtain the results of [27] under weaker conditions. At the same time, in addition, we obtain new results on the uniformly stability and integrabilty of solutions of the considered system. Further, two examples are given to illustrate the validity and feasibility of the main results of this paper.

Contribution

All the authors have equal contribution in this paper and there is no competing interest.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Cemil Tunç http://orcid.org/0000-0003-2909-8753