Outer-independent k-rainbow domination

ABSTRACT

An outer-independent k-rainbow dominating function of a graph G is a function f from $V\left(G\right)$ to the set of all subsets of $\{1,2,\dots ,k\}$ such that both the following hold: (i) $\{1,\dots ,k\}=\bigcup _{u\in N\left(v\right)}f\left(u\right)$ whenever v is a vertex with $f\left(v\right)=\mathrm{\varnothing }$, and (ii) the set of all $v\in V\left(G\right)$ with $f\left(v\right)=\mathrm{\varnothing }$ is independent. The outer-independent k-rainbow domination number of G is the invariant ${\gamma }_{oir}^k\left(G\right)$, which is the minimum sum (over all the vertices of G) of the cardinalities of the subsets assigned by an outer-independent k-rainbow dominating function. In this paper, we initiate the study of outer-independent k-rainbow domination. We first investigate the basic properties of the outer-independent k-rainbow domination and then we focus on the outer-independent 2-rainbow domination number and present sharp lower and upper bounds for it.

KEYWORDS:

• k-rainbow dominating function
• k-rainbow domination
• outer-independent domination

1. Introduction

In general, we follow the notation and graph theory terminology in [1]. Specifically, let $G=\left(V\right(G),E(G\left)\right)$ be a finite simple graph. For any vertex u in G, the open neighbourhood of u, written $N\left(u\right)$, is the set of vertices adjacent to u and the closed neighbourhood of u is the set $N\left[u\right]=N\left(u\right)\cup \left\{u\right\}$. The degree of a vertex $u\in V\left(G\right)$ is $\mathrm{deg}\left(v\right)=|N\left(v\right)|$. The minimum and maximum degrees of G are denoted by $\delta \left(G\right)$ and $\mathrm{\Delta }\left(G\right)$, respectively. A leaf is a vertex of degree one, and a support vertex is a vertex adjacent to a leaf. We denote the sets of all leaves and all support vertices of G by $L\left(G\right)$ and $S\left(G\right)$, respectively. For a vertex $v\in V\left(G\right)$, the set of leaf neighbours of v is denoted by $L\left(v\right)$. If $A\subset V\left(G\right)$, then $N\left(A\right)$ (respectively, $N\left[A\right]$) denotes the union of open (closed) neighbourhoods of all vertices of A. (If the graph G under consideration is not clear we write $N_G\left(u\right)$, and so on.) We denote by $P_n$ and $C_n$ the path and cycle on n vertices, respectively. The distance between two vertices u and v in a connected graph G is the length of a shortest uv-path in G. The diameter of a graph G, denoted by $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}\left(G\right)$, is the greatest distance between two vertices of G. For a vertex v in a rooted tree T, let $C\left(v\right)$ and $D\left(v\right)$ denote the set of children and descendants of v, respectively and let $D\left[v\right]=D\left(v\right)\cup \left\{v\right\}$. Also, the depth of v, $\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{h}\left(v\right)$, is the largest distance from v to a vertex in $D\left(v\right)$. The maximal subtree at v is the subtree of T induced by $D\left[v\right]$, and is denoted by $T_v$. By $K_{p,q}$ we denote a complete bipartite graph with partite sets of cardinalities p and q. A star is a $K_{1,q}$ and a double star $D{S}_{q,p}$, where $q\ge p\ge 1$, is a tree containing exactly two non-leaf vertices which one is adjacent to p leaves and the other is adjacent to q leaves. By $⟨X⟩$ we denote the induced subgraph of a graph G with vertex set $X\subseteq V\left(G\right)$.

A set $I\subseteq V\left(G\right)$ is independent if no two vertices in I are adjacent. The maximum cardinality of an independent set in G equals the independence number ${\beta }_0\left(G\right)$. A vertex cover of a graph G is a set of vertices that covers all the edges. The minimum cardinality of a vertex cover is denoted by ${\alpha }_0\left(G\right)$. The following theorem due to Gallai.

Theorem 1.1

[2]

Let G be a graph. A subset I of $V\left(G\right)$ is independent if and only if $V\left(G\right)-I$ is a vertex cover of G. In particular, ${\beta }_0\left(G\right)=|V\left(G\right)|-{\alpha }_0\left(G\right)$.

A set $D\subseteq V\left(G\right)$ in G is called a dominating set if $N\left[D\right]=V\left(G\right)$. The domination number $\gamma \left(G\right)$ equals the minimum cardinality of a dominating set in G. For many applications, it is not possible to use an arbitrary dominating set D of G. One possible form of restriction is based on imposing some conditions on the set $V\left(G\right)-D$. Here we concentrate on the property of being outer-independent, i.e. $V\left(G\right)-D$ is independent. Results on outer-independent domination parameters can be found e.g. in [3–7].

For a positive integer k we denote the set $\{1,2,\dots ,k\}$ by $\left[k\right]$. The power set (that is, the set of all subsets) of $\left[k\right]$ is denoted by $2^{\left[k\right]}$. Let G be a graph and let f be a function that assigns to each vertex a subset of $\left[k\right]$; that is, $f:V\left(G\right)\to 2^{\left[k\right]}$. The weight, $\omega \left(f\right)$, of f is defined as $\omega \left(f\right)=\sum _{v\in V\left(G\right)}|f\left(v\right)|$. The function f is called a k-rainbow dominating function (a kR-function) on G if for each vertex $v\in V\left(G\right)$ with $f\left(v\right)=\mathrm{\varnothing }$ the condition $\bigcup _{u\in N\left(v\right)}f\left(u\right)=\{1,\dots ,k\}$ is fulfilled. Given a graph G, the minimum weight of a k-rainbow dominating function is called the k-rainbow domination number of G, which we denote by ${\gamma }_r^k\left(G\right)$. The concept of rainbow domination was introduced in [8] and has been studied extensively [9–15].

Here we introduce and study a new variant of a k-rainbow dominating function. A k-rainbow dominating function $f:V\left(G\right)\to 2^{\left[k\right]}$ is an outer-independent k-rainbow dominating function (an OIkRD-function) on G if the set $\{v\in V(G)\mid f(v)=\mathrm{\varnothing }\}$ is independent. The outer-independent k-rainbow domination number ${\gamma }_{oir}^k\left(G\right)$ is the minimum weight of an OIkRD-function on G. An OIkRD-function of weight ${\gamma }_{oir}^k\left(G\right)$ is called a ${\gamma }_{oir}^k$-function. Since any OIkRD-function is a kRD-function, we have (1) ${\gamma }_r^k\left(G\right)\le {\gamma }_{oir}^k\left(G\right).$(1) In this paper, we initiate the study of outer-independent k-rainbow domination. We first investigate the basic properties of the outer-independent k-rainbow domination and then we focus on the outer-independent 2-rainbow domination number and present sharp lower and upper bounds for it.

2. Preliminary results

In this section, we present basic properties of outer-independent k-rainbow domination number ${\gamma }_{oir}^k\left(G\right)$. We begin with three simple observations.

Observation 2.1

If $G_1,G_2,..,G_r$ are all components of a graph G, then ${\gamma }_{oir}^k\left(G\right)={\gamma }_{oir}^k\left(G_1\right)+{\gamma }_{oir}^k\left(G_2\right)+\cdots +{\gamma }_{oir}^k\left(G_r\right)$.

Observation 2.2

For any graph G of order n, $min\{n,k\}\le {\gamma }_{oir}^k\left(G\right)\le n$. In particular, ${\gamma }_{oir}^k\left(G\right)=n$ whenever $k\ge n$.

Observation 2.3

For any OIkRD-function f on a graph G, the set $\{v\in V(G)\mid f(v)\ne \mathrm{\varnothing }\}$ is a vertex cover of G. Hence ${\alpha }_0\left(G\right)+I\left(G\right)\le \omega \left(f\right)$, where $I\left(G\right)$ is the set of all isolated vertices of G. In particular, ${\alpha }_0\left(G\right)\le {\alpha }_0\left(G\right)+I\left(G\right)\le {\gamma }_{oiR}^k\left(G\right)$.

Notice also that the outer-independent domination is the same as the outer-independent 1-rainbow domination if we view an outer-independent dominating set D as an outer-independent 1-rainbow dominating function f defined by $f\left(v\right)=\left\{1\right\}$ when $v\in D$ and $f\left(v\right)=\mathrm{\varnothing }$ otherwise. Therefore here we concentrate on the case when a graph G is connected and $n-1\ge k\ge 2$.

Now we characterize all connected graphs of order $n\ge k+1$ attaining the lower bound in Observation 2.2.

Theorem 2.1

Let $k\ge 2$ be a positive integer and let G be a connected graph of order $n\ge k+1$. Then ${\gamma }_{oir}^k\left(G\right)=k$ if and only if $G=H_G\vee \overline{K_{n-h}}$, where $H_G$ is a graph of order $h\le k$.

Proof.

First assume that $G=H_G\vee \overline{K_{n-h}}$, where $H_G$ is a graph of order $h\le k$. Define a function $f:V\left(G\right)\to 2^{\left[k\right]}$ by $f\left(x\right)=\mathrm{\varnothing }$ for $x\in V\left(\overline{K_{n-h}}\right)$ and $f\left(x\right)\ne \mathrm{\varnothing }$ for $x\in V\left(H_G\right)$ in such way that $\bigcup _{x\in V\left(H_G\right)}f\left(x\right)=\{1,2,\dots ,k\}$ and $\sum _{x\in V\left(H_G\right)}|f\left(x\right)|=k$. Obviously, f is an OIkRD-function on G with $\omega \left(f\right)=k$. Therefore ${\gamma }_{oir}^k\left(G\right)=k$.

Conversely, assume that ${\gamma }_{oir}^k\left(G\right)=k$. Let f be a ${\gamma }_{oir}^k$-function on G. Since $n\ge k+1$, there exists a vertex v with $f\left(v\right)=\mathrm{\varnothing }$. This implies that $\bigcup _{x\in N\left(v\right)}f\left(x\right)=\{1,2,\dots ,k\}$ and $f\left(x\right)\ne f\left(v\right)$ for all $x\in N\left(v\right)$. Moreover, $k={\gamma }_{oir}^k\left(G\right)=\omega \left(f\right)=\sum _{x\in V\left(G\right)}|f\left(x\right)|\ge \sum _{x\in N\left(v\right)}|f\left(x\right)|\ge |\{1,2,\dots ,k\}|=k$. Hence $f\left(u\right)=\mathrm{\varnothing }$ for all $u\in V\left(G\right)-N\left(v\right)$. Since v was chosen arbitrarily, $G=⟨N\left(v\right)⟩\vee ⟨V\left(G\right)-N\left(v\right)⟩$, where a graph $⟨V\left(G\right)-N\left(v\right)⟩$ has no edges.

Theorem 2.2

Let $k\ge 2$ be a positive integer and let G be a connected graph of order $n\ge k+2$. Then ${\gamma }_{oir}^k\left(G\right)=k+1$ if and only if the following holds:

1. there is no h-order graph $H_G$, $h\le k$, such that $G=H_G\vee \overline{K_{n-h}}$.

2. there exist two nonempty disjoint vertex sets A, B such that: (i) $|A|+|B|\le k+1$ and $|B|\le 2$, (ii) every vertex of $V\left(G\right)-(A\cup B)$ is adjacent to every vertex of $A\cup B$ except at most one vertex in B, (iii) $V\left(G\right)-(A\cup B)$ is independent, and (iv) for each $x\in B$, $N\left(x\right)⊈A\cup B$ or $A⊈N\left(x\right)$.

Proof.

First assume that G satisfies (I) and (II). It follows from Theorem 2.1 and (I) that ${\gamma }_{oir}^k\left(G\right)\ge k+1$. Now define the function $f:V\left(G\right)\to 2^{\left[k\right]}$ by $f\left(x\right)=\mathrm{\varnothing }$ for $x\in V\left(G\right)-A\cup B$, $f\left(x\right)=\left\{k\right\}$ for $x\in B$, and $f\left(x\right)\ne \mathrm{\varnothing }$ for $x\in A$ such that $\bigcup _{x\in A}f\left(x\right)=\{1,2,\dots ,k\}$ and $\sum _{x\in A}|f\left(x\right)|=k$ when $|B|=1$ and by $f\left(x\right)=\mathrm{\varnothing }$ for $x\in V\left(G\right)-A\cup B$, $f\left(x\right)=\left\{k\right\}$ for $x\in B$, and $f\left(x\right)\ne \mathrm{\varnothing }$ for $x\in A$ such that $\bigcup _{x\in A}f\left(x\right)=\{1,2,\dots ,k-1\}$ and $\sum _{x\in A}|f\left(x\right)|=k-1$ when $|B|=2$. Obviously, f is an OIkRD- function of G with $\omega \left(f\right)=k+1$ and thus ${\gamma }_{oir}^k\left(G\right)=k+1$.

Conversely, assume that ${\gamma }_{oir}^k\left(G\right)=k+1$. It follows from Theorem 2.1 that G satisfies (I). Now we show that G satisfies (II). Let f be a ${\gamma }_{oir}^k$-function on G. Choose f so that $D_f=\{u\in V(G)\mid f(u)\ne \mathrm{\varnothing }\}$ is as small as possible. Since $\omega \left(f\right)=k+1$, there exists a colour, say k, which appears exactly twice and each other colour appears exactly once. Hence there are two vertices, say z and w, such that $f\left(z\right)\cap f\left(w\right)=\left\{k\right\}$. Since $n\ge k+2$, there exists a vertex v with $f\left(v\right)=\mathrm{\varnothing }$ which implies that $\bigcup _{x\in N\left(v\right)}f\left(x\right)=\{1,2,\dots ,k\}$ and that $f\left(x\right)\ne \mathrm{\varnothing }$ for each $x\in N\left(v\right)$.

Now let $A=D_f-\{x\in \{z,w\}\mid |f(x)|=1\}$ and $B=\{z,w\}-A$. Since $k\ge 2$, we have $A\ne \mathrm{\varnothing }$. On the other hand, if $B=\mathrm{\varnothing }$, then the function g defined by $g\left(z\right)=f\left(z\right)-\left\{k\right\}$ and $g\left(x\right)=f\left(x\right)$ otherwise, is an OIkRD-function of G with weight less that ${\gamma }_{oir}^k\left(G\right)$ which is a contradiction. Thus A and B are non-empty sets. Since f is an OIkRD-function, the set $V\left(G\right)-(A\cup B)$ is independent, that is G satisfies (iii).

It follows from ${\gamma }_{oir}^k\left(G\right)=k+1$ that $|A|+|B|\le k+1$ and so (i) holds. Since for each vertex $u\in A$, $f\left(u\right)$ has a colour which is not appeared in other vertices, every vertex in $V\left(G\right)-(A\cup B)$ is adjacent to every vertex of A. Also since the colour k appears exactly in $f\left(z\right)$ and $f\left(w\right)$, each vertex of $V\left(G\right)-(A\cup B)$ must be adjacent to one of the vertices z and w. Hence (ii) holds.

Finally, if for some $w\in B$, $N\left(w\right)\subseteq A\cup B$ and $A\subseteq N\left(w\right)$, then the function g defined on G by $g\left(w\right)=\mathrm{\varnothing }$, $g\left(a\right)=f\left(a\right)\cup \left\{k\right\}$ for some $a\in A$ and $g\left(x\right)=f\left(x\right)$ otherwise, is a ${\gamma }_{oir}^k\left(G\right)$-function which contradicts the choice of f. Thus (iv) holds and the proof is complete.

Proposition 2.1

For any graph G of order n, ${\alpha }_0\left(G\right)+I\left(G\right)={\gamma }_{oir}^1\left(G\right)\le {\gamma }_{oir}^2\left(G\right)\le \cdots \le {\gamma }_{oir}^k\left(G\right)\le n$. If G has no isolated vertices, then ${\alpha }_0\left(G\right)={\gamma }_{oir}^1\left(G\right)$.

Proof.

Let $f_{s+1}$ be a ${\gamma }_{oir}^{s+1}$-function on G, $1\le s\le k-1$. Define the function $h_s:V\left(G\right)\to 2^{\left[s\right]}$ as follows: $h_s\left(u\right)=f_{s+1}\left(u\right)$ when $s+1\notin f_{s+1}\left(u\right)$, $h_s\left(u\right)=\left\{1\right\}$ when $f_{s+1}\left(u\right)=\{s+1\}$, and $h_s\left(u\right)=f_{s+1}\left(u\right)-\{s+1\}$ otherwise. Clearly $h_s$ is an OIsRD-function and so ${\gamma }_{oir}^s\left(G\right)\le \omega \left(h_s\right)\le {\gamma }_{oir}^{s+1}\left(G\right)$.

If C is a minimum vertex cover of G, then the function $g:V\left(G\right)\to \{\mathrm{\varnothing },\{1\left\}\right\}$ defined by $g\left(v\right)=\left\{1\right\}$ when $v\in C\cup I\left(G\right)$ and $g\left(v\right)=\mathrm{\varnothing }$ otherwise, is an OI1RD-function on G with weight $|C|+|I\left(G\right)|={\alpha }_0\left(G\right)+|I\left(G\right)|$. The equality ${\gamma }_{oir}^k\left(G\right)={\alpha }_0\left(G\right)+|I\left(G\right)|$ now follows by Observation 2.3.

Finally, the right side inequality follows by Observation 2.2.

Proposition 2.2

For any graph G, ${\gamma }_{oir}^k\left(G\right)\le k{\alpha }_0\left(G\right)+|I\left(G\right)|$. If $\delta \left(G\right)\ge 1$ then ${\gamma }_{oir}^k\left(G\right)\le k{\alpha }_0\left(G\right)$.

Proof.

Let C be any minimum vertex cover set of G and define the function $f:V\left(G\right)\to 2^{\left[k\right]}$ by $f\left(u\right)=\left[k\right]$ for $u\in C$, $f\left(u\right)=\left\{1\right\}$ when $u\in I\left(G\right)$, and $f\left(u\right)=\mathrm{\varnothing }$ otherwise. Clearly f is an OIkRD-function on G which immediately implies the required.

The bounds in Proposition 2.2 are attainable. Let G be a graph such that each vertex is either a leaf or a support vertex and let each support vertex of G is adjacent to at least k + 1 leaves. Then clearly $S\left(G\right)$ is a minimum vertex cover set and the function $f:V\left(G\right)\to 2^{\left[k\right]}$ defined as $f\left(u\right)=\left[k\right]$ when u is a support vertex and $f\left(u\right)=\mathrm{\varnothing }$ when u is a leaf, is an OIkRD-function on G of minimum weight. Thus ${\gamma }_{oir}^k\left(G\right)=k{\alpha }_0\left(G\right)$.

We will say that a graph G is a vertex cover outer independent k-rainbow graph, a VCOI-k-rainbow graph for short, if ${\gamma }_{oir}^k\left(G\right)=k{\alpha }_0\left(G\right)$.

Proposition 2.3

A graph G with no isolated vertex, is VCOI-k-rainbow if and only if it has a ${\gamma }_{oir}^k$-function f such that for each vertex x, either $f\left(x\right)=\mathrm{\varnothing }$ or $f\left(x\right)=\left[k\right]$.

Proof.

Assume that G is a VCOI-k-rainbow graph and let D be a minimum vertex cover set of G. Then the function $f:V\left(G\right)\to 2^{\left[k\right]}$ defined by $f\left(x\right)=\left[k\right]$ for $x\in D$ and $f\left(x\right)=\mathrm{\varnothing }$ otherwise, is an OIkRD-function on G which implies that $k{\alpha }_0\left(G\right)={\gamma }_{oir}^k\left(G\right)\le \omega \left(f\right)=k|D|=k{\alpha }_0\left(G\right)$. Thus all inequalities in this chain must be equality and so ${\gamma }_{oir}^k\left(G\right)=\omega \left(f\right)$, yielding f is a ${\gamma }_{oir}^k\left(G\right)$-function satisfying that for each vertex x either $f\left(x\right)=\mathrm{\varnothing }$ or $f\left(x\right)=\left[k\right]$.

Conversely, assume that there exists a ${\gamma }_{oir}^k\left(G\right)$-function h such that for each vertex x, either $h\left(x\right)=\mathrm{\varnothing }$ or $h\left(x\right)=\left[k\right]$. Since the set $A_h=\{v\in V(G)\mid h(v)\ne \mathrm{\varnothing }\}$ is a vertex cover set of G, we have $k{\alpha }_0\left(G\right)\le k|A_h|={\gamma }_{oir}^k\left(G\right)$. By Proposition 2.2 we deduce that ${\gamma }_{oir}^k\left(G\right)=k{\alpha }_0\left(G\right)$ and this implies that G is a VCOI-k-rainbow graph.

Proposition 2.4

Let H be an induced subgraph of a graph G. Then ${\gamma }_{oir}^k\left(G\right)\le {\gamma }_{oir}^k\left(H\right)+|V\left(G\right)|-|V\left(H\right)|$.

Proof.

Let f be a ${\gamma }_{oir}^k$-function on H. Define an OIkRD-function h on G as follows: $h\left(x\right)=f\left(x\right)$ when $x\in V\left(H\right)$ and $h\left(x\right)=\left\{1\right\}$ otherwise. Since $\omega \left(h\right)=\omega \left(f\right)+|V\left(G\right)|-|V\left(H\right)|$, we have the desired inequality.

Observation 2.4

Let f be an OIkRD-function on a graph G and $a_i=|\{v\in V(G)\mid i\in f(v\left)\right\}|$ for each $1\le i\le k$. Then $\omega \left(f\right)=a_1+a_2+\cdots +a_k$.

Theorem 2.3

Let G be a graph of order at least two and $k^{\prime }>k$. Then ${\gamma }_{oir}^{k^{\prime }}\left(G\right)\le {\gamma }_{oir}^k\left(G\right)+(k^{\prime }-k)\lfloor \frac{{\gamma }_{oir}^k\left(G\right)}{k}\rfloor$.

Proof.

Let f be a ${\gamma }_{oir}^k$-function on G, and $a_i=|\{v\in V(G)\mid i\in f(v\left)\right\}|$, $1\le i\le k$. Assume without loss of generality that $a_1\ge a_2\ge \cdots \ge a_k$.

Define $g:V\left(G\right)\to 2^{\left[k\right]}$ by $g\left(v\right)=f\left(v\right)\cup \{k+1,\dots ,k^{\prime }\}$ when $k\in f\left(v\right)$ and $g\left(v\right)=f\left(v\right)$ otherwise. Clearly g is an OIkRD-function on G. This fact and Observation 2.4 lead to $\begin{array}{rl}{\gamma }_{oir}^{k^{\prime }}\left(G\right)& \le \omega \left(g\right)={\gamma }_{oir}^k\left(G\right)+(k^{\prime }-k)a_k\\ & \le {\gamma }_{oir}^k\left(G\right)+(k^{\prime }-k)⌊\frac{{\gamma }_{oir}^k\left(G\right)}{k}⌋.\end{array}$

Corollary 2.1

Let $k^{\prime }>k$ be two positive integers and G a graph of order at least two. Then ${\gamma }_{oir}^{k^{\prime }}\left(G\right)\le k^{\prime }⌊\frac{{\gamma }_{oir}^k\left(G\right)}{k}⌋.$

3. Outer-independent 2-rainbow domination number

In this section, we focus on outer-independent 2-rainbow domination. An OI2RD-function f on a graph G can be represented by the ordered 4-tuple $(V_0,V_1,V_2,V_{1,2})$ (or $(V_0^f,V_1^f,V_2^f,V_{1,2}^f)$ to refer f) of $V\left(G\right)$, where $V_0=\{v\in V(G)\mid f(v)=\mathrm{\varnothing }\}$, $V_1=\{v\in V(G)\mid f(v)=\{1\left\}\right\}$, $V_2=\{v\in V(G)\mid f(v)=\{2\left\}\right\}$ and $V_{1,2}=\{v\in V(G)\mid f(v)=\{1,2\left\}\right\}$. In this representation, its weight is $\omega \left(f\right)=|V_1|+|V_2|+2|V_{1,2}|$.

By Theorem 2.1 we immediately obtain

Corollary 3.1

For any graph G of order $n\ge 2$, $2\le {\gamma }_{oir}^2\left(G\right)\le n$. Moreover ${\gamma }_{oir}^2\left(G\right)=2$ if and only if G is $\overline{K_2}$ or $G=K_{1,n-1}$ or $G=K_{2,n-2}$ or $G=K_2\vee \overline{K_{n-2}}$.

3.1. Outer-independent 2-rainbow domination versus domination parameters

A function $f:V\left(G\right)\to \{0,1,2\}$ is an outer-independent Roman dominating function (OIRD-function) on G if every vertex $u\in V$ for which $f\left(u\right)=0$ is adjacent to at least one vertex v for which $f\left(v\right)=2$ and $\{v\mid f(v)=0\}$ is an independent set. The outer-independent Roman domination number ${\gamma }_{oiR}\left(G\right)$ is the minimum weight of an OIRD-function on G. Outer-independent Roman domination was introduced by Abdollahzadeh Ahangar et al. in [3]. Clearly, if $f=(V_0,V_1,V_2)$ is a ${\gamma }_{oiR}\left(G\right)$-function, then the function $g=(V_0,V_1,\mathrm{\varnothing },V_2)$ is an outer-independent 2-rainbow dominating function on a graph G and so (2) ${\gamma }_{oiR}\left(G\right)\ge {\gamma }_{oir}^2\left(G\right).$(2) Abdollahzadeh Ahangar et al. proved the following bounds on ${\gamma }_{oiR}\left(G\right)$.

Proposition 3.1

[3]

If G is a connected triangle-free graph of order $n\ge 2$ and maximum degree Δ, then ${\gamma }_{oiR}\left(G\right)\le n-\mathrm{\Delta }+1$.

Proposition 3.2

[3]

Let G be a connected graph of order n. If G has girth $g<\mathrm{\infty }$, then ${\gamma }_{oiR}\left(G\right)\le n+\lceil \frac{g}{2}\rceil -g$.

Next results are immediate consequences of Propositions 3.1, 3.2 and inequality (2(2) ${\gamma }_{oiR}\left(G\right)\ge {\gamma }_{oir}^2\left(G\right).$(2) ).

Corollary 3.2

If G is a connected triangle-free graph of order $n\ge 2$ and maximum degree Δ, then ${\gamma }_{oir}^2\left(G\right)\le n-\mathrm{\Delta }+1$. This bound is sharp for all stars $K_{1,n-1}$, $n\ge 2$.

Corollary 3.3

Let G be a connected graph of order n. If G has girth $g<\mathrm{\infty }$, then ${\gamma }_{oir}^2\left(G\right)\le n+\lceil \frac{g}{2}\rceil -g$.

In the following, we provide an upper bound on ${\gamma }_{oiR}\left(G\right)$ in terms of ${\gamma }_{oir}^2\left(G\right)$ for arbitrary graphs G.

Theorem 3.1

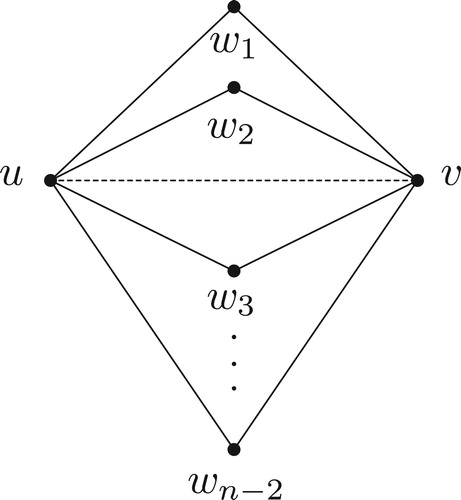
For any graph G, ${\gamma }_{oiR}\left(G\right)\le \frac{3}{2}{\gamma }_{oir}^2\left(G\right)$. This bound is sharp for the family $\mathcal{F}$ of graphs illustrated in Figure 1.

Figure 1. The graph $\mathcal{F}$.

Proof.

Let $f=(V_0,V_1,V_2,V_{1,2})$ be a ${\gamma }_{oir}^2\left(G\right)$-function and without loss of generality $|V_1|\ge |V_2|$. Then $g=(V_0,V_1,V_2\cup V_{1,2})$ is an OIRD-function on G implying that $\begin{array}{rl}{\gamma }_{oiR}\left(G\right)& \le \omega \left(g\right)=|V_1|+2|V_2|+2|V_{1,2}|\\ & =\omega \left(f\right)+|V_2|\le \frac{3}{2}{\gamma }_{oir}^2\left(G\right).\end{array}$

The notion of outer-independent Italian domination in graphs was introduced in [16]. An outer-independent Italian dominating function (OIID-function) on a graph G is a function $f:V\left(G\right)\to \{0,1,2\}$ such that every vertex $v\in V\left(G\right)$ with $f\left(v\right)=0$ has at least two neighbours assigned 1 under f or one neighbour w with $f\left(w\right)=2$ and the set of all vertices assigned 0 under f is independent. The weight of an OIID-function f is the value $\omega \left(f\right)=\sum _{u\in V\left(G\right)}f\left(u\right)$. The minimum weight of an OIID-function on a graph G is called the outer-independent Italian domination number ${\gamma }_{oiI}\left(G\right)$ of G. Clearly, if $f=(V_0,V_1,V_2,V_{1,2})$ is a ${\gamma }_{oir}^2\left(G\right)$-function, then the function $g=(V_0,V_1\cup V_2,V_2)$ is an outer-independent Italian dominating function of G and so (3) ${\gamma }_{oir}^2\left(G\right)\ge {\gamma }_{oiI}\left(G\right).$(3) In [16], the authors proved that ${\gamma }_{oiI}\left(C_n\right)=\lceil \frac{n}{2}\rceil$ for $n\ge 3$ and ${\gamma }_{oiI}\left(K_{p,q}\right)=q$ for $p\ge q\ge 2$. Using these we obtain the next results.

Proposition 3.3

For $n\ge 3$, ${\gamma }_{oir}^2\left(C_n\right)=\lceil \frac{n}{2}\rceil$.

Proof.

By (3(3) ${\gamma }_{oir}^2\left(G\right)\ge {\gamma }_{oiI}\left(G\right).$(3) ), we have ${\gamma }_{oir}^2\left(C_n\right)\ge \lceil \frac{n}{2}\rceil$. Let $C_n:v_1{v}_2\dots v_n{v}_1$ be a cycle and define $f:V\left(G\right)\to 2^{\left[2\right]}$ by $f\left(v_{4i+1}\right)=\left\{1\right\}$, $f\left(v_{4i+3}\right)=\left\{2\right\}$ for $i\ge 0$ and $f\left(x\right)=\mathrm{\varnothing }$ otherwise. Clearly f is an OI2RD-function of $C_n$ and hence ${\gamma }_{oir}^2\left(C_n\right)\le \lceil \frac{n}{2}\rceil$. Thus ${\gamma }_{oir}^2\left(C_n\right)=\lceil \frac{n}{2}\rceil$.

Proposition 3.4

For $p\ge q\ge 2$, ${\gamma }_{oir}^2\left(K_{p,q}\right)=q$.

Proof.

It follows from (3(3) ${\gamma }_{oir}^2\left(G\right)\ge {\gamma }_{oiI}\left(G\right).$(3) ) that ${\gamma }_{oir}^2\left(K_{p,q}\right)\ge q$. Let $X=\{x_1,\dots ,x_q\}$ and $Y=\{y_1,\dots ,y_p\}$ be the bipartite sets of $K_{p,q}$ and define $f:V\left(K_{p,q}\right)\to 2^{\left[2\right]}$ by $f\left(x_1\right)=\left\{2\right\}$, $f\left(x_i\right)=\left\{1\right\}$ for $2\le i\le q$ and $f\left(x\right)=\mathrm{\varnothing }$ otherwise. Clearly f is an OI2RD-function of $K_{p,q}$ and hence ${\gamma }_{oir}^2\left(K_{p,q}\right)\le q$. Therefore ${\gamma }_{oir}^2\left(K_{p,q}\right)=q$.

Fan et al. [16] proved the following bound on  ${\gamma }_{oiI}\left(G\right)$.

Theorem 3.2

For any connected graph G of order $n\ge 2$ with minimum degree δ and maximum degree Δ, ${\gamma }_{oiI}\left(G\right)\ge ⌈n\delta /(\delta +\mathrm{\Delta })⌉.$

Next result is an immediate consequence of Theorem 3.2 and inequality (3(3) ${\gamma }_{oir}^2\left(G\right)\ge {\gamma }_{oiI}\left(G\right).$(3) ).

Corollary 3.4

For any connected graph G of order $n\ge 2$ with minimum degree δ and maximum degree Δ, ${\gamma }_{oir}^2\left(G\right)\ge \lceil n\delta /(\delta +\mathrm{\Delta })\rceil .$ This bound is sharp for cycles.

Fan et al. [16] proved the following Nordhaus–Gaddum type result for outer-independent Italian domination number.

Theorem 3.3

For any graph G on n vertices, $n-1\le {\gamma }_{oiI}\left(G\right)+{\gamma }_{oiI}\left(\overline{G}\right).$

As an immediate consequence we have:

Corollary 3.5

For any graph G on n vertices, $n-1\le {\gamma }_{oir}^2\left(G\right)+{\gamma }_{oir}^2\left(\overline{G}\right)\le 2n.$ The upper bound is sharp for $K_2$ and the lower bound is sharp for a graph G obtained from $K_{10}$ with vertex set $\{u_1^j,u_2^j|1\le j\le 5\}$ by adding new vertices $v_1,v_2,v_3,v_4,v_5$ and joining $v_j$ to $u_1^j$ and $u_2^j$ for $2\le j\le 5$ and joining $v_1$ to all vertices in $K_{10}$.

3.2. Trees

Here we present sharp upper and lower bounds on the outer-independent 2-rainbow domination number of trees. First we show that the outer-independent 2-rainbow domination number and the outer-independent Italian domination number of a tree are equal.

Theorem 3.4

For any tree T, ${\gamma }_{oiI}\left(T\right)={\gamma }_{oir}^2\left(T\right)$.

Proof.

Consider a ${\gamma }_{oiI}$-function $f=(V_0,V_1,V_2)$ on T and let $U_1,U_2,\dots ,U_s$ be the components of the graph $⟨V_1\cup V_2⟩$. Let $T_f$ be the graph whose vertex set is $\{U_1,U_2,\dots ,U_s\}$ and two vertices $U_i$ and $U_j$ are adjacent if and only if there are vertices $u_i\in U_i$, $u_j\in U_j$ and $u_{ij}\in V_0$ such that $u_i{u}_{ij}{u}_j$ is a path in T. If $V_1\ne \mathrm{\varnothing }$, then we may assume that $V_1\cap U_1\ne \mathrm{\varnothing }$. Define $g:V\left(G\right)\to 2^{\left[2\right]}$ as follows: $g\left(x\right)=\{1,2\}$ for $x\in V_2$, $g\left(x\right)=\mathrm{\varnothing }$ for $x\in V_0$, $g\left(x\right)=\left\{1\right\}$ whenever $f\left(v\right)=1$ and either $v\in V_1\cap U_1$ or $v\in U_j$, where the distance $U_1$ and $U_j$ in $T_f$, is even, and $g\left(x\right)=\left\{2\right\}$ otherwise. Clearly g is an OI2RD-function on T with weight $\omega \left(f\right)$ and so ${\gamma }_{oir}^2\left(T\right)\le {\gamma }_{oiI}\left(T\right)$. The result now immediately follows from (3(3) ${\gamma }_{oir}^2\left(G\right)\ge {\gamma }_{oiI}\left(G\right).$(3) ).

Using the results given in [16] and Theorem 3.4, we obtain the following results.

Proposition 3.5

For $n\ge 1$, ${\gamma }_{oir}^2\left(P_n\right)=\lceil \frac{n+1}{2}\rceil$.

Proposition 3.6

For any tree T of order n, ${\gamma }_{oir}^2\left(G\right)\le n-\mathrm{\Delta }+1$.

Theorem 3.5

For any tree T of order $n\ge 2$, ${\gamma }_{oir}^2\left(T\right)\ge \frac{n+3-\ell \left(T\right)}{2},$ where $\ell \left(T\right)$ is the number of leaves of T. This bound is sharp for stars and paths.

As a consequence of Propositions 2.4 and 3.5 we obtain the following result.

Corollary 3.6

For any connected graph G of order n, ${\gamma }_{oir}^2\left(G\right)\le n-\lceil \frac{\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}\left(G\right)+1}{2}\rceil .$

In the sequel we will use the following observation.

Observation 3.1

Let G be a graph.

1. If u is a strong support vertex of G, then there is a ${\gamma }_{oir}^2\left(G\right)$-function f with $f\left(u\right)=\{1,2\}$.

2. If $v_3{v}_2{v}_1$ is a path in G such that ${\mathrm{deg}}_G\left(v_2\right)=2$ and ${\mathrm{deg}}_G\left(v_1\right)=1$, then there is a ${\gamma }_{oir}^2\left(G\right)$-function f with $f\left(v_1\right)=\left\{1\right\}$, $f\left(v_2\right)=\mathrm{\varnothing }$ and $2\in f\left(v_3\right)$.

Proof.

(1) is trivial. To prove (2), let g be a ${\gamma }_{oir}^2\left(G\right)$-function. If $g\left(v_2\right)=\mathrm{\varnothing }$, then let f = g. Assume then that $g\left(v_2\right)\ne \mathrm{\varnothing }$. If $|g\left(v_2\right)|=1$, then since g is a ${\gamma }_{oir}^2\left(G\right)$-function, it follows that $|g\left(v_1\right)|=1$. By the minimality of g, we have $g\left(v_3\right)=\mathrm{\varnothing }$, for otherwise we may assume that $1\in g\left(v_3\right)$ and then the function h defined by $h\left(v_2\right)=\mathrm{\varnothing }$, $h\left(v_1\right)=\left\{2\right\}$ and $h\left(x\right)=g\left(x\right)$ otherwise, is an OI2RD-function of G with smaller weight than g, a contradiction. Hence we may assume that $g\left(v_3\right)=\mathrm{\varnothing }$. But then the function $f:V\left(G\right)\to 2^{\left[2\right]}$ defined by $f\left(v_3\right)=\left\{2\right\}$, $f\left(v_2\right)=\mathrm{\varnothing }$, $f\left(v_1\right)=\left\{1\right\}$ and $f\left(x\right)=g\left(x\right)$ for all $x\in V\left(G\right)-\{v_1,v_2,v_3\}$ is a ${\gamma }_{oir}^2\left(G\right)$-function with desired property. If $|g\left(v_2\right)|=2$, that is, $g\left(v_2\right)=\{1,2\}$, then by the minimality we have $g\left(v_1\right)=g\left(v_3\right)=\mathrm{\varnothing }$. Now the function f defined above is a ${\gamma }_{oir}^2\left(G\right)$-function with desired property.

Next we present an upper bound on outer-independent 2-rainbow domination number of a tree T in terms of the order and its number of support vertices. For any tree T, let $s\left(T\right)$ denote the number its support vertices.

Theorem 3.6

If T is a tree of order at least 3, then ${\gamma }_{oir}^2\left(T\right)\le ⌊\frac{n\left(T\right)+s\left(T\right)}{2}⌋.$ This bound is sharp for all paths $P_{2k}(k\ge 1)$.

Proof.

The proof is by induction on $n\left(T\right)$. It is easy to verify that the statement is true for $n\left(T\right)\le 4$. Hence, let $n\left(T\right)\ge 5$ and assume that every $T^{\prime }$ of order $n\left(T^{\prime }\right)<n\left(T\right)$ with $s\left(T^{\prime }\right)$ support vertices satisfies ${\gamma }_{oir}^2\left(T^{\prime }\right)\le \lfloor \frac{n\left(T^{\prime }\right)+s\left(T^{\prime }\right)}{2}\rfloor$. Let T be a tree of order $n\left(T\right).$ If T is a star, then ${\gamma }_{oir}^2\left(T\right)=2<\lfloor \frac{n\left(T\right)+1}{2}\rfloor$. Likewise, if T is a double star, then ${\gamma }_{oir}^2\left(T\right)=3\mathrm{o}\mathrm{r}4$ and so ${\gamma }_{oir}^2\left(T\right)\le \lfloor \frac{n\left(T\right)+2}{2}\rfloor$ with equality if and only if $T\in \{D{S}_{1,2},D{S}_{2,2},D{S}_{2,3}\}$. Henceforth, we assume that $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}\left(T\right)\ge 4$.

If T has a strong support vertex u with $L\left(u\right)\ge 3$, then let $T^{\prime }=T-w$ where $w\in L\left(u\right)$. Clearly, there exists a ${\gamma }_{oir}^2\left(T^{\prime }\right)$-function f such that $f\left(u\right)=\{1,2\}$ and f can be extended to an OI2RD-function of T by assigning ∅ to w and this implies that ${\gamma }_{oir}^2\left(T\right)\le {\gamma }_{oir}^2\left(T^{\prime }\right)$. Now the result follows by using the induction on $T^{\prime }$ and the facts $n\left(T^{\prime }\right)=n\left(T\right)-1$ and $s\left(T^{\prime }\right)=s\left(T\right)$. Henceforth, we assume that every support vertex of T is adjacent to at most two leaves.

Let $v_1{v}_2\dots v_k$ be a diametrical path in T such that ${\mathrm{deg}}_T\left(v_2\right)$ is as large as possible and root T at $v_k$. We consider the following cases.

Case 1. ${\mathrm{deg}}_T\left(v_2\right)=3$. If ${\mathrm{deg}}_T\left(v_3\right)\ge 3$, then any ${\gamma }_{oir}^2(T-T_{v_2})$-function can be extended to an OI2RD-function of T by assigning $\{1,2\}$ to $v_2$ and ∅ to the leaves adjacent to $v_2$ and so ${\gamma }_{oir}^2\left(T\right)\le {\gamma }_{oir}^2(T-T_{v_2})+2$. Using the induction on $T-T_{v_2}$ and the facts $n(T-T_{v_2})=n\left(T\right)-3$ and $s(T-T_{v_2})=s\left(T\right)-1$, we obtain ${\gamma }_{oir}^2\left(T\right)\le {\gamma }_{oir}^2\left(T^{\prime }\right)+2\le \lfloor \frac{n\left(T^{\prime }\right)+s\left(T^{\prime }\right)}{2}\rfloor +2=\lfloor \frac{n\left(T\right)+s\left(T\right)}{2}\rfloor .$ Hence we assume that ${\mathrm{deg}}_T\left(v_3\right)=2$. If $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}\left(T\right)=4$, then we have ${\gamma }_{oir}^2\left(T\right)=4\le \lfloor \frac{n\left(T\right)+s\left(T\right)}{2}\rfloor .$ Let $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}\left(T\right)\ge 5$. We distinguish the followings.

Subcase 1.1. ${\mathrm{deg}}_T\left(v_4\right)\ge 3$.

If $v_4$ is a support vertex, then any ${\gamma }_{oir}^2(T-T_{v_2})$-function can be extended to an OI2RD-function of T by assigning $\{1,2\}$ to $v_2$ and ∅ to the leaves adjacent to $v_2$ and it follows from the induction hypothesis on $T-T_{v_2}$ and the facts $n(T-T_{v_2})=n-3$ and $s(T-T_{v_2})=s\left(T\right)-1$ that $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \le {\gamma }_{oir}^2(T-T_{v_2})+2\\ & \le ⌊\frac{n(T-T_{v_2})+s(T-T_{v_2})}{2}⌋+2=⌊\frac{n+s}{2}⌋.\end{array}$ Assume next that $v_4$ is not a support vertex. We consider the following situations.

1. $v_4$ has a child $w_2$ with depth one. Let $T^{\prime }=T-T_{w_2}$ and let f be a ${\gamma }_{oir}^2\left(T^{\prime }\right)$-function such that $f\left(v_2\right)=\{1,2\}$. Without loss of generality, we may assume that $|f\left(v_4\right)|\ge 1$ and that $1\in f\left(v_4\right)$. If ${\mathrm{deg}}_T\left(w_2\right)=2$, then the function f can be extended to an OI2RD-function of T by assigning ∅ to $w_2$ and $\left\{2\right\}$ to the leaf-neighbour of $w_2$, and using the induction hypothesis on $T^{\prime }$ and the facts $n\left(T^{\prime }\right)=n\left(T\right)-2$ and $s\left(T^{\prime }\right)=s\left(T\right)-1$ we obtain $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \le {\gamma }_{oir}^2\left(T^{\prime }\right)+1\\ & \le ⌊\frac{n\left(T^{\prime }\right)+s\left(T^{\prime }\right)}{2}⌋+1<⌊\frac{n+s}{2}⌋.\end{array}$If ${\mathrm{deg}}_T\left(w_2\right)=3$, then the function f can be extended to an OI2RD-function of T by assigning a $\{1,2\}$ to $w_2$ and ∅ to its leaf-neighbours, and using the induction hypothesis on $T^{\prime }$ and the facts $n\left(T^{\prime }\right)=n\left(T\right)-3$ and $s\left(T^{\prime }\right)=s\left(T\right)-1$ we obtain $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \le {\gamma }_{oir}^2\left(T^{\prime }\right)+2\le ⌊\frac{n\left(T^{\prime }\right)+s\left(T^{\prime }\right)}{2}⌋+2\\ & =⌊\frac{n+s}{2}⌋.\end{array}$

2. $v_4$ has a child $w_3$ with depth two different from $v_3$. Suppose $v_4{w}_3{w}_2{w}_1$ be a path in T such that ${\mathrm{deg}}_T\left(w_1\right)=1$. First let ${\mathrm{deg}}_T\left(w_2\right)=3$. As in the first paragraph of Case 1, we may assume that ${\mathrm{deg}}_T\left(w_3\right)=2$. Let $T^{\prime }=T-T_{v_3}$ and let f be a ${\gamma }_{oir}^2\left(T^{\prime }\right)$-function such that $f\left(w_2\right)=\{1,2\}$. Without loss of generality, we may assume that $|f\left(v_4\right)|\ge 1$. Then f can be extended to an OI2RD-function of T by assigning $\{1,2\}$ to $v_2$ and ∅ to $v_3$ and all leaves of $v_2$. Using the induction on $T^{\prime }$ and the facts $n\left(T^{\prime }\right)=n\left(T\right)-3$ and $s\left(T^{\prime }\right)=s\left(T\right)-1$ we obtain $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \le {\gamma }_{oir}^2\left(T^{\prime }\right)+2\le ⌊\frac{n\left(T^{\prime }\right)+s\left(T^{\prime }\right)}{2}⌋+2\\ & \le ⌊\frac{n\left(T\right)+s\left(T\right)}{2}⌋.\end{array}$Assume now that ${\mathrm{deg}}_T\left(w_2\right)=2$ and that all children of $w_3$ with depth 1 has degree 2. Let $t_1$ be the number of children of $w_3$ with depth 0 and $t_2$ be the number of children of $w_3$ with depth 1 and let t = 0 if $t_1=0$ and t = 1 if $t_1\ge 1$. Suppose $T^{\prime }=T-T_{w_3}$. Clearly, any ${\gamma }_{oir}^2\left(T^{\prime }\right)$-function can be extended to an OI2RD-function of T by assigning $\left\{1\right\}$ to all leaves at distance 2 from $w_3$, ∅ to all children of $w_3$, and $\{1,2\}$ to $w_3$ if $t_1\ge 1$ and $\left\{2\right\}$ to $w_3$ if $t_1=0$. Using the induction on $T^{\prime }$ and the facts $n\left(T^{\prime }\right)=n\left(T\right)-1-2t_2-t_1$ and $s\left(T^{\prime }\right)=s\left(T\right)-t_2-t$ we obtain $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \le {\gamma }_{oir}^2\left(T^{\prime }\right)+t_2+1+t\\ & \le ⌊\frac{n\left(T^{\prime }\right)+s\left(T^{\prime }\right)}{2}⌋+t_2+1+t\\ & =⌊\frac{n\left(T\right)-1-2t_2-t_1+s\left(T\right)-t_2-t}{2}⌋\\ & +t_2+1+t\\ & \le ⌊\frac{n\left(T\right)+s\left(T\right)}{2}⌋.\end{array}$

Subcase 1.2. ${\mathrm{deg}}_T\left(v_4\right)=2$.

If ${\mathrm{deg}}_T\left(v_5\right)\ge 3$, then any ${\gamma }_{oir}^2(T-T_{v_4})$-function can be extended to an OI2RD-function of T by assigning a $\{1,2\}$ to $v_2$, a $\left\{1\right\}$ to $v_4$ and an ∅ to other vertices in $T_{v_4}$, and it follows from the induction hypothesis and the facts $n(T-T_{v_4})=n\left(T\right)-5$ and $s(T-T_{v_4})=s\left(T\right)-1$ that $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \le ⌊\frac{n(T-T_{v_4})+s(T-T_{v_4})}{2}⌋+3\\ & =⌊\frac{n\left(T\right)+s\left(T\right)}{2}⌋.\end{array}$ Assume that ${\mathrm{deg}}_T\left(v_5\right)=2$. Let $T^{\prime }=T-T_{v_3}$ and f be a ${\gamma }_{oir}^2$-function. By Observation 3.1 (item (2)) we may suppose that $f\left(v_4\right)=\left\{1\right\}$. Then f can be extended to an OI2RD-function of T by assigning a $\{1,2\}$ to $v_2$ and an ∅ to other vertices in $T_{v_3}$, and it follows from the induction hypothesis and the facts $n\left(T^{\prime }\right)=n\left(T\right)-4$ and $s\left(T^{\prime }\right)=s\left(T\right)$ that ${\gamma }_{oir}^2\left(T\right)\le {\gamma }_{oir}^2\left(T^{\prime }\right)+2\le \lfloor \frac{n\left(T\right)+s\left(T\right)}{2}\rfloor .$

Case 2. ${\mathrm{deg}}_T\left(v_2\right)=2$.

By the choice of diametrical path, we deduce that every child of $v_3$ with depth one has degree two. Consider the following subcases.

Subcase 2.1. ${\mathrm{deg}}_T\left(v_3\right)\ge 3$.

First suppose that $v_3$ is a strong support vertex or adjacent to a support vertex except $v_2$. Let $T^{\prime }=T-\{v_1,v_2\}$ and f a ${\gamma }_{oir}^2\left(T^{\prime }\right)$-function. By Observation 3.1, we may assume without loss of generality that $1\in f\left(v_3\right)$. Now f can be extended to an OI2RD-function of T by assigning a $\left\{2\right\}$ to $v_1$ and an ∅ to $v_2$. Now we deduce from the induction hypothesis on $T^{\prime }$ and the facts $n\left(T^{\prime }\right)=n\left(T\right)-2$ and $s\left(T^{\prime }\right)\le s\left(T\right)$ that $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \le {\gamma }_{oir}^2\left(T^{\prime }\right)+1\le ⌊\frac{n\left(T^{\prime }\right)+s\left(T^{\prime }\right)}{2}⌋+1\\ & \le ⌊\frac{n+s}{2}⌋.\end{array}$ Suppose next that $v_3$ is a support vertex with ${\mathrm{deg}}_T\left(v_3\right)=3$. Let $T^{\prime }=T-v_1$ and f a ${\gamma }_{oir}^2\left(T^{\prime }\right)$-function. Since $v_3$ is a strong support vertex we may assume that $f\left(v_3\right)=\{1,2\}$. Now f can be extended to an OI2RD-function of T by assigning a $\left\{1\right\}$ to $v_1$, and as above we have ${\gamma }_{oir}^2\left(T\right)\le \lfloor \frac{n+s}{2}\rfloor .$

Subcase 2.2. ${\mathrm{deg}}_T\left(v_3\right)=2$.

First assume that ${\mathrm{deg}}_T\left(v_4\right)\ge 3$. Let $T^{\prime }=T-\{v_1,v_2,v_3\}$. Then any ${\gamma }_{oir}^2\left(T^{\prime }\right)$-function f can be extended to an OI2RD-function of T by assigning a $\left\{1\right\}$ to $v_1$, a $\left\{2\right\}$ to $v_3$ and an ∅ to $v_2$, and it follows from the induction hypothesis and the facts $n\left(T^{\prime }\right)=n\left(T\right)-3$ and $s\left(T^{\prime }\right)=s\left(T\right)-1$ that $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \le {\gamma }_{oir}^2\left(T^{\prime }\right)+2\le \left[\frac{n\left(T^{\prime }\right)+s\left(T^{\prime }\right)}{2}\right]+2\\ & =⌊\frac{n\left(T\right)+s\left(T\right)}{2}⌋.\end{array}$ Assume next that ${\mathrm{deg}}_T\left(v_4\right)=2$. Let $T^{\prime }=T-\{v_1,v_2\}$ and f a ${\gamma }_{oir}^2\left(T^{\prime }\right)$-function. Observation 3.1 (item (2)), we may assume that $1\in f\left(v_3\right)$. Now f can be extended to an OI2RD-function of T by assigning a $\left\{2\right\}$ to $v_1$ and an ∅ to $v_2$, and we deduce from the induction hypothesis and the facts $n\left(T^{\prime }\right)=n\left(T\right)-2$ and $s\left(T^{\prime }\right)=s\left(T\right)$ that ${\gamma }_{oir}^2\left(T\right)\le {\gamma }_{oir}^2\left(T^{\prime }\right)+1\le \lfloor \frac{n+s}{2}\rfloor$ and this completes the proof.

Next result in an immediate consequence of Theorems 3.4 and 3.6 since the number of support vertices of a tree on $n\ge 3$ vertices is at most $\lfloor \frac{n}{2}\rfloor$.

Corollary 3.7

For any tree T of order $n\ge 3$, ${\gamma }_{oiI}\left(T\right)={\gamma }_{oir}^2\left(T\right)\le \frac{3n}{4}.$

A constructive instruction of trees attaining the bound given in Corollary 3.7 is given in [16].

We close this section by establishing a lower bound on the outer-independent 2-rainbow domination number of a tree in terms of the order and the total outer-independent domination number. Recall that a set S of vertices of a graph G is a total outer-independent dominating set if every vertex from $V\left(G\right)$ has a neighbour in S and the complement of S is an independent set. The total outer-independent domination number ${\gamma }_{oit}\left(G\right)$ of G is the smallest possible cardinality of any total outer-independent dominating set of G. The total outer-independent domination was introduced in [17, 18]. It was observed in [17] that ${\gamma }_{oit}\left(P_n\right)=\left\{\begin{array}{ll}2& \mathrm{i}\mathrm{f}n=2,\\ \lfloor 2n/3\rfloor & \mathrm{i}\mathrm{f}n\ge 3.\end{array}\right.$

Theorem 3.7

For any nontrivial tree T, ${\gamma }_{oir}^2\left(T\right)\ge {\gamma }_{oit}\left(T\right)-⌈\frac{n\left(T\right)}{6}⌉+1.$ Furthermore, this bound is sharp for paths $P_{6k}(k\ge 1)$.

Proof.

The proof is by induction on the order $n\left(T\right)$. If $n\left(T\right)=2$ or $n\left(T\right)=3$, then ${\gamma }_{oir}^2\left(T\right)={\gamma }_{oit}\left(T\right)=2$ and the bound is sharp. Let $n\left(T\right)\ge 4$ and assume that for any tree $T^{\prime }$ of order $n\left(T^{\prime }\right)<n\left(T\right)$, ${\gamma }_{oir}^2\left(T^{\prime }\right)\ge {\gamma }_{oit}\left(T^{\prime }\right)-\lceil \frac{n\left(T^{\prime }\right)}{6}\rceil +1$. Let T be a tree of order $n\left(T\right)$ and $f=(V_0,V_1,V_2,V_{1,2})$ be a ${\gamma }_{oir}^2\left(T\right)$-function. Since for stars and double stars T we have ${\gamma }_{oit}\left(T\right)=2$, so the statement holds. Hence, we assume that T has diameter at least four. If $V_0=\mathrm{\varnothing }$, then by the fact that $\lceil \frac{n\left(T\right)}{6}\rceil \ge 1$ we have ${\gamma }_{oir}^2\left(T\right)=n\left(T\right)\ge {\gamma }_{oit}\left(T\right)$. Therefore we assume that $V_0\ne \mathrm{\varnothing }$. First suppose that T has a support vertex x which is adjacent to two or more leaves. Let u, v be two leaves adjacent to x and $T^{\prime }$ be the tree obtained from T by removing u. Obviously, ${\gamma }_{oit}\left(T\right)={\gamma }_{oit}\left(T^{\prime }\right)$. Also by Observation 3.1, we may assume that $f\left(x\right)=\{1,2\}$ and so all leaves adjacent to x belong to $V_0$. Hence, the function f, restricted to $T^{\prime }$, is a OI2RD-function on $T^{\prime }$, implying that ${\gamma }_{oir}^2\left(T\right)\ge {\gamma }_{oir}^2\left(T^{\prime }\right)$. Applying the inductive hypothesis to $T^{\prime }$, we get ${\gamma }_{oir}^2\left(T\right)={\gamma }_{oir}^2\left(T^{\prime }\right)\ge {\gamma }_{oit}\left(T^{\prime }\right)-\lceil \frac{n\left(T^{\prime }\right)}{6}\rceil +1={\gamma }_{oit}\left(T\right)-\lceil \frac{n\left(T\right)-1}{6}\rceil +1\ge {\gamma }_{oit}\left(T\right)-\lceil \frac{n\left(T\right)}{6}\rceil +1$, as desired. Therefore, we may assume that every support vertex of T is adjacent to exactly one leaf. Suppose $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}\left(T\right)=k-1$, and let $P:=v_1,v_2,\dots ,v_k$ be a diametrical path of T. Root T at $v_k$. Thus, $v_1$ is a leaf of T and ${\mathrm{deg}}_T\left(v_2\right)=2$.

By item (2) of Observation 3.1, there is a ${\gamma }_{oir}^2\left(T\right)$-function g such that $g\left(v_1\right)=\left\{1\right\}$, $g\left(v_2\right)=\mathrm{\varnothing }$ and $2\in g\left(v_3\right)$. Consider the following cases.

Case 1. ${\mathrm{deg}}_T\left(v_3\right)\ge 3$.

Let $T^{\prime }=T-\{v_1,v_2\}$. Since $v_3$ is a support vertex or is adjacent to a support vertex of degree two in $T^{\prime }$, any ${\gamma }_{oit}\left(T^{\prime }\right)$-set containing no leaf, contains $v_3$ and so it can be extended to an OITD-set of T by adding $v_2$ implying that ${\gamma }_{oit}\left(T\right)\le {\gamma }_{oit}\left(T^{\prime }\right)+1$. On the other hand, the function g restricted to $T^{\prime }$ is an OI2RD-function of $T^{\prime }$ of weight at most $\omega \left(g\right)-1$ and we conclude from the induction hypothesis that $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \ge {\gamma }_{oir}^2\left(T^{\prime }\right)+1\\ & \ge {\gamma }_{oit}\left(T^{\prime }\right)-⌈\frac{n\left(T^{\prime }\right)}{6}⌉+1+1\\ & \ge {\gamma }_{oit}\left(T\right)-1-⌈\frac{n\left(T\right)-2}{6}⌉+2\\ & \ge {\gamma }_{oit}\left(T\right)-⌈\frac{n\left(T\right)}{6}⌉+1.\end{array}$ Case 2. ${\mathrm{deg}}_T\left(v_3\right)=2$.

If $|g\left(v_4\right)|\ge 1$ or ${\cup }_{v\in N\left(v_4\right)-\left\{v_3\right\}}g\left(v\right)=\{1,2\}$, then let $T^{\prime }=T-T_{v_3}$. Clearly the function g restricted to $T^{\prime }$ is an OI2RD-function of $T^{\prime }$ of weight at most $\omega \left(g\right)-2$ and so ${\gamma }_{oir}^2\left(T\right)\ge {\gamma }_{oir}^2\left(T^{\prime }\right)+2$. On the other hand, any ${\gamma }_{oit}\left(T^{\prime }\right)$-set can be extended to an OITD-set of T by adding $v_3,v_2$ yielding ${\gamma }_{oit}\left(T\right)\le {\gamma }_{oit}\left(T^{\prime }\right)+2$. It follows from the induction hypothesis that $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \ge {\gamma }_{oir}^2\left(T^{\prime }\right)+2\\ & \ge {\gamma }_{oit}\left(T^{\prime }\right)-⌈\frac{n\left(T^{\prime }\right)}{6}⌉+1+2\\ & \ge {\gamma }_{oit}\left(T\right)-2-⌈\frac{n\left(T\right)-3}{6}⌉+3\\ & \ge {\gamma }_{oit}\left(T\right)-⌈\frac{n\left(T\right)}{6}⌉+1.\end{array}$ Assume that $g\left(v_4\right)=\mathrm{\varnothing }$ and that ${\cup }_{v\in N\left(v_4\right)-\left\{v_3\right\}}g\left(v\right)\ne \{1,2\}$. Since $V_0$ is independent and $g\left(v_4\right)=\mathrm{\varnothing }$, we may assume without loss of generality that $g\left(x\right)=\left\{1\right\}$ for each $x\in N\left(v_4\right)-\left\{v_3\right\}$. First let ${\mathrm{deg}}_T\left(v_4\right)\ge 3$. Assume $T^{\prime }=T-\{v_1,v_2,v_3\}$ and let $T_1$ be the components of $T-\{v_3{v}_4,v_4{v}_5\}$ containing $v_4$. Define $h:V\left(T\right)\to 2^{\left[2\right]}$ by $h\left(x\right)=\{1,2\}-g\left(x\right)$ if $x\in V\left(T_1\right)$ and $|g\left(x\right)|=1$, and $h\left(x\right)=g\left(x\right)$ otherwise. Clearly, h is a ${\gamma }_{oir}^2\left(T\right)$-function and we are in above situation and so we have ${\gamma }_{oir}^2\left(T\right)\ge {\gamma }_{oit}\left(T\right)-\lceil \frac{n}{6}\rceil +1$.

Now let ${\mathrm{deg}}_T\left(v_4\right)=2$. Assume that $T^{\prime }=T-\{v_1,v_2,v_3,v_4\}$. Then the function g restricted to $T^{\prime }$ is an OI2RD-function of $T^{\prime }$, implying that ${\gamma }_{oir}^2\left(T\right)\ge {\gamma }_{oir}^2\left(T^{\prime }\right)+2$. On the other hand, any ${\gamma }_{oit}\left(T^{\prime }\right)$-set can be extended to an total outer-independent set of T by adding $v_2,v_3,v_4$, yielding ${\gamma }_{oit}\left(T\right)\le {\gamma }_{oit}\left(T^{\prime }\right)+3$. We deduce from the induction hypothesis on $T^{\prime }$ that $\begin{array}{rl}{\gamma }_{oir}^2\left(T\right)& \ge {\gamma }_{oir}^2\left(T^{\prime }\right)+2\\ & \ge {\gamma }_{oit}\left(T^{\prime }\right)-⌈\frac{n\left(T^{\prime }\right)}{6}⌉+1+2\\ & \ge {\gamma }_{oit}\left(T\right)-3-⌈\frac{n\left(T\right)-4}{6}⌉+3\\ & ={\gamma }_{oit}\left(T\right)-⌈\frac{n\left(T\right)-10}{6}⌉+1\\ & \ge {\gamma }_{oit}\left(T\right)-⌈\frac{n\left(T\right)}{6}⌉+1.\end{array}$ This completes the proof.

We conclude this paper with an open problem.

Problem. Prove or disprove: for any non-trivial connected graph G of order n, ${\gamma }_{oir}^2\left(G\right)\ge {\gamma }_{oit}\left(G\right)-\lceil \frac{n}{6}\rceil +1$.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Qiong Kang http://orcid.org/0000-0001-8123-9184

Vladimir Samodivkin http://orcid.org/0000-0001-7934-5789

Marzieh Soroudi http://orcid.org/0000-0002-6677-6835

Additional information

Funding

This work was supported by the Natural Science Foundation of Guangdong Province under grant 2018A0303130115.