On total edge irregularity strength of polar grid graph

Abstract

For a graph $G$, an edge irregular total $r$-labelling $\pi :V\cup E\to \left\{1,2,3,\dots ,r\right\}$ is a labelling for edges and vertices of a graph $G$ in such a way that the weights of any two different edges are distinct. The minimum for which $G$ admits an edge irregular total $r$-labelling is called total edge irregularity strength of $G$, $tes\left(G\right)$. In this paper, the exact value of total edge irregularity strength of the polar grid graph was determined. We have also determined the total edge irregularity strength for a polar grid graph.

Keywords:

• Total edge irregularity strength
• polar grid graph
• labelling graph

2010 Mathematics subject classification:

• 05C78

1. Introduction

Graph labelling is an extremely useful tool for making a lot of problems in different areas of human life very easy to be handled in a mathematical way. So, it is an important branch in graph theory and has a lot of applications in many fields, for instance, coding theory, astronomy, communication network and optimal circuit layouts.

A labelling of a simple, connected and undirected graph $G\left(V,E\right)$ that is defined as a function that assigns some set of elements of a graph $G$ with a set of positive or non-negative integer. According to a domain of a labelling, we have three types of it. The first one vertex labels if the domain is a vertex-set, the second is edge labelling when edge-set is the domain and finally, total labelling that its domain is the union of edge-set and vertex-set.

Bača et al. [1] defined an edge irregular total $r-$labelling of a graph $G$ as a labelling $\theta :V\cup E\to \left\{1,2,3,\dots ,\text{r}\right\}$ such that every two distinct edges $lm$ and $l^{\ast }{m}^{\ast }$ of a graph $G$ have distinct weights, i.e. $w_{\theta }\left(\text{pq}\right)\ne w_{\theta }\left(p^{\ast }{q}^{\ast }\right)$. If a graph $G$ admits an edge irregular total $r$-labelling and $r$ is minimum then we say that $G$ has a total edge irregularity strength denoted by $tes\left(G\right)$. Furthermore, in [1], for any graph $G$, a lower bound of $tes\left(G\right)$ is given by (1) $tes\left(G\right)\ge max\left\{\frac{|E\left(G\right)|+2}{3},\frac{\mathrm{\Delta }G+1}{2}\right\}$(1) Since then, many authors try to find exact values for the total edge irregularity strength of graphs. Ivanĉo et al. [2] proved that $tes\left(T\right)$ is equal its lower bound where $T$ is any tree. In [3,4] authors determined the exact value of total edge irregularity strength for complete bipartite graph, complete graph and the corona of the path to path, a star and cycle. Ahmad et al. [5] determined $tes\left(G\right)$ that $G$ is generalized helm graph $H_n^m$ with $n\ge 3$, $m\ge 4$. On the other hand, in [6–8] the total edge irregularity strengths for fan graph, wheel graph, triangular Book graph, friendship graph, centralized uniform theta graphs and large graphs are investigated. For definitions, applications and terminology are not mentioned in our paper, see [5,8–26].

In this paper, the exact value of total edge irregularity strength of the polar grid graph was determined.

2. Main results

In this section, we determined the total edge irregularity strength of a polar grid graph $P_{3,n},n\ge 3$, and a polar grid graph $P_{m,3},m\ge 3$. Finally, the exact value of the total edge irregularity strength of a generalized polar grid graph $P_{m,n}$ was determined.

Theorem 2.1.

Let $P_{3,n}$ be a polar grid graph with $3n+1$ vertices and $6n$ edges, $n\ge 3$. Then $tes\left(P_{3,n}\right)=2n+1$

Proof: Since $|V\left(P_{3,n}\right)|=3n+1$, $|E\left(P_{3,n}\right)|=6n$. Then by (1) we have $tes\left(P_{3,n}\right)\ge 2n+1.$

For the inverse inequality, we sufficient to show the existence of an edge irregular total labelling with $r=2n+1.$ Let $r=2n+1$ and $\pi :V\cup E\to \left\{1,2,3,\dots ,r\right\}$ is a total $r$-labelling defined as $\pi \left(v_0\right)=1,$ $\pi \left(v_i\right)=\left\{\begin{array}{ll}i& \text{for}1\le i\le 2n\\ r& \text{for}2n+1\le i\le 3n\end{array}\right.,$ $\pi \left(v_0{v}_i\right)=i\text{for}1\le i\le n,$ $\pi \left(v_i{v}_{i+n}\right)=\left\{\begin{array}{ll}n+1& \text{for}1\le i\le n\\ i& \text{for}n+1\le i\le 2n\end{array}\right.,$ $\pi \left(v_i{v}_{i+1}\right)=\left\{\begin{array}{ll}1& \begin{array}{l}\text{for}1\le i<2n+1,\\ i\notin \left\{n,2n\right\}\end{array}\\ 2\left(i+1-r\right)& \text{for}2n+1\le i\le 3n-1\end{array}\right.,$ $\pi \left(v_n{v}_1\right)=n+1,$ $\pi \left(v_{2n}{v}_{n+1}\right)=n+1$ $\pi \left(v_{3n}{v}_{2n+1}\right)=2n.$

Obviously, all edges and vertex labels are at most $r$. Also, the weights of edges under the labelling $\pi$ are given by: $W_{\pi }\left(v_0{v}_i\right)=2i+1\text{for}1\le i\le n,$ $W_{\pi }\left(v_i{v}_{i+n}\right)=2i+r\text{for}1\le i\le 2n,$ $W_{\pi }\left(v_i{v}_{i+1}\right)=2i+2\text{for}1\le i\le 3n-1,i\notin \left\{n,2n\right\},$ $W_{\pi }\left(v_n{v}_1\right)=r+1,$ $W_{\pi }\left(v_{2n}{v}_{n+1}\right)=2r,$ $W_{\pi }\left(v_{3n}{v}_{2n+1}\right)=2r+2n.$

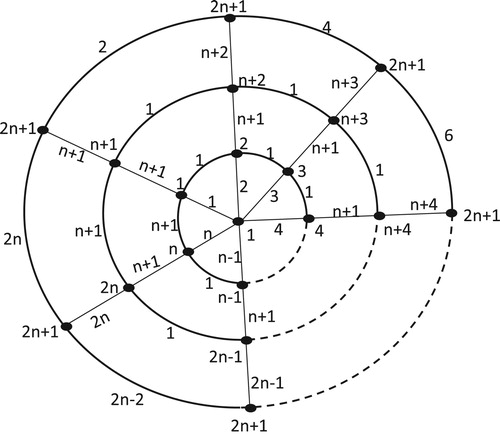
It is clear that the weights for any two different edges in $P_{3,n}$ are distinct (Figure 1). Therefore, $\pi$ is an edge irregular total $r$-labelling f $P_{3,n}$. Hence $tes\left(P_{3,n}\right)=2n+1$

Theorem 2.2.

Let $m\ge 3$ and $P_{m,3}$ be a polar grid graph with $3m+1$ vertices and $6m$ edges. Then $tes\left(P_{m,3}\right)=2m+1$Proof: Since $|V\left(P_{m,3}\right)|=3m+1$, $|E\left(P_{m,3}\right)|=6m$. Then from (1) we have $tes\left(P_{m,3}\right)\ge 2m+1$

To prove the invers inequality, we need to show that there exist an edge irregular total $r$-labelling, $r=2m+1$, for a graph $P_{m,3}.$ Suppose that $r=2m+1$ and $\pi :V\cup E\to \left\{1,2,3,\dots ,r\right\}$ is a total $r$-labelling. The proof is divided into three cases as follows:

Case 1: $m\equiv 0\left(mod3\right).$

Figure 1. A polar grid graph $P_{3,n}$.

Define $\pi$ as follows: $\pi \left(v_0\right)=1,$ $\pi \left(v_i\right)=\left\{\begin{array}{ll}i& \text{for}1\le i\le 2\\ r& \text{for}2m+1\le i\le 3m\end{array}\right.,$ $\pi \left(v_0{v}_i\right)=i\text{for}1\le i\le 3,$ $\pi \left(v_{i-3}{v}_i\right)=\left\{\begin{array}{ll}4& \text{for}4\le i\le 2m+1\\ i-r+4& \text{for}2m+2\le i\le 2m+4\\ 2\left(i-r\right)+1& \text{for}2m+5\le i\le 3m\end{array}\right.,$ $\pi \left(v_i{v}_{i+1}\right)=\left\{\begin{array}{ll}1& \begin{array}{l}\text{for}1\le i\le 2m-1,\\ i\notin \left\{3,6,\dots ,2m-3\right\}\end{array}\\ 2\left(i-r\right)+2& \text{for}2m+1\le i\le 3m-1,\\ & \begin{array}{l}i\notin \{2m+3,2m+6,\\ \dots ,3m-3\}\end{array}\end{array}\right.$ $\pi \left(v_i{v}_{i-2}\right)=\left\{\begin{array}{ll}4& \text{for}i\in \left\{3,6,\dots ,2m\right\}\\ 2\left(i-r\right)+2& \text{for}i\in \{2m+3,\\ & 2m+6,\dots .,3m\}\end{array}\right..$

It is easy to check that the greatest label is $r$. Next, the weights of edges of $P_{m,3}$ are given by: $w_{\pi }\left(v_0{v}_i\right)=2i+1\text{for}1\le i\le 3,$ $w_{\pi }\left(v_{i-3}{v}_i\right)=2i+1\text{for}4\le i\le 3m,$ $\begin{array}{rl}& w_{\pi }\left(v_i{v}_{i+1}\right)=2i+2\text{for}1\le i\le 3m-1,\\ & i\notin \left\{3,6,9,\dots ,3m-3\right\},\end{array}$ $w_{\pi }\left(v_i{v}_{i-2}\right)=2i+2\text{for}i\in \left\{3,6,9,\dots ,3m\right\},$

It is easy to check that the edge- weights of edges are pairwise distinct. So, $tes\left(P_{m,3}\right)=2m+1.$

Case 2: $m\equiv 1\left(mod3\right).$

Define $\pi$ as follows: $\pi \left(v_0\right)=1,$ $\pi \left(v_i\right)=\left\{\begin{array}{ll}i& \text{for}1\le i\le 2m\\ r& \text{for}2m+1\le i\le 3m\end{array}\right.,$ $\pi \left(v_0{v}_i\right)=i\text{for}1\le i\le 3,$ $\pi \left(v_{i-3}{v}_i\right)=\left\{\begin{array}{ll}4& \text{for}4\le i\le 2m+1\\ i-r+4& \text{for}2m+2\le i\le 2m+4\\ 2\left(i-r\right)+1& \text{for}2m+5\le i\le 3m\end{array}\right.,$ $\pi \left(v_i{v}_{i+1}\right)=\left\{\begin{array}{ll}1& \begin{array}{l}\text{for}1\le i\le 2m,\\ i\notin \left\{3,6,\dots ,2m-2\right\}\end{array}\\ 2\left(i-r\right)+2& \begin{array}{l}\text{for}2m+2\le i\le 3m-1,\\ i\notin \{2m+4,2m+7,\\ \dots ,3m-3\}\end{array}\end{array}\right.,$ $\pi \left(v_i{v}_{i-2}\right)=\left\{\begin{array}{ll}4& \text{for}i\in \left\{3,6,\dots ,2m+1\right\}\\ 2\left(i-r\right)+2& \begin{array}{l}\text{for}i\in \{2m+4,2m+7,\\ \dots .,3m\}\end{array}\end{array}\right..$

It is clear that the largest label is $r$. The edge- weights are given by: $w_{\pi }\left(v_0{v}_i\right)=2i+1\text{for}1\le i\le 3,$ $w_{\pi }\left(v_{i-3}{v}_i\right)=2i+1\text{for}4\le i\le 3m,$ $\begin{array}{rl}& w_{\pi }\left(v_i{v}_{i+1}\right)=2i+2\text{for}1\le i\le 3m-1,\\ & i\notin \left\{3,6,9,\dots ,3m-3\right\},\end{array}$ $w_{\pi }\left(v_i{v}_{i-2}\right)=2i+2\text{for}i\in \left\{3,6,9,\dots ,3m\right\}.$

It implies that the weights of edges are distinct. Then, $tes\left(P_{m,3}\right)=2m+1.$

Case 3: $m\equiv 2\left(mod3\right).$

$\pi$ is defined as follows: $\pi \left(v_0\right)=1,$ $\pi \left(v_i\right)=\left\{\begin{array}{ll}i& \text{for}1\le i\le 2m\\ r& \text{for}2m+1\le i\le 3m\end{array}\right.,$ $\pi \left(v_0{v}_i\right)=i\text{for}1\le i\le 3,$ $\pi \left(v_{i-3}{v}_i\right)=\left\{\begin{array}{ll}4& \text{for}4\le i\le 2m+1\\ i-r+4& \text{for}2m+2\le i\le 2m+4\\ 2\left(i-r\right)+1& \text{for}2m+5\le i\le 3m\end{array}\right.,$ $\pi \left(v_i{v}_{i+1}\right)=\left\{\begin{array}{ll}1& \begin{array}{l}\text{for}1\le i\le 2m,\\ i\notin \left\{3,6,\dots ,2m-1\right\}\end{array}\\ 2\left(i-r\right)+2& \text{for}2m+1\le i\le 3m-1,\\ & i\notin \{2m+2,2m+5\dots ,\\ & 3m-3\}\end{array}\right.$ $\pi \left(v_i{v}_{i-2}\right)=\left\{\begin{array}{ll}4& \text{for}i\in \left\{3,6,\dots ,2m-1\right\}\\ 5& \text{for}i=2m+2\\ 2\left(i-r\right)+2& \text{for}i\in \{2m+5,\\ & 2m+8,\dots .,3m\}\end{array}\right.,$

Obviously, the greatest label is $r$. Also, the weights of the edges of the graph $P_{m,3}$ are given by: $w_{\pi }\left(v_0{v}_i\right)=2i+1\mathrm{f}\mathrm{o}\mathrm{r}1\le i\le 3,$ $w_{\pi }\left(v_{i-3}{v}_i\right)=2i+1\mathrm{f}\mathrm{o}\mathrm{r}4\le i\le 3m,$ $\begin{array}{rl}& w_{\pi }\left(v_i{v}_{i+1}\right)=2i+2\text{for}1\le i\le 3m-1,\\ & i\notin \left\{3,6,\dots ,2m-1,2m+2,2m+5,\dots ,3m-3\right\},\end{array}$ $w_{\pi }\left(v_i{v}_{i-2}\right)=\left\{\begin{array}{ll}2r+5& \text{for}i=2m+2\\ 2i+2& \text{for}i\in \{3,6,\dots ,2m-1,\\ & 2m+5,\dots ,3m-3\}\end{array}\right..$From the above equations it is clear that the edge- weights are distinct. So $\pi$ is an edge irregular total $r$-labelling, $r=2m+1$. Hence $tes\left(P_{m,3}\right)=2m+1.$

Theorem 2.3.

If $P_{m,n}$ is a polar grid graph with $nm+1$ vertices and $2mn$ edges, $m\ge 3,n\ge 3$. Then $tes\left(P_{m,n}\right)=\frac{2mn+2}{3}.$

Proof: Since $|V\left(P_{m,n}\right)|=nm+1$, $|E\left(P_{m,n}\right)|=2mn$, then by (1) $tes\left(P_{m,n}\right)\ge \frac{2mn+2}{3}.$

To prove the inverse of previous inequality, it is necessary to show that there exists an edge irregular total $r$-labelling for $P_{m,n}$ with $r=\frac{2mn+2}{3}$ as follows:

Let $r=\frac{2mn+2}{3}$ and a total $r$-labelling $\eta :V\cup E\to \left\{1,2,3,\dots ,r\right\}$ is defined as: $\eta \left(v_0\right)=1,$ $\eta \left(v_i\right)=\left\{\begin{array}{ll}i& \text{for}1\le i\le \frac{2mn+2}{3}\\ r& \text{for}\frac{2mn+2}{3}+1\le i\le mn\end{array}\right.,$ $\eta \left(v_0{v}_i\right)=i\text{for}1\le i\le n,$ $\eta \left(v_{i-n}{v}_i\right)=\left\{\begin{array}{ll}n+1& \text{for}n+1\le i\le \frac{2mn+2}{3}\\ i-r+n+1& \begin{array}{l}\text{for}\frac{2mn+2}{3}+1\\ \le i\le \frac{2mn+2}{3}+n-1\end{array}\\ 2\left(i-r\right)+1& \begin{array}{l}\text{for}\frac{2mn+2}{3}\\ +n\le i\le mn\end{array}\end{array}\right.,$ $\eta \left(v_i{v}_{i+1}\right)=\left\{\begin{array}{ll}1& \begin{array}{l}\text{for}1\le i\le \frac{2mn+2}{3}-1,\\ i\notin \left\{n,2n,3n,\dots ,k\right\},\\ k=Pn,P\in Z^{+}\end{array}\\ 2\left(i-r+1\right)& \begin{array}{l}\text{for}\frac{2mn+2}{3}\le i\le mn,\\ i\ne k+sn,s\in \left\{1,2,\dots ,l\right\},\\ k+ln=mn\end{array}\end{array}\right.$ $\eta \left(v_i{v}_{i-n+1}\right)=\left\{\begin{array}{ll}n+1& \text{for}i\in \left\{n,2n,\dots .,k\right\},k<r-1\\ s\frac{mn}{3}& \begin{array}{l}\text{for}i=k+sn,s\in \left\{1,2,\dots ,l\right\},\\ k+ln=mn\end{array}\end{array}\right..$

Obviously, the greatest label is $r=\frac{2mn+2}{3}$. The weights of the edges of $P_{m,n}$ expressed as: $w_{\eta }\left(v_0{v}_i\right)=2i+1\text{for}1\le i\le n,$ $w_{\eta }\left(v_{i-n}{v}_i\right)=2i+1\text{for}n+1\le i\le mn,$ $w_{\eta }\left(v_i{v}_{i-n+1}\right)=\left\{\begin{array}{ll}2i+2& \begin{array}{l}\text{for}i\in \left\{n,2n,\dots .,k\right\}\\ k=Pn,P\in Z^{+},\\ k<r-1\end{array}\\ 2r+s\frac{mn}{3}& \begin{array}{l}\text{for}i=k+sn,\\ s\in \left\{1,2,\dots ,l\right\},\\ k+ln=mn\end{array}\end{array}\right..$

Upon checking, it was found that the weights of any two different edges are different. Hence $\eta$ is an edge irregular total $r$-labelling for being $r=\frac{2mn+2}{3}$, i.e. $tes\left(P_{m,n}\right)\ge \frac{2mn+2}{3}.$

3. Conclusion

In this paper, we have determined the total edge irregularity strength for a polar grid graph $P_{3,n},n\ge 3$, and a polar grid graph $P_{m,3},m\ge 3$. Finally, the exact value of total edge irregularity strength for a generalized polar grid graph $P_{m,n}$ was determined.

Acknowledgements

The author expresses his sincere thanks to the reviewers for valuable comments and suggestions, which helped to improve the quality of the paper.

Disclosure statement

No potential conflict of interest was reported by the author.

ORCID

F. Salama http://orcid.org/0000-0002-3555-7349