On the fractional-order model of HIV-1 infection of CD4⁺ T-cells under the influence of antiviral drug treatment

ABSTRACT

In this article, the fractional-order model, namely HIV-1 infection of CD4⁺ T-cells combined with the effect of antiviral drug treatment, is investigated. The model includes three unknown factors, (i) the uninfected CD4⁺ T-cells, (ii) the infected CD4⁺ T-cells, and (iii) the density of virions in the plasma. The most effective techniques such as the variation-of-parameters method, the variational iteration method, the homotopy perturbation method and the adomian decomposition method are implemented to tackle the mathematical models of Caputo’s fractional derivative. Graphical illustration and numerical results are presented to show the validity and accuracy of the obtained results. It is found that the fractional-order model can be easily solved by means of analytical approaches with less computational cost and the HPM technique is slightly better than others. It is also perceived that the fractional-order approximate solutions can get closer to classical approximate solutions when $\delta \to 1$.

KEYWORDS:

• Fractional-order HIV-1 infection model
• Caputo’s fractional derivative
• analytical and numerical results

1. Introduction

Fractional calculus is a generalized interpretation of the classical one. A salient feature of the fractional-order derivative is its description of memory and the hereditary properties of various materials [1]. The study of fractional-order partial differential equations (PDEs) and ordinary differential equations (ODEs) is widely available in the literature due to their enormous applications in areas such as applied mathematics, physics, electrical circuit theory, viscoelasticity, biomedical sciences, and control theory [2–6].

Acquired immunodeficiency syndrome (AIDS) is caused by human immunodeficiency virus (HIV). HIV attacks several cells especially affecting the CD4⁺ T-cells which play a vital role in the immune system of our body. Several mathematical models are at hand in the literature to better perceive the interplay between HIV and the immune system of human being, associated with therapeutic strategies [7–10]. Bonhoeffer et al. [11] introduced the following model: (1) $\begin{array}{rl}\frac{\text{d}x}{\text{d}t}& =a-\text{β}x-\gamma xy,\\ \frac{\text{d}y}{\text{d}t}& =\gamma xy-by\end{array}$(1) in which $x$ and $y$ are the densities of infected cells and virus-creating cells, respectively, whereas $a$, $\text{β}$,$\gamma$ and $b$ describe the rate of creation of infected cells, the natural death rate of infected cells, the infection rate of uninfected cells and the death rate of virus-creating cells, respectively.

The model (1) is extended by Tuckwell and Wan [12], related to HIV-1 infection: (2) $\begin{array}{rl}\frac{\text{d}x}{\text{d}t}& =q^{\mathrm{\prime }}-\sigma x-\text{β}xz,\\ \frac{\text{d}y}{\text{d}t}& =\text{β}xz-\rho y,\\ \frac{\text{d}z}{\text{d}t}& =ay-\gamma z,\end{array}$(2) subject to the initial conditions (3) $x\left(0\right)=l_1,y\left(0\right)=l_2,z\left(0\right)=l_3.$(3) Here, $x$, $y$ and $z$ show uninfected CD4⁺ T-cells, infected CD4⁺ T-cells and the density of virions (virus in its infective form) contained in the plasma, respectively. Here, $q^{\mathrm{\prime }}$, $\sigma$, $\text{β}$, $\rho$, $a$ and $\gamma$ are constant coefficients interpreting the production rate of CD4⁺ T-cells, natural death rate, rate of infected CD4⁺ cells from uninfected CD4⁺ cells, the death rate of virus-producing cells, the production rate of virions viruses by the infected cells, and, the death rate of virus particles, respectively. When the drug therapy is initiated, it affects the virus-producing cells. If the drug therapeutic effect is less, a portion of infected cells will be improved, while the rest of the infected cells will resume virus production [13]. Several works have been carried out to investigate the fractional-order models of HIV [14,15]. For the similar studies, a few more techniques, such as the predictor corrector method [16], the fractional approximation method involving non-singular kernel [17], the generalized Euler method [18] and the collocation method based on Muntz-Legendre polynomials [19], Elzaki projected the differential transform method [20], the variation-of-parameters method (VPM) [21–23], the variational iteration method (VIM) [24–26], the homotopy perturbation method (HPM) [27–35] and the adomian decomposition method (ADM) [36–40] have been successively employed to solve these types of models. The most relevant techniques that might be useful to handle the said model can be seen in [41–50].

In this work, the main emphasis is given to explore the best approach to find approximate numerical results to solve the following the fractional-order model of HIV-1 infection of CD4⁺ T-cells incorporating the influence of drug therapy [51]: (4) $\begin{array}{rl}{D}_t^{\delta }\left(x\right)& =q^{\mathrm{\prime }}-\sigma x-\text{β}xz,\\ D_t^{\delta }\left(y\right)& =\text{β}xz-\rho y,0<\delta <1,\\ D_t^{\delta }\left(z\right)& =ay-\gamma z.\end{array}$(4) Here, $D_t^{\delta }(.)$ signifies Caputo’s form of a fractional derivative [52]. This particular operator is used to cope with the fractional-order sense of the model (4).

2. Preliminaries

2.1 Gamma function

The generalization of the factorial function is defined as follows. (5) $\mathrm{\Gamma }\left(z\right)={\int }_0^{\mathrm{\infty }}{e}^{-t}{t}^{z-1}\text{d}t,\mathrm{\Re }\left(z\right)>0.$(5)

The operator is defined as (6) $\begin{array}{rl}{D}_t^{\delta }f& =\frac{1}{\mathrm{\Gamma }\left(n-\delta \right)}{\int }_0^t{\left(t-p\right)}^{n-\delta -1}{f}^n\left(p\right)dp,\\ & n-1<\delta \le n,n\in N,t>0,\end{array}$(6)

2.2 Mittag–Leffler function

The generalized exponential function, known as the Mittag–Leffler function, is defined as (7) $E_{\delta }\left(z\right)=\sum _{k=0}^{\mathrm{\infty }}\frac{z^k}{\mathrm{\Gamma }\left(k\delta +1\right)},\delta >0,\delta \in R,z\in C.$(7)

2.3 Reimann–Liouville fractional integral

The Reimann–Liouville fractional integral is defined as (8) $J^{\delta }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\delta \right)}{\int }_0^t{\left(t-p\right)}^{\delta -1}f\left(p\right)dp,\delta >0,t>0,$(8) where $f\left(t\right)\in C_{\mu },\mu \ge 1$ and $\mathrm{\Gamma }\left(\delta \right)$ signify the Gamma function.

2.4 Caputo’s fractional differential operator

The operator is defined as (9) $\begin{array}{rl}{D}_t^{\delta }f& =\frac{1}{\mathrm{\Gamma }\left(n-\delta \right)}{\int }_0^t{\left(t-p\right)}^{n-\delta -1}{f}^n\left(p\right)dp,\\ & n-1<\delta \le n,n\in N,t>0,\end{array}$(9) where $\alpha >0,t>a,$ and $\alpha ,a,t\in R,$ is known as the Caputo’s fractional differential operator.

3. Methodologies

3.1. Variation-of-parameters method

The VPM yields iterative results which quickly approach the exact solution, if such a solution is available. Discretization, linearization, calculation of adomian’s polynomials, etc., are not required in the VPM for solving a non-linear problem. The VPM furnishes significant numerical results in the case of non-existence of the exact solution. By using the VPM, the following iterative scheme is formulated for the following model (4): (10) $\begin{array}{rl}{x}_{n+1}\left(t\right)& =l_1+J^{\delta }\lambda (t,s)[q^{\mathrm{\prime }}-\sigma x_n-\text{β}{x}_n{z}_n],\\ y_{n+1}\left(t\right)& =l_2+J^{\delta }\lambda (t,s)[\text{β}{x}_n{z}_n-\rho y_n],\\ z_{n+1}\left(t\right)& =l_3+J^{\delta }\lambda (t,s)[\alpha y_n-\gamma z_n].\end{array}$(10) $J^{\delta }$ and $l_1,l_2,l_3$ are fractional integral and initial guesses (given in Equation (3)), respectively. Furthermore, $\lambda$ being a multiplier avoids successive implementation of integrals, whose value can be known by the Wronskian’s technique and presently we have $\lambda =1$. We finally get approximate solutions: $x\left(t\right)$, $y\left(t\right)$, and $z\left(t\right)$ in iterative forms by using Equation (10).

3.2. Variational iteration method

Iterations by the VIM quickly converge to the exact solution. This method does not require linearization, discretization and the calculation of adomian polynomials, etc., for solving a non-linear problem. We can freely select an initial guess in this method. The VIM gives promising numerical results, when no exact solution exists. By using the VIM, the following correction functional is formulated for model (4): (11) $\begin{array}{rl}{x}_{n+1}\left(t\right)& =x_n+J^{\delta }\lambda (t,s)\left[D_t^{\delta }\right(x_n)-q^{\mathrm{\prime }}+\sigma x_n+\text{β}{x}_n{z}_n],\\ y_{n+1}\left(t\right)& =y_n+J^{\delta }\lambda (t,s)\left[D_t^{\delta }\right(y_n)-\text{β}{x}_n{z}_n+\rho y_n],\\ z_{n+1}\left(t\right)& =z_n+J^{\delta }\lambda (t,s)\left[D_t^{\delta }\right(z_n)-\sigma y_n+\gamma z_n].\end{array}$(11) subject to conditions given in Equation (3), where $J^{\delta }$, $\lambda$, are fractional integral and Lagrange’s multiplier, respectively. The $\lambda$ avoids successive integrals and could be acquired by the variational theory, $y_0$ is an initial approximation and for $\delta =1$, $\lambda \left(t,s\right)=-1$. The VIM will finally yield iterations for approximate solutions of Equation (4) by using Equation (3).

3.3. Adomian decomposition method

ADM does not require perturbation, linearization and transformation. One of the main features is its rapid convergence towards the solution. This method considers the solutions for $x\left(t\right)$, $y\left(t\right)$, and $z\left(t\right)$ as the following series (12) $x\left(t\right)=\sum _{n=0}^{\mathrm{\infty }}{x}_n,y\left(t\right)=\sum _{n=0}^{\mathrm{\infty }}{y}_n,$(12) and (13) $z\left(t\right)=\sum _{n=0}^{\mathrm{\infty }}{z}_n.$(13) The non-linear term in Equation (4) is expressed as (14) $xz=\sum _{n=0}^{\mathrm{\infty }}{A}_n,$(14) where $A_n$ are adomian polynomials.

Using ADM, containing fractional integral $J^{\delta },$ the following scheme is formed (15) $\begin{array}{rl}{x}_0& =l_1,\\ x_{n+1}\left(t\right)& =J^{\delta }\left[-\sigma x_n-\text{β}{A}_n\right],\end{array}$(15) (16) $\begin{array}{rl}{y}_0& =l_2,\\ y_{n+1}\left(t\right)& =J^{\delta }\left[\text{β}{A}_n-\rho y_n\right],\end{array}$(16) (17) $\begin{array}{rl}{z}_0& =l_3,\\ z_{n+1}\left(t\right)& =J^{\delta }\left[a{y}_n-\gamma z_n\right].\end{array}$(17)

By obtaining the desired number of iterations and substituting them in Equation (12), we obtain approximate solutions: $x\left(t\right)$, $y\left(t\right)$, and $z\left(t\right)$.

3.4. Homotopy perturbation method

The HPM does not require transformation, linearization and discretization. The method contains traditional perturbation method and homotopy (in topology). Using the HPM, the following homotopy is constructed: (18) $\begin{array}{rl}& (1-s)\left(\frac{{\mathrm{\partial }}^{\delta }x}{\mathrm{\partial }{t}^{\delta }}-\frac{\mathrm{\partial }{x}_0}{\mathrm{\partial }t}\right)\\ & +s\left(\frac{{\mathrm{\partial }}^{\delta }x}{\mathrm{\partial }{t}^{\delta }}-q^{\mathrm{\prime }}+\sigma x+\text{β}{x}_n{z}_n\right)=0,\end{array}$(18) where $s\in \left[0,1\right]$ is known as an embedding parameter. From Equation (14), we have (19) $\left(\frac{{\mathrm{\partial }}^{\delta }x}{\mathrm{\partial }{t}^{\delta }}-\frac{\mathrm{\partial }{x}_0}{\mathrm{\partial }t}\right)=s\left(q^{\mathrm{\prime }}-\sigma x-\text{β}{x}_n{z}_n-\frac{\mathrm{\partial }{x}_0}{\mathrm{\partial }t}\right)=0,$(19) We suppose a solution for $x$ (20) $x\left(t\right)=x_0+s^1{x}_1+s^2{x}_2+s^3{x}_3\dots ,$(20) Using Equation (20) in Equation (19) and collecting the same powers of $s$, we obtain (21) $\begin{array}{rl}{s}^0:\left(\frac{{\mathrm{\partial }}^{\delta }x}{\mathrm{\partial }{t}^{\delta }}-\frac{\mathrm{\partial }{x}_0}{\mathrm{\partial }t}\right)& =0,\end{array}$(21) (22) $\begin{array}{rl}{s}^1:\left(\frac{{\mathrm{\partial }}^{\delta }{x}_1}{\mathrm{\partial }{t}^{\delta }}\right)& =q^{\mathrm{\prime }}-\sigma x_0-\text{β}{x}_0{z}_0-\frac{\mathrm{\partial }{x}_0}{\mathrm{\partial }t},\end{array}$(22) (23) $\begin{array}{rl}{s}^2:\left(\frac{{\mathrm{\partial }}^{\delta }{x}_2}{\mathrm{\partial }{t}^{\delta }}\right)& =-\sigma x_1-\text{β}{x}_0{z}_1-\text{β}{x}_1{z}_0,\end{array}$(23) (24) $\begin{array}{rl}{s}^3:\left(\frac{{\mathrm{\partial }}^{\delta }{x}_3}{\mathrm{\partial }{t}^{\delta }}\right)& =-\sigma x_2-\text{β}{x}_2{z}_0-\text{β}{x}_1{z}_1-\text{β}{x}_0{z}_2,\end{array}$(24)

and so on.

Similarly, the solution for $y$ is supposed as (25) $y\left(t\right)=y_0+s^1{y}_1+s^2{y}_2+s^3{y}_3\dots ,$(25) which leads to (26) $\begin{array}{rl}{s}^0:\left(\frac{{\mathrm{\partial }}^{\delta }y}{\mathrm{\partial }{t}^{\delta }}-\frac{\mathrm{\partial }{y}_0}{\mathrm{\partial }t}\right)& =0,\end{array}$(26) (27) $\begin{array}{rl}{s}^1:\left(\frac{{\mathrm{\partial }}^{\delta }{y}_1}{\mathrm{\partial }{t}^{\delta }}\right)& =\text{β}{x}_0{z}_0-\rho y_0-\frac{\mathrm{\partial }{y}_0}{\mathrm{\partial }t},\end{array}$(27) (28) $\begin{array}{rl}{s}^2:\left(\frac{{\mathrm{\partial }}^{\delta }{y}_2}{\mathrm{\partial }{t}^{\delta }}\right)& =\text{β}{x}_0{z}_1-\text{β}{x}_1{z}_0-\rho y_1,\end{array}$(28) (29) $\begin{array}{rl}{s}^3:\left(\frac{{\mathrm{\partial }}^{\delta }{y}_3}{\mathrm{\partial }{t}^{\delta }}\right)& =\text{β}{x}_0{z}_2+\text{β}{x}_1{z}_1+\text{β}{x}_2{z}_0-\rho y_2,\end{array}$(29)

and so on.

With the same contrast, the solution for $z$ is supposed as (30) $z\left(t\right)=z_0+s^1{z}_1+s^2{z}_2+s^3{z}_3\dots ,$(30) and this leads to (31) $\begin{array}{rl}{s}^0:\left(\frac{{\mathrm{\partial }}^{\delta }z}{\mathrm{\partial }{t}^{\delta }}-\frac{\mathrm{\partial }{z}_0}{\mathrm{\partial }t}\right)& =0,\end{array}$(31) (32) $\begin{array}{rl}{s}^1:\left(\frac{{\mathrm{\partial }}^{\delta }{z}_1}{\mathrm{\partial }{t}^{\delta }}\right)& =a{y}_0-2z_0-\frac{\mathrm{\partial }{z}_0}{\mathrm{\partial }t},\end{array}$(32) (33) $\begin{array}{rl}{s}^2:\left(\frac{{\mathrm{\partial }}^{\delta }{z}_2}{\mathrm{\partial }{t}^{\delta }}\right)& =a{y}_1-2z_1,\end{array}$(33) (34) $\begin{array}{rl}{s}^3:\left(\frac{{\mathrm{\partial }}^{\delta }{z}_3}{\mathrm{\partial }{t}^{\delta }}\right)& =a{y}_2-2z_2,\end{array}$(34)

and so forth

By setting $s=1$ in Equations (20), (25) and (30), we obtain (35) $\begin{array}{rl}x\left(t\right)& =x_0+x_1+x_2+x_3\dots ,\\ y\left(t\right)& =y_0+y+y_2+y_3\dots ,\\ z\left(t\right)& =z_0+z_1+z_2+z_3\dots ,\end{array}$(35) Using Equations (22), (27) and (32) in Equation (35), we finally come up with approximate solutions$x\left(t\right)$, $y\left(t\right)$, and $z\left(t\right)$.

4. Results and discussion for the fractional-order HIV model (4)

We have numerically figured out three terms $l_1=100,l_2=0,l_3=1$ of the infinite series for $x$, $y$ and $z$ by using ADM and HPM, whereas the fourth-order approximations are attained by using VPM and VIM. However, the number of terms and order of approximations can further be extended for the desired accuracy. Numerical values of parameters [53] for model (4) are $q^{\mathrm{\prime }}=0.272\left(\text{day}/\text{m}{\text{m}}^3\right)$, $\sigma =0.00136\left(day/m{m}^3\right)$, $\text{β}=0.00027\left(day/virion/m{m}^3\right)$, $\rho =0.33\left(day/m{m}^3\right),$ $a=50$ $\gamma =2.0\left(\text{day}\right)$, and the initial conditions are (36) $l_1=100,l_2=0,l_3=1$(36)

4.1. Variation-of-parameters method

We use the VPM to solve model (4) along with the initial conditions (36) for finding approximate solutions:

(37) $\begin{array}{rl}x\left(t\right)& \approx 100+\frac{\text{0}\text{.10900 }{t}^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }+\frac{\text{0}\text{.09539759608}{t}^{2\delta }}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }(\delta +0.5)}-\frac{0.5236883859{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.3333333\right)\mathrm{\Gamma }\left(\delta +0.6666666\right)}\\ & +\frac{0.0001204660201{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.3333333\right)\mathrm{\Gamma }\left(\delta +0.6666666\right)}\\ & -\frac{0.0007176426450{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta +0.3333333\right)\mathrm{\Gamma }\left(\delta +0.6666666\right){\left(t^{\delta }\right)}^4}{{\left(2^{\delta }\right)}^{10}{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2{\left(\mathrm{\Gamma }\left(\delta +0.5\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}\\ & -\frac{0.0000004262581863{\left(2^{\delta }\right)}^2{\left(t^{\delta }\right)}^4}{{\left(4^{\delta }\right)}^4{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}\\ & +\frac{0.0005476017674{\left(4^{\delta }\right)}^4\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right){\left(t^{\delta }\right)}^5}{{\left(5^{\delta }\right)}^5{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right){\left(2^{\delta }\right)}^4\mathrm{\Gamma }\left(\delta +0.5\right)}\\ & +\frac{0.0000001458455726{\left(2^{\delta }\right)}^{10}{\left(\mathrm{\Gamma }\left(\delta +0.5\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right){\left(t^{\delta }\right)}^5}{{\left(3^{\delta }\right)}^3{\left(5^{\delta }\right)}^5{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^3{\delta }^3\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right)\mathrm{\Gamma }\left(\delta +0.3333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}\\ & -\frac{0.0000007057588881{\left(5^{\delta }\right)}^5\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right){\left(t^{\delta }\right)}^6}{{\left(6^{\delta }\right)}^6{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^3{\delta }^3\mathrm{\Gamma }\left(\delta +0.1666\right){\left(\mathrm{\Gamma }\left(\delta +0.333\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(\mathrm{\Gamma }\left(\delta +0.666666\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.8333\right){\left(3^{\delta }\right)}^3}.\end{array}$(37) (38) $\begin{array}{rl}y\left(t\right)& \approx \frac{0.02700t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }-\frac{0.1114529084{\left(t^{\delta }\right)}^2}{\mathrm{\Gamma }\left(\delta \right)\delta {\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right)}+\frac{0.5992287273{\left(t^{\delta }\right)}^3}{\mathrm{\Gamma }\left(\delta \right)\delta {\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}\\ & -\frac{0.0001204660201{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(t^{\delta }\right)}^3}{{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}+\frac{0.0001204660201{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(t^{\delta }\right)}^3}{{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta +0.3333333\right)\mathrm{\Gamma }\left(\delta +0.6666666\right)}\\ & +\frac{0.0007176426450{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right){\left(t^{\delta }\right)}^4}{{\left(4^{\delta }\right)}^4{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2{\left(2^{\delta }\right)}^2{\left(\mathrm{\Gamma }\left(\delta +0.5\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}\\ & -\frac{0.0007176426450{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta +0.3333333\right)\mathrm{\Gamma }\left(\delta +0.6666666\right){\left(t^{\delta }\right)}^4}{{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2{\left(2^{\delta }\right)}^2{\left(\mathrm{\Gamma }\left(\delta +0.5\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}\\ & +\frac{0.00008636827680{\left(2^{\delta }\right)}^2{\left(t^{\delta }\right)}^4}{{\left(4^{\delta }\right)}^4{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}\\ & +\frac{0.0005476017674{\left(t^{\delta }\right)}^5{\left(4^{\delta }\right)}^4\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}{{\delta }^2{\left(5^{\delta }\right)}^5{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right){\left(2^{\delta }\right)}^4\mathrm{\Gamma }\left(\delta +0.5\right)}\\ & -\frac{0.0000001458455726{\left(2^{\delta }\right)}^2{\left(\mathrm{\Gamma }\left(\delta +0.5\right)\right)}^2{\left(t^{\delta }\right)}^5{\left(4^{\delta }\right)}^4\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}{{\left(3^{\delta }\right)}^3{\left(5^{\delta }\right)}^5{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^3{\delta }^3\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right)\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}\\ & +\frac{0.0000007057588881{\left(5^{\delta }\right)}^5\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right){\left(t^{\delta }\right)}^6}{{\left(3\right)}^{9\delta }{\left(2\right)}^{6\delta }{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^3{\delta }^3\mathrm{\Gamma }\left(\delta +0.166666\right){\left(\mathrm{\Gamma }\left(\delta +0.333333\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(\mathrm{\Gamma }\left(\delta +0.666666\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.833333\right)}.\end{array}$(38) (39) $\begin{array}{rl}z\left(t\right)& \approx 1-2\frac{t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }+\frac{9.482628103{\left(t^{\delta }\right)}^2}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.5\right)}-\frac{50.22058020{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.3333333333\right)\mathrm{\Gamma }\left(\delta +0.6666666\right)}\\ & -\frac{0.01307540449{\left(2^{\delta }\right)}^2{\left(t^{\delta }\right)}^4}{{\left(4^{\delta }\right)}^4{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.2500000000\right)\mathrm{\Gamma }\left(\delta +0.7500000000\right)}.\end{array}$(39)

4.2. Variational iteration method

We use the VIM to solve model (4) along with the initial conditions (36) for finding approximate solutions:

(40) $\begin{array}{rl}x\left(t\right)& \approx 100+\frac{\text{0}\text{.10900}{t}^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }+\frac{\text{0}\text{.09539759608}{\left(t^{\delta }\right)}^2}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }(\delta +0.5)}+\frac{\text{0}\text{.0001204660201}{\left(2^{\delta }\right)}^2\mathrm{\Gamma }(\delta +0.5){\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3{\left(\mathrm{\Gamma }\right(\delta \left)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +\text{0}\text{.333333}\right)\mathrm{\Gamma }(\delta +\text{0}\text{.666666})}\\ & -\frac{0.5243248872{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}-\frac{0.0000004262581863{\left(t^{\delta }\right)}^4}{{\left(2^{\delta }\right)}^6{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}\\ & -\frac{0.0004939860275{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right){\left(t^{\delta }\right)}^4}{{\left(2^{\delta }\right)}^{10}{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2{\left(\mathrm{\Gamma }\left(\delta +0.5\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}\\ & -\frac{0.0005476017674{\left(2^{\delta }\right)}^4\mathrm{\Gamma }\left(\delta +0.250\right)\mathrm{\Gamma }\left(\delta +0.750\right){\left(t^{\delta }\right)}^5}{{\left(5^{\delta }\right)}^5{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.5\right)\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right)}\\ & +\frac{0.00000014584{\left(2^{\delta }\right)}^{10}{\left(\mathrm{\Gamma }\left(\delta +0.5\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right){\left(t^{\delta }\right)}^5}{{\left(3^{\delta }\right)}^3{\left(5^{\delta }\right)}^5{\delta }^3{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^3\mathrm{\Gamma }\left(\delta +0.3333\right)\mathrm{\Gamma }\left(\delta +0.66666\right)\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right)}\\ & -\frac{0.00000070575888{\left(5^{\delta }\right)}^5\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right){\left(t^{\delta }\right)}^6}{{\left(2^{\delta }\right)}^6{\left(3^{\delta }\right)}^9{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^3{\delta }^3{\left(\mathrm{\Gamma }\left(\delta +0.333\right)\right)}^2{\left(\mathrm{\Gamma }\left(\delta +0.666\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.1666666\right)\mathrm{\Gamma }\left(\delta +0.5\right)\mathrm{\Gamma }\left(\delta +0.833333\right)}.\end{array}$(40) (41) $\begin{array}{rl}y\left(t\right)& \approx \frac{0.02700t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }-\frac{0.1114529084{\left(t^{\delta }\right)}^2}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.5\right)}-\frac{0.0001204660201{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}\\ & +\frac{0.5993341599{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}+\frac{0.00049398602{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta +0.3333\right)\mathrm{\Gamma }\left(\delta +0.6666\right){\left(t^{\delta }\right)}^4}{{\left(2^{\delta }\right)}^{10}{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2{\left(\mathrm{\Gamma }\left(\delta +0.5\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right)}\\ & -\frac{0.0000001458455726{\left(2^{\delta }\right)}^{10}{\left(\mathrm{\Gamma }\left(\delta +0.5\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.25\right)\mathrm{\Gamma }\left(\delta +0.75\right){\left(t^{\alpha }\right)}^5}{{\left(3^{\delta }\right)}^3{\left(5^{\delta }\right)}^5{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^3{\delta }^3\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right)}\\ & +\frac{0.0000007057588881{\left(5^{\delta }\right)}^5\mathrm{\Gamma }\left(\delta +0.2\right)\mathrm{\Gamma }\left(\delta +0.4\right)\mathrm{\Gamma }\left(\delta +0.6\right)\mathrm{\Gamma }\left(\delta +0.8\right){\left(t^{\delta }\right)}^6}{{\left(3^{\delta }\right)}^9{\left(2^{\delta }\right)}^6{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^3{\delta }^3{\left(\mathrm{\Gamma }\left(\delta +0.333333\right)\right)}^2{\left(\mathrm{\Gamma }\left(\delta +0.666666\right)\right)}^2\mathrm{\Gamma }\left(\delta +0.166666\right)\mathrm{\Gamma }\left(\delta +0.5\right)\mathrm{\Gamma }\left(\delta +0.833333\right)}\end{array}$(41) (42) $\begin{array}{rl}z\left(t\right)& \approx 1-\frac{2t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }+\frac{9.482628103{\left(t^{\delta }\right)}^2}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.5\right)}-\frac{50.22058020{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}\end{array}$(42)

4.3. Adomian decomposition method

We use the ADM to solve model (4) along with the initial conditions (36) for finding the following approximate solutions:

(43) $\begin{array}{rl}x\left(t\right)& \approx 100+\frac{0.10900t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }+\frac{0.544t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }-\frac{0.09618343122{\left(t^{\delta }\right)}^2}{\mathrm{\Gamma }\left(\delta \right)\delta {\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right)}-\frac{0.5236883860{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}\\ & +\frac{0.0001204660201{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(t^{\delta }\right)}^3}{{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.66666\right)}\end{array}$(43) (44) $\begin{array}{rl}y\left(t\right)& \approx \frac{0.02700t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }-\frac{0.1113227394{\left(t^{\delta }\right)}^2}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.5\right)}+\frac{0.5992287274{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}\\ & -\frac{0.0001204660201{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}.\end{array}$(44) (45) $\begin{array}{rl}z\left(t\right)& \approx 1-2\frac{t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }+\frac{9.482628103{\left(t^{\delta }\right)}^2}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.5\right)}-\frac{50.22058020{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}.\end{array}$(45)

4.4. Homotopy perturbation method

Now we use the HPM to solve model (4) along with the initial conditions (36) for finding the approximate solutions:

(46) $\begin{array}{rl}x\left(t\right)& \approx 100+\frac{\text{0}\text{.10900}{t}^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }+\frac{\text{0}\text{.09023342771}{\left(t^{\delta }\right)}^2}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }(\delta +0.5)}-\frac{\text{0}\text{.5243076594}{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }(\delta +\text{0}\text{.3333})\mathrm{\Gamma }(\delta +\text{0}\text{.66666})}\\ & +\frac{0.0001204660201{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}.\end{array}$(46) (47) $\begin{array}{rl}y\left(t\right)& \approx \frac{0.02700t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }-\frac{0.1114529084{\left(t^{\delta }\right)}^2}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.5\right)}+\frac{0.5993313064{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}\\ & -\frac{0.0001204660201{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta +0.5\right){\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3{\left(\mathrm{\Gamma }\left(\delta \right)\right)}^2{\delta }^2\mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}.\end{array}$(47) (48) $\begin{array}{rl}z\left(t\right)& \approx 1-2\frac{t^{\delta }}{\mathrm{\Gamma }\left(\delta \right)\delta }+\frac{9.482628103{\left(t^{\delta }\right)}^2}{{\left(2^{\delta }\right)}^2\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.5\right)}-\frac{50.22058020{\left(t^{\delta }\right)}^3}{{\left(3^{\delta }\right)}^3\mathrm{\Gamma }\left(\delta \right)\delta \mathrm{\Gamma }\left(\delta +0.333333\right)\mathrm{\Gamma }\left(\delta +0.666666\right)}.\end{array}$(48)

4.5. Validation

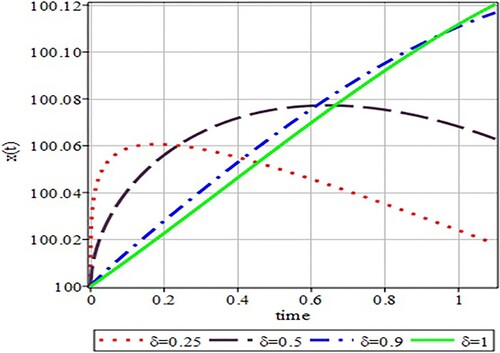
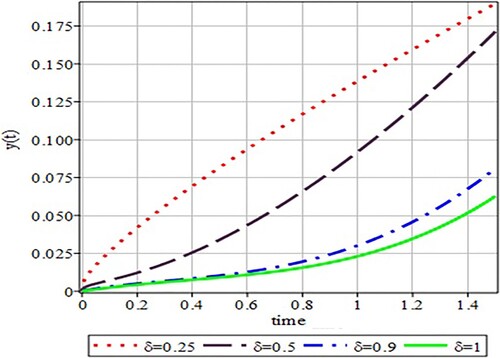
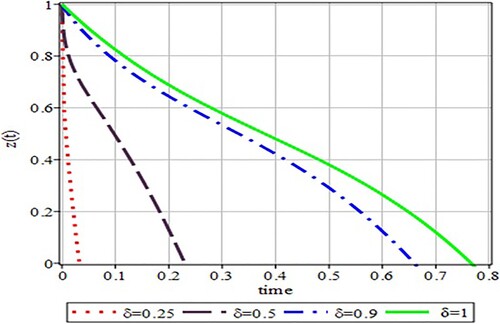
This section is devoted to see the accuracy of results obtained by the VPM, VIM, HPM and ADM. Tables 1Table 2.–3 represent numerical results for different fractional orders. These results show the dynamism of the approximate analytical methods. One can observe that the HPM technique is slightly better than the rest of approaches that is why for illustration, only the analytical results obtained by using the HPM have been chosen. Figures 1Figure 2.–3 have been plotted by considering $\delta =0.25,0.5,0.9,$ and $\delta =1$, respectively. It is observed that the fractional-order approximate solutions can be seen to get closer towards the classical approximate solution when $\delta \to 1$.

Figure 1. Behaviour of $x\left(t\right)$ for different values of $\delta$, showing uninfected CD4⁺ T-cells’ dynamics.

Figure 2. Behaviour of $y\left(t\right)$ for different values of $\delta$, showing infected CD4⁺ T-cells’ dynamics.

Figure 3. Behaviour of $z\left(t\right)$ for different values of $\delta$, showing dynamics of virions’ density.

Table 1. Absolute errors for $x\left(t\right).$

t	$\delta$	$\text{VPM}$	$\text{VIM}$	$\text{HPM}$	$\text{ADM}$
0.02	0.25	8.8202E − 03	8.3675E − 03	8.3599E − 03	1.0443E − 01
	0.90	5.5299E − 05	9.0066E − 07	8.9583E − 07	8.3631E − 03
	1.00	2.1400E − 05	2.0000E − 07	2.0000E − 07	5.4397E − 03
0.06	0.25	1.0700E − 02	1.9077E − 02	1.9057E − 02	1.2936E − 01
	0.90	3.8839E − 04	1.7413E − 05	1.7396E − 05	2.2463E − 02
	1.00	1.8860E − 04	5.2000E − 06	5.2000E − 06	1.6314E − 02
0.10	0.25	1.0461E − 02	2.7986E − 02	2.7953E − 02	1.4067E − 01
	0.90	9.4855E − 04	6.9151E − 05	6.9094E − 05	3.5531E − 02
	1.00	5.1420E − 04	2.4100E − 05	2.4100E − 05	2.7174E − 02

Table 2. Absolute errors for $y\left(t\right)$.

t	$\delta$	$\text{VPM}$	$\text{VIM}$	$\text{HPM}$	$\text{ADM}$
0.02	0.25	9.5628E − 03	9.5644E − 03	9.5567E − 03	9.5668E − 03
	0.90	1.0246E − 06	1.0248E − 06	1.0241E − 06	1.0622E − 06
	1.00	2.2025E − 07	2.2029E − 07	2.2013E − 07	2.3478E − 07
0.06	0.25	2.1801E − 02	2.1806E − 02	2.1785E − 02	2.1801E − 02
	0.90	1.9898E − 05	1.9901E − 05	1.9887E − 05	2.0161E − 05
	1.00	5.9470E − 06	5.9480E − 06	5.9435E − 06	6.0747E − 06
0.10	0.25	3.1980E − 02	3.1989E − 02	3.1955E − 02	3.1976E − 02
	0.90	7.9035E − 05	7.9047E − 05	7.8988E − 05	7.9669E − 05
	1.00	2.7533E − 05	2.7538E − 05	2.7516E − 05	2.7879E − 05

Table 3. Absolute errors for $z\left(t\right)$.

t	$\delta$	$\text{VPM}$	$\text{VIM}$	$\text{HPM}$	$\text{ADM}$
0.02	0.25	8.0117E − 01	8.0117E − 01	8.0111E − 01	8.0111E − 01
	0.90	8.5870E − 05	8.5870E − 05	8.5870E − 05	8.5870E − 05
	1.00	1.8459E − 05	1.8459E − 05	1.8459E − 05	1.8459E − 05
0.06	0.25	1.8263E + 00	1.8263E + 00	1.8261E + 00	1.8261E + 00
	0.90	1.6675E − 03	1.6675E − 03	1.6675E − 03	1.6675E − 03
	1.00	4.9839E − 04	4.9839E − 04	4.9838E − 04	4.9838E − 04
0.10	0.25	2.6790E + 00	2.6790E + 00	2.6787E + 00	2.6787E + 00
	0.90	6.6232E − 03	6.6232E − 03	6.6231E − 03	6.6231E − 03
	1.00	2.3074E − 03	2.3074E − 03	2.3073E − 03	2.3073E − 03

5. Conclusion

We applied approximate analytical methods such as the VPM, VIM, HPM and ADM to solve the fractional-order model of HIV-1 infection of CD4⁺ T-cells comprising the effect of the anti-viral drug therapy. The proposed work contains the approximate solutions, showing the memory patterns of uninfected CD4⁺ T-cells, infected CD4⁺ T-cells and the density of virions in plasma, which could be helpful in predicting the improvements for the treatment of AIDS. The proposed methods reflect high accuracy for fractional orders: $0.25,0.5,0.9$ and the classical one is $\delta =1$. The overall performance of the employed methods shows their efficacy, simplicity, and the approach is straightforward. These methods can be very promising for a wide class of fractional-order systems of the applied nature.

Disclosure statement

No potential conflict of interest was reported by the authors.