Effects of radiative heat and magnetic field on blood flow in an inclined tapered stenosed porous artery

ABSTRACT

A porous tapered inclined stenosed artery under the influence of magnetic field with radiation was considered. The momentum and energy equations with thin radiation governing the blood flow in the inclined artery were obtained taking the flow to be Newtonian. These equations were simplified under assumptions of mild stenosis, non-dimensionalized and solved using Differential Transform Method (DTM). The DTM were coded on Mathematica software to obtain expressions for velocity, temperature and the volumetric flow rate of the blood. The results presented graphically show that the velocity of the blood flow and the blood temperature decreases as the radiation parameter (N) increases.

KEYWORDS:

• Heat transfer
• magnetic field
• magnetohydrodynamic flow
• stenosis
• inclined porous artery
• differential transform method

Nomenclature

$(r,\theta ,z)$	=	Cylindrical polar coordinate system
$(v_r,v_{\theta },v_z)$	=	Velocity components
$L$	=	Length of the artery under consideration
$\gamma$	=	Angle of inclination of artery
$M$	=	Applied magnetic field
$q_r$	=	Radiation
$\rho$	=	Flow density
$\mu \left(r\right)$	=	Variable viscosity
${\mu }_0$	=	Coefficient of viscosity of plasma
$\nu$	=	Dynamic viscosity
$\alpha$	=	Coefficient of thermal expansion
$k_1$	=	Permeability of the porous medium
$\tau$	=	Wall shear stress
${\tau }_s$	=	Wall shear stress at the maximum height of the stenosis
$h\left(r\right)$	=	Hematocrit
$H$	=	Maximum hematocrit at the midline of the artery
$m$	=	Velocity shape parameter
$H_r$	=	Hematocrit parameter
$d\left(z\right)$	=	Radius of tapered artery in the region of stenosis
$d_0$	=	Radius of the non-tapered artery in the non-stenotic region
$n$	=	Stenosis shape parameter
$b$	=	Length of stenosis
$\xi$	=	Tapering parameter
$\phi$	=	Tapered angle
$\delta$	=	Maximum height of the stenosis at some location $z$
$R_e$	=	Reynolds number
$E_f$	=	Electric filed
$\sigma$	=	Stefan-Boltzmann constant
${\alpha }_v$	=	Radiation absorption coefficient
$T$	=	Local temperature of the blood
$T_0$	=	Temperature of the blood at the stenotic region
$P_r$	=	Prandtl number
$E_c$	=	Eckert number
$G_r$	=	Grashof number
$\mathrm{\Theta }$	=	Temperature parameter
$Z$	=	Porosity parameter
$N$	=	Radiation absorption parameter

1. Introduction

Blood is a suspension of erythrocytes (red blood cells), leukocytes (white blood cells), and platelets in an aqueous electrolyte solution known as plasma. In normal blood, erythrocytes constitute $45\mathrm{\%}$ of the total volume of blood. This volumetric fraction of the erythrocytes defines an important variable called hematocrit.

Stenosis, a constriction in blood vessels, is one of the leading causes of death in many countries of Africa and the world at large. Severe stenosis reduces the blood supply, thereby causing critical flow conditions which results in serious effects called carotid artery blockage, a major contributing factor to strokes [1]. This results from the brain not receiving enough blood as the plague builds up and hardens down the artery. When the brain lacks adequate supply of blood, the cells in it begin to die. This leads to severe disability or death of an individual. Due to these risks, it is important to watch out for the symptoms of a carotid artery blockage, like the Transient Ischemic Attack (TIA) and stroke, so that proper measures can be taken before the condition gets worse.

The study of fluid dynamics has enabled many researchers to examine the mathematical and physical behaviour of fluid flow for use in medicine and other industrial applications.

Under several conditions, the enhanced heat transfer property and thermal conductivity of fluids, such as nanofluids which contain nanoparticles that further enhance the thermal conductivity of the fluid, have been observed by some researchers in the past years. For example, Ellahi [2] studied the effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe. Hassan et al. [3] examined the convective heat transfer flow of nanofluid in a porous medium over wavy surface. Alamri et al. [4], through a novel perspective of Cattaneo–Christov heat flux model, studied the effects of mass transfer on MHD second grade fluid towards stretching cylinder.

In the past decades, many investigators have displayed interest in problems arising from blood flow mechanism and characteristics under different conditions and influence of external factors.

The idea of electromagnetic fields in medical research was first given by Kollin [5] and the possibility that the application of magnetic field to blood would regulate its movement in human system was later studied by Korchevskii and Marochnik [6]. Abdullah et al. [7] and Bose and Banerjee [8] discussed magnetic particle capture for biomagnetic fluid flow in stenosed aortic.

The above mentioned authors observed that the effect of magnetic field is to slow down the speed of blood. But, they did not analyse the magnetic effect on blood flow through an inclined artery. If a magnetic field is applied to an electrically conducting fluid in motion, electric and magnetic fields are induced which interact and a body force known as Lorentz force is produced, and has a propensity to either assist or oppose the fluid motion. Chakraborty et al. [9] analysed the suspension of blood flow through an inclined tube with an axially non-symmetric stenosis.

In the case of stenosis when the cholesterol deposits on the wall of the artery, the artery-clogging blood which clots inside the lumen of the coronary artery is considered as being equivalent to a fictitious porous medium. This case is particularly examined by some researchers. Elnaqeeb et al. established a cu-blood flow model through a catheterized mild stenotic artery with a thrombosis. El-Shahed [10] presented a model for pulsatile blood flow through a stenosed porous artery under the effect of periodic body acceleration. Akbarzadeh [11] presented a numerical simulation of the effect of periodic body acceleration and periodic body pressure gradient on magneto-hydrodynamic (MHD) blood flow through porous artery. All of these published works, however, do not include the analysis of blood flow characteristics through an inclined artery with the applied magnetic field, which was presented by Srivastava [1].

Blood viscosity, although constant in real physiological system, it may vary in ratio of hematocrit or depend on temperature and pressure [12]. Bhatti et al. [13], using a clot blood model, analysed heat transfer on peristaltically induced motion of particle-fluid suspension with variable viscosity. Elnaqeeb et al. [14] studied the hemodynamic characteristics of gold nanoparticle blood flow through a tapered stenosed vessel with variable nanofluid viscosity. Massoudi and Christie [15], Pantokratoras [16], Nadeem and Akbar [17] analysed the influence of heat transfer with temperature dependent viscosity. Petrofsky et al. [18] examined the effect of the moisture content of heat source on the blood flow response of the skin through data. Prakash et al. [19] developed a model for bifurcated arteries to analytically study the effects of heat source on magneto-hydrodynamic (MHD) blood flow.

In this work, we present combined effects of an external heat source (radiation) and magnetic field on an inclined tapered stenosed porous artery, considering variable viscosity of the blood flow. Under well-defined boundary conditions, the resulting non-linear differential equations of the model have been solved numerically using Differential Transform Method (DTM).

2. Mathematical formulation of the problem

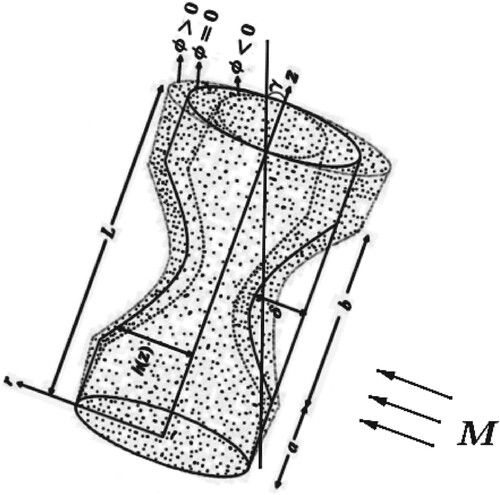
Let $(r,\theta ,z)$ be the cylindrical polar coordinate system, and let $v_r$, $v_{\theta }$ and $v_z$ be the velocity components in the r, θ and z directions, respectively. Consider blood flow through a tapered stenosed artery in the axial direction of the artery with length L and inclined at an angle γ with externally applied magnetic field M and radiation $q_r$ (see Figure 1).

Figure 1. Geometry of an inclined non-tapered artery.

Blood can be seen as a suspension of red blood cells in plasma. Consider an incompressible flow of the blood such that the density ρ is uniform throughout. Viscosity, $\mu \left(r\right)$ however, varies as the blood flows in the radial direction. Einstein's model of variable viscosity is [20]: (1) $\mu \left(r\right)={\mu }_0(1+\lambda h(r\left)\right),$(1) where ${\mu }_0$ is the coefficient of viscosity of plasma, λ is a constant which takes the value 2.5 for blood (suspension of red blood cells which are considered to be of spherical shape) and $h\left(r\right)$ is the volume fraction of the red blood cells, known as hematocrit.

The analysis will be carried out using the following empirical formulas for hematocrit [21]: (2) $h\left(r\right)=H\left[1-{\left(\frac{r}{d_0}\right)}^m\right],$(2) and (3) $H_r=\lambda H,$(3) where H represents the maximum hematocrit at the mid line of the artery, m represents the parameter which determines the shape of the velocity profile of blood ($m\ge 2$) and $H_r$ is the volumetric ratio of red blood cells in the blood and is known as the hematocrit parameter.

Consider a tapered stenosed porous artery inclined at an angle γ with an externally applied magnetic field (M) as shown in Figure 1. Let $d\left(z\right)$ be the radius of the tapered artery in the region of stenosis, with [21]: (4) $d\left(z\right)=d_0+\xi z,$(4) then, the geometry of the stenosis in dimensionless form is defined by [21,22]:

(5) $h\left(z\right)=\left\{\begin{array}{ll}d\left(z\right)\left[1-\eta \left(b^{n-1}(z-a)-(z-a{)}^n\right)\right],& a\le z\le a+b,\\ d\left(z\right),& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right.$(5) where $d_0$ is the radius of the non-tapered artery in the non-stenotic region, n is a parameter which determines the shape of the constriction profile (n = 2 for a symmetrically shaped stenosis and $n\ge 2$ for a non-symmetric stenosis), b is the length of the stenosis and ξ is the tapering parameter defined by $\xi =\tan \phi$, where φ is the tapered angle which assumes value $\phi <0$, $\phi >0$ and $\phi =0$ in the converging, diverging and non-tapered regions, respectively.

Let δ be the maximum height of the stenosis at the location [21]: (6) $z=a+\frac{b}{n^{n/(n-1)}},$(6) then, we define the parameter η in (5(5) $h\left(z\right)=\left\{\begin{array}{ll}d\left(z\right)\left[1-\eta \left(b^{n-1}(z-a)-(z-a{)}^n\right)\right],& a\le z\le a+b,\\ d\left(z\right),& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right.$(5) ) by [21]: $\eta =\frac{\delta n^{n/(n-1)}}{d_0{b}^n(n-1)}.$ Hence, for our model, we make the following assumptions:

• The artery is a circular cylindrical tube with finite length.

• Blood is incompressible Newtonian fluid (the artery is large enough that a Newtonian model is appropriate [23]).

• The blood flows steadily in the axial direction and a uniform magnetic field (M) is applied in the radial direction (perpendicular to the flow).

• The flow is axisymmetric. This implies that $v_r$, $v_z$ and p do not depend on θ, and we write $(r,\theta ,z)=(r,0,z)$.

• The stenosis is mild and is symmetrical about the axis of the artery.

• The temperature difference of the blood and artery is very high. This ensures that radiative heat transfer is valid.

• The dimensionless magnetic Reynolds number $R_e$ is small ($R_e\ll 1$) so that the induced magnetic field is negligible compared to the applied magnetic field [24].

• The electric field $E_f=0$ since the flow is not subjected to any applied voltage.

Under these assumptions, the governing equations for the steady, axisymmetric flow of blood through an inclined tapered artery with mild stenosis are given by (7) $\begin{array}{rl}& \frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}+\frac{v_r}{r}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}=0,\end{array}$(7) (8) $\begin{array}{rl}& \rho \left[v_r\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}+v_z\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }z}\right]\\ & =-\frac{\mathrm{\partial }\overline{P}}{\mathrm{\partial }r}+\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left[2\mu \frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}\right]\\ & +2\frac{\mu }{r}\left[\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}-\frac{v_r}{r}\right]\\ & +\frac{\mathrm{\partial }}{\mathrm{\partial }z}\left[\mu \left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }r}\right)\right],\end{array}$(8) (9) $\begin{array}{rl}& \rho \left[v_r\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }r}+v_z\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}\right]\\ & =-\frac{\mathrm{\partial }\overline{P}}{\mathrm{\partial }z}+\frac{\mathrm{\partial }}{\mathrm{\partial }z}\left[2\mu \frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}\right]\\ & +\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left[\mu r\left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }r}\right)\right]-{\sigma }_1{\mu }_m^2{H}_0^2{v}_z\\ & +\rho g\alpha (T-T_0)\cos \gamma -\frac{\mu v_z}{k_1},\end{array}$(9) (10) $\begin{array}{rl}& \rho c_p\left[v_r\frac{\mathrm{\partial }T}{\mathrm{\partial }r}+v_z\frac{\mathrm{\partial }T}{\mathrm{\partial }z}\right]\\ & =\frac{k}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r\frac{\mathrm{\partial }T}{\mathrm{\partial }r}\right)+k\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{z}^2}\\ & +2\mu \left[{\left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}\right)}^2+{\left(\frac{v_r}{r}\right)}^2+{\left(\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}\right)}^2\right]\\ & +\mu {\left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }r}\right)}^2-\mathrm{\partial }{q}_r/\mathrm{\partial }r.\end{array}$(10) The most general differential equation for the radiative flux $q_r$ is the transport equation [25]: (11) $\frac{{\mathrm{\partial }}^2{q}_r}{\mathrm{\partial }{r}^2}-3{\alpha }_v^2{q}_r-16{\alpha }_v\sigma T^3\frac{\mathrm{\partial }T}{\mathrm{\partial }r}=0,$(11) where σ is the Stefan–Boltzmann constant.

We assume that blood is optically thin, so that ${\alpha }_v\ll 1$ [25]. Then, if T is the local temperature of the blood, and $T_0$ is the temperature of the blood at the stenotic region, (11(11) $\frac{{\mathrm{\partial }}^2{q}_r}{\mathrm{\partial }{r}^2}-3{\alpha }_v^2{q}_r-16{\alpha }_v\sigma T^3\frac{\mathrm{\partial }T}{\mathrm{\partial }r}=0,$(11) ) can be simplified to [25]: (12) $\frac{\mathrm{\partial }{q}_r}{\mathrm{\partial }r}=4{\alpha }_v^2(T-T_0),$(12) Equations (7(7) $\begin{array}{rl}& \frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}+\frac{v_r}{r}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}=0,\end{array}$(7) )–(10(10) $\begin{array}{rl}& \rho c_p\left[v_r\frac{\mathrm{\partial }T}{\mathrm{\partial }r}+v_z\frac{\mathrm{\partial }T}{\mathrm{\partial }z}\right]\\ & =\frac{k}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r\frac{\mathrm{\partial }T}{\mathrm{\partial }r}\right)+k\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{z}^2}\\ & +2\mu \left[{\left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}\right)}^2+{\left(\frac{v_r}{r}\right)}^2+{\left(\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}\right)}^2\right]\\ & +\mu {\left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }r}\right)}^2-\mathrm{\partial }{q}_r/\mathrm{\partial }r.\end{array}$(10) ) are dimensional equations of motion which govern the flow of blood in the stenosed artery under the influence of radiation and magnetic field. These equations are not easy to solve by the number of parameters they include. This number of parameters, however, can be reduced by introducing non-dimensional groups.

We therefore introduce the following non-dimensional variables into (7(7) $\begin{array}{rl}& \frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}+\frac{v_r}{r}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}=0,\end{array}$(7) )–(10(10) $\begin{array}{rl}& \rho c_p\left[v_r\frac{\mathrm{\partial }T}{\mathrm{\partial }r}+v_z\frac{\mathrm{\partial }T}{\mathrm{\partial }z}\right]\\ & =\frac{k}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r\frac{\mathrm{\partial }T}{\mathrm{\partial }r}\right)+k\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{z}^2}\\ & +2\mu \left[{\left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}\right)}^2+{\left(\frac{v_r}{r}\right)}^2+{\left(\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}\right)}^2\right]\\ & +\mu {\left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }r}\right)}^2-\mathrm{\partial }{q}_r/\mathrm{\partial }r.\end{array}$(10) ) to get the equivalent non-dimensional equations of motion [21,26]:

(13) $\begin{array}{rl}& v_r=\frac{u{u}_0\delta }{b},r=r^{\prime }{d}_0,z=z^{\prime }b,v_z=w^{\prime }{u}_0,h=h^{\prime }{d}_0,\\ & \overline{P}=\frac{u_{0}b{\mu }_{0}P}{d_0^2},R_e=\frac{\rho b{u}_0}{{\mu }_0},\mathrm{\Theta }=\frac{T-T_0}{T_0},P_r=\frac{\mu c_p}{k},\\ & E_c=\frac{u_0^2}{c_p{T}_0},Z=\frac{k_1}{d_0^2},M^2=\frac{\sigma H_0^2{d}_0^2}{{\mu }_0},N^2=\frac{4d_0^2{\alpha }_v^2}{k},\\ & G_r=\frac{g\alpha d_0^3{T}_0}{{\nu }^2}.\end{array}$(13) where $R_e$, $P_r$, $E_c$, $G_r$, Θ, Z, M, and N, respectively, represent the Reynolds number, Prandtl number, Eckert number, Grashof number, temperature parameter, porosity parameter, magnetic field parameter and radiation absorption parameter. The term $\nu ={\mu }_0/\rho$ is the dynamic viscosity, α is the coefficient of thermal expansion, and $k_1$ is the permeability of the porous medium.

In order to adopt simple notations, we will drop the prime (${}^{\prime }$) on r, z, w and h. This basically changes nothing since we now have them in their dimensionless forms and by considering $d_0=1$.

We assumed a symmetrically shaped mild stenosis in which (14) $\frac{\delta }{d_0}\ll 1,$(14) and the conditions of [21,27] (15) $\begin{array}{rl}& \frac{R_e\delta n^{1/(n-1)}}{b}\ll 1,\end{array}$(15) (16) $\begin{array}{rl}& d_0{n}^{1/(n-1)}\sim \mathcal{O}\left(1\right),\end{array}$(16) then, the pressure gradient in the r-direction is negligible compared to the pressure gradient in the z-direction, that is, $\frac{\mathrm{\partial }P}{\mathrm{\partial }r}\ll \frac{\mathrm{\partial }P}{\mathrm{\partial }z}.$ Also, condition (14(14) $\frac{\delta }{d_0}\ll 1,$(14) ) implies $\mathrm{\partial }{v}_r/\mathrm{\partial }z\ll 1$. Therefore, given conditions (14(14) $\frac{\delta }{d_0}\ll 1,$(14) )–(16(16) $\begin{array}{rl}& d_0{n}^{1/(n-1)}\sim \mathcal{O}\left(1\right),\end{array}$(16) ), the no-slip boundary condition, and that $h\left(z\right)$, defined in (5(5) $h\left(z\right)=\left\{\begin{array}{ll}d\left(z\right)\left[1-\eta \left(b^{n-1}(z-a)-(z-a{)}^n\right)\right],& a\le z\le a+b,\\ d\left(z\right),& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right.$(5) ), is the geometry of the stenosis in non-dimensional form, then (7(7) $\begin{array}{rl}& \frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}+\frac{v_r}{r}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}=0,\end{array}$(7) )–(10(10) $\begin{array}{rl}& \rho c_p\left[v_r\frac{\mathrm{\partial }T}{\mathrm{\partial }r}+v_z\frac{\mathrm{\partial }T}{\mathrm{\partial }z}\right]\\ & =\frac{k}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r\frac{\mathrm{\partial }T}{\mathrm{\partial }r}\right)+k\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{z}^2}\\ & +2\mu \left[{\left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }r}\right)}^2+{\left(\frac{v_r}{r}\right)}^2+{\left(\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}\right)}^2\right]\\ & +\mu {\left(\frac{\mathrm{\partial }{v}_r}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }r}\right)}^2-\mathrm{\partial }{q}_r/\mathrm{\partial }r.\end{array}$(10) ) in their non-dimensional forms, respectively, become (17) $\begin{array}{rl}& \frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}=0,\end{array}$(17) (18) $\begin{array}{rl}& \frac{\mathrm{\partial }P}{\mathrm{\partial }r}=0,\end{array}$(18) (19) $\begin{array}{rl}& \frac{\mathrm{\partial }P}{\mathrm{\partial }z}=\left[\frac{1}{r}+H_r\left(\frac{1}{r}-(m+1)r^{m-1}\right)\right]\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\\ & +\left[1+H_r(1-r^m)\right]\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right)\\ & -w\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}(1-r^m)\right)+G_r\mathrm{\Theta }\cos \gamma ,\end{array}$(19) (20) $\begin{array}{rl}& \frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r\frac{\mathrm{\partial }\mathrm{\Theta }}{\mathrm{\partial }r}\right)+E_c{P}_r{\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right)}^2-N^2\mathrm{\Theta }=0.\end{array}$(20) The corresponding boundary conditions are

• the axisymmetric boundary conditions of the flow axial velocity at the mid line of the artery (21) $\frac{\mathrm{\partial }w}{\mathrm{\partial }r}=0,\frac{\mathrm{\partial }\mathrm{\Theta }}{\mathrm{\partial }r}=0\mathrm{a}\mathrm{t}r=0,$(21)

• and the no-slip boundary conditions at the wall of the artery (22) $w=0,\mathrm{\Theta }=0,\mathrm{a}\mathrm{t}r=h\left(z\right),$(22) where $h\left(z\right)$, defined by (23) $\begin{array}{rl}h\left(z\right)& =(1+{\xi }^{\prime }z)[1-{\eta }^{\prime }((z-a^{\prime })-(z-a^{\prime }{)}^n)]\\ & \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}{a}^{\prime }\le z\le a^{\prime }+1,\end{array}$(23) is the geometry of the stenosis when the radius $d_0$ of the artery is of unit length.

In (23(23) $\begin{array}{rl}h\left(z\right)& =(1+{\xi }^{\prime }z)[1-{\eta }^{\prime }((z-a^{\prime })-(z-a^{\prime }{)}^n)]\\ & \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}{a}^{\prime }\le z\le a^{\prime }+1,\end{array}$(23) ), ${\eta }^{\prime }$, $a^{\prime }$ and ${\xi }^{\prime }$ are defined as follows: ${\eta }^{\prime }=\frac{{\delta }^{\prime }{n}^{n/(n-1)}}{(n-1)}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\delta }^{\prime }=\frac{\delta }{d_0},a^{\prime }=\frac{a}{b},{\xi }^{\prime }=\frac{\xi b}{d_0}.$

3. Solution of the problem

The Differential Transform Method (DTM) was used to solve the system of Equations (17(17) $\begin{array}{rl}& \frac{\mathrm{\partial }{v}_z}{\mathrm{\partial }z}=0,\end{array}$(17) )–(20(20) $\begin{array}{rl}& \frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r\frac{\mathrm{\partial }\mathrm{\Theta }}{\mathrm{\partial }r}\right)+E_c{P}_r{\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right)}^2-N^2\mathrm{\Theta }=0.\end{array}$(20) ) with boundary conditions (21(21) $\frac{\mathrm{\partial }w}{\mathrm{\partial }r}=0,\frac{\mathrm{\partial }\mathrm{\Theta }}{\mathrm{\partial }r}=0\mathrm{a}\mathrm{t}r=0,$(21) )–(22(22) $w=0,\mathrm{\Theta }=0,\mathrm{a}\mathrm{t}r=h\left(z\right),$(22) ). The DTM, which is based on the Taylor series expansion of a function, is an alternative method for obtaining analytic Taylor series solution of differential equations. That is, for an analytic function $f\left(x\right)$, the differential transform at the point x = 0 is defined as follows: (24) $F\left(k\right)=\frac{H^k}{k!}{f}^{\left(k\right)}\left(0\right),$(24) while the differential inverse transform of $F\left(k\right)$, in real application, is (25) $f\left(x\right)=\sum _{k=0}^n{\left(\frac{x}{H}\right)}^{k}F\left(k\right).$(25) The differential spectrum of $F\left(k\right)$ is defined in the interval $x\in [0,H]$, where H is a constant whose value is generally taken as 1.

First, we write the momentum equation (19(19) $\begin{array}{rl}& \frac{\mathrm{\partial }P}{\mathrm{\partial }z}=\left[\frac{1}{r}+H_r\left(\frac{1}{r}-(m+1)r^{m-1}\right)\right]\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\\ & +\left[1+H_r(1-r^m)\right]\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right)\\ & -w\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}(1-r^m)\right)+G_r\mathrm{\Theta }\cos \gamma ,\end{array}$(19) ) and the energy equation (20(20) $\begin{array}{rl}& \frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(r\frac{\mathrm{\partial }\mathrm{\Theta }}{\mathrm{\partial }r}\right)+E_c{P}_r{\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right)}^2-N^2\mathrm{\Theta }=0.\end{array}$(20) ) respectively as follows: (26) $\begin{array}{rl}& (1+H_r)r^{-1}\frac{\mathrm{\partial }w}{\mathrm{\partial }r}-H_r(m+1)r^{m-1}\frac{\mathrm{\partial }w}{\mathrm{\partial }r}+(1+H_r)\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{r}^2}\\ & -H_r{r}^m\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{r}^2}-\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)w+\frac{H_r}{Z}{r}^{m}w\\ & +G_r\mathrm{\Theta }\cos \gamma -\frac{\mathrm{\partial }P}{\mathrm{\partial }z}=0,\end{array}$(26) and (27) $r^{-1}\frac{\mathrm{\partial }\mathrm{\Theta }}{\mathrm{\partial }r}+\frac{{\mathrm{\partial }}^2\mathrm{\Theta }}{\mathrm{\partial }{r}^2}+E_c{P}_r{\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right)}^2-N^2\mathrm{\Theta }=0,$(27) and obtain their respective differential transforms. Let the differential transform of $w\left(r\right)$ and $\mathrm{\Theta }\left(r\right)$ be $W\left(k\right)$ and $G\left(k\right)$, respectively, then (26(26) $\begin{array}{rl}& (1+H_r)r^{-1}\frac{\mathrm{\partial }w}{\mathrm{\partial }r}-H_r(m+1)r^{m-1}\frac{\mathrm{\partial }w}{\mathrm{\partial }r}+(1+H_r)\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{r}^2}\\ & -H_r{r}^m\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{r}^2}-\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)w+\frac{H_r}{Z}{r}^{m}w\\ & +G_r\mathrm{\Theta }\cos \gamma -\frac{\mathrm{\partial }P}{\mathrm{\partial }z}=0,\end{array}$(26) ) and (27(27) $r^{-1}\frac{\mathrm{\partial }\mathrm{\Theta }}{\mathrm{\partial }r}+\frac{{\mathrm{\partial }}^2\mathrm{\Theta }}{\mathrm{\partial }{r}^2}+E_c{P}_r{\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right)}^2-N^2\mathrm{\Theta }=0,$(27) ) become (28) $\begin{array}{rl}& (1+H_r)\sum _{l=0}^k\delta (k-l+1)(l+1)W(l+1)\\ & -H_r(m+1)\sum _{l=0}^k\delta (k-l-m+1)(l+1)W(l+1)\\ & +(1+H_r)(k+1)(k+2)W(k+2)\\ & -H_r\sum _{l=0}^k\delta (k-l-m)(l+1)(l+2)W(l+2)\\ & -\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)W\left(k\right)+\frac{H_r}{Z}\sum _{l=0}^k\delta (k-l-m)W\left(l\right)\\ & +G_r\cos \gamma G\left(k\right)-\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\delta \left(k\right)=0,\end{array}$(28) and (29) $\begin{array}{rl}& \sum _{l=0}^k\delta (k-l+1)(l+1)G(l+1)\\ & +E_c{P}_r\sum _{l=0}^k(k-l+1)W(k-l+1)(l+1)W(l+1)\\ & +(k+1)(k+2)G(k+2)-N^{2}G\left(k\right)=0.\end{array}$(29) Applying Equation (24(24) $F\left(k\right)=\frac{H^k}{k!}{f}^{\left(k\right)}\left(0\right),$(24) ) in the boundary conditions, taking H = 1, we find that $\begin{array}{rl}W\left(0\right)& =\frac{1}{0!}w\left(h\right(z\left)\right)=a_1,G\left(0\right)=\frac{1}{0!}\mathrm{\Theta }\left(h\right(z\left)\right)=a_2,\\ W\left(1\right)& =\frac{1}{1!}{w}^{\prime }\left(0\right)=0,G\left(1\right)=\frac{1}{1!}{\mathrm{\Theta }}^{\prime }\left(0\right)=0,\end{array}$ where $a_1$ and $a_2$ are constants which can be determined by using the boundary conditions (22(22) $w=0,\mathrm{\Theta }=0,\mathrm{a}\mathrm{t}r=h\left(z\right),$(22) ).

From (28(28) $\begin{array}{rl}& (1+H_r)\sum _{l=0}^k\delta (k-l+1)(l+1)W(l+1)\\ & -H_r(m+1)\sum _{l=0}^k\delta (k-l-m+1)(l+1)W(l+1)\\ & +(1+H_r)(k+1)(k+2)W(k+2)\\ & -H_r\sum _{l=0}^k\delta (k-l-m)(l+1)(l+2)W(l+2)\\ & -\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)W\left(k\right)+\frac{H_r}{Z}\sum _{l=0}^k\delta (k-l-m)W\left(l\right)\\ & +G_r\cos \gamma G\left(k\right)-\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\delta \left(k\right)=0,\end{array}$(28) ), we obtain: (30) $\begin{array}{rl}& W(k+2)\\ & =\frac{H_r(m+1)\sum _{l=0}^k\delta (k-l-m+1)(l+1)W(l+1)}{(1+H_r)(k+1)(k+2)}\\ & +\frac{\delta \left(k\right)}{(1+H_r)(k+1)(k+2)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\\ & +\frac{W\left(k\right)\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)}{(1+H_r)(k+1)(k+2)}\\ & +\frac{H_r\sum _{l=0}^k\delta (k-l-m)(l+1)(l+2)W(l+2)}{(1+H_r)(k+1)(k+2)}\\ & -\frac{G_r\cos \gamma G\left(k\right)}{(1+H_r)(k+1)(k+2)}\\ & -\frac{H_r\sum _{l=0}^k\delta (k-l-m)W\left(l\right)}{Z(1+H_r)(k+1)(k+2)}\end{array}$(30) and from (29(29) $\begin{array}{rl}& \sum _{l=0}^k\delta (k-l+1)(l+1)G(l+1)\\ & +E_c{P}_r\sum _{l=0}^k(k-l+1)W(k-l+1)(l+1)W(l+1)\\ & +(k+1)(k+2)G(k+2)-N^{2}G\left(k\right)=0.\end{array}$(29) ), we obtain

(31) $\begin{array}{rl}& G(k+2)\\ & =\frac{N^{2}G\left(k\right)}{(k+1)(k+2)}\\ & -\frac{\sum _{l=0}^k\delta (k-l+1)(l+1)G(l+1)}{(k+1)(k+2)}\\ & -\frac{E_c{P}_r\sum _{l=0}^k\delta (k-l+1)W(k-l+1)(l+1)W(l+1)}{(k+1)(k+2)}\end{array}$(31) for k = 0, 1, 2, 3 and m = 2.

Hence, (32) $\begin{array}{rl}w\left(r\right)& =a_1+\left\{\frac{a_1}{2(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{G_r\cos \gamma }{2(1+H_r)}{a}_2+\frac{1}{2(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right\}{r}^2\\ & +\left\{\frac{1}{24(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+\frac{H_r}{Z}\right]\\ & \left.-a_1{H}_r\frac{1}{Z}-\frac{1}{2}{N}^2{a}_2{G}_r\cos \gamma \right\}{r}^4\end{array}$(32) (33) $\begin{array}{rl}\mathrm{\Theta }\left(r\right)& =a_2+\frac{N^2{a}_2}{2}{r}^2+\left\{\frac{N^4{a}_2}{24}-\frac{E_c{P}_r}{12(1+H_r{)}^2}\right.\\ & \left.{\left[a_1\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)+\frac{\mathrm{\partial }P}{\mathrm{\partial }z}-a_2{G}_r\cos \gamma \right]}^2\right\}{r}^4\end{array}$(33) The boundary conditions (22(22) $w=0,\mathrm{\Theta }=0,\mathrm{a}\mathrm{t}r=h\left(z\right),$(22) ) imply: (34) $\begin{array}{rl}& w\left(h\right(z\left)\right)\\ & =a_1+\left\{\frac{a_1}{2(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{G_r\cos \gamma }{2(1+H_r)}{a}_2+\frac{1}{2(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right\}{h}^2\\ & +\left\{\frac{1}{24(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+\frac{H_r}{Z}\right]\\ & \left.-a_1{H}_r\frac{1}{Z}-\frac{1}{2}{N}^2{a}_2{G}_r\cos \gamma \right\}{h}^4=0,\end{array}$(34) (35) $\begin{array}{rl}& \mathrm{\Theta }\left(h\right(z\left)\right)\\ & =a_2+\frac{N^2{a}_2}{2}{h}^2\\ & +\left\{\frac{N^4{a}_2}{24}-\frac{E_c{P}_r}{12(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\phantom{{\left.+\frac{\mathrm{\partial }P}{\mathrm{\partial }z}-a_2{G}_r\cos \gamma \right]}^2}\right.\\ & \left.{\left.+\frac{\mathrm{\partial }P}{\mathrm{\partial }z}-a_2{G}_r\cos \gamma \right]}^2\right\}{h}^4=0.\end{array}$(35) The Wolfram Mathematica 11.3 software was used to solve (34(34) $\begin{array}{rl}& w\left(h\right(z\left)\right)\\ & =a_1+\left\{\frac{a_1}{2(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{G_r\cos \gamma }{2(1+H_r)}{a}_2+\frac{1}{2(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right\}{h}^2\\ & +\left\{\frac{1}{24(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+\frac{H_r}{Z}\right]\\ & \left.-a_1{H}_r\frac{1}{Z}-\frac{1}{2}{N}^2{a}_2{G}_r\cos \gamma \right\}{h}^4=0,\end{array}$(34) ) and (35(35) $\begin{array}{rl}& \mathrm{\Theta }\left(h\right(z\left)\right)\\ & =a_2+\frac{N^2{a}_2}{2}{h}^2\\ & +\left\{\frac{N^4{a}_2}{24}-\frac{E_c{P}_r}{12(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\phantom{{\left.+\frac{\mathrm{\partial }P}{\mathrm{\partial }z}-a_2{G}_r\cos \gamma \right]}^2}\right.\\ & \left.{\left.+\frac{\mathrm{\partial }P}{\mathrm{\partial }z}-a_2{G}_r\cos \gamma \right]}^2\right\}{h}^4=0.\end{array}$(35) ) simultaneously for $a_1$ and $a_2$. The values obtained for $a_1$ and $a_2$ were then substituted into (32(32) $\begin{array}{rl}w\left(r\right)& =a_1+\left\{\frac{a_1}{2(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{G_r\cos \gamma }{2(1+H_r)}{a}_2+\frac{1}{2(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right\}{r}^2\\ & +\left\{\frac{1}{24(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+\frac{H_r}{Z}\right]\\ & \left.-a_1{H}_r\frac{1}{Z}-\frac{1}{2}{N}^2{a}_2{G}_r\cos \gamma \right\}{r}^4\end{array}$(32) ) and (33(33) $\begin{array}{rl}\mathrm{\Theta }\left(r\right)& =a_2+\frac{N^2{a}_2}{2}{r}^2+\left\{\frac{N^4{a}_2}{24}-\frac{E_c{P}_r}{12(1+H_r{)}^2}\right.\\ & \left.{\left[a_1\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)+\frac{\mathrm{\partial }P}{\mathrm{\partial }z}-a_2{G}_r\cos \gamma \right]}^2\right\}{r}^4\end{array}$(33) ) to obtain full expressions for the velocity profile, $w\left(r\right)$ and temperature profile, $\mathrm{\Theta }\left(r\right)$. The expressions are not shown due to their lengths.

4. Volumetric flow rate

The volumetric flow rate, $Q_v$ is defined as (36) $Q_v=2\pi {\int }_0^{h}rw\mathrm{d}r,$(36) where w is the obtained axial velocity and r is the artery radius.

Substituting (32(32) $\begin{array}{rl}w\left(r\right)& =a_1+\left\{\frac{a_1}{2(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{G_r\cos \gamma }{2(1+H_r)}{a}_2+\frac{1}{2(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right\}{r}^2\\ & +\left\{\frac{1}{24(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+\frac{H_r}{Z}\right]\\ & \left.-a_1{H}_r\frac{1}{Z}-\frac{1}{2}{N}^2{a}_2{G}_r\cos \gamma \right\}{r}^4\end{array}$(32) ) into (36(36) $Q_v=2\pi {\int }_0^{h}rw\mathrm{d}r,$(36) ), and integrating, we obtain (37) $\begin{array}{rl}{Q}_v& =a_1\pi h^2+\left\{\frac{a_1\pi }{4(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{\pi G_r\cos \gamma }{4(1+H_r)}{a}_2+\frac{\pi }{4(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right\}{h}^4\\ & +\left\{\frac{\pi }{72(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right]\phantom{\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)}\\ & \left.-\frac{\pi }{3Z}{a}_1{H}_r-\frac{\pi }{6}{N}^2{a}_2{G}_r\cos \gamma \phantom{\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)}\right\}{h}^6.\end{array}$(37) The values obtained for $a_1$ and $a_2$ are substituted into (37(37) $\begin{array}{rl}{Q}_v& =a_1\pi h^2+\left\{\frac{a_1\pi }{4(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{\pi G_r\cos \gamma }{4(1+H_r)}{a}_2+\frac{\pi }{4(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right\}{h}^4\\ & +\left\{\frac{\pi }{72(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right]\phantom{\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)}\\ & \left.-\frac{\pi }{3Z}{a}_1{H}_r-\frac{\pi }{6}{N}^2{a}_2{G}_r\cos \gamma \phantom{\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)}\right\}{h}^6.\end{array}$(37) ) to have expressions for the volumetric flow rate. The expression is not shown due to its length.

5. Wall shear stress

The wall shear stress, τ of the blood flow is defined as (38) $\tau ={\mu }_0{\left[\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right]}_{r=h}.$(38) Substituting (32(32) $\begin{array}{rl}w\left(r\right)& =a_1+\left\{\frac{a_1}{2(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{G_r\cos \gamma }{2(1+H_r)}{a}_2+\frac{1}{2(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right\}{r}^2\\ & +\left\{\frac{1}{24(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+\frac{H_r}{Z}\right]\\ & \left.-a_1{H}_r\frac{1}{Z}-\frac{1}{2}{N}^2{a}_2{G}_r\cos \gamma \right\}{r}^4\end{array}$(32) ) into (38(38) $\tau ={\mu }_0{\left[\frac{\mathrm{\partial }w}{\mathrm{\partial }r}\right]}_{r=h}.$(38) ) and differentiating with respect to r, we obtain (39) $\begin{array}{rl}\tau & =\left[\frac{a_1}{(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{a_2{G}_r\cos \gamma }{(1+H_r)}+\frac{1}{(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]h\\ & +\left\{\frac{1}{12(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right]\\ & \left.-\frac{4a_1{H}_r}{Z}\phantom{\left[8H_r+M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right]}-N^2{a}_2{G}_r\cos \gamma \right\}{h}^3.\end{array}$(39) The values obtained for $a_1$ and $a_2$ are substituted into (39(39) $\begin{array}{rl}\tau & =\left[\frac{a_1}{(1+H_r)}\left(M^2+\frac{1}{Z}+\frac{H_r}{Z}\right)\right.\\ & \left.-\frac{a_2{G}_r\cos \gamma }{(1+H_r)}+\frac{1}{(1+H_r)}\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]h\\ & +\left\{\frac{1}{12(1+H_r{)}^2}\left[a_1\left(M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right)\right.\right.\\ & \left.-a_2{G}_r\cos \gamma +\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right]\cdot \left[8H_r+M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right]\\ & \left.-\frac{4a_1{H}_r}{Z}\phantom{\left[8H_r+M^2+\frac{1}{Z}+H_r\frac{1}{Z}\right]}-N^2{a}_2{G}_r\cos \gamma \right\}{h}^3.\end{array}$(39) ) to have expression for the wall shear stress. The expression is not shown due to its length.

The wall shear stress, ${\tau }_s$ at the maximum height of the stenosis located at $z^{\prime }=\frac{z}{b}=\frac{a}{b}+\frac{1}{n^{n/(n-1)}},$ (the stenosis throat) is computed by assuming a negligible value of ξ in (23(23) $\begin{array}{rl}h\left(z\right)& =(1+{\xi }^{\prime }z)[1-{\eta }^{\prime }((z-a^{\prime })-(z-a^{\prime }{)}^n)]\\ & \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}{a}^{\prime }\le z\le a^{\prime }+1,\end{array}$(23) ), and putting $h=1-\delta$ [21]. Hence, we have (40) ${\tau }_s={\left[\tau \right]}_{h=(1-\delta )}.$(40)

6. Results and discussion

The numerical results are simulated in the figures below in order to have greater insight into the qualitative analysis of the results. The magnetic field parameter (M), heat radiation parameter (N), the angle of inclination (γ) of the artery and the height of the stenosis (δ) were simulated through graphs plotted using the Mathematica software.

The following values of the various parameters were used [21,26]: $\begin{array}{rl}& \mathrm{\partial }P/\mathrm{\partial }z=0.3,M=1.5,Z=0.3,H_r=1,\\ & G_r=2,\gamma =\pi /3,N=1.5,\\ & B_r=E_c{P}_r=2,\xi =0.002,a=0.25,b=1,\\ & d_0=1,n=2,z=0.5,\delta =0.1,\mathrm{a}\mathrm{n}\mathrm{d}\\ & h=\mathrm{0.923.}\end{array}$ Figure 2(a–d), respectively, show the effects of heat radiation, magnetic field, the angle of inclination of the artery and the height of stenosis on the velocity profile of blood.

Figure 2. Effects on blood velocity. (a) Effects of heat radiation on blood velocity. (b) Effects of magnetic field on blood velocity. (c) Effects of the inclination angle on blood velocity. (d) Effects of the stenosis height on blood velocity.

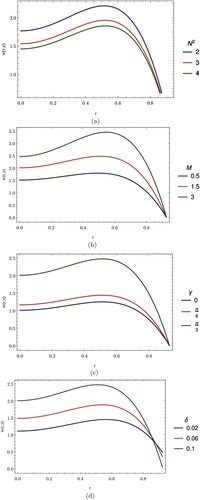
Figure 2(a) describes how the velocity of blood varies with heat radiation. We see that the velocity of blood decreases with an increasing heat radiation.

Figure 2(b) shows the behaviour of the axial velocity with the applied magnetic field. We see that the velocity increases as the magnetic field parameter increases. This occurs because the magnetic field is applied to a moving electrically conducting fluid and as these fields interact, the Lorentz force produced assists the motion of the blood.

Figure 2(c) shows the behaviour of the velocity of blood with the artery inclination angle. As the inclination angle of the artery increases from 0 to $\pi /3$, the velocity of blood flow increases.

Figure 2(d) indicates the behaviour of the velocity profile of blood as the stenotic height varies. It shows that the velocity of blood flow increases as the height of stenosis increases, but changes behaviour as the stenosis height approaches its maximum value.

Figure 3(a–d), respectively, show the effects of heat radiation, magnetic field, the angle of inclination of the artery and the height of stenosis on blood temperature.

Figure 3. Effects on blood temperature. (a) Effects of the heat radiation on blood temperature. (b) Effects of magnetic field on blood temperature. (c) Effects of the inclination angle on blood temperature. (d) Effects of the stenosis height on blood temperature.

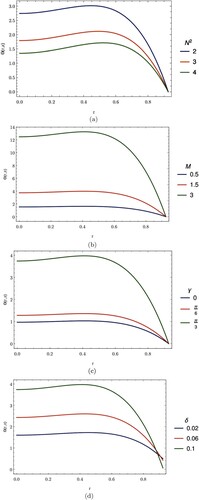
Figure 3(a) displays the effects of radiative heat transfer to blood flow on the blood temperature. We see that the temperature of blood decreases as the heat source parameter increases.

Figure 3(b) represents how blood temperature varies with the applied magnetic field. It can be seen that the temperature increases as the magnetic field parameter increases.

Figure 3(c) shows how blood temperature varies as the inclination angle of the artery varies. It shows that the temperature of blood increases as the inclination angle increases.

Figure 3(d) indicates the behaviour of the temperature of blood with the height of the stenosis. The temperature of blood increases as the height of stenosis increases.

Figure 4(a,b), respectively, show the effect of heat radiation, magnetic field, and the angle of inclination of the artery on the volumetric flow rate of blood.

Figure 4. Effects on volumetric flow rate. (a) Effects of the heat radiation on volumetric flow rate. (b) Effects of magnetic field on volumetric flow rate. (c) Effects of the inclination angle on volumetric flow rate.

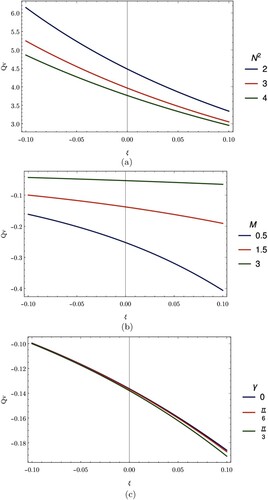
Figure 4(a) indicates the behaviour of the volumetric flow rate in the diverging, converging and non-tapered regions of the artery with change of heat radiation parameter. The volumetric flow rate of blood decreases with an increasing heat radiation.

Figure 4(b) shows the behaviour of the volumetric flow rate, $Q_v$ in the diverging, converging and non-tapered regions of the artery as the applied magnetic field parameter changes. It is noted that as the magnetic field increases, the volumetric flow rate increases in the diverging, converging and non-tapered regions.

Figure 4(c) shows the variation of the volumetric flow rate in the diverging, converging and non-tapered regions of the artery with the inclination angle of the artery. It is seen that the volumetric flow rate decreases as the inclination angle increases from 0 to $\pi /3$.

Figure 5(a,b), respectively, show the variation of the wall shear stress at stenosis throat for different values of heat radiation and magnetic field parameters.

Figure 5. Variation of wall shear stress at stenosis throat. (a) Effects of wall shear stress at stenosis throat with the heat radiation. (b) Effects of wall shear stress at stenosis throat with the magnetic field.

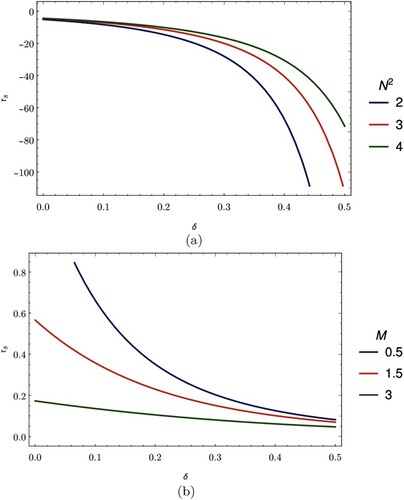
Figure 5(a) depicts how the wall shear stress changes with a change in the radiation parameter. It is noted that, increasing the value of the radiation parameter raises the value of the wall shear stress at the stenosis throat.

Figure 5(b) shows that the wall shear stress decreases as the magnetic field parameter increases. We have seen that the magnetic field speeds up the blood flow and this allows the blood to flow with a reduced interaction with the walls of the artery, hence producing a minimal shear.

7. Conclusions

The electrically conducting blood in motion and the effects of an external magnetic field and heat radiation on the blood flow in an inclined tapered stenosed porous artery have been studied through this work. The mathematical formulation for the momentum and energy equations was obtained for the blood flow considered to be Newtonian. The resulting equations of motion were solved numerically using the Differential Transform Method (DTM). Various fluid parameters were introduced and used to study the effect of heat radiation and magnetic field on the velocity, temperature, volumetric flow rate and the wall shear stress of the blood. The following are the findings obtained:

1. An increase in the magnetic field parameter, M increases the velocity and temperature profiles of the blood flow due to the presence of the Lorentz force which assists the motion of the blood. The curves representing the volumetric flow rate show that the volumetric flow rate increases as the magnetic field parameter increases and is greater in the converging region as compared to the diverging region. It is however observed that the wall shear stress decreases at the stenosis throat as the magnetic field parameter increases.

2. Under the influence of heat radiation and magnetic field, there is a greater variation in the volumetric flow rate of an inclined artery in the converging region than in the diverging region.

3. By increasing the heat radiation parameter, we observed that the curves representing both the velocity and temperature profiles deviate rapidly from the origin. The volumetric flow rate varies inversely with the heat radiation parameter for converging, diverging and non-tapered regions of the artery.

4. The velocity and temperature profiles increase as the angle of inclination, γ of the artery increases. With the increase of inclination angle of the artery, it is observed that the volumetric flow rate will increase more in the converging region than in the non-tapered and diverging regions of the artery.

5. By increasing the height of stenosis, we observed that the velocity and temperature profiles increase, as the curves representing them shift away from the origin.

Acknowledgments

Authors are sincerely thankful to the African Institute for Mathematical Sciences, Cameroon for providing the platform which served as the foundation of this work.

Disclosure statement

No potential conflict of interest was reported by the authors.