Generalized KdV equation involving Riesz time-fractional derivatives: constructing and solution utilizing variational methods

Abstract

In this work, the time-fractional generalized Korteweg de Vries (TFGKdV) is derived by utilizing the method of a semi-inverse and the variational principles. Based on the initial condition relying on the dispersion and nonlinear coefficients, we can apply the He’s variational iteration to construct an approximated solution for the TFGKdV equation. Finally, we study the impact of the fractional derivatives on the propagation and the structure of the solitary waves obtained from the solution of TFGKdV equation.

KEYWORDS:

• Solitary waves
• Riemann–Liouville fractional derivative
• Riesz fractional derivative
• KdV equation
• the method of He’s variational iteration

1. Introduction

Indeed, the fractional calculus recently employs to describe the majority physical and engineering processes that in some cases, gives an adequate description of such models in a comparison of integer-order derivatives. Although the majority of the physical real world is described by non-conservative systems, the majority of methods in classical mechanics transact with the conservative systems. This motivates the study such systems by constructing the equations of motion using the fractional derivatives notations. These types of equations are non-conservative systems. Thence, the usage of fractional calculus is the best for describing the physical real world (see, e.g. [1–15]).

From another perspective, the KdV equation appeared for the first time in 1895 as a one-dimensional evolution equation describing the waves of an along surface gravity propagation in a water shallow canal [16]. It also appeared in a numeral of diverse physical phenomena as hydromagnetic collision-free waves, ion-acoustic waves, stratified waves interior, lattice dynamics, physics of plasma, etc. [17]. It is also utilized as a model to inspect some phenomena in theoretical physics arising in quantum mechanics. It is employed as an example of the construction of wave shock construction, the dynamics of fluid, continuum mechanics, Solitons, turbulence, mass transport, aerodynamics and boundary layer behaviour. Moreover, there are many studies about the higher dimension of the KdV equation from the point of the study the bifurcation and constructing travelling wave solution (see, e.g. [18]). It is well known in physics that the whole phenomena are regarded as non-conservative systems, therefore, the best description of them is obtained by employing the fractional differential equations. There are various methods can be applied to construct the solution of these equations. For instance, the Fourier transformation, Laplace transformation and iteration method [19,20], operational method [21] and series solution method that is applied successfully in various works such as [22]. The majority of these methods are only valid for the fractional differential equations with linear and constant coefficients. For nonlinear fractional differential equations, there are some techniques for studying the existence and multiplicity of their solution, for example, the theories of a fixed point, the theory of Leray–Shauder, Adomian decomposition and the variational iteration method [23–42]. In [43], the authors studied the impact of the fractional derivatives on the prorogation and the formulation of the solitary waves corresponding to certain type of KdV equation in the form (1) $\frac{\mathrm{\partial }}{\mathrm{\partial }t}v\left(x,t\right)+av\left(x,t\right)\frac{\mathrm{\partial }}{\mathrm{\partial }x}v\left(x,t\right)+\gamma \frac{{\mathrm{\partial }}^3}{\mathrm{\partial }{x}^3}v\left(x,t\right)=0$(1) where $a,\gamma$ are constants. In [44], other study involves certain generalization of KdV Equation (1) in the form (2) $\frac{\mathrm{\partial }}{\mathrm{\partial }t}v\left(x,t\right)+av(x,t{)}^p\frac{\mathrm{\partial }}{\mathrm{\partial }x}v\left(x,t\right)+\gamma \frac{{\mathrm{\partial }}^3}{\mathrm{\partial }{x}^3}v\left(x,t\right)=0$(2)

where $p>0$. It is clear that Equation (1) can be obtained as special case from Equation (2) when $p=1$.

In the present work, we consider a (1 + 1) dimension KdV equation in a general form that is expressed as [45] (3) $\begin{array}{rl}& \frac{\mathrm{\partial }}{\mathrm{\partial }t}v\left(x,t\right)+\left[av\left(x,t\right)+bv{\left(x,t\right)}^2+cv{\left(x,t\right)}^3+d\right]\frac{\mathrm{\partial }}{\mathrm{\partial }x}v\left(x,t\right)\\ & +\gamma \frac{{\mathrm{\partial }}^3}{\mathrm{\partial }{x}^3}v\left(x,t\right)=0\end{array}$(3) where $a,b,c$ and d are arbitrary constants characterizing the nonlinearity terms and linear term, $\gamma$ is a constant which denotes to the dispersion, $v\left(x,t\right)$ is the field variable, $x\in R$ points out a coordinate of the space in the field propagation direction and $t\in T=\left[0,t_0\right]$ refers the time, respectively. To our knowledge, the (1 + 1) KdV Equation (3) with time-fractional derivative is not studied previously and based on the time-fractional of this equation can be effectively employed to examine and analyse the higher-order wave dispersion instead of the integer-order KdV equation when solved may not completely confirm the solitary waves. Moreover, the real physical problem possesses the non-local property that means the next stat of the system does not depend only on its current state but upon all its historical state. This motivates us to study the (1 + 1) KdV equation with time-fractional derivative.

This article is presented as the following type: Section 2 contains the deduction of the TFGKdV equation utilizing the variational principles. Section 3 involves the solution of the TFGKdV equation by employing He’s variational iteration method that is presented in short in the Appendix in order to have a self-contained article. Section 4 discusses and graphically illustrates the influence of the fractional derivatives on the propagation and formation of the resulting solitary waves.

2. Construction of the TFGKdV equation

Equation (3) is transformed to its corresponding potential equation by putting v(x, t) = W_x(x, t) in it. Thus, we have (4) $\begin{array}{rl}& w_{xt}\left(x,t\right)+\left[a{w}_x\right(x,t)+b{w}_x{\left(x,t\right)}^2\\ & +c{w}_x{\left(x,t\right)}^3+d\left]w_{xx}\right(x,t)+\gamma w_{xxxx}(x,t)=0,\end{array}$(4) where $w\left(x,t\right)$ indicates the potential function and the subscripts denote the partial derivative of the function with respect to the given variable. We apply the semi-inverse method [46,47] to construct the Lagrangian function corresponding to Equation (3). The functional associated with the potential Equation (4) reads as (5) $\begin{array}{rl}\mathrm{\Im }& ={\int }_{\mathrm{\Omega }}w\left(x,t\right)\left[c_1{w}_{xt}\right(x,t)+[c_{2}a{w}_x\left(x,t\right)+c_{3}b{w}_x{\left(x,t\right)}^2\\ & +c_{4}c{w}_x{\left(x,t\right)}^3+c_{5}d\left]w_{xx}\right(x,t)+\\ & +c_6\gamma w_{xxxx}\left(x,t\right)]\text{d}\mathrm{\Omega },\end{array}$(5) where $\text{d}\mathrm{\Omega }=\text{d}x\text{d}t$ and $c_i,i=1,2,\dots ,6$ refer to constants demanding calculation for their values. We integrate by parts and take into our consideration $w_t{|}_R=w_x{|}_T=w_x{|}_R=0$, we get (6) $\begin{array}{rl}\mathrm{\Im }& ={\int }_{\mathrm{\Omega }}\left[-c_1{w}_x{w}_t-\frac{a{c}_2}{2}{w}_x^3-\frac{c_{3}b}{3}{w}_x^4-\frac{c{c}_4}{4}{w}_x^5\right.\\ & -\left.c_{5}d{w}_x^2+c_6\gamma {w_{xx}}^2\phantom{\frac{c_{3}b}{3}}\right]\text{d}\mathrm{\Omega }.\end{array}$(6)

The constants c_i can be determined by calculating the variation of the functional (6) and deriving the condition of the optimum variation. We integrate the variation of the functional (6) by parts, the condition of the optimum variation reads as (7) $\begin{array}{rl}& 2c_1{w}_{xt}+\left[3a{c}_2{w}_x+4b{c}_3{w}_x^2+5c{c}_4{w}_x^3+2d{c}_5\right]w_{xx}\\ & +2\gamma c_6{w}_{xxxx}=0.\end{array}$(7)

It is well known that Equations (4) and (7) are equivalent and thus by comparing them, we obtain (8) $c_1=-c_5=c_6=\frac{1}{2},c_2=\frac{1}{3},c_3=\frac{1}{4},c_4=\frac{1}{5}.$(8)

Thus, the Lagrangian corresponding to the generalized KdV equation can be directly obtained from the functional (6) and it is expressed as (9) $\begin{array}{rl}L\left(w_t,w_x,w_{xx}\right)& =-\frac{1}{2}{w}_x{w}_t-\frac{a}{6}{w}_x^3-\frac{b}{12}{w}_x^4-\frac{c}{20}{w}_x^5\\ & -\frac{d}{2}{w}_x^2+\frac{\gamma }{2}{w}_{xx}^2.\end{array}$(9)

We assume that the fractional Lagrangian corresponding to the time-fractional version of the generalized KdV equation has (10) $\begin{array}{rl}\mathcal{L}{(}_0{D}_t^{\alpha }w,w_x,w_{xx})& =-\frac{1}{2}{w}_x{}_0^{}{D}_t^{\alpha }w-\frac{a}{6}{w}_x^3-\frac{b}{12}{w}_x^4\\ & -\frac{c}{20}{w}_x^5-\frac{d}{2}{w}_x^2+\frac{\gamma }{2}{w}_{xx}^2,\end{array}$(10) where ${}_0^{}{D}_t^{\alpha }w$ denotes the left Riemann–Liouville fractional derivative function [19,20,48] and it is expressed as (11) $\begin{array}{rl}{}_a^{}{D}_t^{\alpha }f\left(t\right)& =\frac{1}{\mathrm{\Gamma }\left(k-\alpha \right)}\frac{d^k}{\text{d}{t}^k}{\int }_a^t{\left(t-\tau \right)}^{k-\alpha -1}f\left(\tau \right)\text{d}\tau ,\\ & k-1\le \alpha <k,t\in \left[a,b\right].\end{array}$(11)

The functional corresponding TFGKdV admits the form (12) $\mathrm{\Im }\left(w\right)={\int }_{\mathrm{\Omega }}\mathcal{L}({}_0^{}{D}_t^{\alpha }w,w_x,w_{xx})\text{d}\mathrm{\Omega },$(12)

According to Agrawal’s method [49,50], the following theorem can be proved.

Theorem 1:

The Euler–Lagrange equation making the functional (12) extremum takes the form (13) ${}_t^{}{D}_{t_0}^{\alpha }\left(\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{}_0^{}{D}_t^{\alpha }w}\right)-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{w}_x}\right)+\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\left(\frac{\mathrm{\partial }\mathcal{L}}{\mathrm{\partial }{w}_{xx}}\right)=0,$(13) where ${}_t^{}{D}_{t_0}^{\alpha }u\left(x,t\right)$ refers to right Riemann–Liouville fractional derivative which can be read as [19,20,48] (14) ${}_t{D}_{t_0}^{\alpha }f\left(t\right)=\frac{{\left(-1\right)}^k}{\mathrm{\Gamma }\left(k-\alpha \right)}\frac{d^k}{\text{d}{t}^k}{\int }_t^{t_0}{\left(\tau -t\right)}^{k-\alpha -1}f\left(\tau \right)\text{d}\tau .$(14)

Applying Theorem 1 to the functional (12), we obtain (15) $\begin{array}{rl}& \frac{1}{2}\left[{}_0^{}{D}_t^{\alpha }{w}_x-{}_t^{}{D}_{t_0}^{\alpha }{w}_x\right]+\left(a{w}_x+b{w}_x^2+c{w}_x^3+d\right)w_{xx}\\ & +\gamma w_{xxxx}=0.\end{array}$(15) Setting again $w_x=v$ in Equation (15), we get (16) $\frac{1}{2}\left[{}_0{D}_t^{\alpha }v-{}_t^{}{D}_{t_0}^{\alpha }v\right]+\left(av+b{v}^2+c{v}^3+d\right)v_x+\gamma v_{xxx}=0.$(16) Indeed the first two terms in Equation (16) represents the Riesz fractional derivative which is defined as [19,20,48] (17) $\begin{array}{rl}{}_0^R{D}_t^{\alpha }f\left(t\right)& =\frac{1}{2}\left[{}_0^{}{D}_t^{\alpha }f\left(t\right)+{\left(-1\right)}^k{}_t^{}{D}_{t_0}^{\alpha }f\left(t\right)\right]\\ & =\frac{1}{2}\frac{1}{\mathrm{\Gamma }\left(k-\alpha \right)}\frac{d^k}{\text{d}{t}^k}{\int }_0^{t_0}{|t-\tau |}^{k-\alpha -1}f\left(\tau \right)\text{d}\tau .\end{array}$(17) Now, we restrict ourselves with $0\le \alpha <1$. Thus, taking into account Equation (17), TFGKdV Equation (16) becomes (18) $\begin{array}{rl}& {}_0^R{D}_t^{\alpha }v\left(x,t\right)+\left[av\left(x,t\right)+bv{\left(x,t\right)}^2+cv{\left(x,t\right)}^3+d\right]\frac{\mathrm{\partial }}{\mathrm{\partial }}v\left(x,t\right)\\ & +\gamma \frac{{\mathrm{\partial }}^3}{\mathrm{\partial }{x}^3}v\left(x,t\right)=0,0\le \alpha <1,t\in \left[0,t_0\right].\end{array}$(18) To complete our study, we are going to construct the solution of TFGKdV Equation (18) by employing the variational iteration methods. In addition, we will discuss and graphically illustrate the impact of the fractional derivatives on the propagation and formation of the resulting solitary waves.

3. Solution of TFGKdV equation

In this section, we employ the method of variational iteration to find the solution of TFGKdV Equation (18). Let ${}_0^R{D}_t^{1-\alpha }$ act on Equation (18) form the left side and taking into account the following formula [19,20,48]: (19) $\begin{array}{rl}{}_a^R{D}_t^{\alpha }\left[{}_a^R{D}_t^{\text{β}}\right]& ={}_a^R{D}_t^{\alpha +\text{β}}f\left(t\right)-\sum _{j=1}^k{}_a^R{D}_t^{\text{β}-j}f\left(t\right){|}_{t=a}\frac{{\left(t-a\right)}^{-\alpha -j}}{\mathrm{\Gamma }\left(1-\alpha -j\right)},\\ & k-1\le \text{β}<k.\end{array}$(19)

We obtain (20) $\begin{array}{rl}& \frac{\mathrm{\partial }v}{\mathrm{\partial }t}-{}_0^R{D}_t^{\alpha -1}v{|}_{t=0}\frac{t^{\alpha -2}}{\mathrm{\Gamma }\left(\alpha -1\right)}\\ & +{}_0^R{D}_t^{\alpha -1}\left[av+b{v}^2+c{v}^3+d\right]\frac{\mathrm{\partial }v}{\mathrm{\partial }x}+\gamma \frac{{\mathrm{\partial }}^{3}v}{\mathrm{\partial }{x}^3}=0.\end{array}$(20)

Thus, the iteration correctional functional corresponding Equation (20) is (21) $\begin{array}{rl}{v}_{n+1}\left(x,t\right)& =v_n\left(x,t\right)+{\int }_0^t\lambda \left(\tau \right)\left(\frac{\mathrm{\partial }{v}_n}{\mathrm{\partial }\tau }-{}_0^R{D}_{\tau }^{\alpha -1}{v}_n{|}_{\tau =0}\right.\\ & +\frac{{\tau }^{\alpha -2}}{\mathrm{\Gamma }\left(\alpha -1\right)}{}_0^R{D}_{\tau }^{\alpha -1}\left[(a{\tilde{v}}_n+b{\tilde{v}}_n^2+c{\tilde{v}}_n^3\right.\\ & +\left.\left.d)\frac{\mathrm{\partial }{\tilde{v}}_n}{\mathrm{\partial }x}+\gamma \frac{{\mathrm{\partial }}^3{\tilde{v}}_n}{\mathrm{\partial }{x}^3}\right]\right)\text{d}\tau ,\end{array}$(21) where $\lambda \left(\tau \right)$ is the Lagrange multiplier while $\delta v_n=0$ is the restriction variation. Taking into account the restricted variation $\delta {\tilde{v}}_n=0,$ the variation of (21) becomes (22) $\begin{array}{rl}\delta v_{n+1}& =\delta v_n+{\int }_0^t\lambda \left(\tau \right)\delta \frac{\mathrm{\partial }{v}_n}{\mathrm{\partial }\tau }\text{d}\tau \\ & =\delta v_n+\lambda \left(\tau \right)\delta v_n{|}_{\tau =t}-{\int }_0^t\frac{\mathrm{\partial }\lambda \left(\tau \right)}{\mathrm{\partial }\left(\tau \right)}\delta v_n=0.\end{array}$(22)

This relation gives (23) $\frac{\mathrm{\partial }\lambda \left(\tau \right)}{\mathrm{\partial }\tau }=0,1+\lambda \left(\tau \right)=0.$(23)

Thus, the Lagrange multiplier is $-1$ and so the correction functional (21) admits the form (24) $\begin{array}{rl}{v}_{n+1}\left(x,t\right)& =v_n\left(x,t\right)-{\int }_0^t\left(\frac{\mathrm{\partial }{v}_n}{\mathrm{\partial }\tau }-{}_0^R{D}_{\tau }^{\alpha -1}{v_n|}_{\tau =0}\right.\\ & \times \frac{{\tau }^{\alpha -2}}{\mathrm{\Gamma }\left(\alpha -1\right)}+{}_0^R{D}_{\tau }^{\alpha -1}\left[(a{\tilde{v}}_n+b{\tilde{v}}_n^2\right.\\ & \times \left.+\left.c{\tilde{v}}_n^3+d)\frac{\mathrm{\partial }{\tilde{v}}_n}{\mathrm{\partial }x}+\gamma \frac{{\mathrm{\partial }}^3{\tilde{v}}_n}{\mathrm{\partial }{x}^3}\right]\right)\text{d}\tau .\end{array}$(24)

As a result of $0\le \alpha <1,$ we have that $\alpha -1$ is negative and so the operator ${}_0^R{D}_{\tau }^{\alpha -1}$ will be converted to Riesz fractional integral ${}_0^R{I}_{\tau }^{1-\alpha }$ which is read as [19,20,48] (25) $\begin{array}{rl}{}_0^R{I}_t^{\alpha }f\left(t\right)& =\frac{1}{2}\left[{}_a^{}{I}_t^{\alpha }f\left(t\right)+{}_t^{}{I}_b^{\alpha }f\left(t\right)\right],\\ & =\frac{1}{2\mathrm{\Gamma }\left(\alpha \right)}{\int }_a^b{|t-\tau |}^{\alpha -1}f\left(\tau \right)\text{d}\tau ,\alpha >0.\end{array}$(25) where ${}_a^{}{I}_t^{\alpha }f\left(t\right)$ and ${}_t^{}{I}_b^{\alpha }f\left(t\right)$ are the left and the right Riemann–Liouville fractional integral respectively.

Physically, it is well known that the right Riemann–Liouville fractional derivative with respect to the independent variable time t points out the future status of the process [49]. For this reason, in what follows, the right Riemann–Liouville fractional derivative will be set equal to zero. We can choose the state variables initial value to be the solution zero-order correction, i.e. (26) $v_0\left(x,t\right)=A\text{sec}{\text{h}}^2\left(Bx\right),$(26) in which $A,B$ are constants. To build the solution first-order approximation, setting $n=1$ in Equation (24), utilizing (26) and after some tedious manipulations, we get (27) $\begin{array}{rl}{v}_1\left(x,t\right)& =A\text{sec}{\text{h}}^2\left(Bx\right)+\frac{2AB{t}^{\alpha }\sinh \left(Bx\right)}{\mathrm{\Gamma }\left(\alpha +1\right){\cosh }^9\left(Bx\right)}\\ & \times [\left(4B^2\gamma +1\right){\cosh }^6\left(Bx\right)+\left(aA-12B^2\gamma \right)\\ & \times {\cosh }^4\left(Bx\right)+b{A}^2{\cosh }^2\left(Bx\right)+c{A}^3]\end{array}$(27)

Putting n = 2 in Equation (24) and using the expression (27), we obtain (28) $\begin{array}{rl}{v}_2\left(x,t\right)& =A\text{sec}{\text{h}}^2\left(Bx\right)+\frac{2AB{t}^{\alpha }\sinh \left(Bx\right)}{\mathrm{\Gamma }\left(\alpha +1\right){\cosh }^9\left(Bx\right)}\\ & \times \left[\right(4B^2\gamma +1\left){\cosh }^6\right(Bx)+(aA-12B^2\gamma )\\ & \times {\cosh }^4\left(Bx\right)+b{A}^2{\cosh }^2\left(Bx\right)+c{A}^3]\\ & +\frac{4A{B}^2{t}^{2\alpha }}{\mathrm{\Gamma }\left(2\alpha +1\right){\cosh }^{16}\left(Bx\right)}\left[\frac{1}{7}{\left(4B^2\gamma +1\right)}^2\right.\\ & \times {\cosh }^{14}\left(Bx\right)+\frac{1}{14}(-1008\times {\gamma }^2{B}^4\\ & +80A{B}^{2}a\gamma -120B^2\gamma +8aA-3\left){\cosh }^{12}\right(Bx)\\ & +\frac{1}{7}(120A^2{B}^{2}b\gamma +1680{\gamma }^2{B}^4-176A{B}^{2}a\gamma \\ & +3A^2{a}^2+6b{A}^2+60B^2\gamma -5aA\left){\cosh }^{10}\right(Bx)\\ & +\frac{1}{14}(544A^3{B}^{2}c\gamma -824A^2{B}^{2}b\gamma -2520{\gamma }^2{B}^4\\ & +16A^{3}ab+294A{B}^{2}a\gamma +16c{A}^3-7A^2{a}^2\\ & -14b{A}^2\left){\cosh }^8\right(Bx)+\frac{A^2}{7}(-816A{B}^{2}c\gamma \\ & +10A^{2}ac+5A^2{b}^2+306b\gamma B^2-9Aab-9Ac)\\ & \times {\cosh }^6\left(Bx\right)+\frac{1}{14}(24A^{2}bc+1122\gamma c{B}^2\\ & -22Aac-11A{b}^2)A^3\left({\cosh }^4\left(Bx\right)\right.\\ & +\left.\left.\frac{c{A}^5}{7}\left(7Ac-13b\right){\cosh }^2\left(Bx\right)-\frac{15A^6{c}^2}{14}\right)\right]\\ & +\frac{40A^2{B}^3{t}^{3\alpha }\mathrm{\Gamma }\left(2\alpha \right)}{\mathrm{\Gamma }\left(3\alpha \right){\mathrm{\Gamma }}^2\left(\alpha +1\right){\cosh }^{23}Bx}\left[\right(4B^2\gamma +1)\\ & \times {\cosh }^6\left(Bx\right)+\left(-12B^2\gamma +aA\right){\cosh }^4\left(Bx\right)\\ & +b{A}^2{\cosh }^2\left(Bx\right)+c{A}^3]\left[\frac{a\left(4B^2\gamma +1\right)}{15}\right.\\ & \times {\cosh }^{12}\left(Bx\right)+\frac{1}{30}(24A{B}^{2}b\gamma -60a\gamma B^2\\ & +4A{a}^2+6bA-3a\left){\cosh }^{10}\right(Bx)\end{array}$(28) $\begin{array}{rl}& +\frac{1}{30}(48A^2{B}^{2}c\gamma -152A{B}^{2}b\gamma +16A^{2}ab\\ & +60a\gamma B^2+12A^{2}c-5A{a}^2-8bA\left)\text{cos}{\text{h}}^8\right(Bx)\\ & +\frac{1}{30}(-276A{B}^{2}c\gamma +26A^{2}ac+14A^2{b}^2\\ & +144b\gamma B^2-19Aab-15Ac\left)A\text{cos}{\text{h}}^6\right(Bx)\\ & +\frac{1}{15}\left(21A^{2}bc+126\gamma B^{2}c-15Aac-8A{b}^2\right)\\ & \times A{}^2{\cosh }^4(Bx{)}^{}+\frac{A^{4}c}{30}\left(30Ac-47b\right){\cosh }^2\left(Bx\right)\\ & \times \left.-\frac{11A^5{c}^2}{10}\right]+\frac{3A^3{B}^4{t}^{4\alpha }{\sinh }^2\left(Bx\right)}{{\mathrm{\Gamma }}^3\left(\alpha +1\right)\mathrm{\Gamma }\left(4\alpha \right){\cosh }^{30}\left(Bx\right)}\\ & \times \left[2b\right(4B^2\gamma +1\left){\cosh }^{10}\right(Bx)+(32A{B}^{2}c\gamma \\ & -60b\gamma B^2+4Aab+8Ac-3b\left){\cosh }^8\right(Bx)\\ & +(-212A{B}^{2}c\gamma +14A^{2}ac+6A^2{b}^2+60b\gamma B^2\\ & -5Aab-11Ac\left){\cosh }^6\right(Bx)+A(28A^{2bc}\\ & +201\gamma B^{2}c-17Aac-7A{b}^2\left){\cosh }^4\right(Bx)\\ & +2c{A}^3\left(13Ac-16b\right)\times {\cosh }^2\left(Bx\right)-29A^4{c}^2]\\ & \times \left[\right(4B^2\gamma +1\left){\cosh }^6\right(Bx)-(12B^2\gamma +aA)\\ & \times {\cosh }^4\left(Bx\right)+b{A}^2{\cosh }^2\left(Bx\right)+c{A}^3{]}^2\\ & +\frac{32c{A}^4{B}^5{t}^{5\alpha }{\sinh }^3\left(Bx\right)}{5{\mathrm{\Gamma }}^4\left(\alpha +1\right)\mathrm{\Gamma }\left(5\alpha \right){\cosh }^{37}\left(Bx\right)}\left[2\right(4B^2\gamma +1)\\ & \times {\cosh }^8\left(Bx\right)+\left(4aA-60B^2\gamma -3\right){\cosh }^6\left(Bx\right)\\ & +(6b{A}^2+60B^2\gamma -5aA){\cosh }^4\left(Bx\right)\\ & +A^2\left(8Ac-7b\right)\text{ cos}{\text{h}}^2\left(Bx\right)-9c{A}^3]\\ & \times \left[\right(4B^2\gamma +1\left)\text{cos}{\text{h}}^6\right(Bx)+(aA-12B^2\gamma )\\ & \times {\cosh }^4\left(Bx\right)+b{A}^2{\cosh }^2\left(Bx\right)+c{A}^3{]}^3.\end{array}$

In a similar way, we can find higher-order approximations employing the Maple package. Notice, the exact solution appears as an infinite approximation.

4. Interpretation of the results

Indeed, the evolution equations that are knowing as nonlinear partial differential equation have a particular type of elementary solutions naming as solitons possess the form of localized waves that preserve their attributes also after interaction between them, and then behave somewhat alike as particles. Despite one of the numerous reasons for occurring the solitary waves is the balancing script among the dispersion and nonlinearity, these waves can also be resulted due to different balancing effects. This motivates us to study and investigate in detail the influence of the fractional-order derivatives on the propagation and the structure of the obtained solitary waves from the time-fractional derivative for the KdV equation. To achieve our aims, we employ the method of semi-inverse [32,33] to find the Lagrangian function corresponding to the generalized KdV Equation (3). The Lagrangian function for the TFGKdV is assumed in an analogous style involving the left Riemann–Liouville derivative and consequently, we utilize the variational principles [49–51] to derive the Euler–Lagrange equation that gives immediately the TFGKdV. Although we start with left Riemann Liouville derivative, the obtained time-fractional KdV contains the Riesz Riemann derivatives. Moreover, we applied He’s method to construct a solution for the time-fractional generalized KdV. Assuming the initial value for the solution is postulated as $A\text{sec}{\text{h}}^2\left(Bx\right)$ and utilizing the Maple to perform the iterations of He’s method up to five iterations. To complete our study, we investigate the influence of the fractional derivative of different values of the order $\alpha =1,\left(3/4\right),\left(1/2\right),\gamma =1.$ In the follows, we assumed the nonlinearity coefficients are $a=-b=1,c=2,d=0.5$, and the dispersion $\gamma =1.$ while the amplitude of the initial solution is the unit and the constant $B=1/24$. 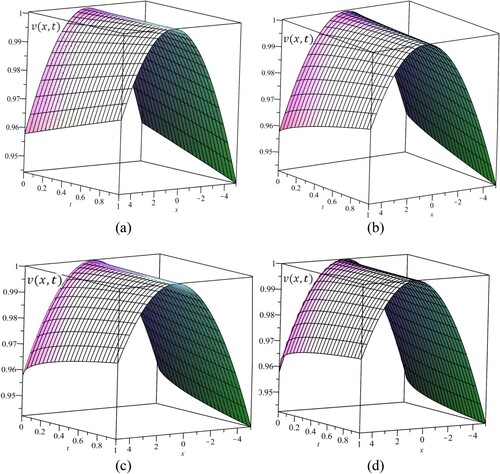Figure 1 displays the 3D solution for the TFGKdV equation with time t and space x for several values of the fractional-order α.

Figure 1. 3D graph for the $v\left(x,t\right)$ for the fractional-order of several values (a) $\alpha =1$, (b) $\alpha =3/4$, (c) $\alpha =1/2$ and (d) $\alpha =1/4$.

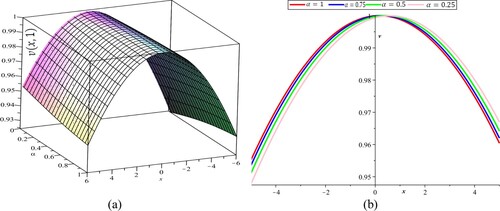
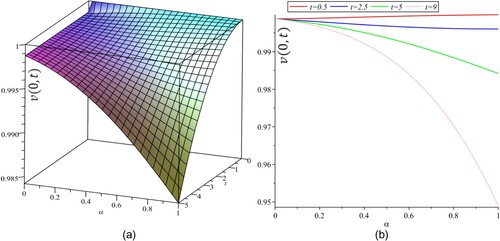
It is clear that for diverse values of the fractional-order α, the solution $u\left(x,t\right)$ remains a single soliton solution. This indicates the balancing script among the dispersion and nonlinearity remains true despite of the width and amplitude of the soliton are altered. The $\text{2D}$ and $\text{3D}$ figures appearing in Figure 2 outline the change of the structure of the soliton (width and amplitude) as a result of altering the fractional-order. This means that an increment in the fractional-order implies an increment in the altitude and the amplitude of the solitary wave solution. Figure 3 clarifies the effect of different values of the fractional-order on the amplitude of the soliton when x takes a certain value, say $x=0$. It is clear at a fixed value of the time $t$, the raise of the fractional-order implies a reducing the amplitude of the soliton wave solution.

Figure 2. (a) 3D graph and (b) 2D graph for $v\left(x,t\right)$ which relies only on x when the time $t=1$ for the fractional-order $\alpha$ with several values.

Figure 3. The distribution function amplitude for v(0; t) that depends only on the fractional-order $\alpha$ (a) 3D graph and (b) 2D graph.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

The authors acknowledge the Deanship of Scientific Research at King Faisal University for the financial support under Nasher Track [grant number 186034].

Appendix (He’s variational iteration method)

This method that has been developed by He (see, e.g. [52–57]) was utilized successfully to study wave equation that is either linear or nonlinear or wave-like equations in unbounded and bounded domains. Several researchers proved the reliability and efficiency of this method to be applicable to a large class of scientific applications to a large class of linear or nonlinear scientific applications (see, e.g. [58–61]). Furthermore, this method was proved sturdier than the current techniques, for instance, the Adomian method [62,63], perturbation method, etc. The method gives quickly convergent successive approximations of the exact solution in the case of its existence; or else, a few approximations can be utilized for numerical purposes. The computational procedures for the perturbation method are not an easy task, particularly, when the nonlinearity degree increases. Furthermore, the Adomian method possesses a difficult algorithm that is employed to find the Adomian polynomial that is required for nonlinear problems. While the present method does not demand specific requirements, such as small parameters, linearization and so on, for nonlinear operators. This method is considered an adjustment for the generic method of Lagrange multiplier [56,57]. It has been utilized successfully to construct the solution for integer nonlinear differential equations (see, e.g. [32,33]). In addition, it can be employed to build the solution fractional differential equations whether they are nonlinear or linear (see, e.g. [34–36]).

Consider the nonlinear partial differential equation (A1) $\hat{L}v\left(x,t\right)+\hat{N}v\left(x,t\right)=h\left(x,t\right),$(A1) where $\hat{L}$ and $\hat{N}$ represent the nonlinear and linear operator while h(x, t) acts the inhomogeneous term. Utilizing the iteration correction functional as [32,33], the $\left(n+1\right)\text{th}$ approximated solution for Equation (29) can be written as (A2) $\begin{array}{rl}{v}_{n+1}\left(x,t\right)& =v_n\left(x,t\right)+{\int }_0^t\lambda \left(\tau \right)\left[\hat{L}{v}_n\right(x,\tau )+\hat{N}{\tilde{v}}_n(x,\tau )\\ & -h\left(x,\tau \right)]\text{d}\tau ,n\ge 0,\end{array}$(A2) where λ(τ) represents the Lagrange multiplier that can be determined optimally by employing the variational theory while ${\tilde{v}}_n\left(x,t\right)$ is a restricted variation function, i.e. $\delta {\tilde{v}}_n\left(x,t\right)=0.$ The zeroth approximation $v_0\left(x,t\right)$ can be chosen as a solution of $\hat{L}v\left(x,t\right)=0$ or can be selected as the initial value $v\left(x,0\right)$. The exact solution for Equation (29) can be obtained when $n\to \mathrm{\infty },$ i.e. (A3) $v\left(x,t\right)=\underset{n\to \mathrm{\infty }}{lim}{v}_n\left(x,t\right).$(A3) Finally, we can summarize He’s variational method in the following algorithm:

Algorithm:

Step (1): Consider an equation in the form of Equation (29).

Step (2): Formulate Equation (30) which is considered the $\left(n+1\right)\text{th}$ approximated solution of Equation (29).

Step (3): Determine the Lagrange multiplier.

Step (4): Find the zeroth approximated solution, which can be taken as a solution for $\hat{L}v\left(x,t\right)=0$ or can be selected as an initial value.

Step (5): Insert the value of the Lagrange multiplier into Step (2) and find the approximated solutions for different values of $n$.

Step (6): For larger values of $n$, the approximated solution will be tended to the exact solution.

Step (7): Stop.