Analytic approximate solutions for some nonlinear Parabolic dynamical wave equations

Abstract

In this paper, modified variational iteration algorithm-II is investigated for finding approximate solutions of nonlinear Parabolic equations. Comparisons of the MVIA-II with trigonometric B-spline collocation method, variational iteration method, homotopy perturbation transform method, Adomian decomposition method, and modified variational iteration method are carried out, which show that the proposed algorithm (MVIA-II) is robust one. Some nonlinear Parabolic equations are given to demonstrate the implementation and accuracy of the MVIA-II.

KEYWORDS:

• Modified variational iteration algorithm-II
• Newell–Whitehead equation
• Fisher equations
• Allen-Cahn equation
• MVIA-I

1. Introduction

The exceptional advancement of nonlinear sciences and engineering during the most recent two decades, several analytical and numerical methods [1,2] including the sine-Gordon expansion, Adomian's decomposition [1], Finite difference [2], Variational iteration algorithm-I [5], Backlund transformation, Homotopy Pade [3], Variational principle [4], Jacobi elliptic function expansion [5], implicit-explicit [6], tanh-coth [7], Homotopy Analysis [8], Fourier pseudo-spectral [9], Hirota's bilinear [10], Homotopy Perturbation [11], Finite volume [12], lattice Boltzmann [13], generalized $\left(G^{\mathrm{\prime }}/G\right)-$ expansion method [14,15] are presented to solve different type differential equations. Most of these approaches have their inbuilt insufficiencies including divergent results, calculation of Adomian's polynomials, un-realistic assumptions, limited convergence, very lengthy calculations and non-compatibility with the nonlinearity of physical problem [16]. Encouraged and inspired by the continuous study in this area, we employ a moderately new strategy which is called modified variational iteration algorithm-II to find the mathematical solution of the general nonlinear parabolic equation [17] arises in quantum mechanics, plasma physics and mathematical biology of the form (1) $\frac{\mathrm{\partial }v}{\mathrm{\partial }t}=\frac{{\mathrm{\partial }}^{2}v}{\mathrm{\partial }{x}^2}+\alpha v+\text{β}{v}^n,$(1) where $\alpha \text{and}\text{β}$ are non zero real constants. Equation (1) gives rise to three widely known models. It becomes Allen-Cahn equation when $n=3,\alpha =1\text{and}\text{β}=-1$, which has various applications in quantum mechanics, biology and plasma physics [18]. If for $\text{β}=-\text{β}\text{and}n=3$, then Equation (1) turn out to be Newell–Whitehead (NW) equation, which appears in various study for describing the Rayleigh -Benard convection of binary fluid mixtures. While for $n=2\text{and}\text{β}=-\alpha$ this equation reduced to Fishers equation.

The AC equation is the indispensable model for numerous physical phenomena and helps as a model for the study of separation of phase in binary, isotropic and isothermal mixtures. It is well notorious that wave phenomena of fluid dynamics are demonstrated by bell-shaped $\text{sec}h$ or $\text{tan}h$ solutions and kink shaped solutions. To find analytical as well as numerical solutions of this model, numerous approaches can be found in the literature like the finite difference method has been applied by Yokuş and Bulut [19] for the mathematical computation of Ac equation and has been shown that the proposed technique is more stable than the Fourier-Von Neumann technique for solving these type equations. Hariharan and Kannan [17] developed Haar wavelet or transform technique for this type equations, Bulut et al. [20] used Bernoulli sub-equation function technique to gain exponential prototype structures to the AC model. Yang et al. [6] studied the stability of the Implicit-Explicit approaches for AC equation [37], Gui and Zhao [21] studied the qualitative properties of travelling wave solution of the AC equation. Jeong and Kim [22] proposed an explicit hybrid numerical method based on splitting technique and obtained analytical solution of Allen-Cahn equation, while the combination of Quasi-Newton, reproducing kernel and finite difference methods are utilized by Niu et al. [23]. Hou and Leng [23] considered a finite difference technique for the approximations of one-dimensional AC equation. Recently, Chen et al. [24] derived a posteriori error approximation based on the elliptic reconstruction method for AC equation by applying Crank–Nicolson finite element technique.

The Newell-Whitehead equation which is also known as Newell–Whitehead–Segel equation explains the dynamical behaviour near the bifurcation point for the Rayleigh-Benard convection of binary fluid mixtures [7]. In recent years, many authors have studied this equation and for the numerical solution of this type equation, different approaches have been employed like Ezzati and Shakibi [25] applied multiquadric quasi-interpolation and Adomian's decomposition methods for the numerical treatment of NW equation. Homotopy Pade and Homotopy analysis methods have been employed by Kheiri et al. [3], Sakaguchi [26] studied Zigzag instability of the NW equation numerically, while, Antoniou [27] obtained analytic solution of the NW equation by using Riccati equation method.

The well-known Fisher's equation combines logistic nonlinearity with diffusion. It was Fisher [28] who presented for the first time, the renowned equation is known as Fisher equation, to define the propagation of a mutant gene, which has many applications and encountered in population dynamics, chemical kinetics, flame propagation, neurophysiology and autocatalytic chemical reactions [29–31]. Many researchers have explained this model by different methods like Harihar an et al. [32] have presented Haar wavelet technique for the mathematical treatment of Fisher's equation. Homotopy analysis technique has been employed for the analytical solution of Fisher equation by Babolian and Saeidian [8]. Ismail et al. [1] have employed Adomian decomposition technique for the approximate solution, Zhang et al. [33] employed discontinuous Galerkin technique for numerical solution, Moghimi and Hejazi [34] have used Variational iteration method and by Modified pseudospectral method is investigated by Javidi [35]. Triki and Wazwaz [36] proposed a trial equation method for exact soliton solutions have been obtained for the first time of the Fisher equation. It is worth referencing that Wazwaz made a nitty-gritty investigation for solitons and kink solutions of Newell–Whitehead, Allen-Cahn and Fisher equations using tanh–coth approach [7] and analytical solutions of these equations are attained by Adomian decomposition method [37].

In the last two decades, the variational iteration method has been broadly employed for the analytic approximate solutions of different types of PDEs [38–43]. The originator himself advanced this method and now variational iteration algorithms have attracted more researchers. These algorithms are employed as an alternative to obtain a precise and a reliable solution of the nonlinear PDEs models which reduce complexities counter in the process conventional methods like finite element procedures, finite difference and, Adomian decomposition method etc. [44–53].

The main endeavour of this article is to introduce a numerical algorithm to approximate the Newell–Whitehead (NW), Allen–Cahn (AC) and Fisher's equations. It is to be worth mentioning that such model equations arise commonly in various branches of science, engineering and physics, the proposed algorithm is completely well-suited with the complications of such problems as well as easy to implement and use. Numerical results are very accurate and encouraging.

This article is composed as follows; in Section [2], modified variational iteration algorithm-II is depicted. In Section [3], To check the dependability of new presented technique, some problems are incorporated and results are shown in the form of absolute error for various values of parameters used in the models, and in the last segment [4], a nitty gritty conclusion is discussed.

2. Description of the method

In order to convey the elementary idea of MVIA-II, we consider. (2) $L\left(v\right)+N\left(v\right)=g,$(2) where $L\left(v\right)$ is a linear, $N\left(v\right)$ is a nonlinear operator and $g$ is the source term. For any nonzero scalar $\lambda$, we have (3) $\lambda \left[L\left(v\right)+N\left(v\right)-g\right]=0,$(3) By taking the integral from 0 to $\varsigma$, we get, (4) ${\int }_0^{\varsigma }\lambda \left[L\left(v\right)+N\left(v\right)-g\right]ds,$(4) The above relation can be rewritten as: (5) $v_n\left(\varsigma \right)=v_n\left(\varsigma \right)+{\int }_0^{\varsigma }\lambda \left[L\left(v\right)+N\left(v\right)-g\right]ds,$(5) From Equation (5), one can find The relation of recurrence of VIM given below, (6) $v_{n+1}\left(\varsigma \right)=v_n\left(\varsigma \right)+{\int }_0^{\varsigma }\left[L\left\{v_n\left(s\right)\right\}+N\left\{v_n\left(s\right)\right\}-g\right]ds,$(6)

For a given $v_0\left(\varsigma \right)$, approximate solution $v_{n+1}\left(\varsigma \right)$ of equation (5) can be obtained, and the Equation (6) is known as variational iteration method, where the unknown scalar $\lambda$ is known as the Lagrange multiplier [54], its values can be obtained by using the optimality conditions. (7) $v_{n+1}\left(\varsigma \right)=v_n\left(\varsigma \right)+{\int }_0^{\varsigma }\lambda \left[L\left\{v_n\left(s\right)\right\}+\widetilde{N\left\{v_n\left(s\right)\right\}}-g\right]ds,$(7) In the above recurrence relation $\widetilde{v_n\left(s\right)}$ is considered as a restricted variation. which in turn gives $\delta \widetilde{v_n\left(s\right)}=0$.

According to He et al. [55,56], a more summarizing iteration formula can be made, known as variational iteration algorithm-II (VIA-II), (8) $v_{n+1}\left(\varsigma \right)=v_0\left(\varsigma \right)+{\int }_0^{\varsigma }\lambda \left[N\left\{v_n\left(s\right)\right\}-g\right]ds,$(8) The sequence of approximants obtained gives us the exact solution $v\left(\varsigma \right)$, where (9) $v\left(\varsigma \right)={\text{Lim}}_{n\to \mathrm{\infty }}{v}_n\left(\varsigma \right).$(9) An auxiliary parameter $h$ can be presented into the iterative algorithm: VIA-II, which is employed to improve the accurateness and ability of the procedure. By introducing $h$, in MVIA-II and summarizing the procedure; (10) $\left\{\begin{array}{l}{v}_0\left(\varsigma \right)\text{is}\text{a}\text{proper}\text{initial}\text{approximation},\\ v_1\left(\varsigma ,h\right)=v_0\left(\varsigma \right)+h{\int }_0^{\varsigma }\lambda \left(s\right)\left[L\right\{v_0\left(s\right)\}\\ +N\left\{v_0\left(s\right)\right\}-g\left(s\right)]ds,\\ v_{n+1}\left(\varsigma ,h\right)=v_0\left(\varsigma ,h\right)+h{\int }_0^{\varsigma }\lambda \left(s\right)\\ \left[N\left\{v_n\left(s,h\right)\right\}-g\left(s,h\right)\right]ds,\\ n=1,2,3,\dots \end{array}\right.$(10) This algorithm is named as MVIA-II and utilized here to investigate some nonlinear Parabolic equations numerically.

3. Numerical applications

In order to demonstrate the implementation, precision and effectiveness of the planned algorithm, five different types of nonlinear Parabolic equations have been solved in this section. Two test problems are for Allen–Cahn equation, two for Newell–Whitehead equation and the other one test problem is for the Fisher equation. We compute the absolute error described by the below relation $E_j=|v_j^{\text{exact}}-V_j^{\text{approximate}}|.$Also, all the numerical computation work has been made by using Mapple and Matlab R2015a.

3.1. Test Problem 1 (Allen–Cahn equation)

First, consider the Equation (1) with the values of constants as $n=3,\alpha =1\text{and}\text{β}=-1$, which gives the AC equation of the following form [57], (11) $\frac{\mathrm{\partial }v}{\mathrm{\partial }t}=\frac{{\mathrm{\partial }}^{2}v}{\mathrm{\partial }{x}^2}+v-v^3,$(11)

With initial-boundary conditions: $\begin{array}{rl}v\left(x,0\right)& =-0.5+0.5\tan h\left(0.3536x\right),\\ v\left(0,t\right)& =-0.5+0.5\tan h\left(0.75t\right).\end{array}$ $v\left(1,t\right)=-0.5+0.5\tan h\left(0.3536-0.75t\right),$The exact solution of the above system as follows from [57]: (12) $v\left(x,t\right)=-0.5+0.5\text{tan}h\left(0.3536x-0.75t\right).$(12)

The relation of recurrence of VIM for Equation (11) is given by, (13) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_n\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\\ & \times \left\{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }-\stackrel{~}{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right.\\ & \left.-\widetilde{v_n\left(x,\varsigma ,h\right)+}\widetilde{v_n{\left(x,\varsigma ,h\right)}^3}\phantom{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }}\right\}d\varsigma ,\end{array}$(13) The value of $\lambda \left(\varsigma \right)$ can be obtained by the variational principle [58–60] or using the optimality condition, $\frac{\mathrm{\partial }{v}_{n+1}\left(x,t,h\right)}{\mathrm{\partial }{v}_n\left(x,t,h\right)}=0$We obtained the value of $\lambda \left(\varsigma \right)$, which is $\lambda \left(\varsigma \right)=-1$. By putting the value of $\lambda \left(\varsigma \right)$ in equation (13) gives (14) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_n\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\left\{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }\right.\\ & -\frac{{\mathrm{\partial }}^2{v}_n(x,\varsigma ,h)}{\mathrm{\partial }{x}^2}-v_n(x,\varsigma ,h)\\ & +\left.v_n\left(x,\varsigma ,h{)}^3\right)\phantom{\frac{{\mathrm{\partial }}^2{v}_n(x,\varsigma ,h)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma ,\end{array}$(14)

According to our proposed scheme (10), the following iterative formula is obtained (15) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_0\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\left\{-\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}\right.\\ & \left.-v_n\left(x,\varsigma ,h\right)+v_n{\left(x,\varsigma ,h\right)}^3)\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma ,\end{array}$(15) We consider the initial approximation $v_0\left(x,t\right)$ as, $v_0\left(x,t\right)=-0.5+0.5\tan h\left(0.3536x\right).$Then from The relation of recurrence of VIM (14), we get the following other iterations, $\begin{array}{rl}{v}_1(x,t,h)& =\text{tan}h\left(\right(221\ast x\left)/625\right)/2\\ & -(h\ast t\ast \text{exp}((442\ast x)/625)\\ & \ast (585989\ast \text{exp}(442\ast x\left)/625\right)\\ & +585886\left)\right)/(390625\ast \text{exp}((442\ast x)/625)\\ & +1{)}^{\wedge }3-1/2,\end{array}$ $⋮$ $⋮$

For obtained approximate solution, the following residual function can be used to find a valid value of h, (16) $\begin{array}{rl}{r}_3\left(x,t,h\right)& =\frac{\mathrm{\partial }{v}_3\left(x,t,h\right)}{\mathrm{\partial }t}-\frac{{\mathrm{\partial }}^2{v}_3\left(x,t,h\right)}{\mathrm{\partial }{x}^2}\\ & -v_3\left(x,t,h\right)+v_3(x,t,h{)}^3.\end{array}$(16)

The norm 2 of residual function (16) for 3rd-order approximate solution for $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$ is (17) $e_3\left(h\right)={\left[\frac{1}{{\left(11\right)}^2}\sum _{i=0}^{10}\sum _{j=0}^{10}{\left\{r_3\left(\frac{i}{10},\frac{j}{10},h\right)\right\}}^2\right]}^{\frac{1}{2}}$(17)

The residual function (17) can be utilized for the approximation of $e_3\left(h\right)$ and an appropriate value of the $h$ can be found out by making the $e_3\left(h\right)$ minimum. The value of the auxiliary parameter is determined to be 0.956746100718808 when the minimum value of $e_3\left(h\right)$ is obtained which is 0.768386328622880561E-3. More precise and accurate results can be obtained when the number of iterations is increased. Utilizing the value of $h$ in $v_3\left(x,t,h\right)$ in the domain $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$, the following results are obtained.

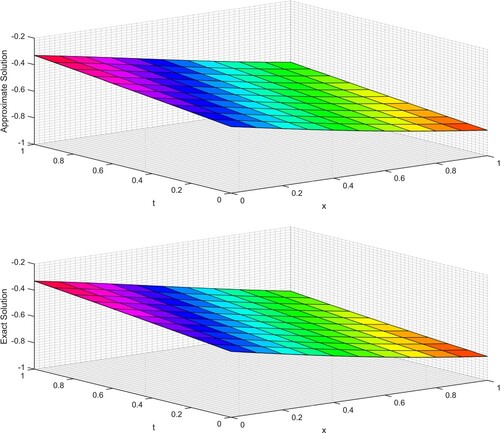
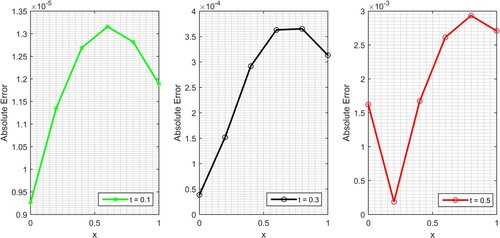
The numerical solutions of Test Problem (1) are reported in Tables 1 and 2. To prove the efficiency of the MVIA-II, comparison in terms of absolute errors is carried out the proposed technique and trigonometric B-spline collocation technique are reported in Table 1, while the comparison of MVIA-II and exact solutions are presented in Table 2. In comparison with [61] results, one can ensure that the results of MVIA-II are more accurate, efficient and reliable. Graphical results of Allen-Cahn equation corresponding Test Problem (1) are shown in Figures 1 and 2. In the first one, the behaviour of exact and MVIA-II solutions has been shown while in second the absolute errors graphs have been plotted for $t=0.001$ and $t=0.005$. It is cleared from figures that the MVIA-II can handle the nonlinear Parabolic equations precisely (Figure 3).

Figure 1. (Left): Behavior of exact and (Right): approximate solution for Test Problem 1.

Figure 2. Comparing the curves of absolute errors for different time levels for Test Problem 1.

Figure 3. Comparing the curves of absolute errors for different time levels for the Test Problem 2.

Table 1. Comparison in the form of absolute errors for Test Problem 1.

	$t=0.001$		$t=0.005$		$t=0.009$		$t=0.01$
$x$	Present	TBS [57]	Present	TBS [57]	Present	TBS [57]	Present	TBS [57]
0.1	1.620 E-05	2.448 E-04	8.101 E-05	9.687 E-04	1.454 E-04	1.492 E-03	1.621 E-04	1.606 E-03
0.2	1.614 E-05	2.000 E-04	8.073 E-05	1.016 E-03	1.445 E-04	1.761 E-03	1.615 E-04	1.935 E-03
0.3	1.604 E-05	1.797 E-04	8.024 E-05	9.082 E-04	1.433 E-04	1.644 E-03	1.606 E-04	1.826 E-03
0.4	1.590 E-05	1.594 E-04	7.956 E-05	8.052 E-04	1.418 E-04	1.465 E-03	1.593 E-04	1.632 E-03
0.5	1.572 E-05	1.410 E-04	7.869 E-05	7.124 E-04	1.399 E-04	1.296 E-03	1.576 E-04	1.444 E-03
0.6	1.551 E-05	1.242 E-04	7.764 E-05	6.280 E-04	1.378 E-04	1.143 E-03	1.555 E-04	1.273 E-03
0.7	1.526 E-05	1.091 E-04	7.643 E-05	5.520 E-04	1.353 E-04	1.003 E-03	1.531 E-04	1.116 E-03
0.8	1.499 E-05	9.502 E-05	7.505 E-05	4.824 E-04	1.326 E-04	8.536 E-04	1.504 E-04	9.434 E-04
0.9	1.468E-05	8.886 E-05	7.535 E-05	3.725 E-04	1.296 E-04	6.009 E-04	1.441E-04	6.534 E-04

Table 2. Comparison of the numerical results for Test Problem 1.

			Approximate solution		Absolute errors
$x$	$t$	Exact solution	Present	TBS [57]	Present
0.1	0.001	−0.48270191	−0.48268570	−0.48294667	1.620E−05
0.2	0.002	−0.46544517	−0.46541289	−0.46584916	3.228 E−05
0.3	0.003	−0.44827076	−0.448222628	−0.44881129	4.813 E−05
0.4	0.004	−0.43121885	−0.43115521	−0.43186126	6.363 E−05
0.5	0.005	−0.41432848	−0.41424978	−0.41504090	7.869 E−05
0.6	0.006	−0.39763717	−0.39754397	−0.39839276	9.320 E−05
0.7	0.007	−0.38118064	−0.38107357	−0.38195995	1.071 E−04
0.8	0.008	−0.36499250	−0.36487227	−0.36571227	1.202 E−04
0.9	0.009	−0.34910400	−0.34897140	−0.34910129	1.326 E−04

3.2. Test Problem 2 (Allen–Cahn equation)

Consider the Equation (1) with the values of constants as $n=3,\alpha =1\text{and}\text{β}=-1$, which gives the AC equation of the following form [57], (18) $\frac{\mathrm{\partial }v}{\mathrm{\partial }t}=\frac{{\mathrm{\partial }}^{2}v}{\mathrm{\partial }{x}^2}+v-v^3,$(18) Having the initial condition: $v\left(x,0\right)={\left(1+e^{-\frac{\sqrt{2}}{2}x}\right)}^{-1},$

And boundary conditions $\begin{array}{rl}v\left(0,t\right)& ={\left(1+e^{-\frac{3}{2}t}\right)}^{-1},\\ v\left(1,t\right)& ={\left(1+e^{-\frac{\sqrt{2}}{2}\left(1+\frac{3\sqrt{2}}{2}t\right)}\right)}^{-1},\end{array}$and exact solution from [57], which is: (19) $v\left(x,t\right)={\left(1+e^{-\frac{\sqrt{2}}{2}\left(x+\frac{3\sqrt{2}}{2}t\right)}\right)}^{-1}.$(19)

The relation of recurrence of VIM for Equation (18) is given by, (20) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_n\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\\ & \times \left\{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }-\stackrel{~}{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right.\\ & \left.-\widetilde{v_n\left(x,\varsigma ,h\right)}+\widetilde{v_n{\left(x,\varsigma ,h\right)}^3}\phantom{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }}\right\}d\varsigma .\end{array}$(20) The value of $\lambda \left(\varsigma \right)$ can be obtained by the variational principle [58–60] or using the optimality condition, $\frac{\mathrm{\partial }{v}_{n+1}\left(x,t,h\right)}{\mathrm{\partial }{v}_n\left(x,t,h\right)}=0$We obtained the value of $\lambda \left(\varsigma \right)$, which is $\lambda \left(\varsigma \right)=-1$. By putting the value of $\lambda \left(\varsigma \right)$ in equation (20) gives (21) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_n\left(x,t,h\right)-h{\int }_0^t\left\{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }\right.\\ & -\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}-v_n\left(x,\varsigma ,h\right)\\ & \left.+v_n{\left(x,\varsigma ,h\right)}^3\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma .\end{array}$(21)

According to our proposed scheme (10), the following iterative formula is obtained (22) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_0\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\left\{-\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}\right.\\ & \left.-v_n\left(x,\varsigma ,h\right)+v_n{\left(x,\varsigma ,h\right)}^3\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma ,\end{array}$(22)

We consider the initial approximation $v_0\left(x,t\right)$ as, $v_0\left(x,t\right)={\left(1+e^{-\frac{\sqrt{2}}{2}x}\right)}^{-1}.$Then from The relation of recurrence of VIM (22), we get the following other iterations, $\begin{array}{rl}{v}_1\left(x,t,h\right)& =\left(\text{exp}\right(\left(2^{\wedge }\right(1/2)\ast x)/2)\\ & \ast (2\ast \text{exp}(\left(2^{\wedge }\right(1/2)\ast x)/2)+3\ast h\ast t\\ & +2\left)\right)/(2\ast (\text{exp}\left(\right(2^{\wedge }\left(1/2\right)\ast x\left)/2\right)\\ & +1{)}^{\wedge }2),\end{array}$ $\begin{array}{rl}{v}_2\left(x,t,h\right)& =1/\left(\text{exp}\right(-\left(2^{\wedge }\right(1/2)\ast x)/2)+1)\\ & +(3\ast h\ast t\ast \text{exp}(\left(2^{\wedge }\right(1/2)\ast x)/2)\\ & \ast (96\ast \text{exp}(2^{\wedge }\left(1/2\right)\ast x)\\ & +16\ast \text{exp}(2\ast 2^{\wedge }(1/2)\ast x)\\ & +64\ast \text{exp}\left(\right(2^{\wedge }\left(1/2\right)\ast x\left)/2\right)\\ & +64\ast \text{exp((3}\ast 2^{\wedge }\ast x\left)/2\right)+12\ast h\ast t\\ & -24\ast h^{\wedge }2\ast t^{\wedge }2\ast \text{exp}\left(2^{\wedge }\right(1/2)\ast x)\\ & -9\ast h^{\wedge }3\ast t^{\wedge }3\ast \text{exp}\left(2^{\wedge }\right(1/2)\ast x)\\ & -24\ast h^{\wedge }2\ast t^{\wedge }2\ast \text{exp}\left(\right(3\ast 2^{\wedge }\left(1/2\right)\\ & \ast x\left)/2\right)-12\ast h\ast t\ast \text{exp}(2\ast 2^{\wedge }(1/2)\ast x)\\ & +24\ast h\ast t\ast \text{exp}\left(\right(2^{\wedge }\left(1/2\right)\ast x\left)/2\right)\\ & -24\ast h\ast t\ast \text{exp}\left(\right(3\ast 2^{\wedge }\left(1/2\right)\ast x\left)/2\right)\\ & +16\left)\right)/(32\ast (\text{exp}\left(\right(2^{\wedge }\left(1/2\right)\ast x\left)/2\right)\\ & +1{)}^{\wedge }6),\end{array}$ $⋮$ $⋮$ For obtained approximate solution $v_4\left(x,t,h\right)$, the following residual function can be used to find a valid value of h, (23) $\begin{array}{rl}{r}_4\left(x,t,h\right)& =\frac{\mathrm{\partial }{v}_4\left(x,t,h\right)}{\mathrm{\partial }t}-\frac{{\mathrm{\partial }}^2{v}_4\left(x,t,h\right)}{\mathrm{\partial }{x}^2}-v_4\left(x,t,h\right)\\ & +v_4(x,t,h{)}^2\end{array}$(23)

The norm 2 of residual function (23) with respect to $h$ for $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$ is: (24) $e_4\left(h\right)={\left[\frac{1}{{11}^2}\sum _{i=0}^{10}\sum _{j=0}^{10}{\left\{r_4\left(\frac{i}{10},\frac{j}{10},h\right)\right\}}^2\right]}^{\frac{1}{2}}$(24) The residual function (24) can be utilized for the approximation of $e_4\left(h\right)$ and an appropriate value of the $h$ can be found out by making the $e_4\left(h\right)$ minimum. The value of the auxiliary parameter is determined to 0.846053479477633 when the minimum value of $e_4\left(h\right)$ is 0.874216890183716032E-2. More precise and accurate results can be obtained when the number of iterations is increased. 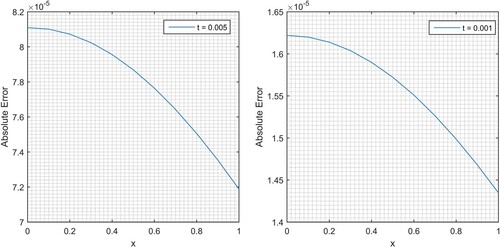By means of this value of $h$ in $v_4\left(x,t,h\right)$ in the domain $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$, error b/w the exact and MVIA-II solutions can be seen in Figure 4, while the Comparison in the form of absolute errors of MVIA-II and TBS [42] for different values of $t$ are presented in Table 3.

Figure 4. Absolute error graph for x = 1 for Test Problem 3.

Table 3. Comparison of the numerical results for Test Problem 2.

	$t=0.001$		$t=0.005$		$t=0.009$		$t=0.01$
$x$	Present	TBS [57]	Present	TBS [57]	Present	TBS [57]	Present	TBS [57]
0.1	3.765 E-05	2.509 E-04	2.882 E-04	1.127 E-03	5.187 E-04	1.917 E-03	5.763 E-04	2.108 E-03
0.2	5.744 E-05	3.351 E-04	2.871 E-04	1.715 E-03	5.165 E-04	3.100 E-03	5.738 E-04	3.446 E-03
0.3	5.708 E-05	4.389 E-04	2.852 E-04	2.233 E-03	5.131 E-04	4.085 E-03	5.700E-04	4.555 E-03
0.4	5.658 E-05	5.456 E-04	2.827 E-04	2.768 E-03	5.084 E-04	5.057 E-03	5.648 E-04	5.639 E-03
0.5	5.595 E-05	6.542 E-04	2.795 E-04	3.314 E-03	5.025 E-04	6.042 E-03	5.582 E-04	6.735 E-03
0.6	5.519 E-05	7.626 E-04	2.756 E-04	3.857 E-03	4.956 E-04	7.028 E-03	5.505 E-04	7.830 E-03
0.7	5.432 E-05	8.697 E-04	2.712 E-04	4.399 E-03	4.875 E-04	7.968 E-03	5.415 E-04	8.850 E-03
0.8	5.333 E-05	9.653 E-04	2.662 E-04	4.902 E-03	4.785 E-04	8.510 E-03	5.314 E-04	9.353 E-03
0.9	5.224 E-05	1.161 E-03	2.607 E-04	4.617 E-03	4.685 E-04	7.136 E-03	5.203 E-04	7.685 E-03

Table 4. Comparison of the numerical results for Test Problem 3.

			Approximate solution		Absolute errors
$t$	$x$	Exact Solution	Present	VIM [62]	Present	VIM [62]
0	1	0.159466223943033	0.159466223943033	0.1594662239430331	2.498E−16	0
0.2	1	0.193509037431178	0.193509600917448	0.1935090374311784	5.635E−07	2.1E−06
0.4	1	0.231630452841077	0.231629619298055	0.2316304528410767	8.335E−07	5.3E−05
0.6	1	0.273447260416673	0.273433638969862	0.2734472604166732	1.362E−05	3.2E−04
0.8	1	0.318375189312876	0.318317204172162	0.3183751893128759	5.799E−05	1.1E−02
1	1	0.365661380536344	0.365500671580091	0.3656613805363442	1.607E−04	2.6E−02

3.3. Test Problem 3 (Newell–Whitehead equation)

Consider the Equation (1) with the values of constants as $n=2,\alpha =1\text{and}\text{β}=-1$, which gives the NW equation of the following form (25) $\frac{\mathrm{\partial }v}{\mathrm{\partial }t}=\frac{{\mathrm{\partial }}^{2}v}{\mathrm{\partial }{x}^2}+v-v^2,$(25) having initial condition: $v\left(x,0\right)={\left(1+e^{\frac{x}{\sqrt{6}}}\right)}^{-2}$

and exact solution from [62], which is: (26) $v\left(x,t\right)={\left(1+e^{\frac{x}{\sqrt{6}}-\frac{5}{6}t}\right)}^{-2}.$(26)

By applying MVIA-I, The relation of recurrence of VIM for Equation (25) is given by, (27) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_n\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\left\{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }\right.\\ & -\stackrel{~}{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}-\widetilde{v_n\left(x,\varsigma ,h\right)}\\ & \left.+\widetilde{v_n{\left(x,\varsigma ,h\right)}^2}\right\}d\varsigma ,\end{array}$(27) The value of $\lambda \left(\varsigma \right)$ can be obtained by the variational principle [58–60] or using the optimality condition, $\frac{\mathrm{\partial }{v}_{n+1}\left(x,t,h\right)}{\mathrm{\partial }{v}_n\left(x,t,h\right)}=0$We obtained the value of $\lambda \left(\varsigma \right)$, which is $\lambda \left(\varsigma \right)=-1$. By putting the value of $\lambda \left(\varsigma \right)$ in equation (27) gives in the following iterative structure: (28) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_n\left(x,t,h\right)-h{\int }_0^t\left\{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }\right.\\ & -\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}-v_n\left(x,\varsigma ,h\right)\\ & +\left.v_n{\left(x,\varsigma ,h\right)}^2\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma .\end{array}$(28) According to our proposed scheme (10), the following iterative formula is obtained (29) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_0\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\left\{-\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}\right.\\ & \left.-v_n\left(x,\varsigma ,h\right)+v_n{\left(x,\varsigma ,h\right)}^2\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma ,\end{array}$(29) We consider the initial approximation $v_0\left(x,t\right)$ as, $v_0\left(x,t\right)=\frac{1}{{\left(1+e^{\frac{x}{\sqrt{6}}}\right)}^2}.$Then from The relation of recurrence of VIM (29), we get the following other iterations, $\begin{array}{rl}{v}_1\left(x,t,h\right)& =(3\ast exp(\left(6^{\wedge }\left(1/2\right)\ast x\right)/6)+5\ast h\ast t\\ & \ast exp\left(\left(6^{\wedge }\left(1/2\right)\ast x\right)/6\right)+3)/\\ & \times \left(3\ast (exp\left(\left(6^{\wedge }\left(1/2\right)\ast x\right)/6\right)+1{)}^{\wedge }3\right),\end{array}$ $\begin{array}{rl}{v}_2(x,t,h)& =1/\left(\text{exp}\right(\left(6^{\wedge }\right(1/2)\ast x)/6)+1{)}^{\wedge }2\\ & +(h\ast ((5\ast t\ast \text{exp}(\left(6^{\wedge }\right(1/2)\ast x)/6)\\ & \ast (36\ast \text{exp}(\left(6^{\wedge }\right(1/2)\ast x)/2)\\ & +108\ast \text{exp}\left(\right(6^{\wedge }\left(1/2\right)\ast x\left)/3\right)\\ & -15\ast h\ast t+30\ast h\ast t\ast \text{exp}\left(\right(6^{\wedge }\left(1/2\right)\\ & \ast x\left)/2\right)+45\ast h\ast t\ast \text{exp}\left(\right(6^{\wedge }\left(1/2\right)\\ & \ast x\left)/3\right)+36\left)\right)/108-(5\ast t\ast \text{exp}((6^{\wedge }\\ & \times \left(1/2\right)\ast x\left)/3\right)\ast (20\ast h^{\wedge }2\ast t^{\wedge }2\\ & -108\left)\right)/108\left)\right)/\left(\text{exp}\right(\left(6^{\wedge }\right(1/2)\ast x)/6)\\ & +1{)}^{\wedge }6,\end{array}$ $⋮$ $⋮$

For obtained approximate solution $v_4\left(x,t,h\right)$, the following residual function can be used to find a valid value of h, (30) $\begin{array}{rl}{r}_4\left(x,t,h\right)& =\frac{\mathrm{\partial }{v}_4\left(x,t,h\right)}{\mathrm{\partial }t}-\frac{{\mathrm{\partial }}^2{v}_4\left(x,t,h\right)}{\mathrm{\partial }{x}^2}-v_4\left(x,t,h\right)\\ & +v_4(x,t,h{)}^2\end{array}$(30)

The norm 2 of residual function (30) with respect to $h$ for $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$ is: (31) $e_4\left(h\right)={\left[\frac{1}{{11}^2}\sum _{i=0}^{10}\sum _{j=0}^{10}{\left\{r_4\left(\frac{i}{10},\frac{j}{10},h\right)\right\}}^2\right]}^{\frac{1}{2}}$(31) The residual function (31) can be utilized for the approximation of $e_4\left(h\right)$ and an appropriate value of the $h$ can be found out by making the $e_4\left(h\right)$ minimum. The value of the auxiliary parameter is determined to be1.00001765132560 when the minimum value of $e_4\left(h\right)$ is achieved. More precise and accurate results can be obtained when the number of iterations is increased. By means of this value of $h$ in $v_4\left(x,t,h\right)$ in the domain $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$, error b/w the exact and MVIA-II solutions can be seen in Figure 4, while the comparison of MVIA-II and exact solutions, as well as Comparison in the form of absolute errors with VIM, is presented in Table 4, which show that the proposed technique can handle the Newell–Whitehead equations precisely.

Table 5. Comparison of the numerical results for Test Problem 4.

	$t=0.1$		$t=0.3$		$t=0.5$
$x$	Present	HPTM [63]	Present	HPTM [63]	Present	HPTM [63]
0.1	9.2588440E-06	1.221229E-4	3.8573053E-05	3.022038E-3	16215066 E-03	1.245533E-2
0.2	1.1350216E-05	1.328287E-4	1.5193154 E-04	3.415236E-3	1.8704859 E-04	1.462723E-2
0.4	1.2689898E-05	1.352957E-4	2.9185887E-04	3.602846E-3	1.6733416E-03	1.597269E-2
0.6	1.3157393E-05	1.296021E-4	3.6312075E-04	3.570756E-3	2.6144372 E-03	1.636664E-2
0.8	1.2819577E-05	1.168616E-4	3.6523601E-04	3.333532E-3	2.9338374 E-03	1.580592E-2
1.0	11888620E-05	9.893015E-5	3.1331675E-04	2.929772E-3	2.7080923 E-03	1.440339E-2

3.4. Test Problem 4 (Newell–Whitehead equation)

Consider the Equation (1) with the values of constants as $n=4,\alpha =1\text{and}\text{β}=-1$, which gives the NW equation of the following form the [63] (32) $\frac{\mathrm{\partial }v}{\mathrm{\partial }t}=\frac{{\mathrm{\partial }}^{2}v}{\mathrm{\partial }{x}^2}+v-v^4,0<x<1,t>0,$(32) having the initial condition: $v\left(x,0\right)={\left(1+e^{\frac{3x}{\sqrt{10}}}\right)}^{-\frac{2}{3}},$and exact solution from [63], which is: (33) $v\left(x,t\right)={\left[\frac{1}{2}\text{tan}h\left\{-\frac{3}{2\sqrt{10}}\left(x-\frac{7}{\sqrt{10}}t\right)\right\}+\frac{1}{2}\right]}^{\frac{2}{3}}$(33)

The relation of recurrence of VIM for Equation (32) is given by, (34) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_n\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\left\{\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }\right.\\ & -\stackrel{~}{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}-\widetilde{v_n\left(x,\varsigma ,h\right)}\\ & \left.+\widetilde{v_n{\left(x,\varsigma ,h\right)}^4}\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma ,\end{array}$(34)

The value of $\lambda \left(\varsigma \right)$ can be obtained by the variational principle [58–60] or using the optimality condition, $\frac{\mathrm{\partial }{v}_{n+1}\left(x,t,h\right)}{\mathrm{\partial }{v}_n\left(x,t,h\right)}=0$We obtained the value of $\lambda \left(\varsigma \right)$, which is $\lambda \left(\varsigma \right)=-1$. By putting the value of $\lambda \left(\varsigma \right)$ in equation (34) gives in the following iterative structure: (35) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_n\left(x,t,h\right)-h{\int }_0^t\\ & \times \left\{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }-\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}\right.\\ & \left.-v_n\left(x,\varsigma ,h\right)+v_n{\left(x,\varsigma ,h\right)}^4\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma ,\end{array}$(35)

According to our proposed scheme (10), the following iterative formula is obtained (36) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_0\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\\ & \times \left\{-\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}-v_n\left(x,\varsigma ,h\right)\right.\\ & \left.+v_n{\left(x,\varsigma ,h\right)}^2)\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma ,\end{array}$(36)

We consider the initial approximation $v_0\left(x,t\right)$ as, $v_0\left(x,t\right)={\left(1+e^{\frac{3x}{\sqrt{10}}}\right)}^{\frac{-2}{3}},$Then from The relation of recurrence of VIM (36), we get the following other iterations, $\begin{array}{rl}{v}_1\left(x,t,h\right)& =\left(\right(1/\left(\text{exp}\right((3\ast {10}^{\wedge }(1/2)\ast x)/10)+1){)}^{\wedge }\\ & \times \left(5/3\right)\ast (5\ast \text{exp}((3\ast {10}^{\wedge }(1/2)\ast x)/10)\\ & +7\ast h\ast t\ast \text{exp}\left(\right(3\ast {10}^{\wedge }\left(1/2\right)\ast x\left)/10\right)\\ & +5\left)\right)/5,\end{array}$ $⋮$ $⋮$

For obtained approximate solution, the following residual function can be used to find a valid value of h (37) $\begin{array}{rl}{r}_4\left(x,t,h\right)& =\frac{\mathrm{\partial }{v}_4\left(x,t,h\right)}{\mathrm{\partial }t}-\frac{{\mathrm{\partial }}^2{v}_4\left(x,t,h\right)}{\mathrm{\partial }{x}^2}-v_4\left(x,t,h\right)\\ & +v_4(x,t,h{)}^4\end{array}$(37)

The norm 2 of residual function (37) for 4th-order approximation with respect to $h$ for $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$ is (38) $e_4\left(h\right)={\left[\frac{1}{{11}^2}\sum _{i=0}^{10}\sum _{j=0}^{10}{\left\{r_4\left(\frac{i}{10},\frac{j}{10},h\right)\right\}}^2\right]}^{\frac{1}{2}}$(38)

The residual function (38) can be utilized for the approximation of $e_4\left(h\right)$ and an appropriate value of the $h$ can be found out by making the $e_4\left(h\right)$ minimum. The value of the auxiliary parameter is determined to be 0.999795976281803 when the minimum value of $e_4\left(h\right)$ is 0.347702197150023600e-3. More precise and accurate results can be obtained when the number of iterations is increased.

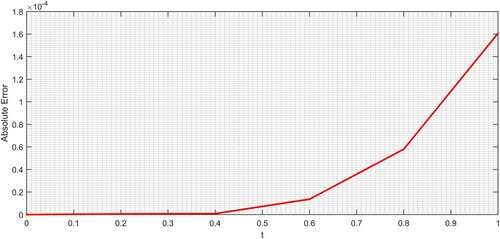
Utilizing the value of $h$ in $v_4\left(x,t,h\right)$ in the domain $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$, the comparison of exact and MVIA-II solutions can be seen in Figure 5 for different values of $t$, while to prove the effectiveness of the suggested technique for various values of $t,x$ and absolute errors in Table 5 along with the results of homotopy perturbation transform technique given in [63]. One can ensure that the results of MVIA-II are more accurate and can be obtained in a very short time.

Figure 5. Comparing the curves of absolute errors for different time levels for the Test Problem 4.

3.5. Test Problem 5 (Fisher equation)

Consider the Equation (1) with the values of constants as $n=2,\alpha =6\text{and}\text{β}=-6$, which gives the Fisher equation of the form [64], (39) $\frac{\mathrm{\partial }v}{\mathrm{\partial }t}=\frac{{\mathrm{\partial }}^{2}v}{\mathrm{\partial }{x}^2}+6v\left(1-v\right),$(39) having the initial condition: $v\left(x,0\right)=(1+e^x{)}^{-2},$And exact solution from [64], which is: (40) $v\left(x,t\right)=(1+e^{x-5t}{)}^{-2}.$(40)

The relation of recurrence of VIM for Equation (39) is given by, (41) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_n\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\left\{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }\right.\\ & -\stackrel{~}{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}-6\widetilde{v_n}\left(x,\varsigma ,h\right)\\ & \times \left.\left(\widetilde{1-v_n}\left(x,\varsigma ,h\right)\right)\phantom{\frac{\mathrm{\partial }{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }\varsigma }}\right\}d\varsigma ,\end{array}$(41)

The value of $\lambda \left(\varsigma \right)$ can be obtained by the variational principle [58–60] or using the optimality condition, $\frac{\mathrm{\partial }{v}_{n+1}\left(x,t,h\right)}{\mathrm{\partial }{v}_n\left(x,t,h\right)}=0$We obtained the value of $\lambda \left(\varsigma \right),$ which is $\lambda \left(\varsigma \right)=-1.$ By putting value of $\lambda \left(\varsigma \right)$ in equation (39) gives (42) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_0\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\left\{-\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}\right.\\ & \left.-6v_n\left(x,\varsigma ,h\right)\left(1-v_n\left(x,\varsigma ,h\right)\right)\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma ,\end{array}$(42) According to our proposed scheme (10), the following iterative formula is gained (43) $\begin{array}{rl}{v}_{n+1}\left(x,t,h\right)& =v_0\left(x,t,h\right)+h{\int }_0^t\lambda \left(\varsigma \right)\\ & \times \left\{-\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}-v_n\left(x,\varsigma ,h\right)\right.\\ & \left.\times \left(1-v_n{\left(x,\varsigma ,h\right)}^2\right)\phantom{\frac{{\mathrm{\partial }}^2{v}_n\left(x,\varsigma ,h\right)}{\mathrm{\partial }{x}^2}}\right\}d\varsigma ,\end{array}$(43) We consider the initial approximation $v_0\left(x,t\right)$ as, $v_0\left(x,t\right)=(1+e^x{)}^{-2},$Then from The relation of recurrence of VIM (43), we get the following other iterations, $\begin{array}{rl}{v}_1\left(x,t,h\right)& =\left(exp\left(x\right)+10\ast h\ast t\ast exp\left(x\right)+1\right)/\\ & \times (exp\left(x\right)+1{)}^{\wedge }3,\end{array}$ $\begin{array}{rl}{v}_2\left(x,t,h\right)& =1/\left(\text{exp}\right(x)+1{)}^{\wedge }2-(h\ast (5\ast t\ast \text{exp}\\ & \times (2\ast x)\ast (40\ast h^{\wedge }2\ast t^{\wedge }2-6)\\ & -5\ast t\ast \text{exp}\left(x\right)\ast (6\ast \text{exp}(2\ast x)\\ & +2\ast \text{exp}(3\ast x)-5\ast h\ast t+15\ast h\ast t\\ & \ast \text{exp}(2\ast x)+10\ast h\ast t\ast \text{exp}(3\ast x)+2\left)\right))\\ & /\left(\text{exp}\right(x)+1{)}^{\wedge }6,\end{array}$ $⋮$ $⋮$ For obtained approximate solution, the following residual function can be used to find a valid value of h (44) $\begin{array}{rl}{r}_3\left(x,t,h\right)& =\frac{\mathrm{\partial }{v}_3\left(x,t,h\right)}{\mathrm{\partial }t}-\frac{{\mathrm{\partial }}^2{v}_3\left(x,t,h\right)}{\mathrm{\partial }{x}^2}\\ & -6v_3\left(x,t,h\right)\left(1-v_3\left(x,\varsigma ,h\right)\right).\end{array}$(44) The norm 2 of residual function (44) for 3rd-order approximation with respect to $h$ for $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$ is (45) $e_3\left(h\right)={\left[\frac{1}{{\left(11\right)}^2}\sum _{i=0}^{10}\sum _{j=0}^{10}{\left\{r_3\left(\frac{i}{10},\frac{j}{10},h\right)\right\}}^2\right]}^{\frac{1}{2}}$(45) The residual function (45) can be utilized for the approximation of $e_3\left(h\right)$ and an appropriate value of the $h$ can be found out by making the $e_3\left(h\right)$ minimum. The value of the auxiliary parameter is determined to be 0.971647912904180 when the minimum value of $e_3\left(h\right)$ is obtained which is 0.617775361521317526e-1. More precise and accurate results can be obtained when the number of iterations is increased. Utilizing the value of $h$ in $v_3\left(x,t,h\right)$ in the domain $\left(x,t\right)ϵ\left[0,1\right]\times \left[0,1\right]$, the following results are obtained.

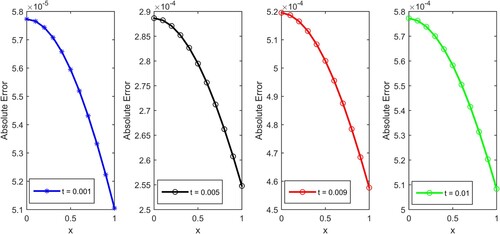
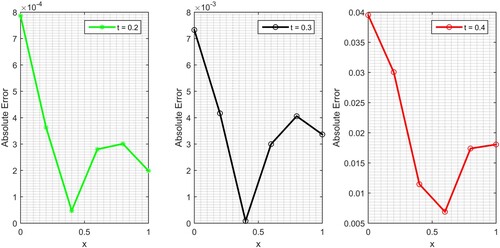
Comparison of results of the MVIA-II with the results produced by approaches reported in [64] is shown in Table 5, which demonstrate that the overall results of proposed MVIA-II are either better or same with the results of [64], where modified variational iteration method and Adomian decomposition method are employed. In Figure 6, the absolute error graphs are plotted for $t=0.2$, $t=0.3$ and $t=0.4$. It is cleared from figure and table that the proposed MVIA-II can handle the fisher equation accurately.

Figure 6. Absolute error graph for different times for Test Problem 6.

Table 6. Comparison in the form of absolute errors for Test Problem 6.

	$t=0.2$			$t=0.4$
$x$	Present	ADM [64]	MVIM [64]	Present	ADM [64]	MVIM [64]
0	7.8637525 E-04	7.22002 E-03	2.69962 E-03	3.9521338 E-02	5.75298 E-02	5.01844 E-02
0.2	3.6257440 E-04	9.89049 E-03	2.15566 E-03	3.0056850 E-02	1.6115 E-01	5.27127 E-02
0.4	4.7452743 E-05	1.09765 E-02	1.136097 E-03	1.1467670 E-02	1.39113 E-01	4.12072 E-02
0.6	2.7987518 E-04	1.04039 E-02	7.38299 E-04	6.8928130 E-03	1.51579 E-01	2.25459 E-02
0.8	3.0106076 E-04	8.50732 E-03	5.73101 E-04	1.73835851 E-02	1.43529 E-01	5.28693 E-03
1.0	1.9885243 E-04	5.87222 E-03	9.07727 E-04	1.8052646 E-02	1.19333 E-01	4.23672 E-03

4. Conclusions

In this article, we have studied and analyzed an iterative algorithm named as modified variational iteration algorithm-II for solving Allen–Cahn, Newell–Whitehead and Fisher equations with different parameters and presented in great detail, including tabulated numerical results and figures. This modified algorithm makes simple the computational work and results of high degree precision can be gotten in limited iterations as compared to other known approaches like variational iteration method, trigonometric B-spline collocation method, homotopy perturbation transform method, modified variational iteration method and Adomian decomposition method.

The proposed method will be able to use without using discretization, shape parameter, Adomian polynomials, transformation, linearization or restrictive assumptions and thus are particularly perfect with the expanded and flexible nature of the physical problems. Furthermore, the modification based upon the auxiliary parameter is easier to use and is more user friendly. The main advantage is that the auxiliary parameter involved in the MVIA-II is able to control the convergence rate and its optimum value can be determined.

Hence, we infer that the proposed algorithm is a reliable and proficient incredible scientific instrument for tackling nonlinear Parabolic problems in science and engineering.

Disclosure statement

No potential conflict of interest was reported by the author(s).