Evolution of ambiguous numbers under the actions of a Bianchi group

Abstract

In this paper we study some combinatorial properties of biquadratic irrational number field $\mathbb{Q}\left(i,\sqrt{3}\right)$, under the action of a Bianchi group ${\mathrm{\Gamma }}_3=PSL\left(2,O_3\right)$. In this experiment it is revealed that a special class of elements exists; that is, for an element $\xi$ its conjugate $\overline{\xi }$ has different signs in the closed path (orbits) for the action of ${\mathrm{\Gamma }}_3$ over $\mathbb{Q}\left(i,\sqrt{3}\right)$, known as ambiguous numbers. It is also proved that the orbit $\mathrm{\Gamma }\xi$ defined on a finite number of ambiguous numbers succeeding a unique closed path.

KEYWORDS:

• Group action
• Bianchi group
• biquadratic irrational field
• orbits

2010 AMS CLASSIFICATIONS:

• Primary 05C25
• Secondary 20H20

1. Introduction

A significant portion of the combinatorial group theory is about exploring the subgroups of projective special linear group over the ring of complex numbers, that is, $PSL\left(2,C\right)$. The study of $PSL(2,C)$ (or $PGL(2,C)$) comprising all Linear Fractional Transformations (LFTs), with complex coefficients, was one of the mainstream topics of mathematics in the last century and played an important role in the development of Lobachevskian geometry (Non-Euclidean geometry). A special class of discrete subgroups of projective special linear groups $PSL\left(2,C\right)$ are the groups of the form $PSL(2,O_r)$, where $O_r$ is the ring of integers in the imaginary quadratic irrational number field $\mathbb{Q}\left(\sqrt{-r}\right)$. The ring of integers $O_r$ has a Euclidean algorithm only when $r\in \left\{1,2,3,7,11\right\}$ while only two rings of integers for $r=1,2$; that is, $O_1$ and $O_3$ have non-trivial units $(\ne \pm 1)$. The groups ${\mathrm{\Gamma }}_r=PSL(2,O_r)$ with $r$ and $O_r$ as above are known as Bianchi groups (see [1–7]). The Bianchi group ${\mathrm{\Gamma }}_3=PSL\left(2,O_3\right)$ can be represented finitely with three generators that satisfy seven relations. The LFTs concerned to three generators $x,$ $y$ and $t$ are $x:z\mapsto -\frac{1}{z}$, $y:z\mapsto \frac{w^{-1}z}{w}$ and $t:z\mapsto \frac{z-1}{z},$ where $w=\frac{-1+\sqrt{3}i}{2}.$ In [8], the finite presentation of ${\mathrm{\Gamma }}_3$ is $⟨x,y,t|x^2,{\left(xy\right)}^2,{\left(xyt\right)}^3,y^3,t^3,{\left(yx{t}^{-1}\right)}^3,t^{-1}ytyx{t}^{-1}{y}^{-1}{t}^{-1}{y}^{-1}x⟩$. The biquadratic irrational number field $\mathbb{Q}(\sqrt{k_1},\sqrt{k_2})$ formed by adjoining $\sqrt{k_1}$ and $\sqrt{k_2}$, where $k_1$ and $k_2$ are square-free integers, is called biquadratic field over $\mathbb{Q}$ [9]. The elements of the field $\mathbb{Q}\left(\sqrt{k_1},\sqrt{k_2}\right)$ are of the form: $q_0+q_1\sqrt{k_1}+q_2\sqrt{k_2}+q_3\sqrt{k_1{k}_2}$, where $q_0,q_1,q_2,q_3\in \mathbb{Q}$. It is known that ${\mathrm{\Gamma }}_3$ acts on $\mathbb{Q}\left(i,\sqrt{r}\right)$, where $r$ is a positive square-free [9–11]. The generators $x,y$ and $t$ of ${\mathrm{\Gamma }}_3$ have fixed points $\pm i,0$ and $1\pm \sqrt{3i}/2$, respectively. All fixed points are placed in a biquadratic field $\mathbb{Q}\left(i,\sqrt{3}\right)$, where $\sqrt{3}$ and $i$ are zeroes of an irreducible ring of polynomial, that is, $\left(q^2-3\right)\left(q^2+1\right)$ over $Q$, for more detail [10,12,13]. The action of ${\mathrm{\Gamma }}_3$ on $\mathbb{Q}\left(i,\sqrt{3}\right)$ deserves special treatment because $\mathbb{Q}\left(i,\sqrt{3}\right)$ has all the fixed points of generators of ${\mathrm{\Gamma }}_3$ and these actions are also differentiated from $\mathbb{Q}\left(i,\sqrt{r}\right)$, where $r$ is a positive square-free [10]. Mushtaq in [14] defined a coset diagram for the modular group $PSL\left(2,Z\right)$ and after that many authors used the coset graph to study different group theoretic properties, while considering the action on certain base fields accordingly, for details see [9,10,12–21] and some related number theoretic applications in [22,23]. The elements of $\mathbb{Q}\left(i,\sqrt{3}\right)$ are of the form $u+v\sqrt{3}$, where $u,v\in \mathbb{Q}\left(i\right)$ can be written as $\xi =\frac{\left(\alpha +\text{β}i\right)+\left(\gamma +\delta i\right)\sqrt{3}}{e},$ where $\alpha ,\text{β},\gamma ,\delta ,e\in \mathbb{Q}$. The actions of ${\mathrm{\Gamma }}_3$ over $\mathbb{Q}\left(i,\sqrt{3}\right)$ behave special under this situation and show certain elements of $\mathbb{Q}\left(i,\sqrt{3}\right)$ of the form $\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$. Therefore, these elements deserve a special kind of classification. There always exist two conjugates [24], namely $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ and $\frac{\alpha -\text{β}\sqrt{3}}{\gamma }$, over $\mathbb{Q}$ and field $\mathbb{Q}\left(i,\sqrt{3}\right)$ has also a conjugate of $\xi$ again, so we have a conjugate of $\xi$ over irrational number field $\mathbb{Q}\left(i\right)$ that is $\frac{\alpha -\text{β}\sqrt{3}}{\gamma }$. The element $\xi \in \mathbb{Q}\left(i,\sqrt{3}\right)$ is a real quadratic irrational number, if $\xi$ and $\overline{\xi }$ are both positive (or both negative), where $\alpha ,\text{β},$ and $\gamma \in \mathbb{Q}$ are said to be a completely positive (or completely negative). In [13,19], Mushtaq discussed and defined a special type of numbers known as ambiguous numbers and proved that an ambiguous number exists if $\xi$ and its conjugate $\overline{\xi }$ have opposite signs. The action of Bianchi group ${\mathrm{\Gamma }}_3$ has played a very important role in the classification of the orbits of $\mathbb{Q}\left(i,\sqrt{3}\right)$. For detailed results and discussion related to Bianchi groups readers referred to [1–3,5,10,15,25–33]. It is obvious to see the application of group theory to mechanics and physics to construct models, drive differential equations and investigate their structures [34–36].

The major contributions of this work are listed below.

1. This paper presents a novel graphical study of the action of Bianchi group $PSL\left(2,O_3\right)$ on the bi-quadratic irrational field.

2. We have discovered a new class of elements of the bi-quadratic irrational field, possessing some interesting properties, known as ambiguous numbers.

3. We proved that ambiguous numbers in the coset diagram form one and only one closed path (orbit) for $\mathrm{\Gamma }\xi .$

2. Action of $PSL\left(2,O_3\right)$ over $\mathbb{Q}\left(i,\sqrt{3}\right)$

We have clarified how ambiguous numbers would create a path from one ambiguous number to the next in the following proposition.

Proposition 2.1

Let ${\mathrm{\Gamma }}_3$ act on $\mathbb{Q}\left(\text{I},\sqrt{3}\right)$ and $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }\in \mathbb{Q}\left(i,\sqrt{3}\right)$ be a completely positive or negative number. Then there exist two types of sequences; $x\left(\xi \right),x^3\left(\xi \right),\dots ,$ ${\text{x}}^{\text{m}}\left(\xi \right)$ are completely negative and $x^2\left(\xi \right),x^4\left(\xi \right),\dots ,x^n\left(\xi \right)$ are completely positive, where m and n are odd and even numbers, respectively.

Proof

Suppose $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }\in \mathbb{Q}\left(i,\sqrt{3}\right)$ is completely positive, then either $\alpha ,\delta ,\gamma >0$ or $\alpha ,\delta ,\gamma <0$. If $\alpha ,\delta ,\gamma >0$, then $x\left(\xi \right)=\frac{-\alpha +\text{β}\sqrt{3}}{\gamma }$, where $\delta =\frac{{\alpha }^2-3{\text{β}}^2}{\gamma }$. Here, ${\alpha }_1⟨0,{\gamma }_1⟩0$ & ${\delta }_1>0$, so $x\left(\xi \right)$ is completely negative. Again, $x^2\left(\xi \right)=\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$, where $\gamma =\frac{{\alpha }^2-3{\text{β}}^2}{\delta }$. Here, ${\alpha }_2>0,{\gamma }_2>0$ & ${\delta }_2>0,$ therefore $x^2\left(\xi \right)$ is completely positive. Inductively, we deduce that $x^3\left(\xi \right),x^5\left(\xi \right),\dots ,x^m\left(\xi \right)$ are completely negative numbers and $x^4\left(\xi \right),$ $x^6\left(\xi \right),\dots ,x^n\left(\xi \right)$ are completely positive numbers. Suppose $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ is completely a negative real quadratic irrational number, then either $\alpha <0$ & $\delta ,\gamma >0$ or $\alpha >0$ & $\delta ,\gamma <0$. If $\alpha >0$ & $\delta ,\gamma <0$, then $x\left(\xi \right)$ is completely a negative number and ${\text{x}}^2\left(\xi \right)$ is completely a positive number. Inductively, we come up with the sequences $x^5\left(\xi \right),x^7\left(\xi \right),\dots ,x^m\left(\xi \right)$ and $x^6\left(\xi \right),x^8\left(\xi \right),\dots ,x^n\left(\xi \right)$ such that $x^5\left(\xi \right),x^7\left(\xi \right),\dots ,x^m\left(\xi \right)$ are completely negative numbers and $x^6\left(\xi \right),x^8\left(\xi \right),\dots ,x^n\left(\xi \right)$ are completely positive numbers.

Remark 2.2

Let $\mathrm{\Gamma }\xi$ be an orbit and $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }\in \mathbb{Q}\left(i,\sqrt{3}\right),$ then $\text{β}$ remains the same in $\mathrm{\Gamma }\xi$.

Lemma 2.3

Let ${\mathrm{\Gamma }}_3$ act on $\mathbb{Q}\left(i,\sqrt{3}\right)$ and $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ is completely a positive (negative) real quadratic irrational number, then $t\left(\xi \right)$ is completely positive and $t^2\left(\xi \right)$ is completely a negative number.

Proof

Suppose $\xi \in \mathbb{Q}\left(i,\sqrt{3}\right)$ is completely a positive number, then either $\alpha ,\delta ,\gamma >0$ or $\alpha ,\delta ,\gamma <0.$ If $\alpha ,\delta ,\gamma >0,$ then $t\left(\xi \right)=\frac{\delta -\alpha +\text{β}\sqrt{3}}{\delta },$ where ${\alpha }_1=\delta -\alpha ,{\delta }_1$ and ${\gamma }_1$ are all positive numbers. So, $t\left(\xi \right)$ is completely a positive number. Similarly, it can be proved that $t^2\left(\xi \right)$ is completely a negative number. Next, if $\alpha ,\delta ,\gamma <0$, then $t\left(\xi \right)$ is completely a positive number and $t^2\left(\xi \right)$ is a completely negative number.

Suppose $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ $\in \mathbb{Q}\left(i,\sqrt{3}\right)$ is completely a negative real quadratic irrational number, then either $\alpha >0$ & $\delta ,\gamma <0$ or $\alpha <0$ & $\delta ,\gamma >0$. If $\alpha <0$ & $\delta ,\gamma >0$, then $t\left(\xi \right)$ and $t^2\left(\xi \right)$ are completely positive and negative numbers, respectively. In the same way, if $\alpha >0$ & $\delta ,\gamma <0,$ then $t\left(\xi \right)$ is completely positive and the other one is negative.

Lemma 2.4

Let ${\mathrm{\Gamma }}_3$ act on $\mathbb{Q}\left(\text{I},\sqrt{3}\right)$, then the transformation $x$ maps one ambiguous number to another.

Proof

Let $\xi \in \mathbb{Q}\left(i,\sqrt{3}\right)$ be an ambiguous number, and because of the fact that $\xi \overline{\xi }<0$, then $\left(x\left(\xi \right)x\left(\overline{\xi }\right)\right)=\frac{{\alpha }^2-3{\text{β}}^2}{{\delta }^2}<0$ as ${\alpha }^2-3{\text{β}}^2<0$ and ${\delta }^2>0$. Hence, $x\left(\xi \right)$ is an ambiguous number.

Lemma 2.5

If $x\left(\xi \right)$ is an ambiguous number, then $\xi$ is also an ambiguous number.

Proof

Consider $x\left(\xi \right)$ is an ambiguous number and $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }\in \mathbb{Q}\left(i,\sqrt{3}\right)$ is not an ambiguous number; therefore, $\xi \overline{\xi }\ge 0.$ This means that $\frac{{\alpha }^2-3{\text{β}}^2}{{\gamma }^2}\ge 0$ implies that ${\alpha }^2-3{\text{β}}^2\ge 0$ as ${\gamma }^2\ne 0$. Hence $\left(x\left(\xi \right)\overline{x\left(\xi \right)}\right)\ge 0$, which is contradiction to the fact that $x\left(\xi \right)$ is an ambiguous number. Thus, our supposition is wrong and $\xi$ is an ambiguous number.

Theorem 2.6

Let ${\mathrm{\Gamma }}_3$ act on $\mathbb{Q}\left(i,\sqrt{3}\right)$ and if $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ is an ambiguous number, then $y\left(\xi \right)$ and $y^2\left(\xi \right)$ do not exist.

Proof

Suppose $\xi$ is an ambiguous number then by definition $\xi \overline{\xi }<0$, then $y\left(\xi \right)=\frac{\xi w^{-1}}{w}=\left(\right(-\alpha -\text{β}\sqrt{3})+(\alpha \sqrt{3}+3\text{β}\left)i\right)/2\gamma$. Since the imaginary part of $y\left(\xi \right)$ is $\frac{\alpha \sqrt{3}+3\text{β}}{2\gamma }$. Therefore, $y\left(\xi \right)$ is an ambiguous only if the imaginary part of the equation is zero, that is $\frac{\left(\alpha \sqrt{3}+3\text{β}\right)i}{2\gamma }=0$. But $i\ne 0$ implies that $\frac{\alpha \sqrt{3}+3\text{β}}{2\gamma }=0$. The real part will also be equal zero if $\alpha =\text{β}=\gamma =0$. Therefore, $\xi =\mathrm{\infty }$ is not an ambiguous number, that’s why $\text{β}$ and $\gamma$ cannot be zero. This proves that $y\left(\xi \right)$ is not an ambiguous number. Also, $y^2\left(\xi \right)=\left(\left(-\alpha -\text{β}\sqrt{3}\right)-\left(\alpha \sqrt{3}+3\text{β}\right)i\right)/2\gamma$ implies that $\frac{\alpha \sqrt{3}+3\text{β}}{2\gamma }$ is an imaginary part of this equation and hence $y^2\left(\xi \right)$ is an ambiguous number only if $\frac{\left(\alpha \sqrt{3}+3\text{β}\right)i}{2\gamma }=0$. But, $i\ne 0$ implies that $\frac{\alpha \sqrt{3}+3\text{β}}{2\gamma }=0$. If $\alpha ,\text{β}$ and $\gamma$ are zero, then the real part of the equation will also be equal to zero. Hence $\xi =\mathrm{\infty }$ is not an ambiguous number, that’s why $\text{β}$ and $\gamma$ cannot be zero. Hence, $y^2\left(\xi \right)$ is not an ambiguous number.

Proposition 2.7

Consider the action of ${\mathrm{\Gamma }}_3$ over $\mathbb{Q}\left(i,\sqrt{3}\right)$, then

1. If $\xi$ is a negative ambiguous number, then $t\left(\xi \right)$ is an ambiguous number and $t^2\left(\xi \right)$ is completely a negative number.

2. If $\xi$ is a positive ambiguous number, then $t^2\left(\xi \right)$ is an ambiguous number and $t\left(\xi \right)$ is completely a positive number.

Proof

:

(i) Suppose $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ is a negative ambiguous number, then $\left(t\left(\xi \right)\overline{t\left(\xi \right)}\right)=\frac{{(\delta -\alpha )}^2-3{\text{β}}^2}{\delta }<0.$So, $t\left(\xi \right)$ is an ambiguous number. Also $t^2\left(\xi \right)=-\left(\frac{\gamma -\alpha +\text{β}\sqrt{3}}{\delta }\right),$ which is completely a negative number.

(ii) Suppose $\xi$ is a positive ambiguous number, then $t\left(\xi \right)$ is also a positive number. That is, $t\left(\xi \right)=\frac{\xi -1}{\xi }=\frac{\delta -\alpha +\text{β}\sqrt{3}}{\delta }$and $t^2\left(\xi \right)=-\left(\frac{\gamma -\alpha +\text{β}\sqrt{3}}{\delta }\right)$is completely a negative number. So, $\left(t^2\left(\xi \right)\overline{t^2\left(\xi \right)}\right)=\frac{{(\gamma -\alpha )}^2-3{\text{β}}^2}{{\delta }^2}<0.$Therefore,

Table

$\xi$	$t\left(\xi \right)$	$t^2\left(\xi \right)$
$-$	$+$	$-$
$+$	$+$	$-$

Hence $t^2\left(\xi \right)$ is ambiguous, if $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ is a positive ambiguous number.

Example 2.8

For illustration, suppose $\xi =\frac{2+2\sqrt{3}}{2}.$ Here $\alpha =2,\text{β}=2$ and $\gamma =2.$ Where $\delta =\frac{{\alpha }^2-3{\text{β}}^2}{\gamma }=-4,$ implies that $\delta \gamma =-8<0.$ This shows that $\xi$ is an ambiguous number. Now $x\left(\xi \right)=\frac{-2+2\sqrt{3}}{-4},$ therefore, ${\alpha }_1=-2,{\gamma }_1=-4$ and ${\delta }_1=2,$which implies ${\delta }_1{\gamma }_1=-8<0.$ Hence, it proves that $x\left(\xi \right)$ is an ambiguous number. Now $t\left(\xi \right)=\frac{-6+2\sqrt{3}}{-4},{\alpha }_2=-6,{\gamma }_2=-4$ and ${\delta }_2=-6,$ implies that ${\delta }_2{\gamma }_2=24>0.$ So, $t\left(\xi \right)$ is not an ambiguous number. Also, for $t^2\left(\xi \right)=\frac{2\sqrt{3}}{4},{\gamma }_3=4$ and ${\delta }_3=-3,$ implies ${\delta }_3{\gamma }_3=-12<0.$ That is $t^2\left(\xi \right)$ also an ambiguous number.

Lemma 2.9

Let ${\mathrm{\Gamma }}_3$ act on $\mathbb{Q}\left(i,\sqrt{3}\right)$ and $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }\in \mathbb{Q}\left(i,\sqrt{3}\right)$, then the transformations $x\left(\xi \right),t\left(\xi \right)$ and $t^2\left(\xi \right)$ contained an integer.

Proof

Suppose $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$, where $\alpha ,\text{β},\gamma \in \mathbb{Z}$. Since $x\left(\xi \right)=\frac{-\alpha +\text{β}\sqrt{3}}{\delta }$, here, ${\alpha }_1=-\alpha ,{\gamma }_1=\delta ,{\delta }_1=\frac{{\alpha }^2-3{\text{β}}^2}{\gamma }$. So, ${\delta }_1$ is also an integer because $\alpha ,\text{β}$ and $\gamma$ are integers. Hence $x\left(\xi \right)$ has an integer $\delta$. Again, $t\left(\xi \right)=\frac{\delta -\alpha +\text{β}\sqrt{3}}{\delta }.$ Here, ${\alpha }_1=\delta -\alpha ,{\gamma }_1=\delta$, therefore, ${\delta }_1=\frac{{\delta }^2+{\alpha }^2-2\delta x-3{\text{β}}^2}{\delta }=\delta +\gamma -2\alpha \in \mathbb{Z}$Hence, ${\delta }_1$ is an integer.

Also, $t^2\left(\xi \right)=-\left(\frac{\gamma -\alpha +\text{β}\sqrt{3}}{\delta }\right)$, here, ${\alpha }_2=\gamma -\alpha ,{\gamma }_2=\delta$,

Therefore, ${\delta }_2=\frac{{\gamma }^2+{\alpha }^2-2\gamma \alpha -3{\text{β}}^2}{\delta }=\delta +\gamma -2\alpha \in \mathbb{Z}$So, ${\delta }_2$ is an integer, which shows that $t$ ($\xi )$ and $t^2\left(\xi \right)$ have an integer $\delta .$

Lemma 2.10

Let ${\mathrm{\Gamma }}_3$ act on $\mathbb{Q}\left(i,\sqrt{3}\right)$, then there exists a finite number of ambiguous numbers in the orbit $\mathrm{\Gamma }\xi .$

Proof

By the definition of ambiguous numbers, $\xi \overline{\xi }<0$ implies $\frac{{\alpha }^2-3{\text{β}}^2}{{\gamma }^2}<0.$ Also, ${\alpha }^2-3{\text{β}}^2<0,$ then the condition ${\alpha }^2<3{\text{β}}^2$ satisfies for the constant value of $\text{β}$, if the value of $\alpha$ is finite. For the numbers of the form $\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ in $\mathrm{\Gamma }\xi$ the value of $\text{β}$ remains the same, by remark 2 2, whereas $\alpha ,\text{β}$ and $\gamma \in \mathbb{Q}$. It is clear from lemma 2.9 that $\delta$ is an integer and the value of $\gamma$ is also finite if $\gamma$ divides ${\alpha }^2-3{\text{β}}^2$. So in orbit $\mathrm{\Gamma }\xi$ the value of $\text{β}$ is fixed and the values of $\alpha$ and $\gamma$ are finite. This shows that only finite ambiguous numbers of the form $\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ exist in $\mathrm{\Gamma }\xi$ orbit.

Theorem 2.11

If ${\mathrm{\Gamma }}_3$ acts on $\mathbb{Q}\left(i,\sqrt{3}\right)$, then ambiguous numbers of the form $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ in the coset diagram form one and only one closed path (orbit) for $\mathrm{\Gamma }\xi .$

Proof

Suppose $\xi =\frac{\alpha +\text{β}\sqrt{3}}{\gamma }$ is an ambiguous number. Now, taking the action of the transformations $x$ and $t$, we have the following information (which traces the path). (1) $\begin{array}{rl}x\left(\xi \right)& =\frac{-\alpha +\text{β}\sqrt{3}}{\delta }.\end{array}$(1) (2) $\begin{array}{rl}t\left(\xi \right)& =\frac{\delta -\alpha +\text{β}\sqrt{3}}{\delta }.\end{array}$(2) (3) $\begin{array}{rl}{t}^2\left(\xi \right)& =-\left(\frac{\gamma -\alpha +\text{β}\sqrt{3}}{\delta }\right).\end{array}$(3) (4) $\begin{array}{rl}t\left(2.1\right)& =\frac{\gamma +\alpha +\text{β}\sqrt{3}}{\gamma }.\end{array}$(4) (5) $\begin{array}{rl}{t}^2\left(2.1\right)& =-\left(\frac{\alpha +\delta +\text{β}\sqrt{3}}{\gamma }\right).\end{array}$(5) (6) $\begin{array}{rl}x\left(2.4\right)& =\frac{-\gamma -\alpha +\text{β}\sqrt{3}}{\delta }\text{, where }\\ \delta & =\frac{(\gamma +{\alpha }^2)-3{\text{β}}^2}{\gamma }.\end{array}$(6) (7) $\begin{array}{rl}t\left(2.6\right)& =\frac{2\gamma +\alpha +\text{β}\sqrt{3}}{\gamma }.\end{array}$(7) (8) $\begin{array}{rl}{t}^2\left(2.6\right)& =-\left(\frac{\delta +\gamma +\alpha +\text{β}\sqrt{3}}{\gamma }\right).\end{array}$(8) (9) $\begin{array}{rl}x\left(2.7\right)& =\frac{-2\gamma -\alpha +\text{β}\sqrt{3}}{\delta }.\end{array}$(9) (10) $\begin{array}{rl}t\left(2.9\right)& =\frac{3\gamma +\alpha +\text{β}\sqrt{3}}{\gamma }.\end{array}$(10) (11) $\begin{array}{rl}{t}^2\left(2.9\right)& =-\left(\frac{2\gamma +\alpha +\delta +\text{β}\sqrt{3}}{\gamma }\right).\end{array}$(11) (12) $\begin{array}{rl}x\left(2.10\right)& =\left(\frac{-3\gamma -\alpha +\text{β}\sqrt{3}}{\delta }\right).\end{array}$(12) (13) $\begin{array}{rl}t\left(2.12\right)& =\frac{4\gamma +\alpha +\text{β}\sqrt{3}}{\gamma }.\end{array}$(13) (14) $\begin{array}{rl}{t}^2\left(2.12\right)& =-\left(\frac{3\gamma +\alpha +\delta +\text{β}\sqrt{3}}{\gamma }\right).\end{array}$(14) (15) $\begin{array}{rl}x\left(2.13\right)& =\frac{-4\gamma -\alpha +\text{β}\sqrt{3}}{\delta }.\end{array}$(15) (16) $\begin{array}{rl}t\left(2.15\right)& =\frac{5\gamma +\alpha +\text{β}\sqrt{3}}{\gamma }.\end{array}$(16) (17) $\begin{array}{rl}{t}^2\left(2.15\right)& =-\left(\frac{4\gamma +\alpha +\delta +\text{β}\sqrt{3}}{\gamma }\right).\end{array}$(17) (18) $\begin{array}{rl}x\left(2.16\right)& =\frac{-5\gamma -\alpha +\text{β}\sqrt{3}}{\delta }.\end{array}$(18) (19) $\begin{array}{rl}t\left(2.18\right)& =\frac{6\gamma +\alpha +\text{β}\sqrt{3}}{\gamma }.\end{array}$(19) (20) $\begin{array}{rl}{t}^2\left(2.18\right)& =-\left(\frac{5\gamma +\alpha +\delta +\text{β}\sqrt{3}}{\gamma }\right).\end{array}$(20) (21) $\begin{array}{rl}x\left(2.19\right)& =\frac{-6\gamma -\alpha +\text{β}\sqrt{3}}{\delta }.\end{array}$(21) (22) $\begin{array}{rl}t\left(2.21\right)& =\frac{7\gamma +\alpha +\text{β}\sqrt{3}}{\gamma }.\end{array}$(22) (23) $\begin{array}{rl}{t}^2\left(2.21\right)& =\frac{-6\gamma -\alpha -\delta +\text{β}\sqrt{3}}{\gamma }.\end{array}$(23) It is clear from the above discussion 1–23 and Figure 1. if we have a positive ambiguous number $\xi$, then the transformation $t$ ($\xi )$ is also a completely positive  number and $t^2\left(\xi \right)$ is an ambiguous number. If $\xi$ is a negative ambiguous number, then the transformation $t^2\left(\xi \right)$ is also a completely negative number and $t$($\xi )$ is an ambiguous number, by theorem 2.4, generator $x$ is used to join these ambiguous numbers to another ambiguous numbers.

Figure 1. Closed path.

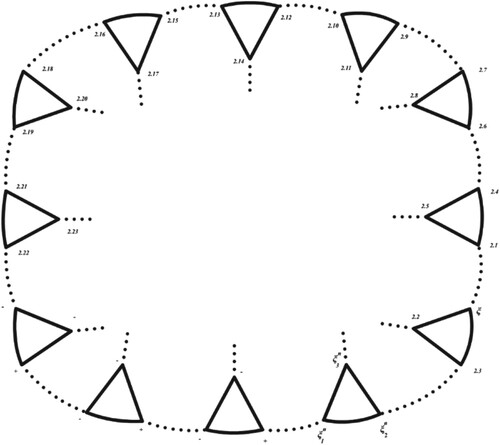
Through inductive hypothesis, as demonstrated in Figure 1 and by virtue of lemma 2.10, there exist finite ambiguous numbers. Now, if we start from one vertex, that is an ambiguous number ${\xi }_2^n$ (superscript in ${\xi }_2^n$ is pointed as the number of triangle and subscript is pointed as the number of vertex of triangle labelled by ambiguous numbers) $n$ is an odd number; after a finite number of steps, that is, $x\left({\xi }_2^n\right)={\xi }_1^1,$ because the generator $x$ maps one ambiguous number to the next. Hence, there exists a sequence, $\xi ={\xi }_1^1,{\xi }_2^1,{\xi }_1^2,{\xi }_2^2,\dots {\xi }_1^n,{\xi }_2^n,{\xi }_1^1=\xi$of ambiguous numbers that forms a unique closed path.

3. Conclusion

In this work, we have discussed group theoretical aspects of the actions of a Bianchi group ${\mathrm{\Gamma }}_3$ on $\mathbb{Q}\left(\text{i},\sqrt{3}\right)$. Since the closed path can be defined as the path where the vertices of the initial and the terminal (end) coincide, the closed path of ambiguous numbers as a closed path with all ambiguous numbers at its vertices. We have proved that for the orbit $\mathrm{\Gamma }\xi$, there exist a finite number of ambiguous numbers, where they form a unique closed path.

Acknowledgement

This research project was supported by a grant from the Research Center of the Center for Female Scientific and Medical Colleges, Deanship of Scientific Research, King Saud University.

Disclosure statement

No potential conflict of interest was reported by the author(s).