Solitary and shocklike wave solutions for the Gardner equation in dusty plasmas

Abstract

The propagation of dust ion acoustic waves (DIAWs) for two-temperature ions with isothermal electrons in dusty plasmas has been investigated. Using the reductive perturbation method, the Gardner equation is derived. Many analytical solutions have been presented for small but finite amplitude acoustic waves, e.g. solitary and shocklike waves. The effects of many parameters on the feature of the shocklike waves have been studied for the dusty plasma system. The results of this study could be helpful for understanding the existence of nonlinear potential structures those are observed in various cosmic dust-laden plasmas, such as Saturn's E-ring, noctilucent clouds, Halley's comet and interstellar molecular clouds.

Keywords:

• Dusty plasma
• Gardner equation
• extended tanh method

1. Introduction

In the recent years, multicomponent plasmas, including ions, electrons, positrons and dust grains which considered as dusty plasmas, are taking the importance of the research works since dusty plasmas can be found in many space objects like Earth's magnetosphere, Saturn's E-ring, noctilucent clouds, white dwarfs, etc. [1–3]. Dusty plasma is an ionized gas containing dust particles from ${10}^{-3}$ m to ${10}^{-9}$ m and these are in charge both positively and negatively [4,5]. On the other hand, most of the cases studying electron–ion plasmas in the presence/absence of dust particles, in general, ions are considered to be positive, whereas it is found that negative ions [6,7] can also be present in both space plasmas [8] and laboratory experiments [9]. Thus it is really interesting to study the role the dust particles in a plasma system containing both positively and negatively charged ions to see how they significantly change the wave characteristics in astrophysical compact objects studied in the previous works [1,2,4,5,8–10].

Many authors have studied the nonlinear wave propagation in multicomponent plasmas in the presence of dust particles [1,2,4–9,11]. Nonlinear structures associated with dust-ion-acoustic waves are really interesting topics to study because of its wide applications in space as well as laboratory dusty plasmas. Magnetized plasma system containing inertial positive and negative mobile ions and opposite polarity dusts has been studied [12,13] for different electron distribution like Maxwellian [14], vortex [12,15] and non-thermal [13,16].

Recently, a fully nonlinear propagation of dust-acoustic waves (DAWs) was investigated using superthermal electrons and ions where both follow kappa distribution where the reductive perturbation method was used to analyse both long and small amplitudes in the nonlinear waves [17], Sagdeev potential and Korteweg–de Vries (KdV) equation were derived, and Extended homogeneous balance method was applied for obtaining the exact travelling wave solutions for the KdV equation. Also, using the hydrodynamic equations of positive and negative ions, nonthermal electrons, as well as solar wind streaming protons and electrons and Poisson equation, the ion acoustic waves (IAWs) were studied by the Gardner equation [18], the effect of the number densities and velocities of the streaming particles on the feature of the shocklike waves was studied.

There are many recognized methods for solving nonlinear evaluations equations, among those methods, Inverse Scattering method, bilinear transformation, the tanh method, extended homogeneous balance method, F-expansion method, general expansion method and (G ´ /G) method [17–23]. Now, choosing a suitable model to derive an acceptable exact solution is the most challenging objective in this field of plasma science because it takes us more insight into the physical aspects of the nonlinear wave equations than it seems to be so. Here, we choose the extended tanh method (ETM) to solve the reduced nonlinear ordinary differential equation from the Gardner equation and study the dust ion acoustic waves for our plasmas model. ETM introduces a unifying method for exact [24–26] as well as approximate solutions in direct and consistent way [27]. The standard tanh method and its modified versions, all depend on the balance method, where the linear terms of highest order are balanced with the highest order nonlinear terms of the reduced equation to obtain the exact analytical solutions for the nonlinear evaluation equations (NLEE's) include soliton, periodic and rational solutions, peakons, breathers, casps and compacton solutions [17,18,28–30].

In this paper, we have obtained periodical, soliton, rational, explosive/blow up, shocklike wave solutions for the Gardner equation. It is shown that the feature of the shocklike waves can be modified by the effects of parameters like electron and ion densities or hot ion, cold ion, dust and electron temperature in our dusty plasma model to study the DIAWs. This model can be found in various cosmic dust-laden plasmas.

The paper is organized as follows. The governing equations for the plasma model are presented in Section 2. In Section 3, the Gardner equation which describing the system that has been derived using the reductive perturbation method. In Section 4, we apply the extended tanh method to solve the Gardner equation. The discussion and numerical results are presented in Section 5. Finally, the results are summarized in Section 6.

2. Considered model

We consider a dusty plasma system of collisionless, and unmagnetized four-components plasma consisting of negatively charged dust particles ($n_d$), isothermal electrons ($n_e$), and two-temperature isothermal ions ($n_{il}$ and $n_{ih}$). The dimensionless basic equations are given by (1) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_d}{\mathrm{\partial }t}+\frac{\mathrm{\partial }(n_d{u}_d)}{\mathrm{\partial }x}=0,\end{array}$(1) (2) $\begin{array}{rl}& \frac{\mathrm{\partial }{u}_d}{\mathrm{\partial }t}+u_d\frac{\mathrm{\partial }{u}_d}{\mathrm{\partial }x}+\sigma n_d\frac{\mathrm{\partial }{n}_d}{\mathrm{\partial }x}-\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }x}=0.\end{array}$(2) For dust, and the Poisson's equation (3) $\frac{{\mathrm{\partial }}^2\varphi }{\mathrm{\partial }{x}^2}=n_d+n_e-n_{il}-n_{ih},$(3) and the electrons and ions distributions are given by (4) $\begin{array}{rl}{n}_e& ={\mu }_e\exp ({\mathrm{\Delta }}_e\varphi ),\end{array}$(4) (5) $\begin{array}{rl}{n}_{il}& ={\mu }_{il}\exp (-{\mathrm{\Delta }}_{il}\varphi ),\end{array}$(5) (6) $\begin{array}{rl}{n}_{ih}& ={\mu }_{ih}\exp (-{\mathrm{\Delta }}_{ih}\varphi ),\end{array}$(6) where ${\mu }_e=n_{e0}/Z_d{n}_{d0}$, ${\mu }_{il}=n_{il0}/Z_d{n}_{d0}$, ${\mu }_{ih}=n_{ih0}/Z_d{n}_{d0}$, ${\mathrm{\Delta }}_e=T_{\mathrm{eff}}/Z_d{T}_e$, ${\mathrm{\Delta }}_{il}=T_{\mathrm{eff}}/Z_d{T}_{il}$ and ${\mathrm{\Delta }}_{ih}=T_{\mathrm{eff}}/Z_d{T}_{ih}$

where $T_{\mathrm{eff}}$ is the effective temperature and $\frac{1}{T_{\mathrm{eff}}}=[\frac{n_{il0}}{T_{il}}+\frac{n_{ih0}}{T_{ih}}+\frac{n_{e0}}{T_e}]$ Here, $n_d$, $u_d$ and φ refer to the number density, fluid velocity of the dust grains and the electrostatic potential, respectively. The densities $n_d$ and $n_q$ (q = il, ih, e) are normalized by $n_{d0}$ and $Z_d{n}_{d0}$, respectively, and φ is normalized by $T_{\mathrm{eff}}/e{Z}_d$. The space and time are normalized by the positive ion Debye length ${\lambda }_{Dd}=(T_{\mathrm{eff}}/4\pi n_{d0}{e}^2{Z}_d^2{)}^{1/2}$ and the positive ion plasma period ${\omega }_{pd}^{-1}=(4\pi n_{d0}{e}^2{Z}_d^2/m_d{)}^{-1/2}$, respectively, $\sigma =\frac{T_d}{T_e},{\beta }_1=\frac{T_{il}}{T_e},{\beta }_2=\frac{T_{ih}}{T_e}\mathrm{and}\beta =\frac{T_{il}}{T_{ih}},$ with temperature $T_e$ for electrons, temperature $T_{il}$ for cold ions and temperature $T_{ih}$ for hot ions in units of energy, respectively, where the neutrality condition is given by [17,18,31–33] (7) $1={\mu }_{il}+{\mu }_{ih}-{\mu }_e,$(7)

3. Derivation of the Gardner equation

Using the reductive perturbation technique, the independent variables can be stretched as [17] (8) $\xi =ϵ(x-\lambda t)\mathrm{and}\tau ={ϵ}^{3}t,$(8) where ($0<ϵ\ll 1)$, and λ is the wave propagation speed [17,18,31–33]. The dependent variables are expanded as (9) $\mathrm{\Psi }={\mathrm{\Psi }}^{(0)}+\sum _{n=1}^{\mathrm{\infty }}{ϵ}^n{\mathrm{\Psi }}^{(n)},$(9) where (10) $\mathrm{\Psi }=\{n_d,n_e,n_{il},n_{ih},u_d,\varphi {\}}^T$(10) and (11) ${\mathrm{\Psi }}^{(0)}=\{1,{\mu }_e,{\mu }_{il},{\mu }_{ih},0,0{\}}^T.$(11) Employing the variable stretching in Equation (8(8) $\xi =ϵ(x-\lambda t)\mathrm{and}\tau ={ϵ}^{3}t,$(8) ) and the expansions of Equations (9(9) $\mathrm{\Psi }={\mathrm{\Psi }}^{(0)}+\sum _{n=1}^{\mathrm{\infty }}{ϵ}^n{\mathrm{\Psi }}^{(n)},$(9) )–(11(11) ${\mathrm{\Psi }}^{(0)}=\{1,{\mu }_e,{\mu }_{il},{\mu }_{ih},0,0{\}}^T.$(11) ) into Equations (1(1) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_d}{\mathrm{\partial }t}+\frac{\mathrm{\partial }(n_d{u}_d)}{\mathrm{\partial }x}=0,\end{array}$(1) )–(7(7) $1={\mu }_{il}+{\mu }_{ih}-{\mu }_e,$(7) ), we may now isolate distinct orders in ε and derive the corresponding variable contributions. The lowest-order equations in ε yield (12) $n_d^{(1)}=\frac{1}{(\sigma -{\lambda }^2)}{\varphi }^{(1)},u_d^{(1)}=\frac{\lambda }{(\sigma -{\lambda }^2)}{\varphi }^{(1)},$(12) and (13) $\begin{array}{rl}{n}_e^{(1)}& ={\mu }_e{\mathrm{\Delta }}_e{\varphi }^{(1)},n_{il}^{(1)}={\mu }_{il}{\mathrm{\Delta }}_{il}{\varphi }^{(1)},\\ n_{ih}^{(1)}& ={\mu }_{ih}{\mathrm{\Delta }}_{ih}{\varphi }^{(1)},\end{array}$(13) Then Poisson equation gives (14) $\frac{1}{(\sigma -{\lambda }^2)}+{\mu }_e{\mathrm{\Delta }}_e+{\mu }_{il}{\mathrm{\Delta }}_{il}+{\mu }_{ih}{\mathrm{\Delta }}_{ih}=0,$(14) which is the compatibility condition.

The next order in ε yields (15) $\begin{array}{rl}{n}_d^{(2)}& =\frac{1}{(\sigma -{\lambda }^2)}{\varphi }^{(2)}-\frac{(3{\lambda }^2+\sigma )}{2(\sigma -{\lambda }^2{)}^3}{\varphi }^{(1)2},\end{array}$(15) (16) $\begin{array}{rl}{u}_d^{(2)}& =\frac{\lambda }{(\sigma -{\lambda }^2)}{\varphi }^{(2)}\\ & -\frac{1}{2}(\frac{(3{\lambda }^2+\sigma )}{(\sigma -{\lambda }^2{)}^2}-\frac{\lambda }{(\sigma -{\lambda }^2)}){\varphi }^{(1)2},\end{array}$(16) (17) $\begin{array}{rl}{n}_e^{(2)}& ={\mu }_e{\mathrm{\Delta }}_e{\varphi }^{(2)}+\frac{1}{2}{\mu }_e{\mathrm{\Delta }}_e^2{\varphi }^{(1)2},\end{array}$(17) (18) $\begin{array}{rl}{n}_{il}^{(2)}& =-{\mu }_{il}{\mathrm{\Delta }}_{il}{\varphi }^{(2)}+\frac{1}{2}{\mu }_{il}{\mathrm{\Delta }}_{il}^2{\varphi }^{(1)2},\end{array}$(18) (19) $\begin{array}{rl}{n}_{ih}^{(2)}& =-{\mu }_{ih}{\mathrm{\Delta }}_{ih}{\varphi }^{(2)}+\frac{1}{2}{\mu }_{ih}{\mathrm{\Delta }}_{ih}^2{\varphi }^{(1)2},\end{array}$(19) while the Poisson's equation gives (20) $-\frac{(3{\lambda }^2+\sigma )}{2(\sigma -{\lambda }^2{)}^3}+\frac{1}{2}{\mu }_e{\mathrm{\Delta }}_e^2-\frac{1}{2}{\mu }_{il}{\mathrm{\Delta }}_{il}^2-\frac{1}{2}{\mu }_{ih}{\mathrm{\Delta }}_{ih}^2=0.$(20) The next order in ε the Poisson's equation gives the Gardner equation as follows: (21) $\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\tau }+\mathrm{\Gamma }\varphi \frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\xi }+\mathrm{\Omega }{\varphi }^{{}^2}\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\xi }+\mathrm{\Lambda }\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }{\xi }^3}=0,$(21) where we replace ${\varphi }^{(1)}$ by φ for simplicity. The coefficients Γ, Λ and Ω are given as (22) $\begin{array}{rl}\mathrm{\Gamma }& =\frac{(\sigma -{\lambda }^2{)}^2}{2\lambda }[\frac{3{\lambda }^2+\sigma }{(\sigma -{\lambda }^2{)}^3}\\ & +\frac{{\mu }_{il}(1-{\beta }_1^2)+{\mu }_{ih}{\beta }^2(1-{\beta }_2^2)+{\beta }_1^2}{({\mu }_{il}(1+{\beta }_1)+{\mu }_{ih}\beta (1+{\beta }_2)-{\beta }_1{)}^2}],\end{array}$(22) (23) $\begin{array}{rl}\mathrm{\Lambda }& =\frac{(\sigma -{\lambda }^2{)}^2}{2\lambda },\\ \mathrm{\Omega }& =\frac{3(\sigma -{\lambda }^2{)}^2}{2\lambda }[\frac{2{\lambda }^2}{(\sigma -{\lambda }^2{)}^4}-\frac{3{\lambda }^2+\sigma }{(\sigma -{\lambda }^2{)}^5}\\ & -\frac{1}{6}\frac{{\mu }_{il}(1+{\beta }_1^3)+{\mu }_{ih}{\beta }^3(1+{\beta }_2^3)-{\beta }_1^3}{({\mu }_{il}(1+{\beta }_1)+{\mu }_{ih}\beta (1+{\beta }_2)-{\beta }_1{)}^3}],\end{array}$(23) where (24) $\sigma =\frac{T_d}{T_e},{\beta }_1=\frac{T_{il}}{T_e},{\beta }_2=\frac{T_{ih}}{T_e}\mathrm{and}\beta =\frac{T_{il}}{T_{ih}}.$(24)

4. Analytical solutions of the Gardner equation using extended tanh method

For a nonlinear evaluation equation (25) $P(u,u_x,u_t,u_y,u_{xx},\dots )=0,$(25) using extended tanh method (see [17,26]), we try to find its solution in the following form: (26) $u=\sum _{i=0}^n{a}_i{\varphi }^i(\zeta )$(26) Considering the Gardner Equation (21(21) $\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\tau }+\mathrm{\Gamma }\varphi \frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\xi }+\mathrm{\Omega }{\varphi }^{{}^2}\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\xi }+\mathrm{\Lambda }\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }{\xi }^3}=0,$(21) ) in the form (27) $\frac{\mathrm{\partial }u}{\mathrm{\partial }t}+\mathrm{\Gamma }u\frac{\mathrm{\partial }u}{\mathrm{\partial }\eta }+\mathrm{\Lambda }{u}^{{}^2}\frac{\mathrm{\partial }u}{\mathrm{\partial }\eta }+\mathrm{\Omega }\frac{{\mathrm{\partial }}^{3}u}{\mathrm{\partial }{\eta }^3}=0.$(27) We try to find travelling wave solution for Equation (27(27) $\frac{\mathrm{\partial }u}{\mathrm{\partial }t}+\mathrm{\Gamma }u\frac{\mathrm{\partial }u}{\mathrm{\partial }\eta }+\mathrm{\Lambda }{u}^{{}^2}\frac{\mathrm{\partial }u}{\mathrm{\partial }\eta }+\mathrm{\Omega }\frac{{\mathrm{\partial }}^{3}u}{\mathrm{\partial }{\eta }^3}=0.$(27) ) in the form (28) $u(\eta ,t)=u(\omega ),\omega =\eta -\epsilon t,$(28) where $\mathit{\epsilon }$ is a constant. The transformation Equation (28(28) $u(\eta ,t)=u(\omega ),\omega =\eta -\epsilon t,$(28) ) reduces Equation (27(27) $\frac{\mathrm{\partial }u}{\mathrm{\partial }t}+\mathrm{\Gamma }u\frac{\mathrm{\partial }u}{\mathrm{\partial }\eta }+\mathrm{\Lambda }{u}^{{}^2}\frac{\mathrm{\partial }u}{\mathrm{\partial }\eta }+\mathrm{\Omega }\frac{{\mathrm{\partial }}^{3}u}{\mathrm{\partial }{\eta }^3}=0.$(27) ) to an ordinary differential equation [17,26]: (29) $-\lambda U^{\mathrm{\prime }}+\mathrm{\Gamma }U{U}^{\mathrm{\prime }}+\mathrm{\Lambda }{U}^2{U}^{\mathrm{\prime }}+\mathrm{\Omega }{U}^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}=0.$(29) By integrating Equation (29(29) $-\lambda U^{\mathrm{\prime }}+\mathrm{\Gamma }U{U}^{\mathrm{\prime }}+\mathrm{\Lambda }{U}^2{U}^{\mathrm{\prime }}+\mathrm{\Omega }{U}^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}=0.$(29) ) w.r.t ω twice, we obtain (30) $-\lambda U+\frac{\mathrm{\Gamma }}{2}{U}^2+\frac{\mathrm{\Lambda }}{3}{U}^3+\mathrm{\Omega }{U}^{\mathrm{\prime }\mathrm{\prime }}=0.$(30) Balancing $U^{\mathrm{\prime }\mathrm{\prime }}$ with $U^3$ yields m = 1. Therefore, we are looking for the solution in the form of (31) $U=a_0+a_1\varphi .$(31) From Equations (31(31) $U=a_0+a_1\varphi .$(31) ) and (26(26) $u=\sum _{i=0}^n{a}_i{\varphi }^i(\zeta )$(26) ) in Equation (30(30) $-\lambda U+\frac{\mathrm{\Gamma }}{2}{U}^2+\frac{\mathrm{\Lambda }}{3}{U}^3+\mathrm{\Omega }{U}^{\mathrm{\prime }\mathrm{\prime }}=0.$(30) ), we get a polynomial equation of φ. Then, by the steps of the extended tanh method, we may obtain a system of over determined algebraic equation by using the symbolic manipulation package MATHEMATICA. we obtain two sets of solutions with many types as discussed below.

For the first set, the kink solutions (32) $u_1(x,t)=\frac{\sqrt{6\lambda }}{\mathrm{\Lambda }}\tanh \left(\frac{\sqrt{-\lambda }}{\mathrm{\Omega }}\zeta \right),$(32) and travelling wave solutions (33) $u_2(x,t)=\frac{\sqrt{6\lambda }}{\mathrm{\Lambda }}\coth \left(\frac{\sqrt{-\lambda }}{\mathrm{\Omega }}\zeta \right).$(33) However, for periodic solutions (34) $\begin{array}{rl}{u}_3(x,t)& =\frac{i\sqrt{6\lambda }}{\mathrm{\Lambda }}\tan \left(\frac{\sqrt{\lambda }}{\mathrm{\Omega }}\zeta \right),\end{array}$(34) (35) $\begin{array}{rl}{u}_4(x,t)& =-\frac{i\sqrt{6\lambda }}{\mathrm{\Lambda }}\cot \left(\frac{\sqrt{\lambda }}{\mathrm{\Omega }}\zeta \right),\end{array}$(35) and the rational solutions (36) $u_5(x,t)=-\frac{i\sqrt{6\mathrm{\Omega }}}{\zeta \sqrt{\mathrm{\Lambda }}}.$(36) For the second set, the kink solutions (37) $u_6(x,t)=-\frac{\mathrm{\Gamma }}{2\mathrm{\Lambda }}-\frac{i\sqrt{\mathrm{\Omega }}\sqrt{-\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}\tanh \left(\frac{\zeta \sqrt{-\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}}{2\sqrt{6}}\right)}{2\sqrt{\mathrm{\Lambda }}},$(37) and travelling wave solutions (38) $u_7(x,t)=-\frac{\mathrm{\Gamma }}{2\mathrm{\Lambda }}-\frac{i\sqrt{\mathrm{\Omega }}\sqrt{\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}\coth \left(\frac{\zeta \sqrt{-\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}}{2\sqrt{6}}\right)}{2\sqrt{\mathrm{\Lambda }}},$(38) and we can obtain periodic solutions (39) $\begin{array}{rl}{u}_8(x,t)& =\frac{i\sqrt{\mathrm{\Omega }}\sqrt{\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}\tan \left(\frac{\zeta \sqrt{\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}}{2\sqrt{6}}\right)}{2\sqrt{\mathrm{\Lambda }}}-\frac{\mathrm{\Gamma }}{2\mathrm{\Lambda }},\end{array}$(39) (40) $\begin{array}{rl}{u}_9(x,t)& =\frac{i\sqrt{\mathrm{\Omega }}\sqrt{\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}\cot \left(\frac{\zeta \sqrt{\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}}{2\sqrt{6}}\right)}{2\sqrt{\mathrm{\Lambda }}}-\frac{\mathrm{\Gamma }}{2\mathrm{\Lambda }},\end{array}$(40) and rational solutions (41) $u_{10}(x,t)=-\frac{\mathrm{\Gamma }\zeta +2\sqrt{6}i\sqrt{\mathrm{\Omega }}\sqrt{\mathrm{\Lambda }}}{2\zeta \mathrm{\Lambda }}.$(41)

5. Discussion

The use of the extended tanh method gives rise to many travelling wave solutions that were formally derived for the Gardner equation. The obtained solutions include many types like rational, periodical, singular and solitary wave solutions. Therefore, our model gives almost the main spectrum of the DPs behaviour under different conditions. For example, solutions (34(34) $\begin{array}{rl}{u}_3(x,t)& =\frac{i\sqrt{6\lambda }}{\mathrm{\Lambda }}\tan \left(\frac{\sqrt{\lambda }}{\mathrm{\Omega }}\zeta \right),\end{array}$(34) ) and (35(35) $\begin{array}{rl}{u}_4(x,t)& =-\frac{i\sqrt{6\lambda }}{\mathrm{\Lambda }}\cot \left(\frac{\sqrt{\lambda }}{\mathrm{\Omega }}\zeta \right),\end{array}$(35) ) are periodic solutions, and Equation (36(36) $u_5(x,t)=-\frac{i\sqrt{6\mathrm{\Omega }}}{\zeta \sqrt{\mathrm{\Lambda }}}.$(36) ) is the rational solution, which may help for explaining some physical phenomena, while solution (33(33) $u_2(x,t)=\frac{\sqrt{6\lambda }}{\mathrm{\Lambda }}\coth \left(\frac{\sqrt{-\lambda }}{\mathrm{\Omega }}\zeta \right).$(33) ) is explosive/blow up solution, the shocklike wave solution in Equation (37(37) $u_6(x,t)=-\frac{\mathrm{\Gamma }}{2\mathrm{\Lambda }}-\frac{i\sqrt{\mathrm{\Omega }}\sqrt{-\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}\tanh \left(\frac{\zeta \sqrt{-\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}}{2\sqrt{6}}\right)}{2\sqrt{\mathrm{\Lambda }}},$(37) ) [see [34] for more details], which is our main interest because of its unexplained origin, are presented in Figure 1. The potential is found to be decreased with increasing of time in a nonlinear shape. In the beginning, there is no change in potential with time but after a time period it suddenly decreases sharply, almost close to zero potential. However, in the opposite polarity we see the opposite condition where potential drops in a very short-period and after that, there is no change for a long period. There is no change in potential with the change in position. It is important to note here that from Figure 1 these changes in potential structure are due to the effect of ions with two-temperatures. The effects of dust particles were less effective than ions in the wave structures, thus we do not show them for further discussion.

Figure 1. Three-dimensional profile of the shocklike pulse [given by Equation (40(40) $\begin{array}{rl}{u}_9(x,t)& =\frac{i\sqrt{\mathrm{\Omega }}\sqrt{\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}\cot \left(\frac{\zeta \sqrt{\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}}{2\sqrt{6}}\right)}{2\sqrt{\mathrm{\Lambda }}}-\frac{\mathrm{\Gamma }}{2\mathrm{\Lambda }},\end{array}$(40) )] for $\lambda =1.7,$ ${\mu }_{il}=0.1$, ${\mu }_{ih}=0.01,$ ${\beta }_1=0.07$, ${\beta }_2=0.87$ and $\sigma =0.01$.

To study the nonlinear properties of the shocklike waves, we express the solution of Equation (37(37) $u_6(x,t)=-\frac{\mathrm{\Gamma }}{2\mathrm{\Lambda }}-\frac{i\sqrt{\mathrm{\Omega }}\sqrt{-\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}\tanh \left(\frac{\zeta \sqrt{-\frac{{\mathrm{\Gamma }}^2}{\mathrm{\Omega }\mathrm{\Lambda }}}}{2\sqrt{6}}\right)}{2\sqrt{\mathrm{\Lambda }}},$(37) ) in the form (42) $u(\eta )=\frac{1}{2}{\varphi }_m[1-\tanh \left(\frac{2\eta }{W}\right)],$(42) with boundary condition $u(\eta )\to 0$ at $\eta \to \mathrm{\infty }$, where ${\varphi }_m$ and W are the amplitude and width of the shocklike/double layers, respectively, and are given by [see [34] for more details] (43) ${\varphi }_m=-\frac{\mathrm{\Gamma }}{\mathrm{\Lambda }}\mathrm{and}W=2\frac{\sqrt{-12\mathrm{\Omega }/\mathrm{\Lambda }}}{\left|{\varphi }_m\right|},$(43) what measures the spatial extension (width) of the localized pulse.

Figure 2 shows that with the increasing values of ${\beta }_1$ the potential values decrease with same rate whereas at the beginning there is very few change, almost negotiable. In Figure 3, we have seen the same characteristics for the changing values of ${\beta }_2$. But in this case, there is a notable change from ${\beta }_2=0.01$ to ${\beta }_2=0.02$ comparing from ${\beta }_2=0.02$ to ${\beta }_2=0.03$. This means that after a sudden value of ${\beta }_2$ there will be no change wave potential. Thus comparing between Figures 2 and 3, we can say that ${\beta }_1$ has greater effects on wave structure to decrease the potential than ${\beta }_2$.

Figure 2. Shocklike wave profile [given by Equation (54)] for $\lambda =1.7,$ ${\mu }_{il}=0.1$, ${\mu }_{ih}=0.01$, ${\beta }_2=0.87$, $\sigma =0.01$ and different values of ${\beta }_1=0.01$ (solid curve), 0.02 (dotted curve) and 0.03 (dashed curve).

Figure 3. Shocklike wave profile [given by Equation (54)] for $\lambda =1.7,$ ${\mu }_{il}=0.1$, ${\mu }_{ih}=0.01,$ ${\beta }_1=0.02$, $\sigma =0.01$ and different values of ${\beta }_2=0.1$ (solid curve), 0.2 (dotted curve) and 0.3 (dashed curve).

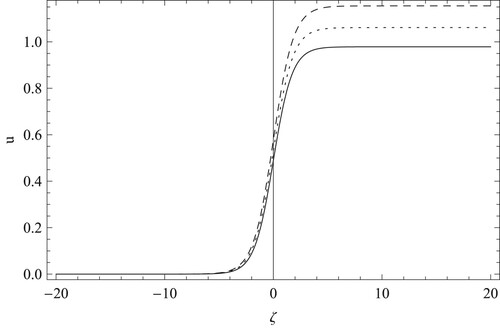
When we look at Figure 4 then we see that with increasing values of σ the potential increases, opposite characteristics of Figures 2 and 3. However, note that the increasing rate is also changing with increasing value of σ thus we do not see (very tiny) change where $\sigma =0.1$ and 0.2. This is also a notable point to compare with Figures 2 and 3. Figure 5 is also showing same phenomena like Figure 4 for the change of values in ${\mu }_{il}$ whereas the increasing rate is really higher that other three figures for the effects of ${\beta }_1$, ${\beta }_2$, and σ whereas the increasing rate is showing a very sharp curve comparing other three figures. Figure 6 is same as shown in Figure 5 where solid, dotted and dashed lines are for ${\mu }_{ih}=0.1$, 0.3 and 0.5. In this case, the increasing rate is almost same for the change in values of ${\mu }_{ih}$ and higher potential is found at lower values of ${\mu }_{ih}$ comparing ${\mu }_{il}$ as shown in Figure 5. Observing the effects of different plasma parameters of this model, we can say that due to the effect of ${\beta }_2$ and ${\mu }_{il}$, the change in potential structure is very sharp (where the changing rate is low and high) shown in Figures 3 and 5 comparing the effects of ${\beta }_1$, σ and ${\mu }_{ih}$ as shown in Figures 2, 4 and 6.

Figure 4. Shocklike wave profile [given by Equation (54)] for $\lambda =1.7,$ ${\mu }_{il}=0.1$, ${\mu }_{ih}=0.01,$ ${\beta }_1=0.02$, ${\beta }_2=0.2$ and different values of $\sigma =0.3$ (solid curve), 0.4 (dotted curve) and 0.5 (dashed curve).

Figure 5. Shocklike wave profile [given by Equation (54)] for $\lambda =1.7,$ ${\mu }_{ih}=0.01,$ ${\beta }_1=0.02$, $\sigma =0.3$, ${\beta }_2=0.2$ and different values of ${\mu }_{il}=0.1$ (solid curve), 0.11 (dotted curve) and 0.13 (dashed curve).

Figure 6. Shocklike wave profile as shown in Figure 5 where ${\mu }_{ih}=0.1$ (solid curve), ${\mu }_{ih}=0.3$ (dotted curve) and ${\mu }_{ih}=0.5$ (dashed curve).

6. Conclusion

We have derived the Gardner equation for the investigation of small but finite amplitude dust plasma waves. The extended tanh method has been successfully employed to show up different types of solutions of the Gardner equation. The transformation formulas are used in our nonlinear wave equations to show that our analysis of the Gardner equation is applicable to any nonlinear behaviour. We have studied the dust ion acoustic waves (DIAWs) for the present dusty plasma model. To study the nonlinear wave dynamics in the astrophysical compact objects for both space and laboratory, there are many plasma parameters in the plasma systems, but it is really complicated to study all parameters in one framework [12–16]. Thus we consider a model of dusty plasma system containing negatively charged dust particles, isothermal electrons and two-temperature isothermal ions deriving the exact analytical solutions for the nonlinear evaluation equation [17,18,28–30]. For this model, we have studied the DIAW's by observing the effects of various parameters like electron and ion densities or hot ion, cold ion, dust and electron temperatures on the feature of the shocklike waves in our dusty plasma model. We have found that ions significantly change the potential structure more than comparing dust particles. It is observed that increasing ${\beta }_1$ or ${\beta }_2$ causes to decrease the shocklike wave amplitude as depicted in Figures 2 and 3 while Figures 4 and 5 show that the enhancement in σ or ${\mu }_{il}$ causes to increase the shocklike wave amplitude. This dusty plasma model can be found in many astrophysical objects.

Acknowledgments

We would like to thank Rustaq College of Education, Rustaq, Sultanate of Oman for supporting this research.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This research was funded by Rustaq College of Education, Ministry of Higher Education, Sultanate of Oman.