Numerical study on factional differential-algebraic systems by means of Chebyshev Pseudo spectral method

Abstract

A numerical treatment to a system of Caputo fractional order differential- algebraic equations (SFDAEs) is presented throughout this article. The suggested method based upon the shifted Chebyshev pesedu- spectral method (SCPSM). The shifted Chebyshev polynomials (SCPs) are handled to reduce the SFDAEs into the solution of linear/ nonlinear systems of algebraic equations. By using some tested applications, the effectiveness and the accuracy of the suggested approach are demonstrated graphically. Also numerical comparisons between the proposed technique with other numerical methods in the existing literature are held. The numerical results show that the proposed technique is computationally efficient, accurate and easy to implement.

KEYWORDS:

• Fractional differential equations
• Chebyshev polynomials
• fractional differential algebraic equations
• spectral collocation methods
• Caputo fractional derivative

1. Introduction

Nowadays, the fractional differential equations (FDEs) have gained increased appearances in varied problems in various fields of physics, chemistry, biology, applied science and engineering, this is due to their accuracy in modelling these problems [1–8]. Consequently, the development of analytical and numerical algorithms for FDEs is an interested topic for many researches [9–16].

Many physical phenomena's are obviously designated by a system of differential-algebraic equations (SDAEs). These types of systems follow in the displaying of the mechanical systems subject to constraints, power systems, electrical networks, optimal control, chemical process and in other numerous applications [17]. SFDAEs have currently confirmed to be a suitable devise in the displaying of the numerous engineering and physical problems such as non-integer order optimal controller design, electrochemical processes, complex biochemical [18].

The approximate and numerical solutions of these types of systems have been a focus of several researchers especially the nonlinear systems, because most of these systems don't have exact solutions. Numerical methods to solve SDAEs have been given such as, the numerical algorithms for computing the matrix Green's operator [19], implicit Runge–Kutta method [20], Padé approximation method [21,22], homotopy perturbation method [23], Adomain decomposition method [24] and variation iteration method (VIM) [25].

While methods like, the homotopy analysis method (HAM) [26], the Adomian decomposition method (ADM) [27], the variational iteration method [27], fractional differential transform method [28], the generalized triangular function operational matrices [29], the Bezier curves method [30], and Gegenbauer tau method [31] have been successfully applied for SFDAEs.

In this paper, we apply the SCPSM to solve the following SFDAEs [31]: (1) $\left\{\begin{array}{l}\begin{array}{l}{D}_{\ast }^{{\alpha }_i}{y}_i\left(t\right)=f_i(t,y_1,y_2,\cdots y_n,{y^{\mathrm{\prime }}}_1,{y^{\mathrm{\prime }}}_2,\cdots ,{y^{\mathrm{\prime }}}_n),\\ i=1,2,\cdots ,l-1,t\ge 0,0<{\alpha }_i\le 1,\end{array}\\ y_i=g_i\left(t,y_1,y_2,\cdots y_n\right),i=l,l+1,\cdots ,n\end{array}\right.$(1) With the initial conditions: (2) $y_i\left(0\right)=a_i,i=1,2,\cdots ,n.$(2) where $D_{\ast }^{{\alpha }_i}$ is the Caputo fractional derivative of order ${\alpha }_i$. When ${\alpha }_i=1$, the SFDAEs is reduced to the classical SDAEs. The proposed technique is one of the known spectral methods, which have been widely used in many fields. These methods are characterized by their speed of convergence and the high level of accuracy.

For FDEs, the spectral collocation method (also called pseudo-spectral method) is more applicable and commonly applied to numerically solve different types of the fractional differential equations [15,32]. In collocation technique, expansion coefficients are determined by constructing the approximate solution to satisfy the differential equation at some applicably selected points from the domain identified as collocation points. Recently, various types of orthogonal polynomials and collocation points are used in spectral collocation approximations [15,32].

CPs have many useful properties. These polynomials present, among others, very good properties in the approximation of functions. This encourages many researchers for using these polynomials for solving different types of differential equations and FDEs [32–35].

The proposed technique used the properties of Chebyshev polynomials (CPs) to reduce the SFDAEs into a system of algebraic equation which is greatly simplifying the problem. To the best of our knowledge, the numerical treatment of SFDAEs has not been established by using SCPSM yet.

To check the accuracy of the suggested method, five numerical applications including comparisons between our obtained results with those achieved by using other existing methods are presented. This article is prescribed as follows: The basic definition of the Caputo fractional derivative and the main properties of the CPs are summarized in Section 2. In Section 3, the necessary theorems of the upper bound of errors and the convergence analysis of the fractional derivatives of the SCPs are explained. Section 4 contains the procedures for the implementation of the suggested method to nonlinear FDAEs. Some applications are discussed in Section 5. Finally, a brief conclusion finishes the paper in Section 6.

2. Preliminaries and notations

2.1. Caputo fractional derivatives

Definition 2.1:

A real function $f\left(t\right),t>0,$ is assumed to be in the space $C_{\mu ,}\mu \in \mathrm{\Re },$ if there exists a real number $p>\mu$ such that $f\left(t\right)=t^{p}g\left(t\right)$ where $g\left(t\right)\in C\left(0,\mathrm{\infty }\right),$ and is assumed to be in space $C_{\mu }^m$ if and only if $f^{\left(m\right)}\in C_{\mu },m\in \mathbb{N}.$

Definition 2.2

The fractional derivative $D_{\ast }^{\alpha }$ of $f\left(t\right)$ in the Caputo sense is defined as (3) $D_{\ast }^{\alpha }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(m-\alpha \right)}{\int }_0^t(t-s{)}^{m-\alpha -1}{f}^{\left(m\right)}\left(s\right)ds$(3) For $m-1<\alpha \le m,m\in \mathbb{N},t>0,f\left(t\right)\in C_{-1}^m$

Caputo derivatives have the following properties: (4) $\begin{array}{rl}& D_{\ast }^{\alpha }\left(\lambda f\left(t\right)+\mu g\left(t\right)\right)=\lambda D_{\ast }^{\alpha }f\left(t\right)+\mu D_{\ast }^{\alpha }g\left(t\right),\\ & \lambda \text{and}\mu \text{are}\text{constants}\end{array}$(4) $D_{\ast }^{\alpha }C=0,C\text{is}\text{a}\text{constant}$ (5) $D_{\ast }^{\alpha }{t}^n=\left\{\begin{array}{ll}0& \text{for}n\in {\mathbb{N}}_0\text{and}n<\lceil \alpha \rceil \\ \frac{\mathrm{\Gamma }\left(n+1\right)}{\mathrm{\Gamma }\left(n+1-\alpha \right)}{t}^{n-\alpha }& \text{for}n\in {\mathbb{N}}_0\text{and}n\ge \lceil \alpha \rceil \end{array}\right.$(5) where $\lceil \alpha \rceil$ is the ceiling function and ${\mathbb{N}}_0=\left\{0,1,2,\cdots \right\}.$ For $\alpha \in \mathbb{N},$ the Caputo fractional derivative agrees with the integer order derivative. More details in [12,13].

2.2. Main properties of the CPs

The CPs, $T_n\left(z\right)$ of degree $n$ are determined by the following recurrence relation [32–34] $\begin{array}{rl}{T}_{n+1}\left(z\right)& =2z{T}_n\left(z\right)-T_{n-1}\left(z\right),T_0\left(z\right)=1,\\ T_1\left(z\right)& =z,n=1,2,\cdots \end{array}$The analytic form of $T_n\left(z\right)$ is defined by (6) $T_n\left(z\right)=n\sum _{i=0}^{\left[\frac{n}{2}\right]}(-1{)}^i{2}^{n-2i-1}\frac{\left(n-i-1\right)!}{\left(i\right)!\left(n-2i\right)!}{z}^{n-2i},$(6) where $\left[\frac{n}{2}\right]$ is the integer part of $\frac{n}{2}$.

The SCPs $T_n^{\ast }\left(t\right)$ of degree n defined in the interval $\left[0,L\right]$, constructed by offering the change of variable $z=\left(\frac{2}{L}t-1\right)$ and defined by (7) $T_n^{\ast }\left(t\right)=n\sum _{k=0}^n(-1{)}^{n-k}\frac{2^{nk}\left(n+k-1\right)!}{L^k\left(2k\right)!\left(n-k\right)!}{t}^k,n=1,2,\dots$(7) The square integrable function $f\left(t\right)$ in $\left[0,L\right],$ can be approximated using the first $\left(m+1\right)$ terms of the SCPs as (8) $f_m\left(t\right)=\sum _{i=0}^m{c}_i{T}_i^{\ast }\left(t\right)$(8) Where the coefficients $c_i$ are given by (9) $\begin{array}{rl}{c}_0& =\frac{1}{\pi }{\int }_0^L\frac{f\left(t\right)T_i^{\ast }\left(t\right)}{\sqrt{Lt-t^2}}dt,\\ c_i& =\frac{2}{\pi }{\int }_0^L\frac{f\left(t\right)T_i^{\ast }\left(t\right)}{\sqrt{Lt-t^2}}dt,i=1,2,\dots .m\end{array}$(9)

3. The approximation of the fractional derivatives of the SCPs and its convergence analysis

The approximate formulation of the non-integer derivatives, the truncating error and the convergence analysis of the SCPs are considered in the following theorems.

Theorem 2.1:

(Chebyshev truncation theorem) [32]

The error in approximating $x\left(t\right)$ by the sum of its $m$-terms is bounded by the sum of the absolute values of all neglected coefficient. If (10) $\begin{array}{r}{x}_m\left(t\right)=\sum _{k=0}^m{c}_k{T}_k\left(t\right),\end{array}$(10) then (11) $\begin{array}{r}{E}_T\left(m\right)=|x\left(t\right)-x_m\left(t\right)|\le \sum _{k=m+1}^{\mathrm{\infty }}|c_k|,t\in \left[-1,1\right]\end{array}$(11)

Theorem 2 .2:

Let $f\left(t\right)$ be approximated by SCPs as in (8) and suppose that $\alpha >0$, then (12) $D_{\ast }^{\alpha }\left(f_m\left(t\right)\right)=\sum _{i=\alpha }^m\sum _{k=\alpha }^i{c}_i{\psi }_{i,k}^{\left(\alpha \right)}{t}^{k-\alpha }$(12) Where ${\psi }_{i,k}^{\left(\alpha \right)}$ is given by (13) ${\psi }_{i,k}^{\left(\alpha \right)}=(-1{)}^{i-k}\frac{2^{2k}i\left(i+k-1\right)!\mathrm{\Gamma }\left(k+1\right)}{L^k\left(i-k\right)!\left(2k\right)!\mathrm{\Gamma }\left(k+1-\alpha \right)}$(13) For Proof, see [32].

Theorem 2.3

[32,35]

The Caputo fractional derivative of order $\alpha$ for the SCPs can be expressed in terms of the SCPs themselves as in the following form (14) $D_{\ast }^{\alpha }\left(T_i^{\ast }\left(t\right)\right)=\sum _{k=\alpha }^i\sum _{j=0}^{k-\alpha }{\theta }_{i,j,k}{T}_j^{\ast }\left(t\right),$(14) where (15) $\begin{array}{rl}{\theta }_{i,j,k}& =\frac{{(-1)}^{i-k}2i\left(i+k-1\right)!\mathrm{\Gamma }\left(k-\alpha +\frac{1}{2}\right)L^{k-\alpha }}{\begin{array}{c}{h}_j\mathrm{\Gamma }\left(k+\frac{1}{2}\right)\left(i-k\right)!\mathrm{\Gamma }\left(k-\alpha +j+1\right)\\ \mathrm{\Gamma }\left(k-\alpha -j+1\right)\end{array}},\\ & j=0,1,\cdots \end{array}$(15) Theorem 3.4 [32,35]

The error $|E_T\left(m\right)|=|D_{\ast }^{\alpha }u\left(t\right)-D_{\ast }^{\alpha }{u}_m\left(t\right)|$ in approximating $D_{\ast }^{\alpha }u\left(t\right)by{D}_{\ast }^{\alpha }{u}_m\left(t\right)$ is bounded by: (16) $|E_T\left(m\right)|\le \left|\sum _{i=m+1}^{\mathrm{\infty }}{c}_i\left(\sum _{k=\alpha }^i\sum _{j=0}^{k-\alpha }{\theta }_{i,j,k}\right)\right|$(16)

4. Solution to the SFDAEs

In this section we will explain the main steps of the procedure of applying the SCPSM for solving the following SFDAEs: (17) $\left\{\begin{array}{l}\begin{array}{l}{D}_{\ast }^{{\alpha }_i}{y}_i\left(t\right)=f_i(t,y_1,y_2,\cdots y_n,{y^{\mathrm{\prime }}}_1,{y^{\mathrm{\prime }}}_2,\cdots ,{y^{\mathrm{\prime }}}_n),\\ i=1,2,\cdots ,l-1,t\ge 0,0<{\alpha }_i\le 1,\end{array}\\ y_i=g_i\left(t,y_1,y_2,\cdots y_n\right),i=l,l+1,\cdots ,n\end{array}\right.$(17) Subject to the initial conditions (18) $y_i\left(0\right)=a_i,i=1,2,\cdots ,n.$(18) Step 1: Approximate $y_i\left(t\right)$ by using the SCPs as: (19) $y_i\left(t\right)=y_{i,mi}\left(t\right)=\sum _{j=0}^{m_i}{c}_{ij}{T}_j^{\ast }\left(t\right),$(19) Step 2: Use Eq. (12) to approximate the Caputo fractional derivatives, then the SFDAEs (17) is reduced to (20) $\left\{\begin{array}{l}\sum _{j=\alpha }^{mi}\sum _{k=\alpha }^j{c}_{ij}{\psi }_{j,k}^{\left({\alpha }_i\right)}{t}^{k-\alpha }=f_i\left(t,\sum _{j=0}^{m_1}{c}_{1j}{T}_j^{\ast }\left(t\right),\cdots ,\right.\\ \left.\sum _{j=0}^{m_n}{c}_{nj}{T}_j^{\ast }\left(t\right),\sum _{j=0}^{m_1}{c}_{1j}{T}_j^{\ast \mathrm{\prime }}\left(t\right),\cdots ,\sum _{j=0}^{m_n}{c}_{nj}{T}_j^{\ast \mathrm{\prime }}\left(t\right)\right),\\ \text{For}i=1,2,\cdots ,l-1,0<{\alpha }_i\le 1,\text{and}\\ \sum _{j=0}^{m_i}{c}_{ij}{T}_j^{\ast }\left(t\right)=g_i\left(t,\sum _{j=0}^{m_1}{c}_{1j}{T}_j^{\ast }\left(t\right),\cdots ,\sum _{j=0}^{m_n}{c}_{nj}{T}_j^{\ast }\left(t\right)\right)\\ \text{for}i=l,l+1,\cdots ,n\end{array}\right.$(20) Step 3: Approximate the initial conditions (18) by using SCPs: (21) $\sum _{j=0}^{m_i}{c}_{ij}{T}_j^{\ast }\left(0\right)=a_i,i=1,2,\dots n.$(21) Step 4: Collocate Eq. (20) at the $(\sum _{i=1}^n{m}_i+n(1-\lceil {\alpha }_i\rceil )$ points. For a suitable collocation points, use the of the SCPs roots, $T_{m_i+1-\lceil {\alpha }_i\rceil }^{\ast }\left(t\right)$.

Step 5: The obtained equations of the previous step 4 with Eq. (21) represent a system of linear/nonlinear algebraic equations which contain $\sum _{i=1}^n{m}_i+n$ of unknowns; $c_{ij}$, $i=1,2,\dots n,j=0,1,\dots m,$

Step 6: Solve the algebraic system by using the Newton iteration method to obtain the unknowns.

Step 7: The approximated solutions will be $\begin{array}{rl}{y}_{i,mi}\left(t\right)& =c_{i0}{T}_0^{\ast }\left(t\right)+c_{i1}{T}_1^{\ast }\left(t\right)+\cdots c_{i{m}_i}{T}_{m_i}^{\ast }\left(t\right),\\ & i=1,2,\cdots n\end{array}$

5. Numerical applications

In this section five numerical applications of SFDAEs are solved by the proposed technique; the applications include variable and constant coefficient linear\ nonlinear SFDAEs

Application 5.1:

Consider the following variable coefficient linear SFDAE [27–29] (22) $\left\{\begin{array}{l}{D}_{\ast }^{\alpha }x\left(t\right)-t{y}^{\mathrm{\prime }}\left(t\right)+x\left(t\right)-\left(1+t\right)y\left(t\right)=0,0<\alpha \le 1\\ y\left(t\right)-\sin \left(t\right)=0.\end{array}\right.$(22) With the initial conditions (23) $x\left(0\right)=1,y\left(0\right)=0.$(23) For the special case at $\alpha =1,$ system (22) has exact solution: (24) $x\left(t\right)=e^{-t}+tsin\left(t\right),y\left(t\right)=sin\left(t\right).$(24) By implementing the proposed technique using $m_1=m_2=5$, $x\left(t\right)=\sum _{j=0}^5{c}_j{T}_j^{\ast }\left(t\right)$ and $y\left(t\right)=\sum _{j=0}^5{b}_j{T}_j^{\ast }\left(t\right)$ to Eq. (22), we obtain (25) $\left\{\begin{array}{l}\sum _{n=1}^5\sum _{r=0}^{n-1}{c}_n{\psi }_{n,r}^{\left(\alpha \right)}{t}^{r-\alpha }-t\sum _{j=0}^5{b}_j{T}_j^{\ast \mathrm{\prime }}\left(t\right)+\sum _{j=0}^5{c}_j{T}_j^{\ast }\left(t\right)\\ -\left(1+t\right)\sum _{j=0}^5{b}_j{T}_j^{\ast }\left(t\right)=0,\\ \sum _{j=0}^5{b}_j{T}_j^{\ast }\left(t\right)-sin\left(t\right)=0,\end{array}\right.$(25) And the approximated equations for the initial conditions will be (26) $\sum _{j=0}^5{c}_j{T}_j^{\ast }\left(0\right)=1\text{and}\sum _{j=0}^5{b}_j{T}_j^{\ast }\left(0\right)=0.$(26) The equations obtained by collocating system (25) at the first five roots of the SCPs $T_5^{\ast }\left(t\right)$ with Eqs. (26) represent a system of linear algebraic equations which contains twelve equations for twelve unknowns; $c_j$ and $b_j,j=0,1,\dots ,5$. These unknowns are obtained by using Newton iteration method.

For $\alpha =1$. The estimated solutions are $\begin{array}{rl}x\left(t\right)& =1.+\text{t }(-0.9999+\text{t }(1.498+\text{t }(-0.154\\ & +\left(-0.1527+0.018\text{ t}\right)\text{ t}\left)\right))\\ y\left(t\right)& =2.34188\times {10}^{-17}+t(0.999+t(0.00005\\ & +t(-0.1672+(0.00090+0.0075t\left)t\right)\left)\right)\end{array}$Figure 1(a,b) shows the performance of the approximate solutions; $x\left(t\right)$ and $y\left(t\right)$ respectively, of the Application 5.1 at $m=5$ for different values of $\alpha$ ($\alpha$ = 0.75, $\alpha$ = 0.85, $\alpha$ = 0.95, $\alpha$ = 1) with the exact solutions at $\alpha =1$. it is easy to see that the obtained solutions are continuously depended on the fractional derivative and the estimated solutions are in good agreement with the exact solution at $\alpha =1.$ The Absolute errors between the exact solution and the approximate solution of Application 5.1 at different values of $m$ ($m=5,10,15,20$) with their CPU time are tabulated in Table 1. Executing time of this problem is measured using Mathematica 10 software on CPU Intel(R) Core(TM) i3, it's apparent that the solution doesn't require much CPU time. It is remarkable that the proposed technique is very effective even with using few terms of SCPs and the overall errors can be made smaller by adding more terms of SCPs.

Figure 1. The behaviours of $x\left(t\right)$ and $y\left(t\right)$ of Application 5.1 for different values of $\alpha$ with the exact solutions at $\alpha =1$. (a) $x\left(t\right)$, (b) $y\left(t\right)$.

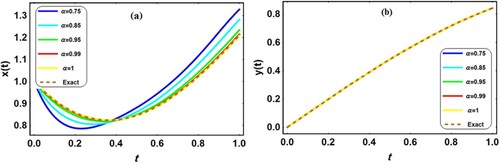
Table 1. Absolute error of $x\left(t\right)$ of Application 5.1 for different values of $m$.

Absolute error of $x\left(t\right)$ of Application 5.1
t	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}0.\\ 3.8569\times {10}^{-6}\\ 9.0051\times {10}^{-6}\\ 3.9128\times {10}^{-6}\\ 5.1621\times {10}^{-6}\\ 9.0323\times {10}^{-6}\\ 4.0753\times {10}^{-6}\\ 5.2983\times {10}^{-6}\\ 9.7923\times {10}^{-6}\\ 3.5209\times {10}^{-6}\\ 3.0737\times {10}^{-6}\end{array}$	$\begin{array}{c}3.3307\times {10}^{-16}\\ 1.3878\times {10}^{-14}\\ 9.5480\times {10}^{-15}\\ 1.0769\times {10}^{-13}\\ 1.2346\times {10}^{-13}\\ 2.6978\times {10}^{-14}\\ 1.2734\times {10}^{-13}\\ 1.1668\times {10}^{-13}\\ 4.7074\times {10}^{-14}\\ 5.3291\times {10}^{-15}\\ 2.1094\times {10}^{-14}\end{array}$	$\begin{array}{c}4.4409\times {10}^{-16}\\ 2.2205\times {10}^{-16}\\ 1.1102\times {10}^{-16}\\ 3.3307\times {10}^{-16}\\ 3.3307\times {10}^{-16}\\ 2.2204\times {10}^{-16}\\ 2.2204\times {10}^{-16}\\ 1.1102\times {10}^{-16}\\ 4.4409\times {10}^{-16}\\ 4.4409\times {10}^{-16}\\ 4.4409\times {10}^{-16}\end{array}$	$\begin{array}{c}1.1102\times {10}^{-16}\\ 1.1102\times {10}^{-16}\\ 1.1102\times {10}^{-16}\\ 1.1102\times {10}^{-16}\\ 0.\\ 1.1102\times {10}^{-16}\\ 0.\\ 1.1102\times {10}^{-16}\\ 0.\\ 0.\\ 2.2204\times {10}^{-16}\end{array}$
CPU	0.0312	0.0624	0.140401	0.265202

In Table 2 the approximate numerical solutions for $x\left(t\right)$ for $\alpha =0.75\text{and}1$ are compared with the solutions given by VIM [27], HAM [28] and TF [29]. These numerical results demonstrate the harmony between our method and the other numerical methods used in the comparisons.

Table 2. Approximate solution of $x\left(t\right)$ obtained by our proposed method with the results in [27–29].

Approximate solution of $x\left(t\right)$ Application 5.1
	$\alpha =0.75$				$\alpha =1$
t	VIM [27]	HAM [28]	TF [29]	SCPSM	VIM [27]	HAM [28]	TF [29]	SCPSM	Exact
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{l}1\\ 0.8492996\\ 0.8016697\\ 0.7978998\\ 0.8250871\\ 0.8760143\\ 0.9454581\\ 1.0290756\\ 1.1229594\\ 1.2234365\\ 1.32697591\end{array}$	$\begin{array}{c}1\\ 0.8492995\\ 0.8016696\\ 0.7979000\\ 0.8250873\\ 0.8760146\\ 0.9454582\\ 1.0290755\\ 1.1229592\\ 1.2234363\\ 1.3269757\end{array}$	$\begin{array}{c}1\\ 0.8492966\\ 0.8016674\\ 0.7978979\\ 0.8250855\\ 0.8760129\\ 0.9454568\\ 1.0290744\\ 1.1229582\\ 1.2234354\\ 1.3269747\end{array}$	$\begin{array}{c}1.\\ 0.8495402\\ 0.8015908\\ 0.7973782\\ 0.8251602\\ 0.8760693\\ 0.9451350\\ 1.0291829\\ 1.1230337\\ 1.2233991\\ 1.3269025\end{array}$	$\begin{array}{c}1\\ 0.9148207\\ 0.8584646\\ 0.8294742\\ 0.8260873\\ 0.8462434\\ 0.8875971\\ 0.9475376\\ 1.0232138\\ 1.1115638\\ 1.2093504\end{array}$	$\begin{array}{c}1\\ 0.9148208\\ 0.8584646\\ 0.8294743\\ 0.8260874\\ 0.8462434\\ 0.8875971\\ 0.9475377\\ 1.0232138\\ 1.1115639\\ 1.2093505\end{array}$	$\begin{array}{c}1\\ 0.9148207\\ 0.8584645\\ 0.8294741\\ 0.8260872\\ 0.8462431\\ 0.8875968\\ 0.9475373\\ 1.0232134\\ 1.1115633\\ 1.2093498\end{array}$	$\begin{array}{c}1\\ 0.9148208\\ 0.8584646\\ 0.8294743\\ 0.8260874\\ 0.8462434\\ 0.8875971\\ 0.9475377\\ 1.0232138\\ 1.1115639\\ 1.2093504\end{array}$	$\begin{array}{c}1\\ 0.9148208\\ 0.8584646\\ 0.8294743\\ 0.8260874\\ 0.8462434\\ 0.8875971\\ 0.9475377\\ 1.0232138\\ 1.1115639\\ 1.2093504\end{array}$

Application 5.2:

Consider the following nonlinear SFADE [27–29] (27) $\left\{\begin{array}{l}{D}_{\ast }^{\alpha }x\left(t\right)=1+x\left(t\right)+z\left(t\right)x\left(t\right),\\ D_{\ast }^{\alpha }z\left(t\right)=y\left(t\right)-x^2\left(t\right)-z\left(t\right)\\ y\left(t\right)=x^2\left(t\right)\end{array}\right.$(27) With $0<\alpha \le 1$ and initial conditions (28) $x\left(0\right)=y\left(0\right)=z\left(0\right)=1.$(28) For the special case when $\alpha =1,$ the exact solution is $x\left(t\right)=e^t,y\left(t\right)=e^{2t},z\left(t\right)=e^{-t}$.

By employing the proposed technique using $m_1=m_2=m_3=5$, $x\left(t\right)=\sum _{j=0}^5{c}_j{T}_j^{\ast }\left(t\right),$ $y\left(t\right)=\sum _{j=0}^5{b}_j{T}_j^{\ast }\left(t\right)$ and $z\left(t\right)=\sum _{j=0}^5{a}_j{T}_j^{\ast }\left(t\right)$

We obtain a system of nonlinear algebraic equations which contains eighteen equations for eighteen unknowns; $c_j$, $b_{j}and{a}_j,j=0,1,\dots ,5$. These unknowns are obtained by using Newton iteration method.

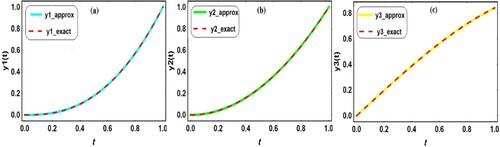
For $\alpha =1$. The estimated solutions will be $\begin{array}{rl}x\left(t\right)& =0.9999+t(3.0001+t(2.4967+t(0.85017\\ & +(0.0904+0.0737t)t\left)\right)\\ y\left(t\right)& =1.+t(6.00725+t(13.647+t(19.38\\ & +t(4.417+11.9554t)\left)\right))\\ z\left(t\right)& =1.+t(-0.99999+t(0.4997+t(-0.1652\\ & +(0.0385-0.0051t)t\left)\right))\end{array}$The numerical solutions of Application 5.2 are shown graphically through Figure 2 and tabulated in Table 3(a–c) and Table 4(4a and 4b). From Figure 2, it is easy to conclude that the obtained solutions are continuously depend on the fractional derivative and the estimated solutions are in good agreement with the exact solution at $\alpha =1$. Table 3(a–c) show the effectiveness of the suggested technique even with using few terms of SCPs and the accuracy of the method is increased by adding more terms of the SCPs. Also the solutions do not need much CPU time to produce very accurate numerical solutions.

Table 3. (a) Absolut errors of $x\left(t\right)$ of Application 5.2 for different values of $m$.

Absolute errors of $x\left(t\right)$ for Application 5.2
$t$	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}0.\\ 1.047\times {10}^{-6}\\ 2.565\times {10}^{-6}\\ 1.299\times {10}^{-6}\\ 1.208\times {10}^{-6}\\ 2.393\times {10}^{-6}\\ 1.083\times {10}^{-6}\\ 1.576\times {10}^{-6}\\ 2.854\times {10}^{-6}\\ 9.906\times {10}^{-7}\\ 2.289\times {10}^{-7}\end{array}$	$\begin{array}{c}0.\\ \phantom{,,}2.89\times {10}^{-15}\\ \phantom{,,}1.11\times {10}^{-15}\\ \phantom{,,}3.86\times {10}^{-14}\\ \phantom{,,}3.44\times {10}^{-14}\\ 3.109\times {10}^{-15}\\ 4.707\times {10}^{-14}\\ 2.443\times {10}^{-14}\\ 7.105\times {10}^{-15}\\ 1.599\times {10}^{-14}\\ 1.243\times {10}^{-14}\end{array}$	$\begin{array}{c}1.11\times {10}^{-16}\\ 2.22\times {10}^{-16}\\ 0.\\ 0.\\ 0.\\ 0.\\ 0.\\ 4.44\times {10}^{-16}\\ 0.\\ 4.44\times {10}^{-16}\\ 4.44\times {10}^{-16}\end{array}$	$\begin{array}{c}1.11\times {10}^{-16}\\ 0.\\ 2.22\times {10}^{-16}\\ 2.22\times {10}^{-16}\\ 0.\\ 2.22\times {10}^{-16}\\ 0.\\ 0.\\ 0.\\ 8.88\times {10}^{-16}\\ 0.\end{array}$
CPU	$0.0468$	$0.156001$	$0.343202$	$0.655204$
(b). Absolute errors of $y\left(t\right)$ of Application 5.2 for different values of $m$.
Absolute errors of $y\left(t\right)$ for Application 5.2
t	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}\phantom{,.}1.11\times {10}^{-16}\\ 3.961\times {10}^{-5}\\ 1.208\times {10}^{-5}\\ 1.008\times {10}^{-4}\\ 1.401\times {10}^{-4}\\ 0.789\times {10}^{-5}\\ 2.118\times {10}^{-4}\\ 2.768\times {10}^{-4}\\ 0.146\times {10}^{-4}\\ 4.097\times {10}^{-4}\\ 4.740\times {10}^{-4}\end{array}$	$\begin{array}{c}0.\\ \phantom{,.}2.31\times {10}^{-11}\\ 4.694\times {10}^{-11}\\ 4.060\times {10}^{-11}\\ 4.213\times {10}^{-11}\\ 1.247\times {10}^{-10}\\ 6.500\times {10}^{-11}\\ 1.016\times {10}^{-10}\\ 2.075\times {10}^{-10}\\ 2.374\times {10}^{-10}\\ 2.717\times {10}^{-10}\end{array}$	$\begin{array}{c}1.11\times {10}^{-16}\\ 1.55\times {10}^{-15}\\ 6.66\times {10}^{-16}\\ 0.\\ 4.44\times {10}^{-16}\\ 4.44\times {10}^{-16}\\ 4.44\times {10}^{-16}\\ 2.66\times {10}^{-15}\\ 3.55\times {10}^{-15}\\ 8.88\times {10}^{-16}\\ 8.88\times {10}^{-16}\end{array}$	$\begin{array}{c}1.11\times {10}^{-16}\\ 8.88\times {10}^{-16}\\ 6.66\times {10}^{-16}\\ 2.22\times {10}^{-16}\\ 4.44\times {10}^{-16}\\ 1.33\times {10}^{-15}\\ 1.33\times {10}^{-15}\\ 3.55\times {10}^{-15}\\ 2.66\times {10}^{-15}\\ 8.88\times {10}^{-16}\\ 8.88\times {10}^{-16}\end{array}$
CPU	$0.0468$	$0.156001$	$0.343202$	$0.655204$
(c) Absolute errors of $z\left(t\right)$ of Application 5.2 for different values of $m$.
Absolute errors of $z\left(t\right)$ for Application 5.2
$t$	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}0.\\ 4.177\times {10}^{-7}\\ 9.684\times {10}^{-7}\\ 4.224\times {10}^{-7}\\ 5.275\times {10}^{-7}\\ 9.102\times {10}^{-7}\\ \phantom{,,}3.77\times {10}^{-7}\\ 5.693\times {10}^{-7}\\ 9.534\times {10}^{-7}\\ 2.568\times {10}^{-7}\\ 1.549\times {10}^{-7}\end{array}$	$\begin{array}{c}0.\\ 1.665\times {10}^{-15}\\ \phantom{,,}7.77\times {10}^{-16}\\ 1.266\times {10}^{-14}\\ 1.366\times {10}^{-14}\\ 1.665\times {10}^{-15}\\ 1.499\times {10}^{-14}\\ 1.160\times {10}^{-14}\\ 2.165\times {10}^{-15}\\ 3.053\times {10}^{-15}\\ 2.220\times {10}^{-15}\end{array}$	$\begin{array}{c}0.\\ 1.11\times {10}^{-16}\\ 1.11\times {10}^{-16}\\ 0.\\ 0.\\ 1.11\times {10}^{-16}\\ 0.\\ 1.665\times {10}^{-16}\\ 5.551\times {10}^{-17}\\ 5.551\times {10}^{-17}\\ 5.551\times {10}^{-17}\end{array}$	$\begin{array}{c}0.\\ 1.11\times {10}^{-16}\\ 0.\\ 1.11\times {10}^{-16}\\ 0.\\ 0.\\ 0.\\ 5.55\times {10}^{-17}\\ 0.\\ 5.55\times {10}^{-17}\\ 0.\end{array}$
CPU	$0.0468$	$0.156001$	$0.343202$	$0.655204$

Table 4(a,b) demonstrate the accuracy of the proposed technique when compared with the numerical methods in [27–29].

Figure 2. The behaviours of $x\left(t\right),y\left(t\right)\text{and}z\left(t\right)$ of Application 5.2 for different values of $\alpha$ with the exact solutions at $\alpha$ = 1, $m=5$; (a) $x\left(t\right)$, (b) $y\left(t\right)$, (c) $z\left(t\right)$.

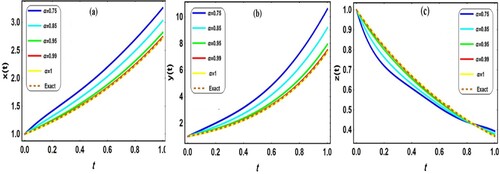
Table 4. (a) The approximate solution of $x\left(t\right)$ of Application 5.2 with comparisons by [27–29].

Approximate solution of $x\left(t\right)$ Application 5.2
	$\alpha =0.75$				$\alpha =1$
t	VIM [27]	HAM [28]	TF [29]	SCPSM	VIM [27]	HAM [28]	TF [29]	SCPSM	Exact
$\begin{array}{l}0\\ 0.1\\ 0.2\\ 0.3\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1\end{array}$	$\begin{array}{c}1\\ 1.218706\\ 1.400027\\ 1.584126\\ 1.776908\\ 1.981386\\ 2.199744\\ 2.433882\\ 2.685623\\ 2.956809\\ 3.249362\end{array}$	$\begin{array}{c}1\\ 1.218706\\ 1.400027\\ 1.584127\\ 1.776908\\ 1.981386\\ 2.199745\\ 2.433883\\ 2.685624\\ 2.956813\\ 3.249374\end{array}$	$\begin{array}{c}1\\ 1.218704\\ 1.400026\\ 1.584129\\ 1.776908\\ 1.981386\\ 2.199745\\ 2.433884\\ 2.685625\\ 2.956813\\ 3.249370\end{array}$	$\begin{array}{c}1\\ 1.218641\\ 1.400325\\ 1.584803\\ 1.777029\\ 1.981671\\ 2.200299\\ 2.434116\\ 2.685985\\ 2.957288\\ 3.249887\end{array}$	$\begin{array}{c}1\\ 1.1051709\\ 1.2214027\\ 1.3498588\\ 1.4918246\\ 1.6487212\\ 1.8221188\\ 2.0137527\\ 2.2255409\\ 2.4596031\\ 2.7182818\end{array}$	$\begin{array}{c}1\\ 1.1051709\\ 1.2214027\\ 1.3498588\\ 1.4918246\\ 1.6487212\\ 1.8221188\\ 2.0137527\\ 2.2255409\\ 2.4596031\\ 2.7182818\end{array}$	$\begin{array}{c}1\\ 1.1051709\\ 1.2214028\\ 1.3498589\\ 1.4918249\\ 1.6487215\\ 1.8221191\\ 2.0137531\\ 2.2255415\\ 2.4596038\\ 2.7182827\end{array}$	$\begin{array}{c}1\\ 1.1051709\\ 1.2214027\\ 1.3498588\\ 1.4918246\\ 1.6487212\\ 1.8221188\\ 2.0137527\\ 2.2255409\\ 2.4596031\\ 2.7182818\end{array}$	$\begin{array}{l}1\\ 1.1051709\\ 1.2214027\\ 1.3498588\\ 1.4918246\\ 1.6487212\\ 1.82211880\\ 2.0137527\\ 2.2255409\\ 2.4596031\\ 2.7182818\end{array}$
(b) The approximate solution of $z\left(t\right)$ of Application 5.2 with comparisons by [24–26].
Approximate solution of $z\left(t\right)$ Application 5.2
	$\alpha =0.75$				$\alpha =1$
t	VIM [27]	HAM [28]	TF [29]	SCPSM	VIM [27]	HAM [28]	TF [29]	SCPSM	Exact
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}1\\ 0.828250\\ 0.732584\\ 0.660337\\ 0.602121\\ 0.553602\\ 0.512285\\ 0.476555\\ 0.445294\\ 0.445294\\ 0.393120\end{array}$	$\begin{array}{c}1\\ 0.828250\\ 0.732584\\ 0.660337\\ 0.602121\\ 0.553602\\ 0.512285\\ 0.476554\\ 0.445292\\ 0.417682\\ 0.393108\end{array}$	$\begin{array}{c}1\\ 0.828247\\ 0.732582\\ 0.660335\\ 0.602119\\ 0.553601\\ 0.512283\\ 0.476553\\ 0.445291\\ 0.417681\\ 0.393107\end{array}$	$\begin{array}{c}1.\\ 0.828489\\ 0.732506\\ 0.659818\\ 0.602193\\ 0.553657\\ 0.511963\\ 0.476661\\ 0.4453663\\ 0.4176448\\ 0.3930353\end{array}$	$\begin{array}{c}1\\ 0.9048374\\ 0.8187307\\ 0.7408182\\ 0.6703200\\ 0.6065306\\ 0.5488116\\ 0.4965853\\ 0.4493289\\ 0.4065696\\ 0.3678794\end{array}$	$\begin{array}{c}1\\ 10.9048374\\ 0.8187307\\ 0.7408182\\ 0.6703200\\ 0.6065306\\ 0.5488116\\ 0.4965853\\ 0.4493289\\ 0.4065696\\ 0.3678794\end{array}$	$\begin{array}{c}1\\ 0.9048373\\ 0.8187306\\ 0.7408181\\ 0.6703199\\ 0.6065305\\ 0.5488115\\ 0.4965851\\ 0.4493288\\ 0.4065695\\ 0.3678793\end{array}$	$\begin{array}{c}1\\ 0.9048374\\ 0.8187307\\ 0.7408182\\ 0.6703200\\ 0.6065306\\ 0.5488116\\ 0.4965853\\ 0.4493289\\ 0.4065696\\ 0.3678794\end{array}$	$\begin{array}{c}1\\ 0.9048374\\ 0.8187307\\ 0.7408182\\ 0.6703200\\ 0.6065306\\ 0.5488116\\ 0.4965853\\ 0.4493289\\ 0.4065696\\ 0.3678794\end{array}$

Table 5. (a) The absolute error of $y\left(t\right)$ of Application 5.3 for different values of $m$.

Absolute error of $y\left(t\right)$ of Application 5.3
$t$	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{l}1.041\times {10}^{-17}\\ 1.050\times {10}^{-5}\\ 3.803\times {10}^{-5}\\ 4.376\times {10}^{-5}\\ 1.750\times {10}^{-5}\\ 2.615\times {10}^{-5}\\ 5.738\times {10}^{-5}\\ 4.610\times {10}^{-5}\\ 1.821\times {10}^{-5}\\ 1.020\times {10}^{-4}\\ 9.876\times {10}^{-5}\end{array}$	$\begin{array}{l}1.332\times {10}^{-17}\\ 4.109\times {10}^{-10}\\ 2.770\times {10}^{-9}\\ 2.431\times {10}^{-8}\\ 3.239\times {10}^{-9}\\ 1.368\times {10}^{-8}\\ 3.409\times {10}^{-8}\\ 3.292\times {10}^{-8}\\ 1.005\times {10}^{-8}\\ 3.692\times {10}^{-8}\\ 1.840\times {10}^{-8}\end{array}$	$\begin{array}{l}3.284\times {10}^{-17}\\ 1.746\times {10}^{-12}\\ 6.319\times {10}^{-12}\\ 1.306\times {10}^{-11}\\ 7.637\times {10}^{-12}\\ 1.426\times {10}^{-11}\\ 4.268\times {10}^{-12}\\ 8.064\times {10}^{-12}\\ 1.290\times {10}^{-11}\\ 2.085\times {10}^{-11}\\ 1.604\times {10}^{-11}\end{array}$	$\begin{array}{l}\phantom{..}1.400\times {10}^{-17}\\ \phantom{..}5.187\times {10}^{-16}\\ \phantom{..}4.025\times {10}^{-15}\\ \phantom{..}6.314\times {10}^{-15}\\ \phantom{..}6.883\times {10}^{-15}\\ \phantom{..}1.280\times {10}^{-14}\\ 8.3267\times {10}^{-16}\\ \phantom{..}2.110\times {10}^{-15}\\ \phantom{..}1.932\times {10}^{-14}\\ \phantom{..}1.477\times {10}^{-14}\\ 1.1880\times {10}^{-14}\end{array}$
CPU	$0.0468$	$0.124801$	$0.280802$	$0.624004$
(b) The absolute error of $z\left(t\right)$ of Application 5.3 for different values of $m$.
Absolute error of $z\left(t\right)$ of Application 5.3
$t$	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{l}6.939\times {10}^{-17}\\ 0.311\times {10}^{-4}\\ 7.933\times {10}^{-4}\\ 3.911\times {10}^{-4}\\ 4.916\times {10}^{-4}\\ 9.533\times {10}^{-4}\\ 4.156\times {10}^{-4}\\ 8.154\times {10}^{-4}\\ 1.488\times {10}^{-3}\\ 3.739\times {10}^{-4}\\ 4.594\times {10}^{-4}\end{array}$	$\begin{array}{l}\phantom{,,}7.378\times {10}^{-17}\\ 5.9767\times {10}^{-8}\\ \phantom{,,}3.579\times {10}^{-8}\\ \phantom{,,}6.205\times {10}^{-7}\\ \phantom{,,}7.183\times {10}^{-7}\\ \phantom{,,}1.107\times {10}^{-7}\\ \phantom{,,}9.743\times {10}^{-7}\\ \phantom{,,}8.533\times {10}^{-7}\\ \phantom{,,}2.033\times {10}^{-7}\\ \phantom{,,}2.737\times {10}^{-7}\\ \phantom{,,}2.410\times {10}^{-7}\end{array}$	$\begin{array}{l}9.365\times {10}^{-18}\\ 1.577\times {10}^{-10}\\ 4.831\times {10}^{-10}\\ 6.830\times {10}^{-10}\\ 7.139\times {10}^{-10}\\ 8.918\times {10}^{-10}\\ 8.890\times {10}^{-10}\\ 1.009\times {10}^{-9}\\ 9.193\times {10}^{-10}\\ 2.701\times {10}^{-10}\\ 8.629\times {10}^{-11}\end{array}$	$\begin{array}{l}2.166\times {10}^{-18}\\ 9.966\times {10}^{-14}\\ 1.469\times {10}^{-13}\\ 5.939\times {10}^{-13}\\ 5.010\times {10}^{-13}\\ 6.661\times {10}^{-15}\\ 6.933\times {10}^{-13}\\ 8.002\times {10}^{-13}\\ 2.218\times {10}^{-13}\\ 3.106\times {10}^{-13}\\ 3.042\times {10}^{-14}\end{array}$
CPU	$0.0468$	$0.124801$	$0.280802$	$0.624004$
(c) The absolute error of $w\left(t\right)$ of Application 5.3 for different values of $m$.
Absolute error of w(t) of Application 5.3
t	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{l}1.735\times {10}^{-18}\\ 1.264\times {10}^{-5}\\ 3.836\times {10}^{-5}\\ 3.800\times {10}^{-5}\\ 1.012\times {10}^{-5}\\ 2.615\times {10}^{-5}\\ 4.621\times {10}^{-5}\\ 3.241\times {10}^{-5}\\ 1.686\times {10}^{-5}\\ 8.196\times {10}^{-5}\\ 1.211\times {10}^{-4}\end{array}$	$\begin{array}{l}6.967\times {10}^{-18}\\ 4.109\times {10}^{-10}\\ 2.770\times {10}^{-9}\\ 2.431\times {10}^{-8}\\ 3.239\times {10}^{-9}\\ 1.368\times {10}^{-8}\\ 3.409\times {10}^{-8}\\ 3.292\times {10}^{-8}\\ 1.005\times {10}^{-8}\\ 3.692\times {10}^{-8}\\ 1.840\times {10}^{-8}\end{array}$	$\begin{array}{l}4.058\times {10}^{-17}\\ 1.746\times {10}^{-12}\\ 6.319\times {10}^{-12}\\ 1.306\times {10}^{-11}\\ 7.637\times {10}^{-12}\\ 1.426\times {10}^{-11}\\ 4.268\times {10}^{-12}\\ 8.064\times {10}^{-12}\\ 1.290\times {10}^{-11}\\ 2.085\times {10}^{-11}\\ 1.604\times {10}^{-11}\end{array}$	$\begin{array}{l}3.535\times {10}^{-17}\\ 4.302\times {10}^{-16}\\ 3.997\times {10}^{-15}\\ 6.384\times {10}^{-15}\\ 6.883\times {10}^{-15}\\ 1.277\times {10}^{-14}\\ 6.661\times {10}^{-16}\\ 1.998\times {10}^{-15}\\ 1.910\times {10}^{-14}\\ 1.466\times {10}^{-14}\\ 1.210\times {10}^{-14}\end{array}$
CPU	$0.0468$	$0.124801$	$0.280802$	$0.624004$

Table 6. (a) The absolute error of $x\left(t\right)$ of Application 5.4 for different values of $m$.

Absolute error of the approximate values $x\left(t\right)$ for Application 5.4
t	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}1.282\times {10}^{-16}\\ 1.197\times {10}^{-16}\\ 9.021\times {10}^{-17}\\ 8.327\times {10}^{-17}\\ 8.327\times {10}^{-17}\\ 1.110\times {10}^{-16}\\ 1.110\times {10}^{-16}\\ 1.665\times {10}^{-16}\\ 0.\\ 1.110\times {10}^{-16}\\ 0.\end{array}$	$\begin{array}{c}1.127\times {10}^{-17}\\ 5.204\times {10}^{-18}\\ 6.940\times {10}^{-18}\\ 1.388\times {10}^{-17}\\ 0.\\ 0.\\ 0.\\ 0.\\ 0.\\ 0.\\ 0.\end{array}$	$\begin{array}{c}1.635\times {10}^{-16}\\ 1.769\times {10}^{-16}\\ 1.735\times {10}^{-16}\\ 1.388\times {10}^{-16}\\ 1.110\times {10}^{-16}\\ 1.110\times {10}^{-16}\\ 1.110\times {10}^{-16}\\ 1.110\times {10}^{-16}\\ 0.\\ 1.110\times {10}^{-16}\\ 0.\end{array}$	$\begin{array}{c}1.132\times {10}^{-17}\\ 1.735\times {10}^{-18}\\ 1.388\times {10}^{-17}\\ 1.388\times {10}^{-17}\\ 0.\\ 0.\\ 0.\\ 0.\\ 0.\\ 0.\\ 0.\end{array}$
CPU	$0.0312$	$0.124801$	$0.296402$	$0.608404$
(b) The absolute error of $y\left(t\right)$ of Application 5.4 for different values of $m$.
Absolute error of the approximate values $y\left(t\right)$ for Application 5.4
$t$	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}2.776\times {10}^{-17}\\ 3.751\times {10}^{-17}\\ 1.735\times {10}^{-17}\\ 7.112\times {10}^{-17}\\ 1.388\times {10}^{-16}\\ 1.596\times {10}^{-16}\\ 1.110\times {10}^{-16}\\ 1.110\times {10}^{-16}\\ 2.220\times {10}^{-16}\\ 6.661\times {10}^{-16}\\ 6.661\times {10}^{-16}\end{array}$	$\begin{array}{c}3.964\times {10}^{-17}\\ 6.204\times {10}^{-17}\\ 1.453\times {10}^{-17}\\ 1.388\times {10}^{-17}\\ 4.163\times {10}^{-17}\\ 5.551\times {10}^{-17}\\ 8.327\times {10}^{-17}\\ 5.551\times {10}^{-17}\\ 1.110\times {10}^{-16}\\ 1.110\times {10}^{-16}\\ 0.\end{array}$	$\begin{array}{c}5.217\times {10}^{-17}\\ 2.004\times {10}^{-17}\\ 9.476\times {10}^{-17}\\ 1.509\times {10}^{-16}\\ 8.327\times {10}^{-17}\\ 1.110\times {10}^{-16}\\ 8.327\times {10}^{-17}\\ 1.665\times {10}^{-16}\\ 1.665\times {10}^{-16}\\ 3.331\times {10}^{-16}\\ 4.441\times {10}^{-16}\end{array}$	$\begin{array}{c}2.133\times {10}^{-17}\\ 2.263\times {10}^{-17}\\ 2.927\times {10}^{-17}\\ 1.041\times {10}^{-17}\\ 1.735\times {10}^{-17}\\ 1.249\times {10}^{-16}\\ 1.110\times {10}^{-16}\\ 8.327\times {10}^{-17}\\ 5.551\times {10}^{-17}\\ 0.\\ 0.\end{array}$
CPU	$0.0312$	$0.124801$	$0.296402$	$0.608404$
(c) The absolute error of $z\left(t\right)$ of Application 5.4 for different values of $m$.
Absolute error of the approximate values $z\left(t\right)$ for Application 5.4
$t$	$m=5$	$m=10$	$m=15$	$m=20$
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}0.\\ 8.88\times {10}^{-16}\\ 2.22\times {10}^{-16}\\ 6.66\times {10}^{-16}\\ 4.44\times {10}^{-16}\\ 6.66\times {10}^{-16}\\ 1.78\times {10}^{-15}\\ 1.33\times {10}^{-15}\\ 4.44\times {10}^{-16}\\ 4.44\times {10}^{-16}\\ 1.77\times {10}^{-15}\end{array}$	$\begin{array}{c}1.110\times {10}^{-16}\\ 3.997\times {10}^{-15}\\ 3.331\times {10}^{-15}\\ 1.554\times {10}^{-15}\\ 8.882\times {10}^{-16}\\ 3.553\times {10}^{-15}\\ 1.332\times {10}^{-15}\\ 1.332\times {10}^{-15}\\ 4.885\times {10}^{-15}\\ 2.665\times {10}^{-15}\\ 1.776\times {10}^{-15}\end{array}$	$\begin{array}{c}0.\\ 3.109\times {10}^{-15}\\ 1.332\times {10}^{-15}\\ 6.661\times {10}^{-16}\\ 2.220\times {10}^{-16}\\ 2.220\times {10}^{-16}\\ 8.882\times {10}^{-16}\\ 0.\\ 4.441\times {10}^{-16}\\ 2.665\times {10}^{-15}\\ 2.665\times {10}^{-15}\end{array}$	$\begin{array}{c}2.220\times {10}^{-16}\\ 1.998\times {10}^{-15}\\ 1.776\times {10}^{-15}\\ 8.882\times {10}^{-16}\\ 1.776\times {10}^{-15}\\ 1.998\times {10}^{-15}\\ 1.332\times {10}^{-15}\\ 0.\\ 8.882\times {10}^{-16}\\ 2.665\times {10}^{-15}\\ 3.109\times {10}^{-15}\end{array}$
CPU	$0.0312$	$0.124801$	$0.296402$	$0.608404$

Table 7. (a) Numerical comparison between the approximate solutions of $y_1\left(t\right)$ of Application 5.5 with SGOM [31] at $m=3andm=5$.

Approximate solution of $y_1\left(t\right)$ of Application 5.5
	$m=3$		$m=5$
$t$	SGOM [31]	SCPSM	SGOM [31]	SCPSM
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}0\\ 2.31\times {10}^{-3}\\ 1.84\times {10}^{-3}\\ 7.94\times {10}^{-4}\\ 8.99\times {10}^{-5}\\ 2.42\times {10}^{-5}\\ 5.07\times {10}^{-4}\\ 1.18\times {10}^{-3}\\ 1.47\times {10}^{-3}\\ 6.46\times {10}^{-4}\\ 2.15\times {10}^{-3}\end{array}$	$\begin{array}{c}1.665\times {10}^{-16}\\ 2.44\times {10}^{-4}\\ 1.70\times {10}^{-3}\\ 2.54\times {10}^{-3}\\ 2.21\times {10}^{-3}\\ 8.08\times {10}^{-4}\\ 1.20\times {10}^{-3}\\ 3.10\times {10}^{-3}\\ 3.91\times {10}^{-3}\\ 2.21\times {10}^{-3}\\ 2.56\times {10}^{-3}\end{array}$	$\begin{array}{c}\phantom{,}1.30\times {10}^{-17}\\ 1.66\times {10}^{-4}\\ 3.60\times {10}^{-5}\\ 4.54\times {10}^{-5}\\ 4.43\times {10}^{-5}\\ 9.10\times {10}^{-5}\\ 3.86\times {10}^{-5}\\ 4.56\times {10}^{-6}\\ 4.36\times {10}^{-5}\\ 9.67\times {10}^{-5}\\ 1.23\times {10}^{-4}\end{array}$	$\begin{array}{c}\phantom{,,}4.13\times {10}^{-16}\\ \phantom{,,}1.36\times {10}^{-4}\\ \phantom{,,}6.99\times {10}^{-5}\\ \phantom{,,}1.44\times {10}^{-4}\\ \phantom{,,}2.17\times {10}^{-4}\\ \phantom{,,}7.44\times {10}^{-5}\\ 1.497\times {10}^{-4}\\ \phantom{,,}2.39\times {10}^{-4}\\ \phantom{,,}6.89\times {10}^{-5}\\ \phantom{,,}2.03\times {10}^{-4}\\ \phantom{,,}7.87\times {10}^{-5}\end{array}$
CPU	–	$0.0156$	–	$0.0312$
(b) Numerical comparison between the approximate solutions of $y_2\left(t\right)$ of Application 5.5 with SGOM [31] at $m=3\text{and}m=5$.
Approximate solution of $y_2\left(t\right)$ of Application 5.5
	$m=3$		$m=5$
t	SGOM [31]	SCPSM	SGOM [31]	SCPSM
$\begin{array}{l}0.\\ 0.1\\ 0.2\\ 0.4\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.\end{array}$	$\begin{array}{c}0\\ 2.46\times {10}^{-5}\\ 3.66\times {10}^{-6}\\ 3.93\times {10}^{-4}\\ 3.58\times {10}^{-4}\\ 2.92\times {10}^{-4}\\ 2.27\times {10}^{-4}\\ 1.96\times {10}^{-4}\\ 2.28\times {10}^{-4}\\ 3.56\times {10}^{-4}\\ 6.10\times {10}^{-4}\end{array}$	$\begin{array}{c}\phantom{,,}5.55\times {10}^{-17}\\ \phantom{,,}5.09\times {10}^{-5}\\ \phantom{,,}9.16\times {10}^{-6}\\ 1.\phantom{,,}36\times {10}^{-4}\\ \phantom{,,}2.84\times {10}^{-4}\\ 4.092\times {10}^{-4}\\ \phantom{,,}4.67\times {10}^{-4}\\ \phantom{,,}4.13\times {10}^{-4}\\ \phantom{,,}2.03\times {10}^{-4}\\ \phantom{,,}2.09\times {10}^{-4}\\ \phantom{,,}8.66\times {10}^{-4}\end{array}$	$\begin{array}{c}3.68\times {10}^{-17}\\ 3.41\times {10}^{-5}\\ 3.52\times {10}^{-5}\\ 2.92\times {10}^{-5}\\ 2.68\times {10}^{-5}\\ 2.88\times {10}^{-5}\\ 3.05\times {10}^{-5}\\ 2.76\times {10}^{-5}\\ 2.04\times {10}^{-5}\\ 1.93\times {10}^{-5}\\ 4.96\times {10}^{-5}\end{array}$	$\begin{array}{c}1.28\times {10}^{-16}\\ 6.09\times {10}^{-6}\\ 2.40\times {10}^{-5}\\ 2.30\times {10}^{-5}\\ 1.43\times {10}^{-6}\\ 2.46\times {10}^{-5}\\ 3.47\times {10}^{-5}\\ 1.61\times {10}^{-5}\\ 2.34\times {10}^{-5}\\ 0.43\times {10}^{-5}\\ 4.18\times {10}^{-5}\end{array}$
CPU	–	$0.0156$	–	$0.0312$
(c) Numerical comparison between the approximate solutions of $y_3\left(t\right)$ of Application 5.5 with SGOM [31] at $m=3\text{and}m=5$.
Approximate solution of $y_3\left(t\right)$ of Application 5.5
	$m=3$		$m=5$
t	SGOM [31]	SCPSM	SGOM [31]	SCPSM
$\begin{array}{l}0\\ 0.1\\ 0.2\\ 0.3\\ 0.4\\ 0.5\\ 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1\end{array}$	$\begin{array}{c}0\\ 4.38\times {10}^{-3}\\ 3.31\times {10}^{-3}\\ 2.20\times {10}^{-3}\\ 1.78\times {10}^{-4}\\ 2.44\times {10}^{-4}\\ 2.16\times {10}^{-3}\\ 2.70\times {10}^{-3}\\ 9.37\times {10}^{-4}\\ 4.90\times {10}^{-3}\\ 4.98\times {10}^{-3}\end{array}$	$\begin{array}{c}\phantom{..}2.43\times {10}^{-17}\\ 2.55\times {10}^{-4}\\ 1.50\times {10}^{-4}\\ 2.14\times {10}^{-4}\\ 7.16\times {10}^{-4}\\ 1.21\times {10}^{-3}\\ 1.50\times {10}^{-3}\\ 1.35\times {10}^{-3}\\ 4.72\times {10}^{-4}\\ 1.49\times {10}^{-3}\\ 4.98\times {10}^{-3}\end{array}$	$\begin{array}{c}\phantom{..}6.28\times {10}^{-17}\\ 2.98\times {10}^{-4}\\ 3.68\times {10}^{-5}\\ 6.16\times {10}^{-5}\\ 1.62\times {10}^{-4}\\ 1.53\times {10}^{-4}\\ 4.67\times {10}^{-5}\\ 1.85\times {10}^{-5}\\ 6.68\times {10}^{-5}\\ 1.74\times {10}^{-4}\\ 2.96\times {10}^{-4}\end{array}$	$\begin{array}{c}\phantom{..}1.47\times {10}^{-17}\\ 1.32\times {10}^{-5}\\ 8.79\times {10}^{-5}\\ 7.76\times {10}^{-5}\\ 1.93\times {10}^{-5}\\ 1.24\times {10}^{-4}\\ 1.42\times {10}^{-4}\\ 2.56\times {10}^{-5}\\ 1.61\times {10}^{-4}\\ 1.79\times {10}^{-4}\\ 4.46\times {10}^{-4}\end{array}$
CPU	–	$0.0156$	–	$0.0312$

Application 5.3:

Consider the following variable coefficient nonlinear SFDAEs [29] (29) $\left\{\begin{array}{l}{D}_{\ast }^{\alpha }y\left(t\right)=y\left(t\right)-z\left(t\right)w\left(t\right)+\sin \left(t\right)+t\text{cos}\left(t\right),\\ D_{\ast }^{\alpha }z\left(t\right)=tw\left(t\right)+y^2\left(t\right)+se{c}^2\left(t\right)\\ -t^2\left(\cos \left(t\right)+si{n}^2\left(t\right)\right)\\ y\left(t\right)=w\left(t\right)-t\left(\cos \left(t\right)-sin\left(t\right)\right)\end{array}\right.$(29) where $0<\alpha \le 1$ and initial conditions: (30) $y\left(0\right)=z\left(0\right)=w\left(0\right)=0$(30) At $\alpha =1.$ The exact solution is: $y\left(t\right)=tsin\left(t\right),z\left(t\right)=\tan \left(t\right),w\left(t\right)=tcos\left(t\right)$.

By applying our proposed technique using $m_1=m_2=m_3=5$, $y\left(t\right)=\sum _{j=0}^5{c}_j{T}_j^{\ast }\left(t\right)$, $z\left(t\right)=\sum _{j=0}^5{b}_j{T}_j^{\ast }\left(t\right)$ and $w\left(t\right)=\sum _{j=0}^5{a}_j{T}_j^{\ast }\left(t\right)$ to the fractional system (5–8), we obtain a system of linear algebraic equations with unknowns; $c_j$, $b_{j}and{a}_j,j=0,1,\dots ,5$. These unknowns are attained by using Newton iteration method. For $\alpha =1$, the estimated solutions will be $\begin{array}{rl}y\left(t\right)& =-1.56\times {10}^{-17}+t(-0.0002+t(1.004\\ & +t(-0.013+(-0.1584+0.009t\left)t\right)\left)\right)\\ z\left(t\right)& =-5.898\times {10}^{-17}+t(1.007+t(-0.17\\ & +t(1.17+t(-1.478+1.025t\left)\right)\left)\right)\\ w\left(t\right)& =-2.776\times {10}^{-17}+t(0.9998+t(0.005\\ & +t(-0.52(0.03146+0.025t\left)t\right)\left)\right)\end{array}$

The numerical solutions of Application 5.3 are shown graphically through Figure 3 and the absolute errors between our approximate solutions and the exact solutions for different values of m with their CPU time are given in Table 5(a–c)

Application 5.4:

Consider the following nonlinear SFDAEs [26] (31) $\left\{\begin{array}{l}{D}_{\ast }^{\alpha }x\left(t\right)=x^2\left(t\right)-y\left(t\right)+2t\\ D_{\ast }^{\alpha }y\left(t\right)=2z\left(t\right)-2\left(t+1\right),\\ tz\left(t\right)=-y\left(t\right)+3x^2\left(t\right)+t\end{array}\right.0<\alpha \le 1$(31) with the initial conditions (32) $x\left(0\right)=0,y\left(0\right)=0,z\left(0\right)=1$(32) At $\alpha =1.$ System (31) has exact solution: $x\left(t\right)=t^2,y\left(t\right)={\text{t}}^4,z\left(t\right)=2t^3+t+1$. By using our proposed technique using $m_1=m_2=m_3=5,$ $x\left(t\right)=\sum _{j=0}^5{c}_j{T}_j^{\ast }\left(t\right),$ $y\left(t\right)=\sum _{j=0}^5{b}_j{T}_j^{\ast }\left(t\right)$ and $z\left(t\right)=\sum _{j=0}^5{a}_j{T}_j^{\ast }\left(t\right)$ to the fractional system (5–6), we obtain a system of linear algebraic equations with unknowns; $c_j$, $b_{j}and{a}_j,j=0,1,\dots ,5$. These unknowns are gained by using Newton iteration method.

Figure 3. The behaviour of $y\left(t\right),z\left(t\right)\text{and}w\left(t\right)$ of Application 5.3 for different values of $\alpha$ with exact solutions $\alpha =1$; (a) $y\left(t\right)$, (b) $z\left(t\right)$, (c) $w\left(t\right)$.

For $\alpha =1$, the estimated solutions are $\begin{array}{rl}x\left(t\right)& =-5.974\times {10}^{-17}+t(2.884\times {10}^{-17}\\ & +t(-1.44\times {10}^{-15}+(1.835\times {10}^{-15}\\ & -\left(7.275\times {10}^{-16}t\right)t\left)\right))\\ y\left(t\right)& =-5.55\times {10}^{-17}+t(-2.33\times {10}^{-15}\\ & +t(1.2\times {10}^{-14}+t(-1.896\times {10}^{-14}\\ & +\left(1.-3.4\times {10}^{-16}t\right)t\left)\right))\\ z\left(t\right)& =1.+t(0.99+t(4.619\times {10}^{-13}+t(1.9999\\ & +(1.546\times {10}^{-12}t-6.17\times {10}^{-13}t)t\left)\right))\end{array}$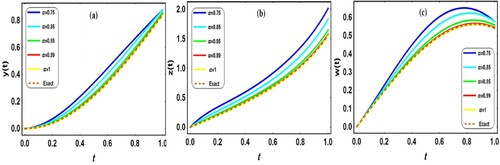The numerical solutions of Application 5.4 are shown graphically through Figure 4 and the absolute errors for different values of $m$ are tabulated in Table 6(a–c).

Figure 4. The behaviours of $y\left(t\right),z\left(t\right)\text{and}w\left(t\right)$ Application 5.4 for different values of $\alpha$ with exact solutions at $\alpha =1$; (a) $x\left(t\right)$, (b) $y\left(t\right)$, (c) $z\left(t\right)$.

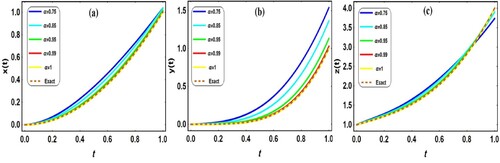
Application 5.5:

Consider the following SFDAEs [31] (33) $\left\{\begin{array}{l}{D}_{\ast }^{0.5}{y}_1\left(t\right)+2y_1\left(t\right)-\frac{\mathrm{\Gamma }\left(\frac{7}{2}\right)}{\mathrm{\Gamma }\left(3\right)}{y}_2\left(t\right)+y_3\left(t\right)\\ =2t^{\frac{5}{2}}+\sin \left(t\right)\\ D_{\ast }^{0.5}{y}_2\left(t\right)+y_2\left(t\right)+y_3\left(t\right)=\frac{\mathrm{\Gamma }\left(3\right)}{\mathrm{\Gamma }\left(5/2\right)}{t}^{\frac{3}{2}}+t^2+\sin \left(t\right),\\ 2y_1\left(t\right)+y_2\left(t\right)-y_3\left(t\right)=2t^{\frac{5}{2}}+t^2-\sin \left(t\right),t\in \left[0,1\right]\end{array}\right.$(33) with the initial conditions (34) $y_1\left(0\right)=y_2\left(0\right)=y_3\left(0\right)=0$(34) The exact solution of this problem is (35) $y_1\left(t\right)=t^{\frac{5}{2}},y_2\left(t\right)=t^2,y_3\left(t\right)=\text{sin}\left(t\right)$(35) By using our proposed technique using $m_1=m_2=m_3=5,$ $y_1\left(t\right)=\sum _{j=0}^5{c}_j{T}_j^{\ast }\left(t\right),$ $y_2\left(t\right)=\sum _{j=0}^5{b}_j{T}_j^{\ast }\left(t\right)$ and $y_3\left(t\right)=\sum _{j=0}^5{a}_j{T}_j^{\ast }\left(t\right)$ to the fractional system (33), we obtain a system of linear algebraic equations with unknowns; $c_j$, $b_{j}and{a}_j,j=0,1,\dots ,5$. These unknowns are obtained by solving the algebraic system. Then the estimated solutions are $\begin{array}{rl}{y}_1\left(t\right)& =-4.13\times {10}^{-16}+t(-0.003+t(-0.003\\ & +t(0.25+t(1.199+(-0.645+0.199t)t\left)\right))\\ y_2\left(t\right)& =1.28\times {10}^{-16}+t(0.0002+t(0.0002\\ & +t(0.99+t(0.016+(-0.023+0.01t)t\left)\right))\\ y_3\left(t\right)& =1.47\times {10}^{-16}+t(0.999+t(0.0198\\ & +t(-0.25+(0.115-0.0458t\left)t\right)\left)\right)\end{array}$The numerical results of Application 5.5 are graphically illustrated in Figure 5. A numerical comparison between our attained solutions with the results in [31] is tabulated in Table 7(a–c). The numerical results demonstrate the effectiveness and the accuracy of the proposed technique even by using a few terms of SCPs, and our obtained results are quite similar to the results given by SGOM [31].

5. Conclusion

Through this paper, The SCPSM method has been extended to solve the linear and nonlinear SFDAEs. The numerical results of some tested applications were a good evidence for the applicability and efficiency of the suggested method. A specific advantage of the suggested implementation is that it transfers the fractional differential equations into a system of algebraic equations which is easier to solve. Also, satisfactory results are obtained by using a few terms of the SCPs, and the efficiency of the anticipated method is increased by using more terms of SCPs. The obtained solutions are continuously depended on the fractional derivative and this note confirms the physical meaning of the behaviour of the solution for the proposed real problems. Also the solutions do not require much CPU time.

Figure 5. The behaviours of the approximate and exact solutions of Application 5.5. (a) $y_1\left(t\right)$ (b) $y_2\left(t\right)$ (c) $y_3\left(t\right)$.

Acknowledgement

The author is very grateful to the referees for carefully reading the paper and for their comments and suggestions which have improved the paper.

Disclosure statement

No potential conflict of interest was reported by the author(s).