?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
This work employs two new modified computational schemes to find the exact travelling and solitary wave solutions of the general modified Degasperis-Procesi Camassa-Holm (DP CH) equation that is used to illustrate the dynamical behaviour of shallow water. These schemes are the modified exponential expansion and the modified Khater methods that are used to formulate the computational solutions in various formulas such as trigonometric, hyperbolic, exponential functions. The obtained solutions are explained and figured out their substantial contributions in three different types of sketches (three, two-dimensional, and contour plots).
1. Introduction
The nonlinear partial differential equations (NPDEs) have so many essential applications in various fields of engineering and science, such as heat transfer, fluid mechanics, chemistry, thermodynamic, physics, micro electro-mechanic system, etc. These equations have been being employed to describe many complex phenomena [Citation1–10]. So, finding the exact and numerical solutions of these model have been being attracted the attention of many researchers in various branches of science. Consequently, a variety of practical, accurate solution methods have been being developed to be used for solving LPDEs, such as the auxiliary equation method [Citation11,Citation12], the Jacobi elliptic function expansion method [Citation13,Citation14], the – expansion method [Citation15,Citation16], the modified Kudryashov method [Citation17,Citation18], the first integral method [Citation19,Citation20], the new extended direct algebraic method [Citation21,Citation22], the sine-Gordon expansion method [Citation23,Citation24], the Khater method [Citation25,Citation26], the sub-equation method [Citation27,Citation28], the extended sinh-Gordon equation expansion method [Citation29,Citation30] and so on.
In this sense, we are going to employ two modified recent computational schemes (the modified exponential expansion and modified Khater methods) to find the exact travelling and solitary wave solutions of the dimensionless form of the general modified Degasperis-Procesi Camassa-Holm (GM-DP-CH) equation that is given by [Citation31,Citation32]
(1)
(1) where
is any real number, including
also
is the function of displacement and time and used to explain the dynamical behaviour of the shallow water. Equation (1) is a member of a great mathematical integrable equation family that studies the shallow water physical properties. This family is given by
(2)
(2) Equation (2) gives the Camassa-Holm (CH) equation [Citation33] when
, and provides the Degasperis-Procesi with (DP) equation [Citation34] when
Both of CH and DP equations are bi-Hamiltonian and have an associated isospectral problem. Additionally, they admit peaked solitary wave solutions. Equation (2) is just an integrable family of the equation in case
but it is not for any other values of
Using the next wave transformation
where
is an arbitrary constant on Equation (1) leads to
(3)
(3)
Balancing the highest order derivative term and nonlinear term
in Equation (3) leads to
The rest sections in this paper are organized as follows. Section 2 studies the performance of the modified exponential expansion method [Citation35,Citation36], and the modified Khater method [Citation37–40] on the GM-DP-CH equation. Section 3 gives the conclusion.
2. Application
In this section, the modified exponential expansion method and the modified Khater method are used to find novel solitary wave solutions of the GM-DP-CH equation. These solutions have a significant role in discovering more physical properties of the dynamics of the shallow water waves.
The modified exponential expansion method.
Applying this scheme to Equation (3) leads to the following general solution
(4)
(4) where
are arbitrary constants. Also,
is the solution function of the next ODE;
(5)
(5) where
are arbitrary constants. Substituting Equation (4) along (5) into Equation (3) and collecting all terms with the same power of
lead to a system of algebraic equations. Solving this system yields
Family I:
Family II
Thus, the solitary wave solutions of the GM-DP-CH are given based on family I by
For
(6)
(6)
(7)
(7)
For
(8)
(8) For
(9)
(9) For
(10)
(10)
(11)
(11)
While, the solitary wave solutions of the GM-DP-CH are given based on family II by
For
(12)
(12)
(13)
(13)
For
(14)
(14)
For Figures –
(15)
(15)
(16)
(16)
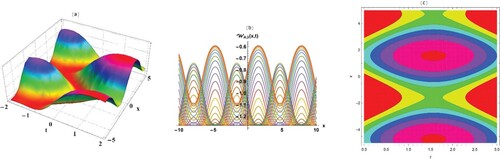
Figure 1. Dark-wave solutions of Equation (6) when in three, two-dimensional, and contour plot in two-dimensional plots.
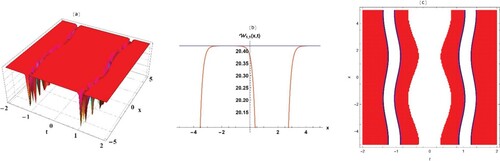
Figure 2. Bright wave solutions of Equation (7) when in three, two-dimensional, and contour plot in two-dimensional plots.
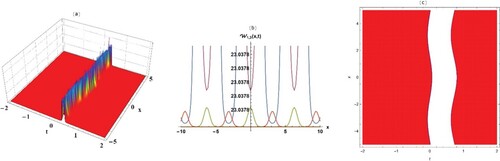
Figure 3. Dark-wave solutions of Equation (12) when in three, two-dimensional, and contour plot in two-dimensional plots.
2.2. Modified Khater method
Applying this scheme to Equation (3) leads to the following general solution
(17)
(17) where
are arbitrary constants. Also,
satisfies
(18)
(18) where
are arbitrary constants. Substituting Equa-tion (17) along (18) into Equation (3) and collecting all terms with the same power of
lead to a system of algebraic equations. Solving this system yields
Family A
Family B
Consequently, the solitary wave solutions of the GM-DP-CH are given based on family A by
For
(19)
(19)
(20)
(20)
For
(21)
(21)
(22)
(22)
For
(23)
(23)
For
(24)
(24)
For
(25)
(25)
Consequently, the solitary wave solutions of the GM-DP-CH are given based on family B by
For
(26)
(26)
(27)
(27)
For
(28)
(28)
(29)
(29)
For
(30)
(30)
For
(31)
(31)
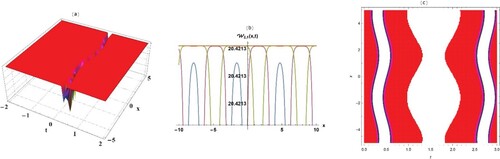
For Figures and
(32)
(32)
3. Results and discussion
In this section, we discuss our obtained results of the GM-DP-CH equation through two used employed analytical schemes (The modified exponential expansion method and the modified Khater method). Firstly, we show the difference between our two used schemes and then we go for the coincide and difference between the obtained solutions by each one of the above-mentioned schemes. Finally, we show the novelty and originality of our paper:
Used schemes:
The modified exponential expansion method and the modified Khater method have been employed to evaluate the exact travelling wave solutions of the GM-DP-CH equation. Both of these methods depend on auxiliary equation (5), (19) that play an essential role in finding the exact solutions that we have found however, Equations (5), (19) are equal when
. This equivalence makes the obtained solutions of both methods are also equal.
Obtained results:
We can find the equivalence between the solutions that have been obtained via the above-mentioned schemes. We shall show the equivalence solutions as follows:
Equations (6), (7) are equal to Equations (17), (18) when
. However the discussed equivalence between the used methods but the modified Khater method has obtained more solutions than modified exponential expansion method that explains the superiority of the modified Khater method over the modified exponential expansion method.
Previous obtained solutions:
Comparing our obtained results with that have been obtained Linares, F., Ponce, G., & Sideris, T. C (2019), shows the novelty of our solutions where the studied the property of for the solutions of properties of solutions to the IVP associated to the Camassa-Holm equation on the line related to the regularity and the decay of solutions but all our solutions in this paper is completely different from that have been obtained in their paper.
4. Conclusion
We succeed in constructing many distinct formulas of exact travelling and solitary wave solutions of the GM-DP-CH equation via the modified exponential expansion method and the modified Khater method. These obtained computational solutions explain the dynamical behaviour of shallow-water waves. Moreover, for further explanation of our obtained solutions, some distinct types of sketches were given in two, three-dimensional, and contour plots. The powerful and capable of both methods have been verified. The ability of both methods for applying to other nonlinear partial differential equation with an-integer and fractional order have been illustrated. Our future papers will aim to show the accuracy of the obtained solutions in this paper by applying numerical scheme to this model to illustrate the absolute error between exact and numerical solutions.
Acknowledgements
B. Almohsen is Supported by Researchers Supporting Project number (RSP-2020/158), King Saud University, Riyadh, Saudi Arabia.
Data Availability
All data used for the findings in this research are available publicly in manuscript.
Disclosure statement
No potential conflict of interest was reported by the author(s).
Additional information
Funding
References
- Yue C, Khater MM, Attia RA, et al. The plethora of explicit solutions of the fractional KS equation through liquid–gas bubbles mix under the thermodynamic conditions via Atangana–baleanu derivative operator. Adv Differ Equ. 2020;2020(1):1–12.
- Baleanu D, Fernandez A, Akgül A. On a fractional operator combining proportional and classical differintegrals. Mathematics. 2020;8(3):360.
- Khater MM, Park C, Lu D, et al. Analytical, semi-analytical, and numerical solutions for the Cahn–allen equation. Adv Differ Equ. 2020;2020(1):1–12.
- Akgül A. A novel method for a fractional derivative with non-local and non-singular kernel. Chaos. Solitons & Fractals. 2018;114:478–482.
- Akgül EK. Solutions of the linear and nonlinear differential equations within the generalized fractional derivatives. Chaos: An Interdisciplinary J Nonlinear Sci. 2019;29(2):023108.
- Houwe A, Inc M, Doka SY, et al. Chirped solitons in negative index materials generated by Kerr nonlinearity. Results Phys. 2020;17. doi:10.1016/j.rinp.2020.103097.
- Korpinar Z, Inc M, Bayram M, et al. New optical solitons for Biswas Arshed equation with higher order dispersions and full nonlinearity. Optik (Stuttg). 2020;206; doi:10.1016/j.ijleo.2019.163332.
- Yépez-Martínez H, Gómez-Aguilar JF. Fractional sub-equation method for Hirota–satsuma-coupled KdV equation and coupled mKdV equation using the Atangana’s conformable derivative. Waves Random Complex Media. 2019;29(4):678–693.
- Aslan EC, Inc M. Optical soliton solutions of the NLSE with quadratic-cubic-Hamiltonian perturbations and modulation instability analysis. Optik (Stuttg). 2019;196:162661.
- Pinar Z. On the explicit solutions of fractional Bagley-Torvik equation arises in engineering. An Int J Optimization Control: Theories & Applications (IJOCTA). 2019;9(3):52–58.
- Abdel-Aty AH, Khater M, Attia RA, et al. Exact traveling and nano-solitons wave solitons of the ionic waves propagating along microtubules in living cells. Mathematics. 2020;8(5):697.
- Morales-Delgado VF, Gómez-Aguilar JF, Taneco-Hernandez MA. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville-Caputo sense. AEU-Int J Electron Commun. 2018;85:108–117.
- Li J, Attia RA, Khater MM, et al. The new structure of analytical and semi-analytical solutions of the longitudinal plasma wave equation in a magneto-electro-elastic circular rod. Mod Phys Lett B. 2020;34(12). doi:10.1142/S0217984920501237
- Jajarmi A, Yusuf A, Baleanu D, et al. A new fractional hrsv model and its optimal control: a non-singular operator approach. Physica A. 2020;547; doi:10.1016/j.physa.2019.123860.
- Yue C, Khater MM, Inc M, et al. Abundant analytical solutions of the fractional nonlinear (2 + 1)-dimensional BLMP equation arising in incompressible fluid. Int J Mod Phys B. 2020. doi:10.1142/S0217979220500848.
- Houwe A, Abbagari S, Salathiel Y, et al. Complex traveling-wave and solitons solutions to the Klein-Gordon-Zakharov equations. Results in Physics. 2020. doi:10.1016/j.rinp.2020.103127.
- Khater MM, Attia RA, Alodhaibi SS, et al. Novel soliton waves of two fluid nonlinear evolutions models in the view of computational scheme. Int J Mod Phys B. 2020. doi:10.1142/S0217979220500964.
- Yépez-Martínez H, Gómez-Aguilar JF, Atangana A. First integral method for non-linear differential equations with conformable derivative. Math Model Nat Phenom. 2018;13(1):14.
- Yue C, Khater MM, Attia RA, et al. Computational simulations of the couple Boiti–leon–pempinelli (BLP) system and the (3 + 1)-dimensional Kadomtsev–petviashvili (KP) equation. AIP Adv. 2020;10(4):045216.
- Yépez-Martínez H, Gómez-Aguilar JF. M-derivative applied to the dispersive optical solitons for the Schrödinger-Hirota equation. The European Physical Journal Plus. 2019;134(3):93.
- Yepez-Martinez H, Gomez-Aguilar JF. M-derivative applied to the soliton solutions for the Lakshmanan–porsezian–daniel equation with dual-dispersion for optical fibers. Opt Quantum Electron. 2019;51(1):31.
- Khater MM, Attia RA, Lu D. Computational and numerical simulations for the nonlinear fractional Kolmogorov–petrovskii–piskunov (FKPP) equation. Phys Scr. 2020;95(5):055213.
- Lavalle G, Grenier N, Mergui S, et al. Solitary waves on superconfined falling liquid films. Phys Rev Fluids. 2020;5(3). doi:10.1103/PhysRevFluids.5.032001
- la Forgia G, Tokyay T, Adduce C, et al. Bed shear stress and sediment entrainment potential for breaking of internal solitary waves. Adv Water Resour. 2020;135. doi:10.1016/j.advwatres.2019.103475.
- Khater MM, Attia RA, Abdel-Aty AH, et al. Analytical and semi-analytical ample solutions of the higher-order nonlinear Schrödinger equation with the non-Kerr nonlinear term. Results Phys. 2020;16; doi:10.1016/j.rinp.2020.103000.
- El-Ganaini S, Zayed EM. Short comment on “the extended simplest equation method and the (G′/G,1/G)-expansion method”. Optik (Stuttg). 2020;206; doi:10.1016/j.ijleo.2020.164258.
- Arqub OA, Al-Smadi M. Fuzzy conformable fractional differential equations: novel extended approach and new numerical solutions. Soft comput. 2020; 24: 12501–12522.
- Hyder AA, Barakat MA. General improved Kudryashov method for exact solutions of nonlinear evolution equations in mathematical physics. Phys Scr. 2020;95(4):045212.
- Ali A, Seadawy AR, Baleanu D. Propagation of harmonic waves in a cylindrical rod via generalized Pochhammer-Chree dynamical wave equation. Results Phys. 2020. doi:10.1016/j.rinp.2020.103039
- Ganji DD, Abdollahzadeh M. Exact travelling solutions for the Lax’s seventh-order KdV equation by sech method and rational exp-function method. Appl Math Comput. 2008;206(1):438–444.
- Biswas A, Konar S, Zerrad E. Soliton Perturbation Theory for the general modified Degasperis-Procesi Camassa-Holm equation. Int. J. Mod. Math. 2007;2:35–40.
- Abbasbandy S. Solitary wave solutions to the modified form of Camassa–holm equation by means of the homotopy analysis method. Chaos. Solitons & Fractals. 2009;39(1):428–435.
- Linares F, Ponce G, Sideris TC. Properties of solutions to the Camassa-Holm equation on the line in a class containing the peakons. In Asymptotic analysis for nonlinear dispersive and wave equations. Cornell University; 2016. arXiv:1609.06212v3.
- Gao Q, Zhang S, Zhang J. Adaptive moving knots meshless method for Degasperis-Procesi equation with conservation laws. Appl Numer Math. 2019;142:90–101.
- Kadkhoda N, Jafari H. Analytical solutions of the Gerdjikov–ivanov equation by using exp (− φ (ξ))-expansion method. Optik (Stuttg). 2017;139:72–76.
- Khater MM. Exact traveling wave solutions for the generalized Hirota-Satsuma couple KdV system using the exp (φ (ξ))-expansion method. Cogent Math. 2016;3(1). doi:10.1080/23311835.2016.1172397.
- Khater MM, Lu D, Attia RA. Dispersive long wave of nonlinear fractional Wu-Zhang system via a modified auxiliary equation method. AIP Adv. 2019;9(2):025003.
- Khater MM, Attia RA, Abdel-Aty AH, et al. Analytical and semi-analytical ample solutions of the higher-order nonlinear Schrödinger equation with the non-Kerr nonlinear term. Results in Physics. 2020;16. doi:10.1016/j.rinp.2020.103000.
- Ali AT, Khater MM, Attia RA, et al. Abundant numerical and analytical solutions of the generalized formula of Hirota-Satsuma coupled KdV system. Chaos Solitons Fractals. 2020;131. doi:10.1016/j.chaos.2019.109473.
- Attia RA, Lu D, Ak T, et al. Optical wave solutions of the higher-order nonlinear Schrödinger equation with the non-Kerr nonlinear term via modified Khater method. Mod Phys Lett B. 2020;34(05):20500.