A new parametric differential operator generalized a class of d'Alembert's equations

Abstract

The studies in operator theory are attracting many researchers. The central aim of this investigation is to formulate a special parametric differential operator (PDO) based on the error function in the open unit disk. The suggested operator is related to the well-known Carlson–Shaffer operator and the differential operator due to Salagean. We express a class of analytic functions to study its performance in view of the geometric function theory. As application, we employ PDO to present the conformable d'Alembert's equation. We discuss the univalent solution of the suggested equation and study some of its geometric behaviours.

Keywords:

• Univalent function
• analytic function
• subordination and superordination
• open unit disk
• fractional differential operator
• fractional calculus

2020 Mathematics Subject Classifications:

• 30C55
• 30C45

1. Introduction

A class of parametric differential operators (PDO) is a special class of parametric equations. Parametric equations are generally utilized to define the coordinates of the points that make up a geometric shape such as a curve or surface, in which situation the formulas are cooperatively known as a parametric representation or parameterization of the image. The PDOs are normally employed in kinematics, where the arc of a graph is characterized by equations depending on time as the parameter. Nevertheless, parameters can characterize other physical magnitudes (such as geometric variables as in our study) or can be picked randomly for convenience. Parameterizations are non-unique; additional set of parametric equations can require the same graph.

The complex differential equation has attracted many researchers taking the general form ${\lambda }^{\left(k\right)}\left(\xi \right)+a_{k-1}{\lambda }^{(k-1)}\left(\xi \right)+\cdots +a_k=0,$ where $\lambda \left(\xi \right)$ is an analytic function in a complex domain with non zero coefficients. Classes of this formula are investigated widely. Most of these studies are focused on the connection problem and its boundary. For example, Pommerenke investigated [1] the second order; Heittokangas [2] studied a special case of the kth order, while Walter [3] presented a meromorphic solution for a class of complex differential equation. Later, the equation is generalized by using fractional calculus in the open unit disk [4–6].

The theory of differential and integral operators is a study of the various classes of operators over function spaces. The operators can have structures which are formulated abstractly by their characteristics. During the times, this theory becomes very interesting in applications not only in mathematics, but in other subjects especially physics. Nowadays, the fractional, fractal and conformable operators play a major role developing applications in engineering, medical studies including the dynamic of recent pandemic, economic and computer sciences. More applications of this theory is appeared, when some classes of differential and integral operators are extended to the complex plane [7–9].

One of the most important recent operators in the complex plane is the conformable differential operator [10] and generalized by a fractional differential operator in [11]. The basic idea of the parametric differential operator (PDO) came from the controller system, which is employed by Anderson and Ulness [12] to define the well-known PDO for a real variable. The main aim of this study is to suggest a special PDO based on the error function in the open unit disk then use it to generalize the D'Alembert's equation. To study the analytic univalent solution of the generalized equation, we formulate a class of analytic functions, investigating its behaviour in view of the geometric function theory.

2. Methodology

This section displays the method and concepts that we will employ in our study.

2.1. Error function

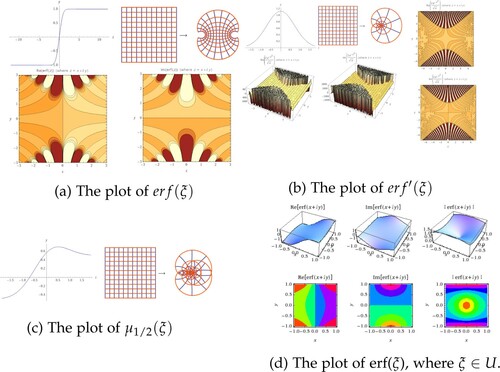
The error function singed by the three letters  erf, is an odd complex function $\left(\mathrm{e}\mathrm{r}\mathrm{f}\right(-\xi )=-\mathrm{e}\mathrm{r}\mathrm{f}(-\xi \left)\right)$ of a complex variable formulating by the integral $\mathrm{e}\mathrm{r}\mathrm{f}\left(\xi \right)=\frac{2}{\sqrt{\pi }}{\int }_0^{\xi }{e}^{-{\zeta }^2}\mathrm{d}\zeta ,$ where the integral is a special sigmoid function (see Figure 1) having the series $\begin{array}{rl}\mathrm{e}\mathrm{r}\mathrm{f}\left(\xi \right)& =\frac{2}{\sqrt{\pi }}\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n{\xi }^{2n+1}}{n!(2n+1)}\\ & =\frac{2\xi e^{-{\xi }^2}}{\sqrt{\pi }}\mathcal{M}(1,\frac{3}{2};{\xi }^2)\\ & =\frac{2}{\sqrt{\pi }}\left(\xi -\frac{{\xi }^3}{3}+\frac{{\xi }^5}{10}-\frac{{\xi }^7}{42}+\frac{{\xi }^9}{216}-\cdots \right),\end{array}$ where $\mathcal{M}$ indicates the confluent hypergeometric function. The k th derivatives of $\mathrm{e}\mathrm{r}\mathrm{f}\left(\xi \right)$ are given by the formula $\begin{array}{rl}& \frac{\mathrm{d}\left[\mathrm{e}\mathrm{r}\mathrm{f}\right(\xi \left)\right]}{\mathrm{d}\xi }=\frac{2}{\sqrt{\pi }}{e}^{-{\xi }^2}=\frac{2}{\sqrt{\pi }}-\frac{2{\xi }^2}{\sqrt{\pi }}+\frac{{\xi }^4}{\sqrt{\pi }}+O\left({\xi }^5\right),\dots ,\\ & {\mathrm{e}\mathrm{r}\mathrm{f}}^{\left(k\right)}\left(\xi \right)=\frac{2(-1{)}^{k-1}}{\sqrt{\pi }}{\mathit{H}}_{k-1}\left(\xi \right)e^{-{\xi }^2}=\frac{2}{\sqrt{\pi }}\frac{{\mathrm{d}}^{k-1}}{\mathrm{d}{\xi }^{k-1}}\left(e^{-{\xi }^2}\right),\\ & k\ge 1,\end{array}$ where H indicates the Hermite polynomials. In the open unit disk $U:=\{\xi \in \mathbb{C}:|\xi |<1\},$ the error function satisfies $\mathrm{e}\mathrm{r}\mathrm{f}\left({\mathrm{e}\mathrm{r}\mathrm{f}}^{-1}\left(\xi \right)\right)=\xi ,$ where $\begin{array}{rl}{\mathrm{e}\mathrm{r}\mathrm{f}}^{-1}\left(\xi \right)& =\sum _{n=0}^{\mathrm{\infty }}\frac{{\sigma }_n}{2n+1}{\left(\frac{\sqrt{\pi }}{2}\xi \right)}^{2n+1}\\ & =\frac{1}{2}\sqrt{\pi }\left(\xi +\frac{\pi }{12}{\xi }^3+\frac{7{\pi }^2}{480}{\xi }^5+\frac{127{\pi }^3}{40320}{\xi }^7\right.\\ & \left.+\frac{4369{\pi }^4}{5806080}{\xi }^9+\frac{34807{\pi }^5}{182476800}{\xi }^{11}+\cdots \right),\end{array}$ where ${\sigma }_0=1,{\sigma }_1=1,{\sigma }_2=\frac{7}{6},\dots$

Figure 1. Three graphs of error function including PDO of order $\nu =0.5,{\kappa }_p={\kappa }_d=0.5$.

2.2. Parametric differential operator (PDO)

Anderson and Ulness [12] formulated a new conformable differential operator based on the control theory. The proportional-derivative controller for controller output μ at time τ with two tuning parameters has the structure (1) $\begin{array}{r}\mu \left(\tau \right)={\kappa }_p\mathrm{e}\mathrm{r}\mathrm{f}\left(\tau \right)+{\kappa }_d\frac{\mathrm{d}}{\mathrm{d}\tau }\mathrm{e}\mathrm{r}\mathrm{f}\left(\tau \right),\end{array}$(1) where ${\kappa }_p$ indicates the proportional gain, ${\kappa }_d$ presents the derivative gain, and erf is the error between the state variable and the process variable (see [13]).

For a fractional value $\nu \in [0,1]$, (1(1) $\begin{array}{r}\mu \left(\tau \right)={\kappa }_p\mathrm{e}\mathrm{r}\mathrm{f}\left(\tau \right)+{\kappa }_d\frac{\mathrm{d}}{\mathrm{d}\tau }\mathrm{e}\mathrm{r}\mathrm{f}\left(\tau \right),\end{array}$(1) ) can be considered for a complex variable $\xi \in U$ as follows: (2) $\begin{array}{rl}{\mu }_{\nu }\left(\xi \right)& =\left(\frac{{\kappa }_p(\nu ,\xi )}{{\kappa }_p(\nu ,\xi )+{\kappa }_d(\nu ,\xi )}\right)\mathrm{\Xi }\left(\xi \right)\\ & +\left(\frac{{\kappa }_d(\nu ,\xi )}{{\kappa }_p(\nu ,\xi )+{\kappa }_d(\nu ,\xi )}\right)\xi {\mathrm{\Xi }}^{\prime }\left(\xi \right),\end{array}$(2) ${\kappa }_p(\nu ,\xi )\ne -{\kappa }_d(\nu ,\xi )$, $\begin{array}{rl}& \underset{\nu \to 0}{lim}{\kappa }_p(\nu ,\xi )=1,\underset{\nu \to 1}{lim}{\kappa }_p(\nu ,\xi )=0,\\ & {\kappa }_p(\nu ,\xi )\ne 0,\mathrm{\forall }\xi \in U,\nu \in (0,1),\end{array}$ and $\begin{array}{rl}& \underset{\nu \to 0}{lim}{\kappa }_d(\nu ,\xi )=0,\underset{\nu \to 1}{lim}{\kappa }_d(\nu ,\xi )=1,\\ & {\kappa }_d(\nu ,\xi )\ne 0,\mathrm{\forall }\xi \in U\nu \in (0,1).\end{array}$ Note that $\begin{array}{rl}\mathrm{\Xi }\left(\xi \right)& =\frac{\sqrt{\pi }}{2}erf\left(\xi \right)\\ & =\left(\xi -\frac{{\xi }^3}{3}+\frac{{\xi }^5}{10}-\frac{{\xi }^7}{42}+\frac{{\xi }^9}{216}-\cdots \right),\end{array}$ where ${\mu }_{\nu }\left(\xi \right)$ is called the complex controller output. This type of controller has been suggested for the first time in 2007 by Tomasz et al. [14]. Later it has been used in many applications in engineering and physics, especially in the thermal dynamics for boiling, cooling and optical studies (see [15–17]).

2.3. Normalized class of analytic functions

To study the operator ${\mu }_{\nu }$ geometrically in U, we need to consider the class of normalized analytic functions denoting by Λ and structuring by the formula (3) $\begin{array}{r}\varphi \left(\xi \right)=\xi +\sum _{n=2}^{\mathrm{\infty }}{\phi }_n{\xi }^n,\xi \in U.\end{array}$(3) It is clear that ${\mu }_{\nu }\left(\xi \right)\in \mathrm{\Lambda }.$ Two functions $\varphi \left(\xi \right)$ and $\psi \left(\xi \right)=\xi +\sum _{n=2}^{\mathrm{\infty }}{\psi }_n{\xi }^n$ are convoluted if and only if they satisfy the structure [18] $\begin{array}{rl}\varphi \left(\xi \right)\ast \psi \left(\xi \right)& =\left(\xi +\sum _{n=2}^{\mathrm{\infty }}{\phi }_n{\xi }^n\right)\ast \left(\xi +\sum _{n=2}^{\mathrm{\infty }}{\psi }_n{\xi }^n\right)\\ & =\xi +\sum _{n=2}^{\mathrm{\infty }}{\phi }_n{\psi }_n{\xi }^n.\end{array}$ Based on the above information, we formulate a new linear operator ${\mathcal{L}}_{\nu }:\mathrm{\Lambda }\to \mathrm{\Lambda }$ as follows $\begin{array}{rl}{\mathcal{L}}_{\nu }\varphi \left(\xi \right)& =\varphi \left(\xi \right)\ast {\mu }_{\nu }\left(\xi \right)\\ & =\left(\xi +\sum _{n=2}^{\mathrm{\infty }}{\phi }_n{\xi }^n\right)\ast \left(\xi +\sum _{n=2}^{\mathrm{\infty }}{ϵ}_n{\xi }^n\right)\\ & =\xi +\sum _{n=2}^{\mathrm{\infty }}{\phi }_n{ϵ}_n{\xi }^n\\ & =\xi +\left(\frac{-A}{3}-B\right){\phi }_3{\xi }^3+\frac{1}{10}(A+5B){\phi }_5{\xi }^5\\ & +\frac{1}{42}(-A-7B){\phi }_7{\xi }^7+O\left({\xi }^9\right),\end{array}$ where $A:={\kappa }_p/({\kappa }_p+{\kappa }_d)$ and $B:={\kappa }_d/({\kappa }_p+{\kappa }_d).$ The class of linear operators in U is investigated, for the first time, by Carlson and Shaffer [19] (recent advance work can be located in [20, 21]) when they introduced the convoluted linear operator $L(a,c)\varphi \left(\xi \right)=\text{β}(a,c,\xi )\ast \varphi \left(\xi \right),$ where β indicates the incomplete beta function. Since $L(a,a)\varphi \left(\xi \right)=\varphi \left(\xi \right)$ and $L(2,1)\varphi \left(\xi \right)=\xi {\varphi }^{\prime }\left(\xi \right),$ then we have the relation $\begin{array}{rl}{\mu }_{\nu }\left(\xi \right)& =\left(\frac{{\kappa }_p(\nu ,\xi )}{{\kappa }_p(\nu ,\xi )+{\kappa }_d(\nu ,\xi )}\right)L(a,a)\mathrm{\Xi }\left(\xi \right)\\ & +\left(\frac{{\kappa }_d(\nu ,\xi )}{{\kappa }_p(\nu ,\xi )+{\kappa }_d(\nu ,\xi )}\right)L(2,1)\mathrm{\Xi }\left(\xi \right)\\ & :={\mu }_{\nu }(a;\xi )\end{array}$ As a conclusion, ${\mathcal{L}}_{\nu }\varphi \left(\xi \right)$ admits a linear combination of special types of the Carlson–Shaffer operator in U. Proceeding, we introduce the following generalized parametric differential operator (4) $\begin{array}{r}{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right):={\mu }_{\nu }(a;\xi )\ast \varphi \left(\xi \right),\xi \in U\end{array}$(4) Note that, the special case ${\mathcal{L}}_1\left(a\right)\varphi \left(\xi \right)$ represents the Salagean differential operator [22], when ${\kappa }_p=0$.Next subsection is deal with the generalized D'Alembert's equation using (4(4) $\begin{array}{r}{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right):={\mu }_{\nu }(a;\xi )\ast \varphi \left(\xi \right),\xi \in U\end{array}$(4) ). In this place, we refer to different types of the D'Alembert's equation, which can be located in [23–30].

2.4. D'Alembert's equation

In this part, we shall generalize D'Alembert's equation [31] $f\left(\xi \right)=\xi F\left(f^{\prime }\right(\xi \left)\right)+G\left(f^{\prime }\right(\xi \left)\right),\xi \in U.$ This type of differential equations has applications in the wave theory. For example, $(1-a)\varphi \left(\xi \right)+a\xi {\varphi }^{\prime }\left(\xi \right)=\xi$ has a solution $\varphi \left(\xi \right)=c{\xi }^{(a-1)/a}+\xi ,a\ne 0.$ Assuming $c=0,$ we have $\varphi \left(\xi \right)=\xi .$ Employing the operator (4(4) $\begin{array}{r}{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right):={\mu }_{\nu }(a;\xi )\ast \varphi \left(\xi \right),\xi \in U\end{array}$(4) ), then the conformable D'Alembert's equation can be viewed as follows: (5) $\begin{array}{rl}{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)& =\xi F\left(\right[{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){]}^{\prime })\\ & +G\left(\right[{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){]}^{\prime }),\xi \in U.\end{array}$(5) We deal with the following class of the conformable d'Alembert's Equation

Definition 2.1

Consider the normalized functions $\varphi ,g\in \mathrm{\Lambda }.$ Then the function ϕ is in the class ${\mathcal{A}}_{\nu }(a,g(\xi \left)\right)$ if it satisfies the Ma-Minda type [32] of subordination inequality $(1-a){\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)+a\xi \left[{\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){]}^{\prime }\prec g(\xi ),$ where ≺ indicates the subordination notion [33].

Our aim is to collect all the inequalities that bring the above subordination using a class of Equation (5(5) $\begin{array}{rl}{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)& =\xi F\left(\right[{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){]}^{\prime })\\ & +G\left(\right[{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){]}^{\prime }),\xi \in U.\end{array}$(5) ). In other words, we shall present the suitable value of a that satisfies the above subordination providing $\nu \in [0,1]$. Moreover, we shall study the following class $S_a^{\ast \nu }\left(\mathrm{ð}\right)=\{\varphi \in \mathrm{\Lambda }:\frac{\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }}{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}\prec \mathrm{ð}\left(\xi \right),\mathrm{ð}\in \mathcal{C}\},$ where $\mathcal{C}$ is the class of convex univalent functions in U.

2.5. Lemmas

To illustrate our result, we need the following lemma ([33], pp. 139–140).

Lemma 2.2

Let $\upsilon \in \mathrm{\Lambda }.$ Then

1. $\upsilon \left(\xi \right)+a\xi {\upsilon }^{\prime }\left(\xi \right)\prec (1+a)\xi +a{\xi }^2\Rightarrow \upsilon \left(\xi \right)\prec \xi ,$when $a\in (0,1/3];$

2. $\xi {\upsilon }^{\prime }\left(\xi \right)[1+\upsilon (\xi \left)\right]+a{\upsilon }^2\left(\xi \right)\prec \xi +(1+a){\xi }^2\Rightarrow \upsilon \left(\xi \right)\prec \xi ,$ when $|1+a|\le 1/4;$

3. $\left[\xi {\upsilon }^{\prime }\right(\xi )-\upsilon (\xi \left)\right]e^{a\left(\upsilon \right(\xi \left)\right)}+e^{\upsilon \left(\xi \right)}\prec e^{\xi }\Rightarrow \upsilon \left(\xi \right)\prec \xi ,$when $|a-1|\le \pi /2;$

4. $\xi {\upsilon }^{\prime }\left(\xi \right)(1+a\upsilon (\xi \left)\right)+\upsilon \left(\xi \right)\prec 2\xi +a{\xi }^2\Rightarrow \upsilon \left(\xi \right)\prec \xi ,$ when $|a|\le 1/2;$

5. $\xi {\upsilon }^{\prime }\left(\xi \right)e^{a\upsilon \left(\xi \right)}+\upsilon \left(\xi \right)\prec \xi (1+a\xi e^{a\xi })\Rightarrow \upsilon \left(\xi \right)\prec \xi ,$when $|a|\le 1;$

6. $\upsilon \left(\xi \right)+\frac{\xi {\upsilon }^{\prime }\left(\xi \right)}{1+a\upsilon \left(\xi \right)}\prec \xi \Rightarrow \upsilon \left(\xi \right)\prec \xi ,$ when $|a|\le 1;$

and the solution is sharp.

Lemma 2.3

[33]

Assume that υ is univalent in U and V is analytic in a domain contains $\upsilon \left(U\right).$ If $\xi {\upsilon }^{\prime }\left(\xi \right)V\left(\upsilon \right(\xi \left)\right)$ is starlike then $\xi v^{\prime }\left(\xi \right)V\left(v\right(\xi \left)\right)\prec \xi {\upsilon }^{\prime }\left(\xi \right)V\left(\upsilon \right(\xi \left)\right)\Rightarrow v\left(\xi \right)\prec \upsilon \left(\xi \right)$ and υ is the best dominant.

3. Results

We start our first result:

Theorem 3.1

Let $\upsilon \in \mathrm{\Lambda }.$ If one of the following inequalities holds

1. $(1-a)\left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi \left)\right)+2a\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }+a^2{\xi }^2({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{″}\prec (1+a)\xi +a{\xi }^2$ when $a\in (0,1/3];$

2. $\left(\xi \right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{\prime }+a{\xi }^2\left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi \left){)}^{″}\right)(1+(1-a\left)\right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right))+a\xi ({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{\prime })\prec \xi +(1+a){\xi }^2,$when $|1+a|\le 1/4;$

3. $\exp \left(\right(1-a\left)\right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\left)+a\xi \right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{\prime }\left)\times \right(\left(a{\xi }^2\right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{″}+(1-a)\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }+(a-1\left)\right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\left)\right)e^a+1)\prec e^{\xi },$ when $|a-1|\le \pi /2;$

4. $\left(\right(1-a\left)\right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\left)+\right(1+a\left)\xi \right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{\prime }+a{\xi }^2\left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi \left){)}^{″}\right)+\left(a\right(1-a\left)\right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right))+a^2\xi ({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{\prime }\left)\right(\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }+a{\xi }^2({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{″})\prec 2\xi +a{\xi }^2,$ when $|a|\le 1/2;$

5. $(1-a)\left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi \left)\right)+(a+\exp (a\left(\right(1-a\left)\right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right))+a\xi ({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\left)\right)\left)\right)\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }+a\exp (a\left(\right(1-a\left)\right({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{\prime }+a\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi \left)\right)\left)\right){\xi }^2\left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{″}\prec \xi (1+a\xi e^{a\xi }),$ when $|a|\le 1;$

6. $(1-a){\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)+a\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }+\frac{\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }+a{\xi }^2({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right){)}^{″}}{1+a(1-a)\left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi \left)\right)+a^2\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }}\prec \xi ,$when $|a|\le 1;$

then $\varphi \in {\mathcal{A}}_{\nu }(a,\xi )$.

Proof.

Consider $\varphi \in \mathrm{\Lambda }.$ By letting $\upsilon \left(\xi \right):=(1-a)\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)+a\xi {\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^{\prime }$ in Lemma 2.2 such that $\xi {\upsilon }^{\prime }\left(\xi \right)=\xi {\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^{\prime }+a{\xi }^2{\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^{″}$ and $\begin{array}{rl}a{\upsilon }^2\left(\xi \right)& =a(1-a){\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^2\\ & +2a^2(1-a)\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)\times \xi {\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^{\prime }\\ & +a^3{\xi }^2[{\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^{\prime }{]}^2,\end{array}$ we have from the condition inequalities $(1-a){\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)+a\xi \left[{\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){]}^{\prime }\prec \xi ,$ which leads to $\varphi \in {\mathcal{A}}_{\nu }(a,\xi ).$

The next result indicates that every univalent solution of D'Alembert's equation is the best dominant for all other solutions.

Theorem 3.2

Let $g\in \mathcal{C}$ (the class of convex univalent analytic functions in U). Assume that ${\varphi }_1\in \mathrm{\Lambda }$ is a univalent solution in U of the conformable D'Alembert's equation ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)+a\xi \left[{\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){]}^{\prime }=g(\xi ).$ If ϕ and ${\varphi }_1\in {\mathcal{A}}_{\nu }(a,g)$ then $\varphi \left(\xi \right)\prec {\varphi }_1\left(\xi \right).$

Proof.

Suppose that $\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]=(1-a){\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)+a\xi \left[{\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){]}^{\prime }.$ Clearly, $\mathrm{\Theta }\left[\varphi \right(0\left)\right]=g\left(0\right)=0;$ and since $\varphi ,{\varphi }_1\in \mathrm{\Lambda }$ then $\varphi \left(0\right)={\varphi }_1\left(0\right)=0.$ Moreover, we have $\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]=(1-a){\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)+a\xi \left[{\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){]}^{\prime }\prec g(\xi )$ and $\begin{array}{rl}& \mathrm{\Theta }\left[{\varphi }_1\right(\xi \left)\right]\\ & =(1-a){\mathcal{L}}_{\nu }\left(a\right){\varphi }_1\left(\xi \right)+a\xi \left[{\mathcal{L}}_{\nu }\right(a\left){\varphi }_1\right(\xi ){]}^{\prime }\prec g(\xi ).\end{array}$ Thus, in view of [33] , Theorem 3.4.c, $\varphi \left(\xi \right)\prec {\varphi }_1\left(\xi \right)$ such that ${\varphi }_1$ is the best dominant of the last subordination.

We proceed to present more information about solutions of Bernoulli's equation. Next two results indicate that a solution of Bernoulli's equation can be considered as a solution of the Briot–Bouquet equation. More interesting outcome is that the equation has a positive real solution and univalent.

Theorem 3.3

Let g be analytic and λ be analytic starlike function in U. Assume that $\varphi \in \mathrm{\Lambda }$ is a solution of Bernoulli's equation $\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]=g\left(\xi \right),$ where $\begin{array}{rl}\mathrm{\Re }\left(\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]\right)& =\mathrm{\Re }\left((1-a){\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)+a\xi \left[{\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){]}^{\prime }\right)\\ & >0.\end{array}$ Then ϕ is a solution of the Briot–Bouquet equation $\varphi \left(\xi \right)+\frac{{\varphi }^{\prime }\left(\xi \right)\lambda \left(\xi \right)}{\varphi \left(\xi \right){\lambda }^{\prime }\left(\xi \right)}=g\left(\xi \right)$ such that $\mathrm{\Re }\left(\varphi \right(\xi \left)\right)>0.$

Moreover, if $\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]\in {\mathcal{S}}^{\ast }\left(\alpha \right)$ (starlike of order α) then $\varphi \in {\mathcal{A}}_{\nu }(a,\frac{\xi }{(1-\xi {)}^{2-2\alpha }}),\alpha \in [0,1],|\xi |\in (0.21,0.3)$ and ${\left(\mathrm{\Theta }\left[\sigma \right(\xi \left)\right]\right)}^{\prime }\prec {\left(\frac{\xi }{(1-\xi {)}^{2-2\alpha }}\right)}^{\prime }.$

Proof.

Since λ is starlike analytic function in U then $\mathrm{\Re }\left(\frac{\xi {\lambda }^{\prime }\left(\xi \right)}{\lambda \left(\xi \right)}\right)>0,\xi \in U.$ Define a function $Q:U\to U$ as follows: $Q\left(\xi \right):=\left(\frac{\xi {\lambda }^{\prime }\left(\xi \right)}{\lambda \left(\xi \right)}\right)\mathrm{\Theta }\left[\varphi \right(\xi \left)\right].$ Thus, $\mathrm{\Re }\left(Q\right(\xi \left)\right)>0.$ According to [33] , Theorem 3.4j, the Briot–Bouquet equation $\varphi \left(\xi \right)+\frac{{\varphi }^{\prime }\left(\xi \right)\lambda \left(\xi \right)}{\varphi \left(\xi \right){\lambda }^{\prime }\left(\xi \right)}=g\left(\xi \right)$ such that $\mathrm{\Re }\left(\varphi \right(\xi \left)\right)>0.$

Since $\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]\in {\mathcal{S}}^{\ast }\left(\alpha \right)$ then in view of [18], Corollary 2.2, there is a probability measure $\omega \in \mathrm{\partial }U$ such that $\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]={\int }_{\mathrm{\partial }U}\frac{\xi }{(1-t\xi {)}^{2-2\alpha }}\mathrm{d}\omega \left(\xi \right).$ That is, $\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]$ satisfies the majority inequality $\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]\ll \frac{\xi }{(1-\xi {)}^{2-2\alpha }}.$ But, $\frac{\xi }{(1-\xi {)}^{2-2\alpha }}$ is starlike in U, then in virtue of [34], Corollary 2, we have $\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]\prec \frac{\xi }{(1-\xi {)}^{2-2\alpha }},|\xi |\in (0.21,0.3),$ which leads to $\varphi \in {\mathcal{A}}_{\nu }(a,\frac{\xi }{(1-\xi {)}^{2-2\alpha }}),\alpha \in [0,1],|\xi |\in (0.21,0.3).$ The last part comes immediately from [34], Theorem 3.

Corollary 3.4

Consider d'Alembert's equation (6) $\begin{array}{r}\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]=\frac{\xi }{(1-\xi {)}^{2-2\alpha }},|\xi |\in (0.21,0.3).\end{array}$(6) Then the solution is defined by the hypergeometric function as follows: $\varphi \left(\xi \right)=\frac{\xi {}_2{F}_1(1+\frac{1}{a},2-2\alpha ,2+\frac{1}{a},\xi )}{(a+1)}+c{\xi }^{-1/a},$ where c is a real constant, $\alpha ,\nu \in [0,1]$ and $a\ne 0$.

Theorem 3.5

Let $\varphi \in S_a^{\ast \nu }\left(\mathrm{ð}\right),$ where $\mathrm{ð}$ is convex univalent function in U. Then $\begin{array}{r}{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \xi \exp \left({\int }_0^{\xi }\frac{\mathrm{ð}\left(\hslash \right(z\left)\right)-1}{z}\mathrm{d}z\right),\end{array}$ where $\hslash \left(\xi \right)$ is analytic in U, with $\hslash \left(0\right)=0$ and $|\hslash \left(\xi \right)|<1$. In addition, for $|\xi |=\eta$, ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)$ fulfills the relation $\begin{array}{rl}& \exp \left({\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(-\eta \left)\right)-1}{\eta }\right)\mathrm{d}\eta \\ & \le \left|\frac{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}{\xi }\right|\le \exp \left({\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(\eta \left)\right)-1}{\eta }\right)\mathrm{d}\eta .\end{array}$

Proof.

By the definition of $\varphi \in S_a^{\ast \nu }\left(\mathrm{ð}\right),$ we obtain $\left(\frac{\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }}{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}\right)\prec \mathrm{ð}\left(z\right),z\in U,$ which satisfies that there is an analytic function with $\hslash \left(0\right)=0$ and $|\hslash \left(\xi \right)|<1$ confirming $\left(\frac{\xi \left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }}{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}\right)=\mathrm{ð}\left(\hslash \right(\xi \left)\right),\xi \in U.$ Proceeding, we get $\left(\frac{\left({\mathcal{L}}_{\nu }\right(a\left)\varphi \right(\xi ){)}^{\prime }}{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}\right)-\frac{1}{\xi }=\frac{\mathrm{ð}\left(\hslash \right(\xi \left)\right)-1}{\xi }.$ Integrating yields $\log {\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)-\log \xi ={\int }_0^{\xi }\frac{\mathrm{ð}\left(\hslash \right(z\left)\right)-1}{z}\mathrm{d}z.$ Accordingly, we attain (7) $\begin{array}{r}\log \frac{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}{\xi }={\int }_0^{\xi }\frac{\mathrm{ð}\left(\hslash \right(z\left)\right)-1}{z}\mathrm{d}z.\end{array}$(7) In virtue of the subordination, we have ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \xi \exp \left({\int }_0^{\xi }\frac{\mathrm{ð}\left(\hslash \right(z\left)\right)-1}{z}\mathrm{d}z\right).$ Note that $\mathrm{ð}$ transforms the disk $0<|\xi |<\eta <1$ onto a convex symmetric domain with x-axis, which yields $\mathrm{ð}(-\eta |\xi |)\le \mathrm{\Re }\left(\mathrm{ð}\right(\hslash \left(\eta \xi \right)\left)\right)\le \mathrm{ð}\left(\eta |\xi |\right),\eta \in (0,1).$ Thus, we have the conclusion $\mathrm{ð}(-\eta )\le \mathrm{ð}(-\eta |\xi |),\mathrm{ð}\left(\eta |\xi |\right)\le \mathrm{ð}\left(\eta \right)$ and $\begin{array}{rl}& {\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(-\eta |\xi |\left)\right)-1}{\eta }d\eta \\ & \le \mathrm{\Re }\left({\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(\eta \left)\right)-1}{\eta }d\eta \right)\le {\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(\eta |\xi |\left)\right)-1}{\eta }d\eta .\end{array}$ Equation (7(7) $\begin{array}{r}\log \frac{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}{\xi }={\int }_0^{\xi }\frac{\mathrm{ð}\left(\hslash \right(z\left)\right)-1}{z}\mathrm{d}z.\end{array}$(7) ) implies that $\begin{array}{rl}& {\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(-\eta |\xi |\left)\right)-1}{\eta }d\eta \\ & \le \log \left|\frac{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}{\xi }\right|\le {\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(\eta |\xi |\left)\right)-1}{\eta }d\eta .\end{array}$ This leads to $\begin{array}{rl}& \exp \left({\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(-\eta |\xi |\left)\right)-1}{\eta }\mathrm{d}\eta \right)\\ & \le \left|\frac{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}{\xi }\right|\le \exp \left({\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(\eta |\xi |\left)\right)-1}{\eta }\mathrm{d}\eta \right).\end{array}$ Thus, we obtain $\begin{array}{rl}& \exp \left({\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(-\eta \left)\right)-1}{\eta }\right)\mathrm{d}\eta \\ & \le \left|\frac{{\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)}{\xi }\right|\le \exp \left({\int }_0^1\frac{\mathrm{ð}\left(\hslash \right(\eta \left)\right)-1}{\eta }\right)\mathrm{d}\eta .\end{array}$

Corollary 3.6

Let $\varphi \in S_a^{\ast \nu }\left(\frac{1+\xi }{1-\xi }\right)$. Then ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \frac{\xi }{(1-\xi {)}^2},\xi \in U,$ where $\frac{\xi }{(1-\xi {)}^2}$ is the extreme starlike function in U.

Proof.

Clearly, the function $\mathrm{ð}\left(\xi \right):=\frac{1+\xi }{1-\xi }$ is convex univalent in U (see [33]). Therefore, by letting $\hslash \left(z\right)=z$ in Theorem 3.5, we have ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \xi \exp \left(2{\int }_0^{\xi }\frac{\mathrm{d}z}{1-z}\right),\xi \in U,$ consequently, we obtain ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \frac{\xi }{(1-\xi {)}^2},\xi \in U$

Corollary 3.7

Let $\varphi \in S_a^{\ast \nu }\left(e^{\xi }\right)$. Then $\begin{array}{rl}& {\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \xi \exp \left(\mathrm{C}\mathrm{h}\mathrm{i}\left(\xi \right)+\mathrm{S}\mathrm{h}\mathrm{i}\left(\xi \right)-\gamma \right),\xi \in U,\end{array}$ $\begin{array}{rl}& =\xi +{\xi }^2+\frac{3{\xi }^3}{4}+\frac{17{\xi }^3}{36}+\frac{19{\xi }^4}{72}+\frac{27{\xi }^5}{200}+O\left({\xi }^6\right),\end{array}$ where γ is Euler constant, $\mathrm{C}\mathrm{h}\mathrm{i}\left(\xi \right)$ and $\mathrm{S}\mathrm{h}\mathrm{i}\left(\xi \right)$ are the hyperbolic cosine and sine integrals, respectively $\mathrm{C}\mathrm{h}\mathrm{i}\left(\xi \right):=\ln \xi +\gamma +{\int }_0^{\xi }\frac{\cosh \tau -1}{\tau }\mathrm{d}\tau$ and $\mathrm{S}\mathrm{h}\mathrm{i}\left(\xi \right):={\int }_0^{\xi }\frac{\sinh \tau }{\tau }\mathrm{d}\tau =\xi +\frac{1}{8}{\xi }^3+\cdots .$

Proof.

Clearly, the function $\mathrm{ð}\left(\xi \right):=e^{\xi }$ is convex univalent in U (see [33]). Thus, by putting $\hslash \left(z\right)=z$ in Theorem 3.5, we obtain ${\mathcal{L}}_{\nu }\varphi \left(\xi \right)\prec \xi \exp \left({\int }_0^{\xi }\frac{e^z-1}{z}dz\right),\xi \in U,$ consequently, we obtain ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \xi \exp \left(\mathrm{C}\mathrm{h}\mathrm{i}\left(\xi \right)+\mathrm{S}\mathrm{h}\mathrm{i}\left(\xi \right)-\gamma \right),\xi \in U.$

Corollary 3.8

Let $\varphi \in S_a^{\ast \nu }\left(e^{\xi }\right)$. Then ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \frac{\xi }{1-\xi },\xi \in U,$ where $\frac{\xi }{1-\xi }$ is the extreme convex function in U.

Proof.

From Corollary 3.7, we obtain ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \xi \exp \left(\mathrm{C}\mathrm{h}\mathrm{i}\left(\xi \right)+\mathrm{S}\mathrm{h}\mathrm{i}\left(\xi \right)-\gamma \right),\xi \in U.$ The majority of the coefficients implies that $\xi \exp \left(\mathrm{C}\mathrm{h}\mathrm{i}\left(\xi \right)+\mathrm{S}\mathrm{h}\mathrm{i}\left(\xi \right)-\gamma \right)\prec \frac{\xi }{1-\xi },$ which indicates that ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \frac{\xi }{1-\xi },\xi \in U.$

Corollary 3.9

Let $\varphi \in S_a^{\ast \nu }(1+\xi e^{\xi }),\mathrm{\Re }\left(\xi \right)>0,\xi \in U$. Then ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \frac{\xi }{1-\xi },\xi \in U,$ where $\frac{\xi }{1-\xi }$ is the extreme convex function in U.

Proof.

Let $p\left(\xi \right)=1+\xi e^{\xi },\mathrm{\Re }\left(\xi \right)>0,\xi \in U.$ A computation shows that $\begin{array}{rl}1+\mathrm{\Re }\left(\frac{\xi p^{″}\left(\xi \right)}{p^{\prime }\left(\xi \right)}\right)& =1+\mathrm{\Re }\left(\frac{\xi (\xi +2)e^{\xi }}{(\xi +1)e^{\xi }}\right)\\ & =1+\mathrm{\Re }\left(\frac{\xi (\xi +2)}{(\xi +1)}\right)\\ & >0,\mathrm{\Re }\left(\xi \right)>0,|\xi |\le 0.381966\cdots \end{array}$ This condition is sufficient to prove that $p\left(\xi \right)$ is convex in U provided $\mathrm{\Re }\left(\xi \right)>0,|\xi |\le \mathrm{0.381966.}$ Then, by assuming $\hslash \left(\xi \right)=\xi$ then in view of Theorem 3.5, we have $\begin{array}{rl}& {\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \xi \exp \left({\int }_0^{\xi }\frac{p\left(z\right)-1}{z}\mathrm{d}z\right)\Rightarrow \\ & {\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \xi \exp \left({\int }_0^{\xi }{e}^z\mathrm{d}z\right)\Rightarrow \\ & {\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \xi \exp \left(e^{\xi }-1\right).\end{array}$ Since $\xi \exp (e^{\xi }-1)=\xi +{\xi }^2+{\xi }^3+\frac{5{\xi }^3}{6}+\frac{5{\xi }^4}{8}+O\left({\xi }^5\right),$ which is majorized by the convex function $\xi /(1-\xi )$ then we have $\xi \exp (e^{\xi }-1)\prec \frac{\xi }{1-\xi },\xi \in U,$ and consequently, we attain ${\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\prec \frac{\xi }{1-\xi },\xi \in U.$

Finally, we have the following result

Theorem 3.10

Let $\varphi \in \mathrm{\Lambda }.$ Then the subordination $\begin{array}{rl}1+\frac{\xi {\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^{″}}{{\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^{\prime }}-\frac{\xi {\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^{\prime }}{\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}\prec \frac{2a\xi }{1+a\xi },& \\ a\in (0,1/\sqrt{2}]& \end{array}$ implies $\frac{\xi {\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}^{\prime }}{\left({\mathcal{L}}_{\nu }\left(a\right)\varphi \left(\xi \right)\right)}\prec (1+a\xi {)}^2,$ where the function $(1+a\xi {)}^2$ indicates the Limacon domain.

Proof.

In view of [35] , Lemma 2, the function $\frac{2a\xi }{1+a\xi }$ is starlike in U. But $\frac{\xi {\left((1+a\xi {)}^2\right)}^{\prime }}{(1+a\xi {)}^2}=\frac{2a\xi }{1+a\xi }.$ Thus, by consuming $V\left(u\right)=1/u$ and $\upsilon \left(\xi \right)=(1+a\xi {)}^2$ in Lemma 2.3, then we have the desire assertion.

Example 3.11

• Let ${\kappa }_d=\left(\nu \right),{\kappa }_p=(1-\nu ),c=0,\nu =\alpha =0.5$ and $a=1,$ then the solution of (6(6) $\begin{array}{r}\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]=\frac{\xi }{(1-\xi {)}^{2-2\alpha }},|\xi |\in (0.21,0.3).\end{array}$(6) ) is formulated by $\begin{array}{rl}\varphi \left(\xi \right)& =\xi {}_{2}F1(1,2,3,\xi ))\\ & =\xi +\frac{2{\xi }^2}{3}+\frac{{\xi }^3}{2}+\frac{2{\xi }^4}{5}+\frac{{\xi }^5}{3}+\frac{2{\xi }^6}{7}+O\left({\xi }^7\right)\\ & =-2\left(\frac{\xi +\log (1-\xi )}{\xi }\right)\in \mathrm{\Lambda }.\end{array}$

• Let $\alpha =1/4,a=1,\nu =0.5$ and $c=0,$ then the solution takes the formula $\begin{array}{rl}\varphi \left(\xi \right)& =c{\xi }^{-1/a}+\frac{\left({\xi }_2{F}_1\right(1.5,1+1/a,2+1/a,\xi \left)\right)}{a+1}\\ & =\xi +{\xi }^2+0.9375{\xi }^3+0.875{\xi }^4+0.820313{\xi }^5\\ & +0.773438{\xi }^6+O\left({\xi }^7\right)\in \mathrm{\Lambda }.\end{array}$

• Let $\alpha =0.9,a=1,\nu =0.5$ and $c=0,$ then the solution admits the following series $\begin{array}{rl}\varphi \left(\xi \right)& =c{\xi }^{-1/a}+\frac{\left({\xi }_2{F}_1\right(0.2,1+1/a,2+1/a,\xi \left)\right)}{a+1}\\ & =\xi +0.133333{\xi }^2+0.06{\xi }^3+0.0352{\xi }^4\\ & +0.0234667{\xi }^5+0.016896{\xi }^6+O\left({\xi }^7\right)\in \mathrm{\Lambda }.\end{array}$

• Let $\alpha =0.1,a=1,\nu =0.5$ and $c=0,$ then the solution admits the following series $\begin{array}{rl}\varphi \left(\xi \right)& =c{\xi }^{-1/a}+\frac{\left({\xi }_2{F}_1\right(1.8,1+1/a,2+1/a,\xi \left)\right)}{a+1}\\ & =\xi +1.2{\xi }^2+1.26{\xi }^3+1.27{\xi }^4+1.27{\xi }^5\\ & +1.27{\xi }^6+O\left({\xi }^7\right)\in \mathrm{\Lambda }.\end{array}$

Figure 2 shows the behaviour of solutions of Equation (6(6) $\begin{array}{r}\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]=\frac{\xi }{(1-\xi {)}^{2-2\alpha }},|\xi |\in (0.21,0.3).\end{array}$(6) ) for different values of α. In view of Theorem 3.1, we selected the maximum value of at $a=1.$ We confirm that the solution $\varphi \in \mathrm{\Lambda }$ (the class of normalized analytic univalent functions). Note that the functional $F(\ell ,\mathrm{♭},\complement ;\xi ):={\xi }_2{F}_1(\ell ,\mathrm{♭},\complement ;\xi )$ is starlike function in U (see [33], Corollary 4.5.f.1) under the conditions $\ell \in [-1,1],\mathrm{♭}\ge 0$ and $\complement >1+\mathrm{m}\mathrm{a}\mathrm{x}\{2+|\ell +\mathrm{♭}-2|,1-(\ell -1\left)\right(\mathrm{♭}-1\left)\right\}.$

Figure 2. The behaviour of solutions $\varphi \left(\xi \right)$ of the conformable d'Alembert's Equation (6(6) $\begin{array}{r}\mathrm{\Theta }\left[\varphi \right(\xi \left)\right]=\frac{\xi }{(1-\xi {)}^{2-2\alpha }},|\xi |\in (0.21,0.3).\end{array}$(6) ).

For example, when $\alpha =0.99,$ we have the solution $\varphi \left(\xi \right)={\xi }_2{F}_1(0.02,2,3;\xi ),$ which is starlike in U.

4. Conclusion

The above study showed that a linear combination of special types of the Carlson–Shaffer linear operator can be suggested to define a new parametric fractional operator. Some of its geometric presentations are discussed. Moreover, we formulated a class of analytic functions involving the operator in terms of D'Alembert's equation. The sharp solutions is investigated using the subordination results. For future works, one can develop the PDO using quantum calculus.

Acknowledgments

The authors would like to express their full thanks to the respected reviewers for the deep comments, which improved our paper.

Disclosure statement

No potential conflict of interest was reported by the author(s).