Dynamical properties of dust-ion-acoustic wave solutions in a nonextensive collisional dusty plasma

Abstract

Dynamical properties of dust-ion-acoustic waves (DIAWs) are analysed in a collisional nonextensive dusty plasma composing of mobile ions, q-nonextensive electrons and stationary dust grains with slight collisions between dusts and ions. Reductive perturbation technique (RPT) is practiced to acquire the damped Korteweg-de Vries (DKdV) equation. In absence of collision between dusts and ions, the damping term vanishes and the DKdV equation reduces to the KdV equation. Bifurcation analysis of the dynamical system obtained from the KdV equation is carried out. Analytical solitary wave solution and numerical periodic wave solution of the KdV equation are presented. Approximate analytical DIAW solutions for the DKdV equation are furnished using the novel $\left(G^{\prime }/G\right)$-expansion technique. As an outcome, novel approximate analytical solutions of DIAWs are obtained for the DKdV equation. The application of our work is significant to explore nonextensive plasma environment, such as, ionosphere of Earth.

Keywords:

• Dusty plasma
• nonextensive distribution
• $\left(G^{\prime }/G\right)$-expansion method
• damped KdV equation
• collisional plasma

1. Introduction

The interpretation of DIAWs in dusty plasmas has been a rapidly growing research area for last few decades [1, 2]. Some interesting works have been reported in various areas of plasma environments, namely, ring of planets, plasma or gas tails, interplanetary state, interstellar clouds, and the Earth's ionosphere [3, 4]. The presence of dust particles in dusty plasmas initiates new novel eigenmodes, for example, dust-acoustic wave, DIAW, dust lattice mode, etc. It is important to note that dust particles are negatively charged and taken as immobile because of their weighty concentration [5]. With rise in electron population, the DIAW phase velocity diminishes [6, 7]. Recently, DIAWs were examined in both cases theoretically and practically. DIAW was also examined in collisionless [8] plasma as a limiting situation, but it is not well framed in some real situations [9]. Ghosh et al. [10] reported influence of damping on DIAWs. Losseva et al. [11] investigated evolution of weakly dissipative hybrid DIA solitary wave in a collisional plasma. The work [12] reported the impacts of fluctuation of dust charge on soliton of the modified KdV-Burger equation in dusty plasmas. Popel et al. [13] examined experimentally that wave speed is much greater than the wave speed of theoretical situation. Losseva et al. [14] examined arbitrary amplitude DIAWs in dusty plasma. Kruskal [15] reported that gravity wave in inviscid fluid can be modelled the KdV equation asymptotically. Some researchers theoretically and experimentally studied solitary and shock DIAWs [16–19] in dusty plasmas. Ashraf et al. [20] reported behaviours of obliquely travelling DIAWs in a nonextensive dusty plasma. Bacha et al. [21] reported DIAW solitons in non-Maxwellian dusty plasmas. Tribeche and Zerguini [22] investigated DIAWs with effects of undulations of dust charge and instability in a collisional dusty plasma. Later, it was reported that the plasma system having Gaussian distributed dust grains supports DIAW soliton feature in presence of collisional effect [23]. Similarly, works [24–27] reported the solution of the damped KdV equation in different plasma systems through the classical approach.

The $\left(G^{\prime }/G\right)$-expansion technique was discovered by Wang et al. [28]. The technique was reported to be a influential technique for achieving the exact solutions of different nonlinear evolution equation (NEE) types. This expansion extended the range of applicability of solution for the NEEs. The $\left(G^{\prime }/G\right)$-expansion was generalized and later, its improved version was implemented in order to achieve the wave solutions [29, 30]. This technique has an advantage over the existing techniques. It directly corresponds to new exact solutions accompanied by new variables. It is known that the exact solutions reveal the inner dynamics and solutions of NEEs in the physical phenomena. With the help of this method, the researcher solve their numerical results and compare its correctness and analyse the stability of their result [31]. The implementation of the $\left(G^{\prime }/G\right)$-expansion and its improved version was imitated to examine the exact solution for the mKdV equation by Sahoo and Ray [32]. In plasmas, there exist few works reported on the direct utilization of the $\left(G^{\prime }/G\right)$-expansion. The works in plasmas include the exact solution of the KdV-Burger equations in non-Maxwellian plasmas [33] and the KdV equation in Thomas-Fermi plasmas [34] using the $\left(G^{\prime }/G\right)$-expansion. However, there is no study reported regarding the solution for the DKdV equation using the $\left(G^{\prime }/G\right)$-expansion technique in plasma systems.

The q-nonextensive distribution introduced by Tsallis [35] describes the charge of particles with higher inter-collision range. This distribution generalizes the Boltzmann–Gibbs (BG) entropy [36, 37]. The high range inter-collisions are well described by the non-Maxwellian distributions, such as nonextensive, superthermal, nonthermal, etc. The works [38, 39] support that the non-Maxwellian particles can be well characterized by the nonextensive distribution. The parameter q represents the potential or strength of nonextensive distribution with wide ranges from $-1<q<1$ and q>1. The classical Maxwellian limit is achieved for $q\to 1$. The physical importance of q was discussed elaborately in the work [40]. The author obtained the expression $k_B\mathrm{\nabla }{T}_e+(1-q)Q\mathrm{\nabla }\varphi =0$, for a system which describes the relation between q, temperature gradient $T_e$ and the potential energy. The above expression clearly depicts that $q\ne 1$ [40]. Furthermore, the temperature gradient determines that $q\ne 1$ for $\mathrm{\nabla }{T}_e\ne 0$ and q = 1 for $\mathrm{\nabla }{T}_e=0$. This implies that plasma becomes isothermal when $q\to 1$ and it describes the BG statistics while, for $q\ne 1$ describes the Tsallis statistics. Therefore, it is concluded that the Tsallis generalization can be applied to explore non-isothermal feature in plasmas [40, 41]. The nonextensive distribution is extensively used for the plasma particles and its applications are observed in nonlinear gravitational model [42], plasma dynamics [38, 43], astrophysical and cosmological scenarios [44], and Hamiltonian systems [45] with long-range interaction. The effects of nonextensive plasma particles on different travelling waves are reported in works [46–49]. The detailed deduction of nonextensive distribution for electrons can be referred from the work [50]. Using bifurcation analysis, Samanta et al. [51] initiated the investigation of DIAW under magnetic effects in dusty plasmas. Later many researchers [52–55] started using the same analysis to examine nonlinear waves in plasmas. Recently, Tamang et al. [56] examined solitary DIAW solutions under the DKdV and DmKdV equations in collisional nonextensive dusty plasmas employing bifurcation theory of dynamical systems [57]. Very recently, Seadawy et al. [58] reported the shock solution of DmKdV equation in collisional nonextensive dusty plasma using two different extended mapping techniques. Here, we aim to achieve approximate analytical solutions for the DKdV equation for which we consider the $\left(G^{\prime }/G\right)$-expansion technique as this technique is sought to bestow extensive and various solutions which are not reported earlier in collisional nonextensive dusty plasmas.

The orientation of the work is given as: in Section 2, we consider model equations for a collisional dusty plasma. In Section 3, we obtain the DKdV equation using RPT. The condition is discussed where the DKdV equation is reduced into the KdV equation. Bifurcation analysis of the KdV equation is done and its analytical and numerical solutions are presented. Section 4 contains analytical solution of the DKdV equation and its analysis. Finally, Section 5 presents the concluding remark.

2. Model equations

An unmagnetized dusty plasma is considered which is composed of mobile ions, q-nonextensive electrons and stationary dust grain with sight of collision between the dust and ion particles. Here, the number density of N dust species is denoted by $n_{dj}$ having charge $Q_{dj}$(=$e{Z}_{dj}$) with the number of charge ($Z_{dj}$) occupying on j dust grain, where $j=1,2,3\cdots ..N$. The motions of DIAWs are given by [23] (1) $\begin{array}{rl}& \frac{\mathrm{\partial }n}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(nu\right)=0,\end{array}$(1) (2) $\begin{array}{rl}& n\left(\frac{\mathrm{\partial }u}{\mathrm{\partial }t}+u\frac{\mathrm{\partial }u}{\mathrm{\partial }x}\right)=-\frac{\mathrm{\partial }P}{\mathrm{\partial }x}-v_{id}nu-n\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }x},\end{array}$(2) (3) $\begin{array}{rl}& \frac{\mathrm{\partial }P}{\mathrm{\partial }t}+u\frac{\mathrm{\partial }P}{\mathrm{\partial }x}+3P\frac{\mathrm{\partial }u}{\mathrm{\partial }x}=0,\end{array}$(3) (4) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^2\varphi }{\mathrm{\partial }{x}^2}={\delta }_1+{\delta }_2\{1+(q-1)\varphi \text{β}{\}}^{\frac{1}{q-1}+\frac{1}{2}}-n.\end{array}$(4) At equilibrium, the charge neutrality state holds $n_0=\sum _{j=1}^N{Z}_{dj0}{n}_{djo}+n_{e0}$ resulting into ${\delta }_1=1-{\delta }_2$, where  ${\delta }_1=\frac{\left(\sum _{j=1}^N{Z}_{dj0}{n}_{djo}\right)}{n_0}$ and ${\delta }_2=\frac{n_{e0}}{n_0}$. Here, $\text{β}=T_i/T_e$, where $T_{i,e}$ is temperature of ions and electrons. Here $n_0$ and $n_{e0}$ are number densities of ions and electrons at equilibrium. The normalization of physical quantities are given by: the quantities $n_{i0},C_i$ and $\frac{K{T}_i}{e}$ normalize number density of ions (n), velocity of ions (u), and electronic potential ϕ, respectively, where $C_i=(\frac{K{T}_i}{m_i}{)}^{\frac{1}{2}}$. The quantities ${\omega }_p^{-1}$ and ${\lambda }_D=(\frac{K{T}_i}{4\pi e^2{n}_{i0}}{)}^{\frac{1}{2}}$ normalize time t and space coordinate x, respectively, where ${\omega }_p=(\frac{4\pi e^2{n}_{i0}}{m_i}{)}^{\frac{1}{2}}$. Here $T_i$ is the temperatures of ions and ${\nu }_{id}$ is collisional frequency between ions and dusts.

3. Derivation of the DKdV equation

We consider the following stretching coordinates: (5) $\xi ={ϵ}^{\frac{1}{2}}(x-Mt),\mathrm{a}\mathrm{n}\mathrm{d}\tau ={ϵ}^{\frac{3}{2}}t,$(5) with ϵ as measure of the weak dispersion while, the wave phase velocity is denoted by M. Expansions of n, u, ϕ, P and $v_{id}$ are given by: (6) $\left\{\begin{array}{l}n=1+ϵn_1+{ϵ}^2{n}_2+\cdots ,\\ u=0+ϵu_1+{ϵ}^2{u}_2+\cdots ,\\ \varphi =0+ϵ{\varphi }_1+{ϵ}^2{\varphi }_2+\cdots ,\\ P=1+ϵP_1+{ϵ}^2{P}_2+\cdots ,\\ v_{id}\sim {ϵ}^{\frac{3}{2}}{v}_{id0}.\end{array}\right.$(6) Substituting Equations (5(5) $\xi ={ϵ}^{\frac{1}{2}}(x-Mt),\mathrm{a}\mathrm{n}\mathrm{d}\tau ={ϵ}^{\frac{3}{2}}t,$(5) )–(6(6) $\left\{\begin{array}{l}n=1+ϵn_1+{ϵ}^2{n}_2+\cdots ,\\ u=0+ϵu_1+{ϵ}^2{u}_2+\cdots ,\\ \varphi =0+ϵ{\varphi }_1+{ϵ}^2{\varphi }_2+\cdots ,\\ P=1+ϵP_1+{ϵ}^2{P}_2+\cdots ,\\ v_{id}\sim {ϵ}^{\frac{3}{2}}{v}_{id0}.\end{array}\right.$(6) ) in Equation (1(1) $\begin{array}{rl}& \frac{\mathrm{\partial }n}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(nu\right)=0,\end{array}$(1) ), we get (7) $\begin{array}{rl}& {ϵ}^{\frac{5}{2}}\frac{\mathrm{\partial }{n}_1}{\mathrm{\partial }\tau }-M{ϵ}^{\frac{3}{2}}\frac{\mathrm{\partial }{n}_1}{\mathrm{\partial }\xi }-M{ϵ}^{\frac{5}{2}}\frac{\mathrm{\partial }{n}_2}{\mathrm{\partial }\xi }\\ & +{ϵ}^{\frac{3}{2}}\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\xi }+{ϵ}^{\frac{5}{2}}\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }\xi }+{ϵ}^{\frac{5}{2}}\frac{\mathrm{\partial }}{\mathrm{\partial }\xi }\left(n_1{u}_1\right)=0.\end{array}$(7) We obtain the following by comparing the terms ${ϵ}^{\frac{3}{2}}$ and ${ϵ}^{\frac{5}{2}}$, (8) $\begin{array}{rl}& {ϵ}^{\frac{3}{2}}:n_1=\frac{1}{M}{u}_1,\end{array}$(8) (9) $\begin{array}{rl}& {ϵ}^{\frac{5}{2}}:\frac{\mathrm{\partial }{n}_1}{\mathrm{\partial }\tau }-M\frac{\mathrm{\partial }{n}_2}{\mathrm{\partial }\xi }+\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }\xi }+\frac{\mathrm{\partial }}{\mathrm{\partial }\xi }\left(n_1{u}_1\right)=0.\end{array}$(9) Substituting Equations (5(5) $\xi ={ϵ}^{\frac{1}{2}}(x-Mt),\mathrm{a}\mathrm{n}\mathrm{d}\tau ={ϵ}^{\frac{3}{2}}t,$(5) )–(6(6) $\left\{\begin{array}{l}n=1+ϵn_1+{ϵ}^2{n}_2+\cdots ,\\ u=0+ϵu_1+{ϵ}^2{u}_2+\cdots ,\\ \varphi =0+ϵ{\varphi }_1+{ϵ}^2{\varphi }_2+\cdots ,\\ P=1+ϵP_1+{ϵ}^2{P}_2+\cdots ,\\ v_{id}\sim {ϵ}^{\frac{3}{2}}{v}_{id0}.\end{array}\right.$(6) ) in Equation (2(2) $\begin{array}{rl}& n\left(\frac{\mathrm{\partial }u}{\mathrm{\partial }t}+u\frac{\mathrm{\partial }u}{\mathrm{\partial }x}\right)=-\frac{\mathrm{\partial }P}{\mathrm{\partial }x}-v_{id}nu-n\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }x},\end{array}$(2) ), we get (10) $\begin{array}{rl}& {ϵ}^{\frac{5}{2}}(\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\tau }-M\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }\xi })-{ϵ}^{\frac{3}{2}}(M\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\xi })\\ & =-{ϵ}^{\frac{3}{2}}(\frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\xi }+\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\xi })\\ & -{ϵ}^{\frac{5}{2}}(\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }\xi }+v_{ido}{u}_1+\frac{\mathrm{\partial }{\varphi }_2}{\mathrm{\partial }\xi }+n_1\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\xi })\end{array}$(10) We obtain the following by comparing the terms ${ϵ}^{\frac{3}{2}}$ and ${ϵ}^{\frac{5}{2}}$, (11) $\begin{array}{rl}& {ϵ}^{\frac{3}{2}}:M\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\xi }=\frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\xi }+\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\xi },\end{array}$(11) (12) $\begin{array}{rl}& {ϵ}^{\frac{5}{2}}:\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\tau }-M\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }\xi }=-\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }\xi }-v_{ido}{u}_1-\frac{\mathrm{\partial }{\varphi }_2}{\mathrm{\partial }\xi }-n_1\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\xi }.\end{array}$(12) Substituting Equations (5(5) $\xi ={ϵ}^{\frac{1}{2}}(x-Mt),\mathrm{a}\mathrm{n}\mathrm{d}\tau ={ϵ}^{\frac{3}{2}}t,$(5) )–(6(6) $\left\{\begin{array}{l}n=1+ϵn_1+{ϵ}^2{n}_2+\cdots ,\\ u=0+ϵu_1+{ϵ}^2{u}_2+\cdots ,\\ \varphi =0+ϵ{\varphi }_1+{ϵ}^2{\varphi }_2+\cdots ,\\ P=1+ϵP_1+{ϵ}^2{P}_2+\cdots ,\\ v_{id}\sim {ϵ}^{\frac{3}{2}}{v}_{id0}.\end{array}\right.$(6) ) in Equation (3(3) $\begin{array}{rl}& \frac{\mathrm{\partial }P}{\mathrm{\partial }t}+u\frac{\mathrm{\partial }P}{\mathrm{\partial }x}+3P\frac{\mathrm{\partial }u}{\mathrm{\partial }x}=0,\end{array}$(3) ), we get (13) $\begin{array}{rl}& {ϵ}^{\frac{5}{2}}(\frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\tau }-M\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }\xi }+u_1\frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\xi }+3\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }\xi }+3P_1\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\xi })\\ & +{ϵ}^{\frac{3}{2}}(3\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\xi }-M\frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\xi })=0.\end{array}$(13)

We obtain the following by comparing the terms ${ϵ}^{\frac{3}{2}}$ and ${ϵ}^{\frac{5}{2}}$, (14) $\begin{array}{rl}& {ϵ}^{\frac{3}{2}}:P_1=\frac{3}{M}{u}_1,\end{array}$(14) (15) $\begin{array}{rl}& {ϵ}^{\frac{5}{2}}:\frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\tau }-M\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }\xi }+u_1\frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\xi }+3\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }\xi }+3P_1\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\xi }=0.\end{array}$(15) Substituting Equations (5(5) $\xi ={ϵ}^{\frac{1}{2}}(x-Mt),\mathrm{a}\mathrm{n}\mathrm{d}\tau ={ϵ}^{\frac{3}{2}}t,$(5) )–(6(6) $\left\{\begin{array}{l}n=1+ϵn_1+{ϵ}^2{n}_2+\cdots ,\\ u=0+ϵu_1+{ϵ}^2{u}_2+\cdots ,\\ \varphi =0+ϵ{\varphi }_1+{ϵ}^2{\varphi }_2+\cdots ,\\ P=1+ϵP_1+{ϵ}^2{P}_2+\cdots ,\\ v_{id}\sim {ϵ}^{\frac{3}{2}}{v}_{id0}.\end{array}\right.$(6) ) in Equation (4(4) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^2\varphi }{\mathrm{\partial }{x}^2}={\delta }_1+{\delta }_2\{1+(q-1)\varphi \text{β}{\}}^{\frac{1}{q-1}+\frac{1}{2}}-n.\end{array}$(4) ), we get (16) $\begin{array}{rl}{ϵ}^2\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{\xi }^2}& =ϵ(a{\delta }_2\text{β}{\varphi }_1-n_1)\\ & +{ϵ}^2(a{\delta }_2\text{β}{\varphi }_2+\frac{(3-q)}{4}\left(a{\delta }_2{\text{β}}^2{\varphi }_1^2\right)-n_2),\end{array}$(16) where a = $\frac{q+1}{2}$.

We obtain the following by comparing the terms ${ϵ}^{\frac{3}{2}}$ and ${ϵ}^{\frac{5}{2}}$, (17) $\begin{array}{rl}& ϵ:n_1=a{\delta }_2\text{β}{\varphi }_1,\end{array}$(17) (18) $\begin{array}{rl}& {ϵ}^2:\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{\xi }^2}=a{\delta }_2\text{β}{\varphi }_2+\frac{(3-q)}{4}a{\delta }_2{\text{β}}^2{\varphi }_1^2-n_2.\end{array}$(18)

From Equations (8(8) $\begin{array}{rl}& {ϵ}^{\frac{3}{2}}:n_1=\frac{1}{M}{u}_1,\end{array}$(8) ), (11(11) $\begin{array}{rl}& {ϵ}^{\frac{3}{2}}:M\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\xi }=\frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\xi }+\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\xi },\end{array}$(11) ), (14(14) $\begin{array}{rl}& {ϵ}^{\frac{3}{2}}:P_1=\frac{3}{M}{u}_1,\end{array}$(14) ) and (17(17) $\begin{array}{rl}& ϵ:n_1=a{\delta }_2\text{β}{\varphi }_1,\end{array}$(17) ), we obtain (19) $M^2=3+\frac{1}{a\text{β}{\delta }_2}.$(19) From Equations (7(7) $\begin{array}{rl}& {ϵ}^{\frac{5}{2}}\frac{\mathrm{\partial }{n}_1}{\mathrm{\partial }\tau }-M{ϵ}^{\frac{3}{2}}\frac{\mathrm{\partial }{n}_1}{\mathrm{\partial }\xi }-M{ϵ}^{\frac{5}{2}}\frac{\mathrm{\partial }{n}_2}{\mathrm{\partial }\xi }\\ & +{ϵ}^{\frac{3}{2}}\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }\xi }+{ϵ}^{\frac{5}{2}}\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }\xi }+{ϵ}^{\frac{5}{2}}\frac{\mathrm{\partial }}{\mathrm{\partial }\xi }\left(n_1{u}_1\right)=0.\end{array}$(7) )–(19(19) $M^2=3+\frac{1}{a\text{β}{\delta }_2}.$(19) ), we obtain the damped KdV (DKdV) equation as (20) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}+C\psi =0,$(20) here we put ${\varphi }_1=\psi$, $A=B(\frac{12}{(M^2-3{)}^3}+\frac{3}{(M^2-3{)}^2}-\frac{(3-q)}{2}a{\delta }_2{\text{β}}^2)$, where $B=\frac{(M^2-3{)}^2}{2M}$ and $C=\frac{v_{id0}}{2}.$

It is important to note that in absence of dust-ion collision, the collisional parameter ${\nu }_{id0}$ becomes 0, then the above damped KdV (DKdV) Equation (20(20) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}+C\psi =0,$(20) ) reduces to the KdV equation given by (21) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}=0.$(21) Now, we use new variable $\eta =\xi -v\tau$ as wave transformation, where v is speed of wave. Using the transformation η into the KdV Equation (21(21) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}=0.$(21) ), one can obtain (22) $\frac{d^2\psi }{d{\eta }^2}=\frac{1}{B}(v\psi -\frac{A}{2}{\psi }^2),$(22) which further can be written as the following dynamical system (DS) (23) $\left\{\begin{array}{l}\frac{\mathrm{d}\psi }{\mathrm{d}\eta }=y,\\ \frac{\mathrm{d}y}{\mathrm{d}\eta }=\frac{1}{B}\left(v-\frac{A}{2}\psi \right)\psi .\end{array}\right.$(23) Now, we examine phase portrait of the DS (23(23) $\left\{\begin{array}{l}\frac{\mathrm{d}\psi }{\mathrm{d}\eta }=y,\\ \frac{\mathrm{d}y}{\mathrm{d}\eta }=\frac{1}{B}\left(v-\frac{A}{2}\psi \right)\psi .\end{array}\right.$(23) ) which corresponds to the KdV Equation (21(21) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}=0.$(21) ). The DS (23(23) $\left\{\begin{array}{l}\frac{\mathrm{d}\psi }{\mathrm{d}\eta }=y,\\ \frac{\mathrm{d}y}{\mathrm{d}\eta }=\frac{1}{B}\left(v-\frac{A}{2}\psi \right)\psi .\end{array}\right.$(23) ) has two singular points $S_0$ and $S_1$ at $(0,0)$ and $(\frac{2v}{A},0)$, respectively. Determinant of the Jacobian matrix $J=-\frac{1}{B}(v-A\psi )$ is less than 0 for singular point $S_0$, and greater than 0 at $S_1$. Therefore, the theory of planar dynamical systems [57] suggests that the singular point at which det J<0 is a saddle and det J>0 is a centre.

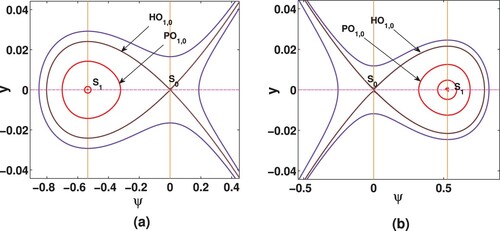
Figure 1 shows two phase portraits of the DS (23(23) $\left\{\begin{array}{l}\frac{\mathrm{d}\psi }{\mathrm{d}\eta }=y,\\ \frac{\mathrm{d}y}{\mathrm{d}\eta }=\frac{1}{B}\left(v-\frac{A}{2}\psi \right)\psi .\end{array}\right.$(23) ) for cases in $-1<q<0$ and 0<q<1. However, the subextensive range of q is valid for q>1, but in this case, the DS (23(23) $\left\{\begin{array}{l}\frac{\mathrm{d}\psi }{\mathrm{d}\eta }=y,\\ \frac{\mathrm{d}y}{\mathrm{d}\eta }=\frac{1}{B}\left(v-\frac{A}{2}\psi \right)\psi .\end{array}\right.$(23) ) shows same feature as shown in range 0<q<1. The singular point $S_0$ of the dynamical system is a saddle and $S_1$ is a centre in both the cases. A closed loop forming around the centre at singular point $S_1$ is called a periodic orbit (PO${}_{1,0}$) and it has zero separatrix. An orbit that begins at $S_0$, forms a loop enclosing $S_1$ and ends at $S_0$ is defined as homoclinic orbit (HO${}_{1,0}$). Here, the subscript “1, 0 ” denotes one singular point and zero separatrix. The PO${}_{1,0}$ shown in phase portrait Figure 1 is related to periodic wave solution (PWS) and HO${}_{1,0}$ is related to solitary solution. Since, the corresponding solutions exist in two opposite region of the phase portrait. Therefore, we have rarefactive solitary wave (RSW) solution for $-1<q<0$ of DIAW and compressive solitary wave (CSW) solution in 0<q<1.

Figure 1. Phase portrait of the DS (23(23) $\left\{\begin{array}{l}\frac{\mathrm{d}\psi }{\mathrm{d}\eta }=y,\\ \frac{\mathrm{d}y}{\mathrm{d}\eta }=\frac{1}{B}\left(v-\frac{A}{2}\psi \right)\psi .\end{array}\right.$(23) ) for (a) q = −0.1, v = 0.1 (b) q = 0.4 v = 0.03 with ${\nu }_{id0}=0$, $\text{β}=0.4$ and $\delta =0.5$.

Equation (22(22) $\frac{d^2\psi }{d{\eta }^2}=\frac{1}{B}(v\psi -\frac{A}{2}{\psi }^2),$(22) ) can be expressed as (24) $\frac{{\mathrm{d}}^2\psi }{\mathrm{d}{\eta }^2}+\frac{\mathrm{d}V}{\mathrm{d}\psi }=0,$(24) where V is the potential energy function corresponding to the DS (23(23) $\left\{\begin{array}{l}\frac{\mathrm{d}\psi }{\mathrm{d}\eta }=y,\\ \frac{\mathrm{d}y}{\mathrm{d}\eta }=\frac{1}{B}\left(v-\frac{A}{2}\psi \right)\psi .\end{array}\right.$(23) ) and it is given by (25) $V\left(\psi \right)=-\frac{1}{2B}v{\psi }^2+\frac{A}{6B}{\psi }^3.$(25) Therefore, the Hamiltonian function ($H(\psi ,y)$) corresponding to the DS (23(23) $\left\{\begin{array}{l}\frac{\mathrm{d}\psi }{\mathrm{d}\eta }=y,\\ \frac{\mathrm{d}y}{\mathrm{d}\eta }=\frac{1}{B}\left(v-\frac{A}{2}\psi \right)\psi .\end{array}\right.$(23) ) is given by (26) $H(\psi ,y)=\frac{y^2}{2}-\frac{v}{2B}{\psi }^2+\frac{A}{6B}{\psi }^3.$(26)

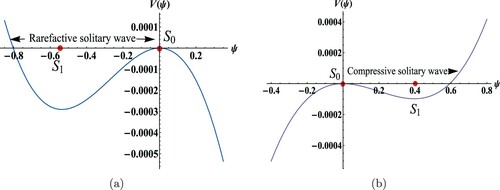
Considering fixed values of parameters $q,v,\text{β},\delta$ as Figure 1, we present potential energy function $V\left(\psi \right)$ with respect to ψ in Figure 2. It is clearly observed from Figures 2(a,b) that the curves contain one local maximum and minimum points. Figure 2(a,b) also provides the information of existence of rarefactive and compressive solitary wave solutions shown by two regions traced by the potential curve.

Figure 2. Potential energy function curve of the KdV equation (21(21) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}=0.$(21) ) with same data values as Figure 1 (a) and (b), respectively.

In phase plane analysis, we show nonlinear homoclinic and periodic orbits which correspond to solitary and periodic DIAW solutions, respectively. 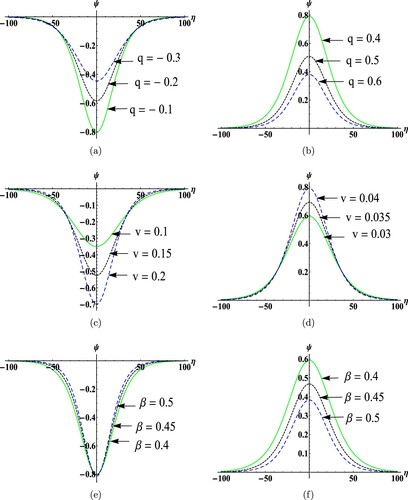Thus, we derive analytical form of solitary wave solution of the KdV equation (21(21) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}=0.$(21) ) as (27) $\psi =\frac{3v}{A}{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left(\sqrt{\frac{v}{4B}}\eta \right).$(27) It is clear that height ($\frac{3v}{A}$) and width ($\frac{4B}{v}$) of the solitary wave are influenced by system parameters $q,v$ and β. For A<0, we get rarefactive solitary DIAW, and for A>0, we get compressive solitary DIAW solution. Therefore, in Figure 3, we show impacts of $q,v$ and β on RSW and CSW solutions of the KdV equation (21(21) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}=0.$(21) ) while other values are fixed as Figure 1(a,b), respectively. Height of RSW and CSW solutions diminishes as q increases, while, it extends when speed of the wave (v) is increased. We also observe that for higher temperature of ions as compared to electrons, only width of RSW diminishes and there is no significant change in its height. Whereas, both width and height of CSW diminish as temperature of ions rises through the parameter β.

Figure 3. RSW and CSW solutions of the KdV equation (21(21) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}=0.$(21) ) with same data values as Figure 1(a,b), respectively.

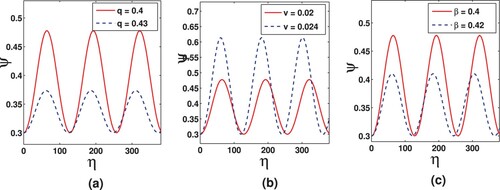
In Figures 4 and 5, the impacts of $q,v$ and β on PWS are presented numerically in ranges $-1<q<0$ and 0<q<1, respectively. It is seen that the height of PWS decreases significantly as q increases, while it declines as value of speed of wave (v) is increased. However, with rise in temperature of ions than that of electrons, the height of PWS gradually rises while, its width shrinks as shown in Figure 4(c). Whereas, under the range 0<q<1 as shown in Figure 5(c), both height and width of PWS diminish with rise in temperature ratio $\left(\text{β}\right)$.

Figure 4. Periodic solution of the KdV equation (21(21) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}=0.$(21) ) with same data values as Figure 1(a).

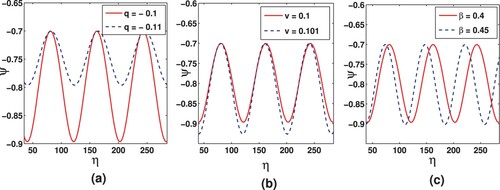
Figure 5. Periodic solution the KdV equation (21(21) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}=0.$(21) ) with same data values as Figure 1(b).

4. Approximate analytical solutions

We can inspect a general nonlinear partial differential equation for (28) $F\left(\psi ,\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau },\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi },\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{\tau }^2},\frac{{\mathrm{\partial }}^2\xi }{\mathrm{\partial }{\xi }^2},\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }\tau \mathrm{\partial }\xi },\dots \right)=0,$(28) where $\psi =\psi (\xi ,\tau )$ is to be determined and F is a polynomial consisting of different order partial derivatives of ψ.

The above equation is reduced to a nonlinear ordinary differential equation (ODE) (29) $F(q,q^{\prime },q^{″},q^{‴},\dots )=0,$(29) by applying the following transformation (30) $\psi (\xi ,\tau )=\psi \left(\eta \right),\eta =\xi -v\tau ,$(30) with v being the travelling wave velocity. It is to be mentioned that derivative with respect to η is denoted by ${}^{\prime }$. Then, Equation (29(29) $F(q,q^{\prime },q^{″},q^{‴},\dots )=0,$(29) ) is to be integrated.

The solution to nonlinear ODE is acquired directly by $\left(G^{\prime }/G\right)$-expansion technique. Some important steps are mentioned below.

4.1. The $\left(G^{\prime }/G\right)$-expansion technique

The following steps are mentioned of the $\left(G^{\prime }/G\right)$-expansion technique [28]:

Step I: Consider the solution of Equation (29(29) $F(q,q^{\prime },q^{″},q^{‴},\dots )=0,$(29) ) in terms of a polynomial in $\left(G^{\prime }/G\right)$ as (31) $\psi \left(\eta \right)=\sum _{i=1}^n{a}_i(G^{\prime }/G{)}^i,a_n\ne 0,$(31) where $a_i$ are unknown constants, $i=0,1,2,\dots ,n$. Here, the linear ODE is (32) $G^{″}+\lambda G^{\prime }+\mu G=0,$(32) which is called auxiliary equation having constants λ and µ.

Step II: Equation (29(29) $F(q,q^{\prime },q^{″},q^{‴},\dots )=0,$(29) ) shows n positive integer obtained by the homogeneous balance between the nonlinear term and the highest order derivative.

Step III: We substitute Equation (31(31) $\psi \left(\eta \right)=\sum _{i=1}^n{a}_i(G^{\prime }/G{)}^i,a_n\ne 0,$(31) ) into the nonlinear ODE (29(29) $F(q,q^{\prime },q^{″},q^{‴},\dots )=0,$(29) ), where $G\left(\eta \right)$ holds Equation (32(32) $G^{″}+\lambda G^{\prime }+\mu G=0,$(32) ). Then, collect the terms having like powers of $(G^{\prime }/G{)}^i$ of the polynomial, where $i=0,1,2,\dots$. Finally, we equate each term of the polynomial and a set of equations in $a_i$ to zero, where $v,\mu$ and λ are to be calculated.

Step IV: Using solutions of Equation (32(32) $G^{″}+\lambda G^{\prime }+\mu G=0,$(32) ) into (31(31) $\psi \left(\eta \right)=\sum _{i=1}^n{a}_i(G^{\prime }/G{)}^i,a_n\ne 0,$(31) ), we obtain the approximate solutions of (28(28) $F\left(\psi ,\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau },\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi },\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{\tau }^2},\frac{{\mathrm{\partial }}^2\xi }{\mathrm{\partial }{\xi }^2},\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }\tau \mathrm{\partial }\xi },\dots \right)=0,$(28) ) after calculating $a_i$, $v,\mu ,\lambda$, $i=0,1,2,\dots n$.

4.2. Implementation of $\left(G^{\prime }/G\right)$-expansion technique on DKdV equation

In the current section, the $\left(G^{\prime }/G\right)$-expansion technique is implemented on the DKdV equation (20(20) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}+C\psi =0,$(20) ) to extract approximate analytical solutions. The transformation (30(30) $\psi (\xi ,\tau )=\psi \left(\eta \right),\eta =\xi -v\tau ,$(30) ) is considered which reduces Equation (20(20) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}+C\psi =0,$(20) ) to (33) $-v\frac{\mathrm{d}\psi }{\mathrm{d}\eta }+A\psi \frac{\mathrm{d}\psi }{\mathrm{d}\eta }+B\frac{{\mathrm{d}}^3\psi }{\mathrm{d}{\eta }^3}+C\psi =0.$(33) The homogeneous balance between $\frac{{\mathrm{d}}^3\psi }{\mathrm{d}{\eta }^3}$ and $\psi \frac{\mathrm{d}\psi }{\mathrm{d}\eta }$ is taken under Equation (33(33) $-v\frac{\mathrm{d}\psi }{\mathrm{d}\eta }+A\psi \frac{\mathrm{d}\psi }{\mathrm{d}\eta }+B\frac{{\mathrm{d}}^3\psi }{\mathrm{d}{\eta }^3}+C\psi =0.$(33) ) and obtain the value of the positive integer n as (34) $3+n=n+(1+n)\Rightarrow n=2.$(34) Hence the solution of Equation (33(33) $-v\frac{\mathrm{d}\psi }{\mathrm{d}\eta }+A\psi \frac{\mathrm{d}\psi }{\mathrm{d}\eta }+B\frac{{\mathrm{d}}^3\psi }{\mathrm{d}{\eta }^3}+C\psi =0.$(33) ) is assumed in $\left(G^{\prime }/G\right)$ polynomial as (35) $\psi \left(\eta \right)=a_0+a_1\left(G^{\prime }/G\right)+a_2(G^{\prime }/G{)}^2,a_2\ne 0,$(35) here $G=G\left(\eta \right)$ holds the auxiliary equation of order 2 (36) $G^{″}+\lambda G^{\prime }+\mu G=0.$(36) Finally, we substitute the solution ansatz (35(35) $\psi \left(\eta \right)=a_0+a_1\left(G^{\prime }/G\right)+a_2(G^{\prime }/G{)}^2,a_2\ne 0,$(35) ) in (33(33) $-v\frac{\mathrm{d}\psi }{\mathrm{d}\eta }+A\psi \frac{\mathrm{d}\psi }{\mathrm{d}\eta }+B\frac{{\mathrm{d}}^3\psi }{\mathrm{d}{\eta }^3}+C\psi =0.$(33) ) considering the auxiliary Equation (36(36) $G^{″}+\lambda G^{\prime }+\mu G=0.$(36) ) which yields a $\left(G^{\prime }/G\right)$ polynomial equation. Collecting all the terms of $(G^{\prime }/G{)}^i,i=0,1,\dots ,5$ and comparing each of them to zero, we get (37) $\begin{array}{rl}& (G^{\prime }/G{)}^0:-a_0{a}_{1}A\mu -a_{1}B{\lambda }^2\mu -6a_{2}B\lambda {\mu }^2\\ & -2a_{1}B{\mu }^2+a_{1}v\mu +C{a}_0=0\\ & (G^{\prime }/G{)}^1:-a_0{a}_{1}A\lambda -a_1^{2}A\mu -2a_0{a}_{2}A\mu \\ & -a_{1}B{\lambda }^3-14a_{2}B{\lambda }^2\mu \\ & -8a_{1}B\lambda \mu -16a_{2}B{\mu }^2+a_{1}v\lambda +2a_{2}v\mu +C{a}_1=0\\ & (G^{\prime }/G{)}^2:-a_1^{2}A\lambda -2a_0{a}_{2}A\lambda -3a_1{a}_{2}A\mu \\ & -a_0{a}_{1}A-8a_{2}B{\lambda }^3\\ & -7a_{1}B{\lambda }^2-52a_{2}B\lambda \mu \\ & -8a_{1}B\mu +2a_{2}v\lambda +a_{1}v+C{a}_2=0\\ & (G^{\prime }/G{)}^3:-3a_1{a}_{2}A\lambda -2a_2^{2}A\mu \\ & -a_1^{2}A-2a_0{a}_{2}A-38a_{2}B{\lambda }^2\\ & -12a_{1}B\lambda -40a_{2}B\mu +2a_{2}v=0\\ & (G^{\prime }/G{)}^4:-2a_2^{2}A\lambda -3a_1{a}_{2}A-54a_{2}B\lambda -6a_{1}B=0\\ & (G^{\prime }/G{)}^5:-2a_2^{2}A-24a_{2}B=0.\end{array}$(37) We simplify the set of algebraic Equation (37(37) $\begin{array}{rl}& (G^{\prime }/G{)}^0:-a_0{a}_{1}A\mu -a_{1}B{\lambda }^2\mu -6a_{2}B\lambda {\mu }^2\\ & -2a_{1}B{\mu }^2+a_{1}v\mu +C{a}_0=0\\ & (G^{\prime }/G{)}^1:-a_0{a}_{1}A\lambda -a_1^{2}A\mu -2a_0{a}_{2}A\mu \\ & -a_{1}B{\lambda }^3-14a_{2}B{\lambda }^2\mu \\ & -8a_{1}B\lambda \mu -16a_{2}B{\mu }^2+a_{1}v\lambda +2a_{2}v\mu +C{a}_1=0\\ & (G^{\prime }/G{)}^2:-a_1^{2}A\lambda -2a_0{a}_{2}A\lambda -3a_1{a}_{2}A\mu \\ & -a_0{a}_{1}A-8a_{2}B{\lambda }^3\\ & -7a_{1}B{\lambda }^2-52a_{2}B\lambda \mu \\ & -8a_{1}B\mu +2a_{2}v\lambda +a_{1}v+C{a}_2=0\\ & (G^{\prime }/G{)}^3:-3a_1{a}_{2}A\lambda -2a_2^{2}A\mu \\ & -a_1^{2}A-2a_0{a}_{2}A-38a_{2}B{\lambda }^2\\ & -12a_{1}B\lambda -40a_{2}B\mu +2a_{2}v=0\\ & (G^{\prime }/G{)}^4:-2a_2^{2}A\lambda -3a_1{a}_{2}A-54a_{2}B\lambda -6a_{1}B=0\\ & (G^{\prime }/G{)}^5:-2a_2^{2}A-24a_{2}B=0.\end{array}$(37) ) and the following (38) $\begin{array}{rl}{a}_0& =-\frac{4\mu B}{A},a_1=-\frac{12\lambda B}{A},a_2=-\frac{12B}{A},\\ v& =\frac{3{\lambda }^{3}B+12\lambda \mu B-C}{3\lambda },\end{array}$(38) where $\lambda ,\mu$ are constants.

We import the solution in the expression (35(35) $\psi \left(\eta \right)=a_0+a_1\left(G^{\prime }/G\right)+a_2(G^{\prime }/G{)}^2,a_2\ne 0,$(35) ) and find the general solution as (39) $\psi \left(\eta \right)=-\frac{4\mu B}{A}-\frac{12\lambda B}{A}\left(G^{\prime }/G\right)-\frac{12B}{A}(G^{\prime }/G{)}^2,$(39) where $\eta =\xi -\frac{3{\lambda }^{3}B+12\lambda \mu B-C}{3\lambda }\tau$.

Finally, the general solution of Equation (36(36) $G^{″}+\lambda G^{\prime }+\mu G=0.$(36) ) is substituted in the general solution (39(39) $\psi \left(\eta \right)=-\frac{4\mu B}{A}-\frac{12\lambda B}{A}\left(G^{\prime }/G\right)-\frac{12B}{A}(G^{\prime }/G{)}^2,$(39) ) and following travelling wave solutions of Equation (20(20) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\tau }+A\psi \frac{\mathrm{\partial }\psi }{\mathrm{\partial }\xi }+B\frac{{\mathrm{\partial }}^3\psi }{\mathrm{\partial }{\xi }^3}+C\psi =0,$(20) ) are acquired as follows:

The hyperbolic function travelling wave solution for ${\lambda }^2-4\mu >0$ is given by (40) $\begin{array}{rl}& {\psi }_1\left(\eta \right)\\ & =-\frac{4\mu B}{A}-\frac{6\lambda \sqrt{{\lambda }^2-4\mu }B}{A}\\ & \left(\frac{C_1\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }{C_1\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }\right)\\ & -\frac{3({\lambda }^2-4\mu )B}{A}\\ & {\left(\frac{C_1\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }{C_1\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }\right)}^2,\end{array}$(40) with $C_1$ and $C_2$ being arbitrary constants.

The trigonometric function travelling wave solution for ${\lambda }^2-4\mu <0$ is given by (41) $\begin{array}{rl}& {\psi }_2\left(\eta \right)\\ & =-\frac{4\mu B}{A}-\frac{6\lambda \sqrt{4\mu -{\lambda }^2}B}{A}\\ & \left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)\\ & -\frac{3(4\mu -{\lambda }^2)B}{A}\\ & {\left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)}^2,\end{array}$(41) where $C_3$ and $C_4$ are arbitrary constants.

The rational function solution for ${\lambda }^2-4\mu =0$ is given by (42) $\begin{array}{rl}{\psi }_3\left(\eta \right)& =-\frac{4\mu B}{A}-\frac{12\lambda B}{A}\frac{C_6}{C_5+C_6\eta }\\ & -\frac{12B}{A}{\left(\frac{C_6}{C_5+C_6\eta }\right)}^2,\end{array}$(42) where $C_5$ and $C_6$ are arbitrary constants.

5. Graphical illustrations

Graphs of the approximate solutions (40(40) $\begin{array}{rl}& {\psi }_1\left(\eta \right)\\ & =-\frac{4\mu B}{A}-\frac{6\lambda \sqrt{{\lambda }^2-4\mu }B}{A}\\ & \left(\frac{C_1\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }{C_1\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }\right)\\ & -\frac{3({\lambda }^2-4\mu )B}{A}\\ & {\left(\frac{C_1\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }{C_1\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }\right)}^2,\end{array}$(40) ), (41(41) $\begin{array}{rl}& {\psi }_2\left(\eta \right)\\ & =-\frac{4\mu B}{A}-\frac{6\lambda \sqrt{4\mu -{\lambda }^2}B}{A}\\ & \left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)\\ & -\frac{3(4\mu -{\lambda }^2)B}{A}\\ & {\left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)}^2,\end{array}$(41) ) and (42(42) $\begin{array}{rl}{\psi }_3\left(\eta \right)& =-\frac{4\mu B}{A}-\frac{12\lambda B}{A}\frac{C_6}{C_5+C_6\eta }\\ & -\frac{12B}{A}{\left(\frac{C_6}{C_5+C_6\eta }\right)}^2,\end{array}$(42) ) obtained for the DKdV equation are presented by considering different sets of physical parameters q, β, ${\delta }_2$, λ, µ and ${\nu }_{id}$ using the Wolfram Mathematica 11.

Figure 6 represents solution (40(40) $\begin{array}{rl}& {\psi }_1\left(\eta \right)\\ & =-\frac{4\mu B}{A}-\frac{6\lambda \sqrt{{\lambda }^2-4\mu }B}{A}\\ & \left(\frac{C_1\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }{C_1\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }\right)\\ & -\frac{3({\lambda }^2-4\mu )B}{A}\\ & {\left(\frac{C_1\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }{C_1\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }\right)}^2,\end{array}$(40) ) of the DKdV equation for DIAWs. Here, Figure 6(a) shows anti 1-soliton solitary wave solution [31] of the DKdV equation with parametric set of $q=7.4,\text{β}=0.6,$ ${\delta }_2=0.7,$ $\lambda =2.001,$ $\mu =1$ and ${\nu }_{id0}=0.09$. Figure 6(b) represents solitary wave solutions of kink type with parametric set of $q=150,\text{β}=0.58,$ ${\delta }_2=0.3,\lambda =30.2,$ $\mu =19,$ ${\nu }_{id0}=0.09$. Figure 6(c) shows rarefactive solitons with parametric set of $q=160,\text{β}=0.6,{\delta }_2=0.7,\lambda =9,$ $\mu =1.9,$ ${\nu }_{id0}=0.09$.

Figure 6. 3D graph of Equation (40(40) $\begin{array}{rl}& {\psi }_1\left(\eta \right)\\ & =-\frac{4\mu B}{A}-\frac{6\lambda \sqrt{{\lambda }^2-4\mu }B}{A}\\ & \left(\frac{C_1\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }{C_1\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }\right)\\ & -\frac{3({\lambda }^2-4\mu )B}{A}\\ & {\left(\frac{C_1\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }{C_1\cosh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta +C_2\sinh \frac{1}{2}\sqrt{{\lambda }^2-4\mu }\eta }\right)}^2,\end{array}$(40) ) with (a) $q=7.4,\text{β}=0.6,{\delta }_2=0.7,\lambda =2.001,$ $\mu =1,$ ${\nu }_{id0}=0.09$. (b) $q=150,\text{β}=0.58,{\delta }_2=0.3,\lambda =30.2,$ $\mu =19,$ ${\nu }_{id0}=0.09$. (c) $q=160,\text{β}=0.6,{\delta }_2=0.7,\lambda =9,$ $\mu =1.9,$ ${\nu }_{id0}=0.09$.

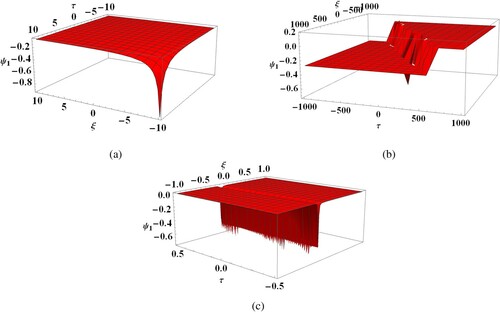
Figure 7 represents the approximate solution (41(41) $\begin{array}{rl}& {\psi }_2\left(\eta \right)\\ & =-\frac{4\mu B}{A}-\frac{6\lambda \sqrt{4\mu -{\lambda }^2}B}{A}\\ & \left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)\\ & -\frac{3(4\mu -{\lambda }^2)B}{A}\\ & {\left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)}^2,\end{array}$(41) ) of the DKdV equation for DIAWs. Here, we clearly observe that Figure 7(a ,b) represent anti-kink type of solitary wave solution for two different sets of parameters. From Figure 7(c), it is visible that the solution (41(41) $\begin{array}{rl}& {\psi }_2\left(\eta \right)\\ & =-\frac{4\mu B}{A}-\frac{6\lambda \sqrt{4\mu -{\lambda }^2}B}{A}\\ & \left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)\\ & -\frac{3(4\mu -{\lambda }^2)B}{A}\\ & {\left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)}^2,\end{array}$(41) ) corresponds to rarefactive periodic solution of the DKdV equation for $q=160,\text{β}=0.3,{\delta }_2=0.6,\lambda =0.2,$ $\mu =2,$ ${\nu }_{id0}=0.01$.

Figure 7. 3D graph of Equation (41(41) $\begin{array}{rl}& {\psi }_2\left(\eta \right)\\ & =-\frac{4\mu B}{A}-\frac{6\lambda \sqrt{4\mu -{\lambda }^2}B}{A}\\ & \left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)\\ & -\frac{3(4\mu -{\lambda }^2)B}{A}\\ & {\left(\frac{-C_3\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }{C_3\cos \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta +C_4\sin \frac{1}{2}\sqrt{4\mu -{\lambda }^2}\eta }\right)}^2,\end{array}$(41) ) with (a) $q=0.98,\text{β}=0.7,{\delta }_2=0.6,\lambda =0.65,$ $\mu =0.1,$ ${\nu }_{id0}=0.01$. (b) $q=86,\text{β}=0.6,{\delta }_2=0.7,\lambda =80,$ $\mu =30,$ ${\nu }_{id0}=0.01$. (c) $q=160,\text{β}=0.3,{\delta }_2=0.6,\lambda =0.2,$ $\mu =2,$ ${\nu }_{id0}=0.01$.

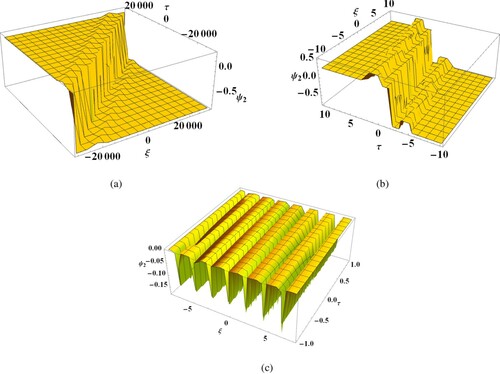
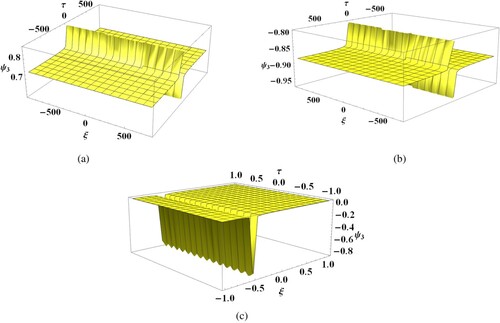
Figure 8 represents the approximate solution (42(42) $\begin{array}{rl}{\psi }_3\left(\eta \right)& =-\frac{4\mu B}{A}-\frac{12\lambda B}{A}\frac{C_6}{C_5+C_6\eta }\\ & -\frac{12B}{A}{\left(\frac{C_6}{C_5+C_6\eta }\right)}^2,\end{array}$(42) ) of the damped KdV equation for DIAWs. It is observed that Figure 8(a ,b) depict singular kink travelling wave solutions for the DIAWs in $-1<q<0$ and 0<q<1 ranges, respectively. For range q>1 with $q=120,\text{β}=0.6,$ ${\delta }_2=0.7,\lambda =1.2,$ $\mu =0.25,$ ${\nu }_{id0}=0.001$, the solution (42(42) $\begin{array}{rl}{\psi }_3\left(\eta \right)& =-\frac{4\mu B}{A}-\frac{12\lambda B}{A}\frac{C_6}{C_5+C_6\eta }\\ & -\frac{12B}{A}{\left(\frac{C_6}{C_5+C_6\eta }\right)}^2,\end{array}$(42) ) corresponds to rarefactive solitary wave solution which is clearly observed in Figure 8(c).

Figure 8. 3D graph of Equation (42(42) $\begin{array}{rl}{\psi }_3\left(\eta \right)& =-\frac{4\mu B}{A}-\frac{12\lambda B}{A}\frac{C_6}{C_5+C_6\eta }\\ & -\frac{12B}{A}{\left(\frac{C_6}{C_5+C_6\eta }\right)}^2,\end{array}$(42) ) with (a) $q=-0.704,\text{β}=0.6,{\delta }_2=0.7,\lambda =9.1,$ $\mu =0.01,$ ${\nu }_{id0}=0.001$. (b) $q=0.98,\text{β}=0.6,{\delta }_2=0.7,\lambda =15,$ $\mu =0.25,$ ${\nu }_{id0}=0.001$. (c) $q=120,\text{β}=0.6,{\delta }_2=0.7,\lambda =1.2,$ $\mu =0.25,$ ${\nu }_{id0}=0.001$.

6. Conclusions

The DIAWs in a nonextensive dusty plasma have been analysed under the damped Korteweg–de Vries (DKdV) equation alongside collision between ions and dusts. The DKdV equation has been acquired using the RPT. In the absence of collision between dusts and ions, the damping coefficient has been vanished. In that case, the reduction of the DKdV equation into the KdV equation has been shown. The DS of the KdV equation has been formed to show bifurcation analysis through phase portraits. In this case, the nonextensive parameter q has been the controlling parameter. Potential energy function has been shown for which the dynamical system of the KdV equation shows regions of periodic and solitary wave solutions. For cases $-1<q<0$ and 0<q<1, analytical solitary wave solution and numerical periodic wave solution of the KdV equation for DIAW have been obtained. It has been observed that nonextensive parameter (q), speed of the wave (v) and temperature ratio of ions to electrons $\left(\text{β}\right)$ effect the solitary and periodic DIAW solutions. Furthermore, in presence of collisional effect, approximate analytical wave solutions of the DKdV equation have been achieved employing the $\left(G^{\prime }/G\right)$-expansion technique. The novel approximate analytical solutions of the DKdV equation have been associated to three different classes, such as, the hyperbolic, trigonometric and rational functions of the travelling wave solutions. It has been perceived that the hyperbolic function solution of DIAW corresponds to anti 1-soliton solitary wave solution, solitary wave solutions of kink type and rarefactive solitary wave solution for different values of q. The trigonometric function solution of DIAW corresponds to anti-kink type of solitary wave with lesser values of q and rarefactive periodic wave for relatively greater values of q. However, the rational function of travelling DIAW solution corresponds to singular kink travelling waves with lesser numbers of q and rarefactive solitary wave with greater numbers of q. The study was carried out considering nonextensive parameter q in the range ($-1<q<0,0<q<1,q>1$), the number density ratio of electrons and ions (${\delta }_2=\frac{n_{e0}}{n_0}<1$) as defined by the relation ${\delta }_1+{\delta }_2=1$, and collisional frequency of ions and dusts (${\nu }_{id0}<1$) because of weak collision between dusts and ions, while, other parameters are constants. Generally, collisional effects between particles are delicate, hence, most of the studies neglect all collisional effects on dust-ion-acoustic waves. While, in some cases, collision effects are strong and cannot be avoided. Normally, the collisional frequency between ions and dust grains is larger, while, the collisional frequencies between dusts and electrons, ions and electrons are weak. Therefore, our study can be applicable to many plasma systems, in which electrons and ions have higher mean free paths than the range of the experimental device or pressure of neutral gas is small so that the collisions between neutral atoms and other particles are neglected. The only effective collision occurs between ions and dust grains. Therefore, we neglect the collisions between dusts and electrons, ions and electrons. We only consider the collision effect between ions and dust grains but, assume that the collisional effect is much weak. All the approximate analytical small-amplitude DIAW solutions obtained for the DKdV equation in collisional nonextensive dusty plasmas have not been reported earlier. Therefore, we can conclude that the approximate analytical solutions of the DKdV equation obtained, applying the $\left(G^{\prime }/G\right)$-expansion technique, have furnished new and significant solutions which can be of great interest for many researchers in Earth's ionosphere [41, 43–46, 59].

Disclosure statement

No potential conflict of interest was reported by the author(s).