Second law analysis of magnetized Casson nanofluid flow in squeezing geometry with porous medium and thermophysical influence

Abstract

This flow investigation analysed the entropy generation rate as an additional enrichment to the rate of heat transfer in Casson nanofluid flow between squeezing disks. The flow is modelled mathematically in PDEs systems, transformed into systems of ODEs via a well-posed transformation, and then solved. In a limiting case, good agreement of the numerical results is achieved. The assumption of variable fluid properties was seen to downsize the fluid velocity and temperature fields but enriches the nanoparticle volume fraction. Entropy number remarkably minimized for thermophysical properties, yield stress, and squeezing impact, while nanoparticle parameters, thermal diffusivity, and viscous dissipation contributed significantly to the system disorderliness. Moreover, findings reveal that thermal irreversibility controls the flow system in the entire channel (approximately $0.3<\eta \le 1$) except near the fixed disk where the other irreversibility dominated. Prandtl, Eckert, and Darcy's number help facilitate the irreversibility distribution phenomenon. With nanoscale mechanism modification nanoparticle volume fraction and energy distributions can easily be achieved.

Keywords:

• Casson nanofluid
• entropy generation
• thermo-physical effect
• porous media
• Bejan number

Nomenclature

English Alphabet

a	=	Stretching rate [$s^{-1}$]
$B{}_0$	=	Magnetic field [Weber/m${}^2$]
Be	=	Bejan number [-]
$B{i}_1$	=	Thermal Biot number [-]
$B{i}_2$	=	Solutal Biot number [-]
$C_p$	=	Specific heat at constant pressure [J/kg.K]
$D_0$	=	Mass diffusivity [m${}^2$/s]
Da	=	Darcy number [-]
Ec	=	Eckert number [-]
$E{c}_r$	=	Local Eckert number [-]
G	=	Dimensionless concentration [-]
$\overline{G}$	=	Fluid concentration [mol.]
${\overline{G}}_h$	=	Wall surface concentration [mol.]
H	=	Dimensionless temperature [-]
$\overline{H}$	=	Fluid temperature [K]
${\overline{H}}_0$	=	Reference temperature [K]
${\overline{H}}_h$	=	Wall surface temperature [K]
Ha	=	Magnetic parameter [-]

Greek Alphabet

α	=	Slip parameter [-]
β	=	Casson parameter [-]
${\kappa }_0$	=	Thermal conductivity [W/mK]
τ	=	Squeezing characteristics parameter [m]
${\mu }_0$	=	Dynamic viscosity [kg m${}^{-1}$s${}^{-1}$]
ν	=	Kinematic viscosity [m${}^2$s${}^{-1}$]
K	=	Permeability constant [$N/A^2$]
$K_D$	=	Dimensionless chemical reaction [-]
Kr	=	Dimensional chemical reaction [${\mathrm{m}}^{-1}$ ${\mathrm{s}}^{-1}$]
$m_1$	=	Variation of viscosity [${\mathrm{N}\mathrm{s}/\mathrm{m}}^2$]
$m_2$	=	Variation of thermal conductivity [W/mK]
$m_3$	=	Variation of mass diffusivity [m${}^2$/s]
Nb	=	Brownian motion parameter [-]
Nt	=	Thermophoresis parameter [-]
Ns	=	Entropy generation number [-]
$\overline{P}$	=	Pressure [N.m${}^{-2}$]
$Pr$	=	Prandtl number [-]
$r_1,r_2,r_3$	=	Coefficient factors [m   $s^{-1}$], [W m${}^{-2}{K}^{-1}$], [m $s^{-1}$]
Sc	=	Schmidt number [-]
$\overline{t}$	=	Time [s]
$\overline{u}$	=	Velocities along $\overline{r}$ direction [m/s]
$\overline{w}$	=	Velocities along $\overline{z}$ direction [m/s]
$V_0$	=	Suction/injection parameter [-]
Z	=	Squeezing parameter [-]
${\xi }_2$	=	Dimensionless thermal conductivity [-]
${\xi }_1$	=	Dimensionless viscosity [-]
${\xi }_3$	=	Dimensionless mass diffusivity [-]
${\rho }_f$	=	Fluid density [kg/m${}^3$]
σ	=	Electric conductivity [s/m]

1. Introduction

In literature, studies show that thermodynamic first law analysis predicts the heat transfer calculations effectively (Atlas et al. [1]). However, energy loss within the flow system due to fluid viscosity, expansion, and contraction of surfaces, convection process, fluid material conductivity, frictional force, chemical reaction, diffusion among others things calls for the second law analysis. Thus, proper utilization of nanoliquids in the squeezing region (expansion and contraction due to thermal expansion or surface movement) requires the proper knowledge of disorderliness caused by the distinct fluid transport variables in any flow geometry. The second law analysis (entropy generation and irreversibility distribution) has found contributing extensive involvement in solar collectors, porous media, turbo-machinery, electronic cooling, heat exchangers, and many more. Hence, this study gains its worth as the need to boost thermal system exergy, energy conversion and management remain essential to minimization of energy loss.

Vast interest in the exploration of nanofluid is observed due to its wide range of applications in engineering and industries such as in the production of electronic microchips, nuclear reactors, industrial cooling, medical sciences, biological fluids, polymers solutions, engine oil to mention but a few. Since its inclusion in the base fluid assisted towards boosting the fluid thermal performance. However, for its proper management and theoretical study (Manjunatha et al. [2]), necessary simulations are required for better usage, prediction and recommendation. Due to the aforementioned principalities, researchers, engineers, and industries found it worth to investigate the dynamics of nanofluid in different flow geometries and base fluids.

Series of demonstration and experimental studies were carried out among which Toghraie et al. [3] employed the L-shaped porous ribs and water/CuO nanofluid for performance evaluation in microchannels. The study identified the percentage of Reynolds number needed for heat transfer improvement. Hybrid nanofluid flow in multilayered porous media by Arasteh et al. [4], an experimental study of hybrid Tungsten oxide (WO3)-MWCNTs/engine oil nanofluids by Aghahadi et al. [5], Rashidi et al. [6, 7] examined the Argon flow in a condensed rough nanochannels and mixed convection flow of Hybrid Nanofluid in Lid-Driven Square Cavity, respectively. Recently, Ruhani et al. [8] gave a statistical investigation via the implementation of equal percentage of ZnO-Ag water hybrid nanofluid. Shafiq et al. [9] presented the sensitivity and numerical analysis of bioconvective tangent hyperbolic nanofluid. Also, a statistical approach to dual solution of Walter's B nanofluid with stratification effect [10]. Steady and unsteady bidirectional stretching surface study by Acharya et al. [11] employed the differential transformed approach for the nanofluid comparative examination. Swimming of microbes in blood flow of nano-bioconvective Williamson fluid by Rana et al. [12].

In thermal system, Nakhchi and co-authors [13–15] investigated the turbulent Cu-water nanofluid flows equipped with perforated conical rings and transverse-cut twisted turbulators. For perforated conical rings, it is discovered that thermal irreversibility dominate the entire tube, they highlight the percentage of Cu-water nanofluid needed for maximum system thermal performance and that thermal entropy degenerate to a raising nanoparticle volume fraction. Thermodynamic second law analysis in moving thin needle with dissipation effect by Khan et al. [16] reveals that the total entropy generated due to fluid friction and heat transfer in air is less than that of water. Buongiorno's nanofluid model by Khan et al. [17] explored squeezing and rotational effects on gyrotactic flow motion and thermodynamic second law analysis. They highlighted that higher thermophoresis and Brownian motion number predict a temperature rise. Aiming at optimizing the entropy generation rate, Zubair et al. [18] observed the effect of joule heating and viscous dissipation in the magnetized flow of Casson nanofluid in a 3-D rotating scene, the results attributed a wider porous media and higher dissipative effect to total entropy rise.

Adesanya et al. [19] enumerated the impact of reactive couple stress fluid while presenting the second law analysis in vertical channel. They mentioned that the couple stress inverse parameter decelerates the Bejan number but contributed to flow disorderliness along the channel. In rotating porous disk, Rashidi et al. [20] highlighted the impact of nanoparticles and MHD on flow motion and the second law of thermodynamics. Das et al. [21] observed the convective cooling and Navier slip impact in their novel entropy generation study while [22] introduced joule heating and dissipation impact on flow through an inclined microchannel. Spectral approach to irreversibility analysis of couple stress fluid by Acharya et al. [23]. Few recent studies on nanofluid and thermodynamic second law analysis include Refs. [24–38].

Series of thermodynamic second law examination in squeezing geometry includes: Butt and Ali [39] study in rotating channel, Qayyum et al. [35] investigation on Williamson fluid between rotating disks, nanofluid Brinkman model by Rajvanshi et al. [40], activation energy and nanoparticle impact on the second-grade fluid by Khan et al. [41], optimization and comparative analysis of different (five) nanoparticles by Ahmad et al. [42], while Ojjela et al. [43] studied Casson fluid examination between parallel disks revivals and show that dissipation effect lowered the irreversibility distribution. Atlas et al. [1] considered modified heat flux and magnetic model in entropy generation investigation through a squeezing channel. They deduced that the squeezing effect diminishes the entropy generation rate.

To identify the thermal characteristics of non-Newtonian fluids, effective estimation and prediction of mass, heat and flow processes, Akolade et al. [44], Meyers et al. [45] and Anyakoha [46] among other authors suggested the consideration of variable thermo fluid properties in non-Newtonian fluid modelling analysis since ‘fluid properties vary significantly when subjected to temperature changes’. Few novel studies of thermophysical impact in squeezing geometry include the work of Akolade et al. [44] on Casson fluid investigation in a horizontal channel, Akolade [47] convective surface, slip, and quadratic convection influence in the parallel disc, Ahmed et al. [48] consideration in carbon nanotubes-based nanofluid. The above literature concluded that temperature-dependent impact predicts the fluid concentration rise but minimization to both energy and fluid velocities. Other works on temperature-dependent variability in different flow geometry include; Olabode et al. [49, 50], Akolade et al. [51, 52], investigation over a slenderized sheet, Gbadeyan et al. [53], Idowu and Falodun [54], Mondal et al. [55] over a vertical plate, Salahuddin et al. [56] in 3-D rotating channel, Akolade and Tijani [57], Abdul Wahab et al. [58], Waqas et al. [59], Basha et al. [60] among others.

Numerous numbers of literature have examined the effect of nanoparticles, porosity, and MHD among others on the thermodynamic second law analysis in squeezing geometry, to the best knowledge of the authors, no attention has been given to the aspect of combined impact of fluid thermal properties (fluid diffusivity, viscosity, and thermal conductivity) with thermodynamic second law analysis in cylindrical squeezing channel, we find these assumptions necessary considering its enormous impact as discussed in Refs. [44, 47, 49], which is the focus of this study. However, the objectives of this study are to: (i) model the flow of non-Newtonian nanofluid in squeezing disc with temperature-dependent properties, (ii) stereotype the governing systems of entropy generation and Bejan number, (iii) implement the workable similarity transformation and collocation approach with Chebysev polynomial as trial basis solution, (iv) perform the comparative study of constant and non-constant temperature dependent assumptions, (v) investigate the pertinent parameters impact on entropy generation rate and irreversibility distribution analysis.

2. Model analysis

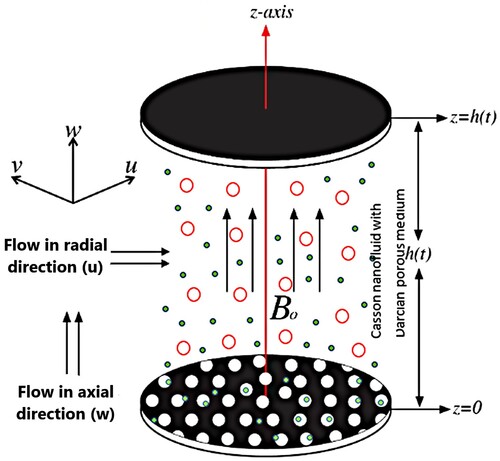
A magnetized, unsteady, squeezing, viscous, and incompressible fluid flow of Casson Nanofluid through a porous medium in between two disks is considered. For proper calculation, prediction and enhancement of nanofluids, this flow examination elucidates the measure of disorderliness on the assumption of variable fluid properties; fluid diffusivity, viscosity, and thermal conductivity. The geometry is assumed porous and filed will Casson nanoparticles. As presented in Figure 1, the radial motion is taken along the $\overline{r}$-axis with velocity $\overline{u}$, and the flow in axial direction z with velocity $\overline{w}$. The magnetic field strength $B_0$ applied perpendicular to the radial flow movement with the lower disk kept fixed and the upper disk squeezing with stretching velocity $U_w=\frac{a\overline{r}}{2(1-\tau \overline{t})}$ both conditioned at distance $h\left(\overline{t}\right)=(\frac{\nu (1-\tau \overline{t})}{a}{)}^{1/2}$ apart.

Figure 1. Model physical abstract.

The rheological model of Casson fluid is as follows (see Refs. [44, 47, 52, 61, 62]), (1) ${\tau }_{ij}=\{\begin{array}{l}(\mu +{\displaystyle \frac{P_y}{\sqrt{2\pi }}})2e_{ij}when\pi >{\pi }_c,\\ (\mu +{\displaystyle \frac{P_y}{\sqrt{2{\pi }_c}}})2e_{ij}when\pi <{\pi }_c,\end{array}$(1) with $P_y=\frac{\mu \sqrt{2\pi }}{\text{β}}$ representing the Casson fluid yield stress, the kinematic viscosity depends on the plastic dynamic fluid density, viscosity and Casson number [44, 53], (2) $\nu =\frac{\mu }{{\rho }_f}{\text{β}}_C,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{\text{β}}_C=(1+\frac{1}{\text{β}}),$(2) with critical value for the model ${\pi }_c$, product of rate of strain tensors $\pi =e_{ij}{e}_{ij}$, rate of strain tensor $e_{ij}$, and component of stress tensor ${\tau }_{ij}$ accordingly.

2.1. Model governing system

The governing model encompassing the dissipative, Magneto-hydrodynamics, and variable fluid properties conveying Casson Nanofluid with porous material are as thus (see Refs. [44, 47, 63–67]); (3) $\begin{array}{rl}& \frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}+\frac{\overline{u}}{\overline{r}}=0,\end{array}$(3) (4) $\begin{array}{rl}& \frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{t}}+\overline{u}\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}+\overline{w}\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}}\\ & =-\frac{1}{{\rho }_f}\frac{\mathrm{\partial }\overline{P}}{\mathrm{\partial }\overline{r}}+\frac{{\mu }_{\omega }{\text{β}}_C}{{\rho }_f}(\frac{{\mathrm{\partial }}^2\overline{u}}{\mathrm{\partial }{\overline{z}}^2}-\frac{\overline{u}}{{\overline{r}}^2}+\frac{1}{\overline{r}}\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}+\frac{{\mathrm{\partial }}^2\overline{u}}{\mathrm{\partial }{\overline{r}}^2})\\ & -\frac{{\text{β}}_C{\mu }_{\omega }}{K(1-\alpha \overline{t})}\overline{u}\\ & -\frac{\sigma }{{\rho }_f}B(\overline{t}{)}^2\overline{u}+\frac{{\text{β}}_C}{{\rho }_f}\{2\frac{\mathrm{\partial }{\mu }_{\omega }}{\mathrm{\partial }\overline{r}}\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}\\ & +\frac{\mathrm{\partial }{\mu }_{\omega }}{\mathrm{\partial }\overline{z}}(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}})\},\end{array}$(4) (5) $\begin{array}{rl}& \frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{t}}+\overline{u}\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\overline{w}\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}\\ & =-\frac{1}{\rho }\frac{\mathrm{\partial }\overline{P}}{\mathrm{\partial }\overline{z}}+\frac{{\mu }_{\omega }{\text{β}}_C}{{\rho }_f}(\frac{{\mathrm{\partial }}^2\overline{w}}{\mathrm{\partial }{\overline{z}}^2}+\frac{1}{\overline{r}}\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{{\mathrm{\partial }}^2\overline{w}}{\mathrm{\partial }{\overline{r}}^2})\\ & -\frac{{\text{β}}_C{\mu }_{\omega }}{K(1-\alpha \overline{t})}\overline{w}\\ & +\frac{{\text{β}}_C}{{\rho }_f}\{2\frac{\mathrm{\partial }{\mu }_{\omega }}{\mathrm{\partial }\overline{z}}\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}+\frac{\mathrm{\partial }{\mu }_{\omega }}{\mathrm{\partial }\overline{r}}(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}})\},\end{array}$(5) (6) $\begin{array}{rl}& \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{t}}+\overline{u}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}+\overline{w}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\\ & =\frac{1}{{\rho }_f{c}_p}[\frac{\mathrm{\partial }{\kappa }_{\omega }}{\mathrm{\partial }\overline{r}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}\\ & +\frac{\mathrm{\partial }{\kappa }_{\omega }}{\mathrm{\partial }\overline{z}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}+{\kappa }_{\omega }(\frac{{\mathrm{\partial }}^2\overline{H}}{\mathrm{\partial }{\overline{z}}^2}+\frac{1}{\overline{r}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}+\frac{{\mathrm{\partial }}^2\overline{H}}{\mathrm{\partial }{\overline{r}}^2})]\\ & +\mathrm{\Omega }[D_{\omega }(\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}+\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}})\\ & +\frac{D_H}{H_m}\{{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\right)}^2\}]\\ & +\frac{{\text{β}}_C{\mu }_{\omega }}{{\rho }_f{c}_p}[2\{{\left(\frac{\overline{u}}{\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}\right)}^2\}\\ & +{(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}})}^2],\end{array}$(6) (7) $\begin{array}{rl}& \frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{t}}+\overline{u}\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}+\overline{w}\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\\ & =\frac{\mathrm{\partial }{D}_{\omega }}{\mathrm{\partial }\overline{r}}\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }{D}_{\omega }}{\mathrm{\partial }\overline{z}}\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\\ & +D_{\omega }(\frac{{\mathrm{\partial }}^2\overline{G}}{\mathrm{\partial }{\overline{z}}^2}+\frac{1}{\overline{r}}\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}+\frac{{\mathrm{\partial }}^2\overline{G}}{\mathrm{\partial }{\overline{r}}^2})\\ & +\frac{D_H}{H_m}(\frac{{\mathrm{\partial }}^2\overline{H}}{\mathrm{\partial }{\overline{z}}^2}+\frac{1}{\overline{r}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}+\frac{{\mathrm{\partial }}^2\overline{H}}{\mathrm{\partial }{\overline{r}}^2})-Kr(\overline{G}-{\overline{G}}_0),\end{array}$(7) subjected to the boundary conditions (see Akolade [47]), (8) $\begin{array}{rl}& \overline{u}={\text{β}}_C\frac{{\mu }_{\omega }}{{\rho }_f}{r}_1\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}},\overline{w}=w_0,-{\kappa }_{\omega }\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}=r_2[{\overline{H}}_h-\overline{H}],\\ & -D_{\omega }\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}=r_3[{\overline{G}}_h-\overline{G}]at\overline{z}=0,\\ & \overline{u}=0,\overline{w}=W_0=\frac{\mathrm{d}h\left(\overline{t}\right)}{\mathrm{d}\overline{t}},\overline{H}={\overline{H}}_h,\\ & \overline{G}={\overline{G}}_{h}at\overline{z}=h\left(\overline{t}\right).\end{array}$(8) Thus, implementing the well-defined similarity variables as presented in Butt and Ali [39], Zubai et al. [18], Qayyum et al. [35], Sobamowo et al. [68], and Hayat et al. [69] alongside the variable fluid properties defined in [44, 47, 53] on the governing partial differential Equations (3(3) $\begin{array}{rl}& \frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}+\frac{\overline{u}}{\overline{r}}=0,\end{array}$(3) )–(8(8) $\begin{array}{rl}& \overline{u}={\text{β}}_C\frac{{\mu }_{\omega }}{{\rho }_f}{r}_1\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}},\overline{w}=w_0,-{\kappa }_{\omega }\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}=r_2[{\overline{H}}_h-\overline{H}],\\ & -D_{\omega }\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}=r_3[{\overline{G}}_h-\overline{G}]at\overline{z}=0,\\ & \overline{u}=0,\overline{w}=W_0=\frac{\mathrm{d}h\left(\overline{t}\right)}{\mathrm{d}\overline{t}},\overline{H}={\overline{H}}_h,\\ & \overline{G}={\overline{G}}_{h}at\overline{z}=h\left(\overline{t}\right).\end{array}$(8) ), (9) $\begin{array}{rl}& \overline{u}=U_w\frac{\mathrm{d}u}{\mathrm{d}\eta },\overline{w}=-{\left(\frac{a\nu }{1-\tau \overline{t}}\right)}^{1/2}u\left(\eta \right)=-\frac{\nu }{h\left(t\right)}u\left(\eta \right),\\ & \eta =\frac{\overline{z}}{h\left(\overline{t}\right)},H\left(\eta \right)=\frac{\overline{H}-{\overline{H}}_0}{{\overline{H}}_h-{\overline{H}}_0},\\ & G\left(\eta \right)=\frac{\overline{G}-{\overline{G}}_0}{{\overline{G}}_h-{\overline{G}}_0},h\left(\overline{t}\right)={\left(\frac{\nu (1-\tau \overline{t})}{a}\right)}^{1/2}\\ & U_w=\frac{a\overline{r}}{2(1-\tau \overline{t})},W_0=\frac{-w_0}{(1-\alpha \overline{t})},\\ & D_{\omega }=D_0[1+m_3(\overline{G}-{\overline{G}}_0\left)\right],{\mu }_{\omega }={\mu }_0{e}^{(-m_1(\overline{H}-{\overline{H}}_0\left)\right)},\\ & {\kappa }_{\omega }={\kappa }_0[1+m_2(\overline{H}-{\overline{H}}_0\left)\right],\\ & B\left(t\right)=B_0(1-\tau \overline{t}{)}^{-1/2},Kr=K_0(1-\tau \overline{t}{)}^{-1}.\end{array}$(9) The dimensionless ODEs accountable for the flow, heat, and mass transfer are as follows: (10) $\begin{array}{rl}& {\text{β}}_C{e}^{-{\xi }_{1}H}[\frac{{\mathrm{d}}^{4}u}{\mathrm{d}{\eta }^4}-2{\xi }_1\frac{\mathrm{d}H}{\mathrm{d}\eta }\frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}-{\xi }_1\frac{{\mathrm{d}}^{2}H}{\mathrm{d}{\eta }^2}\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}\\ & +{\xi }_1^2{\left(\frac{\mathrm{d}H}{\mathrm{d}\eta }\right)}^2\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}-\frac{1}{Da}\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}]\\ & -\frac{Z}{2}[3\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}+\eta \frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}]+u\frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}-H{a}^2\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}=0,\end{array}$(10) (11) $\begin{array}{rl}& [1+{\xi }_{2}H]\frac{{\mathrm{d}}^{2}H}{\mathrm{d}{\eta }^2}+{\xi }_2{\left(\frac{\mathrm{d}H}{\mathrm{d}\eta }\right)}^2\\ & +Pr{\text{β}}_C{e}^{-{\xi }_{1}H}[12E{c}_r{\left(\frac{\mathrm{d}u}{\mathrm{d}\eta }\right)}^2+Ec{\left(\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}\right)}^2]\\ & +Pr\left\{Nb\right[1+{\xi }_{3}G]\frac{\mathrm{d}G}{\mathrm{d}\eta }\frac{\mathrm{d}H}{\mathrm{d}\eta }\\ & +Nt{\left(\frac{\mathrm{d}H}{\mathrm{d}\eta }\right)}^2+(u-Z\frac{\eta }{2})\frac{\mathrm{d}H}{\mathrm{d}\eta }\}=0,\end{array}$(11) (12) $\begin{array}{rl}& [1+{\xi }_{3}G]\frac{{\mathrm{d}}^{2}G}{\mathrm{d}{\eta }^2}+{\xi }_3{\left(\frac{\mathrm{d}G}{\mathrm{d}\eta }\right)}^2+Sc(u-Z\frac{\eta }{2})\frac{\mathrm{d}G}{\mathrm{d}\eta }\\ & +\frac{Nt}{Nb}\frac{{\mathrm{d}}^{2}H}{\mathrm{d}{\eta }^2}-Sc{K}_{D}G=0,\end{array}$(12) subjected to the transformed boundary conditions; (13) $\begin{array}{rl}& \frac{\mathrm{d}u}{\mathrm{d}\eta }=F_1,u=V_0,\frac{\mathrm{d}H}{\mathrm{d}\eta }=\frac{B{i}_1(H-1)}{1+{\xi }_{2}H},\\ & \frac{\mathrm{d}G}{\mathrm{d}\eta }=\frac{B{i}_2(G-1)}{1+{\xi }_{3}G}at\eta =0,\\ & \frac{\mathrm{d}u}{\mathrm{d}\eta }=0,u=\frac{Z}{2},H=F_2,G=F_3,at\eta =1,\end{array}$(13) where, $F_1=\alpha {\text{β}}_C{e}^{-{\xi }_{1}H}\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}$, $F_2=F_3=1$,  $Pr=\frac{\rho c_p\nu }{{\kappa }_f},$  $\alpha =\frac{{\mu }_0}{{\rho }_f{r}_{1}h\left(t\right)},$ $B{i}_1=\frac{r_{2}h\left(t\right)}{{\kappa }_f}$,  $B{i}_2=\frac{r_{3}h\left(t\right)}{D_0}$,  $V_0=\frac{w_0}{ah\left(t\right)}$,  ${\xi }_1=({\overline{H}}_h-{\overline{H}}_0)m_1$,   ${\xi }_2=({\overline{H}}_h-{\overline{H}}_0)m_2$,   ${\xi }_3=({\overline{G}}_h-{\overline{G}}_0)m_3,$   $Sc=\frac{\nu }{D_0}$,   $Z=\frac{\tau }{a}$,   $K_D=\frac{K_0}{a}$,   $Da=\frac{Ka}{{\mu }_0}$,   $H{a}^2=\frac{\sigma B_0^2}{\rho a}$,  $Nb=\frac{\mathrm{\Omega }{D}_0({\overline{G}}_h-{\overline{G}}_0)}{\nu }$,   $Nt=\frac{\mathrm{\Omega }{D}_{\overline{H}}({\overline{H}}_h-{\overline{H}}_0)}{\nu {\overline{H}}_m}$,   $E{c}_r=\frac{{\nu }^2}{4h\left(t{)}^2{C}_p\right({\overline{H}}_h-{\overline{H}}_0)}$,   $Ec=\frac{U_w^2}{C_p({\overline{H}}_h-{\overline{H}}_0)}.$

2.2. Second law analysis

The entropy generation rate for the considered model of squeezing, magnetized and dissipative Casson nanofluid with porous material is as thus [20, 34–36, 70–72]; (14) $\begin{array}{rl}{E}_G& =\frac{{\kappa }_{\omega }}{H_0^2}\{{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\right)}^2\}\\ & +\frac{D_{\omega }}{H_0}\{\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\}\\ & +\frac{{\text{β}}_C{\mu }_{\omega }}{H_0}[2\{{\left(\frac{\overline{u}}{\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}\right)}^2\}\\ & +{(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}})}^2]\\ & +\frac{\sigma }{H_0}B(x{)}^2{\overline{u}}^2+\frac{{\text{β}}_C{\mu }_{\omega }}{K(1-\tau \overline{t}){\overline{H}}_0}({\overline{u}}^2+{\overline{w}}^2)\\ & +\frac{D_{\omega }}{G_k}\{{\left(\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\right)}^2\}.\end{array}$(14) By definition, Equation (14(14) $\begin{array}{rl}{E}_G& =\frac{{\kappa }_{\omega }}{H_0^2}\{{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\right)}^2\}\\ & +\frac{D_{\omega }}{H_0}\{\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\}\\ & +\frac{{\text{β}}_C{\mu }_{\omega }}{H_0}[2\{{\left(\frac{\overline{u}}{\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}\right)}^2\}\\ & +{(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}})}^2]\\ & +\frac{\sigma }{H_0}B(x{)}^2{\overline{u}}^2+\frac{{\text{β}}_C{\mu }_{\omega }}{K(1-\tau \overline{t}){\overline{H}}_0}({\overline{u}}^2+{\overline{w}}^2)\\ & +\frac{D_{\omega }}{G_k}\{{\left(\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\right)}^2\}.\end{array}$(14) ) is sub-divided into:

Heat Transfer Irreversibility (HTI) (15) $\mathrm{H}\mathrm{T}\mathrm{I}=\frac{{\kappa }_{\omega }}{H_0^2}\{{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\right)}^2\}.$(15) Fluid Friction Irreversibility (FFI) (16) $\begin{array}{rl}\mathrm{F}\mathrm{F}\mathrm{I}& =\frac{{\text{β}}_C{\mu }_{\omega }}{H_0}[2\{{\left(\frac{\overline{u}}{\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}\right)}^2\}\\ & +{(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}})}^2]+\frac{{\text{β}}_C{\mu }_{\omega }}{K(1-\tau \overline{t}){\overline{H}}_0}({\overline{u}}^2+{\overline{w}}^2)\\ & +\frac{\sigma }{H_0}B(x{)}^2{\overline{u}}^2.\end{array}$(16)

Mass Transfer Irreversibility (MTI) (17) $\begin{array}{rl}\mathrm{M}\mathrm{T}\mathrm{I}& =\frac{D_{\omega }}{G_k}\{{\left(\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\right)}^2\}\\ & +\frac{D_{\omega }}{H_0}\{\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\}.\end{array}$(17) Applying Equation (9(9) $\begin{array}{rl}& \overline{u}=U_w\frac{\mathrm{d}u}{\mathrm{d}\eta },\overline{w}=-{\left(\frac{a\nu }{1-\tau \overline{t}}\right)}^{1/2}u\left(\eta \right)=-\frac{\nu }{h\left(t\right)}u\left(\eta \right),\\ & \eta =\frac{\overline{z}}{h\left(\overline{t}\right)},H\left(\eta \right)=\frac{\overline{H}-{\overline{H}}_0}{{\overline{H}}_h-{\overline{H}}_0},\\ & G\left(\eta \right)=\frac{\overline{G}-{\overline{G}}_0}{{\overline{G}}_h-{\overline{G}}_0},h\left(\overline{t}\right)={\left(\frac{\nu (1-\tau \overline{t})}{a}\right)}^{1/2}\\ & U_w=\frac{a\overline{r}}{2(1-\tau \overline{t})},W_0=\frac{-w_0}{(1-\alpha \overline{t})},\\ & D_{\omega }=D_0[1+m_3(\overline{G}-{\overline{G}}_0\left)\right],{\mu }_{\omega }={\mu }_0{e}^{(-m_1(\overline{H}-{\overline{H}}_0\left)\right)},\\ & {\kappa }_{\omega }={\kappa }_0[1+m_2(\overline{H}-{\overline{H}}_0\left)\right],\\ & B\left(t\right)=B_0(1-\tau \overline{t}{)}^{-1/2},Kr=K_0(1-\tau \overline{t}{)}^{-1}.\end{array}$(9) ) on the dimensional entropy generation system in Equation (14(14) $\begin{array}{rl}{E}_G& =\frac{{\kappa }_{\omega }}{H_0^2}\{{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\right)}^2\}\\ & +\frac{D_{\omega }}{H_0}\{\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }\overline{z}}\}\\ & +\frac{{\text{β}}_C{\mu }_{\omega }}{H_0}[2\{{\left(\frac{\overline{u}}{\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}\right)}^2\}\\ & +{(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}})}^2]\\ & +\frac{\sigma }{H_0}B(x{)}^2{\overline{u}}^2+\frac{{\text{β}}_C{\mu }_{\omega }}{K(1-\tau \overline{t}){\overline{H}}_0}({\overline{u}}^2+{\overline{w}}^2)\\ & +\frac{D_{\omega }}{G_k}\{{\left(\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{G}}{\mathrm{\partial }\overline{z}}\right)}^2\}.\end{array}$(14) ), produced the dimensionless Equation (18(18) $\begin{array}{rl}Ns& =\frac{E_G}{E_{G_0}^{‴}}=[1+{\xi }_{2}H]{\left(\frac{\mathrm{d}H}{\mathrm{d}\eta }\right)}^2\\ & +{\chi }_1^2{\chi }_2{\chi }_3[1+{\xi }_{3}G]{\left(\frac{\mathrm{d}G}{\mathrm{d}\eta }\right)}^2\\ & +{\chi }_1{\chi }_2[1+{\xi }_{3}G]\frac{\mathrm{d}G}{\mathrm{d}\eta }\frac{\mathrm{d}H}{\mathrm{d}\eta }\\ & +{\text{β}}_{C}PrE{c}_r{\chi }_1{e}^{-{\xi }_{1}H}[(H{a}^2+\frac{1}{Da}){\left(\frac{\mathrm{d}u}{\mathrm{d}\eta }\right)}^2\\ & +{\left(\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}\right)}^2+\frac{Ec}{E{c}_r}\{\frac{1}{Da}{u}^2+\frac{7}{2}{\left(\frac{\mathrm{d}u}{\mathrm{d}\eta }\right)}^2\}].\end{array}$(18) ), (18) $\begin{array}{rl}Ns& =\frac{E_G}{E_{G_0}^{‴}}=[1+{\xi }_{2}H]{\left(\frac{\mathrm{d}H}{\mathrm{d}\eta }\right)}^2\\ & +{\chi }_1^2{\chi }_2{\chi }_3[1+{\xi }_{3}G]{\left(\frac{\mathrm{d}G}{\mathrm{d}\eta }\right)}^2\\ & +{\chi }_1{\chi }_2[1+{\xi }_{3}G]\frac{\mathrm{d}G}{\mathrm{d}\eta }\frac{\mathrm{d}H}{\mathrm{d}\eta }\\ & +{\text{β}}_{C}PrE{c}_r{\chi }_1{e}^{-{\xi }_{1}H}[(H{a}^2+\frac{1}{Da}){\left(\frac{\mathrm{d}u}{\mathrm{d}\eta }\right)}^2\\ & +{\left(\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}\right)}^2+\frac{Ec}{E{c}_r}\{\frac{1}{Da}{u}^2+\frac{7}{2}{\left(\frac{\mathrm{d}u}{\mathrm{d}\eta }\right)}^2\}].\end{array}$(18) Where (19) $\begin{array}{rl}& E_{G_0}^{{}^{‴}}=\frac{{\kappa }_f}{\nu }\frac{({\overline{H}}_h-{\overline{H}}_0{)}^{2}a}{{\overline{H}}_0^2},{\chi }_1=\frac{{\overline{H}}_0}{{\overline{H}}_h-{\overline{H}}_0},\\ & {\chi }_2=\frac{a{D}_0({\overline{G}}_h-{\overline{G}}_0)}{{\kappa }_f\nu },{\chi }_3=\frac{{\overline{G}}_h-{\overline{G}}_0}{G_k}.\end{array}$(19)

Furthermore, we define the Bejan number as the ratio of HTI to Ns (see [73, 74]) i.e. (20) $Be=\frac{HTI}{HTI+FFI+MTI}=\frac{HTI}{Ns}.$(20)

3. Method of solution

Authors seek an approximate solution to the transformed, non-linear, and coupled systems of Equations (10(10) $\begin{array}{rl}& {\text{β}}_C{e}^{-{\xi }_{1}H}[\frac{{\mathrm{d}}^{4}u}{\mathrm{d}{\eta }^4}-2{\xi }_1\frac{\mathrm{d}H}{\mathrm{d}\eta }\frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}-{\xi }_1\frac{{\mathrm{d}}^{2}H}{\mathrm{d}{\eta }^2}\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}\\ & +{\xi }_1^2{\left(\frac{\mathrm{d}H}{\mathrm{d}\eta }\right)}^2\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}-\frac{1}{Da}\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}]\\ & -\frac{Z}{2}[3\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}+\eta \frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}]+u\frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}-H{a}^2\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}=0,\end{array}$(10) )–(13(13) $\begin{array}{rl}& \frac{\mathrm{d}u}{\mathrm{d}\eta }=F_1,u=V_0,\frac{\mathrm{d}H}{\mathrm{d}\eta }=\frac{B{i}_1(H-1)}{1+{\xi }_{2}H},\\ & \frac{\mathrm{d}G}{\mathrm{d}\eta }=\frac{B{i}_2(G-1)}{1+{\xi }_{3}G}at\eta =0,\\ & \frac{\mathrm{d}u}{\mathrm{d}\eta }=0,u=\frac{Z}{2},H=F_2,G=F_3,at\eta =1,\end{array}$(13) ), by employing the well known Chebyshev Collocation Approach (CCA). Without loss of generality, CCA had proved satisfactorily well, efficient, rapid in convergence, stable and simple in handling the models of coupled ODEs and non-linear systems of equations. In particular, CCA have been very efficient for solving squeezing flow problem (see [44, 47]).

3.1. Application of Chebyshev-based collocation method

The assumed trial function of the flow fields; $u\left(\eta \right),H\left(\eta \right)$ and $G\left(\eta \right)$ is assumed as the sum of Chebyshev basis function $T_i\left(\eta \right)$. (21) $\begin{array}{rl}u\left(\eta \right)& =\sum _{i=0}^{\mathrm{\Omega }}{a}_i{T}_i(2\eta -1),H\left(\eta \right)=\sum _{i=0}^{\mathrm{\Omega }}{b}_i{T}_i(2\eta -1),\\ G\left(\eta \right)& =\sum _{i=0}^{\mathrm{\Omega }}{c}_i{T}_i(2\eta -1),\end{array}$(21) $T_i(2\eta -1)$ being the shifted Chebyshev basis function which transforms the basis domain from $[0,1]$ to $[-1,1]$ and, $a_i,b_i$, and $c_i$ are the unknown constants to be determined. Substituting Equation (16(16) $\begin{array}{rl}\mathrm{F}\mathrm{F}\mathrm{I}& =\frac{{\text{β}}_C{\mu }_{\omega }}{H_0}[2\{{\left(\frac{\overline{u}}{\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}\right)}^2\}\\ & +{(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}})}^2]+\frac{{\text{β}}_C{\mu }_{\omega }}{K(1-\tau \overline{t}){\overline{H}}_0}({\overline{u}}^2+{\overline{w}}^2)\\ & +\frac{\sigma }{H_0}B(x{)}^2{\overline{u}}^2.\end{array}$(16) ) into Equation (13(13) $\begin{array}{rl}& \frac{\mathrm{d}u}{\mathrm{d}\eta }=F_1,u=V_0,\frac{\mathrm{d}H}{\mathrm{d}\eta }=\frac{B{i}_1(H-1)}{1+{\xi }_{2}H},\\ & \frac{\mathrm{d}G}{\mathrm{d}\eta }=\frac{B{i}_2(G-1)}{1+{\xi }_{3}G}at\eta =0,\\ & \frac{\mathrm{d}u}{\mathrm{d}\eta }=0,u=\frac{Z}{2},H=F_2,G=F_3,at\eta =1,\end{array}$(13) ), the boundary conditions gives the following sets of algebraic equations. (22) $\begin{array}{rl}& {[\frac{\mathrm{d}}{\mathrm{d}\eta }\sum _{i=0}^{\mathrm{\Omega }}{a}_i{T}_i(2\eta -1)-F_1]}_{\eta =0}=0,\\ & [\phantom{\frac{B{i}_1\left({\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{b}_i{T}_i(2\eta -1)-1}\right)}{(1+{\xi }_2{\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{b}_i{T}_i(2\eta -1)})}}\frac{\mathrm{d}}{\mathrm{d}\eta }\sum _{i=0}^{\mathrm{\Omega }}{b}_i{T}_i(2\eta -1)\\ & -{\frac{B{i}_1\left({\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{b}_i{T}_i(2\eta -1)-1}\right)}{(1+{\xi }_2{\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{b}_i{T}_i(2\eta -1)})}]}_{\eta =0}=0,\\ & {[\sum _{i=0}^{\mathrm{\Omega }}{a}_i{T}_i(2\eta -1)-V_0]}_{\eta =0}=0,\\ & [\phantom{\frac{B{i}_2\left({\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{c}_i{T}_i(2\eta -1)-1}\right)}{(1+{\xi }_3{\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{c}_i{T}_i(2\eta -1)})}}\frac{\mathrm{d}}{\mathrm{d}\eta }{\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{c}_i{T}_i(2\eta -1)}\\ & +{\frac{B{i}_2\left({\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{c}_i{T}_i(2\eta -1)-1}\right)}{(1+{\xi }_3{\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{c}_i{T}_i(2\eta -1)})}]}_{\eta =0}=0,\\ & {\left[{\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{a}_i{T}_i(2\eta -1)}\right]}_{\eta =1}=\frac{Z}{2},\\ & {\left[\frac{\mathrm{d}}{\mathrm{d}\eta }{\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{a}_i{T}_i(2\eta -1)}\right]}_{\eta =1}=0,\\ & {\left[{\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{b}_i{T}_i(2\eta -1)}\right]}_{\eta =1}=F_2,\\ & {\left[{\displaystyle \sum _{i=0}^{\mathrm{\Omega }}{c}_i{T}_i(2\eta -1)}\right]}_{\eta =1}=F_3.\end{array}$(22) Likewise, substituting Equation (16(16) $\begin{array}{rl}\mathrm{F}\mathrm{F}\mathrm{I}& =\frac{{\text{β}}_C{\mu }_{\omega }}{H_0}[2\{{\left(\frac{\overline{u}}{\overline{r}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}\right)}^2+{\left(\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}\right)}^2\}\\ & +{(\frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}})}^2]+\frac{{\text{β}}_C{\mu }_{\omega }}{K(1-\tau \overline{t}){\overline{H}}_0}({\overline{u}}^2+{\overline{w}}^2)\\ & +\frac{\sigma }{H_0}B(x{)}^2{\overline{u}}^2.\end{array}$(16) ) into the transformed systems (10(10) $\begin{array}{rl}& {\text{β}}_C{e}^{-{\xi }_{1}H}[\frac{{\mathrm{d}}^{4}u}{\mathrm{d}{\eta }^4}-2{\xi }_1\frac{\mathrm{d}H}{\mathrm{d}\eta }\frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}-{\xi }_1\frac{{\mathrm{d}}^{2}H}{\mathrm{d}{\eta }^2}\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}\\ & +{\xi }_1^2{\left(\frac{\mathrm{d}H}{\mathrm{d}\eta }\right)}^2\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}-\frac{1}{Da}\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}]\\ & -\frac{Z}{2}[3\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}+\eta \frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}]+u\frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}-H{a}^2\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}=0,\end{array}$(10) )–(12(12) $\begin{array}{rl}& [1+{\xi }_{3}G]\frac{{\mathrm{d}}^{2}G}{\mathrm{d}{\eta }^2}+{\xi }_3{\left(\frac{\mathrm{d}G}{\mathrm{d}\eta }\right)}^2+Sc(u-Z\frac{\eta }{2})\frac{\mathrm{d}G}{\mathrm{d}\eta }\\ & +\frac{Nt}{Nb}\frac{{\mathrm{d}}^{2}H}{\mathrm{d}{\eta }^2}-Sc{K}_{D}G=0,\end{array}$(12) ), residues $R_u$, $R_H$ and $R_G$ are defined. Using collocation approach, residues $R_u(\eta ,a_i,b_i,c_i)$, $R_H(\eta ,a_i,b_i,c_i)$ and $R_G(\eta ,a_i,b_i,c_i)$ are derived and minimized close to zero as follows.

For (23) $\delta (\eta -{\eta }_j)=\{\begin{array}{ll}0,& otherwise,\\ 1,& \eta ={\eta }_j\end{array}$(23) (24) $\begin{array}{rl}& {\int }_0^1{R}_u(\eta ,a_i,b_i,c_i)\mathrm{d}\eta =R_u(\eta ,a_i,b_i,c_i)=0,\\ & \mathrm{f}\mathrm{o}\mathrm{r}j=1,2,\dots ,N-3,\\ & {\int }_0^1{R}_H(\eta ,a_i,b_i,c_i)\mathrm{d}\eta =R_H(\eta ,a_i,b_i,c_i)=0,\\ & \mathrm{f}\mathrm{o}\mathrm{r}j=1,2,\dots ,N-1,\\ & {\int }_0^1{R}_G(\eta ,a_i,b_i,c_i)\mathrm{d}\eta =R_G(\eta ,a_i,b_i,c_i)=0,\\ & \mathrm{f}\mathrm{o}\mathrm{r}j=1,2,\dots ,N-1,\end{array}$(24) where ${\eta }_j$ is the shifted Gauss Lobato collocation points defined as, (25) ${\eta }_j=\frac{1}{2}(1-\cos \left(\frac{j\pi }{N}\right)),forj=0,1\cdots ,N.$(25) Thus, the flow distributions $u\left(\eta \right),H\left(\eta \right)$ and $G\left(\eta \right)$ are obtained from the system of 3N + 3 algebraic equations with 3N + 3 unknown coefficients $a_i,b_i$, and $c_i$. The obtained system of equations are solved via the Newton method with MATHEMATICA 11.3.

4. Results and discussion

For clear insight/prediction of the physical model, the choice of the following pertinent parameters were presumed constant else stated otherwise, Z = 1, ${\xi }_1={\xi }_2={\xi }_3=0.2$, Sc = 1, Ec = 0.1, $E{c}_r=0.1$ Pr = 7.2, Nb = 0.3, Nt = 0.1, Ha = 1, $\alpha =B{i}_1=B{i}_2=0.2$, $V_0=-0.1$, $\text{β}=0.2$, Da = 5, ${\chi }_1=0.1$, ${\chi }_2=0.1$, ${\chi }_3=0.1$, $K_D=0.1$ [35, 43, 44, 47, 53, 67, 75].

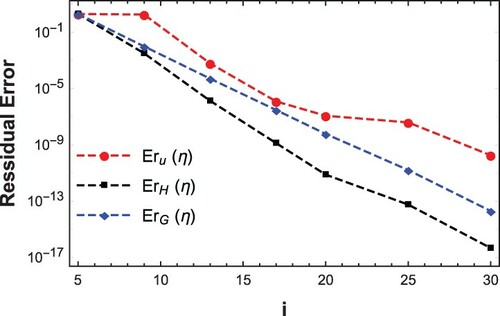
Acknowledgment/validation of the numerical method used (CCA) is highlighted in Tables 1 and 2, CCA work very fine just like other numerical tools: Homotopy Analysis Method (HAM), Differential Transformation Method (DTM), and RKFM as prevailed in the tables, therein, a good agreement of the model is observed in the limiting case. Moreover, Figure 2 shows the residual error analysis of the three profiles $u\left(\eta \right),H\left(\eta \right)$ and $G\left(\eta \right)$, Obviously, the square residual error reduces very close to zero as we increase i. The implication is that, our result approach exact solution as we increase the number of iterations. Evidently, the concentration equation residue reduced drastically and faster compare to the energy and momentum equation, this is attributed to it simplicity compare to the other two which are highly nonlinear and coupled.

Figure 2. Convergence/residual error analysis.

Table 1. Comparison results of Skin friction ($-u^{″}\left(0\right)$) and heat transfer ($-H^{\prime }\left(0\right)$) coefficients for different values of Z when ${\xi }_1={\xi }_2={\xi }_3=0$, Pr = 1, Nb = Nt = 0, $Ec=E{c}_r=0$, $V_0=B{i}_1=1$ $F_1=F_2=F_3=0$ and $\text{β}=\mathrm{\infty }$.

Values			Present result (CCA)		Sobomowo et al. [68] (DTM)		Hayat et al. [69] (HAM)
Da	Ha	Z	$-u^{″}\left(0\right)$	$-H^{\prime }\left(0\right)$	$-u^{″}\left(0\right)$	$-H^{\prime }\left(0\right)$	$-u^{″}\left(0\right)$	$-H^{\prime }\left(0\right)$
$\to \mathrm{\infty }$	1	$-0.2$	12.055564	0.593082	12.05556	0.59308	12.05556	0.59308
		$-0.1$	11.744107	0.592925	11.74411	0.59293	11.74411	0.59293
		0.1	11.117313	0.592609	11.11731	0.59261	11.11731	0.59261
		0.2	10.801983	0.592452	10.801983	0.59245	10.80198	0.59245
1	1	$-0.2$	12.284382	0.592950	12.28438	0.59295	–	–
		$-0.1$	11.967907	0.592793	11.96791	0.59248	–	–
		0.1	11.331126	0.592479	11.33113	0.59248	–	–
		0.2	11.010827	0.592321	11.01083	0.59232	–	–

Table 2. Comparison results of the velocity ($u\left(\eta \right)$) and temperature ($H\left(\eta \right)$) and concentration $\left(G\right(\eta \left)\right)$ profiles for different values of variable $\left(\eta \right)$ when Z = 1.0, ${\xi }_1={\xi }_2={\xi }_3=0$, Ec = 0 $E{c}_r=0.1$, Sc = 1, Pr = 2, Nb = Nt = 0, $\delta =0.1$, $V_0=-0.1$, $\alpha =B{i}_1=B{i}_2=0.2$ $K_D=0.1$, Ha = 1, $Da=5.0$, Pr = 7.2, Nt = Nb = 0.1 and $\text{β}=0.5$.

Variable	Present result (CCA)			Present result (RKFM)
η	$u\left(\eta \right)$	$H\left(\eta \right)$	$G\left(\eta \right)$	$u\left(\eta \right)$	$H\left(\eta \right)$	$G\left(\eta \right)$
0.0	1.0515491957	1.0885349934	$-1.0526618075$	1.0515491961	1.08853499441	$-1.0526618085$
0.2	0.3818078613	$-1.5633431615$	1.51330246046	0.38180786151	$-1.5633431597$	1.5133024582
0.4	$-0.27458238784$	$-4.9503135601$	4.8354888555	$-0.2745823878$	$-4.95031355840$	4.8354888528
0.6	$-0.9423624746$	$-7.6490917951$	7.4388822589	$-0.9423624747$	$-7.64909179143$	7.43888225384
0.8	$-1.6471751043$	$-8.8684776183$	8.534980325	$-1.6471751047$	$-8.8684776132$	8.5349803187
1.0	$-2.4177931369$	$-9.210199661$	8.818448224	$-2.417793137$	$-9.2101996633$	8.818448227

Figures 3–5 reveal the impact of fluid physical characteristics (viscosity, diffusivity, thermal conductivity) to wider porous medium (Da), continuous accumulation of thermophoretic (Nt), and Brownian motion (Nb) parameters as the impact is left not discussed in the literature. As earlier established: ‘impact of distinct flow parameters highlighted the same flow manner for both cases of variable and constant thermophysical effects’ Akolade [44]. However, the impact of Da, Nb, and Nt presented here on the flow fields is of no exception. Figure 3 displayed a velocity rise across the entire axial flow region, a rise in radial velocity around the fixed disk but a reduction at the upper squeezing region, temperature rise, and a reduction in nanoparticle volume fraction to a wider porous medium (i.e. increase in Da). Physically, the free movement of particles is attributed to space provided within the medium among other characteristics. Mathematically, the relation $\frac{1}{Da}$ in Equation (10(10) $\begin{array}{rl}& {\text{β}}_C{e}^{-{\xi }_{1}H}[\frac{{\mathrm{d}}^{4}u}{\mathrm{d}{\eta }^4}-2{\xi }_1\frac{\mathrm{d}H}{\mathrm{d}\eta }\frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}-{\xi }_1\frac{{\mathrm{d}}^{2}H}{\mathrm{d}{\eta }^2}\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}\\ & +{\xi }_1^2{\left(\frac{\mathrm{d}H}{\mathrm{d}\eta }\right)}^2\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}-\frac{1}{Da}\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}]\\ & -\frac{Z}{2}[3\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}+\eta \frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}]+u\frac{{\mathrm{d}}^{3}u}{\mathrm{d}{\eta }^3}-H{a}^2\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{\eta }^2}=0,\end{array}$(10) ) implies that a rise in Da is meant to upsurge the momentum profiles, therein, reduction of velocity at the upper disk is experienced due to the squeezing effect, collision within the fluid particles assisted the fluid temperature which finally resulted to lower fluid concentration since the fluid particles were cut loose (i.e. rise in Da). Furthermore, the fluid velocities and temperature were seen to experience a lower magnitude and higher concentration as variable fluid properties were assumed.

Figure 3. Influence of darcy number (Da) on (a) axial velocity, (b) radial velocity, (c) temperature, (d) nanoparticle concentration.

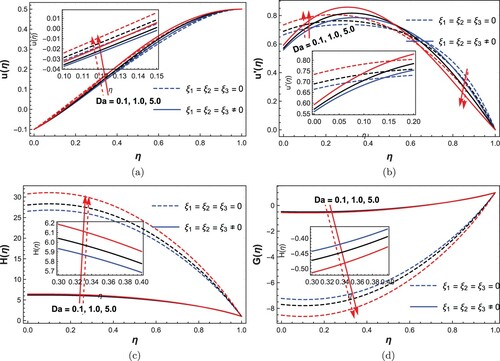
Figure 4. Influence of thermophoresis number (Nt) on (a) temperature, (b) nanoparticle concentration.

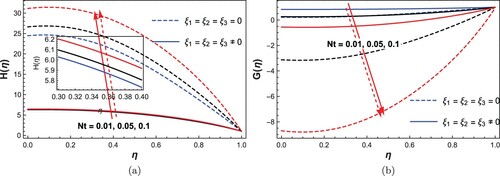
Figure 5. Influence of Brownian motion number (Nb) on (a) temperature, (b) nanoparticle concentration.

The impact of nanoparticle parameters Nb and Nt on the flow model pictured in Figures 4 and 5 identified a rise in fluid temperature and reduction in concentration as Nt rise, while the contrary effect is perceived to increasing magnitude of Nb. Literally, Nb is strongly attributed to the magnitude of nanoparticles, which is associated to thermal diffusion enhancement as the thermal condition of the fluid appreciates. Also, Nt is the parameter that establishes a stronger thermophoretic force which arises from the temperature gradient. It is, therefore, observed that thermal enhancement and nanoparticle species volume fraction is prevailed with increasing Nb and Nt, respectively. As observed, the real prediction of non-Newtonian fluid (Casson) showcases its characteristics as presented in the respective figures. In a nutshell, modification of nanoparticle volume fraction and energy distributions in such flow configuration (Figure 1) can easily be achieved via the nanoscale mechanism.

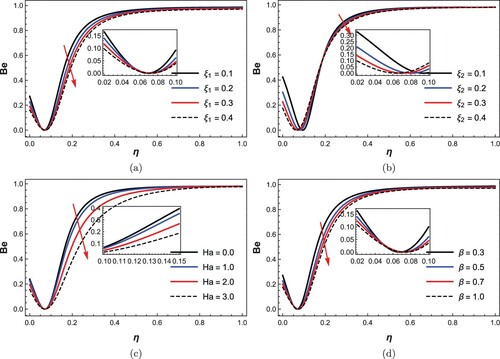
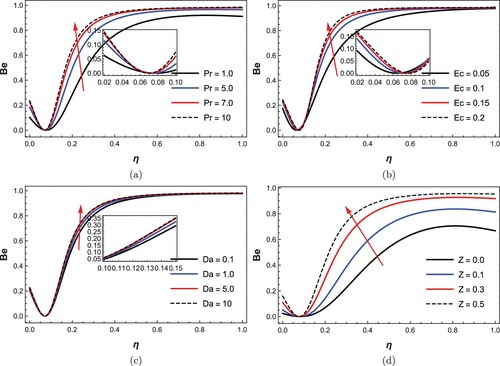
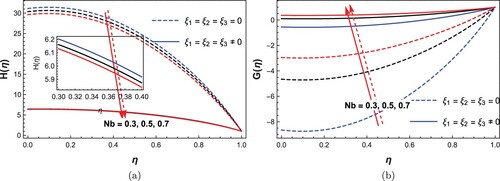
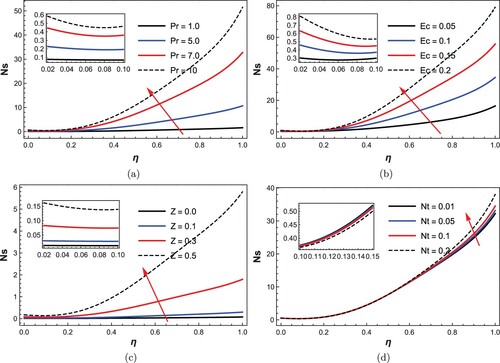
Figures 6–8 display the entropy generation rate for the effects of thermophysical properties, nanofluid representation among other flow parameters; ${\xi }_1$, ${\xi }_2$, Da, β, Pr, Ec, Z, Ha, Nb, Nt. Generally mentioned, disorderliness (entropy) is more prominent near the disks, most significantly at the moving disk. Physically, disturbance in the flow system is felt when there are changes in fluid chemical characteristics, applied force, fluid material conductivity as well as the control mediums. In the figures, Ns minimization is experienced as the fluid thermophysical properties, Brownian motion effect and yield stress of the fluid are encouraged. On the other hand, decrease in thermal diffusivity (Pr), resonance of the disk (squeezing), as well as increase in viscous dissipation (Ec), and thermophoresis number demonstrated a boost to entropy generation rate, significantly near the upper moving disk. Noticeably, the collision between the fluid molecules and nanoparticles referred to as colloidal motion is experienced and thus set the fluid particles off balance. It can be inferred that fluid with high; dissipation, conductivity, squeezing number, and thermophoresis number are set to facilitate a rise in entropy generation via the considered flow medium, while higher variable thermophysical numbers, Brownian motion and lesser yield stress decompose the entropy generation rate. Variation of Darcy and Hartmann numbers characterization on Ns presented in Figure 8 signifies a wavy magnitude rise from the lower disc to the upper moving disc. This may be attributed to the squeezing force that forcefully compresses the flow medium and is set to distribute a non-uniform magnetic field onto the flow system.

Figure 6. Influence of (a) viscosity, (b) thermal conductivity, (c) Brownian motion, (d) Casson number: on entropy generation rate.

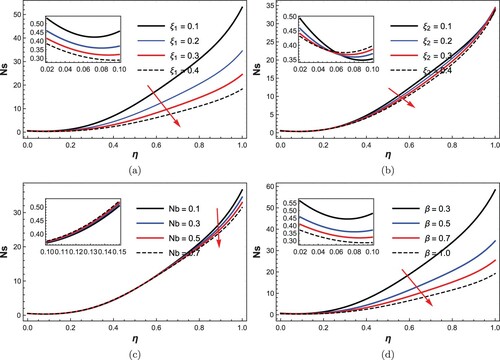
Figure 7. Influence of (a) Prandtl number, (b) Eckert number, (c) squeezing rate, and (d) thermophoresis number: on entropy generation rate.

Figure 8. Influence of (a) darcy number, (b) magnetic number on entropy generation rate.

To predict the dominance of heat and mass transfer disorderliness to the fluid friction disorder, Figures 9 and 10 present the impact of distinct flow parameters ${\xi }_1$, ${\xi }_2$, Da, β, Pr, Ec, Z, Ha on the irreversibility distribution ratio (Bejan number Be). Mathematically, $0<Be\le 1$, for Be<0.5 irreversibility as a result of magnetization, dissipation, and porosity influences dominates, equal contribution when Be = 0.5, while Be>0.5 depicts the dominance of thermal irreversibility. Physically, Be signifies the essential role of thermal irreversibility in the total irreversibility process. Thus, in this study, it is generally perceived that thermal irreversibility controls the flow system throughout the entire channel except near the fixed disk where the other responsibilities were seen to be dominant. Evidently, in the respective Figures 9 and 10, fluid thermophysical properties $({\xi }_1,{\xi }_2)$, Lorentz effect (Ha) and fluid yield stress $\left(\text{β}\right)$ scaled-down the Bejan number as a result of drag force. Contrarily, Prandtl, Eckert, squeezing, and Darcy numbers facilitated a rise to the irreversibility phenomenon. This is not far-fetched since decrease in thermal conductivity resulted in thermal field enhancement, fluid energy does improve significantly due to collision between the fluid molecules and free movement of fluid particles when the travelling medium is wider. However, Z has the tendency of magnifying Be, thereby consolidating the dominance of heat transfer irreversibility over the fluid friction and mass transfer irreversibilities.

Figure 9. Influence of (a) viscosity, (b) thermal conductivity, (c) squeezing rate, (d) Casson number: on irreversibility distribution ratio.

Figure 10. Influence of (a) Prandtl number, (b) Eckert number, (c) Darcy number, (d) magnetic number: on irreversibility distribution ratio.

5. Conclusion

Thermodynamics second law analysis has been considered as the subject of interest in this novel thermophysical, dissipative, and magnetized motion of Casson nanofluid between squeezing disk. The model governing systems has been formed and irreversibility analysis model were stereotyped. Suitable similarity approach is employed and the novel Chebyshev collocation method has been used to solve the highly nonlinear and coupled systems of ODEs numerically. In the limiting case, Table 1 validate the results of the present study with the existing once while 2 compared the numerical results of the employed Chebyshev collocation method with the Runge-Kutta scheme, interestingly, a good agreement is reached. The characterization of model parameters on the considered distributions is elucidated graphically. The observations from the present examination signify that:

• assumption of variable fluid properties lowered the fluid velocities and temperature fields, but its impact upsurges the nanoparticle volume fraction.

• an introduction of Nt is set to boost energy but minimize the fluid concentration rapidly.

• Nb can be seen as a mechanism for energy minimization and nanoparticle volume fraction booster.

• wider flow region aided velocities and temperature fields but reduces the nanoparticle volume fraction.

• thermophysical properties, yield stress, and Brownian motion impact help minimize the entropy generation rate.

• thermophoresis, squeezing, Prandtl, and Eckert number contributed significantly to the system disorderliness.

• thermal irreversibility controls the flow system throughout the entire channel except near the lower fixed disk.

• due to drag/Lorentz force, thermophysical properties, magnetic field effect and, fluid yield stress proof its ability to support the dominance of fluid friction irreversibility over the heat transfer irreversibility, while,

• Prandtl, Eckert, squeezing, and Darcy numbers help facilitate the irreversibility distribution phenomenon.

Interestingly, the present analysis could be helpful in future device fabrication, oil extraction, MHD micropumps, cooling of store grain, micro heat exchanger, modelling, and optimization of thermal conductivity, mass diffusivity, and viscosity rate in this proposed given system. Future work may involve investigation of this study in more complex geometries and introduction of hybrid and ternary nanofluids to enhance the optimality of heat transfer conditions.

Acknowledgments

The authors express their cordial appreciations to the respected Editor in chief and knowledgeable reviewers for valuable comments and suggestions to improve the presentation of this article. M. T. A. and M. M. R. contributed in mathematical modeling, methodology and validation of result by M. T. A., literature analysis by A. O. A. and M. M. R., discussion analysis by M. M. A., I. R., and A. O. A. All authors read and approve to the published version of the manuscript.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Appendix

Algorithm for the numerical integration of the system of the governing equations.